Конспект урока по математике на тему «Площадь. Единицы площади» (3 класс)
Урок математики в 3-м классе по теме: «Площадь. Единицы площади»
Цели урока:
1. Дать представление о площади фигур, познакомить с различными способами сравнения фигур: “на глаз”, путём наложения одной фигуры на другую, с использованием различных единиц измерения площадей.
2. Закрепить знания свойств геометрических фигур.
3. Закрепить умение точно производить измерения и чертить квадрат и прямоугольник.
4. Закрепить знание изученных таблиц умножения и соответствующих случаев деления.
5. Закреплять умение решать задачи
6. Развивать логическое мышление и пространственное воображение.
7. Воспитывать аккуратность при выполнении работы.
Оборудование. Для учащихся: учебник
математики для 3 класса Моро, рабочая тетрадь, линейка, простой карандаш,
цветные карандаши, рабочая тетрадь, листы с заданиями: с фигурами наложения, с
фигурами п.
7, геометрические фигуры: квадраты зелёный 6х6 см, белый 4х4 см,
круги жёлтый и красный диаметром 5 см, прямоугольник 5х3.
Для учителя: образец написания цифр, геометрические фигуры: квадраты зелёный 6х6 см, белый 4х4 см, круги жёлтый и красный диаметром 5 см, прямоугольник 5х3, листы с заданиями: с фигурами наложения, с фигурами п.7(3) образец и заполненный, на доске 3(а), 3(б), 3(в), 4.
ХОД УРОКА
I. Оргмомент.
Начинаем наш урок.
Надеюсь, он пойдёт вам впрок.
Постарайтесь всё понять,
Ответы полные давать.
II. Запись в тетради числа и слов “Классная работа”.
III. Устный счёт и чистописание.
а) Найдите в каждом ряду числа, которые не являются результатом табличного умножения.
6 18 17 12 41
24 30 16 11 28
7 36 27 35 71
Запишите числа 17, 41, 11, 7, 71. Обратите внимание на образцы написания цифр.
Докажите, что оставшиеся числа являются результатом табличного умножения.
б) Из данных чисел выбери пары, произведения и частные, которых
равны 6.
1 4 6 2 54 12 3 36 7 8 24 18 42 48 9
в) Сторона квадрата 2 см. Чему равен периметр? Найди правильное решение.
2+2+2+2=8(см)
2+4=6(см)
4+4+4+4=16(см)
2 • 4=8(см)
4 • 2=8(см)
г) Укажите, какой фигуре соответствует каждый из указанных признаков:
· 4 стороны равны; (квадрат)
· имеет три угла; (треугольник)
· состоит из 4 отрезков; (четырёхугольник)
· все углы прямые; (прямоугольник)
Дайте общее название фигурам – (геометрические).
IV. Сообщение темы урока.
Знание таблиц умножения и соответствующих случаев деления, свойств геометрических фигур понадобится нам при изучении темы нашего урока. Решив примеры на порядок действий и каждому ответу подставить букву, составить слово и узнать тему урока.
24+56:8·3= (45) А 7·7-9 = (40) П (57-22):7+63= (68) Ь 56:7+16= (24) О
36:6·4-(23-17) = (18) Л (80-45):5= (7) Д 5·9-(6+14:2) =(32)Щ
П Л О Щ А Д Ь
40 18 24 32 45 7 68
Итак, тема нашего урока: Площадь.
Единицы площади. Записать
на доске слово ПЛОЩАДЬ.
Сегодня мы выясним, что такое площадь фигуры и как можно сравнить площади фигур.
V. Работа по теме урока.
1. Словарная работа.
Назовите орфограммы в слове “ Площадь”.
— Гласная после шипящих: сочетание ча-ща пиши с буквой а;
— Смягчающий мягкий знак, смягчает предшествующий согласный звук, а сам звука не даёт.
2. Работа с геометрическим материалом.
а) Возьмите зелёный и белый квадраты. Покажите квадрат, который больше.
Как сравнивали?
Видно “ на глаз”.
Про такие фигуры говорят, что площадь зелёного квадрата больше площади белого квадрата.
Как ещё можно сравнить площади этих фигур?
Можно наложить одну на другую.
Наложите и сравните площади квадратов.
Белый квадрат полностью вместился в зелёном, значит площадь зелёного квадрата больше площади белого квадрата.
б) Возьмите жёлтый и красный круги. Сравните площади и покажите
круг, площадь которого меньше.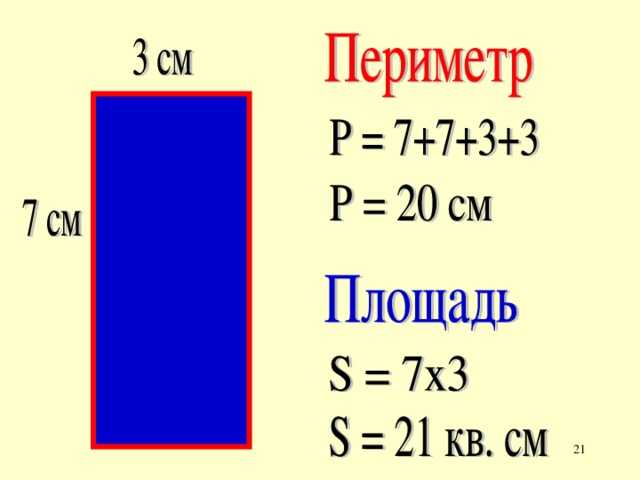
Площади кругов равны, так как при наложении круги полностью совпали.
Что же такое площадь фигуры? Как вы думаете?
Если правильного ответа не будет, учитель сообщает:
Площадь-это место, которое занимает фигура на плоскости.
Как мы сравнивали площади фигур?
“На глаз” и наложением друг на друга.
Физкультминутка. Можно аудио
Встаньте
дружно из-за парт
И скорее стройтесь в ряд!
Повернитесь вправо, влево,
Наконец, присядьте смело!
Поработаем ногами,
Раз, два, три!
Поработаем руками!
Раз, два, три!
Улыбнёмся: день хороший,
И похлопаем в ладоши.
3. Продолжение работы с геометрическим материалом.
Единицы площади.
а) Возьмите фиолетовый прямоугольник и белый квадрат.
Как удобнее сравнивать площади прямоугольника и квадрата “на глаз” или наложением?
Дети пытаются сравнить площади фигур “на глаз” и наложением.
“На глаз” или наложением сравнить площади прямоугольника и
квадрата нельзя, фигуры разные по форме и ни одна полностью не вмещается в
другой.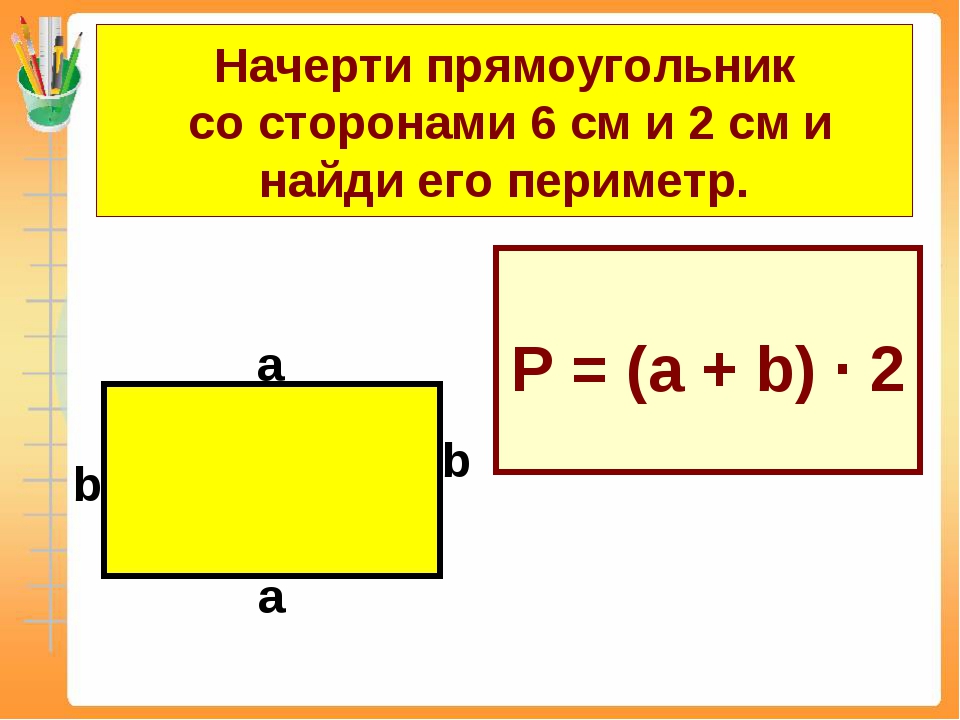
Как же сравнить площади этих фигур?
Ответы детей.
Если правильного ответа не будет, учитель сам предлагает начертить прямоугольник и квадрат в тетради.
а) Назовите общие свойства прямоугольника и квадрата.
Чем отличаются?
б). Вычерчивание прямоугольника и квадрата в тетради.
Измерьте сторону квадрата.
4 см
Начертите квадрат. Укажите на чертеже длину стороны квадрата.
Измерьте длину и ширинку прямоугольника.
5 см, 3 см
Начертите прямоугольник. Укажите длины сторон прямоугольника.
Как же сравнить площади этих фигур?
Ответы детей.
1. Если правильного ответа не будет, обратить внимание детей на то, что, начертив фигуры в тетради, мы разбили их на одинаковые фигуры меньшего размера – клетки тетради.
Можно посчитать клетки.
Посчитайте клетки, I вариант – квадрата, II вариант —
прямоугольника. Сколько клеток поместилось в квадрате, в прямоугольнике?
Запишите числа и сравните их.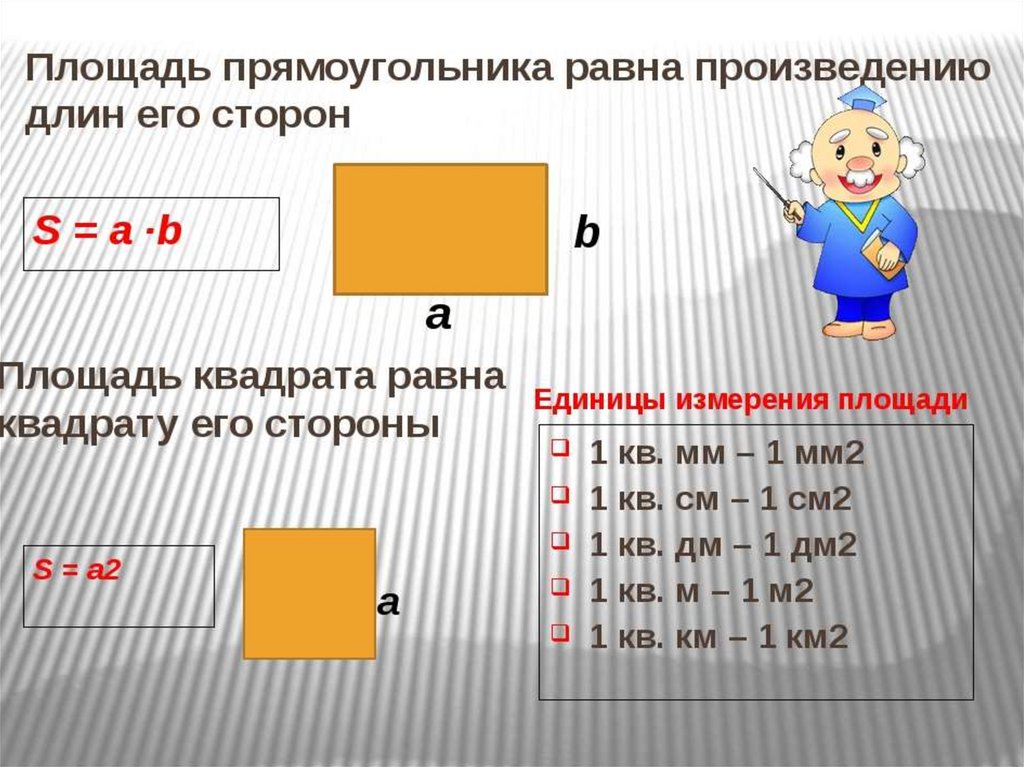
64>60
Сравните площади квадрата и прямоугольника.
Площадь квадрата больше площади прямоугольника.
Большую площадь имеет та фигура, которая содержит большее число клеток.
2. Но площадь фигур можно измерить и другими мерками. Можно разбить фигуру на одинаковые треугольники или большие квадраты.
Демонстрация прямоугольника разбитого на одинаковые треугольники.
3. Разобьём квадрат и прямоугольник на квадраты со стороной 1см. Подсчитайте, сколько квадратов со стороной 1см поместилось в квадрате? В прямоугольнике? Запишите числа и сравните их.
16>15
Сравните площади фигур.
Площадь квадрата больше площади прямоугольника.
Результат сравнения площадей не зависит от выбора единиц измерения.
4. Как удобнее подсчитать квадраты, на которые разбит прямоугольник?
3 ряда по 5 квадратов, 5 • 3 = 15
5 столбцов по 3 квадрата, 3 • 5 = 15
5. Подведём итог наших наблюдений.
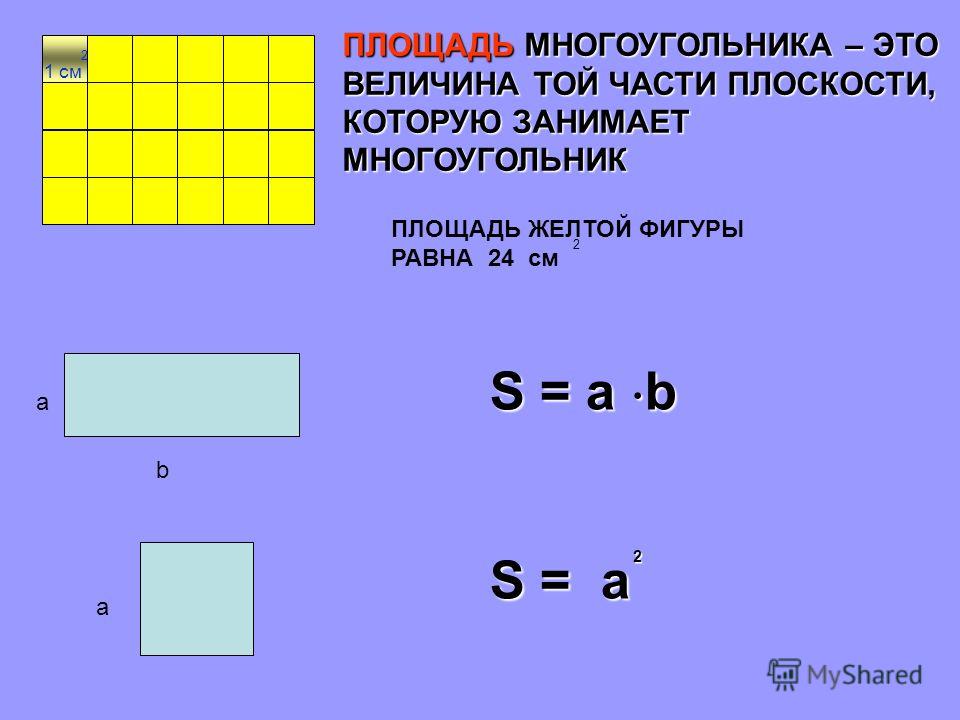
Что же такое площадь фигуры? Площадь-это место, которое занимает фигура на плоскости.
Если обозначить стороны буквами а и b, то при вычислении получаем формулу S=a·b
Как можно сравнить площади фигур? “На глаз” и наложением друг на друга.
Как можно вычислить площадь фигуры? Используя формулу.
Физкультминутка. Можно использовать аудио
Как
же долго мы сидели,
Наши руки онемели,
Наши ноги затекли,
Ими топнем: раз, два, три!
Руки в стороны, дружок,
Раз, два, три, потом — прыжок.
Со здоровьем всё в порядке,
Если делаешь зарядку.
VI.Работа над пройденным материалом.
Учебник математики 3 класс Моро, Бантова и др. 2014 год.
Страница 57, №4.
— От доски длиной 8 метров отпилили часть длиной 2 метра. Во сколько раз больше оставшаяся часть, чем отпиленная?
— О чём говорится в задаче? (О доске от которой отпилили часть.)
— Что нужно узнать в задаче? (Во сколько раз больше оставшаяся часть, чем отпиленная?)
— Что необходимо знать, чтобы сравнить? (Сколько отпилили т
сколько осталось).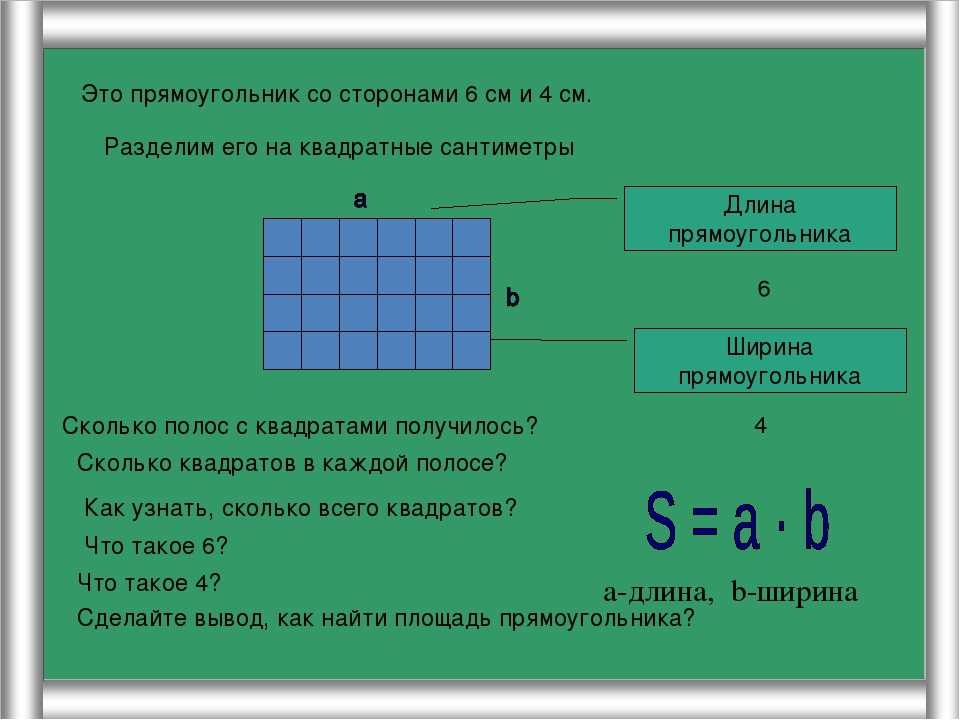
— Запишем задачу кратко.
Было – 8 м
Отпилили – 2 м Во ? раз больше
Осталось — ? м
1) 8-2=6 (м) – осталось
2) 6:2=3 (раза)
Ответ: в 3 раза больше оставшаяся часть, чем отпиленная.
VII. Закрепление.
1) учебник с.57 № 1 (устно).
На рисунке изображены фигуры, которые при наложении не совпадут. Докажите, что их площади равны.
2. Раздели на три фигуры одинаковые по площади, и раскрась разными карандашами.
Построй фигуру равную по площади данной, но другой формы.
3. Задание на развитие пространственного воображения.
Раскрась фигуру. Существует два варианта: а) прямоугольник сверху, а квадрат снизу, б) прямоугольник снизу, а квадрат сверху. Выберите любой вариант.
VIII.
Итог урока.
Завершаем наш урок.
Надеюсь, он пойдёт вам впрок.
Какую тайну мы сегодня открыли?
(Каждая фигура имеет площадь)
— Оценки за урок.
XI. Домашнее задание с пояснением.
Страница 57 №2 (3 и 4 столбики по действиям), №5.
IX. Литература
- http://festival.1september.ru/articles/312140/
- Мокрушина О.А. Поурочные разработки по математике. 3 класс. К УМК М.И. Моро
Периметр и площадь. Почему дети в начальной школе путаются в том, что кажется взрослым очень простым
Нам, взрослым, некоторые вещи кажутся очевидными. Всем мы знаем, как вычислить периметр и площадь у фигуры, например. А вот для детей в началке это сложно. Как им помочь, рассказывает наш блогер, учитель начальных классов Ольга Катаева.
Родители по-разному относятся к вопросу выполнения домашнего задания. Некоторые помогают, корректируют, контролируют. Некоторые делают задания за ребёнка.
А кто-то считает, что выполнение домашнего задания — ответственность ребёнка, и не вмешиваются.
Есть родители, которые предпочитают с детьми не заниматься совсем (это касается не только домашних заданий). Восхищают родители, которые занимаются со своими детьми, помогают им понять то, что решали в классе, разбирают ошибки в контрольных. А есть такие, которые не разбирают материал вместе с ребёнком, а требуют полного заучивания программы, не интересуясь, понял он что-то или нет.
Много раз объясняла родителям, что у детей начальных классов другое мышление
Они не могут думать абстрактными понятиями. Они не могут понять материал, заучив правило или формулу. Чтобы научиться говорить определениями и формулами, младшие школьники должны усвоить понятие на практике.
В начальной школе есть совсем простые темы, а есть темы потруднее. Есть очень трудные. Одна из них — «Площадь и периметр». Взрослым, у которых логическое мышление уже сформировано, эта тема не кажется трудной, поэтому они с лёгкостью объясняют её дома детям, не придерживаясь рекомендаций и объяснений учителя.
Родители помнят, как учили эту тему в школе. Правда, не в начальных классах, а в среднем звене и старшем — то есть тогда, когда начинает формироваться логическое и абстрактное мышление. Поэтому подросткам дают формулы.
Дети начальной школы часто путают понятия «площадь» и «периметр»
Объяснению и повторению этой темы уделяется не так уж много времени. Родители, видя двойки за контрольные с такими заданиями, пытаются по своему объяснить, как решать. Дают формулу на периметр: P=2а+2b, но не объясняют, что она обозначает.
Вспомним формулу площади S=ab. И в той, и в другой формулах присутствует умножение — это первая причина, почему дети путаются (другие причины надо выяснять, это могут быть пространственно-конструктивные нарушения и др.).
Как можно объяснить эту тему, чтобы ребёнок ее понял? Обратимся к определению периметра: «Пери́метр — общая длина границы фигуры», или «Периметр — длина контура замкнутой плоской фигуры», или так: «Периметр — сумма длины всех сторон плоской геометрической фигуры».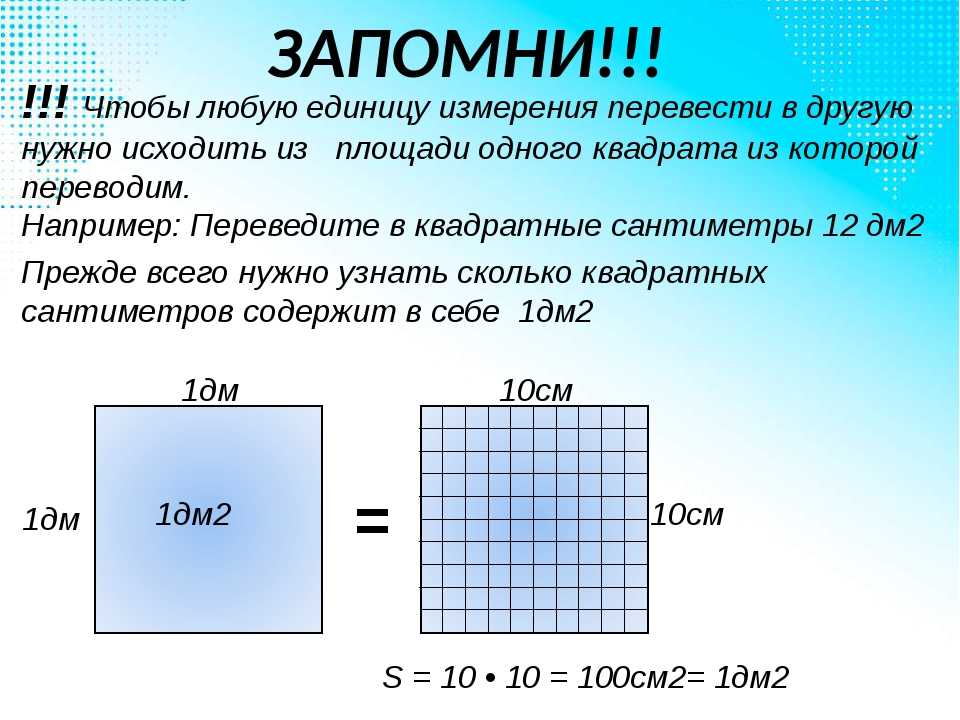
В начальной школе даётся такое определение: «Периметр — это сумма длин всех сторон фигуры». Важно понять, что периметр — это весь контур фигуры, то есть мы складываем вместе длины всех сторон.
Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее). Если фигура — прямоугольник, её делят на равные квадратики и считают их. Так можно делать с небольшими фигурами, которые помещаются в тетрадках.
Находить площадь «Красной площади», которая в Москве, так нельзя
Есть формула. Для нахождения площади больших фигур, прямоугольной формы, достаточно знать длину и ширину и перемножить их (можно ввести ассоциацию с таблицей Пифагора, которая тоже поделена на квадратики и значение произведения находят путём умножения чисел).
Вот оно — существенное отличие: периметр — сложение, площадь — умножение.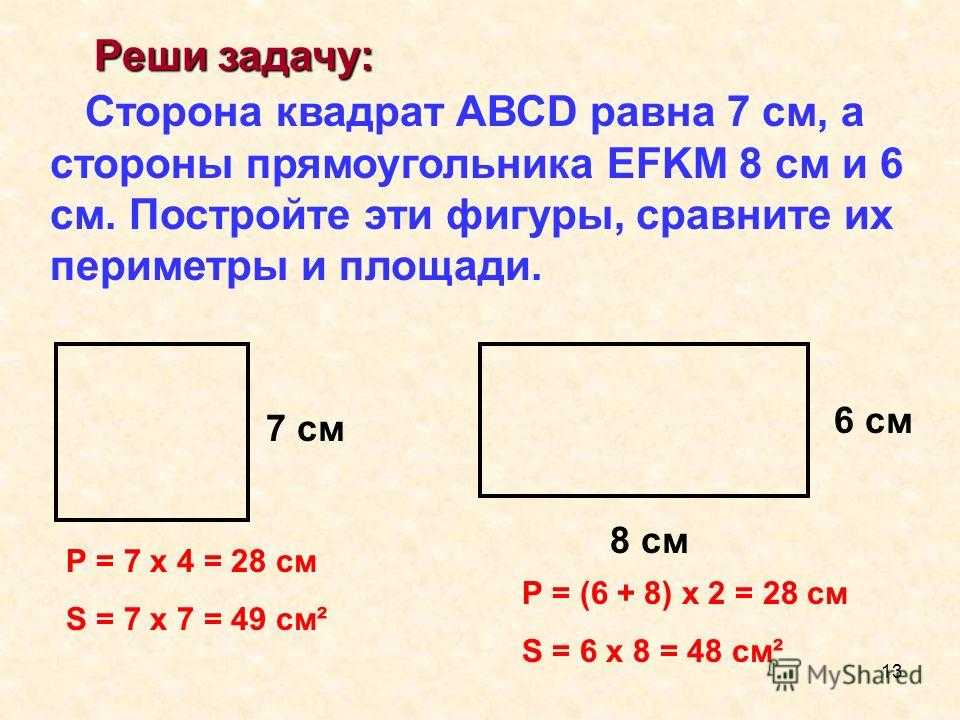
Поэтому в период, когда идёт отработка этих понятий, не следует вводить формулу периметра прямоугольника с умножением. Если ученик поймёт суть понятия «периметр», он сможет найти периметр любого многоугольника. Если зациклить его на формуле для нахождения периметра прямоугольника, школьник не сможет перенести знание для нахождения периметра другой фигуры.
Не надо заучивать с детьми формулы и определения. Надо понимать возрастные особенности младших школьников и объяснять на понятном для них «языке» — через образы, ассоциации, через практику, через действование.
Удачи родителям, которые понимают своих детей и помогают им в нелёгкой учебной жизни.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Фото: Shutterstock / pupunkkop
Площадь — Математика 3-го класса
Площадь — это количество пространства плоской формы или поверхности.
Сколько места занимает эта доска? 🤔
👉 Чтобы это понять, найдем площадь доски !
Совет: Только двумерные объекты имеют площадь. Трехмерные объекты имеют объема .
Обложка книги плоская. Передняя часть двери шкафа плоская. Бумага плоская.
Как найти площадь чего-либо?
Давайте найдем площадь сетки как эта доска
Один из способов найти площадь сетки это подсчитать все квадраты в ней .
Сколько здесь квадратов?
Верно! Есть 30 квадратов.
Площадь доски 30 квадрат шт. . 😀
1 квадрат равен 1 квадратный блок .
Но счет идет довольно медленно. Давайте изучим более быстрый способ.
Использование умножения для нахождения площади
Чтобы найти площадь сетки , такой как прямоугольник или квадрат, просто умножьте на высоту на ширину .
Высота x Ширина = Площадь
Почему это работает? 🤔
Потому что сетки — это просто столбцы , умноженные на на некоторое количество строк! 🤓
Сколько строк и столбцов в нашей сетке?
Что произойдет, если мы умножим количество строк (5) на количество столбцов (6)?
5 x 6 = 30901 😺
Так что помните:
Умножьте на длину и ширину любого прямоугольника или квадрата, чтобы получить его площадь .
Единицы площади
Точно так же, как длина, вес и время, площадь также имеет около единиц из измерений .
Единицы из площадь говорят нам, насколько велика или мала площадь на самом деле.
Представьте, что это размер каждой клетки на доске.
Площадь квадрата шириной 1 см и высотой 1 см составляет 1 квадрат сантиметр.
Квадрат сантиметр единица измерения площади. Записывается как см² .
В Соединенных Штатах люди также иногда используют квадратных дюймов в качестве единицы измерения.
Записывается как кв . дюйма или дюйма² .
👉 Площадь квадрата шириной 1 и высотой 1 равна 1 квадратный дюйм.
Итак, какова площадь нашей доски?
Мы знаем, что это 30 квадратных единиц.
Если площадь каждого квадрата равна 1 см², то площадь доски равна 30 см². 👍
Площадь больших пространств
Что, если мы хотим измерить площадь больших пространств, таких как это травяное поле?
Какую единицу измерения следует использовать? 🤔
😌 Квадратный сантиметр будет слишком мал.
Для больших помещений часто используется единица измерения квадратных метра. Записывается как м² .
Квадрат метр – это площадь, занимаемая квадратом со стороной 1 м. 👍
Теперь измерим площадь двора.
👉 Сетка может помочь нам посчитать квадратные единицы.
Вместо подсчета умножим столбцов на строки.
5 х 9 = ?
Что мы получаем? 45 квадрат штук !
Итак, площадь двора 45 м² .
🎉
В Соединенных Штатах люди часто используют квадратных футов вместо квадратных метра !
1 квадрата фута — это площадь квадрата размером 1 фут на 1 фут. Сокращенно кв. . футов или футов² .
Квадратные футы меньше квадратных метров.
1 м 2 может поместиться чуть более 10 футов².
Теперь завершите практику. Вы узнаете больше и будете помнить дольше. 💪
Площади прямоугольников и квадратов — Математика 3 класса
Прямоугольники и квадраты — две наиболее распространенные формы.
Что такое прямоугольники?
Прямоугольники представляют собой плоские фигуры с 4 прямыми сторонами и 4 прямыми углами.
Вот несколько примеров прямоугольных объектов:
Подсказка : Квадратные углы также называются « прямыми углами ».
Что такое квадраты?
Квадраты — это прямоугольники, у которых все стороны имеют одинаковую длину .
Вот несколько квадратных объектов:
В этом уроке мы научимся находить площади прямоугольников и квадратов.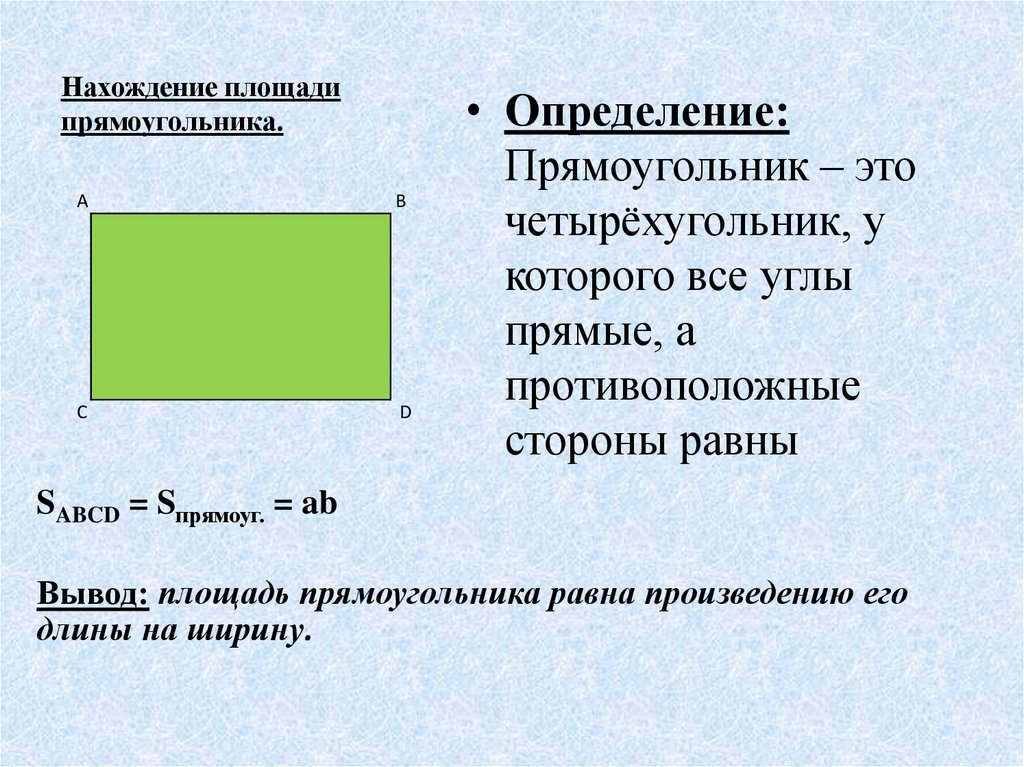
Что такое площадь?
Площадь — это количество места, которое занимает плоская фигура.
Этот зеленый прямоугольник занимает 6 квадратов.
Его площадь равна 6 квадратных единиц .
Мы используем единицу из площадь , чтобы точно знать, насколько велика форма.
Например, если каждый квадрат равен 1 квадратному метру, то площадь зеленого прямоугольника равна 6 квадрата метра .
Совет: Мы можем записать 6 квадратных метров как 6 м² .
Это читается как «6 квадратных метров » .
Площадь прямоугольника
Чтобы найти площадь a прямоугольник , умножьте ширину на высоту.
ширина × высота = площадь
Этот прямоугольник имеет ширину 3 и высоту 2.👇
Давайте умножим ширину на высоту, чтобы найти площадь .
3 × 2 = 6 квадрат
Площадь 6 квадратных единиц !
Такой же ответ мы получаем, подсчитывая каждый квадрат.
😃
Площадь квадрата
Чтобы найти площадь из a квадрат , умножьте на длину любой стороны.
Длина каждой стороны равна 3.
Чтобы найти площадь, умножьте 3 на 3. сантиметры.
Отличная работа! 😺
Давайте потренируемся на примерах!
Найдите площадь этого прямоугольника:
Просто умножьте длину на ширину.
10 × 6 = 60
Площадь этого прямоугольника равна 60 квадрат дюйма (или 60 0 ²) ✅
Убедитесь, что пишет блок из область после номера.
