Что изучает формальная логика: Формальная логика — Психологос

Формальная логика — Психологос

01 октября 2022 г., 21:28

Формальная логика — наука, изучающая формы мысли (понятия, суждения, умозаключения, доказательства) со стороны их логической структуры, отвлекаясь от конкретного содержания мыслей. Это конструирование и исследование правил преобразования высказываний, сохраняющих их истинностное значение безотносительно к содержанию входящих в эти высказывания понятий.

Формальная логика и мышление

Предмет формальной логики — это не все мышление, а только одна его сторона — логические формы мышления. Формальная логика исследует как бы готовые, имеющиеся, уже возникшие мысли — понятия, суждения и т.д. — и устанавливает определенные соотношения (формулы) между ними. Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития этих мыслей — понятий, суждений, умозаключений.

Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития тех или иных мыслей. Она полностью отвлекается, в частности, и от взаимосвязи мышления с чувственным познанием. Иначе говоря, она вовсе не исследует, в отличие от психологии, как конкретно возникает и обогащается содержание нашего мышления на основе ощущений, восприятий и представлений. В логических формулах, например в силлогизме, соотносятся друг с другом уже как бы застывшие, законченные, полностью четко и до конца сформулированные мысли, т.е. результаты, готовые продукты мышления.

• Мышление

Комментарии (3):

Гость, 08 июня 2012 г., 13:12

Спасибо за статью. Очень четко и грамотно дали определение формальной логике. Хотелось бы, чтобы на этом сайте немного больше шире рассматривали такие темы как силлогизм, алогизм и другие составляющие виды этих тем.

1

ответ

Гость, 07 февраля 2020 г., 10:50

Мне даже интересно, какое мышление бывает не логическим?

1

ответ

Гость, 17 июня 2021 г., 18:12

У аутистов диалектическая логика.

Материалы по теме:

01 окт. 2022 г.

Логика

Логика — философская наука, изучающая логические формы человеческого мышления и законы, которым подчиняется мышление. Логика изучает не конкретное содержание действительности, а мысли о ней, их структуру, то, что является общим для мыслей данного типа, независимо от их конкретного содержания. Поэтому при изучении логики для того, чтобы понять сущность процесса мышления, специфическое содержание форм и законов, нужно уметь обобщать конкретные рассуждения, уметь оперировать получаемыми формулами и схемами.

4Подробнее

01 янв. 2006 г.

Мышление

Мышление нередко определяют как способность к решению новых, экстренно возникающих задач в ситуациях, где прежние, уже известные решения не срабатывают. Творческое и конструктивное, развитое мышление действительно способно справляться с такими задачами, но это не значит, что если кто-то не нашел творческого решения в новой для него ситуации, у него мышление отсутствовало. В своих простейших формах мышление, как процесс, это всего лишь переработка информации в потоке течения мыслей, образов и ощущений.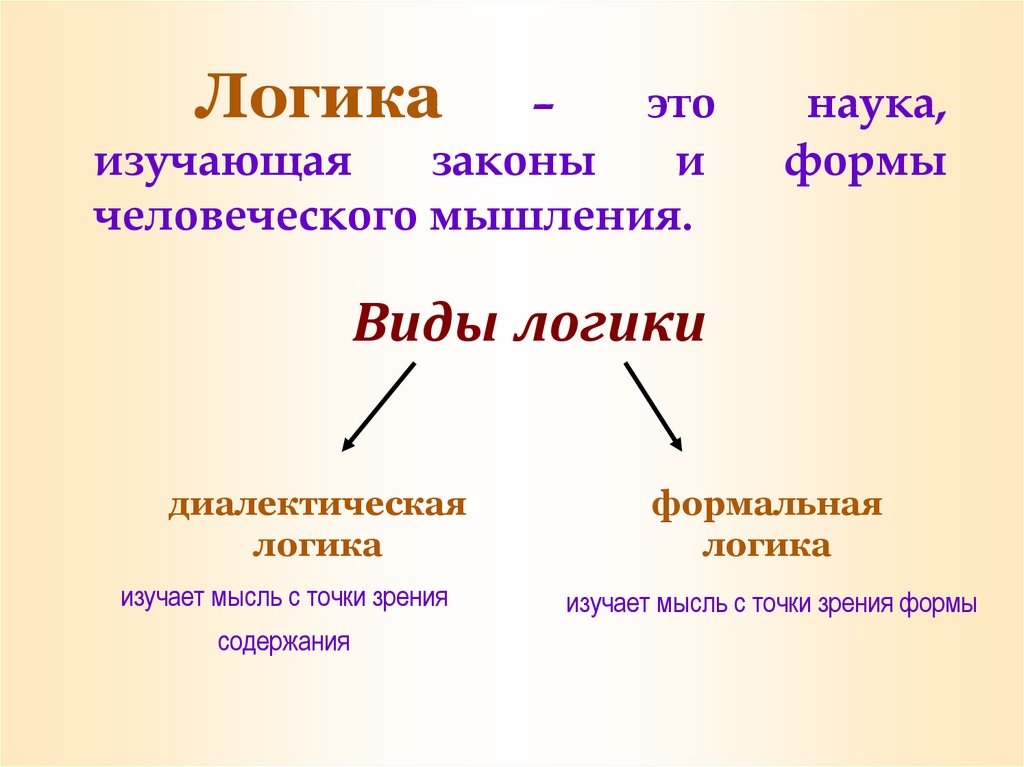

7Подробнее

01 окт. 2022 г.

Мысль

Мысль — упакованный смысл, переданный сознанию (всплывший в сознании) в процессе мышления. Мысль (смысл?) — интересная, имеющая значение связь понятий, связь образа цели и элементов ситуации. «Я понял, как это связано!» «Я понял, что можно сделать!»

6Подробнее

01 окт. 2022 г.

Понятие

Понятие — то, что имеет определение, определенный смысл. Это представление, в котором смысл задан (построен) четким, определенным образом. Смысл понятия (образ понятия) имеет границы и правила его использования.

0Подробнее

01 окт. 2022 г.

Суждение

Суждение — высказывание; умственный акт, выражающий отношение говорящего к содержанию высказываемой мысли. Вынося суждение, мы создаем те опоры, которые считаем соответствующими действительности и потому позволяющими двигаться к истине. Суждение — это отражение связей между предметами и явлениями действительности или между свойствами и признаками. Например, суждение «Металлы при нагревании расширяются», выражает связь между изменениями температуры и объемом металлов. Устанавливая таким образом различные связи и отношения между понятиями, суждения являются высказываниями чего-то о чем-то.

0Подробнее

01 окт. 2022 г.

Теория познания

0Подробнее

01 окт. 2022 г.

Умозаключение — элементарная частица рассуждения

Умозаключение — мыслительная операция, состоящая в получении нового вывода из нескольких суждений. Люди используют умозаключения, когда нужно в чем-то разобраться: вывести следствие, осуществить доказательство, систематизировать знания, проверить гипотезу… Разумное мышление, в отличие от бессвязного или эмоционально заряженного потока мысли, состоит из рассуждений — сложных умственных конструкций. А рассуждения в свою очередь состоят и умозаключений — элементарных мыслительных операций.

2Подробнее

Содержание

Нет новостей

Новые статьи:

• Как отмечать день рождения ребенка?
• Не все праздники — твои!
• Результатник, умеющий наслаждаться
• Лента отчетов, прекрасные авторы и анонимность. Рассказываем подробно!
• «Зима и котик», стихотворение

Популярные статьи:

• Умение договариваться
• Ребенок не слушается. Что делать?
• Что делать мужу, когда жена не хочет секса
• Как разговаривать с мужем
• Можно ли менять свой характер, и как

Хиты недели:

• Как разговаривать с мужем
• Откуда стеснительность и что с нею делать
• Взгляд: как смотреть на собеседника?
• Гнев, злость, ярость. Что делать с собственной агрессивностью?
• Жена не хочет секса. Что делать?

ФОРМАЛЬНАЯ ЛОГИКА | это… Что такое ФОРМАЛЬНАЯ ЛОГИКА?

наука о мышлении, предметом к-рой является исследование умозаключений и доказательств с т. зр. их формы (формы логической) и в отвлечении от их конкретного содержания. Ф. л. является базисной наукой – ее идеи и методы используются как в повседневной практике, напр. в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин.

Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др. формы дедукции (см. Древнегреческая логика). Частично в том же направлении шло развитие логики и в средние века (см.

раздел Схоластическая логика в ст. Схоластика), и в эпоху Возрождения (Галилей, Валла, Раме). Развитие опытного естествознания и математики, усилившееся в 17 в., поставило вопрос о прикладной роли Ф. л., о дальнейшем развитии несиллогистич. форм вывода, характерных для логики науки. (В этой области работали с большим или меньшим успехом Ф. Бэкон, Декарт, Паскаль, авторы Пор-Рояля логики, И. Юнг, Лейбниц и их последователи.) Одна из осн. «логистических» идей Лейбница состояла в том, чтобы свести к «вычислению» не только математические, но и любые умозаключения. Лишь ко 2-й пол. 19 в. относятся ощутимые шаги в реализации этой идеи, когда работами Буля, де Моргана, Джевонса, Шрёдера, Порецкого, Пирса, Фреге, Пеано и др. были заложены основы первых совр. логико-матем. исчислений. «Principia Mathematica» Б. Рассела и А. Уайтхеда открывает совр. этап в развитии Ф. л.

С о в р е м е н н а я Ф. л. является историч. преемником традиц. Ф. л. и в ряде случаев ее прямым продолжением. Расширение и обогащение языка Ф. л., ее осн. понятий в известной мере служат указанием на то, в каком направлении шло развитие Ф. л. от традиционной к современной. В частности, в логич. словаре появились такие понятия, как исчисление и логическое исчисление, математическая индукция, формализация и формализованный язык, независимость, непротиворечивость и полнота, алгоритм и разрешения проблемы, область предметов и переменная, операция и функция и др. неизвестные традиц. Ф. л. понятия. С др. стороны, определ. связь с традицией сохранили такие понятия совр. Ф. л., как аксиома, посылка и постулат, вывод и правило вывода, квантор, следствие и следование (импликация), теорема о дедукции и др., хотя в совр. трактовке этих понятий не сразу узнаются их историч. прообразы.

На протяжении более чем двухтысячелетней истории Ф. л. основную ее цель видели в том, чтобы исследовать, каким образом можно выводить одни высказывания из других. Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см. также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц.

Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании.

Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич. исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф.

л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич. и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики.

В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич. теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см.

Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики.

Т.о., ответ на вопрос «Что такое Ф. л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф.

л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.

М. Новосёлов, Г. Рузавин, П. Таванец. Москва.

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.

Формальная логика | Определение, примеры, символы и факты

Альфред Норт Уайтхед

Смотреть все СМИ

Ключевые люди:

Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано

Похожие темы:

теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод

Просмотреть весь связанный контент →

формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.

Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдений. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.

(Читайте статью Стивена Пинкера о рациональности в «Британнике»). Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают вывод.

Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно различных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.

Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.

Подпишитесь сейчас

Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое обозначает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.

Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.

С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто одновременно и X , и не-9.0027 х . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.

Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую ​​систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.

Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или мысленными конструкциями?

Формальная логика Определение и значение

• Основные определения
• Викторина
• Связанное содержимое
• Примеры
• Британский

Показывает уровень обучения на основе слова с сложностью.

Сохрани это слово!

См. синонимы формальной логики на сайте Thesaurus.com

Показывает уровень обучения в зависимости от сложности слова.

---

сущ.

раздел логики, занимающийся исключительно принципами дедуктивного рассуждения и формой, а не содержанием предложений.

ТЕСТ

МОЖЕТЕ ЛИ ВЫ ОТВЕЧАТЬ НА ЭТИ ОБЫЧНЫЕ ГРАММАТИЧЕСКИЕ СПОРЫ?

Есть грамматические дебаты, которые никогда не умирают; и те, которые выделены в вопросах этой викторины, наверняка снова всех разозлят. Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?

Вопрос 1 из 7

Какое предложение верно?

Происхождение формальной логики

Впервые записано в 1855–1860 гг.

Слова рядом с формальной логикой

формалин, формализм, формальность, формализовать, формальный язык, формальная логика, формально, формальный режим, формальная система, парадная одежда, Форман

Dictionary. com Unabridged Основано на Random House Unabridged Dictionary, © Random House, Inc., 2023

Слова, относящиеся к формальной логике

силлогизм

Как использовать формальную логику в предложении инг который может отслеживать шаги в геометрическом доказательстве или аргумент в формальной логике.

Сила рационального мышления в мире, который кажется неразумным|Ник Ромео|8 октября 2021|Washington Post

Немалое достижение — сделать формальную логику, теорию игр, статистику и байесовские рассуждения восхитительными темами, полными очарования и актуальность.

Сила рационального мышления в мире, который кажется неразумным|Ник Ромео|8 октября 2021 г.|Washington Post

Несмотря на то, что Аристотель изобрел формальную логику, он, по-видимому, не заметил в своих рассуждениях определенной степени цикличности.

Это 10 самых ошибочных научных результатов|Том Зигфрид|10 ноября 2020|Новости науки

Ошибки Антисфена — отчасти зависели от несовершенной формальной логики того времени.

Платон и другие сподвижники Сократа, 3-е изд. Том III (из 4)|George Grote

• Ответ формальной логики (принятый, кроме того, Кантом и которому в той или иной мере следуют все неокантианские логики) однозначен.

  Очерки экспериментальной логики|Джон Дьюи

• Но немыслимо, чтобы большая часть людей проводила всю свою ментальную жизнь с греческим акцентом или с формальной логикой.

  Беседы в Америке|Мэттью Арнольд

• Схоластическое образование того времени уделяло особое внимание формальной логике и метафизике.

  The New Gresham Encyclopedia|Various

• Формальная логика учит, что наш интеллект должен разделять все вещи, но не учит, что он также должен их соединять.

  The Positive Outcome of Philosophy|Joseph Dietzgen

Определения Британского словаря для формальной логики

формальная логика

---

существительное

какие символы используются для точного представления определенные категории выражений.