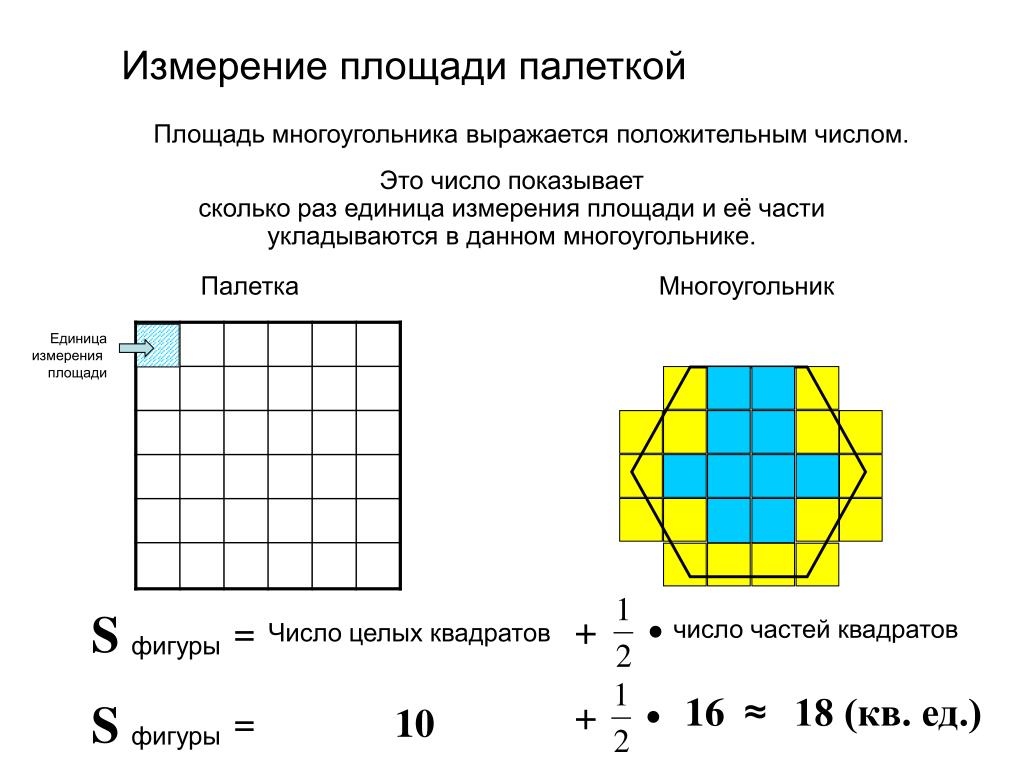
Что такое палетка в математике: Что такое палетка для 3-4 класса по математике и как ею пользоваться?

Содержание

План-конспект урока по математике. Определение площади с помощью палетки. 4 класс

Главная / Начальные классы / Математика

Скачать

2.42 МБ, 1444066.docx Автор: Вероника Анатольевна Ткачева, 21 Фев 2016

План-конспект урока по математике. УМК «Школа России». — 4 класс.

Определение площади с помощью палетки.

Автор: Вероника Анатольевна Ткачева

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	План-конспект урока по математике. Определение площади с помощью палетки. 4 класс	Вероника Анатольевна Ткачева	21 Фев 2016
документ	Конспект урока по математике по теме «Измерение площади фигуры с помощью палетки»	Пономарёва Вера Васильевна	30 Мар 2015
документ	Технологическая карта урока математики в 3 классе «а» по эвристическому обучению. (УМК «система развивающего обучения Л.В. Занкова») Тема урока: Измерение площади с помощью палетки	Богданова Инна Владимировна	4 Ноя 2015
документ	Технологическая карта урока «математика» ПНШ 3 класс «Измерение площади с помощью палетки. Поупражняемся в измерении площадей и повторим пройденное»	Попова Ирина Владимировна	11 Апр 2016
разное	Урок математики в 4 классе. Тема: «Измерение площади фигур с помощью палетки»	Щербаль Светлана Александровна	31 Мар 2015
презентация	Измерение площади с помощью палетки	Земцова Оксана Владимировна	30 Мар 2015
презентация	Измерение площади с помощью палетки	Земцова Оксана Владимировна	30 Мар 2015
документ	«Измерение площади фигур с помощью палетки»	Татьяна Владимировна Кудрявцева	19 Мар 2016
документ	Урок математики в 4 классе по теме «Палетка. Измерение фигуры с помощью палетки» УМК «Школа России»	Микунова Алла Дмитриевна	6 Дек 2015
разное	«Измерение площади фигуры с помощью палетки», технология проблемного обучения	Хисамутдинова Затия Аседулловна	15 Окт 2015
презентация, документ	Конспект урока по математике на тему: «Таблицы мер длины, площади и объема». 4 класс	Сальникова Юлия Николаевна	14 Янв 2016
документ	План-конспект урока по математике(5 класс) на тему:»Площадь. Формула площади прямоугольника. »	Ярыгина Валентина Михайловна	5 Апр 2015
документ	конспект урока по математике « Сравнение по количеству с помощью знаков > и < ». 1 класс	Веневцева Екатерина Александровна	30 Мар 2015
документ	Конспект урока по математике в 4 классе по теме «Поупражняемся в нахождении площади»	Ларченко Галина Викторовна	20 Мар 2016
документ	Конспект урока по математике в 4 классе «Оценка площади»	Кислюнина Наталья Андреевна	28 Фев 2016
документ	План-конспект урока по алгебре 8 класс «Определение степени с целым отрицательным показателем»	Радюшкина Людмила Николаевна	16 Ноя 2015
документ	План-конспект урока по алгебре 7 класс «Определение степени с натуральным показателем»	Радюшкина Людмила Николаевна	16 Ноя 2015
документ	План-конспект урока по алгебре 7 класс по теме:Решение задач с помощью систем уравнений	Краснова Лидия Егоровна	15 Окт 2015
документ	План-конспект урока по алгебре (7 класс) . Урок по теме: «Разложение многочлена на множители с помощью формул сокращённого умножения.»	Макарова Людмила Ивановна	20 Фев 2016
	Урок по математике на тему: «Измерение площади фигур» 4 класс	Харрасова Зиля Мавлияровна	10 Дек 2016
разное	План-конспект урока по математике 1 класс с использованием ЭОР	Черникова Татьяна Владимировна	27 Окт 2015
разное	Практическая работа по теме «Определение пылевого загрязнения воздуха; определение химического загрязнения воздуха с помощью биоиндикаторов; исследование водозапасающей способности зелёных и сфагновых мхов», 10 класс, УМК Пономарёва И. Н.	Шинкарь Лидия Ивановна	21 Мар 2015
разное	Разработка урока по математике в коррекционном классе комплекте 5-9 класс VIII вида «Арифметические действия с числами, полученными при измерении площади .Решение задач»	Прокопова Валентина николаевна	21 Мар 2015
документ	конспект урока по математике по теме»Решение задач с помощью уравнений»	Хафизова Зиля Марсиловна	31 Мар 2015
разное	Конспект урока по математике 4 класс	Назарьева Ирина Владимировна	5 Мая 2015
документ	Конспект урока по математике «Решение задач с помощью формул»	Чеснокова Дарья Михайловна	30 Мар 2015
разное	Конспект урока «Уравнения. Решение задач с помощью уравнений» Урок-сказка по теме: «Уравнение. Решение задач с помощью уравнений», 5 класс	Свечкарева Ирина Михайловна	1 Апр 2015
документ	План конспект урока По учебному предмету «Геометрия» 8 класс Тема: «Площади параллелограмма, треугольника и трапеции»	Романов Юрий Петрович	16 Окт 2015
презентация, документ	Конспект урока математики с презентацией по теме «Час, минута. Определение времени по часам» 2 класс. Школа России.	Ксенофонтова Инесса Амирановна	27 Фев 2016
документ	Рабочие программы по математике для 6,10 и 11 классов,разработка урока «Решение задач с помощью уравнений» 6 класс, тесты по геометрии 10 класс.	Сабурова Халида Загитовна	21 Мар 2015
документ	план урока по теме «задание функции с помощью формулы», математика, 6 класс.	Акинфиева Любовь Михайловна	21 Мар 2015
документ	Раздаточный материал для учащихся 6 класса: 1) Определение протяженности объектов с помощью градусной сетки; 2) Определение географических координат точек.	Денисова Светлана Михайловна	4 Апр 2015
документ	ПЛАН-КОНСПЕКТ УРОКА ГЕОГРАФИИ по теме «Определение географических координат по географической карте» с использованием ЭОР	Морозова Марина Викторовна	21 Мар 2015
разное	Конспект урока по математике с презентацией 4 класс по теме «Единицы длины. Километр.»	Смыкова Олеся Николаевна	30 Мар 2015
документ	Конспект урока по математике по теме: «Деление нацело и деление с остатком», 4 класс.	Фархуллина Гульнара Залиловна	30 Мар 2015
документ	План-конспект урока русского языка во 2 классе по теме «Наблюдение над однокоренными словами. Определение корня слова.	Давыдова Ольга Германовна	4 Апр 2015
презентация, документ	ПЛАН-КОНСПЕКТ УРОКА «Решение задач на проценты с помощью уравнений»	Якименко Евгения Александровна	4 Апр 2015
документ	план-конспект урока по теме «Площади фигур»	Унбаева Гульдан Султановна	21 Мар 2015
разное	План-конспект урока «Образование слов с помощью суффиксов» 5 класс.	Вайзерова Евгения Александровна	7 Дек 2015
документ	План-конспект урока по математике «Виды треугольников» 4 класс, программа «Школа России»	Губко Марина Викторовна	21 Янв 2016

Технологическая карта дистанционного урока Математика. 4 класс Измерение площади фигур с помощью палетки | Начальная школа

Технологическая карта дистанционного урока Математика. 4 класс Измерение площади фигур с помощью палетки

Автор: Лобова Анастасия Вячеславовна

Организация: МБОУ СОШ №4 им. И.Н. Чабанова

Населенный пункт: Краснодарский край, г. Туапсе

Тема урока: «Измерение площади фигур с помощью палетки»

Тип урока: урок изучения нового материала.

Цель урока: познакомить с новым способом измерения площади с помощью палетки

Задачи урока:

Образовательные:

формирование умения вычисления площади фигур очерченных кривой замкнутой линией

Развивающие:

развивать познавательные процессы младших школьников.
развивать математическую речь.
развивать умения сравнивать и анализировать.

Воспитательные:

воспитывать интерес к математике.
развивать способность к самоанализу и самоконтролю.

Личностные:

— умение проявлять учебно–познавательный интерес к учебному заданию;

— адекватно воспринимать оценку учителя и одноклассников.

Метапредметные:

познавательные:

— строить речевое высказывание в устной и письменной форме;

— осуществлять анализ объектов, выделять главное, проводить сравнение.

регулятивные:

— принимать учебную задачу урока;

— учитывать выделенные учителем ориентиры действия в новом учебном материале в сотрудничестве с учителем;

— планировать собственную деятельность в соответствии с поставленной задачей и условиями ее реализации;

— вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок.

коммуникативные:

— строить речевое высказывание в устной и письменной форме по теме урока.

Предметные:

— называть величины и единицы их измерения;

— формулировать понятие площади;

— вычислять площадь с помощью палетки.

Ресурсы: учебник «Математика» 4 класс М.И. Моро, устройство вывода видео информации.

Ход урока

Этапы урока	Деятельность учителя	Деятельность учащихся
1. Организационный момент	Мотивация учащихся на продуктивную деятельность. Проверка готовности обучающихся к уроку.	Учащиеся настраиваются на учебную деятельность.
2.Актуализация знаний	Организация работы по актуализации знаний учащихся. Проведение устного опроса по теме «Величины. Единицы измерения»	Учащиеся называют изученные величины и единицы их измерения.
3.Постановка целей и задач урока.	Создание проблемной ситуации для определения темы и цели урока. Организация работы обучающихся в по теме урока. Обогащение словарного запаса обучающихся. Организация постановки темы и цели урока с использованием опорных слов: узнаю, научусь.	Обучающиеся работают с целью определения границ знания и незнания по теме определения площади криволинейной поверхности. Формулируют цель урока с использованием опорных слов: узнаю, как определяется площадь поверхности очерченной замкнутой кривой линией; научусь измерять площадь поверхности очерченной замкнутой кривой линией.
4.Первичное усвоение новых знаний.	Организация работы с учебником по теме «Измерение площади фигур с помощью палетки». Объяснение правил работы с палеткой средствами мультимедийной презентации. Объяснение использования палетки для измерения площади поверхности очерченной кривой замкнутой линией с помощью учебного видео https://resh. edu.ru/subject/lesson/4577/start/214365/.	Работа с учебником. Знакомство с понятием «палетка». Чтение текста учебника. Работа с учебником. Чтение правила работы с палеткой. Просмотр учебного видео.
5. Физкультурная минутка.	Проведение физкультурной минутки.	Учащиеся выполняют движения физкультурной минутки.
6. Первичное применение полученных знаний на практике.	Организация работы по применению полученных знаний по теме урока в процессе выполнения практико-ориентированного задания. Организация работы с проектом ландшафтного дизайна.	Вычисление площади криволинейной поверхности (пруд и бассейн) с помощью палетки. Выполнение проекта ландшафтного дизайна (работа в группе).
7. Отработка пройденного материала.	Выполнение задания на повторение пройденного материала. Работа с учебником Задание №196. Организация работы по составлению равенств с использованием единиц измерения площади. Организация фронтальной проверки правильности выполненного задания.	Работа с учебником Задание №196. Выполнение записи с использованием единиц измерения площади. Устное комментирование результатов выполненного письменного задания.
8.Домашнее задание	Организация записи домашнего задания. Выполнение карточек на платформе Учи.ру	Обучающиеся выполняют инструкции учителя.
9.Итог урока.	Организация подведения итога урока. Определение общих выводов по теме урока. Акцентирование внимания на конечных результатах учебной деятельности.	Формулируют конечный результат своей работы на уроке.
10.Рефлексия.	Организация работы самоанализа.	Участвуют в рефлексии своей деятельности на уроке.

Используемые источники литературы:

Поурочные разработки по математике. 4 класс (к УМК М.И. Моро и др. («Школа России»)) | Ситникова Татьяна Николаевна, Яценко Ирина Федоровна.
Платформа «Российская электронная школа» https://resh.edu.ru/
Платформа «Учи.ру» https://uchi.ru/

Приложения:

file1.pptx.zip.. 2,3 МБ
file0.docx.. 24,7 КБ

Опубликовано: 28.03.2022

БЕСПЛАТНАЯ ПУБЛИКАЦИЯ БЕСПЛАТНЫЕ КОНКУРСЫ БЕСПЛАТНЫЕ ВЕБИНАРЫ КУРСЫ

Сведения об образовательной организации
Пользовательское соглашение Политика конфиденциальности

© 2010 – 2023, Всероссийский педагогический журнал «Современный урок»
ISSN: 2713 – 282X, УДК 371.321.1(051), ББК 74.202.701, Авт. знак С56
Лицензия на образовательную деятельность № 041875 от 29.12.2021
СМИ ЭЛ № ФС 77 – 65249 от 01.04.2016
Для писем: 125222, Москва, a/я 8
Телефон: +7 (925) 664-32-11
E-mail: [email protected]

16+

Простое упражнение по математике и графическому дизайну

Каждый день нашей жизни мы сталкиваемся с теорией цвета. В большинстве случаев мы не задумываемся об этом дважды. Однако знаете ли вы, что суждения о вашей достоверности на 75% основаны на дизайне вашего веб-сайта? Первое впечатление на 94% связано с внешним видом и дизайном вашего сайта. И 46% клиентов основывают свои решения о покупке на эстетической привлекательности вашего сайта. Действительно, теория цвета и графический дизайн очень важны.

К сожалению, у подавляющего большинства людей ужасный взгляд на графический дизайн, и многие организации экономят на своих проектах. В то время как любой из нас может выбирать цвета, профессиональные графические дизайнеры умеют выбирать цвета, которые просто потрясающе сочетаются друг с другом. Так как они это делают? Они не берут эти цвета из воздуха.

Оказывается, мы можем использовать математику, чтобы лучше понять цвет. Математическая теория цвета, которую мы сегодня рассмотрим, предназначена для веб-дизайна и дизайна приложений, но вы, безусловно, можете использовать ее для покраски дома, согласования модных нарядов или любого другого типа дизайна.

Цветовой круг: основа теории цвета

Исаак Ньютон изобрел цветовой круг в 1666 году. Отображение цветового спектра на круге позволяет нам легко определять отношения между цветами. Вы, наверное, видели цветовой круг, когда учились в начальной школе. Тем не менее, вы можете легко найти цветовые круги, которые используют профессионалы, с помощью быстрого поиска в Google Images. Вот пример одного из них.

Новый взгляд на основные цвета

Пришло время вернуться в начальную школу. Вы помните основные цвета? Я знаю, что ты знаешь. Если вы забыли, они бывают красными, желтыми и синими, или сокращенно RYB. Вы не можете получить основные цвета, комбинируя смеси других цветов.

Знаете ли вы, что это не единственный набор основных цветов? Те основные цвета, которые вы выучили в начальной школе, рассказывают только часть истории. Другой набор основных цветов состоит из красного, зеленого и синего, или RGB. Чего ждать? Нет, это не тип-о. На самом деле в повседневной жизни вы используете основную цветовую схему RGB, а не RYB.

Так как же зеленый может быть основным цветом? Я думал, что желтый и синий дают зеленый. Вы правы, но только частично. Вот остальная часть истории. Основная цветовая схема RYB, которой вас учили в начальной школе, применяется для смешивания цветов краски или чернил. Всякий раз, когда вы смешиваете цвета света, вы используете цветовую схему RGB.

Где мы используем основную цветовую схему RGB?

Он везде. Прежде всего, ваши глаза используют основную цветовую схему RGB для интерпретации цвета. Все, что имеет экран, также использует его. Ваш телефон делает. Как и ваш компьютер и ваш телевизор. Как и те электрические знаки, которые вы видите на автостраде. В следующий раз, когда вы будете в студии или в театре, посмотрите на свет. Вы увидите, что они красные, зеленые и синие.

К счастью, математическая теория цвета остается неизменной, независимо от того, какую основную цветовую схему вы используете.

Математические обозначения цвета

Для того чтобы применить математическую теорию к цвету, нам нужно подставить некоторые числа.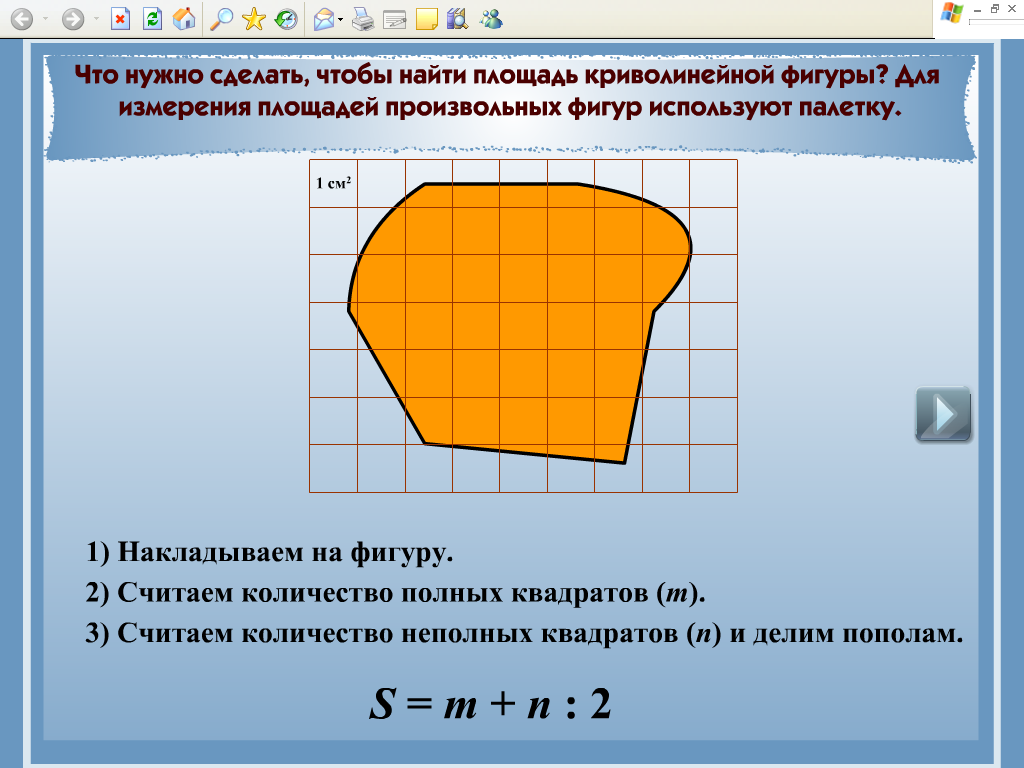 Исаак Ньютон, человек, который изобрел цветовой круг, был одним из величайших математиков всех времен, поэтому большая часть тяжелой работы сделана за нас. Мы просто используем модель RGB, разбивая цвет на красный, зеленый и синий компоненты. Вы можете думать об этом либо как о трехмерном векторе, либо как о матрице 1 × 3.

 цвет = RGB(красный, зеленый, синий)

Итак, какие числа мы вставляем в каждый компонент? От 0 до 100 было бы хорошим предположением. На самом деле это общепринятый способ, но когда вы работаете с компьютерами, есть способ получше. Компьютеры используют двоичную систему, в которой используются степени двойки. Один байт состоит из 8 частей, называемых битами. В результате максимальное значение, которое может содержать байт, равно 2 ⁸ или 256. Мы установим для каждого компонента нашего цвета число от 0 до 255.

 черный = RGB(0, 0, 0)
белый = RGB(255, 255, 255)
красный = RGB(255, 0, 0)
зеленый = RGB(0, 255, 0)
синий = RGB(0, 0, 255)

Выбор системы координат для нашего цветового круга

Чтобы полностью понять теорию цвета, нам нужно изобразить цветовой круг на графике. По умолчанию большинство людей начинают с декартовой ( x, y ) системы координат. И декартовы координаты отлично подходят для теории цвета. Однако есть одна большая загвоздка. Цветовой круг круглый, а это значит, что нам нужно иметь дело с углами. А в декартовой сетке это означает тригонометрию и многое другое.

Не знаю как вы, а мне бы не хотелось приводить сюда синусы и косинусы. К счастью, есть гораздо лучшая система координат. И самое главное, единственная математика, которая вам понадобится, — это сложение и вычитание. Тригонометрия не требуется.

Ввод полярной системы координат

Вместо прямоугольной сетки полярная система координат основана на концентрических окружностях вокруг координаты (0, 0). Вместо ( x, y ) полярные координаты задаются как ( r, θ ). Координата r относится к радиусу или к тому, насколько далеко вы находитесь от начала координат. Тета (θ) — это угол от горизонтальной линии, идущей вправо от начала координат. В градусах тета — это число от 0 до 360.

Преобразуйте RGB в оттенок, насыщенность, яркость (HSL), чтобы сделать математику теории цвета еще проще

Вот где происходит волшебство. Оттенок, насыщенность, яркость или модель HSL — это просто еще один способ обозначения и анализа цветов. Как и RGB, он состоит из трех компонентов. Можете ли вы сказать, какой компонент идеально дополнит нашу полярную систему координат?

Оттенок	Угол на цветовом круге от 0 до 360°. Красный — 0°, зеленый — 120°, синий — 240°.
Насыщенность	Уровень серого в процентах. 0% — это оттенок серого. 100% полноцветный.
Яркость	Насколько светлым или темным является цвет в процентах. 0% — черный, а 100% — белый.

Компонент оттенка идеально накладывается на нашу полярную систему координат. Чтобы выполнить теорию цвета, все, что нам нужно сделать, это добавить или вычесть значения оттенка, чтобы получить дополнительные цвета. Тригонометрия не требуется. Вам даже не нужно прикасаться к значениям насыщенности или яркости. Процесс невероятно прост.

Преобразуйте основной цвет в нотацию HSL. Гайки и болты этого преобразования выходят за рамки этого руководства. Тем не менее, я написал скрипт Python, который выполняет преобразование, чтобы вы могли выполнять свой собственный анализ цвета.
Сложите и/или вычтите углы оттенков, чтобы определить дополнительные цвета. Мы сделаем несколько практических упражнений с этим ниже.
Преобразование цветов вашей цветовой схемы обратно в нотацию RGB.

В приведенных ниже примерах давайте использовать красный в качестве основного цвета, потому что θ = 0 для красного цвета. Таким образом, углы на графиках будут иметь гораздо больше смысла.

Теория комплиментарных цветов

Комплементарный цвет — это цвет, который находится прямо напротив вашего основного цвета на цветовом круге. Математически просто добавьте 180° к оттенку основного цвета и нанесите его на полярную систему координат.

 hue_complimentary = hue_primary + 180
saturation_complimentary = saturation_primary
lightness_complimentary = lightness_primary

Реальный пример дополнительных цветов

Посмотрите на мир спорта Северной Америки, чтобы найти логотипы, в которых используются дополнительные цвета.

Триколор: Теория смежных цветов

Со смежными цветами цель состоит в том, чтобы получить два дополнительных цвета, совместимых с вашим основным цветом. Все три цвета должны быть рядом друг с другом на цветовом круге. Один из соседних цветов должен быть немного холоднее вашего основного цвета. Другой должен быть немного теплее, чем ваш основной цвет.

Смежные цвета лучше всего сочетаются с более приглушенными цветами. Когда они используются с яркими, живыми цветами, они действительно могут подавить ваши чувства.

Несколько слов об углах в теории цвета

Используя полярные координаты, два соседних цвета смещены от основного цвета на один и тот же угол на цветовом круге. Большинство дизайнеров считают, что оптимальным диапазоном является угол от 30° до 45°, но приемлемо любое значение между 20° и 60°. Если вы используете угол менее 20°, цвета будут настолько похожими, что вам будет трудно различить их. Используйте угол больше 60°, и они больше не будут соседними цветами.

В приведенных ниже уравнениях переменная phi ( φ ) представляет угол, на который соседние цвета смещены от основного. На графике ниже φ = 30°.

 оттенок1 = основной_оттенок + фи
оттенок2 = оттенок_основной - фи
насыщенность1 = насыщенность2 = насыщенность_основной
lightness1 = lightness2 = lightness_primary

Соседние цвета для красного, смещение на 30° на цветовом круге

Реальные примеры соседних цветов

Многие компании, с которыми вы взаимодействуете в повседневной жизни, используют соседние цвета.

Триколор: Теория цвета триады

Теория триады цветов идентичен соседним цветам с одним заметным отличием. Вместо того, чтобы смещаться на φ градусов от вашего основного цвета, триадные цвета смещаются на φ градусов от своего дополнительного цвета. Вместо одного дополнительного цвета у вас будет два. Если вы ищете трехцветную схему и имеете яркие цвета, триадные цвета работают намного лучше, чем соседние цвета.

Использование одного триадного цвета также является отличной альтернативой использованию дополнительных цветов. Какой из них использовать, во многом зависит от вашего проекта, но если вам не нравится внешний вид вашей цветовой схемы с использованием дополнительного цвета, попробуйте использовать один триадный цвет. В реальном мире нет более хрестоматийного примера использования одного цвета триады, чем культовый bleu, blanc, et rouge команды Montréal Canadiens. Ну, по крайней мере, детали bleu и rouge .

Монреаль Канадиенс Культовые красные домашние свитера с синей полосой. Изображение предоставлено NBC Sports.

Математически тройные цвета рассчитываются так же, как и соседние цвета, за исключением того, что они смещены от дополнительного цвета. Здесь действуют те же правила для углов. На графиках ниже давайте снова используем 30° в качестве угла смещения.

 hue_complimentary = hue_primary + 180
hue1 = hue_complimentary + phi
hue2 = hue_complimentary - phi
насыщенность1 = насыщенность2 = насыщенность_основной
легкость1 = легкость2 = легкость_основной

Вы видите, откуда «Монреаль Канадиенс» взяли свою цветовую схему?

Реальные примеры цветов триады

Здесь мы вернемся к логотипам спортивных команд. Можете ли вы найти общую нить в цветовых схемах? Обратите внимание, что многие из этих команд используют один цвет триады, как это делают «Монреаль Канадиенс».

Итак, вы заметили что-то общее в цветовых схемах? Красный, белый и синий — невероятно популярная цветовая схема триады в североамериканском спорте.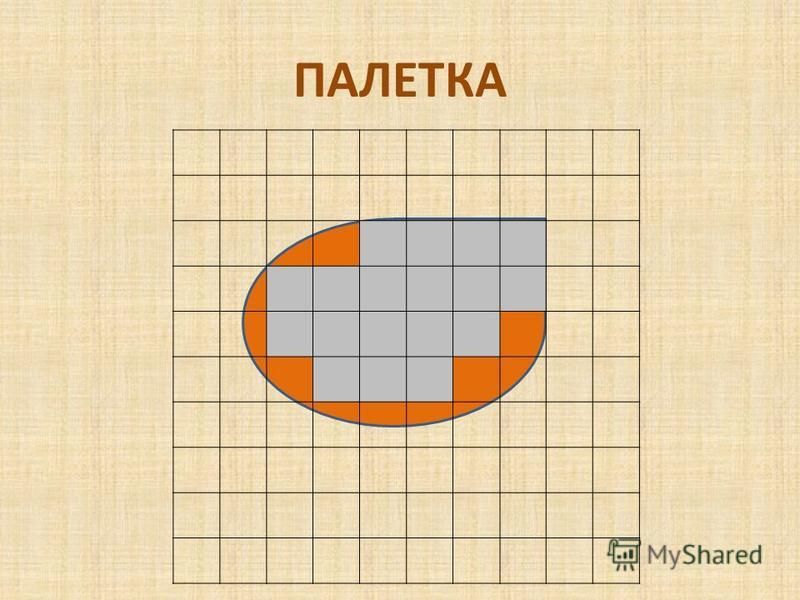 Это имеет смысл, учитывая цветовую схему американского флага. Однако не забывайте, что канадский флаг был синего цвета еще в 19 веке.60-е годы.

Тетрадная цветовая теория: создайте прямоугольник на цветовом круге

Тетрадные цвета сочетают в себе лучшее из дополнительных, смежных и триадных цветов в красивой 4-цветной схеме. Невооруженным глазом невероятно сложно создать хорошую цветовую схему тетрады, но это становится намного проще, когда вы используете математику, стоящую за ней. Если все сделано правильно, если вы нанесете четыре точки на цветовой круг, а затем соедините точки, у вас получится идеальный прямоугольник.

Также называемая «Двойные дополнительные цвета», на самом деле довольно легко придумать цветовую схему тетрады математически.

Начните с основного цвета.
Выберите один из соседних цветов с вашим основным цветом. Неважно, какой.
Вычислите дополнительный цвет из основного цвета.
Триадный цвет — это просто дополнительный цвет к соседнему цвету, который вы выбрали на шаге 2.

 hue_complimentary = hue_primary + 180
hue_adjacent = hue_primary + phi
hue_triad = hue_adjacent + 180 = hue_complimentary + phi
насыщенность1 = насыщенность2 = насыщенность_основной
легкость1 = легкость2 = легкость_основной

Хотя на графике ниже используется угол смещения 30°, я считаю, что цвета тетрады работают намного лучше с большим углом. Во многих наших реальных примерах используются углы от 45 до 60°.

Примеры четырехцветных цветов в реальном мире

Чтобы найти лучшие образцы четырехцветных цветов в реальном мире, вам нужно обратиться к технологической отрасли.

Интересно, что есть одна североамериканская профессиональная спортивная команда, которая невероятно хорошо справляется с цветовой схемой тетрады. Есть предположения, что это за команда? Я дам вам подсказку. Это команда НБА.

Монохроматическое затенение

Наша окончательная теория цвета самая простая. Вам не нужно беспокоиться о преобразовании нотации RGB в HSL. Вы захотите использовать нотацию RGB. Выбросьте и свои полярные координаты. Здесь они не понадобятся.

Монохроматическое затенение — это не что иное, как создание более светлой и более темной версий вашего основного цвета. Секрет успеха заключается в том, что и более светлая, и более темная версии должны быть масштабированы в одинаковой степени по отношению к вашему основному цвету.

Коэффициент масштабирования должен быть выражен в процентах в десятичной форме. Другими словами, используйте 0,25, чтобы масштабировать цвета на 25%. Как и в случае с трехцветными схемами, масштабируйте в меру. От 25 до 60% — довольно безопасный диапазон.

 красный_свет = красный_основной * (1 + коэффициент масштабирования)
зеленый_свет = зеленый_основной * (1 + коэффициент_масштабирования)
синий_свет = синий_основной * (1 + масштабирующий_фактор)
red_dark = red_primary * (1 - коэффициент_масштабирования)
green_dark = green_primary * (1 - коэффициент_масштабирования)
blue_dark = blue_primary * (1 - коэффициент_масштабирования)

Наша стратегия

На наших веб-сайтах мы используем простую стратегию. Мы начинаем с тетрадной цветовой схемы, выбираем из нее первичные и вторичные цвета и при необходимости дополняем их оттенками серого. Однако на самом деле мы используем все 4 цвета.

Первичный цвет
Второстепенный цвет
Акцентный цвет, который экономно используется для дополнения основных и вторичных цветов.
Цвет предупреждения: высококонтрастный цвет, используемый для привлечения внимания к определенным элементам, таким как сообщения об ошибках, предупреждения, объявления о распродажах и т. д.
Серые заголовки, нижние колонтитулы и другие части веб-сайта по мере необходимости.

Мы также используем монохроматическое масштабирование, чтобы сделать кнопки и ссылки темнее, когда вы наводите на них курсор, и сделать их светлее, когда они отключены.

Заключение

Выбор цветовой схемы может быть невероятно сложным. Хотя это не заменит профессионального дизайнера, знание базовой теории цвета поможет вам добиться успеха. Используйте математику теории цвета, чтобы узнать, чего вы хотите, прежде чем нанимать дизайнера. Они смогут работать намного эффективнее, а вы сэкономите немного денег.

Если вы хотите глубже изучить теорию цвета и попробовать математику теории цвета для себя, я поместил скрипты Python в репозиторий Bitbucket. И если у вас есть какие-либо потребности в графическом дизайне или просто общий вопрос, пожалуйста, не стесняйтесь связаться с нами сегодня.

Верхнее фото: Яркие цвета освещают небо пустыни во время захватывающего зимнего восхода солнца
Виттманн, Аризона – декабрь 2017 г. ЕГУ, Физико-математические науки, 55:1 (2021), 36–43

Известия Ереванского государственного университета, серия Физико-математические науки, 2021, том 55, выпуск 1, страницы 36–43
DOI: https://doi.org/10.46991/PYSU:A/2021.55.1.036 (Ми узеру830)

Математика
Два результата по индексу палитры графиков
Смбатян К. С.
Ереванский государственный университет, механико-математический факультет
Полнотекстовый PDF (284 КБ)
Ссылки:
PDF
HTML
DOI: https://doi.org/10.46991/PYSU:A/2021.55.1.036
Реферат: Для заданной правильной раскраски ребер $\alpha$ графа $G$ определим палитру $S_G(v,\alpha)$ вершины $v\in V(G)$ как множество всех цветов, встречающихся на ребрах инцидент с $v$. Индекс палитры $\check{s}(G)$ $G$ – это минимальное количество различных палитр, встречающихся в правильной раскраске ребер $G$. Граф $G$ называется почти двудольным, если существует $v\in V(G)$, такой что $G-v$ является двудольным графом. В этой статье мы даем верхнюю границу индекса палитры почти двудольного графа $G$, используя разложение $G$ на циклы. Мы также обеспечиваем верхнюю границу индекса палитры декартовых произведений графов. В частности, мы показываем, что для любых графов $G$ и $H$ $\check{s}(G\square H)\leq \check{s}(G)\check{s}(H)$.

Рубрики