Что такое регрессия: Регрессия в психологической практике – польза или вред?

Что такое линейная регрессия?

Что такое линейная регрессия?

Это модель машинного обучения, основанная на предположении, что зависимость в наблюдаемых данных можно описать простой прямой. Оказывается, такой моделью можно объяснить большое количество явлений. Помимо этого линейная регрессия хорошо изучена, имеет ряд полезных теоретических свойств, и ввиду своей простоты легко поддаётся интерпретации.

Линейная… регрессия… – всё по порядку

Одна из главных задач машинного обучения – выявить закономерность между наблюдаемыми переменными (их также называют регрессорами, признаками) и целевой. Например, по дозировке препарата и температуре пациента нужно спрогнозировать его давление (наблюдаемые переменные – дозировка и температура, целевая – давление), по дню месяца и влажности воздуха (наблюдаемые переменные)  – температуру воздуха (целевая переменная).

Задача восстановления зависимости между такими парами переменных называется регрессией (regressio — обратное движение, отход).

Зависимости между наблюдаемыми и целевой переменными могут быть любыми, в том числе сколь угодно сложными. Поэтому будем подбирать модель, которая по значениям наблюдаемых переменных будет выдавать значение целевой переменной, “близкое” к истинному, из ограниченного конкретного набора моделей Одним из наиболее простых классов (наборов) моделей является класс линейных моделей. Модель в машинном обучении – это математическая функция, которая (в контексте задачи регрессии) получает на вход значения наблюдаемых переменных, преобразует их, комбинирует и выдаёт значение целевой переменной. 

Линейная модель – модель, которая выражается линейной функцией. Слово “линейная” в названии объясняется тем, что графиком такой функции является прямая. В общем виде линейные функции одной переменной записываются так: h(x) = k*x + b, где k и b – произвольные числа. Пример линейной зависимости – зависимость расстояния от времени (s = v*t).

График линейной функции одной переменной

В случае, когда имеются несколько наблюдаемых переменных, линейные функции имеют вид: h(x_1, x_2, …, x_N) = a_0 + a_1*x_1 + a_2*x_2 + … + a_N*x_N, где a_0, a_1, …, a_N – также произвольные числа. График этой функции – тоже прямая, но уже в N-мерном пространстве.

График линейной функции двух переменных

Теперь соберём всё вместе:

Линейная регрессия – моделирование зависимости между наблюдаемыми и целевыми переменными с помощью линейных функций.

Есть модель, есть данные – пары, состоящие из наборов x-ов (наблюдаемых переменных) и соответствующих y (целевых переменных), последнее, что осталось – подобрать оптимальные коэффициенты, которые стоят перед переменными (например, числа k и b в случае одной наблюдаемой переменной).  Оптимальность коэффициентов определяется функцией потерь, которая отображает, насколько прогнозы модели близки к целевым переменным. Их подбор называется

обучением модели и производится специальными алгоритмами оптимизации (например, градиентным спуском). Эти коэффициенты называют весами модели, поскольку по значению коэффициента можно понять, насколько значима наблюдаемая переменная при нём (вспомним, что предсказание равно сумме произведений коэффициентов и соответствующих наблюдаемых переменных): чем больше коэффициент, тем больший вес имеет наблюдаемая переменная при нём, и наоборот, если коэффициент близок к 0, то переменная при нём практически никак не влияет на прогноз. Поэтому говорят, что линейная регрессия легко интерпретируема, то есть по модели легко можно, какие наблюдаемые переменные важны, а какие – нет.

После этапа обучения модель готова для использования – в полученную функцию (модель) нужно подставить интересующий набор x-ов и вычислить её значение, которое и будет являться прогнозом.

Пример

Представьте, что вы предприниматель, который хочет прорекламировать свой продукт. В рамках рекламной кампании в разные месяцы вы тратите разные суммы денег и получаете соответственно разные показатели прироста выручки. В конце очередного месяца вы планируете бюджет на следующий и задаётесь вопросом: “Даст ли увеличение затрат на рекламу больший прирост выручки?” Зная ответ на этот вопрос, вы сможете более эффективно распределять ваши средства.

Наблюдаемой переменной в этом случае является бюджет на рекламу, то есть данные, которые известны, а целевой переменной – прирост выручки по окончании месяца, то есть данные, которые неизвестны и которые вы хотите спрогнозировать. Пусть x_1, x_2, …, x_10 – количество денег, которые были потрачены на рекламу в прошлых 10 месяцах, а y_1, y_2, …, y_10 – прирост выручки, зафиксированный в конце соответствующего месяца. Если предположить, что зависимость между x и y – линейная, то можно воспользоваться линейной регрессией.

Визуализация модели и собранных данных

Если предположение верно, то обучив линейную регрессию, можно довольно точно описать данные. Как можно видеть на графике выше, все красные точки (пары бюджет-прирост) расположены близко к синей прямой (модели). То, что точки не лежат на прямой, объясняется шумом в обучающих данных, который может быть вызван ошибками при измерениях или сборе данных.

Применимость

Взглянув на график выше, вы можете сделать вывод, что чем больше денег тратится на рекламу, тем больший прирост выручки вы получаете. Однако такое заключение довольно наивно и полагаться на него кажется сомнительной идеей. С большой долей вероятности, начиная с какого-то момента, увеличение трат не будет приводить к значимому приросту.

Собрав ещё немного данных, вы заново строите график и получаете следующее:

Визуализация модели и дополненных данных

Действительно, модель сильно ошибается на новых данных – зелёные точки очень далеки от синей прямой. Более того, можно увидеть, что простой прямой недостаточно, чтобы объяснить все имеющиеся данные: невозможно провести прямую через красные и зелёные точки. В таких случаях говорят, что модель недостаточно выразительна. Данный пример иллюстрирует, что линейная регрессия не всегда применима. Однако существует множество явлений (и довольно сложных), которые ею можно описать. Например, линейная регрессия является фундаментальной моделью в экономике, её также часто применяют в медицине. Для сложных, нелинейных зависимостей используют в том числе и обобщённые линейные модели.

Что почитать

• Градиентный спуск
• Обобщённые линейные модели

Теги:глоссарий, линейная регрессия

Регрессия (Regression) · Loginom Wiki

В теории вероятности и математической статистике это зависимость математического ожидания случайной величины от одной или нескольких других случайных величин.

В отличие от чисто функциональной зависимости y=f(x), где каждому значению независимой переменной x соответствует единственное значение зависимой переменной y, регрессионная зависимость предполагает, что каждому значению переменной x могут соответствовать различные значения y, обусловленные случайной природой зависимости.

Если некоторому значению величины xi соответствует набор значений величин yi1,yi2,…,yin, то зависимость средних арифметических:

¯yi=yi1+yi2+⋯+yinni

от xi и является регрессией в статистическом понимании данного термина.

Типичным примером регрессионной зависимости может быть зависимость между ростом и весом человека. В большинстве случае вес пропорционален росту, но фактически большой рост не всегда означает большой вес. Иными словами, у роста, например, 175 см. может наблюдаться несколько значений веса, скажем 69, 78 и 86 кг. Тогда зависимость между ростом и средним значением указанных весов будет являться регрессионной.

Изучение регрессии в теории вероятностей основано на том, что случайные величины X и Y, имеющие совместное распределение вероятностей, связаны статистической зависимостью: при каждом фиксированном значении X=x, величина Y является случайной величиной с определённым (зависящим от значения x) условным распределением вероятностей.

Регрессия величины Y по величине X определяется условным математическим ожиданием Y, вычисленным при условии, что X=x:E(Y|x)=u(x).

Уравнение y=u(x) называется уравнением регрессии, а соответствующий график — линией регрессии Y по X. Точность, с которой уравнение Y по X отражает изменение Y в среднем при изменении x, измеряется условной дисперсией D величины Y, вычисленной для каждого значения X=x:D(Y|x)=D(x).

Если D(x)=0 при всех значениях x, то можно достоверно утверждать, что Y и X связаны строгой функциональной зависимостью Y=u(X). Если D(x)=0 при всех значениях x и u(x) не зависит от x, то говорят, что регрессионная зависимость Y по X отсутствует.

Линии регрессии обладают следующим замечательным свойством: среди всех действительных функций f(X) минимум математического ожидания E[Y—f(X)]2 достигается для функции f(x)=u(X).

Это означает, что регрессия Y по X даёт наилучшее в указанном смысле представление величины Y по величине X. Это свойство позволяет использовать регрессию для предсказания величины Y по X.

Иными словами, если значение Y непосредственно не наблюдается и эксперимент позволяет регистрировать только X, то в качестве прогнозируемого значения Y можно использовать величину Y=u(X).

Наиболее простым является случай, когда регрессионная зависимость Y по X линейна, т.е. E(Y|x)=b0+b1x, где b0 и b1 – коэффициенты регрессии. На практике обычно коэффициенты регрессии в уравнении y=u(x) неизвестны, и их оценивают по наблюдаемым данным.

Регрессия широко используется в аналитических технологиях при решении различных бизнес-задач, таких как прогнозирование (продаж, курсов валют и акций), оценивание различных бизнес-показателей по наблюдаемым значениям других показателей (скоринг), выявление зависимостей между показателями и т.д.

В Loginom существует специализированный обработчик логистическая регрессия, с помощью которого можно оценивать вероятность того, что событие наступит для конкретного объекта испытания (больной/здоровый, возврат кредита/дефолт и т.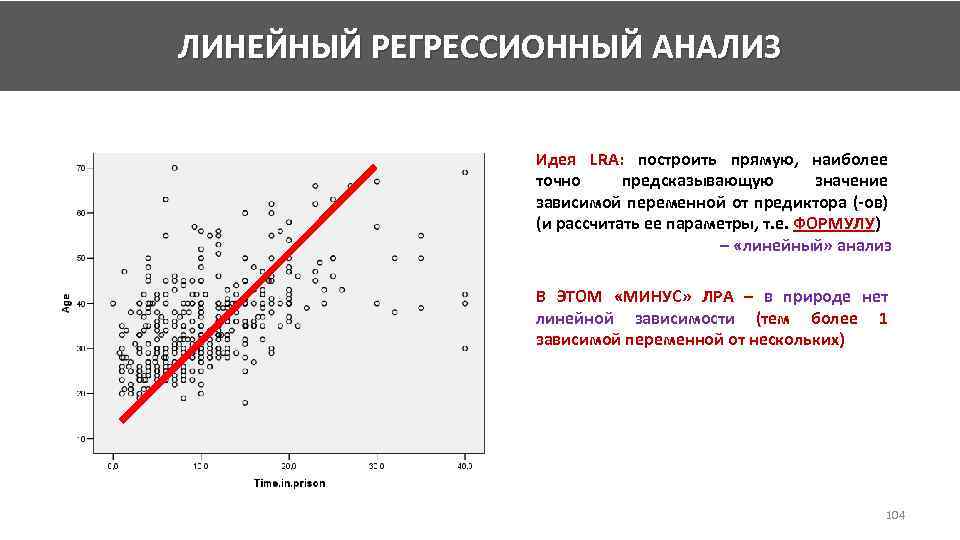

д.). И обработчик линейная регрессия, который может использоваться для решения различных задач, например, прогнозирования и численного предсказания.

Логистическая регрессия является традиционным статистическим инструментом для расчета коэффициентов (баллов) скоринговой карты на основе накопленной кредитной истории. Подробнее в статье «Логистическая регрессия и ROC-анализ — математический аппарат».

О прикладном применении логистической регрессии в двух областях — диагностика заболеваний и оценка кредитоспособности физических лиц узнайте в статье «Применение логистической регрессии в медицине и скоринге».

Что такое нелинейная регрессия? Сравнение с линейной регрессией

К

Уилл Кентон

Полная биография

Уилл Кентон — эксперт в области экономики и инвестиционного законодательства. Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.

Узнайте о нашем редакционная политика

Обновлено 29 мая, 2022

Рассмотрено

Сомер Андерсон

Рассмотрено Сомер Андерсон

Полная биография

​Сомер Дж. Андерсон является дипломированным бухгалтером, доктором бухгалтерского учета и профессором бухгалтерского учета и финансов, который работает в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.

Узнайте о нашем Совет по финансовому обзору

Нелинейная регрессия — это форма регрессионного анализа, в которой данные подгоняются к модели, а затем выражаются в виде математической функции. Простая линейная регрессия связывает две переменные (X и Y) прямой линией (y = mx + b), а нелинейная регрессия связывает две переменные нелинейной (кривой) связью.

Цель модели — сделать сумму квадратов как можно меньше. Сумма квадратов — это мера, которая отслеживает, насколько сильно наблюдения Y отличаются от нелинейной (кривой) функции, используемой для прогнозирования Y.

Он вычисляется путем нахождения разницы между подобранной нелинейной функцией и каждой точкой Y данных в наборе. Затем каждая из этих разностей возводится в квадрат. Наконец, все квадраты цифр складываются вместе. Чем меньше сумма этих квадратов, тем лучше функция соответствует точкам данных в наборе. Нелинейная регрессия использует логарифмические функции, тригонометрические функции, экспоненциальные функции, степенные функции, кривые Лоренца, функции Гаусса и другие методы подбора.

Ключевые выводы

• Как линейная, так и нелинейная регрессия предсказывают отклики Y от переменной (или переменных) X.
• Нелинейная регрессия представляет собой кривую функцию переменной X (или переменных), которая используется для прогнозирования переменной Y.
• Нелинейная регрессия может показывать прогноз роста населения с течением времени.

Моделирование нелинейной регрессии похоже на моделирование линейной регрессии в том смысле, что оба стремятся графически отследить конкретный ответ от набора переменных. Нелинейные модели сложнее разработать, чем линейные модели, потому что функция создается посредством серии приближений (итераций), которые могут возникать в результате проб и ошибок. Математики используют несколько установленных методов, таких как метод Гаусса-Ньютона и метод Левенберга-Марквардта.

Часто модели регрессии, которые на первый взгляд кажутся нелинейными, на самом деле являются линейными. Процедуру оценки кривой можно использовать для определения характера функциональных взаимосвязей в ваших данных, чтобы вы могли выбрать правильную модель регрессии, линейную или нелинейную.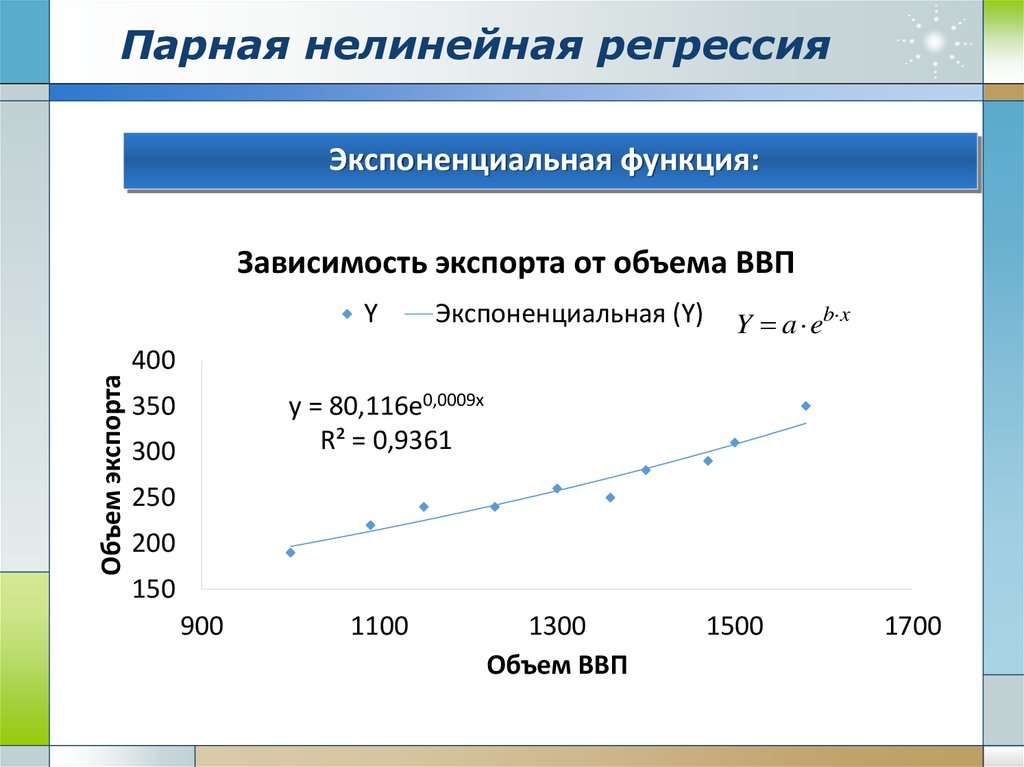 Модели линейной регрессии, хотя они обычно образуют прямую линию, также могут образовывать кривые, в зависимости от формы уравнения линейной регрессии. Точно так же можно использовать алгебру для преобразования нелинейного уравнения, чтобы оно имитировало линейное уравнение — такое нелинейное уравнение называется «внутренне линейным».

Линейная регрессия связывает две переменные прямой линией; нелинейная регрессия связывает переменные с помощью кривой.

Одним из примеров использования нелинейной регрессии является прогнозирование роста населения с течением времени. Диаграмма рассеяния изменения данных о населении с течением времени показывает, что связь между временем и ростом населения, по-видимому, существует, но это нелинейная связь, требующая использования модели нелинейной регрессии. Логистическая модель роста населения может предоставить оценки населения за периоды, которые не были измерены, и прогнозы будущего роста населения.

Независимые и зависимые переменные, используемые в нелинейной регрессии, должны быть количественными. Категориальные переменные, такие как регион проживания или религия, должны быть закодированы как бинарные переменные или другие типы количественных переменных.

Чтобы получить точные результаты от модели нелинейной регрессии, вы должны убедиться, что указанная вами функция точно описывает взаимосвязь между независимыми и зависимыми переменными. Также необходимы хорошие начальные значения. Плохие начальные значения могут привести к тому, что модель не будет сходиться, или решение будет оптимальным только локально, а не глобально, даже если вы указали правильную функциональную форму для модели.

Источники статей

Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.

1. Университет Отаго, Новая Зеландия. «Нелинейный регрессионный анализ».

Множественная линейная регрессия (MLR) Определение, формула и пример

Что такое множественная линейная регрессия (MLR)?

Множественная линейная регрессия (MLR), также известная как множественная регрессия, представляет собой статистический метод, который использует несколько независимых переменных для прогнозирования результата переменной отклика. Целью множественной линейной регрессии является моделирование линейной зависимости между независимыми переменными и переменными отклика (зависимыми). По сути, множественная регрессия является расширением обычной регрессии методом наименьших квадратов (OLS), поскольку она включает более одной объясняющей переменной.

Ключевые выводы

• Множественная линейная регрессия (MLR), также известная как множественная регрессия, представляет собой статистический метод, использующий несколько независимых переменных для прогнозирования результата переменной отклика.
• Множественная регрессия — это расширение линейной (OLS) регрессии, в котором используется только одна независимая переменная.
• MLR широко используется в эконометрике и финансовых выводах.

Формула и расчет множественной линейной регрессии

 у я «=» β 0 + β 1 Икс я 1 + β 2 Икс я 2 + . . . + β п Икс я п + ϵ где, для я «=» н наблюдения: у я «=» зависимая переменная Икс я «=» пояснительные переменные β 0 «=» y-перехват (постоянный термин) β п «=» коэффициенты наклона для каждой независимой переменной ϵ «=» член ошибки модели (также известный как остатки) \begin{align}&y_i = \beta_0 + \beta _1 x_{i1} + \beta _2 x_{i2} + … + \beta _p x_{ip} + \epsilon\\&\textbf{где, для} i = n \textbf{ наблюдения:}\\&y_i=\text{зависимая переменная}\\&x_i=\text{независимые переменные}\\&\beta_0=\text{y-перехват (постоянный член)}\\&\ beta_p=\text{коэффициенты наклона для каждой независимой переменной}\\&\epsilon=\text{член ошибки модели (также известный как остатки)}\end{выровнено} ​yi​=β0​+β1​xi1​+β2​xi2​+. ..+βp​xip​+ϵ, где для i=n наблюдений: yi​=зависимая переменнаяxi​=объясняющие переменныеβ0​=y-отрезок (постоянная термин)βp​= коэффициенты наклона для каждой объясняющей переменнойε= член ошибки модели (также известный как остатки)​

О чем может рассказать множественная линейная регрессия

Простая линейная регрессия — это функция, которая позволяет аналитику или статистику делать прогнозы относительно одной переменной на основе информации, известной о другой переменной. Линейную регрессию можно использовать только при наличии двух непрерывных переменных — независимой переменной и зависимой переменной. Независимая переменная — это параметр, который используется для вычисления зависимой переменной или результата. Модель множественной регрессии распространяется на несколько независимых переменных.

Модель множественной регрессии основана на следующих предположениях:

• Существует линейная зависимость между зависимыми переменными и независимыми переменными
• Независимые переменные не слишком сильно коррелируют друг с другом
• y _i наблюдений выбираются независимо и случайным образом из совокупности
• Остатки должны быть нормально распределены со средним значением 0 и дисперсией σ

Коэффициент детерминации (R-квадрат) — это статистическая метрика, которая используется для измерения того, какая часть вариации результата может быть объяснена вариацией независимых переменных. R ² всегда увеличивается по мере того, как к модели MLR добавляется больше предикторов, даже если предикторы могут быть не связаны с переменной результата.

Таким образом, R ² сам по себе не может использоваться для определения того, какие предикторы следует включить в модель, а какие следует исключить. р ² может принимать значения только от 0 до 1, где 0 означает, что результат не может быть предсказан ни одной из независимых переменных, а 1 означает, что результат может быть предсказан без ошибок по независимым переменным.

При интерпретации результатов множественной регрессии бета-коэффициенты действительны при условии, что все остальные переменные остаются постоянными («все остальные равны»). Выходные данные множественной регрессии могут отображаться горизонтально в виде уравнения или вертикально в виде таблицы.

Пример использования множественной линейной регрессии

Например, аналитик может захотеть узнать, как движение рынка влияет на цену ExxonMobil (XOM). В этом случае их линейное уравнение будет иметь значение индекса S&P 500 в качестве независимой переменной, или предиктора, и цену XOM в качестве зависимой переменной.

На самом деле исход события предсказывают многочисленные факторы. Движение цен ExxonMobil, например, зависит не только от общего состояния рынка. Другие предикторы, такие как цена на нефть, процентные ставки и динамика цен на нефтяные фьючерсы, могут влиять на цену XOM и цены акций других нефтяных компаний. Чтобы понять взаимосвязь, в которой присутствует более двух переменных, используется множественная линейная регрессия.

Множественная линейная регрессия (MLR) используется для определения математической взаимосвязи между несколькими случайными величинами. Другими словами, MLR исследует, как несколько независимых переменных связаны с одной зависимой переменной. Как только каждый из независимых факторов определен для прогнозирования зависимой переменной, информация о нескольких переменных может быть использована для создания точного прогноза уровня их влияния на результирующую переменную. Модель создает зависимость в виде прямой линии (линейной), которая наилучшим образом соответствует всем отдельным точкам данных.

Ссылаясь на приведенное выше уравнение MLR, в нашем примере:

• y _i = зависимая переменная — цена XOM
• x _i1 = процентные ставки
• x _i2 = цена на нефть
• x _i3 = значение индекса S&P 500
• x _i4 = цена фьючерса на нефть
• B ₀ = пересечение оси Y в нулевое время
• B ₁ = коэффициент регрессии, который измеряет единичное изменение зависимой переменной, когда x _i1 changes — изменение цены XOM при изменении процентных ставок
• B ₂ = значение коэффициента, измеряющего единичное изменение зависимой переменной при изменении x _i2 — изменение цены XOM при изменении цен на нефть

Оценки методом наименьших квадратов — B ₀ , B ₁ , B ₂ … B _p — обычно вычисляются с помощью статистического программного обеспечения. Сколько переменных может быть включено в регрессионную модель, в которой каждая независимая переменная дифференцируется числом — 1,2, 3, 4…p. Модель множественной регрессии позволяет аналитику прогнозировать результат на основе информации, предоставленной несколькими независимыми переменными.

Тем не менее, модель не всегда идеально точна, поскольку каждая точка данных может немного отличаться от результата, предсказанного моделью. Остаточное значение E, представляющее собой разницу между фактическим результатом и прогнозируемым результатом, включено в модель для учета таких незначительных отклонений.

Предположим, что мы запускаем нашу модель ценовой регрессии XOM через программное обеспечение для расчета статистики, которое возвращает следующий результат:

Изображение Сабрины Цзян © Investopedia 2020

Аналитик интерпретировал бы этот результат как означающий, что если другие переменные остаются постоянными, цена XOM увеличится на 7,8%, если цена на нефть на рынках увеличится на 1%. Модель также показывает, что цена XOM снизится на 1,5% после повышения процентных ставок на 1%. р ² указывает, что 86,5% колебаний курса акций Exxon Mobil можно объяснить изменениями процентной ставки, цен на нефть, нефтяных фьючерсов и индекса S&P 500.

Разница между линейной и множественной регрессией

Регрессия с помощью обычных линейных квадратов (OLS) сравнивает реакцию зависимой переменной на изменение некоторых независимых переменных. Однако зависимая переменная редко объясняется только одной переменной. В этом случае аналитик использует множественную регрессию, которая пытается объяснить зависимую переменную, используя более одной независимой переменной. Множественные регрессии могут быть линейными и нелинейными.

Множественные регрессии основаны на предположении, что между зависимыми и независимыми переменными существует линейная связь. Он также предполагает отсутствие значительной корреляции между независимыми переменными.

Что делает множественную регрессию множественной?

Множественная регрессия рассматривает влияние более чем одной объясняющей переменной на некоторый интересующий результат.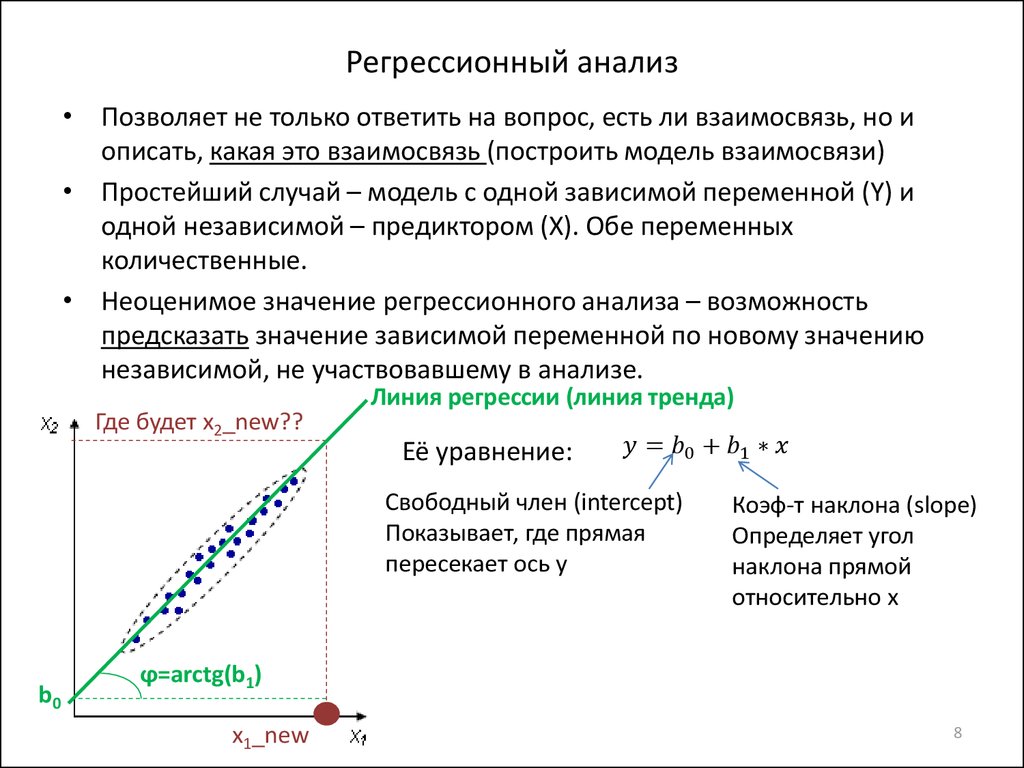 Он оценивает относительное влияние этих объясняющих или независимых переменных на зависимую переменную, когда все остальные переменные в модели остаются постоянными.

Зачем использовать множественную регрессию вместо простой регрессии МНК?

Зависимая переменная редко объясняется только одной переменной. В таких случаях аналитик использует множественную регрессию, которая пытается объяснить зависимую переменную, используя более одной независимой переменной. Модель, однако, предполагает, что между независимыми переменными нет серьезных корреляций.

Можно ли выполнить множественную регрессию вручную?

Маловероятно, поскольку модели множественной регрессии сложны и становятся еще более сложными, когда в модель включается больше переменных или когда увеличивается объем данных для анализа. Для выполнения множественной регрессии вам, вероятно, потребуется использовать специализированное статистическое программное обеспечение или функции в таких программах, как Excel.

Что означает линейность множественной регрессии?

При множественной линейной регрессии модель вычисляет линию наилучшего соответствия, которая минимизирует дисперсии каждой из включенных переменных по отношению к зависимой переменной. Поскольку он соответствует линии, это линейная модель. Существуют также модели нелинейной регрессии с несколькими переменными, такие как логистическая регрессия, квадратичная регрессия и пробит-модели.

Как модели множественной регрессии используются в финансах?

Любая эконометрическая модель, учитывающая более одной переменной, может быть кратной. Факторные модели сравнивают два или более факторов для анализа взаимосвязей между переменными и результирующей производительностью. Фама и французский трехфакторный мод — это такая модель, которая расширяет модель ценообразования капитальных активов (CAPM), добавляя факторы риска размера и риска стоимости к фактору рыночного риска в CAPM (которая сама по себе является регрессионной моделью).