Единицами формальной логики являются: Логика формальная – Гуманитарный портал

Логика формальная – Гуманитарный портал

Формальная логика — это широкая область логических исследований, изучающая идеализированные рассуждения и их системы посредством логических исчислений на основе метода формализации (см. Формализация). Метод формализации подразумевает, что логические рассуждения изучаются в отвлечении от их конкретного содержания; при этом сами логические рассуждения формулируются на некотором точном (формализованном) языке при помощи специального аппарата символов (см. Язык формализованный). Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет. Формализованный язык позволяет избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании рассуждений традиционная логика (см.  Логика), развивавшаяся в рамках философии (см. Философия). Методы формализации дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Определение «формальная логика» было введено И. Кантом с намерением подчеркнуть её ведущую особенность в подходе к изучаемым объектам и отграничить её тем самым от других возможных логик. Способность человеческого мышления к конструктивной языковой деятельности порождает возможность оперировать следующими логическими формами: понятиями, суждениями, умозаключениями, которые представляют собой пространство логических исследований. В качестве наиболее сложного вида логических форм иногда выделяют и теории (см. Теория). Часто эту последовательность воспринимают как некую структурную иерархию. Понятие объявляется наиболее простой из форм мышления, суждение представляется как система понятий, умозаключение как система суждений, а теория как система умозаключений. Эта иерархия недостаточно ясна, и её обоснования порой легко подвергаются критике, однако она часто используется в качестве удобной схемы изложения предметной области формальной логики, что, собственно, подкрепляется многовековой традицией преподавания этой дисциплины. Эти логические формы и лежащие в основе операций с ними законы и принципы, то есть так называемый логический аппарат, составляют основную область исследований формальной логики, а выработка самих эффективных логических аппаратов — её основную цель. В связи с различием логических форм выделяют два основных направления формальной логики: Концептуальный анализ, то есть исследование процедур определения языковых терминов (понятий) и формулировка принципов отношений между ними. Это направление включает в себя широкий спектр теорий, от классификации родо-видовых отношений до конструирования концептуальных «полей». Теория вывода, то есть анализ рассуждений, формализация законов и принципов связи высказываний (суждений) в умозаключениях. Здесь формулируются способы корректного получения суждения, называющегося заключением, из некоторых исходных суждений, называющихся посылками, посредством рассуждения. В рамках теории вывода выделяют логику, рассматривающую дедуктивные рассуждения (см. Дедукция), то есть определённые способы доказательств, и логику, занимающуюся правдоподобными рассуждениями: индукция, аналогия и другие. Кроме того, формальная логика затрагивает и такие вопросы, например, как формализация содержательных теорий, проблема смысла и значения, логические ошибки и парадоксы и многие другие. Самостоятельное выделение этих вопросов достаточно условно, все они погружаются в проблематику основных направлений и тесно переплетены друг с другом. Логика возникла в Древней Греции в рамках философии (см. Философия). История её развития насчитывает около двух с половиной тысячелетий и делится на два основных периода: Традиционная формальная логика (IV век до новой эры — середина XIX века). В развитии традиционной логики, в свою очередь, выделяются три периода: Античная логика (V век до новой эры — середина V века). Схоластическая (Средневековая) логика (середина V века — XV век). Логика Нового времени (XV–XVIII века). Современная (символическая, или математическая) логика (с середины XIX века). Античную и схоластическую логику сейчас объединяет общее название «традиционной логики». Она, кроме историко-философского, по-прежнему имеет важное пропедевтическое значение и, будучи своеобразным стержнем интеллектуальной культуры человека, признается неотъемлемым элементом широкого гуманитарного образования. Новый этап в развитии логики (со второй половины XIX века) был связан с её формализацией и последующей математизацией. В связи с этим новая логика получила название математической (или символической) логики (см. Логика символическая, Логика математическая). Современные логические системы в большинстве своём полностью опираются на формальные математические методы и являются логически интерпретированными исчислениями. Основные разделы математической логики — классические логика высказываний (см. Логика высказываний) и логика предикатов (см. Логика предикатов). Широкое распространение получили исследования модальной логики (см. Логика модальная). Системы логики, отрицающие те или иные фундаментальные законы логики, образовали спектр неклассических логик (см. Логики неклассические). Значительное число различных систем формальной логики обусловлено широкой сферой их приложения. Теоретическая математика, пожалуй, потеряла абсолютно лидирующее место в этом смысле, поскольку не менее интересные приложения осуществляются в областях теоретической физики (квантовая логика), прикладной математики (вычислительная математика и теория алгоритмов), информатики (компьютерные технологии, сети, программирование и исследования в области искусственного интеллекта), гуманитарного знания (лингвистика, юриспруденция, этика) и других. Важным разделом современной формальной логики является металогика (см.  Металогика), в которой исследуются различные проблемы, относящиеся к логическим теориям. Основными здесь являются вопросы о тех свойствах, которыми обладают логические теории: о непротиворечивости, полноте, наличии разрешающих процедур, независимости исходных дедуктивных принципов, а также о различных отношениях между теориями и так далее. В этом смысле металогика является своего рода саморефлексией логики относительно своих построений. Все метатеоретические исследования проводятся на специальном метаязыке, в качестве которого используется естественный язык, обогащённый специальной терминологией и метатеоретическими дедуктивными средствами.

Асмус В. Ф. Логика. 2-е издание. — М., 2001. Бирюков Б. В. Жар холодных чисел и пафос бесстрастной логики. Формализация мышления от античных времён до эпохи кибернетики. — М., 1985. Бочаров В. А., Маркин В. И. Введение в логику. — М., 2008. Гилберт Д., Бернайс П. Основания математики. Логические исчисления и формализация арифметики. — М., 1979. Гладкий А. В. Введение в современную логику. — М., 2001. Непейвода Н. Н. Прикладная логика. 2-е издание, испр. и доп. — Новосибирск, 2000. Смирнов В. А. Формальный вывод и логические исчисления. — М., 1972. Смирнова Е. Д. Формализованные языки и проблемы логической семантики. — М., 1982. Справочная книга по математической логике. В 4-х частях. Ред. Дж. Барвайс. — М., 1982–1983. Тарский А. Введение в логику и методологию дедуктивных наук. — М., 1948 (2-е издание в 2000). Формальная логика. Ред. И. Я. Чупахин, И. Н. Бродский. — Л., 1977. Фрейденталь Х. Язык логики. — М., 1969. Щедровицкий Г. П. О различии исходных понятий «формальной» и «содержательной» логик. — Методология и логика наук. Учёные записки Томского университета. № 41. — Томск, 1962.

Формальная логика — Психологос

01 октября 2022 г., 21:28

Формальная логика — наука, изучающая формы мысли (понятия, суждения, умозаключения, доказательства) со стороны их логической структуры, отвлекаясь от конкретного содержания мыслей. Это конструирование и исследование правил преобразования высказываний, сохраняющих их истинностное значение безотносительно к содержанию входящих в эти высказывания понятий.

Формальная логика и мышление

Предмет формальной логики — это не все мышление, а только одна его сторона — логические формы мышления. Формальная логика исследует как бы готовые, имеющиеся, уже возникшие мысли — понятия, суждения и т.д. — и устанавливает определенные соотношения (формулы) между ними. Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития этих мыслей — понятий, суждений, умозаключений.

Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития тех или иных мыслей. Она полностью отвлекается, в частности, и от взаимосвязи мышления с чувственным познанием. Иначе говоря, она вовсе не исследует, в отличие от психологии, как конкретно возникает и обогащается содержание нашего мышления на основе ощущений, восприятий и представлений. В логических формулах, например в силлогизме, соотносятся друг с другом уже как бы застывшие, законченные, полностью четко и до конца сформулированные мысли, т.

е. результаты, готовые продукты мышления.

• Мышление

Комментарии (3):

Гость, 08 июня 2012 г., 13:12

Спасибо за статью. Очень четко и грамотно дали определение формальной логике. Хотелось бы, чтобы на этом сайте немного больше шире рассматривали такие темы как силлогизм, алогизм и другие составляющие виды этих тем.

1

ответ

Гость, 07 февраля 2020 г., 10:50

Мне даже интересно, какое мышление бывает не логическим?

1

ответ

Гость, 17 июня 2021 г., 18:12

У аутистов диалектическая логика.

Материалы по теме:

01 окт. 2022 г.

Логика

Логика — философская наука, изучающая логические формы человеческого мышления и законы, которым подчиняется мышление. Логика изучает не конкретное содержание действительности, а мысли о ней, их структуру, то, что является общим для мыслей данного типа, независимо от их конкретного содержания.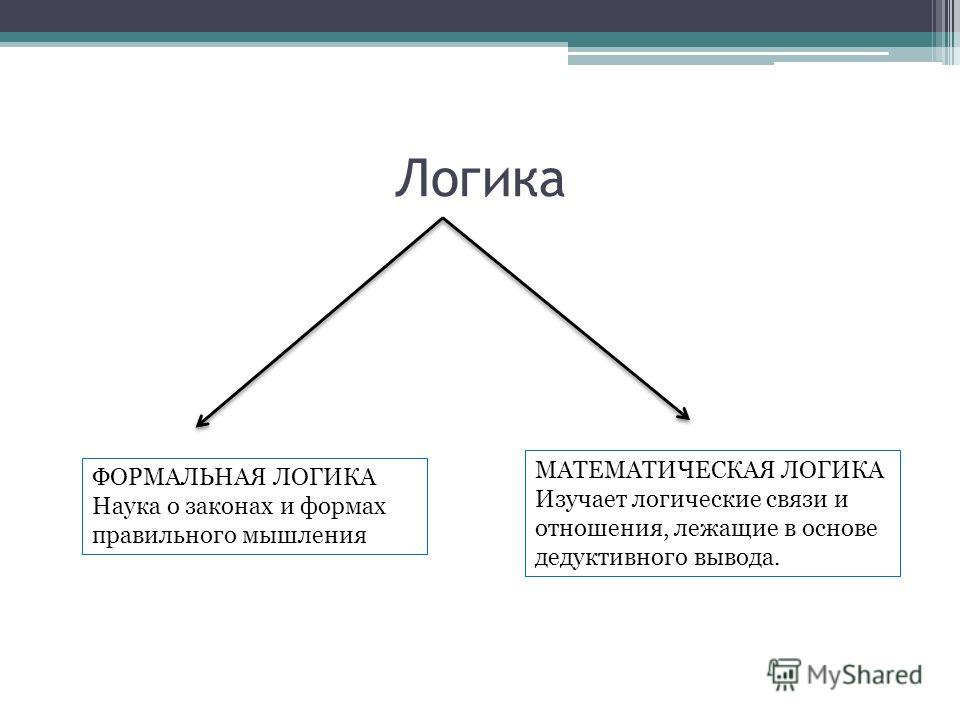 Поэтому при изучении логики для того, чтобы понять сущность процесса мышления, специфическое содержание форм и законов, нужно уметь обобщать конкретные рассуждения, уметь оперировать получаемыми формулами и схемами.

4Подробнее

01 янв. 2006 г.

Мышление

Мышление нередко определяют как способность к решению новых, экстренно возникающих задач в ситуациях, где прежние, уже известные решения не срабатывают. Творческое и конструктивное, развитое мышление действительно способно справляться с такими задачами, но это не значит, что если кто-то не нашел творческого решения в новой для него ситуации, у него мышление отсутствовало. В своих простейших формах мышление, как процесс, это всего лишь переработка информации в потоке течения мыслей, образов и ощущений.

7Подробнее

01 окт. 2022 г.

Мысль

Мысль — упакованный смысл, переданный сознанию (всплывший в сознании) в процессе мышления. Мысль (смысл?) — интересная, имеющая значение связь понятий, связь образа цели и элементов ситуации. «Я понял, как это связано!» «Я понял, что можно сделать!»

6Подробнее

01 окт. 2022 г.

Понятие

Понятие — то, что имеет определение, определенный смысл. Это представление, в котором смысл задан (построен) четким, определенным образом. Смысл понятия (образ понятия) имеет границы и правила его использования.

0Подробнее

01 окт. 2022 г.

Суждение

Суждение — высказывание; умственный акт, выражающий отношение говорящего к содержанию высказываемой мысли. Вынося суждение, мы создаем те опоры, которые считаем соответствующими действительности и потому позволяющими двигаться к истине. Суждение — это отражение связей между предметами и явлениями действительности или между свойствами и признаками. Например, суждение «Металлы при нагревании расширяются», выражает связь между изменениями температуры и объемом металлов. Устанавливая таким образом различные связи и отношения между понятиями, суждения являются высказываниями чего-то о чем-то.

0Подробнее

01 окт. 2022 г.

Теория познания

0Подробнее

01 окт. 2022 г.

Умозаключение — элементарная частица рассуждения

Умозаключение — мыслительная операция, состоящая в получении нового вывода из нескольких суждений. Люди используют умозаключения, когда нужно в чем-то разобраться: вывести следствие, осуществить доказательство, систематизировать знания, проверить гипотезу… Разумное мышление, в отличие от бессвязного или эмоционально заряженного потока мысли, состоит из рассуждений — сложных умственных конструкций. А рассуждения в свою очередь состоят и умозаключений — элементарных мыслительных операций.

2Подробнее

80-310/610 Формальная логика

80-310/610 Формальная логика

Осень 2018

Стив Авуди

12 турецких лир — 1:20

Бейкер Холл A53

9-12 шт.

Введение в формальную логику с приложениями к информатике. Темы включают индуктивно определенные структуры, синтаксис и семантику. логики первого порядка, полноты, компактности и Лёвенгейма-Скулема. теоремы. Дополнительные темы могут также включать определяемость, нестандартность модели арифметической, высшей, интуиционистской и модальной логики.

Предпосылки: либо 80-210, 80-211, 21-127, 15-251, либо согласие инструктор.

---

Новости

---

Информация о курсе

Лекции	TR 12-1:20, BH A53
Чтения	По вторникам в 18:00 в Baker Hall 150
Учебник	Логика и структура, Дирк ван Дален, Springer 2013. Доступно в кампусе по этой ссылке.
Кредит	9-12 шт.
Оценка	50 % домашнее задание, 25 % промежуточное задание, 25 % итоговое задание
Домашнее задание	Еженедельное домашнее задание размещается здесь по четвергам и должно быть выполнено в следующий четверг в классе. Домашнее задание должно быть сдано лично и не будет принято по электронной почте. Поздняя домашняя работа будет принята только в исключительных случаях.
Среднесрочная	Четверг, 11 октября, в классе. Закрытая книга, разрешен один двусторонний лист для заметок.
Окончательный	Четверг, 6 декабря, в классе. Закрытая книга, разрешен один двусторонний лист для заметок.
Темы	Индуктивные определения и доказательства, Синтаксис и семантика логики высказываний, Синтаксис и семантика логики первого порядка, Теория элементарных моделей, Высший порядок, интуиционистская и модальная логика.
Домашняя страница	http://www.andrew.cmu.edu/course/80-310-610/
Онлайн-обсуждение	piazza.com/cmu/fall2018/80310/дом

---

Преподавательский состав

		Офис	Часы работы	Телефон	Электронная почта
Профессор	Стив Авуди	БХ 135F	Ф 11-12	x8-8947	[email protected]
ТП	Мэтью Боуэн	ДХ 4301	Т 3:30-4:30	ххх	[email protected]
ТП	Зесен Цянь	ДХ 4301С	М 3-4	ххх	zesen. [email protected]
ТП	Эндрю Уоррен	ДХ 4301D	Ф 3-4	ххх	[email protected]
Админ. Ассистент	Мэри Грейс Джозеф	БХ 161Н		x8-9459	[email protected]

[email protected]
Стив Аводи

Философия 260: Продвинутая формальная логика

Философия 260: Продвинутая формальная логика Философия 260: Расширенный формальный Логика Осень 2000

Классные заметки

24.08.00

Есть шесть основных логических свойств и отношений, определенных для нас на стр. 24. Это ДЕДУКТИВНАЯ ДЕЙСТВИТЕЛЬНОСТЬ, ЛОГИЧЕСКАЯ СОСТОЯННОСТЬ, ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ, ЛОГИЧЕСКАЯ ИСТИНА, ЛОГИЧЕСКАЯ ЛОЖЬ И ЛОГИЧЕСКАЯ НЕОПРЕДЕЛЕННОСТЬ.

Определения этих терминов указывают на то, что каждый из них выражает общее Отношение истинности или свойство предложений или наборов предложений. Каждое определение апеллирует к понятию возможности, но это неприемлемо расплывчато. Формальное изучение логики пытается предоставить механизм для оценки предложения и наборы предложений для логических свойств и отношений путем придания строгого смысла понятию логической возможности.

Формальные системы:

Формальная система обязательно состоит из двух компонентов и третьего могут быть добавлены.

(1) Формальный язык, состоящий из

(а) словарный запас (набор символов)

(б) грамматика (набор правил для правильных выражений.)

(2) Правила трансформации (набор правил для работы с хорошо сформированными выражения языка).

(3) Семантическая схема (протокол интерпретации или присвоения значений к выражениям языка.)

Примечание: схема толкования не есть толкование, а только способ предоставления одного. Интерпретируемая формальная система иногда называется формальной теория . Одна точка зрения на научные теории состоит в том, что они интерпретируются формальные системы.

Логические и формальные системы:

Логики используют формальные системы для предоставления моделей для оценки логические свойства и отношения. Формальные логические системы предназначены для представлять только те черты естественного языка, которые логически релевантны (т. е. относящийся к оценке шести свойств и отношений.) Логическая система — это любая формальная система, которая может служить этой цели.

В Философии 160 (Формальная логика) вы познакомились с двумя такими логическими системы: сентенциальная логика и логика предикатов. Компоненты две системы были введены неофициально, и вы изучили методы участвует в использовании их для логической оценки.

Логика предложений:

Логика высказываний — это система, в которой предложения являются базовыми логическими единицы, и занимается последствиями того, как предложения соединенные вместе определенными видами соединительного выражения.

Язык SL :

Формальный язык системы сентенциальной логики называется SL . Это не сокращение от словесной логики. Это имя для первый компонент системы. Словарь SL включает символы, которые предназначены для моделирования логической роли отдельных предложений и символы, предназначенные для моделирования особого класса сентенциальных связок.

СОЮЗНОЕ СОЕДИНЕНИЕ ДЛЯ ПРЕДСТАВЛЕНИЯ — это любое выражение, используемое для образования сложных предложений. из других предложений.

Предложная связка используется ИСТИННО-ФУНКЦИОНАЛЬНО тогда и только тогда, когда составное предложение, которое оно генерирует, имеет истинностное значение, которое зависит от (является ли функция от) истинностных значений составного предложения (предложений), из которых образуется соединение.

SL использует заглавные буквы для моделирования предложений.

SL использует пять «истинно-функциональных связок». Эти смоделировать логическую роль многих сентенциальных связок естественного языка.

~     (называется тильда) моделирует логическую роль каждого выражения естественного языка с одинаковым функционировать как НЕ.

&    (называется амперсанд) моделирует логическую роль каждого выражения естественного языка с одинаковым функционировать как И.

Ú     (называется клин) моделирует логическую роль каждого выражения естественного языка с та же функция, что и ИЛИ.

É    (подкова) моделирует логическую роль каждого выражения естественного языка с одинаковым функционировать как ЕСЛИ.

º     (называется тройной bar) моделирует логическую роль каждого выражения на естественном языке с помощью та же функция, что и ЕСЛИ И ТОЛЬКО ЕСЛИ.

Логики-математики и ученые-компьютерщики знакомы с немного другой набор символов для этих связок:
Ø Ù Ú ® «

29.08.00

Формальный синтаксис SL .

Словарь и правила построения правильно построенных предложений SL находятся на стр. 62-63.

Мы используем метаязык (смесь английского языка и некоторых специальных символов) говорить о SL . Мы будем ссылаться на выражения SL с помощью кавычек (одинарных кавычек). Например. мы будем использовать это выражение

(А и Б)

ссылаться (т. е. говорить) на выражение SL

(А и Б)

Также нам потребуется металингвистических переменных . Мы будем использовать

П К Р

как переменные для SL предложений.

Протокол для демонстрации того, что данное выражение является SL предложение:

ШАГ 1: Установите, что все символы являются SL символами.

ШАГ 2: Определите все атомарные предложения. Это SL предложения по правилу 1.

ШАГ 3: Определите все сентенциальные компоненты одной связки. Состояние по каким правилам и каким предыдущим шагам они должны считаться SL фразы.

ШАГ 4. Продолжайте эту процедуру шаг за шагом для более крупных компонентов, пока достигается все рассматриваемое предложение.

  31.08.00

Семантическая схема для SL :

Семантическая схема задается путем определения двух компонентов:

1. Таблицы характеристической истинности для связок SL (стр. 67-8).

2. Концепция Присвоения Ценности Истинности (TVA, стр. 68).

Вместе эти компоненты дают нам основу для присвоения значений истинности ко всем предложениям СЛ .

Таблица истинности — это таблица, содержащая значение истинности SL предложение по любому заданному TVA.

05.09.00

Свойства и отношения TF:

Свойства и отношения TF являются формальными аналогами неформальных логические свойства и отношения, определенные в глоссарии на стр. 24.

Они приведены в глоссарии на стр. 100-1.

Новая логическая концепция — следствие:

Набор из SL предложений можно сказать ПРАВДА-ФУНКЦИОНАЛЬНО ПОСЛЕДУЕТ приговор SL . Это означает, что нет TVA на что члены первого все истинны, а последний ложен.

Сокращено так:

Г |— П

На странице 100 есть двенадцать элементарных предложений метатеории, чьи доказательства зависят от определений свойств и отношений TF и на деталях семантической схемы. Это отличные упражнения.

07.09.00

Обзор SD .

12.09.00

Свойства SD (см. глоссарий на стр. 210).

Набор упражнений 15 на странице 200 содержит три важных положения метатеории. доказательства которых зависят от определений свойств SD и TF. Опять же, это отличные упражнения.

14. 09.00

ПЕРВОЕ ИСПЫТАНИЕ

19.09.00

Основная цель этой части курса:

Показать, что SD -свойства и отношения совпадают с TF-свойства и отношения. т.е. показать, что то, что мы получаем в SD соответствует нашим намерениям, учитывая схему интерпретацию, которую мы выбрали.

Мы докажем, что каждый вывод SD соответствует следствие TF и ​​наоборот. Мы можем выразить это следующим образом:

Где G — набор из SL предложений, а P — SL предложение, G |— P тогда и только тогда, когда G |= P. Мы также докажем один результат чисто семантической метатеории, что SL связки адекватны для представления каждой возможной функции истинности — и один чисто синтаксический результат метатеории, что SD нет допускать противоречивые последствия.

Метод метатеоретического доказательства:

Наши доказательства метатеории будут несколько неформальными. Мы будем использовать метод доказательства, основанного на принципе, родственном математическому индукция.

Слабый принцип математической индукции : Если 1 имеет данное свойство F, и для любого натурального n, если n имеет F, то n + 1 имеет F, то все положительные целые числа имеют F.

Схема аргумента, основанная на этом принципе

        1 имеет F
        Если n имеет F, то n + 1 имеет F
        Каждое натуральное число имеет Ф
 

Сильный принцип математической индукции : Если при любом положительном целое число до n включительно обладает некоторым свойством F, то n + 1 имеет F, то все положительные целые числа имеют F.

Схема аргумента, основанная на этом принципе

        Если каждый m меньше или равное n имеет F, то n + 1 имеет F
        Каждое натуральное число имеет Ф

Гибридный принцип для наших доказательств метатеории:

Принцип доказательства по математической индукции : Если первый член некоторой последовательности обладает свойством F, и для любого n, если каждый член до члена n ^th включительно имеет F, то n+1 ^-й элемент имеет F, то каждый член последовательности имеет F.

Шаги доказательства, основанного на принципе математической индукции:

Чтобы показать , что каждый член некоторого набора элементов { I ₁ I _n } имеет заданное свойство F.

ШАГ ПЕРВЫЙ: закажите товары (по отдельности или группами) в соответствии с некоторыми соответствующими особенность.

[Первый шаг называется заказ .]

ШАГ ВТОРОЙ: показать, что первый элемент (или элементы первой группы) имеет Ф.

[Шаг второй называется этапом основы и является доказательством основы статья .]

ШАГ ТРЕТИЙ: показать, что если каждый элемент до и включая k ^-й элемент (или элементы в группе k ^th ) имеет F, тогда k+1 ^th элемент (элементы в группе k+1 ^th ) имеет F.

[Третий шаг называется индуктивным шагом . Это доказывается формой условного доказательства. Предположим, что предшествуют того, что нужно доказать. это называется индуктивной гипотезой и выводит следствие .]

ШАГ ЧЕТВЕРТЫЙ: каждый элемент имеет свойство.

[Четвертый шаг заключение .]

21.09.00

Некоторые метатеоремы СЛ :

M6.1 SL соединители ~, &, и ты образуют функционально полный набор .

(См. стр. 222, что это означает.)

M6.2 SD — это звук для логической логики.

M6.3 SD — это полный для логической логики.

(См. стр. 229, что они означают.)

M6.4 SL это правда-функционально компактный . (Видеть стр. 245.)

Еще одна вещь, которую я хочу доказать.

M6.5* SD соответствует относительно отрицания .

Это означает, что не существует SL предложения P такого, что Ø |— P и Ø |— ~P.