Индукции пример из жизни: Какие можно привести примеры индукции и дедукции?

Индукция в педагогике: побуждение к поиску — Педагогическая деятельность, педагогический процесс и общие основы педагогики

Хотите знать об этом больше? Робот постарался подобрать для Вас материалы, близкие по теме. Посмотреть Содержание Что такое индукция в построении умозаключений Сравним индукцию с дедукцией В педагогике индукция допускает исключения из общего правила Зачем нужна индукция, если дедукция достоверней Примеры индуктивной логики в педагогической деятельности Что такое индукция в построении умозаключений Ранее мы установили, что при дедукции исходим из общего положения и распространяем выявленное в нём свойство на все частные проявления. Индукция – наоборот, путь от частного к общему. В переводе с латинского inductio означает «наведение», слово произошло от латинского же inducere – повлечь за собой, установить. Имеется в виду наведение на общую мысль, установление некоторой зависимости, вывод, извлечённый из совокупности отдельных фактов. Различают полную и неполную индукцию. При полной индукции обобщение делается на основе абсолютно ВСЕХ частных фактов. В этом случае не бывает исключений из общего правила. Однако такое возможно лишь в точных науках. В гуманитарных и социальных науках, в том числе и в педагогике, преимущественно используется неполная индукция, поэтому именно о ней и пойдёт и речь далее в данной статье. Сравним индукцию с дедукцией При индукции утверждения выстраиваются в обратном порядке. Сравните с дедукцией и почувствуйте разницу: дедукция: «общая идея – наблюдение – конкретный вывод»; индукция: «конкретное наблюдение – сравнение и анализ – общий вывод». Для наглядности возьмём ту же схему с первоклассником Артёмом из предыдущего материала и переставим рассуждения наоборот. Для этого поменяем местами А и С. Дедукция А. Известно: все дети любят играть (общее положение). B. Артём – ребёнок (посылка, тоже известный нам факт). C. Следовательно, Артём любит играть (логический вывод – частное новое утверждение, относящееся к конкретному ребёнку). А теперь индукция C. Нам известно: Артём любит играть (частное утверждение, относящееся к конкретному ребёнку). B. Артём – ребёнок (посылка, тоже известный нам факт). А. Следовательно, все дети любят играть (логический вывод – общее новое положение, относящееся ко всем детям). Всё по-прежнему верно? Нет! Во-первых, очевидно, что гораздо убедительней было к Артёму добавить ещё нескольких детей, основываться не на одном факте, а сразу на нескольких аналогичных – чем больше, тем лучше. А во-вторых… В педагогике индукция допускает исключения из общего правила В индукцию (напомню: в неполную индукцию! – речь тут только о ней) изначально заложена вероятность ошибки. Артём вполне может оказаться особенным ребёнком, отличающимся от ровесников. А если Артём вполне типичен, то есть вероятность, что некоторые другие дети имеют нетипичную для детей нелюбовь к играм. И эта вероятность останется, даже если вместо одного Артёма у нас будет целая выборка из миллиона детей, любящих играть. Ведь «все» в выводе – это ВСЕ без исключения, а исключения в педагогике бывают практически всегда. Зачем нужна индукция, если дедукция достоверней При дедукции логика, что называется, железная. С одной стороны это хорошо, поскольку в самой схеме умозаключения устранена возможность ошибиться (ошибки возможны в посылках, но не в рассуждении). С другой стороны, этого недостаточно, потому что в жизни постоянно возникают ситуации, когда мы не можем быть уверены в истинности посылок, а значит, не можем эффективно применить дедукцию. Поэтому в жизни индукцию мы используем гораздо чаще дедукции, причём это характерно как для взрослых, так и для детей. Однако «бытовое» применение индукции (вне рамок научной логики) сильно увеличивает вероятность ошибки. Именно индукция «виновата» в существовании стереотипных суждений типа «все девчонки – задаваки», «все хорошие учителя строги», «смартфоны всегда мешают учёбе»: имея несколько частных фактов, мы делаем обобщающий вывод, не учитывая возможное существование других частных фактов, противоречащих этому выводу. При грамотном использовании индукция позволяет нам обобщать частные факты, находить общие закономерности, формулировать общие правила. Если фактический материал достаточно обширен, то и обобщения будут максимально верными. Да, из этих правил возможны исключения, но подавляющее большинство частных случаев всё-таки подчиняется правилу. Гораздо проще запомнить правило и несколько исключений, чем пытаться действовать наугад совсем без правил. Дедукция бессильна, когда нам надо осмыслить частные факты, которым нет готовых объяснений, дедуктивным способом невозможно генерировать гипотезу – предположение, достоверность которого можно потом проверить опытным путём. Зато это может индукция! Допустим, что некие подростки Толя, Вася, Рома и Егор и считаются хулиганами. Тогда индукция выдаст следующую логическую цепочку: C. Толя, Вася, Рома и Егор – хулиганы. B. Они подростки. A. Все подростки – хулиганы. Но все ли подростки на самом деле хулиганы? Очевидно, что в этом случае корректней было бы не утверждать, а лишь предположить: A. Возможно, все подростки – хулиганы. Благодаря индукции утверждение превратилось в гипотезу, а это шаг к новому знанию. Таким образом, индукция позволяет выдвинуть гипотезу на основании фактов . Примеры индуктивной логики в педагогической деятельности Пример 1 C. Ирине Сергеевне А., Наталье Петровне Е. и Вячеславу Александровичу М. в прошлом учебном году неоднократно приходилось восстанавливать информацию в электронном журнале. B. Эти учителя несколько лет работают в школе №12. А. Возможно, в работе электронного журнала школы №12 в течение прошлого учебного года происходили технические сбои, после которых всем учителям приходилось восстанавливать информацию. Пример 2 C. Анкетирование показало, что родители Никиты П., Светы У. и ещё двух учеников не удовлетворены преподаванием математики. B. Дети недовольных родителей учатся в 8Б классе. А. Возможно, все родители 8Б класса недовольны преподаванием математики. Пример 3 C. Все дети в классе приобрели навык выполнения данного действия. B. Все дети в классе выполнили данное действие не менее 100 раз. А. Возможно, выполнив данное учебное действие 100 раз, любой ученик гарантированно усвоит его до автоматизма, приобретёт навык его выполнения. В каждом из приведённых примеров заключительное утверждение сформулировано как гипотетическое. Проверка этих предположений позволит дать точный ответ. Так, в первом примере действительно могли иметь место технические проблемы. Но могло и не быть никаких системных сбоев, и тогда, возможно, Ирина Сергеевна и двое её коллег несколько раз восстанавливали информацию из-за своих ошибок в работе с компьютером. Чтобы узнать точно, можно опросить других работников школы: провести анкетирование учителей, побеседовать с завучем, со специалистом, отвечающим за техническое обеспечения работы электронного журнала (наверно, это окажется учитель информатики). Выдвинув гипотезу, можно перейти к её проверке, а проверив, получить точную информацию, которую использовать в дальнейшем, в том числе – в качестве посылок в других умозаключениях.   Роботом установлено, что со статьёй «Индукция в педагогике: побуждение к поиску» тематически связаны: Для ссылки: Сидоров С.В. Индукция в педагогике: побуждение к поиску [Электронный ресурс] // Сидоров С.В. Сайт педагога-исследователя – URL: http://si-sv.com/publ/indukcija_v_pedagogike/20-1-0-728 (дата обращения: 30.05.2023).

Автор(ы): Сидоров С.В. | Опубликовано 08.10.2021 | Просмотров: 4469

SYL.ru — «Семья и Школа»

Содержание

Примеры индукции и дедукции в экономике и других науках

Индукция и дедукция — это взаимосвязанные, дополняющие друг друга методы умозаключения. Происходит целая логическая операция, в которой из суждений на основаниях нескольких выводов рождается новое утверждение. Цель этих методов — вывести новую истину из уже ранее существовавших. Выясним, что это, и приведем примеры дедукции и индукции. Статья подробно ответит на данные вопросы.

Дедукция

В переводе с латинского (дедукцио) обозначает «выведение». Дедукция – это логический вывод частного из общего. Этот ход рассуждений всегда подводится к истинному умозаключению. Метод применяется в тех случаях, когда из общеизвестной истины нужно вывести необходимое заключение о каком-либо явлении. Например, металлы — это теплопроводные вещества, золото — это металл, делаем вывод: золото — теплопроводный элемент.

Родоначальником этой идеи считают Декарта. Он утверждал, что исходный пункт дедукции начинается с интеллектуальной интуиции. Его метод включает в себя следующее:

1. Признание верным лишь того, что познается с максимальной очевидностью. В уме не должно зародиться каких-либо сомнений, то есть судить нужно только на не опровергаемых фактах.
2. Делить исследуемое явление на как можно больше простых частей для дальнейшего легкого их преодоления.
3. Переходить от простого постепенно к более сложному.
4. Составлять общую картину подробно, без каких-либо упущений.

Декарт считал, что с помощью такого алгоритма исследователь сможет найти истинный ответ.

Невозможно постигнуть никакого знания иначе, как путем интуиции, ума и дедукции. Декарт

Индукция

В переводе с латинского (индукцио) обозначает «наведение». Индукция – это логический вывод общего из частных суждений. В отличие от дедукции ход рассуждений приводится к вероятному умозаключению, все потому, что происходит обобщение нескольких оснований, и зачастую делаются поспешные выводы. Например, золото, как и медь, серебро, свинец – твердое вещество. Значит, все металлы — твердые тела. Заключение не верно, так как вывод был поспешным, ведь есть металл, такой как ртуть, а она является жидкостью. Пример дедукции и индукции: в первом случае умозаключение получилось истинным. А во втором — вероятным.

Сфера экономики

Дедукция и индукция в экономике являются методами исследования наравне с такими, как наблюдение, эксперимент, моделирование, метод научных абстракций, анализ и синтез, системный подход, исторический и географический метод. При использовании индуктивного способа исследование берет начало с наблюдения за экономическими явлениями, накапливаются факты, затем на их основе делается обобщение. При применении дедуктивного метода формулируется экономическая теория, потом на основании ее проверяются предполагаемые гипотезы. То есть от теории к фактам, исследование идет от общего к частному.

Приведем примеры дедукции и индукции в экономике. Увеличение стоимости хлеба, мяса, круп и других товаров заставляют нас сделать вывод о подъеме дороговизны в нашей стране. Это индукция. Извещение о повышении стоимости жизни дает думать, что увеличатся цены на газ, свет, другие коммунальные услуги и товары народного потребления. Это дедукция.

Сфера психологии

Впервые рассматриваемые нами явления в психологии упомянул в своих произведениях английский мыслитель Томас Гоббс. Его заслугой стало объединение рационального и эмпирического познания. Гоббс настаивал на том, что истина возможна только одна, достигнутая с помощью опыта и разума. По его мнению, познание начинается с чувственности как первого шага к обобщению. Общие свойства явлений устанавливаются при помощи индукции. Зная действия, можно выяснить причину. После выяснения всех причин нужен противоположный путь, дедукция, которая дает возможность познать новые различные действия и явления. Примеры индукции и дедукции в психологии по Гоббсу показывают, что это взаимозаменяемые, переходящие друг из друга этапы одного познавательного процесса.

Сфера логики

Два вида логического мышления нам знакомы благодаря такому персонажу, как Шерлок Холмс. Артур Конан Дойль обнародовал дедуктивный метод на весь мир. Шерлок начинал наблюдение с общей картины преступления и вел к частному, то есть изучал каждого подозреваемого, каждую деталь, мотивы и физические возможности, и с помощью логических умозаключений вычислял преступника, аргументируя железными доказательствами.

Дедукция и индукция в логике проста, мы, не замечая, используем ее каждый день в обыденной жизни. Зачастую мы реагируем быстро, мгновенно делая ошибочный вывод. Дедукция — более длительное мышление. Чтобы его развить, нужно постоянно давать нагрузку своему мозгу. Для этого можно решать задачи из любой сферы, математические, из физики, геометрии, даже головоломки и кроссворды помогут развитию мышления. Неоценимую помощь окажут книги, справочники, фильмы, путешествия — все, что расширяет кругозор в разных сферах деятельности. Прийти к правильному логическому умозаключению поможет наблюдательность. Каждая, даже самая незначительная, деталь может стать частью одной большой картины.

Приведем пример дедукции и индукции в логике. Вы видите женщину около 40 лет, в руке дамская сумка с не застегивающейся молнией от большого количества тетрадей в ней. Одета скромно, без излишеств и вычурных деталей, на руке тонкие часы и белый след от мела. Вы сделаете вывод, что, скорее всего, она работает учителем.

Сфера педагогики

Метод индукции и дедукции часто применяется и в школьном образовании. Методическую литературу для учителей выстраивают по индуктивному виду. Этот тип мышления широко применим для изучения технических устройств и решения практических задач. А с помощью дедуктивного метода легче описывать большое количество фактов, объясняя их общие принципы или свойства. Примеры дедукции и индукции в педагогике можно наблюдать на любых уроках. Часто в физике или математике учитель дает формулу, а далее в ходе урока учащиеся решают задачи, подходящие под этот случай.

В любой сфере деятельности всегда пригодятся методы индукции и дедукции. И совсем не обязательно для этого быть супер-сыщиком или гением в научных областях. Давайте нагрузку для своего мышления, развивайте мозг, тренируйте память, и в дальнейшем сложные задачи будут решаться на инстинктивном уровне.

что это простыми словами, примеры

Приветствую Вас, друзья!

Дедуктивный метод с успехом применяется и в современном обществе представителями совершенно разных профессий, например, врачами и юристами. Дедукция используется в математике, физике, экономике и научной философии. В данной статье мы попытаемся разобраться что из себя представляет дедуктивный метод, в чём его преимущества и как ему научиться.

Что такое дедуктивный метод?

Дедуктивный метод (от лат. deductio – выведение) — это метод мышления, следствием которого является логический вывод, где частное заключение выводится из общего. Вся суть дедуктивного метода заключается в том, что человек начинает строить логическую цепочку на основе гипотезы, в верности которой он не сомневается. Для того чтобы доказать гипотезу, необходимо провести наблюдения, и сделать умозаключение. В процессе наблюдения применяются общепринятые и признанные факты.

Чтобы было проще понять, что такое дедуктивный метод, обратимся к книге «Думай медленно… решай быстро», автором которой является лауреат Нобелевской премии Даниэль Канеман. В книге описано так называемое «быстрое мышление», которое отвечает за мгновенное познание окружающего пространства. Такой вид мышления заставляет человека классифицировать свои инстинктивные ощущения. На основании этого, человек чаще всего принимает иррациональные решения, которые оказываются ошибочными.

Для того чтобы обеспечить осознанное формирование мыслей, решений, выводов и оценок, необходимо использовать систему «медленного» мышления. Как это проявляется? Например, женщина нашла на столе в гостиной обручальное кольцо своего мужа. Первым порывом, конечно, будет разозлиться на супруга и заподозрить его во всех смертных грехах. Однако, тут же женщина вспоминает, что в их гостиной перегорела лампочка, она попросила мужа заменить её. Лампочка в комнате горит, значит, мужчина выполнил просьбу. Отсюда следует вывод, что ему пришлось принести стремянку и инструменты из гаража. Из-за того, что мужчине пришлось надевать перчатки, он снял кольцо, чтобы ему было сподручнее. После, он просто забыл его надеть, так, как опаздывал на работу. Причина найдена, семейной ссоры удалось избежать – это пример «медленного» мышления, которое помогло женщине увидеть все детали и прийти к правильному выводу.

Подобный тип мышления и является основой дедуктивного метода. Дедукция позволяется исходя из общих фактов сделать частный вывод. Возьмём всё тоже золотое кольцо. Мы знаем, что все металлы способны проводить ток, а золото несомненно является металлом. Отсюда мы можем сделать вывод, что золотое кольцо так же способно пропустить ток. Мы применили знания из общеобразовательной школьной программы, и сделали частный вывод. При этом мы использовали дедуктивный метод мышления.

Примеры дедуктивного метода

Дедуктивное мышление бытовало ещё во времена Аристотеля, который анализировал каждое умозаключение вместе с посылками и выводом. Познание через дедуктивный метод основывается на взаимосвязи составляющих компонентов.

Вернёмся к примеру, с золотым кольцом. Гипотеза А утверждает, что все металлы пропускает ток. Если эта гипотеза верна, то гипотеза Б о том, что золото, как металл, то же пропускает ток, верна. Значит Б гипотеза вытекает из А гипотезы. Если кому-то удастся доказать, что золото не пропускает ток, то это будет означать неверность Б гипотезы. Отсюда можно сделать вывод, что и суждение А окажется ошибочным.

Суждения, которые содержат в себе констатацию непреложных истин, являются посылками. В нашем примере это «металлы пропускают ток» и «золото – это металл». Суждения, вытекающие из посылок и ставящие логическую точку, являются выводом, или следствием. «Золото то же пропускает ток» — это вывод.

Отличия от индуктивного метода

Индуктивный метод является полной противоположностью дедуктивного метода, и основывается на переходе от частного к общему. Более наглядно это можно наблюдать в медицине, когда врач, основываясь на симптоматике пациента ставит диагноз. С точки зрения дедукции, сначала необходимо оценить всю «картину», чтобы сделать правильный вывод. Используя этот метод, врач сначала должен использовать обобщённый термин «простудное заболевание», и отталкиваться от него. Грипп подразумевает, что у человека должны быть симптомы.

Если говорить о различиях, то нужно упомянуть, что дедуктивное мышление является более обобщающим и глобальным. Индуктивное мышление базируется на субъективных предчувствиях. Однако, оба метода являются взаимосвязанными. В начале, до того момента, пока не будет обнаружен общий признак в различных явлениях, движение происходит от частного в общему, то есть применяется индукция. Объединяя частные случаи, индукция позволяет получить общее знание. После установления общего признака, мышление идёт в противоположном направлении – от общего к частному. Это дедуктивный метод.

Где используется дедукция?

Каждый день, сталкиваясь с различными обстоятельствами, наш мозг выстраивает логические цепочки, которые незаметны для многих. Решая с утра что одеть, мы изучаем погоду за окном. У нас в голове есть две посылки: на улице холодно, и теплая одежда защищает от холода. Это два общих знания. Основываясь на этом, мы приходим к пониманию того, что нам необходимо тепло одеться – это вывод.

Дедуктивный метод присутствует в нашей повседневности, но мы можем этого не понимать. Однако, когда дело касается профессиональной деятельности, человек осознанно использует дедукцию для решения конкретных проблем. Метод дедуктивного мышления применяется во многих направлениях:

• споры и дискуссии – используя дедукцию, приводятся очевидные утверждения, с которыми оппоненту приходится согласиться, тем самым принимая вашу точку зрения;
• математика – наглядным примером могут послужить геометрические задачи из школьной программы. Чтобы доказать теорему, ученику необходимо воспользоваться общепринятыми и доказанными аксиомами;
• философия – вся суть метода дедукции здесь заключается в том, что любую гипотезу необходимо обосновать, используя при этом только логические доказательства;
• криминалистика – прибыв на место преступления, эксперт использует общую картину происшествия. Это помогает ему найти отдельные обстоятельства и новые детали;
• наука – учёный за основу своей работы берёт какую-либо гипотезу, которая пока не является доказанной, или опровергнутой. Основываясь на гипотезе, учёный выводит следствия, которые он попытается обнаружить в ходе исследования.

Как научиться дедуктивно мыслить?

Мы уже говорили ранее об образе «медленного» мышления. Если вы хотите изучить дедуктивный метод, вам потребуется наблюдательность. Будьте «въедливыми», старайтесь обратить внимание даже на самые незаметные детали. Начните с малого, например, с изучения расположения мебели в комнате, когда вы будете у кого-то гостить. При разговоре с человеком обратите внимание на то, как он разговаривает, жестикулирует, куда смотрит. Со временем вы научитесь замечать то, что скрыто от чужих глаз.

Если у вас нет маленькой записной книжки, то сейчас самое время её купить. Носите её всегда с собой, чтобы записывать все свои наблюдения. Со временем пространственные описания превратятся в железные факты. Не забывайте и о том, что вам потребуется обширная база знаний. Расширяйте свой кругозор каждый день: читайте, смотрите фильмы и слушайте музыку разных жанров, путешествуйте, знакомьтесь с людьми разных профессий и интересов.

Примеры индуктивных рассуждений

Термин индуктивных рассуждений

относится к рассуждениям, которые используют конкретную информацию и делают более широкое обобщение, которое считается вероятным, но при этом остается открытым для того факта, что вывод не может быть гарантирован на 100%.

Примеры индуктивного рассуждения

Другими словами, вы делаете обоснованное или обоснованное предположение на основе имеющейся у вас информации или данных. Это может звучать правильно, но это не значит, что это правильно. Давайте вместе рассмотрим несколько примеров индуктивных рассуждений. Вы быстро увидите, что это такое.

Реклама

Типы индуктивных рассуждений

Существуют различные степени силы и слабости индуктивных аргументов и рассуждений. Вы также найдете различные типы распространенных индуктивных рассуждений, включая следующие.

Индуктивные обобщения

Используя небольшую выборку, вы делаете обобщение обо всей совокупности. Например:

Мои знакомые левши пользуются ножницами для левшей; поэтому все левши пользуются ножницами для левшей.

Статистическая индукция

Подобно индуктивным обобщениям, статистическая индукция использует небольшой набор статистических данных для обобщения. Например:

Поскольку 95% левшей, которых я видел во всем мире, используют ножницы для левшей, 95% левшей во всем мире используют ножницы для левшей.

Причинно-следственный вывод

При индуктивном умозаключении при причинно-следственном выводе вы используете индуктивную логику для установления причинно-следственной связи между предпосылкой и гипотезой. Например:

Летом на нашем пруду водятся утки. Поэтому лето принесет на наш пруд уточек.

Аналогическая индукция

В этом типе индуктивного рассуждения вы выдвигаете гипотезу, анализируя две похожие посылки и их сходство, например:

Мэри и Джим левши и пользуются ножницами для левшей.

Билл тоже левша.

Вывод: Билл тоже пользуется ножницами для левшей.

Прогностическая индукция

Здесь вы можете сделать вывод о будущем, используя информацию из прошлого. Например:

Раньше к нашему пруду всегда прилетали утки. Поэтому этим летом на наш пруд прилетят утки.

Эти типы индуктивных рассуждений работают в аргументах и ​​при выдвижении гипотез в математике или естественных науках. Теперь, когда вы рассмотрели типы индуктивных рассуждений, посмотрите еще несколько примеров, которые помогут вам понять.

Реклама

Примеры индуктивных рассуждений

Чтобы лучше понять индуктивную логику, просмотрите несколько различных примеров. Посмотрите, сможете ли вы сказать, какой тип индуктивного рассуждения задействован.

• Дженнифер всегда уходит в школу в 7 утра. Дженнифер всегда приходит вовремя. Таким образом, Дженнифер предполагает, что если она сегодня пойдет в школу в 7 утра, то успеет вовремя.
• Стоимость товара составила 1 доллар США. Стоимость труда по изготовлению изделия составила 0,50 доллара. Продажная цена товара составила 5 долларов. Таким образом, товар всегда приносит хорошую прибыль магазинам, продающим его.
• Каждый ураган в этой области приходит с севера. Вдалеке я вижу большое облако пыли. С севера идет новая буря.
• Боб показывает большое кольцо с бриллиантом своему другу Ларри. Боб сказал Ларри, что планирует жениться на Джоан. Должно быть, Боб удивил Джоан сегодня вечером кольцом с бриллиантом.
• Стул в гостиной красный. Стул в столовой красный. Стул в спальне красный. Все стулья в доме красные.
• Каждый раз, когда вы едите арахис, вы начинаете кашлять. У вас аллергия на арахис.
• Все кошки, которых вы видели, мурлыкают. Поэтому все кошки должны мурлыкать.
• Майкл только что переехал сюда из Чикаго. У Майкла рыжие волосы. Поэтому у всех жителей Чикаго рыжие волосы.
• Дети в этом доме громко кричат, когда играют в своей спальне. Я слышу, как дети кричат ​​в этом доме. Поэтому дети должны играть в своей спальне.
• Все цыплята, которых мы видели, были коричневыми. Все цыплята в этой области должны быть коричневыми.
• Джон отличный пловец. В его семье есть бассейн. Сестра Джона, Мэри, должно быть, тоже отлично плавает.
• Все коричневые собаки в парке сегодня маленькие собаки. Поэтому все маленькие собаки должны быть коричневыми.
• Все дети в этом детском саду любят играть с Lego. Все дети должны любить играть с Lego.
• Рэй — футболист. Все остальные футболисты школьной команды весят более 170 фунтов. Следовательно, Рэй должен весить более 170 фунтов.
• Практически каждый дом на Южной улице разваливается. Шерри живет на Южной улице. Ее дом, вероятно, разваливается.
• Каждый год в мае бывает гроза. Поскольку это май, у нас будет гроза.

Реклама

Зарезервируйте свои рассуждения

Как видите, индуктивное рассуждение граничит с высокой вероятностью. Но это не делает его обязательно фактическим. Пока вы занимаетесь этим, подумайте о сестре индуктивных рассуждений: дедуктивных рассуждениях. Это еще одна форма логики, которая поможет вам сделать правильные выводы.

Чтобы проверить свои факты, вы можете сформулировать собственную гипотезу. Затем вы можете протестировать его, выполнив следующие простые шаги.

Штатный писатель

примеров контрпримеры — Какие есть хорошие, элементарные и, может быть, тоже интересные доказательства по индукции?

$\begingroup$

Я провожу разовое занятие/беседу о концепции бесконечности для некоторых (талантливых) старшеклассников. Я хочу научить их доказательству по индукции, и я хочу, чтобы они сделали несколько упражнений (вы изучаете математику, работая!). Поэтому я ищу простые, элементарные и, возможно, интересные упражнения для тех, у кого практически нет опыта в доказательстве утверждений. Несколько примеров, которые пришли на ум: 9n \leq 1+nx$ для всех $x \geq -1$.

Я просмотрел ветку Примеры математической индукции, но большинство, если не все приведенные здесь примеры, я думаю, слишком сложны для аудитории.

Приветствуются любые предложения! Результат и его индукционное доказательство не обязательно должны быть на 100% строгими, цель состоит в том, чтобы проиллюстрировать индукционное доказательство в простых условиях.

• индукция
• примеры-контрпримеры

$\endgroup$

5

$\begingroup$

Моими любимыми доказательствами по индукции всегда были доказательства из реальной жизни. Например, вот тот, который мне всегда нравился:

.

В одиночном турнире по бадминтону каждый игрок играл против всех остальных ровно один раз, и в каждой игре определялся победитель. После всех игр каждый игрок перечислил имена всех игроков, которых она победила, а также имена всех игроков, побежденных игроками, побежденными ею. Например, если $A$ побеждает $B$, а $B$ побеждает $C$. тогда в список $A$ включены как $B$, так и $C$. Докажите, что хотя бы один игрок назвал имена всех остальных игроков.

А вот еще один-

В спортивном турнире с участием $n$ игроков каждая пара играет ровно один матч друг против друга. Розыгрышей нет. Докажите, что игроков можно расположить в таком порядке $P_1,P_2,\dots ,P_n$, что $P_i$ побеждает $P_{i+1}\;∀i=1,2,\dots ,n−1$

$\endgroup$

$\begingroup$

Во-первых: я все еще думаю, что вы можете извлечь несколько довольно простых примеров/доказательств по индукции из той нити, которую вы связываете, например, мозаику с тромино или Ханойскими башнями.

Так что внимательно просмотрите этот список, и действительно есть несколько подходящих, которые не слишком сложны

Если вы выполняете комбинацию слабой и сильной индукции, вот некоторые из моих любимых:

1. Количество способов $S_n$ подняться по $n$ лестнице, где вы поднимаетесь либо по $1$, либо по $2$ лестнице за раз. время является числом Фибоначи, так как для вашего первого шага вы можете либо подняться по лестнице на $1$, и в этом случае вы можете сделать оставшиеся $n-1$ шагов $S_{n-1}$ способами, либо подняться по лестнице на $2$ , и в этом случае вы можете выполнить оставшиеся $n-2$ шагов $S_{n-2}$ способами, поэтому $S_n = S_{n-1} + S_{n-2}$, т.е. вы имеете дело с ряд Фибоначчи. Вот видео. Обязательно сначала задайте этот вопрос своей аудитории и заставьте их бороться с ним. Например. они могут вычислить ответ за $3$, $4$ и $5$ шагов… и тогда кто-то может действительно начать распознавать паттерн Фибоначчи… так что тогда возникает вопрос: почему это так, т.

   е. как мы можем на самом деле доказать, что ?

2. За какое минимальное количество разломов можно разбить плитку шоколада, состоящую из $m \times n$ маленьких кусочков, на эти самые кусочки?

Вы можете сначала предложить эту задачу своей аудитории и как бы поиграть с ними, предложив сначала сделать разрыв в середине такта, чтобы получить два куска примерно одинакового размера, может быть более эффективной стратегией, чем отрывать один колонку за раз и разбивая ее на маленькие кусочки один за другим, так как с более крупными фрагментами вы можете покрыть больше отдельных структурных линий одним разрывом, чем с меньшими фрагментами … Но, конечно, не имеет значения, как вы это сделаете: это будет всегда делайте $n-1$ перерывов, чтобы получить $n$ штук, так как каждый перерыв увеличивает количество кусков только на один. И это понимание действительно не требует индукции, но вы можете использовать сильную индукцию, чтобы действительно понять это: первый разрыв разделит такт с $n$ кусочками на кусок с $m$ кусочков и кусок с $n-m$ кусочков.

По индуктивному предположению, для полного распада первого потребуется $m-1$, а для второго потребуется $n-m-1$ разрывов, всего $1 + (m-1) + (n-m-1) = n-1 $ ломается.

3. Эйлеров обход: вы можете провести Эйлеров обход связного графа, который посещает каждое ребро (соединение) ровно один раз, если каждая вершина (узел) имеет четную степень (четное число прикрепленных к ней ребер). Опять же, хорошая вещь в этом заключается в том, что вы можете сначала дать своей аудитории несколько конкретных примеров графиков (например, использовать «Семь мостов Кенигсбурга»), где некоторые из них можно сделать, а другие нет, чтобы они могли почувствовать эту проблему. А затем проведите доказательство с помощью индукции по «размеру» графа (так что это действительно больше похоже на доказательство структурной индукции): сначала начните с произвольного узла $a$ вашего графа и просто начните обход следующих соединений, убедившись, что повторить любой. Теперь сначала отметьте, что когда вы не можете идти дальше, вы должен вернуть в $a$ (хороший вопрос аудитории: почему?). Хорошо, теперь у вас есть тур… но вы, вероятно, оставили некоторые части графика, где определенные соединения никогда не посещались. Но обратите внимание: все эти подграфы должны по-прежнему иметь свойство каждого узла иметь четную степень (опять же: почему?), поэтому по индуктивному предположению вы можете провести Эйлеров тур для каждого из них. И теперь вы можете просто «вставить» эти частичные эйлеровы туры в исходный частичный тур, чтобы сделать все это эйлеровым туром всего графа.

Мне нравятся эти примеры не только потому, что они наглядны и интерактивны, но и потому, что они показывают, что индукция — это не просто слабая математическая индукция. Я вижу, что многие методы лечения начинаются со слабой математической индукции, а иногда даже не переходят к другим формам индукции, и это оказывает студентам медвежью услугу, потому что индукция — гораздо более общее понятие, которое они должны интуитивно понимать, а не теряться в формальных деталях.

Если вы ищете более традиционные алгебраические слабые математические индукции: есть, конечно, сумма всех чисел от $1$ до $n$ .

13.8: Применение электромагнитной индукции

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4839

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснять, как жесткие диски компьютеров и графические планшеты работают с использованием магнитной индукции
• Объясните, как гибридные/электрические транспортные средства и транскраниальная магнитная стимуляция используют магнитную индукцию в своих интересах

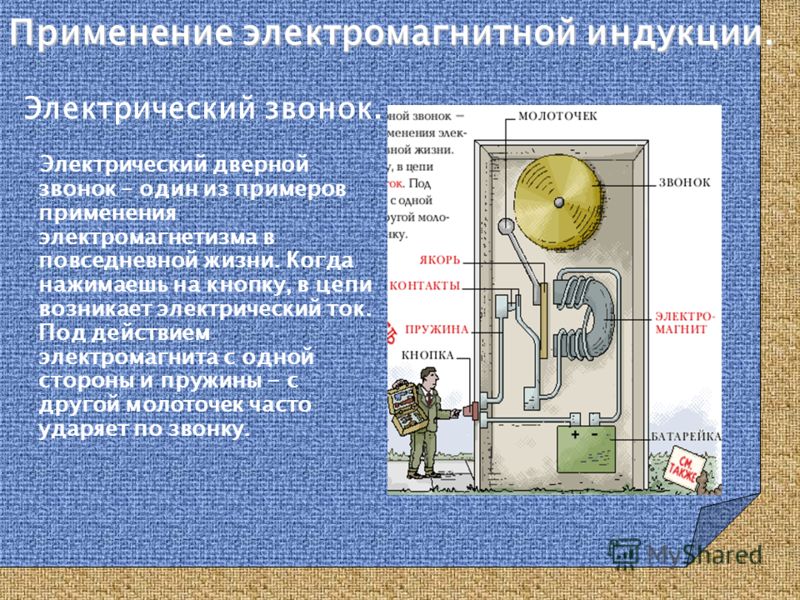
Современное общество имеет множество применений закона индукции Фарадея, которые мы рассмотрим в этой и других главах. На этом этапе позвольте упомянуть несколько, которые связаны с записью информации с использованием магнитных полей.

Некоторые компьютерные жесткие диски применяют принцип магнитной индукции. Записанные данные производятся на вращающемся диске с покрытием. Исторически сложилось так, что чтение этих данных работало по принципу индукции. Однако сегодня большая часть входной информации передается в цифровом, а не в аналоговом виде — на вращающемся жестком диске записывается последовательность нулей или единиц. Поэтому большинство устройств считывания с жестких дисков работают не по принципу индукции, а используют метод, известный как гигантское магнитосопротивление 9 .0045 . Гигантское магнитосопротивление — это эффект большого изменения электрического сопротивления, вызванного приложенным магнитным полем к тонким пленкам чередующихся ферромагнитных и немагнитных слоев. Это один из первых крупных успехов нанотехнологий.

Графические планшеты

или планшетные компьютеры , в которых для рисования цифровых изображений используется специально разработанное перо, также применяют принципы индукции. Обсуждаемые здесь планшеты помечены как пассивные планшеты, поскольку существуют и другие конструкции, в которых для письма используется либо перо с батарейным питанием, либо оптические сигналы. Пассивные планшеты отличаются от планшетов и телефонов с сенсорным экраном, которые многие из нас используют регулярно, но все же их можно обнаружить при подписи на кассе. Под экраном, как показано на рисунке \(\PageIndex{1}\), расположены крошечные провода, идущие по всей длине и ширине экрана. Ручка имеет крошечное магнитное поле, исходящее от кончика. Когда наконечник касается экрана, в проводах ощущается изменяющееся магнитное поле, которое преобразуется в ЭДС индукции, которая преобразуется в линию, которую вы только что нарисовали.

Рисунок \(\PageIndex{1}\): Планшет со специальной ручкой для письма — еще одно применение магнитной индукции.

Другим применением индукции является магнитная полоса на обратной стороне вашей личной кредитной карты , которая используется в продуктовом магазине или в банкомате. Это работает по тому же принципу, что и аудио- или видеокассета, в которой головка воспроизведения считывает личную информацию с вашей карты.

Видео

Посмотрите это видео, чтобы увидеть, как фонарики могут использовать магнитную индукцию.

Магнит движется по проводу благодаря вашей механической работе. Индуцированный ток заряжает конденсатор, в котором хранится заряд, который зажжет лампочку, даже если вы не выполняете эту механическую работу.

Электромобили

и гибридные автомобили также используют преимущества электромагнитной индукции. Одним из ограничивающих факторов, препятствующих широкому распространению 100% электрических транспортных средств, является то, что срок службы батареи не так велик, как время, которое вы можете проехать на полном баке бензина. Чтобы увеличить количество заряда батареи во время движения, двигатель может работать как генератор всякий раз, когда автомобиль тормозит, используя создаваемую противо-ЭДС. Эта дополнительная ЭДС может быть вновь полученной накопленной энергией в автомобильном аккумуляторе, что продлит срок службы аккумулятора.

Еще одной современной областью исследований, в которой успешно применяется электромагнитная индукция, является транскраниальная магнитная стимуляция (ТМС) . Множество расстройств, включая депрессию и галлюцинации, можно отнести к нерегулярной локальной электрической активности в головном мозге. При транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозгу. Использование ТМС в качестве диагностического метода хорошо известно.

Видео

Посмотрите это видео на Youtube, чтобы увидеть, как рок-н-ролльные инструменты, такие как электрогитары, используют электромагнитную индукцию для получения сильных ударов.

---

Эта страница под названием 13. 8: Приложения электромагнитной индукции распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. Электромагнитная индукция
   2. жесткие диски
   3. источник@https://openstax. org/details/books/university-physics-volume-2

из класса на кухню – наука в школе

Автор(ы): Пауло Андре, Ана Рита Бастос и Руте Феррейра

Изучите электромагнитную индукцию и одно из ее хорошо известных применений – индукционную плиту – с помощью этих практических занятий.

Многие современные устройства основаны на электромагнитной индукции. Закон индукции Фарадея, сформулированный в 1831 году, описывает, как переменное магнитное поле индуцирует электродвижущую силу (ЭДС). Применение этого закона включает:

• генераторы, производящие большую часть потребляемой в мире электроэнергии
• поезда на магнитной подушке
• индукционные плиты на кухне
• звукосниматели для электрогитары
• площадки для беспроводной передачи энергии, используемые для зарядки мобильных устройств.

Преподавание закона индукции Фарадея в старших классах является сложной задачей. Учащиеся в возрасте 16–19 лет должны применять как математические расчеты, так и концептуальное понимание для изучения науки, лежащей в основе электромагнитной индукции, и изучения ее применения в повседневной жизни.

В этом упражнении учащиеся получают непосредственный опыт работы с электромагнитной индукцией. Задания подходят для учащихся, изучающих физику, в возрасте 16–19 лет, и на их выполнение уходит около часа, хотя для подготовки к упражнению 2 перед уроком требуется дополнительное время.

Индукционная плита
Luisa Kittner/Pixabay 

В конце занятия учащиеся должны уметь:

• понимать с экспериментальной точки зрения закон индукции Фарадея
• определить параметры, влияющие на применение закона индукции Фарадея
• исследовать взаимосвязь между вариациями магнитного потока и индуцированной электродвижущей силой
• сконструировать электрический генератор, используя катушку и индукционную плиту для питания светодиода

Закон индукции Фарадея гласит, что изменение магнитного окружения проволочной катушки индуцирует электродвижущую силу (ЭДС), представленную как ε :

, где N — число витков катушки, а Φ — магнитный поток через катушку.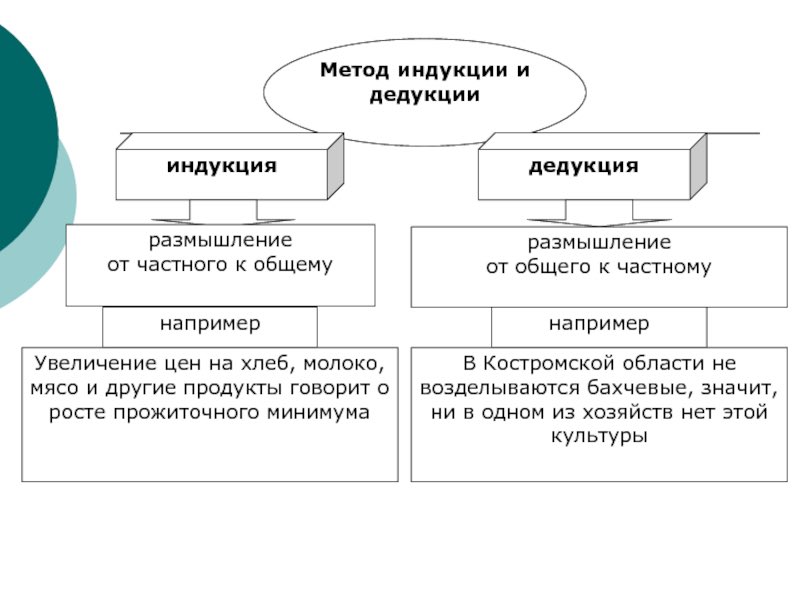

Если масштаб времени мал, производный член d Φ / d t  может быть аппроксимирован до Δ Φ / Δ t . Это приближение особенно полезно, если учащиеся недостаточно знакомы с дифференциальным исчислением.

Магнитный поток зависит от площади катушки A , напряженности магнитного поля B и угла θ , образованный между силовыми линиями магнитного поля и вектором, перпендикулярным (под углом 90°) к плоскости катушки:

Любое изменение напряженности магнитного поля, площади катушки или угла приводит к индуцированной ЭДС, которая может быть измеряется гальванометром и используется для демонстрации принципов индукции. Эта установка показана на рисунке 1.

Рисунок 1: Электрическая цепь с гальванометром и квадратной катушкой в ​​магнитном поле с напряженностью B и направлением.
Изображение предоставлено Пауло Андре

Задание 1: свободно падающий магнит

В этом эксперименте, который должны провести учащиеся, магнитный диполь падает через катушку, индуцируя ЭДС, вызывая кратковременное изменение напряженности магнитного поля. Чтобы наблюдать за изменением ЭДС, катушку можно подключить к гальванометру или светодиоду (LED). Преимущество использования светодиода (рисунок 2) состоит в том, что он создает видимый выходной сигнал (вспышку света), когда индуцированная ЭДС превышает пороговое значение (~ 1,5 В).

Рис. 2. Эксперимент со свободно падающим магнитом со светодиодом
Изображение предоставлено Пауло Андре

Материалы

• Катушка с N > 10 000 витков
• Малый стержневой магнит
• Светодиод
• Линейка
• Смартфон (для съемки свободного падения)

Процедура

1. Подсоедините клеммы катушки к контактным площадкам светодиода. Если требуется пайка, этот шаг должен быть сделан учителем заранее.
2. С помощью линейки поместите магнит на 20 см выше центра катушки (и выровняйте его по центру катушки).
3. Настройте камеру смартфона на запись события, желательно в замедленном режиме.
4. Отпустите магнит и наблюдайте за светодиодом (рис. 3).
5. Поэкспериментируйте с выпуском катушки с разной высоты над катушкой. Какие отличия, если они есть, вы заметили?
6. Теперь поверните катушку на 180º и повторите эксперимент. Наблюдается ли какое-либо изменение?

Рис. 3: Кадры видео, показывающего свободно падающий магнит. Последний кадр —
, когда магнит находится внутри катушки, а светодиод излучает (красный).
Изображение предоставлено Пауло Андре

Обсуждение

Учителя могут обсудить с учениками следующие вопросы, чтобы изучить ключевые понятия:

• Как интенсивность излучения светодиода зависит от расстояния, на котором высвобождается магнит?
• При одинаковом расстоянии падения приводит ли поворот катушки на 180º к различной интенсивности излучения светодиодов?

Учащиеся могут просмотреть свои видеоролики об эксперименте, чтобы найти подтверждение своим ответам, или посмотреть предоставленный видеоролик. В реальной жизни процесс происходит очень быстро, поэтому для уточнения деталей необходимо замедленное видео.

Пояснение

Эксперимент должен показать четкую разницу в интенсивности излучения светодиода по мере увеличения начального расстояния между магнитом и катушкой, что приводит к увеличению скорости магнита и скорости изменения магнитного потока.

Светодиод представляет собой поляризованное устройство, что означает, что он излучает свет только в том случае, если приложенная ЭДС положительна (когда может протекать электрический ток). Является ли ЭДС положительной или отрицательной, зависит от направления движения магнита (какой полюс магнита в данный момент движется через катушку) и в каком направлении катушка подключена к контактным площадкам светодиода.

Мы можем увидеть это более подробно в моделировании, показанном на рисунке 4e. Здесь ЭДС положительна только примерно в половине периода времени, в течение которого магнит находится внутри катушки, и что положительная ЭДС имеет более высокое максимальное значение, чем отрицательная ЭДС из-за ускорения магнита при падении через катушку.

Расширение задания 1: математическое моделирование

Хотя мигающий светодиод указывает на индуцированную ЭДС, возникающую в результате изменения магнитного потока, он не дает количественных значений. Мы можем узнать более точно изменяющиеся значения магнитного потока, когда магнит падает через катушку, используя следующее уравнение:

, где y — координата магнита, y ₀ — координата центра катушки, B _max — максимальное значение напряженности магнитного поля, а σ — параметр, описывающий спад напряженности магнитного поля.

Здесь мы делаем следующие предположения или приближения:

• длина магнита мала по сравнению с катушкой
• вектор его магнитного поля совмещен с его продольной осью
• Φ (магнитный поток через катушку) максимален, когда геометрические центры катушки и магнита совпадают.

Параметр σ (расстояние для B   ~ 37 % от B _max ) можно принять в диапазоне 5–10 мм, полную процедуру экспериментального определения можно найти в Ref. [1].

Для магнита в свободном падении смещение y магнита в момент времени t связано с ускорением свободного падения g уравнением 4:

В таблице 1 приведен пример используемых параметров.

Таблица 1: Примеры значений параметров, использованных для получения результатов на рис. 4.

Параметры	Символ	Значение	Блок
Область катушки	А	250	мм 2
Количество витков катушки	Н	12000
Максимальная напряженность магнитного поля	В макс.	3	мт
Распад магнитного поля	σ	10	мм
Координата центра катушки	г 0	200	мм

Используя значения в таблице 1, уравнениях 3 и 4 и прилагаемой электронной таблице, мы можем создать математическую модель, которая графически отображает эти изменения, как видно из результатов и графиков на рисунке 4. ^[2] Здесь магнитный поток через катушку и ЭДС индукции показаны как функция положения и времени. Магнит освобождается при y = 0 и t = 0 и падает в положительном направлении оси. Катушка отцентрирована в позиции y ₀ .

Рис. 4: а) Экспериментальная схема. b–e) Смоделированные значения для магнита в свободном падении: магнитный поток как функция положения (b) и времени (d), и ЭДС как функция положения (c) и времени (e)
Изображение предоставлено Пауло Андре

Обсуждение

Используя рисунок 4 и электронную таблицу, учителя могут обсудить с учащимися следующие вопросы:

• Как изменяется магнитный поток по мере приближения магнита к центру катушки? (Увеличивается, а после прохождения центра уменьшается – см. рис. 4б.)
• На рисунке 4c что происходит с ЭДС, когда магнит проходит через центр катушки? (Происходит смена знака с отрицательного на положительный.)
• На рисунке 4e форма кривой ЭДС симметрична до и после прохождения магнита через центр катушки? (Нет, она асимметрична, потому что магнит находится в свободном падении, поэтому его скорость со временем увеличивается, а скорость изменения магнитного потока и ЭДС индукции также увеличивается со временем. )

Мероприятие 2: индукционная плита

Реальное применение закона Фарадея — приготовление пищи с использованием индукционной плиты, когда посуда нагревается за счет электрической индукции, а не за счет теплопроводности пламени или электрической плиты. Индукционные плиты генерируют тепло внутри самой посуды, что делает этот метод приготовления более эффективным. Однако все кастрюли должны быть изготовлены из ферромагнитного металла (обычно из чугуна или нержавеющей стали).

Индукционная плита имеет катушку, питаемую переменным электрическим током, под керамической пластиной. Переменный ток создает колеблющееся магнитное поле, которое индуцирует колеблющийся магнитный поток в основании кастрюли, поставленной на плиту. Это создает электрический ток (называемый вихревым током) в основании кастрюли, нагревая его.

В индукционных плитах напряженность магнитного поля обычно мала (~100 мТл), но колеблется с высокой частотой (27 кГц). Это означает, что скорость изменения напряженности магнитного поля очень высока, что приводит к высоким значениям индуцированной ЭДС и, следовательно, к производимому нагреву.

В этом упражнении учащиеся исследуют индуцированные ЭДС вокруг индукционной плиты, опять же, используя светодиод, подключенный к катушке.

Материалы

• Кухонная индукционная плита
• Светодиоды (разные цвета излучения)
• Медная проволока диаметром 0,2 мм для изготовления катушки
• Карандаш
• Бумага
• Клейкая лента

Указание по технике безопасности

Хотя индукционная плита не нагревается, посуда и вода нагреваются, поэтому учащиеся должны быть предупреждены о том, что нельзя прикасаться к ней, и следить за тем, чтобы ручка кастрюли не мешала легко сбить во время эксперимента. Следует проявлять особую осторожность, если учащиеся должны выполнять этап пайки самостоятельно, и это следует делать только под пристальным наблюдением учителя.

Процедура

1. Возьмите карандаш, накройте его листом бумаги (это будет внутренняя часть катушки) и намотайте на него 300–400 витков провода.
2. Наклейте ленту, чтобы закрыть провод и зафиксируйте его на месте; затем уберите карандаш.
3. Удалите эмаль с медных проводов на каждом конце катушки.
4. Припаяйте два светодиода к медным проводам встречно-параллельно (параллельно, но с обратной полярностью друг относительно друга). Этот шаг может выполнять учитель, или ученики могут делать это под наблюдением учителя.
5. Поставьте кастрюлю с водой в центр индукционной плиты.
6. Поместите змеевик рядом с поддоном.
7. Включите варочную панель, начиная с минимальной мощности (рис. 5).
8. Переместите катушку вдоль близлежащих областей варочной панели. Попробуйте выяснить, какие изменения заставляют светодиод становиться ярче или тусклее.

Рис. 5: Катушка возле индукционной плиты с выключенной (слева) и включенной (справа) плитой
Изображение предоставлено Пауло Андре

Обсуждение

Учителя могут обсудить с учениками следующие вопросы, чтобы изучить ключевые понятия.

• Как яркость светодиода зависит от расстояния до варочной панели?
• Изменится ли яркость светодиода при повороте катушки в том же положении?

Учащиеся должны обнаружить, что магнитное поле в основном сосредоточено в области посуды, а интенсивность поля быстро уменьшается по мере удаления от варочной панели. Вращение катушки приводит к изменению ЭДС согласно уравнению (2) из-за изменения угла между катушкой и силовой линией магнитного поля.

Благодарности

Эта работа была разработана в рамках проекта CICECO-Aveiro Institute of Materials (UIDB/50011/2020 & UIDP/50011/2020), Instituto de Telecomunicações (UIDB/50008/2020-UIDP/50008/2020). ) и WinLED (POCI-01-0145-FEDER-030351), финансируемых из национальных фондов через FCT/MEC и, при необходимости, совместно финансируемых FEDER в рамках Партнерства PT2020 через Европейский фонд регионального развития (ERDF) в рамках операционной конкурентоспособности. и Программа интернационализации (POCI).

---

Ссылки

[1] Enrique A et al. (2015) Измерение магнитного поля небольших магнитов с помощью смартфона: очень экономичная лабораторная практика для вводных курсов физики. European Journal of Physics  36 :1–11. doi: 10.1088/0143-0807/36/6/065002

[2] Амрани Д. (2005) Электродвижущая сила: закон индукции Фарадея получает трактовку свободного падения магнита. Физическое образование   40 :313–314. дои: 10.1088/0031-9120/40/4/F02

Ресурсы

• Узнайте больше об индукционных варочных панелях: https://edisontechcenter.org/InductionCooking.html
• Узнайте, как использовать закон Фарадея для создания громкоговорителя: Анта А., Гойри Э. (2018 г.) Волны слуха: как построить громкоговоритель. Наука в школе 45 : 38–42.
• Узнайте больше об использовании закона Фарадея в сейсмографах: Bazanos P (2012) Сборка сейсмографа из металлолома. Наука в школе   23: 25–32.
• Подробное видео, объясняющее закон Фарадея: https://www.youtube.com/watch?v=zRmfNvTzIhk&ab_channel=PhysicsHigh
• Посмотрите забавную демонстрацию закона Фарадея: https://www.youtube.com/watch?v=txmKr69jGBk&amp%3Bab_channel=Veritasium&ab_channel=Veritasium

Автор(ы)

Пауло Андре является профессором телекоммуникационной инженерии Высшего технического института Лиссабонского университета, Португалия. Он имеет докторскую степень в области инженерной физики, и его исследовательские интересы включают устройства и системы фотоники.

Ана Бастос — младший научный сотрудник кафедры физики и Института материалов CICECO Университета Авейру, Португалия. Ее специальные исследовательские интересы включают оптоэлектронные системы, интегральную оптику и оптические коммуникации.

Руте Феррейра — доцент кафедры физики Университета Авейру, Португалия. Она координирует исследования в области информационных и коммуникационных технологий в CICECO-Institute of Materials, University of Aveiro.