Индукция | Краткий Философский Словарь | Онлайн словари по философии
ИНДУКЦИЯ (лат. inductio — наведение) — вид умозаключения и метод исследования, суть которого в восхождении познания от частных, единичных фактов к обобщениям все более высокого порядка. Уже Сократ пользовался индуктивным методом для построения понятий. Его описание дал Аристотель. Был знаком и средневековой схоластике, хотя в ней имел крайне ограниченное значение; при становлении науки Нового времени его апологетами были Г.Галилей и И.Ньютон; но статус универсального научного метода индукция получила в работах Ф. Бэкона, положившего ее в основание опытного, эмпирического познания; Дж. С. Милль разработал индуктивную логику как общую методологию наук. Различают несколько видов индукции. Полная индукция, когда обобщение делается на основе анализа всех объектов данного класса. Такая индукция возможна только при ограниченном, обозримом количестве объектов, что бывает нечасто, поэтому она имеет узкий спектр приложения.
 Несущественные признаки ретушируются, а существенные, наоборот, утрируются. Аналогично мыслится и формирование эмпирических обобщений. Однако сама эта модель указывает на ограничения в использовании индуктивного метода. Представим, что необходимо сформулировать понятие «красота». Возьмем фотографию красивой женщины и фотографию красивой, допустим, лошади. Наложим их друг на друга. Но вряд ли в результате этой операции мы получим «красоту» вообще. Более того, мы вначале должны иметь понятие «красоты», чтобы определить, какой предмет красив, а какой нет. Многочисленные критики (а среди них и Платон, и Августин, Декарт, Кант, Поппер) индуктивного метода как универсального доказывают, что далеко не все общие понятия можно вывести, дедуцировать из опыта. Поэтому индуктивный метод должен быть дополнен дедуктивным.
Несущественные признаки ретушируются, а существенные, наоборот, утрируются. Аналогично мыслится и формирование эмпирических обобщений. Однако сама эта модель указывает на ограничения в использовании индуктивного метода. Представим, что необходимо сформулировать понятие «красота». Возьмем фотографию красивой женщины и фотографию красивой, допустим, лошади. Наложим их друг на друга. Но вряд ли в результате этой операции мы получим «красоту» вообще. Более того, мы вначале должны иметь понятие «красоты», чтобы определить, какой предмет красив, а какой нет. Многочисленные критики (а среди них и Платон, и Августин, Декарт, Кант, Поппер) индуктивного метода как универсального доказывают, что далеко не все общие понятия можно вывести, дедуцировать из опыта. Поэтому индуктивный метод должен быть дополнен дедуктивным.- Назад
- Вперёд
|
Индукция — это познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение. Наиболее широко используемая разновидность индуктивных рассуждений — это перечислительные рассуждения, то есть рассуждения, содержащие переход от посылок, утверждающих, что все известные объекты из некоторой совокупности A обладают свойством P, к заключению, утверждающему, что все — в том числе и неизвестные — объекты из A обладают P. Индукция широко используется во всех областях научного познания, играя важную роль при построении эмпирических знаний и переходе от эмпирического знания к теоретическому. В науке основой индукции являются опыт, эксперимент и наблюдение, в ходе которых собираются отдельные факты. Затем, изучая эти факты, анализируя их, исследователь устанавливает общие и повторяющиеся признаки ряда явлений, входящих в определённый класс. На этой основе он строит индуктивное умозаключение, в качестве посылок которого выступают суждения о единичных объектах и явлениях с указанием их повторяющегося признака, и суждение о классе, включающем данные объекты и явления. В качестве вывода получают суждение, в котором признак, выявленный у совокупности единичных объектов, приписывается всему классу. В индуктивных рассуждениях различают полную и неполную индукцию:
Указанные разновидности неполной индукции играют исключительно важную роль в научном познании. Поскольку индукция тесно связана с развитием опытного познания, она стала применяться уже в глубокой древности, хотя теоретически её простейшие формы начали анализироваться только в античной философии, в частности Сократом, который ввёл понятие индуктивных рассуждений, и Аристотелем, который рассматривал их как вспомогательные средства обоснования посылок силлогизмов (см. Силлогизм). У Аристотеля понимание индукции связывается с обобщением наблюдений и означает, по существу, способ умозаключения, посредством которого производится восхождение от частного к общему. Этот аристотелевский взгляд восприняли философы эпикурейской школы, защищавшие индукцию в споре со стоиками как единственный авторитетный метод доказательства законов природы. Дальнейшее развитие теории индукции отмечается лишь в Новое время, когда активный рост науки, обусловленный накоплением, обобщением и систематизацией обширного эмпирического материала, поставил вопрос об исследовании способов научного открытия, а сами виды индуктивных рассуждений стали изучаться на предмет их надёжности. Важное значение в этом отношении имели сочинения Ф. Бэкона, который начал систематическое изучение индуктивных процедур, рассматривая их как единственно научный способ познания и противопоставив индукцию умозрительным рассуждениям. Поскольку методы аристотелевской силлогистики и индукция через простое перечисление подтверждающих случаев не могли быть использованы для анализа эмпирических обобщений, Бэкон в противовес «Органону» Аристотеля создаёт свой «Новый Органон» (1620), в котором излагает «каноны индукции» как методы открытия новых истин в науке. Позднее теория индукции развивалась в работах Дж. Ст. Милля, который предложил пять методов индуктивных рассуждений (каноны индукции Бэкона-Милля), посредством которых выводятся заключения о причинных связях между явлениями: метод сходства; метод различия; объединённый метод сходства и различия; метод остатков; метод сопутствующих изменений. С философской точки зрения наибольший интерес представляет проблема обоснования индукции — нахождения рационального базиса для признания легитимности индуктивных рассуждений. Важность проблемы обусловлена важностью индуктивных рассуждений для современной науки. Её успешное решение предполагает нахождение ответа на вопрос, на каком основании мы признаем некоторые из индуктивных рассуждений приемлемыми, несмотря на то, что во всяком индуктивном рассуждении истинность посылок не гарантирует истинности заключения. Все ответы, предложенные со времени поставившего этот вопрос Д. Юма, оказались безуспешными — всякая попытка обоснования индукции, предложенная до настоящего момента, в неявной форме предполагала легитимность индукции. В настоящее время определённой популярностью пользуется рассмотрение проблемы индукции, предложенное П. Стросоном, утверждающим, что проект обоснования индукции самопротиворечив. |
|
|
Индукция (философия) — New World Encyclopedia
Индукция — это особая форма рассуждения, в которой посылки аргумента поддерживают вывод, но не гарантируют его. Тема индукции важна в аналитической философии по нескольким причинам и обсуждается в нескольких философских областях, включая логику, эпистемологию и философию науки. Однако самый важный философский интерес к индукции заключается в проблеме того, может ли индукция быть «обоснованной». Эту проблему часто называют «проблемой индукции», и она была открыта шотландским философом Дэвидом Юмом (1711–1776).
Содержание
- 1 Перечислительная индукция
- 1.1 Сильная индукция
- 1.2 Слабая индукция
- 1.
 3 Математическая индукция
3 Математическая индукция
- 2 Неиндуктивные рассуждения
- 2.1 Вычет
- 2.2 Похищение
- 3 Задача индукции
- 4 Новая загадка индукции
- 5 Статистический вывод
- 6 Вероятностный вывод
- 7 Ссылки
- 8 Внешние ссылки
- 8.1 Общие источники по философии
- 9 кредитов
Поэтому было бы целесообразно определить, что философы подразумевают под «индукцией», и отличить ее от других форм рассуждения. Было бы также полезно представить проблему индукции Юма, новую загадку индукции Нельсона Гудмана (1906-1998) и статистический, а также вероятностный вывод в качестве возможных решений этих проблем.
Перечислительная индукция
Тип индукции, которой интересуются философы, известен как перечислительная индукция. Инумеративная индукция (или просто индукция ) бывает двух типов: «сильная» индукция и «слабая» индукция.
Сильная индукция
Сильная индукция имеет следующий вид:
А 1 это Б 1 .
А 2 это Б 2 .
A n это B и .
Таким образом, все As являются Bs.
Пример сильной индукции состоит в том, что все воронов черные, потому что каждый ворон, которого когда-либо наблюдали, был черным.
Слабая индукция
Но заметьте, что нет необходимости делать такой строгий вывод с помощью индукции, потому что есть два типа, второй — слабая индукция. Слабая индукция имеет следующий вид:
А 1 это Б 1 .
А 2 это В 2 .
A n это B n .
Следовательно, следующим A будет B.
Примером слабой индукции является то, что, поскольку каждый ворон, которого когда-либо наблюдали, был черным, следующих наблюдаемых воронов будут черными.
Математическая индукция
Перечислительную индукцию не следует путать с математической индукцией. В то время как перечислительная индукция касается вопросов эмпирических фактов, математическая индукция касается вопросов математических фактов. В частности, математическая индукция — это то, что математики используют, чтобы делать заявления о бесконечном наборе математических объектов. Математическая индукция отличается от нумерационной индукции тем, что математическая индукция гарантирует истинность своих выводов, поскольку она опирается на так называемое «индуктивное определение» (иногда называемое «рекурсивным определением»).
Индуктивные определения определяют множества (обычно бесконечные множества) математических объектов. Они состоят из базового пункта , определяющего основные элементы набора, одного или нескольких индуктивных пунктов , определяющих, как дополнительные элементы генерируются из существующих элементов, и заключительного пункта , предусматривающего, что все элементы в наборе либо базовый или в наборе из-за одного или нескольких применений индуктивного предложения или предложений (Barwise and Etchemendy 2000, 567). Например, множество натуральных чисел (N) можно индуктивно определить следующим образом:
Например, множество натуральных чисел (N) можно индуктивно определить следующим образом:
1. 0 — элемент в N 2. Для любого элемента x, если x — элемент N, то (x + 1) — элемент N. 3. Ничто другое не является элементом N, если оно не удовлетворяет условию (1) или (2).
Таким образом, в этом примере (1) является основным предложением, (2) является индуктивным предложением и (3) является заключительным предложением. Теперь индуктивные определения полезны, потому что, как упоминалось ранее, математические индукции безошибочны именно потому, что они основаны на индуктивных определениях. Рассмотрим следующую математическую индукцию, которая доказывает сумму чисел между 0 и натуральным числом n (S n ) таков, что S n = ½n(n + 1), что является результатом, впервые доказанным математиком Карлом Фредериком Гауссом [1777-1855]:
Во-первых, мы знаем, что 0 = ½(0)(0 + 1) = 0. Предположим теперь, что S m = ½m(m + 1) для некоторого натурального числа m.
Тогда, если S m + 1 представляет S m + (m + 1), отсюда следует, что S m + (m + 1) = ½m(m + 1) + (m + 1). Кроме того, поскольку ½m(m + 1) + (m + 1) = ½m 2 + 1,5m + 1, отсюда следует, что ½m 2 + 1,5м + 1 = (½м + ½)(n + 2). Но тогда (½m + ½)(n + 2) = ½(m + 1)((n + 1) + 1). Поскольку первое поддоказательство показывает, что 0 принадлежит множеству, удовлетворяющему условию S n = ½n(n + 1), а второе поддоказательство показывает, что для любого числа, удовлетворяющего условию S n = ½n(n + 1), естественное число, следующее за ним, удовлетворяет условию S n = ½n(n + 1), то по индуктивному определению N число элементов в N совпадает с набором, удовлетворяющим условию S n = ½n(n + 1). Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел.
Обратите внимание, что приведенная выше математическая индукция безошибочна, поскольку она основана на индуктивном определении N. Однако, в отличие от математических индукций, перечислительные индукции не являются безошибочными, поскольку они не основаны на индуктивных определениях.
Однако, в отличие от математических индукций, перечислительные индукции не являются безошибочными, поскольку они не основаны на индуктивных определениях.
Неиндуктивное рассуждение
Индукция контрастирует с двумя другими важными формами рассуждения: дедукция и абдукция .
Дедукция
Дедукция — это форма рассуждения, при которой посылки аргумента гарантируют заключение. Или, точнее, в дедуктивном рассуждении, если посылки верны, то и вывод верен. Существует несколько форм дедукции, но самая основная из них — 9.0055 modus ponens, , который имеет следующую форму:
Если А, то В
А
Следовательно, В
Выводы уникальны, потому что они гарантируют истинность своих выводов, если посылки верны. Рассмотрим следующий пример дедуктивного аргумента:
Либо Тим занимается бегом, либо играет в теннис.
Тим не играет в теннис.
Следовательно, Тим бежит по дорожке.
Вывод этого аргумента не может быть ложным, если его посылки верны. Теперь рассмотрим следующий индуктивный аргумент:
Теперь рассмотрим следующий индуктивный аргумент:
Все вороны, которых когда-либо наблюдали, были черными.
Следовательно, все вороны черные.
Этот аргумент дедуктивно недействителен, потому что его посылки могут быть истинными, а вывод ложным. Например, некоторые вороны могут быть коричневыми, хотя их еще никто не видел. Таким образом, особенностью индукции является то, что они дедуктивно недействительны.
Похищение
Похищение — это форма рассуждения, посредством которой антецедент выводится из его следствия. Форма похищения ниже:
Если A, то B
B
Следовательно, A
Обратите внимание, что абдукция также дедуктивно недействительна, потому что истинность посылок в абдуктивном аргументе не гарантирует истинность их выводов. Например, даже если у всех собак есть ноги, наличие ног не означает, что они принадлежат собаке.
Абдукция также отличается от индукции, хотя обе формы рассуждений широко используются как в повседневных, так и в научных рассуждениях.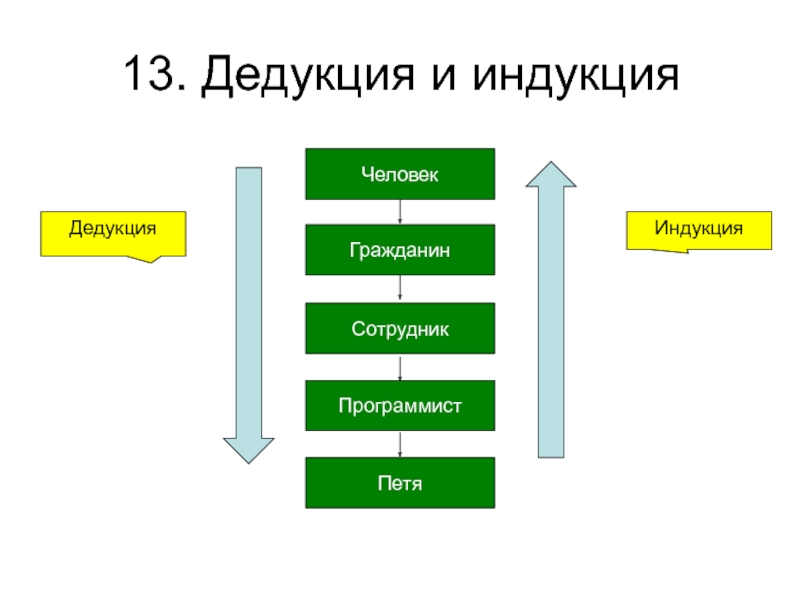 Хотя обе формы рассуждений не гарантируют истинность их выводов, ученые со времен Исаака Ньютона (1643–1727) считали, что индукция — более сильная форма рассуждений, чем абдукция.
Хотя обе формы рассуждений не гарантируют истинность их выводов, ученые со времен Исаака Ньютона (1643–1727) считали, что индукция — более сильная форма рассуждений, чем абдукция.
Проблема индукции
Дэвид Хьюм в своем классическом тексте «Трактат о человеческой природе» усомнился в том, является ли индукция строгой формой рассуждения . В этом тексте Юм утверждает, что индукция является неоправданной формой рассуждения по следующей причине. Считается, что индукции хороши, потому что природа однородна в каком-то глубоком отношении. Например, из небольшой выборки черных воронов можно вывести, что все вороны черные, потому что он полагает, что среди воронов существует закономерность черного цвета, что представляет собой определенное единообразие в природе. Однако почему предполагается, что среди воронов существует закономерность черноты? Чем обосновывается это предположение? Юм утверждает, что известно, что природа однородна либо дедуктивно, либо индуктивно. Однако, по общему признанию, нельзя вывести это предположение, и попытка индуцировать предположение только делает обоснование индукции циркулярным. Таким образом, индукция является неоправданной формой рассуждения. Это проблема индукции Юма.
Таким образом, индукция является неоправданной формой рассуждения. Это проблема индукции Юма.
Вместо того чтобы скептически относиться к индукции, Юм стремился объяснить, как люди производят индукцию, и считал это объяснение хорошим оправданием индукции, которое можно было сделать. Хьюм утверждал, что индукции совершаются из-за привычек . Другими словами, привычка объясняет, почему человек предполагает, что все вороны черные, потому что заранее не видит ничего, кроме черных воронов.
Новая загадка индукции
Нельсон Гудман (1955) поставил под сомнение решение Юма проблемы индукции в его классическом тексте Факты, вымыслы и прогнозы . Хотя Гудман считал Юма выдающимся философом, он считал, что Юм допустил одну серьезную ошибку, отождествив привычку с тем, что объясняет индукцию. Ошибка состоит в том, что у людей легко вырабатывается привычка делать одни наведения, но не делать другие, даже если они подвергаются обоим наблюдениям. Гудман разрабатывает следующий пример grue , чтобы продемонстрировать свою точку зрения:
Предположим, что все наблюдаемые изумруды были зелеными.
Тогда мы легко могли бы предположить, что следующий наблюдаемый изумруд будет зеленым. Но почему зеленый? Предположим, что «злость» — это термин, который применяется ко всем наблюдаемым зеленым вещам или ненаблюдаемым голубым вещам. Тогда все наблюдаемые изумруды также были коричневыми. Тем не менее, никто из нас не стал бы утверждать, что следующий наблюдаемый изумруд будет синим, даже если бы имелись эквивалентные доказательства для этой индукции.
Гудман предвосхищает возражение, что, поскольку «грю» определяется в терминах зеленого и синего, зеленый и синий являются предшествующими и более фундаментальными категориями, чем основными категориями. Однако Гудман отвечает, указывая, что последнее является иллюзией, потому что зеленый и синий могут быть определены с точки зрения грусти и другого термина «блен», где что-то бледнеет только в том случае, если оно наблюдается и синее или ненаблюдаемое и зеленое. Тогда «зеленый» может быть определен как нечто наблюдаемое и мрачное или ненаблюдаемое и синеватое, а «синий» может быть определен как нечто наблюдаемое и сероватое или ненаблюдаемое и мрачное. Таким образом, новая загадка индукции заключается не в том, что оправдывает индукцию, а скорее в том, почему люди делают те или иные индукции, учитывая, что у них есть равных доказательств, чтобы сделать несколько несовместимых индукций?
Таким образом, новая загадка индукции заключается не в том, что оправдывает индукцию, а скорее в том, почему люди делают те или иные индукции, учитывая, что у них есть равных доказательств, чтобы сделать несколько несовместимых индукций?
Решение Гудмана новой загадки индукции состоит в том, что люди проводят индукции, используя знакомые термины, такие как «зеленый», вместо тех, которые включают незнакомые термины, такие как «злой», потому что знакомые термины более укоренились, чем незнакомые термины, которые просто означает, что знакомые термины использовались в большем количестве индукций в прошлом. Таким образом, утверждения, включающие укоренившиеся термины, являются «проецируемыми» и подходят для использования в индуктивных аргументах.
Обратите внимание, что решение Гудмана несколько неудовлетворительно. Хотя он прав в том, что некоторые термины более укоренились, чем другие, он не дает объяснения, почему существует несбалансированное укоренение. Чтобы завершить проект Гудмана, философ Уиллард Ван Орман Куайн (1956–2000) теоретизирует, что укоренившиеся термины соответствуют естественным видам .
Чтобы завершить проект Гудмана, философ Уиллард Ван Орман Куайн (1956–2000) теоретизирует, что укоренившиеся термины соответствуют естественным видам .
Куайн (1969) демонстрирует свою точку зрения с помощью знакомой головоломки философа Карла Хемпеля (1905-1997), известной как «парадокс воронов»:
Предположим, что наблюдение за несколькими черными воронами является доказательством индукции того, что все вороны черные. Тогда, поскольку противопоставление «Все вороны черные» звучит так: «Все нечерные вещи не являются воронами», наблюдение за нечерными вещами, такими как зеленые листья, коричневые баскетбольные мячи и белые бейсбольные мячи, также является доказательством индукции того, что все вороны являются черными. черный. Но как это может быть?
Куайн (1969) утверждает, что наблюдение нечерных вещей не является доказательством индукции того, что все вороны черные, потому что нечерные вещи не образуют естественный вид, а проецируемые термины относятся только к естественным видам (например, «вороны» относятся к вороны). Таким образом, термины являются проектируемыми (и закрепляются), потому что они относятся к естественным видам.
Таким образом, термины являются проектируемыми (и закрепляются), потому что они относятся к естественным видам.
Несмотря на то, что это расширенное решение новой загадки индукции звучит правдоподобно, некоторые из терминов, которые мы используем в естественном языке, не соответствуют естественным видам, тем не менее мы все еще используем их в индукциях. Типичным примером из философии языка является термин «игра», впервые использованный Людвигом Витгенштейном (1889–1951) для демонстрации того, что он называл «фамильными сходствами».
Посмотрите, как компетентные носители английского языка используют термин «игра». Примеры игр: Монополия, карточные игры, Олимпийские игры, военные игры, крестики-нолики и так далее. Итак, что общего у всех этих игр? Витгенштейн сказал бы: «ничего», или если у них есть что-то общее, то это не то, что составляет игр. Так что игры похожи друг на друга, хотя и не образуют вида. Конечно, даже несмотря на то, что игры не являются естественными видами, люди вводят термин «игра». Например, поскольку в недавнем прошлом большинство Олимпийских игр проводились в промышленно развитых городах, большинство Олимпийских игр в ближайшем будущем должно проходить в промышленно развитых городах.
Например, поскольку в недавнем прошлом большинство Олимпийских игр проводились в промышленно развитых городах, большинство Олимпийских игр в ближайшем будущем должно проходить в промышленно развитых городах.
Учитывая сложность решения новой загадки индукции, многие философы объединились с математиками для исследования математических методов обработки индукции. Основным методом математической обработки индукции является статистический вывод, основанный на вероятностных рассуждениях.
Статистический вывод
Вместо того, чтобы спрашивать, все ли вороны черные, потому что все наблюдаемые вороны были черными, статистики спрашивают, какова вероятность того, что вороны черные, при условии, что соответствующая выборка воронов была черной. Вот пример статистического рассуждения:
Предположим, что средняя длина стебля из выборки из 13 растений сои составляет 21,3 см при стандартном отклонении 1,22 см. Тогда вероятность того, что интервал (20,6, 22,1) содержит среднюю длину стебля для всех растений сои, равна 0,9.
5 согласно t-распределению Стьюдента (Сэмюэлс и Витмер, 2003, 189).
Несмотря на привлекательность статистического вывода, поскольку он основан на вероятностных рассуждениях, он действителен ровно настолько, насколько теория вероятностей применима к индуктивным рассуждениям.
Вероятностный вывод
Байесианство — наиболее влиятельная интерпретация теории вероятностей и столь же влиятельная основа для работы с индукцией. Учитывая новые данные, «теорема Байеса» используется для оценки того, насколько должна измениться сила веры в гипотезу.
Ведутся споры о том, что формирует первоначальную степень веры. Объективные байесовцы ищут объективное значение степени вероятности того, что гипотеза верна, и поэтому не избегают философской критики объективизма. Субъективные байесовцы считают, что априорные вероятности представляют собой субъективные степени уверенности, но многократное применение теоремы Байеса приводит к высокой степени согласия в отношении апостериорной вероятности. Следовательно, они не могут обеспечить объективный стандарт для выбора между противоречивыми гипотезами. Теорему можно использовать для получения рационального обоснования веры в некоторую гипотезу, но за счет отказа от объективизма. Такую схему нельзя использовать, например, для объективного выбора между конфликтующими научными парадигмами.
Следовательно, они не могут обеспечить объективный стандарт для выбора между противоречивыми гипотезами. Теорему можно использовать для получения рационального обоснования веры в некоторую гипотезу, но за счет отказа от объективизма. Такую схему нельзя использовать, например, для объективного выбора между конфликтующими научными парадигмами.
Эдвин Джейнс, откровенный физик и байесовец, утверждал, что «субъективные» элементы присутствуют во всех выводах, например, при выборе аксиом для дедуктивного вывода; при выборе начальных степеней уверенности или «априорных вероятностей»; или в выборе вероятностей. Таким образом, он искал принципы для определения вероятностей на основе качественного знания. Максимальная энтропия — обобщение принципа безразличия — и «группы преобразования» — вот два инструмента, которые он создал. Оба пытаются смягчить субъективность назначения вероятностей в конкретных ситуациях, преобразовывая знание особенностей, таких как симметрия ситуации, в однозначный выбор для вероятностных распределений.
«Теорема Кокса», которая выводит вероятность из набора логических ограничений на систему индуктивных рассуждений, побуждает байесовцев называть свою систему индуктивной логикой . Тем не менее вопрос о том, насколько хорошо вероятностный вывод решает первоначальную проблему индукции Юма, а также новую загадку индукции Гудмана, до сих пор является предметом споров в современной философии и, по-видимому, будет обсуждаться еще долгие годы.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Барвайз, Джон и Джон Этчеменди. 2000. Язык, доказательство и логика . Стэнфорд: публикации CSLI.
- Гудман, Нельсон. 1955. Факты, вымыслы и прогнозы . Кембридж: Издательство Гарвардского университета.
- Хьюм, Дэвид. 2002. Трактат о человеческой природе (Дэвид Ф. и Мэри Дж. Нортон, ред.). Оксфорд: Издательство Оксфордского университета.
- Куайн, Западная В.О. 1969. Онтологическая относительность и другие очерки .
 Нью-Йорк: Издательство Колумбийского университета.
Нью-Йорк: Издательство Колумбийского университета. - Сэмюэлс, Майра и Джеффри А. Уитмер. 2003. Статистика наук о жизни . Река Аппер-Сэдл: образование Пирсона.
- Витгенштейн, Людвиг. 2001. Философские исследования (GEM Anscombe, пер.). Оксфорд: Блэквелл.
Внешние ссылки
Все ссылки получены 2 марта 2018 г.
- Индуктивная логика, Стэнфордская философская энциклопедия.
- Дедуктивные и индуктивные аргументы, Интернет-энциклопедия философии.
Общие источники по философии
- Стэнфордская энциклопедия философии.
- Интернет-энциклопедия философии.
- Проект Пайдейя Онлайн.
- Проект Гутенберг.
Кредиты
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3. 0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
- Введение (философия) история
История этой статьи с момента ее импорта в New World Encyclopedia :
- История «Индукции (философия)»
Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
Индукция (философия) — New World Encyclopedia
Индукция — это особая форма рассуждения, в которой посылки аргумента поддерживают вывод, но не гарантируют его. Тема индукции важна в аналитической философии по нескольким причинам и обсуждается в нескольких философских областях, включая логику, эпистемологию и философию науки. Однако самый важный философский интерес к индукции заключается в проблеме того, может ли индукция быть «обоснованной». Эту проблему часто называют «проблемой индукции», и она была открыта шотландским философом Дэвидом Юмом (1711–1776).
Однако самый важный философский интерес к индукции заключается в проблеме того, может ли индукция быть «обоснованной». Эту проблему часто называют «проблемой индукции», и она была открыта шотландским философом Дэвидом Юмом (1711–1776).
Содержание
- 1 Перечислительная индукция
- 1.1 Сильная индукция
- 1.2 Слабая индукция
- 1.3 Математическая индукция
- 2 Неиндуктивные рассуждения
- 2.1 Вычет
- 2.2 Похищение
- 3 Задача индукции
- 4 Новая загадка индукции
- 5 Статистический вывод
- 6 Вероятностный вывод
- 7 Ссылки
- 8 Внешние ссылки
- 8.1 Общие источники по философии
- 9 кредитов
Поэтому было бы целесообразно определить, что философы подразумевают под «индукцией», и отличить ее от других форм рассуждения. Было бы также полезно представить проблему индукции Юма, новую загадку индукции Нельсона Гудмана (1906-1998) и статистический, а также вероятностный вывод в качестве возможных решений этих проблем.
Перечислительная индукция
Тип индукции, которой интересуются философы, известен как перечислительная индукция. Инумеративная индукция (или просто индукция ) бывает двух типов: «сильная» индукция и «слабая» индукция.
Сильная индукция
Сильная индукция имеет следующий вид:
А 1 это Б 1 .
А 2 это Б 2 .
A n это B и .
Таким образом, все As являются Bs.
Пример сильной индукции состоит в том, что все воронов черные, потому что каждый ворон, которого когда-либо наблюдали, был черным.
Слабая индукция
Но заметьте, что нет необходимости делать такой строгий вывод с помощью индукции, потому что есть два типа, второй — слабая индукция. Слабая индукция имеет следующий вид:
А 1 это Б 1 .
А 2 это В 2 .
A n это B n .
Следовательно, следующим A будет B.
Примером слабой индукции является то, что, поскольку каждый ворон, которого когда-либо наблюдали, был черным, следующих наблюдаемых воронов будут черными.
Математическая индукция
Перечислительную индукцию не следует путать с математической индукцией. В то время как перечислительная индукция касается вопросов эмпирических фактов, математическая индукция касается вопросов математических фактов. В частности, математическая индукция — это то, что математики используют, чтобы делать заявления о бесконечном наборе математических объектов. Математическая индукция отличается от нумерационной индукции тем, что математическая индукция гарантирует истинность своих выводов, поскольку она опирается на так называемое «индуктивное определение» (иногда называемое «рекурсивным определением»).
Индуктивные определения определяют множества (обычно бесконечные множества) математических объектов. Они состоят из базового пункта , определяющего основные элементы набора, одного или нескольких индуктивных пунктов , определяющих, как дополнительные элементы генерируются из существующих элементов, и заключительного пункта , предусматривающего, что все элементы в наборе либо базовый или в наборе из-за одного или нескольких применений индуктивного предложения или предложений (Barwise and Etchemendy 2000, 567). Например, множество натуральных чисел (N) можно индуктивно определить следующим образом:
Они состоят из базового пункта , определяющего основные элементы набора, одного или нескольких индуктивных пунктов , определяющих, как дополнительные элементы генерируются из существующих элементов, и заключительного пункта , предусматривающего, что все элементы в наборе либо базовый или в наборе из-за одного или нескольких применений индуктивного предложения или предложений (Barwise and Etchemendy 2000, 567). Например, множество натуральных чисел (N) можно индуктивно определить следующим образом:
1. 0 — элемент в N 2. Для любого элемента x, если x — элемент N, то (x + 1) — элемент N. 3. Ничто другое не является элементом N, если оно не удовлетворяет условию (1) или (2).
Таким образом, в этом примере (1) является основным предложением, (2) является индуктивным предложением и (3) является заключительным предложением. Теперь индуктивные определения полезны, потому что, как упоминалось ранее, математические индукции безошибочны именно потому, что они основаны на индуктивных определениях.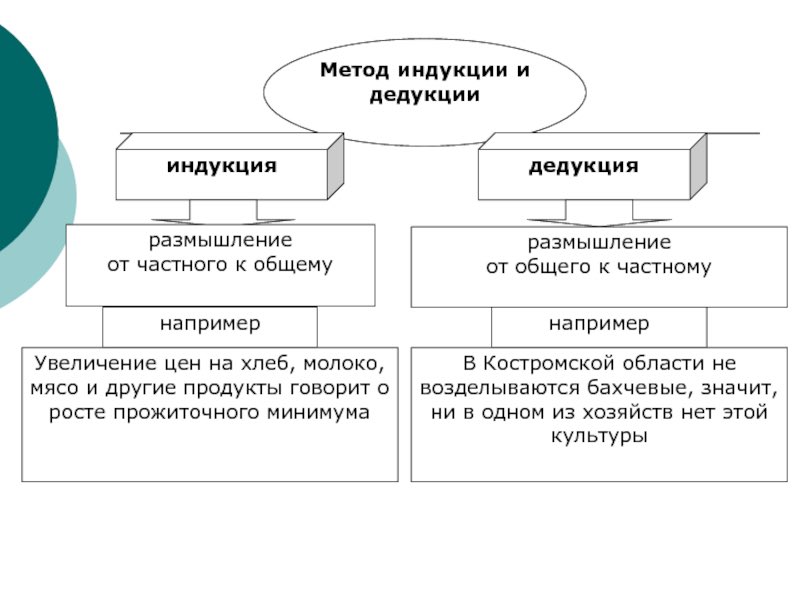 Рассмотрим следующую математическую индукцию, которая доказывает сумму чисел между 0 и натуральным числом n (S n ) таков, что S n = ½n(n + 1), что является результатом, впервые доказанным математиком Карлом Фредериком Гауссом [1777-1855]:
Рассмотрим следующую математическую индукцию, которая доказывает сумму чисел между 0 и натуральным числом n (S n ) таков, что S n = ½n(n + 1), что является результатом, впервые доказанным математиком Карлом Фредериком Гауссом [1777-1855]:
Во-первых, мы знаем, что 0 = ½(0)(0 + 1) = 0. Предположим теперь, что S m = ½m(m + 1) для некоторого натурального числа m. Тогда, если S m + 1 представляет S m + (m + 1), отсюда следует, что S m + (m + 1) = ½m(m + 1) + (m + 1). Кроме того, поскольку ½m(m + 1) + (m + 1) = ½m 2 + 1,5m + 1, отсюда следует, что ½m 2 + 1,5м + 1 = (½м + ½)(n + 2). Но тогда (½m + ½)(n + 2) = ½(m + 1)((n + 1) + 1). Поскольку первое поддоказательство показывает, что 0 принадлежит множеству, удовлетворяющему условию S n = ½n(n + 1), а второе поддоказательство показывает, что для любого числа, удовлетворяющего условию S n = ½n(n + 1), естественное число, следующее за ним, удовлетворяет условию S n = ½n(n + 1), то по индуктивному определению N число элементов в N совпадает с набором, удовлетворяющим условию S n = ½n(n + 1).
Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел.
Обратите внимание, что приведенная выше математическая индукция безошибочна, поскольку она основана на индуктивном определении N. Однако, в отличие от математических индукций, перечислительные индукции не являются безошибочными, поскольку они не основаны на индуктивных определениях.
Неиндуктивное рассуждение
Индукция контрастирует с двумя другими важными формами рассуждения: дедукция и абдукция .
Дедукция
Дедукция — это форма рассуждения, при которой посылки аргумента гарантируют заключение. Или, точнее, в дедуктивном рассуждении, если посылки верны, то и вывод верен. Существует несколько форм дедукции, но самая основная из них — 9.0055 modus ponens, , который имеет следующую форму:
Если А, то В
А
Следовательно, В
Выводы уникальны, потому что они гарантируют истинность своих выводов, если посылки верны. Рассмотрим следующий пример дедуктивного аргумента:
Рассмотрим следующий пример дедуктивного аргумента:
Либо Тим занимается бегом, либо играет в теннис.
Тим не играет в теннис.
Следовательно, Тим бежит по дорожке.
Вывод этого аргумента не может быть ложным, если его посылки верны. Теперь рассмотрим следующий индуктивный аргумент:
Все вороны, которых когда-либо наблюдали, были черными.
Следовательно, все вороны черные.
Этот аргумент дедуктивно недействителен, потому что его посылки могут быть истинными, а вывод ложным. Например, некоторые вороны могут быть коричневыми, хотя их еще никто не видел. Таким образом, особенностью индукции является то, что они дедуктивно недействительны.
Похищение
Похищение — это форма рассуждения, посредством которой антецедент выводится из его следствия. Форма похищения ниже:
Если A, то B
B
Следовательно, A
Обратите внимание, что абдукция также дедуктивно недействительна, потому что истинность посылок в абдуктивном аргументе не гарантирует истинность их выводов. Например, даже если у всех собак есть ноги, наличие ног не означает, что они принадлежат собаке.
Например, даже если у всех собак есть ноги, наличие ног не означает, что они принадлежат собаке.
Абдукция также отличается от индукции, хотя обе формы рассуждений широко используются как в повседневных, так и в научных рассуждениях. Хотя обе формы рассуждений не гарантируют истинность их выводов, ученые со времен Исаака Ньютона (1643–1727) считали, что индукция — более сильная форма рассуждений, чем абдукция.
Проблема индукции
Дэвид Хьюм в своем классическом тексте «Трактат о человеческой природе» усомнился в том, является ли индукция строгой формой рассуждения . В этом тексте Юм утверждает, что индукция является неоправданной формой рассуждения по следующей причине. Считается, что индукции хороши, потому что природа однородна в каком-то глубоком отношении. Например, из небольшой выборки черных воронов можно вывести, что все вороны черные, потому что он полагает, что среди воронов существует закономерность черного цвета, что представляет собой определенное единообразие в природе. Однако почему предполагается, что среди воронов существует закономерность черноты? Чем обосновывается это предположение? Юм утверждает, что известно, что природа однородна либо дедуктивно, либо индуктивно. Однако, по общему признанию, нельзя вывести это предположение, и попытка индуцировать предположение только делает обоснование индукции циркулярным. Таким образом, индукция является неоправданной формой рассуждения. Это проблема индукции Юма.
Однако почему предполагается, что среди воронов существует закономерность черноты? Чем обосновывается это предположение? Юм утверждает, что известно, что природа однородна либо дедуктивно, либо индуктивно. Однако, по общему признанию, нельзя вывести это предположение, и попытка индуцировать предположение только делает обоснование индукции циркулярным. Таким образом, индукция является неоправданной формой рассуждения. Это проблема индукции Юма.
Вместо того чтобы скептически относиться к индукции, Юм стремился объяснить, как люди производят индукцию, и считал это объяснение хорошим оправданием индукции, которое можно было сделать. Хьюм утверждал, что индукции совершаются из-за привычек . Другими словами, привычка объясняет, почему человек предполагает, что все вороны черные, потому что заранее не видит ничего, кроме черных воронов.
Новая загадка индукции
Нельсон Гудман (1955) поставил под сомнение решение Юма проблемы индукции в его классическом тексте Факты, вымыслы и прогнозы . Хотя Гудман считал Юма выдающимся философом, он считал, что Юм допустил одну серьезную ошибку, отождествив привычку с тем, что объясняет индукцию. Ошибка состоит в том, что у людей легко вырабатывается привычка делать одни наведения, но не делать другие, даже если они подвергаются обоим наблюдениям. Гудман разрабатывает следующий пример grue , чтобы продемонстрировать свою точку зрения:
Хотя Гудман считал Юма выдающимся философом, он считал, что Юм допустил одну серьезную ошибку, отождествив привычку с тем, что объясняет индукцию. Ошибка состоит в том, что у людей легко вырабатывается привычка делать одни наведения, но не делать другие, даже если они подвергаются обоим наблюдениям. Гудман разрабатывает следующий пример grue , чтобы продемонстрировать свою точку зрения:
Предположим, что все наблюдаемые изумруды были зелеными. Тогда мы легко могли бы предположить, что следующий наблюдаемый изумруд будет зеленым. Но почему зеленый? Предположим, что «злость» — это термин, который применяется ко всем наблюдаемым зеленым вещам или ненаблюдаемым голубым вещам. Тогда все наблюдаемые изумруды также были коричневыми. Тем не менее, никто из нас не стал бы утверждать, что следующий наблюдаемый изумруд будет синим, даже если бы имелись эквивалентные доказательства для этой индукции.
Гудман предвосхищает возражение, что, поскольку «грю» определяется в терминах зеленого и синего, зеленый и синий являются предшествующими и более фундаментальными категориями, чем основными категориями. Однако Гудман отвечает, указывая, что последнее является иллюзией, потому что зеленый и синий могут быть определены с точки зрения грусти и другого термина «блен», где что-то бледнеет только в том случае, если оно наблюдается и синее или ненаблюдаемое и зеленое. Тогда «зеленый» может быть определен как нечто наблюдаемое и мрачное или ненаблюдаемое и синеватое, а «синий» может быть определен как нечто наблюдаемое и сероватое или ненаблюдаемое и мрачное. Таким образом, новая загадка индукции заключается не в том, что оправдывает индукцию, а скорее в том, почему люди делают те или иные индукции, учитывая, что у них есть равных доказательств, чтобы сделать несколько несовместимых индукций?
Однако Гудман отвечает, указывая, что последнее является иллюзией, потому что зеленый и синий могут быть определены с точки зрения грусти и другого термина «блен», где что-то бледнеет только в том случае, если оно наблюдается и синее или ненаблюдаемое и зеленое. Тогда «зеленый» может быть определен как нечто наблюдаемое и мрачное или ненаблюдаемое и синеватое, а «синий» может быть определен как нечто наблюдаемое и сероватое или ненаблюдаемое и мрачное. Таким образом, новая загадка индукции заключается не в том, что оправдывает индукцию, а скорее в том, почему люди делают те или иные индукции, учитывая, что у них есть равных доказательств, чтобы сделать несколько несовместимых индукций?
Решение Гудмана новой загадки индукции состоит в том, что люди проводят индукции, используя знакомые термины, такие как «зеленый», вместо тех, которые включают незнакомые термины, такие как «злой», потому что знакомые термины более укоренились, чем незнакомые термины, которые просто означает, что знакомые термины использовались в большем количестве индукций в прошлом. Таким образом, утверждения, включающие укоренившиеся термины, являются «проецируемыми» и подходят для использования в индуктивных аргументах.
Таким образом, утверждения, включающие укоренившиеся термины, являются «проецируемыми» и подходят для использования в индуктивных аргументах.
Обратите внимание, что решение Гудмана несколько неудовлетворительно. Хотя он прав в том, что некоторые термины более укоренились, чем другие, он не дает объяснения, почему существует несбалансированное укоренение. Чтобы завершить проект Гудмана, философ Уиллард Ван Орман Куайн (1956–2000) теоретизирует, что укоренившиеся термины соответствуют естественным видам .
Куайн (1969) демонстрирует свою точку зрения с помощью знакомой головоломки философа Карла Хемпеля (1905-1997), известной как «парадокс воронов»:
Предположим, что наблюдение за несколькими черными воронами является доказательством индукции того, что все вороны черные. Тогда, поскольку противопоставление «Все вороны черные» звучит так: «Все нечерные вещи не являются воронами», наблюдение за нечерными вещами, такими как зеленые листья, коричневые баскетбольные мячи и белые бейсбольные мячи, также является доказательством индукции того, что все вороны являются черными.
черный. Но как это может быть?
Куайн (1969) утверждает, что наблюдение нечерных вещей не является доказательством индукции того, что все вороны черные, потому что нечерные вещи не образуют естественный вид, а проецируемые термины относятся только к естественным видам (например, «вороны» относятся к вороны). Таким образом, термины являются проектируемыми (и закрепляются), потому что они относятся к естественным видам.
Несмотря на то, что это расширенное решение новой загадки индукции звучит правдоподобно, некоторые из терминов, которые мы используем в естественном языке, не соответствуют естественным видам, тем не менее мы все еще используем их в индукциях. Типичным примером из философии языка является термин «игра», впервые использованный Людвигом Витгенштейном (1889–1951) для демонстрации того, что он называл «фамильными сходствами».
Посмотрите, как компетентные носители английского языка используют термин «игра». Примеры игр: Монополия, карточные игры, Олимпийские игры, военные игры, крестики-нолики и так далее. Итак, что общего у всех этих игр? Витгенштейн сказал бы: «ничего», или если у них есть что-то общее, то это не то, что составляет игр. Так что игры похожи друг на друга, хотя и не образуют вида. Конечно, даже несмотря на то, что игры не являются естественными видами, люди вводят термин «игра». Например, поскольку в недавнем прошлом большинство Олимпийских игр проводились в промышленно развитых городах, большинство Олимпийских игр в ближайшем будущем должно проходить в промышленно развитых городах.
Итак, что общего у всех этих игр? Витгенштейн сказал бы: «ничего», или если у них есть что-то общее, то это не то, что составляет игр. Так что игры похожи друг на друга, хотя и не образуют вида. Конечно, даже несмотря на то, что игры не являются естественными видами, люди вводят термин «игра». Например, поскольку в недавнем прошлом большинство Олимпийских игр проводились в промышленно развитых городах, большинство Олимпийских игр в ближайшем будущем должно проходить в промышленно развитых городах.
Учитывая сложность решения новой загадки индукции, многие философы объединились с математиками для исследования математических методов обработки индукции. Основным методом математической обработки индукции является статистический вывод, основанный на вероятностных рассуждениях.
Статистический вывод
Вместо того, чтобы спрашивать, все ли вороны черные, потому что все наблюдаемые вороны были черными, статистики спрашивают, какова вероятность того, что вороны черные, при условии, что соответствующая выборка воронов была черной. Вот пример статистического рассуждения:
Вот пример статистического рассуждения:
Предположим, что средняя длина стебля из выборки из 13 растений сои составляет 21,3 см при стандартном отклонении 1,22 см. Тогда вероятность того, что интервал (20,6, 22,1) содержит среднюю длину стебля для всех растений сои, равна 0,9.5 согласно t-распределению Стьюдента (Сэмюэлс и Витмер, 2003, 189).
Несмотря на привлекательность статистического вывода, поскольку он основан на вероятностных рассуждениях, он действителен ровно настолько, насколько теория вероятностей применима к индуктивным рассуждениям.
Вероятностный вывод
Байесианство — наиболее влиятельная интерпретация теории вероятностей и столь же влиятельная основа для работы с индукцией. Учитывая новые данные, «теорема Байеса» используется для оценки того, насколько должна измениться сила веры в гипотезу.
Ведутся споры о том, что формирует первоначальную степень веры. Объективные байесовцы ищут объективное значение степени вероятности того, что гипотеза верна, и поэтому не избегают философской критики объективизма. Субъективные байесовцы считают, что априорные вероятности представляют собой субъективные степени уверенности, но многократное применение теоремы Байеса приводит к высокой степени согласия в отношении апостериорной вероятности. Следовательно, они не могут обеспечить объективный стандарт для выбора между противоречивыми гипотезами. Теорему можно использовать для получения рационального обоснования веры в некоторую гипотезу, но за счет отказа от объективизма. Такую схему нельзя использовать, например, для объективного выбора между конфликтующими научными парадигмами.
Субъективные байесовцы считают, что априорные вероятности представляют собой субъективные степени уверенности, но многократное применение теоремы Байеса приводит к высокой степени согласия в отношении апостериорной вероятности. Следовательно, они не могут обеспечить объективный стандарт для выбора между противоречивыми гипотезами. Теорему можно использовать для получения рационального обоснования веры в некоторую гипотезу, но за счет отказа от объективизма. Такую схему нельзя использовать, например, для объективного выбора между конфликтующими научными парадигмами.
Эдвин Джейнс, откровенный физик и байесовец, утверждал, что «субъективные» элементы присутствуют во всех выводах, например, при выборе аксиом для дедуктивного вывода; при выборе начальных степеней уверенности или «априорных вероятностей»; или в выборе вероятностей. Таким образом, он искал принципы для определения вероятностей на основе качественного знания. Максимальная энтропия — обобщение принципа безразличия — и «группы преобразования» — вот два инструмента, которые он создал. Оба пытаются смягчить субъективность назначения вероятностей в конкретных ситуациях, преобразовывая знание особенностей, таких как симметрия ситуации, в однозначный выбор для вероятностных распределений.
Оба пытаются смягчить субъективность назначения вероятностей в конкретных ситуациях, преобразовывая знание особенностей, таких как симметрия ситуации, в однозначный выбор для вероятностных распределений.
«Теорема Кокса», которая выводит вероятность из набора логических ограничений на систему индуктивных рассуждений, побуждает байесовцев называть свою систему индуктивной логикой . Тем не менее вопрос о том, насколько хорошо вероятностный вывод решает первоначальную проблему индукции Юма, а также новую загадку индукции Гудмана, до сих пор является предметом споров в современной философии и, по-видимому, будет обсуждаться еще долгие годы.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Барвайз, Джон и Джон Этчеменди. 2000. Язык, доказательство и логика . Стэнфорд: публикации CSLI.
- Гудман, Нельсон. 1955. Факты, вымыслы и прогнозы . Кембридж: Издательство Гарвардского университета.
- Хьюм, Дэвид.
 2002. Трактат о человеческой природе (Дэвид Ф. и Мэри Дж. Нортон, ред.). Оксфорд: Издательство Оксфордского университета.
2002. Трактат о человеческой природе (Дэвид Ф. и Мэри Дж. Нортон, ред.). Оксфорд: Издательство Оксфордского университета. - Куайн, Западная В.О. 1969. Онтологическая относительность и другие очерки . Нью-Йорк: Издательство Колумбийского университета.
- Сэмюэлс, Майра и Джеффри А. Уитмер. 2003. Статистика наук о жизни . Река Аппер-Сэдл: образование Пирсона.
- Витгенштейн, Людвиг. 2001. Философские исследования (GEM Anscombe, пер.). Оксфорд: Блэквелл.
Внешние ссылки
Все ссылки получены 2 марта 2018 г.
- Индуктивная логика, Стэнфордская философская энциклопедия.
- Дедуктивные и индуктивные аргументы, Интернет-энциклопедия философии.
Общие источники по философии
- Стэнфордская энциклопедия философии.
- Интернет-энциклопедия философии.
- Проект Пайдейя Онлайн.
- Проект Гутенберг.
Кредиты
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia .

 В научном поиске (см. Методы научного познания) индукция предполагает движение познания от единичных утверждений об отдельных фактах к положениям, носящим более общий характер. В логике (см. Логика) термин «индукция» используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение» и понимается в более узком смысле: как умозаключение, в котором общий вывод строится на основе частных посылок. При этом посылки могут подтверждать или подразумевать истину, но не гарантируют её получения. Этим индукция принципиально отличается от дедукции (см. Дедукция), посредством которой из истинных посылок при соблюдении правил логического вывода всегда получаются истинные заключения.
В научном поиске (см. Методы научного познания) индукция предполагает движение познания от единичных утверждений об отдельных фактах к положениям, носящим более общий характер. В логике (см. Логика) термин «индукция» используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение» и понимается в более узком смысле: как умозаключение, в котором общий вывод строится на основе частных посылок. При этом посылки могут подтверждать или подразумевать истину, но не гарантируют её получения. Этим индукция принципиально отличается от дедукции (см. Дедукция), посредством которой из истинных посылок при соблюдении правил логического вывода всегда получаются истинные заключения. Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P
Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P Ценность индуктивных выводов состоит в том, что они обеспечивают переход от единичных фактов к общим положениям, позволяют обнаруживать зависимости между явлениями, строить эмпирически обоснованные гипотезы и приходить к обобщениям.
Ценность индуктивных выводов состоит в том, что они обеспечивают переход от единичных фактов к общим положениям, позволяют обнаруживать зависимости между явлениями, строить эмпирически обоснованные гипотезы и приходить к обобщениям.
 В этом, собственно, заключается познавательный смысл индукции — абстрагирующая работа мысли помогает получить новое знание при недостатке имеющихся [практических] знаний. Неполнота индукции может обусловливаться не только числом посылок (неполнота в отношении числа посылок), но и их характером (неполнота в отношении характера посылок).
В этом, собственно, заключается познавательный смысл индукции — абстрагирующая работа мысли помогает получить новое знание при недостатке имеющихся [практических] знаний. Неполнота индукции может обусловливаться не только числом посылок (неполнота в отношении числа посылок), но и их характером (неполнота в отношении характера посылок). Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
 Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода.
Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода. В этом процессе обоснование знаний, полученных путём индукции, обязательно предполагает движение от индуктивных обобщений к тому или иному частному случаю. Такого рода вывод представляет собой уже дедуктивное умозаключение. Тем самым индукция дополняется дедукцией, что и обеспечивает переход от вероятностного к достоверному знанию.
В этом процессе обоснование знаний, полученных путём индукции, обязательно предполагает движение от индуктивных обобщений к тому или иному частному случаю. Такого рода вывод представляет собой уже дедуктивное умозаключение. Тем самым индукция дополняется дедукцией, что и обеспечивает переход от вероятностного к достоверному знанию.
 Указанные индуктивные методы являются известными примерами правдоподобных рассуждений (см. Рассуждения правдоподобные). Впоследствии они получили ряд уточнений в работах других исследователей. Однако с помощью «канонов индукции» можно было сделать лишь относительно простые эмпирические обобщения и установить логические отношения между наблюдаемыми свойствами явлений. Когда наука стала исследовать более глубокие законы, раскрывающие сущность и внутренние механизмы явлений, стало очевидным, что эмпирические методы, опирающиеся на индукцию, не в состоянии этого сделать хотя бы потому, что здесь необходимо обращение к абстрактным, теоретическим понятиям. В связи с этим радикально изменился взгляд на индукцию, и вместо логики открытия она стала рассматриваться как метод проверки и обоснования гипотез. В рамках гипотетико-дедуктивного метода (см. Метод гипотетико-дедуктивный) именно эмпирически проверяемые следствия гипотезы могут быть проверены и подтверждены с помощью индуктивно установленных фактов.
Указанные индуктивные методы являются известными примерами правдоподобных рассуждений (см. Рассуждения правдоподобные). Впоследствии они получили ряд уточнений в работах других исследователей. Однако с помощью «канонов индукции» можно было сделать лишь относительно простые эмпирические обобщения и установить логические отношения между наблюдаемыми свойствами явлений. Когда наука стала исследовать более глубокие законы, раскрывающие сущность и внутренние механизмы явлений, стало очевидным, что эмпирические методы, опирающиеся на индукцию, не в состоянии этого сделать хотя бы потому, что здесь необходимо обращение к абстрактным, теоретическим понятиям. В связи с этим радикально изменился взгляд на индукцию, и вместо логики открытия она стала рассматриваться как метод проверки и обоснования гипотез. В рамках гипотетико-дедуктивного метода (см. Метод гипотетико-дедуктивный) именно эмпирически проверяемые следствия гипотезы могут быть проверены и подтверждены с помощью индуктивно установленных фактов. Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики.
Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики. Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов.
Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов. Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.
Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.
 Лекции по истории логики. — М., 1963.
Лекции по истории логики. — М., 1963. Его сфера и границы. — М., 1957.
Его сфера и границы. — М., 1957. — P., 1961.
— P., 1961. 3 Математическая индукция
3 Математическая индукция Тогда, если S m + 1 представляет S m + (m + 1), отсюда следует, что S m + (m + 1) = ½m(m + 1) + (m + 1). Кроме того, поскольку ½m(m + 1) + (m + 1) = ½m 2 + 1,5m + 1, отсюда следует, что ½m 2 + 1,5м + 1 = (½м + ½)(n + 2). Но тогда (½m + ½)(n + 2) = ½(m + 1)((n + 1) + 1). Поскольку первое поддоказательство показывает, что 0 принадлежит множеству, удовлетворяющему условию S n = ½n(n + 1), а второе поддоказательство показывает, что для любого числа, удовлетворяющего условию S n = ½n(n + 1), естественное число, следующее за ним, удовлетворяет условию S n = ½n(n + 1), то по индуктивному определению N число элементов в N совпадает с набором, удовлетворяющим условию S n = ½n(n + 1). Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел.
Тогда, если S m + 1 представляет S m + (m + 1), отсюда следует, что S m + (m + 1) = ½m(m + 1) + (m + 1). Кроме того, поскольку ½m(m + 1) + (m + 1) = ½m 2 + 1,5m + 1, отсюда следует, что ½m 2 + 1,5м + 1 = (½м + ½)(n + 2). Но тогда (½m + ½)(n + 2) = ½(m + 1)((n + 1) + 1). Поскольку первое поддоказательство показывает, что 0 принадлежит множеству, удовлетворяющему условию S n = ½n(n + 1), а второе поддоказательство показывает, что для любого числа, удовлетворяющего условию S n = ½n(n + 1), естественное число, следующее за ним, удовлетворяет условию S n = ½n(n + 1), то по индуктивному определению N число элементов в N совпадает с набором, удовлетворяющим условию S n = ½n(n + 1). Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел. Тогда мы легко могли бы предположить, что следующий наблюдаемый изумруд будет зеленым. Но почему зеленый? Предположим, что «злость» — это термин, который применяется ко всем наблюдаемым зеленым вещам или ненаблюдаемым голубым вещам. Тогда все наблюдаемые изумруды также были коричневыми. Тем не менее, никто из нас не стал бы утверждать, что следующий наблюдаемый изумруд будет синим, даже если бы имелись эквивалентные доказательства для этой индукции.
Тогда мы легко могли бы предположить, что следующий наблюдаемый изумруд будет зеленым. Но почему зеленый? Предположим, что «злость» — это термин, который применяется ко всем наблюдаемым зеленым вещам или ненаблюдаемым голубым вещам. Тогда все наблюдаемые изумруды также были коричневыми. Тем не менее, никто из нас не стал бы утверждать, что следующий наблюдаемый изумруд будет синим, даже если бы имелись эквивалентные доказательства для этой индукции. 5 согласно t-распределению Стьюдента (Сэмюэлс и Витмер, 2003, 189).
5 согласно t-распределению Стьюдента (Сэмюэлс и Витмер, 2003, 189). Нью-Йорк: Издательство Колумбийского университета.
Нью-Йорк: Издательство Колумбийского университета. Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел.
Таким образом, S n = ½n(n + 1) выполняется для всех натуральных чисел. черный. Но как это может быть?
черный. Но как это может быть? 2002. Трактат о человеческой природе (Дэвид Ф. и Мэри Дж. Нортон, ред.). Оксфорд: Издательство Оксфордского университета.
2002. Трактат о человеческой природе (Дэвид Ф. и Мэри Дж. Нортон, ред.). Оксфорд: Издательство Оксфордского университета.