Математика Таблица единиц площади. Измерение площади фигуры с помощью палетки
Материалы к уроку
Конспект урока
|
19. Таблица единиц площади. Измерение площади фигуры с помощью палетки
|
|
Организационный этап
Заливистый школьный звонок Сегодня на уроке мы познакомимся с единицами площади. Научимся измерять площадь фигуры с помощью палетки.
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счет
Задание Вспомним, как найти площадь прямоугольника. Чтобы найти площадь прямоугольника, нужно умножить его длину на ширину. Не забывайте, что площадь будет выражена в соответствующих единицах измерения.
Решите задачи.
Задача 1. Вычислите площадь прямоугольника со сторонами 7 и 2 см. 7 · 2 = 14 (см²). Чтобы найти площадь фигуры, надо длину умножить на ширину. Площадь прямоугольника 14 см².
Задача 2. Площадь прямоугольника 18 дм². 18 : 6 = 3 (дм) Чтобы найти длину неизвестной стороны, надо площадь разделить на длину известной стороны. Длина другой стороны 3 дм.
Задача 3. Площадь прямоугольника 72 м². Длина – 12 м. Во сколько раз ширина прямоугольника меньше его длины? Сразу на вопрос задачи ответить нельзя, т.к. надо знать длины обеих сторон. Сначала узнаем длину второй стороны. 1) 72 : 12 = 6 (м) – ширина прямоугольника. Потом сравним длины. 2) 12 : 2 = 2 (р.) – ширина меньше длины. Мы видим, что ширина меньше длины в 2 раза. |
|
Кто догадался, выполняя задания устного счета, чем мы сегодня будем заниматься на уроке?
|
|
Этап усвоения новых знаний Какие единицы измерения площади вы знаете? Помогите Мудрой Сове заполнить таблицу
1 см² = 100 мм².
1 дм² = 100 см² = 10 000 мм².
Продолжайте заполнять таблицу по аналогии.
Запомните таблицу соотношения единиц площади. 1 см² = 100 мм² 1 дм² = 100 см² = 10 000 мм² 1 м² = 100 дм² = 10 000 см² = 1 000 000 мм² 1 км² = 10 000 дм² = 1 000 000 м² 1 а = 100 м² = 10 000 дм² = 1 000 000 см² 1 га = 100 а = 10 000 м² = 1 000 000 дм² 1 км² = 100 га= 10 000 а |
|
Закончите предложение. Чтобы найти площадь прямоугольника, нужно … Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.
Как найти площадь фигуры, если длины сторон не указаны?
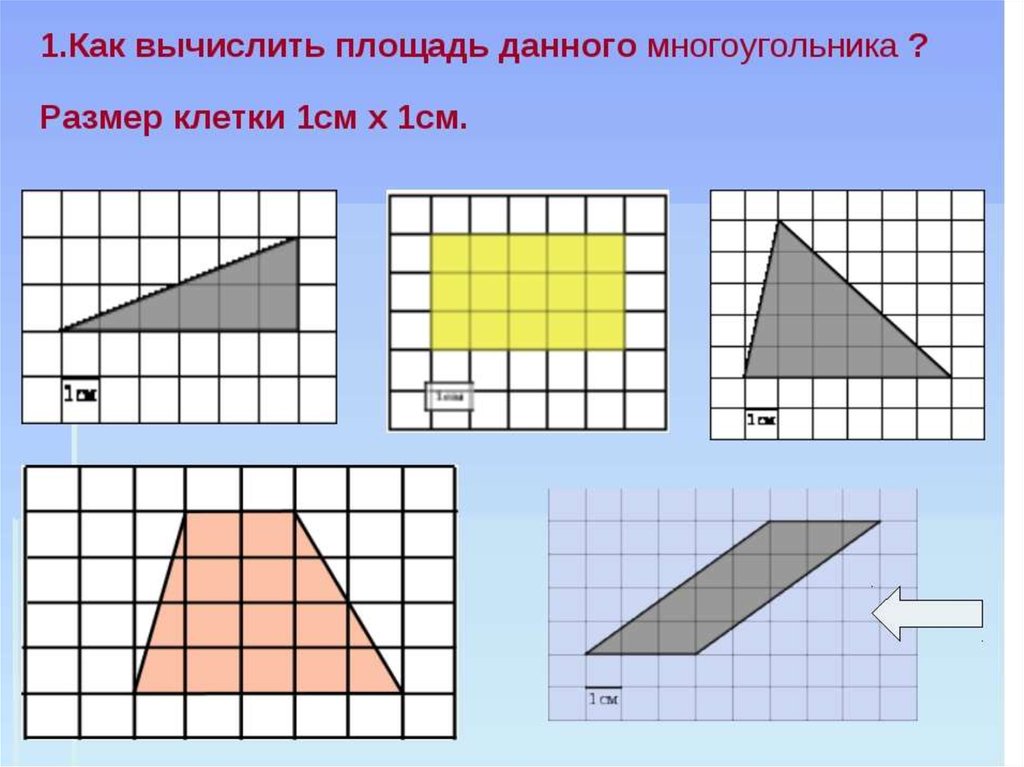
Прямоугольник со сторонами 6 см и 4 см. Разделим фигуру на квадратные сантиметры. Получилось 24 квадрата со стороной 1 см. Площадь – 24 см. Найдите площадь фигуры. Эта фигура не прямоугольной формы. Как быть? Можно как бы поместить нашу фигуру в прямоугольную форму, разбить на квадратные сантиметры и посчитать. Не все квадраты целые. Что будем делать?
Ученые договорились складывать все неполные квадраты и делить их количество на 2. Если таких квадратов получится нечётное количество, то их надо увеличить или уменьшить на 1. Площадь таких фигур можно посчитать приблизительно. Целых квадратов 1, нецелых – 8. Воспользуемся формулой, разделим 8 на 2, будет 4.
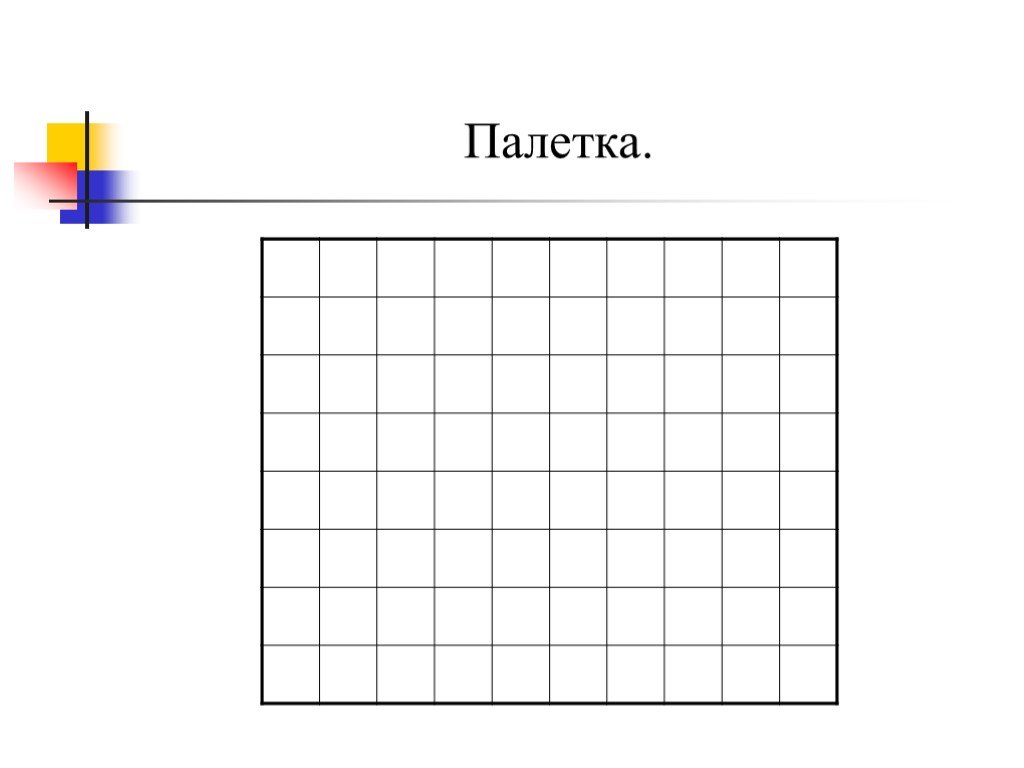
Вы заметили, что самим расчерчивать фигуру на квадраты очень долго? Чтобы сэкономить время и ускорить работу, люди придумали палетку. Палетка – это прозрачная пластинка (плёнка), разделённая на равные квадраты (например, квадратные миллиметры, квадратные сантиметры, квадратные дециметры).
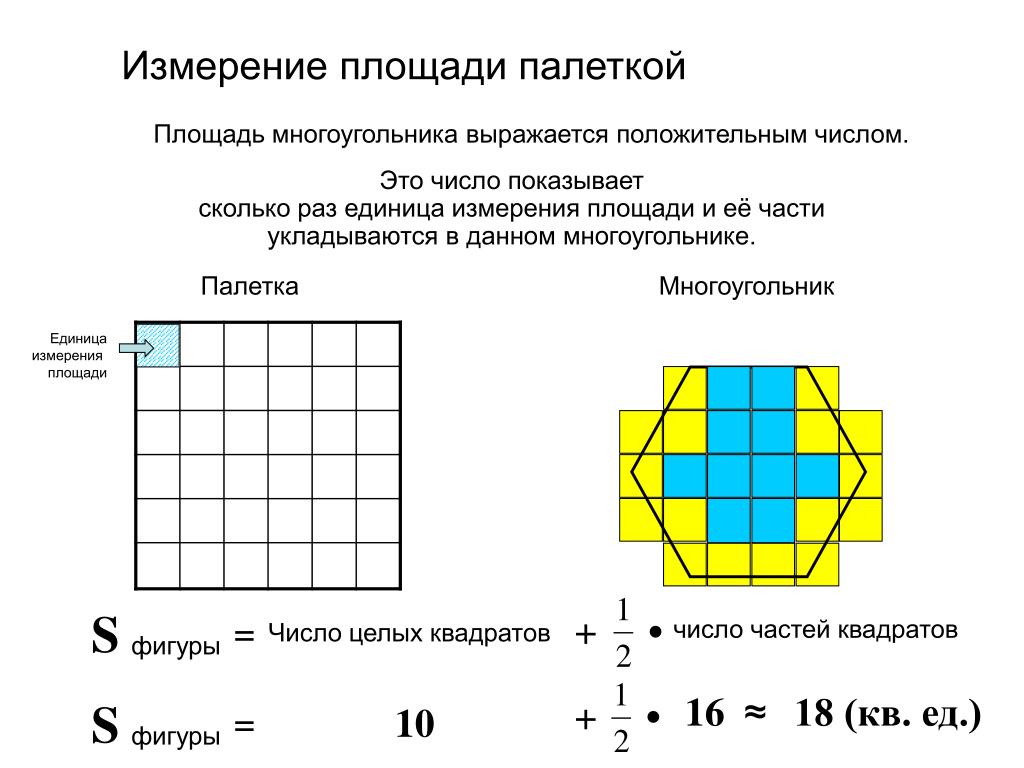
Мудрая Сова решила вывести алгоритм нахождения площади фигуры с помощью палетки. Проверьте, всё ли она сделала правильно. 1. Наложить палетку на фигуру. 2. Подсчитать количество целых квадратов. 3. Подсчитать количество нецелых квадратов. 4. Число нецелых квадратов разделить на 2 и прибавить к числу целых квадратов.
|
|
Закрепление материала
Выберите правильный ответ.
Сантиметр, километр, гектар, дециметр. (Гектар)
100 мм², 10 000 мм², 1000 мм², 100 000 мм². (В 1 дм² содержится 10 000 мм²)
79 см², 790 см², 7900 см², 790 000 см². (790 000 см²)
15 м², 150 м², 1500 м², 15 000 м². (1500 м²)
Найдем площадь кухни: 18 : 2 = 9 (м²) Найдем площадь прихожей: 18 : 3 = 6 (м²) Вычислим площадь квартиры: 18 + 9 + 6 + 4 = 37 (м²) Площадь квартиры 37 м². |
|
Выразите в квадратных сантиметрах 7 дм², 54 м², 2 а. Проверьте себя. 7 дм² = 700 см² 54 м² = 540 000 см² 2 а = 2 000 000 см²
Проверьте работу соседа по парте. 5 км² = 5 000 000 м² 31 а = 310 000 м² 20 га = 200 000 м² |
|
Вычислите площадь фигуры. Целых квадратов 6. Нецелых квадратов 8. Делим 8 на 2, получается 4. 4 плюс 6 – это 10. Площадь данной фигуры приблизительно 10 квадратных сантиметров. |
|
Вычислите площадь фигуры. Целых квадратов нет. Нецелых квадратов 10. Делим 10 на 2, получается 5. Площадь данной фигуры приблизительно 5 квадратных дециметров.
|
|
Этап подведения итогов
Чему научились на уроке? Что такое палетка? Для чего она служит? Как измеряют площадь с ее помощью? Какой формулой пользуются для измерения приблизительной площади фигур?
|
|
Рефлексия
Оцените свою работу на уроке. |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
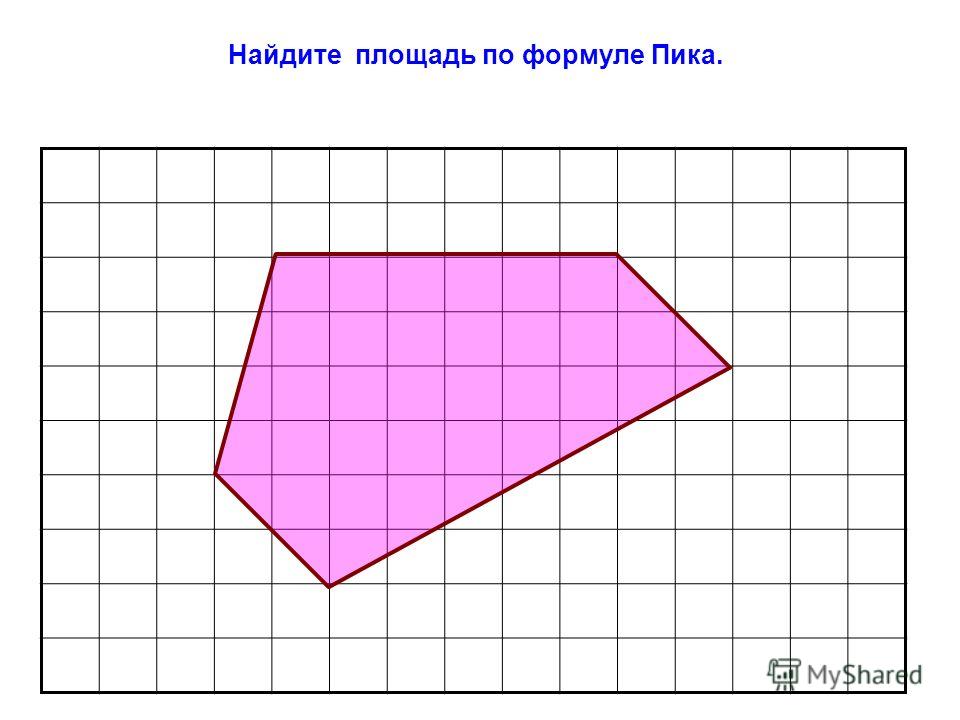
Измерение площади фигуры с помощью палетки.
Муниципальное бюджетное общеобразовательное учреждение
Тёпловская средняя общеобразовательная школа
Методическая разработка
открытого урока математики
по теме:
«Измерение площади фигуры с помощью палетки»
4 класс
(программа «Школа России»)
Разработан
учителем начальных классов
Зиновой А. М.
П. Тёплое
2022 г.
Тема урока: «Измерение площади фигур с помощью палетки»
Уровень образования: начальное общее образование
Класс: 4 класс
Предмет: математика
Тип урока: урок получения новых знаний
Форма урока: урок-путешествие
Используемые учебники и учебные пособия: учебник «Математика» М.И.Моро: 4 класс – Москва: Просвещение, 2020, 1 часть.
Используемая методическая литература:
Поурочные разработки по математике /Т.Н.Ситникова: 4 класс – Москва: Вако, 2018.
М.И.Моро. Методические рекомендации для учителя – Москва: Просвещение, 2018.
Оборудование:
учебник «Математика» М.И.Моро,
тетрадь для учащихся,
компьютер,
мультимедийный проектор,
презентация по теме урока;
карточки для индивидуальной и групповой работы;
палетки.
Цель:Познакомить учащихся со способом нахождения площади фигур различной формы с помощью палетки, закрепить знание единиц площади и единиц длины.
Познавательные УУД
1. Познакомить учащихся со способом нахождения площади фигур различной формы с помощью палетки.
2. Развивать умение использовать способы решения проблем творческого и поискового характера.
3. Совершенствовать вычислительные навыки при решении задач.
Коммуникативные УУД
1. Учить формулировать собственное мнение и позицию.
2. Развивать умение сотрудничать и работать в группе; паре.
Регулятивные
Учить принимать и сохранять цели и задачи учебной деятельности, искать и находить средства их достижения.
Определяют наиболее эффективные способы достижения результата.
Оценивают причины успеха/неуспеха в учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха.
Ход урока:
Деятельность учителя | Деятельность учащихся | УУД |
1.Орг. момент Чтобы спорилось нужное дело Чтобы в жизни не знать неудач, В мир математики отправимся смело В мир примеров и разных задач. Сегодня мы с вами отправимся в очередное путешествие в страну Геометрии. Чтобы вы пожелали себе и своим друзьям перед уроком? 2.Определить тему и цель урока Чтобы узнать, о какой величине пойдёт речь на сегодняшнем уроке, выполните задание на листе №1 Устный счет 1 м =…см 3 дм =…мм 7 см 8 мм =… мм 1 м = …дм 1 км = … м 6 м = …см 1 м2 =…дм2 Проверяем. Какая единица измерения у нас лишняя? Почему? Над какой величиной будем работать? Определите тему нашего урока. Какую цель поставим перед собой? Какими знаниями вы уже владеете в рамках этой темы? 3.Повторение пройденного. Прием «Кластер» Вспомните всё, что вы знаете о площади. Заполните кластер на листе №2. Расскажите о площади по кластеру. Что осталось незаполненным? Значит, на уроке мы узнаем что-то новое. Чего же мы ещё не знаем? Посмотрите на доску. Рассмотрите геометрические фигуры. Назовите их. Площадь каких фигур мы можем найти с помощью формулы? На доске прямоугольник со сторонами 7дм и 2дм. Найдите его площадь. Квадрат со стороной 3см. Найдите его площадь. А как найти площадь у овала? 4.Работа над новым материалом. Выявление причины затруднения. Построение проекта выхода из затруднения. Какая проблема? Можно ли найти площадь криволинейных фигур по формуле? С помощью линейки? Как быть? Оказывается, есть такое приспособление, которое называется палетка. Что вы узнали? Палетка — прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры. С её помощью можно узнать площадь овала. Как это сделать? Коллективное составление кластера «Алгоритм измерение площади фигур с помощью палетки». 1) наложить палетку 2) 3) : 2 4) + ( :2 ) Решение задачи с овалом. Лист №3. 10+14:2=17 см2 Как вы думаете. Ответ будет точный? Где мы можем применять палетку? Каким способом мы определили площадь овала? Что можем записать в наш кластер лист №2? Ф и з к у л ь т м и н у т к а 5.Закрепление нового материала. Прием «Логическая цепочка» наших действий. Выполняем задание 191. 1 фигура=14 см2, 2 фигура=12 см2 Продолжаем работу над единицами измерения площади. Мы постоянно говорим о единицах площади. Можем ли мы эти знания применить в жизни? Где? Как? А можем ли мы измерить площадь нашего класса? С помощью чего? Как записать результат нашего измерения? Дано: Решение: 2 шага=1м а=7 м S=a.b в=5м S=7.5=35 м2 S=? Ответ: S=35м2 Решение геометрической задачи. 6. Итог урока. Возьмите лист №4. Подведём итог нашего урока. Прочитайте утверждения, если вы с ними согласны, то справа в столбике поставьте +, если нет, то -. Прием «Верные и неверные утверждения» Лист №4. |
1. | Площадь – это то, что находится внутри фигуры. | |
2. | Площадь измеряется в мм,см,дм,м,км | |
3. | Площадь – это величина | |
4. | Формула площади прямоугольника S=а. | |
5. | Найти площадь геометрических фигур можно только с помощью линейки |
Достигли мы цели, которую поставили в начале урока? Что нового вы узнали? Оцените себя.
Домашнее задание: тетрадь стр.34 №60, 61
Работают в группах.
Ответ:
Работа по группам.
Ответ: палетка
Работа в парах
Коллективно, один у доски.
Коллективно, один у доски.
Работа индивидуально
Интерес к познанию, к новому учебному материалу, к овладению новыми способами познания
Осуществляют связь компонентов
Навыки сотрудничества со сверстниками в разных ситуациях.
Навыки к исследовательской и поисковой деятельности;
Ищут варианты
Появляется проблема
Решение проблемы
Находят площадь овала.
Делают вывод:
Воспринимать и понимать причины успеха/неуспеха в учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха;
Сравнивают цели учебной деятельности, какими средствами их достигли.
Приложения.
Лист №1
1 м =…см
3 дм =…мм
7 см 8 мм =… мм
1 м = …дм
1 км = … м
6 м = …см
1 м2 =…дм2
Лист №2
Лист №3
Вычисли площадь овала с помощью палетки.
Лист №4
1. | Площадь – это то, что находится внутри фигуры. | |
2. | Площадь измеряется в мм, см, дм, м, км | |
3. | Площадь – это величина | |
4. | Формула площади прямоугольника S = а.в | |
5. | Найти площадь геометрических фигур можно только с помощью линейки |
Площадь прямоугольника — 3 метода
Содержание
В геометрии площадь плоской двумерной формы — это область, покрываемая ею (область, ограниченная периметром) на двумерной плоскости. Другими словами, мы можем сказать, что площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Здесь единичный квадрат относится к квадрату со стороной $1$ единицы. Хорошим примером является графическая бумага. Подсчитав количество квадратов в регионе, вы можете найти площадь этого региона.
Здесь единичный квадрат относится к квадрату со стороной $1$ единицы. Хорошим примером является графическая бумага. Подсчитав количество квадратов в регионе, вы можете найти площадь этого региона.
Прямоугольник — 2D-плоскость Рис. 9{2}$.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Использование площади прямоугольника
Площадь прямоугольника упрощает задачу и помогает нам вычислить пространство, которое занимает наша повседневная жизнь.
Например,
- Если вам нужно покрыть блокнот, вы можете легко подсчитать, сколько бумаги вам понадобится, найдя площадь.
- Если фермеру нужно вспахать свое поле, площадь поля даст ему именно тот регион, который ему нужен.
- Для строительного плана дома нам нужно знать количество плиток, необходимых для пола, что возможно по формуле площади
Формула площади прямоугольника с использованием сторон
Формула площади равна произведению длины и ширины (или ширины) прямоугольника. {2}$ или $12 кв см$. 9{2}$.
{2}$ или $12 кв см$. 9{2}$.
Как вычислить площадь прямоугольника по сторонам?
Площадь прямоугольника равна произведению его длины на ширину. Для нахождения площади прямоугольника используются следующие шаги:
Шаг 1: Запишите длину и ширину прямоугольника
Шаг 2: Преобразование длины и ширины в одни и те же единицы, если единицы длины и ширины не совпадают
Шаг 3: Подставить значения длины и ширины прямоугольника в формулу 9{2}$.
Пример 2: Найдите площадь прямоугольника, длина которого 1,5 м$, а ширина 60 см$.
Длина прямоугольника $l = 1,5 м$
Ширина прямоугольника $w = 60 см$
Обратите внимание, что длина и ширина имеют разные единицы измерения. Итак, вам нужно преобразовать либо $m$ в $cm$, либо $cm$ в $m$.
Преобразуем ширину в $m$.
Ширина $w = 60 см = \frac {60}{100} = 0,60 м$.
Площадь прямоугольника $A = l \times w$
9{2}$ Необходимое количество каменных плит = $\frac {\text{Площадь пути}}{\text{Площадь одной каменной плиты}} = \frac {39 000 000}{260} = 150000$.
Формула площади прямоугольника с использованием диагонали
Вы также можете найти площадь прямоугольника, если известны длины его диагонали и одной из его сторон (длина или ширина). В этом случае вы используете теорему Пифагора, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник длины $l$, ширины $w$ и диагонали $d$. 9{2}$. Площадь прямоугольника зависит от его длины и ширины и рассчитывается путем вычисления произведения длины и ширины.
Практические задачи
- Найдите площадь прямоугольника, длина и ширина которого равны
- Длина = 9 долларов США за единицу $ и ширина = 7 долларов США за единицу $
- Длина = 15 мм$ и ширина = 12 мм$
- Длина = 17 долларов США в дюймах и ширина = 8 долларов США за единицу
- Найдите длину прямоугольника, площадь и ширина которого равны
- Площадь = 9 долларов США{2}$ и ширина = 7 долларов см долларов США
- Площадь прямоугольного забора составляет 500 квадратных футов.
 Если ширина забора 20 футов, то найдите его длину
Если ширина забора 20 футов, то найдите его длину - Найдите площадь прямоугольника, длина которого в $12 см$, а ширина в $3$ меньше
- Сколько квадратов со стороной $2 см$ занимают поверхность прямоугольника длиной $24$ см и шириной $8 см$?
Рекомендуемое чтение
- Что такое длина? (с определением, единицей измерения и преобразованием)
- Вес – определение, единица измерения и преобразование
- Что такое емкость (определение, единицы измерения и примеры)
- Что такое время? (с определением, фактами и примерами)
- Что такое температура? (с определением и единицами измерения)
- Чтение календаря
- Периметр прямоугольника – определение, формула и примеры
- Периметр квадрата – определение, формула и примеры
- Площадь квадрата – определение, формула и примеры 9{2}}$
Что вы подразумеваете под площадью прямоугольника?
Площадь прямоугольника – это область, занимаемая периметром (границей) прямоугольника.
Вам также может понравиться
Как решать линейные уравнения с матрицами (с методом и примерами)
Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости
Читать далее
Правило Крамера – определение, формулы и примеры
Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x
Читать далее
Карточки по математике для печати бесплатно – скачать PDF
Карточки по математикеявляются ценным пособием для учащихся всех возрастов и
. Читать далее
Как найти размеры прямоугольника | Главная Путеводители
Даниэль Смит Обновлено 15 декабря 2021 г.
Нахождение размеров прямоугольника — важный математический навык. Как и при нахождении размеров других геометрических фигур, вы должны следовать основным правилам и уравнениям для формул. Понимание этих принципов на первый взгляд может показаться неважным, но прилежный парень объясняет, что геометрия регулярно используется в повседневной жизни.
Понимание этих принципов на первый взгляд может показаться неважным, но прилежный парень объясняет, что геометрия регулярно используется в повседневной жизни.
Основы прямоугольной геометрии
Разработчики видеоигр используют геометрические вычисления для проектирования своей графики, а архитекторы и дизайнеры используют геометрию для выполнения различных задач. Медицинские работники также часто используют его, особенно в медицинских приложениях, таких как МРТ, рентген, физиотерапия и ядерная визуализация. Вам также может понадобиться найти эти размеры, если вы работаете над проектом по благоустройству дома.
Чтобы найти размеры прямоугольника, вы начнете с нескольких измерений и выберите правильные уравнения, чтобы подставить их. Двумя основными размерами прямоугольника являются длина (L) и ширина (W). Измерьте их в футах и дюймах с помощью рулетки или линейки. Оттуда вы можете вычислить площадь или периметр.
Вы можете упростить расчеты, преобразовав измерения в десятичные числа, чтобы избежать работы с дробями. Если вы используете дюймы, разделите на 12 следующим образом, используя в качестве примера 5 дюймов: 5 дюймов разделить на 12 = 0,42 фута.
Если вы используете дюймы, разделите на 12 следующим образом, используя в качестве примера 5 дюймов: 5 дюймов разделить на 12 = 0,42 фута.
Площадь и периметр: размеры прямоугольника
Важно различать площадь (A) и периметр (P) прямоугольников и квадратов. Согласно Куэмату, площадь — это количество пространства, занимаемое любой фигурой, например прямоугольником. Другими словами, общее количество квадратных единиц, которые могут поместиться в прямоугольник, определяет его фактическую площадь. Периметр — это измерение длины контура фигуры. В то время как площадь измеряется в квадратных единицах, периметр измеряется в футах, дюймах или сантиметрах.
Чтобы определить площадь, используйте это простое уравнение: Площадь = L, умноженная на W. Поскольку вы измеряете площадь в квадратных футах, ваше окончательное число должно отражать это. Если прямоугольник имеет длину 12 футов и ширину 6 футов, его площадь равна 72 квадратных фута. Когда некоторые измерения указаны в футах, а некоторые в дюймах, эти цифры должны быть преобразованы в футы, а затем в квадратные футы. Для этой операции разделите количество дюймов на 12. Например, 7 дюймов ÷ 12 = 0,583 фута.
Когда некоторые измерения указаны в футах, а некоторые в дюймах, эти цифры должны быть преобразованы в футы, а затем в квадратные футы. Для этой операции разделите количество дюймов на 12. Например, 7 дюймов ÷ 12 = 0,583 фута.
Чтобы найти периметр, нужно сложить длины всех четырех сторон. Если у вас есть прямоугольник длиной 10 футов и шириной 8 футов, вы должны использовать уравнение 10 + 10 + 8 + 8 = 36. Это потому, что есть две стороны с длиной 10 футов и две стороны с 8-футовой длиной. ширина стопы.
2D-прямоугольники и 3D-прямоугольные призмы или кубоиды
В некоторых случаях может потребоваться вычислить размеры прямоугольника, который представляет собой просто два измерения. Это может быть полезно, если вы пытаетесь выяснить, какой размер ковра вам нужен для гостиной или если вы планируете прямоугольный огород. Приведенные выше формулы применимы к двумерным прямоугольникам.
В других случаях может потребоваться рассчитать размеры трехмерной фигуры, похожей на прямоугольник, например картонной коробки.


 Длина одной его стороны 6 дм. Найдите длину другой стороны.
Длина одной его стороны 6 дм. Найдите длину другой стороны.  см квадратных миллиметров?
см квадратных миллиметров? 
 1 плюс 4 – 5. Площадь данной фигуры 5 см².
1 плюс 4 – 5. Площадь данной фигуры 5 см².

 Информацию о ней вы найдёте в учебнике на стр.43.
Информацию о ней вы найдёте в учебнике на стр.43.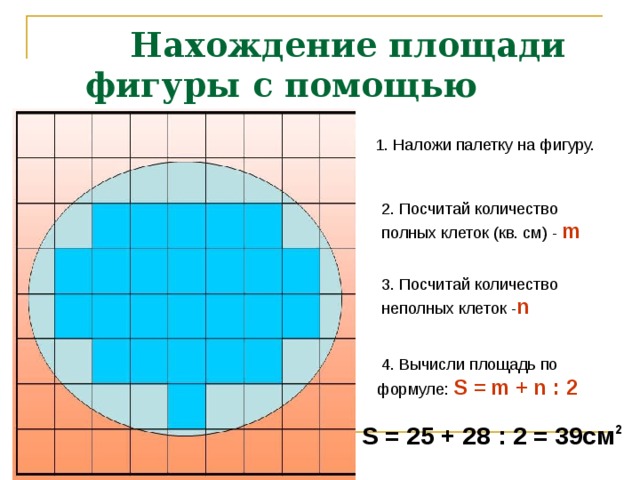 Работа по учебнику стр.44 №196.
Работа по учебнику стр.44 №196. в
в Если ширина забора 20 футов, то найдите его длину
Если ширина забора 20 футов, то найдите его длину