Математика и логика — Математическая составляющая
Математика и логика Поделиться
Лев Дмитриевич Беклемишев
Логика как наука — предмет почти такой же древний, как и математика. В античное время и средние века она была составной частью тривиума (грамматика, риторика, логика/диалектика) — базового уровня образования; математические же предметы (арифметика, геометрия, астрономия и музыка) составляли следующий, более продвинутый, уровень, называемый квадривиум. (От слова «тривиум» происходит одно из любимых математиками выражений «тривиально».) Предметы тривиума понимались как науки о том, как правильно, без ошибок, писать, говорить и, соответственно, рассуждать.
Мы расскажем о том, как и почему возникла математическая логика, что она изучает, какие у неё есть достижения и современные применения.
От Аристотеля к Булю. Основы учения о правильных рассуждениях заложил Аристотель. Он заметил, что корректные умозаключения следуют определённым элементарным схемам, называемым
Силлогистика Аристотеля была не лишена недостатков, однако в целом была выдающейся теорией и стала основой изучения логики на протяжении античности и средних веков. В трудах античных стоиков и средневековых схоластов она была модифицирована и дополнена. В таком виде аристотелевская логика дошла вплоть до середины XIX века, где и встретила революцию, связанную с проникновением в логику математических методов.
Возникновение математической логики полностью изменило представления учёных как о методах исследования логики, так и о том, что составляет сам предмет её изучения.
Аналогия между рассуждениями и вычислениями несколько глубже, чем кажется на первый взгляд. Возникновение логики как математической науки было связано с работами британских учёных Джорджа Буля и Августа де Моргана, которые обнаружили, что с логическими высказываниями можно оперировать как с алгебраическими выражениями. Например, если сложение читать как логическую связку «или», умножение как «и», а равенство как «равносильно», то для любых высказываний $a$, $b$ выполняются законы
$$ a+b=b+a,\quad a\cdot(b+c)=a\cdot b+a\cdot c, $$
как и многие другие привычные нам законы арифметики. Но, помимо этого, в алгебре высказываний выполняется и кое‐что непривычное, например всегда
$$ a+a=a\quad \hbox{и}\quad a+(b\cdot c)=(a+b)\cdot (a+c). $$
Такой взгляд на логику высказываний и силлогистику оказался и неожиданным, и плодотворным. В наше время эту точку зрения разрабатывает область, называемая алгебраической логикой, а одним из её центральных понятий является понятие булевой алгебры, названной так в честь её первооткрывателя. Эта область исследований, через понятие реляционной алгебры, обобщающей булеву, привела в 1960‐х годах к теории реляционных баз данных, в наше время лежащей в основе самых распространённых языков запросов, таких как SQL.
Математизация логики и аксиоматизация математики. Движущей причиной процесса математизации логики был назревший в самой математике на рубеже XIX—XX веков кризис оснований. С одной стороны, во второй половине XIX века в математике получил распространение удобный язык теории множеств, созданной Георгом Кантором. Математики стали уверенно использовать в своих рассуждениях конструкции с бесконечными множествами. Математика, вооружённая теорией множеств, шла от успеха к успеху.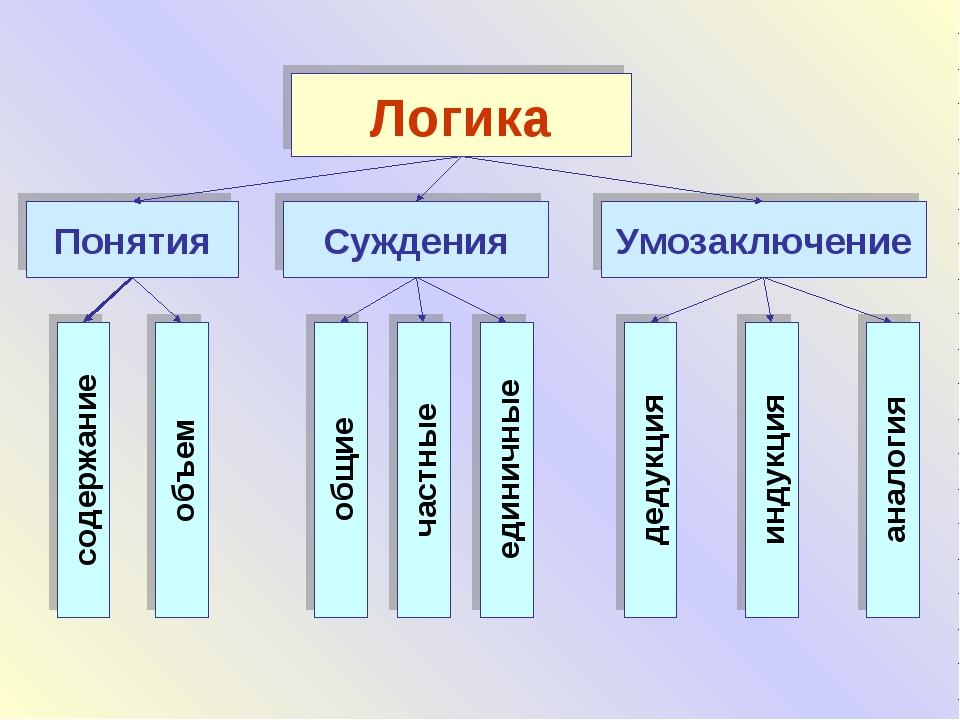
С другой стороны, в самой теории множеств Кантора обнаружились парадоксы, которые указывали на то, что с этой теорией не всё в порядке на самом базовом уровне. Простейший парадокс такого рода, в фольклорном варианте известный как парадокс брадобрея, был придуман Бертраном Расселом: рассмотрим множество $R$ всех тех множеств, которые не содержат сами себя в качестве элемента. Тогда $R\in R$ если и только если $R\notin R$, противоречие.
Такое положение дел заставило многих выдающихся математиков и философов той эпохи (Пеано, Фреге, Рассел, Гильберт, Пуанкаре, Брауэр, Вейль и др.) задуматься об основаниях математики. Их волновали такие фундаментальные вопросы как:
- Что означает доказать математическую теорему? Какие средства при этом законно использовать?
- Что значит выразить то или иное математическое понятие или утверждение на том или ином языке?
- Когда мы говорим об истинности и о доказуемости какого‐либо математического утверждения, имеется ли в виду одно и то же?
Параллельно в математике стали укореняться новые стандарты строгости. Основные области математики — анализ, алгебра, геометрия — были поставлены на аксиоматическую основу. Великий математик Давид Гильберт (1862—1943) был ярким сторонником и пропагандистом аксиоматического метода. Под его влиянием была построена и общепринятая в наше время система аксиом теории множеств, свободная от очевидных парадоксов. Эту аксиоматику предложил в 1908 году Э. Цермело и в дальнейшем дополнили Дж. фон Нейман и А. Френкель. Но где же настоящая гарантия, что полученная система не содержит противоречия? Каким образом это можно установить?
Эти вопросы оказались гораздо сложнее, чем представлялось тогда Гильберту. Они потребовали глубокого изучения аксиоматических систем и их формализации, привели к точному анализу структуры математического высказывания, первым формулировкам строгих математических моделей таких явлений, как доказуемость, выразимость, истинность, и сделали возможным их изучение математическими методами.
Формальные языки. С современной точки зрения область интересов математической логики значительно шире, чем наука о правильных рассуждениях; её можно приблизительно описать, с оговорками и уточнениями, как построение и исследование формальных языков и систем математическими методами
Математическая логика по предмету сво-
ему есть логика, а по методу — математика.(П. С. Порецкий, 1884 год, Казань.)
Формальные и естественные языки имеют общие черты: у тех и у других есть синтаксис (то, как мы говорим или пишем), семантика (смысл того, что написано) и прагматика (то, как используется написанное). Основное отличие заключается в том, что — по крайней мере в идеале — синтаксис и семантика формальных языков могут быть определены на уровне математической строгости и поэтому в принципе поддаются анализу чисто математическими методами.
В наше время формальные языки встречаются в каждом доступном нам электронном устройстве, вроде мобильного телефона, а некоторые из них — языки программирования — даже изучают в школе. Поэтому за примерами далеко ходить не надо. Однако в середине XIX века, когда начался процесс математизации логики, формальных языков ещё не было, их только предстояло создать.
Логика предикатов. Разработчики первых формальных языков и систем, как правило, не думали о том, что эти системы могут быть реально использованы в вычислительных устройствах. (Исключением, видимо, можно считать великого учёного Готфрида Вильгельма Лейбница (1646—1716), который почти за два века до Буля предвосхитил многие идеи математической логики, включая идею формализации языка математики, и даже построил механический арифмометр.)
Первые формальные языки и системы возникли как результат выделения фрагмента естественного языка, достаточного для передачи формулировок математических утверждений и их анализа. Процесс выработки основных категорий этого языка был продолжительным и шёл параллельно с выработкой некоторых ставших в наше время стандартными математических обозначений. (Одним из важных понятий, введённых в это время, стало понятие
Предикатом на множестве $M$ мы называем высказывание, зависящее от $n$ параметров из этого множества (например, «натуральное число $x$ чётно», «точки $x$, $y$ и $z$ плоскости лежат на одной прямой»). Как только фиксированы значения параметров, предикат принимает логическое значение ложь или истина. Таким образом, с формальной точки зрения предикат представляет собой функцию от $n$ аргументов из множества $M$ в $\{0,1\}$.
Не вдаваясь в технические подробности, можно приблизительно описать высказывания логики предикатов как такие, которые можно сформулировать (предполагая заранее заданными обозначения некоторых базовых предикатов) с помощью конструкций $\land$ «и», $\lor$ «или», $\neg$ «не», $\to$ «влечёт» и уже упомянутых кванторов.
Например, текст $\forall{x} \exists{y} (y>x \land P(y))$ выражает неограниченность множества простых чисел, если договориться, что переменные пробегают множество натуральных чисел, «$>$» означает «больше», а $P(y)$ выражает простоту числа $y$. Эти договорённости составляют часть того, что мы назвали семантикой языка логики предикатов.
Удивительный факт, подтверждаемый всей существующей математической практикой, состоит в том, что выразительных средств языка логики предикатов — на первый взгляд очень скромных — достаточно для формулировки любых известных математических результатов. При этом может быть использовано всего лишь одно базовое понятие — предикат принадлежности $x\in y$ «множество $x$ есть элемент множества $y$». (В картине мира аксиоматической теории множеств все объекты, обозначаемые переменными, являются множествами.)
Доказуемость и вычислимость. Выразить в данном языке то или иное осмысленное утверждение — совсем не то же самое, что суметь его доказать. Следующий уровень языка логики предикатов состоит в описании таких текстов, которые следует признать корректными доказательствами. Традиционно этот уровень называется в математической логике исчислением предикатов. Формальное доказательство (в формате, который принято называть гильбертовским, но который существовал и до работ Давида Гильберта) представляет собой конечную цепочку высказываний логики предикатов, каждое из которых либо является аксиомой, либо получается из предшествующих высказываний по одному из постулируемых правил. Минимальный стандартный набор таких правил содержит лишь два: правило, позволяющее из высказываний $A$ и $A\to B$ вывести $B$, и правило, позволяющее из высказывания $A$ вывести $\forall x A$. (Если высказывание $A$ содержит параметр $x$, то формальное доказательство $A$ обосновывает его истинность при всех возможных значениях параметра.)
Таким образом, математическая доказуемость описывается двумя формальными языками — языком утверждений, описанным в предыдущем разделе, и языком доказательств — из которых второй является надстройкой над первым.
Похожая ситуация имеет место и с понятием вычислимости. Языки программирования предназначены для описания алгоритмов. Алгоритм при этом описывается программой — построенным по определённым правилам формальным текстом, который принято называть кодом. Таким образом, первый уровень языка программирования составляет язык текстов программ. Однако, процесс выполнения программы на данном компьютере на данном входе также может быть зафиксирован в виде текста (не важно, сохраняется ли этот текст в ходе работы программы или нет). В теории алгоритмов принято называть такой текст полным протоколом работы программы. То, каким образом порождается этот протокол, и составляет полное описание той или иной вычислительной модели. Для реальных языков программирования, разумеется, такое описание чрезвычайно сложно, однако для простейших моделей, таких как машина Тьюринга, оно гораздо проще.
Теория алгоритмов и создание компьютеров. Математическая логика сыграла важную роль в появлении компьютеров, хотя и не была единственной движущей силой в этом сложном процессе. Именно в математической логике, в попытке дать наиболее общее определение задачи, имеющей алгоритмическое решение, было осознано, что возможно построение универсального вычислительного устройства (машины), которое будет способно решать все теоретически разрешимые алгоритмические задачи.
Одним из первых, кто это понял, был Алан Тьюринг, давший точное определение и наиболее убедительный анализ понятия вычислимой функции в 1936 году. Другими учёными, которые наряду с Тьюрингом пришли к тем же идеям приблизительно в то же время, были Алонзо Чёрч и Эмиль Пост. Этими и другими исследователями в 1930‐х годах были созданы начала теории алгоритмов, которая стала основой понимания работы и построения вычислительных устройств в 40‐е и 50‐е годы. В частности, идея универсальной машины Тьюринга была в дальнейшем технически реализована в компьютерной архитектуре «по фон Нейману», в соответствии с которой программа хранится в памяти устройства и может быть модифицирована в ходе его работы.
На основе этой идеи построены все операционные системы.
Задачей, которую стремились решить пионеры теории алгоритмов, был вопрос, поставленный Гильбертом и названный им по‐немецки Entscheidungsproblem, «проблема решения». Вопрос состоял в том, чтобы найти алгоритм, который по данному утверждению, записанному на языке логики предикатов, давал бы ответ, существует ли формальное доказательство этого утверждения или нет. Если бы такой алгоритм существовал, то все математические проблемы в некотором смысле имели бы чисто механическое решение: как уже упоминалось, на языке логики предикатов можно сформулировать практически любое математическое утверждение, например знаменитую гипотезу о бесконечности числа пар простых чисел‐близнецов. Тогда вопрос о том, выводима ли эта гипотеза из аксиом теории множеств, сводился бы к проверке доказуемости некоторого высказывания в исчислении предикатов. Неудивительно, что исследователи Entscheidungsproblem стремились показать, что требуемого алгоритма в принципе не может существовать.
Если доказать существование того или иного алгоритма можно, предъявив его явно, то для того, чтобы утверждать, что такого алгоритма не существует, необходимо располагать точным математическим описанием того класса задач, которые допускают алгоритмическое решение. Ответ на этот вопрос потребовал разработки формальных языков описания алгоритмов ещё до появления компьютеров. Причём, поскольку цель такой разработки была более теоретическая, чем практическая, исследователи стремились к формулировке наиболее простых для описания и в то же время универсальных вычислительных моделей. Первыми такими моделями были рекурсивные функции Гёделя—Эрбрана, лямбда‐исчисление Чёрча и машины Тьюринга.
Гёдель, хотя и был первым, кто фактически сформулировал универсальный язык программирования, не считал, что найденное им (и французским логиком Эрбраном) понятие является универсальным в смысле способности запрограммировать любой алгоритм.
Первым, кто высказал тезис об универсальности своей вычислительной модели, был Алонзо Чёрч. Он также предъявил доказательство невозможности решения Entscheidungsproblem в рамках этой модели. Исчисление Чёрча было очень простым по форме, но больше напоминало формальное логическое исчисление, чем реальную вычислительную машину. Машины Тьюринга в этом смысле были ближе к будущей реальности, и поверить в тезис Тьюринга о том, что любая задача, имеющая алгоритмическое решение, может быть решена на машине Тьюринга, было намного легче, чем в аналогичный тезис Чёрча (известно, что именно работа Тьюринга смогла убедить Гёделя в справедливости этого тезиса). Тьюринг также показал, что его машины эквивалентны лямбда‐исчислению в смысле вычислительных возможностей, что стало косвенным свидетельством справедливости тезиса Чёрча—Тьюринга, как его теперь принято называть.
Впоследствии многие исследователи предлагали свои вычислительные модели в надежде расширить класс вычислимых функций, впервые описанный Чёрчем и Тьюрингом. Все такие попытки не привели к расширению этого класса, который оказался очень устойчивым. В настоящее время тезис Чёрча—Тьюринга — понимаемый в смысле любой из эквивалентных вычислительных моделей — является одним из краеугольных камней, на которых базируется теория алгоритмов.
Что касается лямбда‐исчисления, то оно долгое время пребывало на обочине математической логики, будучи вытеснено из теории алгоритмов более удобными и интуитивными моделями. Однако во второй половине XX века лямбда‐исчисление и системы на его основе нашли серьёзные практические применения. Лямбда‐исчисление Чёрча стало прообразом так называемых функциональных языков программирования (таких как современный язык Haskell), которые имеют ряд преимуществ по сравнению с традиционными императивными языками и в настоящее время очень активно развиваются.
Алгоритмически неразрешимые проблемы в математике. Вслед за Entscheidungsproblem с точки зрения теории алгоритмов были проанализированы и многие другие математические проблемы, поставленные как вопросы о построении того или иного алгоритма.
Некоторые из таких трудных проблем, остававшихся открытыми десятилетиями, оказались алгоритмически неразрешимыми задачами.
Среди такого рода вопросов наиболее известна 10‐я проблема Гильберта о распознавании разрешимости диофантовых уравнений. Диофантово уравнение — это уравнение вида $P(x_1,…,x_n)=0$, где $P$ — многочлен с целыми коэффициентами от переменных $x_1$, …, $x_n$. Требуется узнать по заданному многочлену $P$, существуют ли целые числа $x_1$, …, $x_n$, удовлетворяющие такому уравнению.
Вопрос Гильберта о построении общего алгоритма, работающего для всех диофантовых уравнений, с самого начала выглядел безнадёжным. С появлением теории алгоритмов исследователи стали предпринимать усилия в попытке доказать неразрешимость этой задачи. Промежуточные результаты в этом направлении получили американские логики Дж. Робинсон, М. Дэвис и Х. Патнэм, на их основе окончательное решение задачи было получено лишь в 1970 году ленинградским математиком Ю. В. Матиясевичем.
В наше время в математике алгоритмические вопросы занимают подобающее им важное место. Математическая логика научила нас тому, что далеко не всякий такой вопрос является разрешимым. Кроме того, даже если алгоритм решения той или иной задачи существует в принципе, не всегда можно говорить о его применимости на практике. Например, выполнение алгоритма может потребовать слишком много времени или памяти компьютера. Такого рода вопросами занимается отдельная область теории алгоритмов — теория сложности вычислений, о которой подробно рассказано в другой статье этого сборника (см. «Теория сложности»).
Теоремы Гёделя и недоказуемые утверждения. Ещё одним открытием, сделанным гениальным австрийским логиком Куртом Гёделем в 1931 году, было явление непополняемости аксиоматических систем. Знаменитые теоремы Гёделя о неполноте не только оказали большое влияние на развитие математической логики и дали толчок к созданию теории алгоритмов, но и стали общекультурным явлением, затронувшим даже творчество писателей и художников.
Гёдель был назван в числе ста наиболее влиятельных личностей XX века по версии журнала Тайм. Однако известность теорем Гёделя приводит и к тому, что часто они интерпретируются в слишком расширительном, метафорическом смысле.
Полными называют такие системы аксиом, в которых доказуемо или опровержимо любое утверждение того же языка (можно говорить о доказуемости в исчислении предикатов из данного множества аксиом). Понятно, что если мы хотим построить систему аксиом для той или иной области математики, нам бы хотелось, чтобы эта система была непротиворечивой и полной — неполнота означает, что мы «забыли» постулировать какие‐то принципы, касающиеся базовых понятий данного языка, и нужно их добавить к списку аксиом.
Теоремы Гёделя относятся к классу аксиоматических систем, удовлетворяющих двум естественным и широким требованиям. Во‐первых, необходимо, чтобы в рассматриваемом формальном языке по меньшей мере было выразимо понятие натурального числа и операции сложения и умножения. На первый взгляд это требование кажется весьма специальным, однако натуральные числа — один из базовых математических объектов, и языки, претендующие на формализацию значительной части математики, должны позволять о них говорить.
Целые числа создал Господь Бог,
всё остальное — дело рук человеческих. (Леопольд Кронекер, 1886 год, Берлин.)
Во‐вторых, должен существовать алгоритм, распознающий, является ли данный текст аксиомой рассматриваемой теории или нет. (Если аксиомы теории нераспознаваемы, то неясно, как можно строить доказательства в такой системе.)
Гёдель показал, что при выполнении этих требований любая система аксиом либо противоречива, либо неполна. Более того, для любой непротиворечивой системы можно явно указать предложение, касающееся арифметики натуральных чисел, которое нельзя ни доказать, ни опровергнуть в данной системе (такие утверждения принято называть независимыми от данной системы аксиом). В частности, это означает, что систему аксиом формальной арифметики нельзя никаким непротиворечивым образом «пополнить»: всегда найдутся независимые от неё арифметические утверждения.
Это составляет содержание так называемой первой теоремы Гёделя.
Вторая теорема Гёделя говорит о том, что утверждение, выражающее непротиворечивость данной аксиоматической системы, не доказуемо в самой системе, если эта система и в самом деле непротиворечива. Если считать, что стандартные математические методы укладываются в рамки аксиоматической теории множеств, то из этой теоремы следует, например, что стандартными математическими методами нельзя установить непротиворечивость теории множеств (и, тем самым, их собственную непротиворечивость).
Теоремы Гёделя позволили построить первые примеры независимых утверждений для сильных систем аксиом, таких как арифметика или даже теория множеств. После работ Гёделя такие примеры были обнаружены среди открытых проблем в различных областях математики. Одной из самых знаменитых открытых проблем в математике была континуум‐гипотеза Кантора, в соответствии с которой всякое бесконечное подмножество множества вещественных чисел либо счётно (равномощно множеству натуральных чисел), либо континуально (равномощно множеству вещественных чисел). В 1938 году Гёдель сумел доказать, что эту гипотезу невозможно опровергнуть в теории множеств, а в 1961 году американский математик Пол Коэн установил её недоказуемость.
Недоказуемые утверждения теоретико‐множественной природы впоследствии были обнаружены в самых разных частях математики — в анализе, алгебре, топологии и др. Сравнительно недавно, в конце 1970‐х годов, были найдены первые простые примеры утверждений из области конечной комбинаторики, независимые от аксиом формальной арифметики и даже от более сильных аксиоматических систем. Принципиальная разница с примерами типа континуум-гипотезы состоит в том, что комбинаторные примеры относятся к конечным и совершенно элементарным объектам, и их можно легко объяснить школьнику. Исследования в направлении поиска естественных примеров независимых утверждений активно ведутся и в наши дни.
Логика в других разделах математики.
Наиболее впечатляющие достижения математической логики, описанные выше, так или иначе связаны с анализом трудных проблем, в том или ином смысле не имеющих решения. Такие проблемы в математике встречаются, по счастью, довольно редко. Для работающих математиков поэтому более ценным является вклад в копилку методов, годных для решения их собственных повседневных задач. Здесь мы упомянем некоторые известные приложения логики такого рода, хотя в целом следует признать, что их не слишком много.
Область математики, которая испытала на себе сильное влияние логических методов — это абстрактная алгебра. Соответствующее направление математической логики — теория моделей — возникло в 1940‐х годах в работах А. И. Мальцева в России и А. Тарского и А. Робинсона в США с прицелом на приложения в алгебре. Первые такие приложения были найдены в 1941 году А. И. Мальцевым, который осмыслил доказанную им (а ранее в более слабой форме Гёделем) теорему о компактности для логики предикатов как общий метод получения локальных теорем в алгебре. Оказалось, что методы универсальной алгебры и методы теории моделей весьма близки и понимание взаимосвязей обогатило обе дисциплины. Некоторые конструкции, впервые найденные в математической логике, стали стандартными в алгебре и анализе, например так называемая конструкция ультрапроизведения, придуманная польским логиком Е. Лосем.
Одним из ярких достижений теории моделей 1960‐х годов стало создание нестандартного анализа Абрахамом Робинсоном. Он описал логическую конструкцию, которая позволила непротиворечиво рассматривать пополнение множества вещественных чисел бесконечно малыми и бесконечно большими числами. С помощью этой конструкции стало возможным дать объяснение исходной интуиции лейбницевских «бесконечно малых» и дать технически простое и интуитивное построение основных результатов математического анализа. В дальнейшем эти методы были также использованы и для получения новых результатов.
Современное направление теории моделей, возникшее в работах 1980‐х годов и активно развивающееся в наши дни, установило новые связи между логическими и алгебро-геометрическими методами.
n$ при $n>2$).
Методы теории доказательств — области математической логики, изучающей формальную доказуемость — также находят применения в «обычной» математике. Одним из успешных современных направлений является proof mining, извлечение конструктивных оценок из априори неконструктивных математических доказательств. Так называемые функциональные интерпретации, первоначально разработанные для анализа формальных систем, оказалось возможным применить и к конкретным содержательным математическим результатам (например, из области вещественного анализа, где интересен вопрос о скорости сходимости того или иного процесса к неподвижной точке и требуется явная оценка этой скорости). Результаты, полученные логическими методами, часто дают совершенно неочевидные усиления исходных теорем.
Логика в компьютерных науках. Если применения математической логики в «обычной» математике достаточно редки, то роль логических методов в информатике и компьютерных науках намного выше. Здесь математическая логика даёт подходящий язык для изучения возникающих задач и набор общих подходов к их решению. Удивительным образом, иногда оказывается, что концепции, сформулированные в математической логике очень давно и с другими целями, обретают новую жизнь в конкретных прикладных областях. Расскажем о некоторых направлениях, в которых логика доказала свою эффективность.
Реляционные базы данных и языки запросов. Многомиллиардная индустрия баз данных связана с технологией хранения больших объёмов структурированных данных, извлечением из них полезной информации и её обновлением. Поиск информации в базе данных осуществляется пользователем на языке запросов, который позволяет найти среди большого массива данных нужные сведения, потратив на это не слишком много времени. Поэтому языки запросов должны сочетать в себе достаточную гибкость для формулировки запросов и одновременно обеспечивать возможность эффективного поиска информации.
В 1960‐х годах американский учёный T.
Кодд понял, что самый обычный язык логики предикатов очень удобен для обеих целей, поскольку позволяет эффективно осуществлять поиск по запросу. Эффективность обеспечивается с помощью аппарата реляционной алгебры — языка операций над отношениями, разработанного до этого в математической логике (в школе Альфреда Тарского) как алгебраический эквивалент языка логики предикатов. Идея Кодда о том, что запросы на языке реляционной алгебры допускают эффективный поиск, была первоначальным стимулом в разработке реляционных баз данных и общеупотребительных в настоящее время языков запросов, таких как SQL. С тех пор теория баз данных и логических языков успешно развиваются рука об руку.
Верификация программ и протоколов. Задача верификации программ, протоколов, аппаратных средств является одной из наиболее трудных и практически важных в компьютерной индустрии. Под верификацией понимается доказательство корректности работы программы (протокола, процессорного чипа, и т. д.), т. е. соответствия того, что реально делает программа, тому, что нам хотелось бы, чтобы она делала. Поскольку программа работает с входными данными, а вариантов входных данных может быть бесконечно много, мы не можем протестировать работу программы на всех возможных входах. На практике применяют методы тестирования, которые увеличивают вероятность обнаружения ошибок, однако полной гарантии надёжности всё‐таки не дают.
Другой путь решения этой проблемы, также активно применяемый на практике, состоит в сведении рассматриваемой задачи к логическому вопросу о соответствии программы её формальной спецификации. Это предполагает формулировку требований к тому, что должна делать программа, на формальном языке спецификаций программ. (В качестве такого языка часто используется язык так называемой темпоральной, или временной, логики, одной из разновидностей модальных логик.)
Подход, называемый model checking, состоит в том, чтобы сопоставить программе граф, представляющий её возможные состояния и переходы между ними.
Это позволяет свести задачу верификации программы к вопросу о выполнимости формулы, задающей спецификацию, в модели, представляющей программу. Для решения задачи проверки выполнимости формулы в данной модели разработаны эффективно работающие алгоритмы, что позволяет на практике верифицировать программы с большим числом состояний. Этот метод особенно хорошо себя зарекомендовал для верификации чипов.
Альтернативный подход, называемый theorem proving, состоит в том, чтобы сопоставить программе логическую формулу, выражающую её корректность, и искать формальное доказательство этой формулы — например, в исчислении предикатов. Этот подход на данный момент не так распространён на практике, как model checking, но продолжает развиваться. Успешность этого метода во многом зависит от эффективности работы пруверов — программ автоматического поиска формальных доказательств. Разработка такого рода систем активно ведётся в наши дни.
Теории типов и функциональное программирование. Парадигма функционального программирования сочетает в себе несколько базовых идей, первоначально возникших в математической логике.
Первая идея — это взгляд на функцию как на объект, к которому может применяться программа наряду с другими данными (аргументы функций в свою очередь могут быть функциями и т. д.). Функциональная программа в целом может рассматриваться как определение некоторой сложной функции, а исполнение программы — как процесс вычисления значения функции на данном аргументе, сводящийся к пошаговому упрощению (редукции) её определения.
Более привычный нам императивный стиль программирования, в традиции Тьюринга и фон Неймана, привязан к понятию состояния памяти компьютера, которое изменяется в результате применения команд, таких как присваивания переменным новых значений. Функциональные программы не предполагают явного хранения состояния вычисления, в них нет присваиваний, а функции больше соответствуют математическому пониманию функций, чем подпрограммы в императивном программировании, которые могут зависеть от внешних переменных и иметь побочные эффекты.
Эти особенности позволяют писать в функциональном стиле более прозрачный код, потенциально содержащий меньше ошибок. Кроме того, функциональные программы допускают хорошее распараллеливание, поскольку разные части определения функции могут быть вычислены независимо.
В последние годы функциональные языки занимают всё более важную нишу среди употребительных языков программирования и применяются в тех областях, где важно иметь надёжные программы, например, в банковской сфере. По существу, первым функциональным языком программирования было лямбда‐исчисление, придуманное Чёрчем как простейшая универсальная вычислительная модель. Идеи лямбда‐исчисления были затем воплощены в одном из первых действующих функциональных языков — языке LISP, а также во многих более современных языках вплоть до Ocaml и Haskell.
Другой ключевой идеей, идущей из математической логики, является идея типа данных, на которой основано подавляющее большинство языков программирования высокого уровня, не обязательно именно функциональных. Использование переменных и функций, которым приписан определённый тип (например, тип «число с плавающей точкой», или тип «массив целых чисел»), позволяет на уровне компиляции проводить контроль типов, что избавляет программы от значительного числа ошибок (связанных с несоответствием значения переменной типу). Развитие языков программирования идёт в сторону усовершенствования и усложнения системы типов, где контролю типов отводится всё большая роль.
Формальные языки с типами (в отличие от бестиповых языков, в которых все переменные имеют один и тот же тип) впервые возникли в фундаментальном труде Б. Рассела и А. Уайтхеда «Основания математики», целью которого было построение математики на основе непротиворечивой системы аксиом теории множеств. В математике эта система, однако, не прижилась и была заменена более простой бестиповой теорией множеств Цермело—Френкеля с аксиомой выбора.
В 1950‐е годы в логике было обнаружено, что в достаточно развитых системах на базе лямбда‐исчисления с типами последние ведут себя в точности как логические высказывания (языка интуиционистской логики), а функциональные программы — как формальные доказательства этих высказываний.
Это явление, описанное здесь, разумеется, очень приблизительно, получило название соответствия Карри—Говарда. Через несколько десятков лет оно послужило основой для создания функциональных языков, в которых возможно написание программ с одновременной верификацией их кода. Наиболее известными языками такого рода являются Coq и Agda, созданные для формализации математических доказательств. В частности, именно на языке Coq удалось построить формальное доказательство гипотезы четырёх красок и ряда других трудных математических результатов. Эти же языки начинают применяться и для задач верификации программ, описанных в предыдущем пункте.
Этими тремя темами мы ограничим избранный список областей информатики, в которых на деле применяются результаты математической логики. Многие не менее важные темы при этом оказались не затронутыми: теория сложности вычислений, теория автоматов и монадическая логика, SAT‐solving, языки авторизации и контроля доступа к информации, логическое программирование и хорнова логика, онтологические базы данных и дескрипционная логика — перечисление можно очень долго продолжать.
Завершая обзор, посмотрим на отдельные области гуманитарных наук, испытавшие на себе влияние методов математической логики. Выбранные нами предметы касаются философии, языкознания и даже теории права. Эти разнообразные темы объединены в одну группу, поскольку связаны с изучением явлений, требующих модификации тех или иных аспектов классической логики.
Неклассические логики. Первые логические системы, отличные от традиционной двузначной, стали появляться ещё в то время, когда процесс формализации классической логики предикатов не был завершён. К настоящему времени неклассические логики представляют собой большое царство, населённое самыми разнообразными и экзотическими представителями (исчисляемое десятками семейств). Мотивации при рассмотрении неклассических логик могут быть самыми разными: попытки точнее передать те или иные свойства естественного языка; попытки построить систему, отвечающую тем или иным философским установкам; попытки расширить язык классической логики новыми выразительными возможностями или, наоборот, сузить выразительные возможности классической логики с тем, чтобы сделать её более эффективной для решения тех или иных задач.
Проведём небольшую экскурсию по «зоопарку» неклассических логик.
Интуиционизм как философское течение возник в самом начале XX века в работах молодого нидерландского математика Л. Э. Я. Брауэра как реакция на кризис оснований математики и теории множеств. Характерной чертой философии Брауэра было желание избавить математику от неконструктивных теорем существования, т. е. утверждений о существовании тех или иных объектов, без возможности предъявить явно их конструкцию. Глубокий анализ привёл Брауэра к идее о том, что сама классическая логика, а именно закон исключённого третьего, является источником таких неконструктивных утверждений в математике. Это потребовало радикально пересмотреть традиционное понимание смысла математических утверждений, логических операций и кванторов.
Хотя сам Брауэр настаивал на неформальном характере своей философии математики — отсюда её название «интуиционизм» в противоположность гильбертовскому «формализму» — к началу 1930‐х годов возникла потребность в уточнении совокупности логических принципов, приемлемых с интуиционистской точки зрения. Решение этой задачи было дано учеником Брауэра А. Гейтингом, который сформулировал общепринятую в настоящее время интуиционистскую логику предикатов, опираясь на предшествовавшую работу А. Н. Колмогорова. Парадоксально, но в результате интуиционизм был также поставлен на прочную формальную основу.
Несмотря на поддержку ряда выдающихся математиков, одним из которых был Герман Вейль, интуиционизм не стал преобладающей философией математики. В настоящее время трудно найти подлинных сторонников этой философии даже среди логиков. Тем не менее, с точки зрения формальной логики, интуиционизм представляет собой стройную и богатую содержательными результатами систему. С течением времени было осознано, что интуиционистская логика скрывается во многих математических структурах, в частности в структурах топологической природы. Например, было обнаружено, что возникшее в работах А.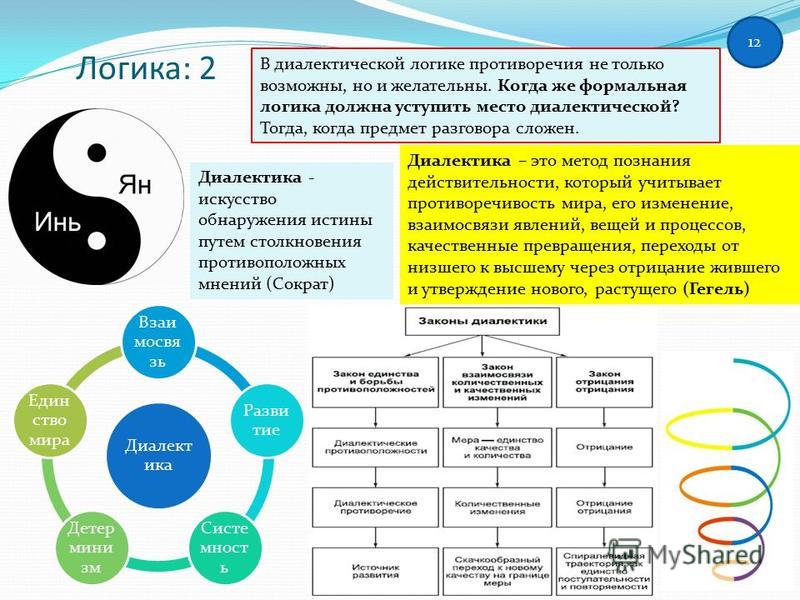
Гротендика понятие топоса можно рассматривать как модель интуиционистской логики.
С другой стороны, интуиционистская логика часто возникает в различных приложениях в компьютерных науках. Это не случайно, поскольку интуиционистская логика теснее связана с понятием вычисления, чем логика классическая. Одним из важнейших проявлений этой связи является уже упомянутое соответствие Карри—Говарда.
Классическая логика допускает интерпретацию в логике интуиционистской, поэтому современная точка зрения на их соотношение состоит в том, что интуиционистская логика не ограничивает, а, наоборот, добавляет в классическую новые выразительные возможности — такие как различие между неконструктивным и конструктивным утверждением о существовании.
Модальная логика. Другим классом логик, обогащающих классическую новыми выразительными возможностями, являются так называемые модальные логики. Язык модальной логики, наряду с обычными связками, содержит новую одноместную логическую связку $ □\, $. Высказывание $□\, A$ в разных контекстах может пониматься совершенно по‐разному, что приводит к разным постулируемым принципам, т. е. разным модальным логикам. Стандартные логические связки, такие как импликация или отрицание, как правило, сохраняют в модальной логике классическую интерпретацию. (Разумеется, могут рассматриваться модальные логики и над другими логиками, например над интуиционистской, однако такие системы в целом сложнее и потому менее распространены.)
Исторически первым, идущим ещё от Аристотеля, прочтением формулы $□\, A$ было высказывание «$A$ необходимо». (Здесь мы говорим о языковой конструкции, присутствующей в нашем естественном языке, а не о каком‐либо математическом понимании того, что значит «необходимо».) Двойственное высказывание «не $A$ не является необходимым» обычно отождествляется с высказыванием «$A$ возможно» и обозначается $◇\, A$.
Перечислим некоторые известные интерпретации модальности, приводящие к интересным и полезным семействам логик.
Логика доказуемости: $□\, A$ означает «$A$ доказуемо» в данной аксиоматической теории, например в теории множеств. При этом высказывания понимаются как высказывания в языке теории множеств, каковым можно считать и само высказывание о доказуемости утверждения $A$. Эта логика интересна тем, что даёт точную математическую семантику модальности и применяется для исследования обычных классических аксиоматических теорий.
Временная логика, описывающая развитие некоторого процесса во времени: $□\, A$ означает «всегда в будущем будет верно $A$». Различные модели течения времени — непрерывное, дискретное или даже ветвящееся — приводят к разным временным логикам. Временные логики, применяемые на практике для верификации программ, используют и некоторые дополнительные связки, например двухместную связку, выражающую «$A$ имеет место до тех пор, пока $B$».
Эпистемическая логика, описывающая знания и обмен информации между несколькими агентами: $□\,_x A$ означает «агенту $x$ известно $A$» (в этой логике, как правило, описываются знания нескольких агентов $x$, $y$, … и каждому из них соответствует своя модальность $□\,_x$, $□\,_y$, …). Эпистемическая логика является частью (формальной) эпистемологии — обширного и важного раздела философии, занимающегося исследованием таких понятий, как знание и вера, того как знание возникает, как оно связано с понятием доказательства (обоснования). Формализм эпистемической логики позволяет построить модели различных аспектов этих явлений и использовать их для анализа тех или иных теоретических положений.
Эпистемическая логика также находит более конкретные применения в компьютерных науках и искусственном интеллекте для описания знания, возникающего в системах с несколькими агентами. Например, условие корректности протокола, связанного с обменом информацией, в котором не должна допускаться утечка информации третьим лицам, может быть сформулировано на языке эпистемической логики.
Деонтическая логика формализует модальности типа долженствования, например $□\, A$ можно понимать как «$A$ требуется» или «$A$ обязательно» (двойственную модальность можно понимать как «$A$ разрешено»).
Такие логики впервые стали рассматриваться в философии и теории права для формализации и анализа различных аспектов правовых систем.
Многозначная логика и нечёткая логика. Многозначные логики возникают, если допускаются другие истинностные значения, помимо классических истины 1 и лжи 0. Например, можно рассматривать промежуточное значение 1/2 и интерпретировать его как «неизвестно». Следующий шаг требует определения того, каким образом вычисляются значения логических связок, и конкретное решение по этому поводу может привести к различным логикам.
Если пойти дальше по пути многозначности, то естественно возникает идея о том, что истинностным значением высказывания может быть любое вещественное число в интервале $[0,1]$ (например, это число может выражать степень нашей уверенности в справедливости высказывания). Такие логики часто называют «нечёткими» (fuzzy), поскольку предикаты в такой системе могут выглядеть как размытые, не имеющие чётких границ. Например, высказывание о том, что видимый цвет является красным, не является чётким в силу неопределённости самого понятия «красный».
Нечёткие логики призваны формализовать рассуждения в условиях неопределённости или неточности информации. Подлинным «отцом» нечёткой логики и теории нечётких множеств был Л. Заде. Он увидел потенциал этой логики для различных инженерных применений, например в такой области, как экспертные системы или теория управления, и сделал очень много для её популяризации.
Немонотонная логика. Классическая логика обладает очевидным свойством монотонности: добавление новых аксиом не отменяет никаких ранее доказанных теорем. В работе с базами данных, где не вся содержащаяся информация может быть верной, появление новой информации может привести к пересмотру уже известных фактов и их отмене. В этом случае свойство монотонности нарушается.
Аргументы и доказательства, приводимые в суде, могут быть оспорены или опровергнуты противной стороной. Процесс выстраивания аргументов, таким образом, на практике выглядит совершенно непохоже на привычные нам дедуктивные математические доказательства.
Эти аспекты изучает теория аргументации — весьма развитая область исследований, связанная с философией, лингвистикой, теорией права и искусственным интеллектом. Формальные модели аргументации во многих случаях базируются на немонотонных логиках.
Паранепротиворечивая логика. Как известно, в классической логике действует закон ex contradictio quodlibet, т. е. из противоречия следует всё что угодно. Поэтому противоречивые классические системы все эквивалентны между собой и, по существу, бесполезны. На практике людям приходится рассуждать в не столь стерильных условиях: не всегда бывает известно, есть ли противоречие в имеющейся информации, на основании которой приходится делать выводы. Логики, приспособленные для рассуждений в условиях возможно противоречивых предположений, называются паранепротиворечивыми. В таких системах возникновение противоречия не приводит к доказуемости всех вообще утверждений.
Можно сказать, что наша обыденная логика (как способ умозаключений на основе имеющейся информации) является одновременно нечёткой, паранепротиворечивой и немонотонной. Разумеется, все эти формальные системы являются лишь приближёнными и грубыми моделями отдельных аспектов той самой «обыденной логики».
Грамматики Хомского и семантика Монтегю. Одной из теорий, соединивших в себе сразу несколько аспектов неклассических логик — кванторы, предикаты, модальности, модели Крипке и лямбда‐абстракцию — является семантика Монтегю. Эта теория, предложенная американским логиком Р. Монтегю в начале 1970‐х годов, представляет собой попытку применить идеи математической логики к трудной задаче описания семантики естественного языка. Она, по существу, положила начало целому направлению в математической лингвистике — формальной семантике. Ранее работы Н. Хомского, создавшего теорию формальных грамматик, произвели революцию в понимании синтаксиса естественных языков. Применения математической логики в лингвистике, из которых мы вскользь упомянули лишь два важных направления, безусловно заслуживают отдельного разговора.
Неужели это всё математика? — недоумённо воскликнет читатель. И да, и нет. Исследователи, применяющие методы математической логики в той или иной области знания, должны прежде всего быть компетентными специалистами именно в этой области и разбираться в постановках специфических для неё задач. Напомним, что многие создатели математической логики — Гёдель, Тьюринг, фон Нейман и др. — не были только лишь «чистыми» математиками.
Тем не менее, используемый в приложениях логический аппарат является самым настоящим математическим аппаратом, даже если он и совсем не похож на ту математику, которой традиционно обучают на математических факультетах университетов. Вопросы, связанные с неклассическими логиками — например, вопросы их полноты относительно семантики Крипке или топологической семантики, вопросы классификации различных семейств неклассических логик — имеют существенную математическую составляющую. Для успешной работы в философской логике, математической лингвистике, теории игр, теории баз данных и других областях приложений этой математикой также нужно овладеть. К счастью, порог входа здесь не так уж высок, и математическую логику с успехом преподают на факультетах компьютерных наук, философии и лингвистики.
Математически наиболее развитые части математической логики — такие, как теория множеств, теория алгоритмов и сложности вычислений, теория моделей или ординальный анализ формальных систем, содержат некоторые из наиболее сложных с математической точки зрения результатов и применяемых методов. Разумеется, современные исследования в этих давно сложившихся областях целиком и полностью лежат в области математики.
Основные подходы к пониманию предмета логики в европейской философии XIX века
Предлагается взгляд на историю формальной логики в Европе XIX века как на три автономных традиции: германскую, британскую и австрийскую. В первой логика понималась как наука о форме мышления, отвлекающаяся от всякого содержания; во второй — как теория рассуждения, сосредоточенная на анализе формы языковых выражений; в третьей — как общая теория науки и -учение о форме предметов вообще.
Описываются основные вехи истории и общие характеристики каждой из традиций.
При описании всех познавательных способностей Кант жёстко разделяет две стороны: форму и содержание. Выделяя два уровня, или «ствола», познания, а именно чувственность и рассудок, он в каждом из них различает эти две составляющие. При этом только чувственность имеет «контакт» с внешним миром, являясь единственным источником содержания знания. Рассудок имеет дело с тем же содержанием, но уже обработанным и упорядоченным чувственностью. Рассудок оперирует с понятиями, которые являются более высоким уровнем познания в сравнении с чувственными наглядным представлением. Собственно, именно Кант тематизировал для логики и эпистемологии категорию понятия. В предшествующей философии было в ходу ‘представление’ [Vorstellung], или, как это преимущественно именовалось в британской философии, ‘идея’ — термин с гораздо более широким смыслом, охватывавшим и ощущение, и восприятие, и продукты абстрактного мышления. Например, для Лейбница различие между такими видами представлений, как понятие и ощущение, состояло только в степени отчетливости. Кант же чётко разделяет два вида представления [Vorstellung] — наглядное представление [Anschauung] и понятие [Begriff], проводя резкую границу между ними. Первое относится к чувственности, второе □ к рассудку, которые являются несводимыми друг к другу познавательными способностями. Словами самого Канта, «логика — наука о рассудке вообще» [1, А52 (В61)]. Впрочем, здесь требуются некоторые уточнения. В «Критике чистого разума» он разделяет общее и частное применение рассудка и, соответственно, общую логику и частные логики. Общая логика отличается тем, что отвлекается от всякого содержания знания, от любого возможного различия в предметах. Под частными логиками он имел в виду то, что сегодня назвали бы методологией той или иной науки. Именно это понимание природы общей логики и предопределило широко известное пренебрежение Канта её познавательными возможностями. Ведь если она не имеет дела ни с каким определенным предметом, то она ничего не говорит о мире, становясь своего рода знанием ни о чём, но о формах всего.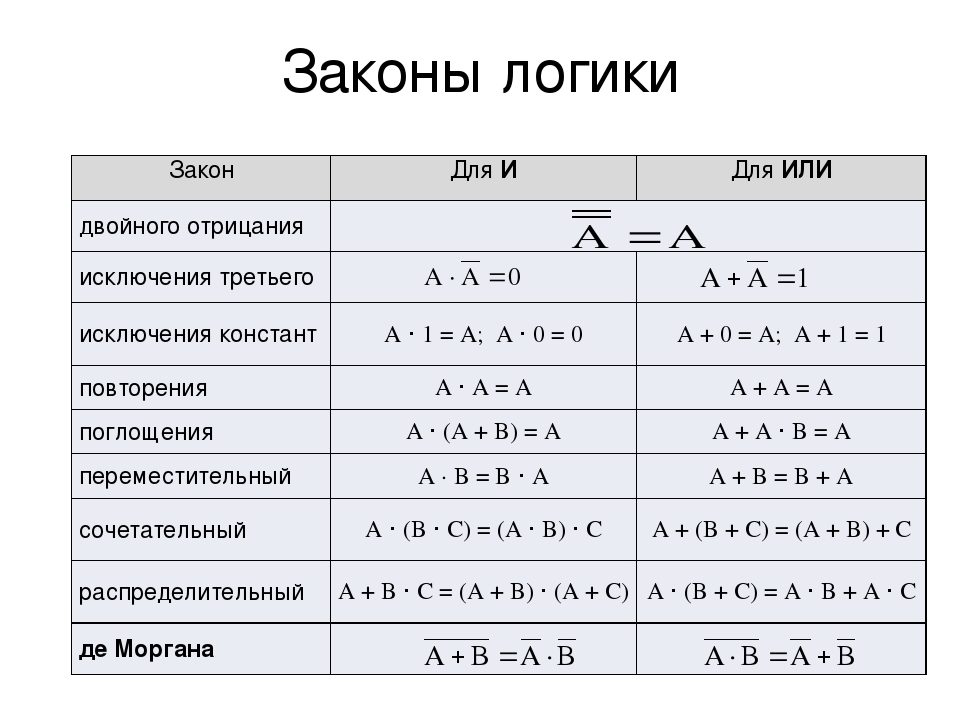
Общая логика, в свою очередь, подразделяется на чистую и прикладную. В рамках чистой логики исследуются только априорные принципы рассудка. В прикладной же логике, которая также отвлекается от всякого содержания, рассматривается применение рассудка с учётом психологических условий, в которых он действует. В рамках последней исследуются источники предрассудков и заблуждений, зависимость применения рассудка от особенностей того или иного субъекта, таких как память, внимание, привычка, сомнение и уверенность и т.д. и т.п. Кантовское понятие общей чистой логики составило основание того, что впоследствии стало именоваться «формальной логикой». У самого Канта нет разновидности логики с таким названием, но он характеризует как формальное всякое рассмотрение, которое не принимает во внимание какого-либо содержания, абстрагируется от предмета. Формально можно рассматривать как чувственность, так и мышление, но ни то, ни другое не даст знания о вещах. Таким образом, для Канта «формальное» представляет собой в первую очередь отрицательную характеристику: формально то, что бессодержательно, беспредметно. Наряду с общей Кант выделяет трансцендентальную логику, в которой принимаются во внимание источники познания и познаваемая реальность. Как раз последняя представляет для него больший интерес и приковывает основное внимание; её он рассматривает как более высокий уровень логики, который в состоянии пролить свет на тайну человеческого мышления. Но что касается общей чистой логики, она остаётся на самом низком и самом простом уровне описания познания, не выходя за границы предписанных ей априорных форм: «Общая чистая логика имеет дело исключительно с априорными принципами» [1, B77]. Поэтому общая логика именно в силу того, что она отвлекается от содержания, может служить лишь отрицательным критерием истины. Как выражается Кант, она может быть каноном для оценки знания, но не органоном для его расширения. Переходя к дедукции априорных форм рассудка, которые также называются категориями, Кант предлагает нам известный набор из двенадцати категорий, которые полностью исчерпывают сферу логики.
Каждая из этих категорий выполняет определенную функцию единства суждения, тем самым давая субъекту возможность совершать то или иное суждение. Причем эти функции единства самостоятельны в том смысле, что они не сводимы друг к другу. Здесь для нас существенны два следствия, которые наиболее отчетливо сформулированы уже не в «Критике чистого разума», а в «Логике». Во-первых, поскольку категорические, гипотетические и дизъюнктивные суждения «основываются на существенно различных функциях рассудка» [2, 503], они не могут преобразовываться друг в друга: «невозможно гипотетическое суждение превратить в категорическое — они совершенно различны по своей природе» [2, 505]. Во-вторых, Кант отвергает, что применение комбинаторно-алгебраических методов может иметь какую бы то ни было пользу для логики: последняя «не есть алгебра, с помощью которой можно было бы открывать какие-либо скрытые истины» [2, 434], более того, по его убеждению, мы не нуждаемся в каких-либо изобретениях для логики именно по той причине, что та содержит только форму мышления. Согласно Канту, истины общей чистой логики — априорны, поскольку они находятся в душе до всякого возможного опыта; — аналитичны, ибо они позволяют не более чем разложение уже имеющегося содержания понятий, не выходящее за их границы; — не принимают во внимание какого-либо предмета знания, они беспредметны. — являются частью теории познания. Действительно, в Германии логика стала рассматриваться как область знания, теснейшим образом связанная с гносеологией, более того, как правило, она рассматривалась как часть последней. 1.2. Якоб Фридрих Фриз и антропологическая логика После Канта обозначились два пути дальнейшего развития логики. Первый был связан с развитием трансцендентальной логики, где она, в руках представителей классического немецкого идеализма, фактически смыкалась с метафизикой. Второй привёл к появлению логики как самостоятельной науки. Именно последний представляет для нас интерес. Среди многочисленных пособий и исследований, изданных в первые два десятилетия после смерти Канта, наибольшее влияние на рассматриваемый нами процесс оказали два автора — Я.Ф. Фриз и И.Ф. Гербарт. Я.Ф. Фриза (1773-1843) часто характеризуют как основателя психологизма в логике и философии. Хотя в этом есть некоторый анахронизм, поскольку в то время антитеза психологизм — антипсихологизм не была актуальна, эту оценку в целом можно признать справедливой. К ней только стоит добавить, что острие его «психологизма» было направлено в первую очередь против спекулятивного идеализма и, не считая сформировавшейся несколько позднее школы Гербарта, было единственной альтернативой этому идеализму в деле формирования научной методологии. Фриз начинает с наблюдения, что выражение Канта «чистая логика» может пониматься двояко: как антропологическое либо как философское учение о законах мышления. Философская, которую он также называет демонстративной, занимается теорией доказательства. Она основана на принципах de omni et de nullo, тождества и противоречия. Основной же вопрос антропологической логи-ки — «как в процессе деятельности человеческого духа возникают понятия имышление» [3. С.3]. Фриз полагает, что тезис Канта относительно завершенности логики уже у Аристотеля касается только первой, а вот во второй ещё могут делаться открытия. В соответствии с этим первая часть его труда, посвященная чистой общей логике — «учение о формах мышления», — состоит из двух разделов — антропологической логики, которая включает в себя описание нашего познания и мышления вообще, учений о понятии и суждении. Во втором разделе, «Философская логика», повествуется о «расчленяющем познании» (Zer-gliederungs-Erkenntnis) и об умозаключении. Вполне естественно, что оригинальность и новизну можно найти только в первом разделе «Системы логики». Второй же раздел добросовестно воспроизводит стандартный набор логического материала, характерный для немецких учебников логики после X. Вольфа и И. Канта. Так, теория суждения обосновывается той же таблицей категорий, что и у Канта. Фриз не ставит под сомнение результаты кантовской дедукции, он только пытается подвести под неё психологическое основание, критикуя при этом Канта за то, что тот пытался строить доказательства там, где возможно только описание. Таким образом, у Фриза психология стала тем основанием логики, каким у Вольфа была онтология, а у Канта теория познания. 1.3. Иоганн ФридрихГербарт Иоганном Фридрихом Гербартом (1776-1841) и его школой был сделан первый ощутимый шаг в направлении онтологической трактовки логики. Гербарт широко известен как основатель своего направления в педагогике, в истории психологии признаются его заслуги как одного из пионеров математизации психологии, но в современной истории философии уделяемое ему внимание ничтожно мало. Это резко контрастирует с той ролью, которую играли его идеи в философском процессе своего времени. Гербарт был одним из первых влиятельных критиков немецкого идеализма, и продолжительное время школа Гербарта была практически единственной силой, которая поддерживала научный дух в философии на фоне безраздельного господства произвольных умозрительных спекуляций. Он определял философию как «обработку понятий». Соответственно, разные разделы философии ведают разными уровнями и видами такой обработки. Так, первый раздел — логика — должен привести понятия к ясности (проведению чётких границ между различными понятиями) и отчётливости (строгому различению признаков отдельного понятия). Метафизика ведает изменением понятий. А эстетика (которая включает этику) учитывает оценку понятий. Таким образом, понятие является основным предметом не только логики, но и философии Гербарта в целом. Согласно Гербарту, анализ понятий в рамках логического исследования исключает всякие вопросы, связанные с их генезисом и с тем, что касается психологии познания. Логика имеет дело с понятиями как с чем-то уже готовым, наперёд заданным и не задаётся вопросом о том, откуда они берутся. Его работа «Основные моменты логики» (1808) открывается словами: «Логика занимается не чем иным, как представлениями; но не актами представления, не способами их получения и происхождения в нас, и не изменениями состояний сознания (Gemutszustande), которые они в нас вызывают». Логика занимается «только тем, что представляется». Это представляемое становится предметом логики, поскольку оно «уже схвачено, выделено, понято. Вот почему это называется понятием» [4. С. 467]. В работе «Учебное введение в философию» (1813) он определяет предмет логики как «мысли, характеризуемые со стороны того, что с помощью их мыслится» [5. С. 77]. Как видим, Гербарт резко отделяет представление как психический акт от представляемого, мышление от мыслимого. Такое различение создает предпосылки для онтологизации предмета логики, что и объясняет гармоничность позднейшей рецепции гербартианства австрийской логико-философской традицией. Гербарт не характеризует понятия как «объективные», как позднее делал Больцано, его описания носят негативный характер — он говорит о том, чем понятия не являются. А именно, они «не есть ни реальные предметы, ни действительные акты мышления» [5. S. 78]. Иначе говоря, понятия принадлежат некой промежуточной сфере между действительными предметами и мышлением (или актами мышления). Любое понятие «имеется как бы в единственном экземпляре»; что же касается отношения между понятиями и мышлением, то «мышление одного и того же понятия может многократно повторяться» в сознании бесчисленных разумных существ, «и при этом не будет происходить размножение понятия» [5. S. 78]. Знаменательны также соображения Гербарта о суждении и его связи с мышлением и мыслимым. Мышление — это «лишь посредник, как бы телега, которая свозит понятия в одно место». Когда понятия встречаются в мышлении, они находятся в «зависшем состоянии (Schweb) и сначала образуют вопрос» [5. S. 91]. Отвечая на этот вопрос, мы совершаем не что иное, как суждение. Нетрудно заметить, что это объяснение природы суждения весьма близко к теориям Брентано и Фреге, которые понимали под последним утверждение (у Брентано также отвергание) помысленного или представленного содержания. Только Гербарт был склонен относить истинностную оценку суждения к компетенции психологии и, как следствие, призывал дистанцироваться от неё, поскольку речь идёт о логике. Он считает, что о суждении можно говорить в двух смыслах — психологическом (признание истины) и логическом (соединение субъекта и предиката). В такой трактовке суждения «в логическом смысле», занимающем промежуточное положение между действительным миром и оценивающими актами сознания, нетрудно увидеть предвосхищение «допущений» Мейнонга, как и «содержания, допускающего вынесение суждения» (beurteilbare Inhalt) Фреге. Гербартовский подход к пониманию предмета логики заметно расходился со взглядами Канта. Если логика занимается не формальной структурой познающего рассудка, но формами мыслимого как такового, то это не может не отразиться и на структуре логического знания. В частности, кантовское учение о категориях, через которые описываются фундаментальные функции рассудка, просто остаётся не у дел. Действительно, Гербарт совершенно осознанно отказался делать категории основанием для логических дистинк-ций. Так, например, принципиальное для Канта различение категорических, гипотетических и разделительных суждений, по мнению Гербарта, «принадлежит целиком языковой форме» [4. С. 473]. Как отмечалось выше, логика, в отличие от педагогики и психологии, находилась на периферии научных интересов Гербарта, он посвятил ей лишь две небольших работы. Подробное и систематическое изложение логики в соответствии с принципами философии Гербарта осуществлено М.В. Дро-бишем (1802-1896) в «Новом изложении логики» (1836). Это был едва ли не лучший немецкий учебник логики, выдержавший пять изданий. Не останавливаясь на его многочисленных достоинствах, отметим некоторые важные моменты, относящиеся к философии логики. Дробиш систематизировал и развил критику фризовского антропологизма, начатую ещё Гербартом. «Совершенно ложно мнение, что можно дать психологическое (антропологическое) обоснование логики» и что этого можно добиться «разложением операций сознания и мышления, памяти и фантазии» [6, s.vii-viii]. Развивая онтологический поворот Гербарта, Дробиш впервые вводит понятие логического объекта, что сопровождается рассуждениями о несовпадении реального и мыслимого объекта. Немало оригинальных идей содержится в его теории суждений. Например, экзистенциальные суждения вместе с безличными образуют «тетические», или абсолютные, суждения, классифицируются как разновидность гипотетического. «X существует» следует понимать как «если есть нечто, то есть X» [6. С. 60-61]. 1.4. Адольф Тренделенбург Решающую роль в окончательном формировании логической дисциплины сыграл берлинский профессор А.Тренделенбург (1802-1872). Его фундаментальный труд «Логические исследования» (1840) по современным меркам скорее представляет собой исследования по философии науки или по теории познания. В первой главе «Логика и метафизика как основополагающие науки» исследуется природа связи науки с логикой и метафизикой, вторая посвящена критике основных принципов формальной логики, третья -критике диалектического метода. В остальных пяти главах предпринимается попытка построить теорию научного метода на основе истолкованных в духе Аристотеля понятий движения, пространства, времени и других. По его мнению, все науки характеризуются единством метода и в силу этого имеют отношение к логике. Таким образом, в логике Тренделенбург видит, в первую очередь, теорию научного метода. Свой идеал логики он находит в трудах древних. Приведём красноречивую цитату: «Науку, рассматривающую вместе и мышление, и сущее, назвали, вслед за Платоном, диалектикой; но, во избежание привходящих понятий (Nebenbegriff), назовём её лучше логикой в широком смысле и к такой логике направим наши «логические исследования»» [7, 11-12]. Здесь концентрированно выражена дальнейшая стратегия Тренделенбурга. Он намерен предложить программу развития логики, избегая двух крайностей: во-первых, формальной логики, которая не принимает во внимание «сущего», во-вторых, гегелевской диалектики. Многообразие философских систем он называет «немецким предрассудком» и «ложной оригинальностью» [7, IX], полагая при этом, что правильный путь указан в глубокой древности Платоном и Аристотелем. Заметим, что именно Тренделенбург является автором термина «формальная логика» как обозначения соответствующего раздела логики. Кант, как мы помним, говорил об «общей чистой логике», которая характеризовалась тем, что она является лишь формальной. Фриз использовал обозначения «философская» или «демонстративная» логика, Твестен — «аналитическая» логика, а чаще просто «аналитика». Термин «формальная логика» также не использовался ни Гербартом, ни Дробишем. Выражение «формальная логика» могло встречаться между делом у разных авторов, например, его можно встретить у Твестена, но оно носило случайный характер дополнительного определения, не имея статуса собственного имени для определенного раздела логики. Только Тренделенбург обозначил то направление логических исследований, которого придерживались Гербарт и Дробиш, как «формальную логику», и только после него это обозначение стало общеупотребимым. По мнению Тренделенбурга, формальная логика стала возможной благодаря Канту, который резко отделил форму от содержания. Это замечание вполне справедливо, но, как мы уже показали, в устах Канта определение «формальный» имеет отчётливый привкус негативной оценки. Поэтому, когда Тренделенбург именно эту характеристику делает отправной, скептическое отношение к описываемой области тем самым уже предопределено са-мим этим фактом. Тренделенбург основное внимание уделяет критике Гербарта, Твестена и Дробиша, по сути, продолжает анти-формалистскую аргументацию Канта, делает её развёрнутой. В частности, серьёзные претензии предъявляются к тезису о том, что понятие есть нечто готовое и заранее данное. Попытки критикуемых авторов привлечь на свою сторону авторитет Лейбница Тренделенбург парирует замечанием, что «когда Лейбниц предлагал исчисление … он делал это не в смысле формальной логики» [7, 23]. Тренделенбург окончательно оформил принятое в Германии понимание места и роли формальной логики в системе логической науки. Что же касается логики в широком смысле, то его заслуга не в предложенных ответах, которые не нашли поддержки, но в самой постановке проблемы необходимости реформы логики. Это проблема стала предметом интенсивнейших обсуждений на протяжении последующего полустолетия, не приводя, однако, ни к какой реальной реформе. 2. Логика и философия в Британии В исторической литературе процесс развития логики в Британии XIX века описывается как постепенное утверждение курса на математизацию последователями Дж. Буля в борьбе с индуктивизмом сторонников Дж.С. Мил-ля. Не ставя под сомнение справедливость этой картины, здесь мы бы хотели обратить внимание на некоторые общие особенности британской логической традиции, оставив без внимания указанную коллизию. Действительно, взгляды сторонников обоих направлений на предмет логических исследований и природу основных понятий логики, как мы надеемся показать, отличались своеобразным единством, что позволяет объединить сторонников несовместимых научных программ в единую традицию, противостоящую континентальной. В Британии критика схоластической логики носила, пожалуй, наиболее радикальный характер. Как следствие, в течение XVII-XVIII вв. логические исследования не вызывали заметного интереса у британских мыслителей. Хотя логика продолжала оставаться университетской дисциплиной, достаточно заметить, что после выхода краткого компендиума Генри Олдрича [8] в 1691 г., вплоть до 20-х гг. XIX в. не было написано ни одного учебника по логике. Сам по себе тот факт, что в течение едва ли не полутора столетий преподавание некоторой дисциплины осуществлялось только по одному учебнику, уникален в истории науки и образования и достаточно свидетельствует об отсутствии интереса к этой области знания. 2.1. Ричард Уэтли: станоелениетрадиции Ситуация резко изменилась после публикации в 1826 г. «Элементов логики» Ричарда Уэтли (1787-1863). Уэтли был воспитанником Оксфордского университета, единственного (из двух) в Англии, где к тому времени сохранилось преподавание логики. Автор не предлагал каких-либо технических новшеств или новаторских теорий. Более того, в содержательном разрезе он, фактически, просто пересказал упомянутый компендиум Олдрича, местами едва ли не копируя фрагменты текста. Но при этом он изложил пребывавшую в забвении и пренебрежении Аристотелеву логику живым языком, насытив текст аргументами в защиту её научной состоятельности и полезности в образовании. Кроме того, некоторые принципиальные подходы и формулировки, предложенные в этой работе Уэтли, не просто стали типичными, но образовали концептуальный базис языка логики и философии логики в Британии. По существу, именно его «Элементы логики» положили начало британской логической традиции XIX века. По мнению Уэтли, логика — объективная наука, подобно химии или математике, и её существо — в раскрытии принципов отдельно от их приложений. Как раз в период работы Уэтли над своей книгой в английском языке формируется понятие науки, «science» в современном смысле, и одной из основных парных оппозиций к термину «science» служило искусство, «art». Поэтому наш автор вполне в духе времени уделяет немалое внимание обоснованию того, что логика представляет собой в первую очередь науку, илишь производным образом — искусство25. В центре внимания логики, по мнению Уэтли, находится рассуждение, или, точнее, «анализ процесса разума в рассуждении» [9. С.29]. Тем самым главной темой, «ядром» логики он делает умозаключение, отводя теориям понятия и суждения подчинённое положение. Причина, по которой эта наука находится в пренебрежении в последние столетия, по мнению Уэтли, в том, что к ней предъявляли завышенные ожидания, и последние были вызваны в том числе и превратным пониманием места понятия и суждения в логике. Как сказали бы сегодня, к логике примешивали методологическую проблематику, нередко за счёт вытеснения собственно логических проблем. В числе этих избыточных тем он указывает стремления выработать «правила образования ясных идей» и «руководство суждением». Но это, считает Уэтли, означает требование «такой системы всеобщего знания, которая научила бы нас значениям всех слов, истинности и ложности — достоверности и недостоверности — каждого высказывания, превосходя тем самым все наши научные дисциплины» [9. С.45-46]. Обвинять логику в том, что она не обеспечивает этого, — «это всё равно, что возражать против оптики за то, что она не даёт зрение слепым, или жаловаться, что очки не помогут тому, кто не умеет читать» [9. С. 46]. Следующий принципиальнейший момент логики Уэтли состоит в той роли, которую он отводит языку. Ставя вопрос о природе элементов, из которых строится рассуждение, он категорически отвергает предположение, что рассуждающий разум оперирует идеями. Рассуждение осуществляется в языке и только в языке. Развёрнутых философских аргументов в пользу своего выбора автор не приводит, для него это имеет характер фундаментального убеждения. Он лишь утверждает, что следствием обратного было бы то, что «некоторый человек, не знающий ни одного произвольного знака, был бы способен рассуждать. Но нет никаких оснований верить, что это возможно, как и в то, что «абстрактные идеи» вообще существуют» [9. С. 48-49]. В дальнейшем он делает ещё более радикальные утверждения, отождествляя с языком и сам предмет логики. «Язык. насколько он служит средством для … умозаключения, составляет предмет логики» [10. С. 111]. A страницей ранее он выразился ещё более категорично: «Логика имеет дело только с языком» [10. С. 110]. При этом Уэтли не предлагает никаких разъяснений относительно того, как это согласуется с приведенным ранее определением, согласно которому предметом логики служит рассуждение. Тезис о том, что логика имеет дело с языком, носит здесь не просто программный характер, он имеет существенные практические следствия. Когда Уэтли обсуждает, в чём состоит формальный характер логики, выясняется, что он имеет в виду не форму мышления, но форму языкового выражения. Если в правильном силлогизме, рассуждает автор, мы будем заменять имена определенных вещей «бессодержательными символами, обеспечивая при этом, чтобы форма выражения оставалась той же самой» [9. С. 58], то невозможно будет принять истинность посылок, не принимая при этом истинность заключения. Поэтому, заключает Уэтли, «сила (или доказательность) рассуждения видна из самой формы выражения и независимо от смысла входящих в него слов» [9. С. 59; 10. С. 13]. Эта мысль воспроизводится при описании природы силлогизма: «Так как логика занимается исключительно исследованием употребления языка26, то из этого следует, что силлогизм (который является аргументом, представленным в регулярной логической форме) есть аргумент, выраженный таким образом, что его доказательность очевидна из самой формы выражения, т.е. без учёта значенийтерминов» [9. С. 105]. Эффект, произвеленный выходом «Элементов», был взрывоподобен. Количество посвященных ей заметок, рецензий с трудом поддаётся подсчёту. В 1850 г. вышло уже 9-е издание «Элементов…». Книга Уэтли была подробнейше проанализирована, среди прочих, Дж. Бентамом (1821), Дж. С. Мил-лем (1828), У. Гамильтоном (1833). Кульминацией процесса, вызванного обсуждением этой книги, стал громогласный и скандальный спор де Моргана и Гамильтона из-за приоритета в квантификации предиката. Как признавался Дж. Буль во введении к «Математическому анализу логики», именно наблюдение за этой полемикой вызвало у него интерес к проблемам логики и желание подвергнуть её математической обработке. Не только Буль, но и Де Морган ссылались на логику Уэтли как на собственно логику. Затруднительно также сказать, для скольких учёных, от Дж.Бентама до Ч. С. Пирса, логика Уэтли стала отправной точкой в их самостоятельных исследованиях. Даже оппоненты, категорически не соглашавшиеся с ключевыми тезисами Уэтли, признавали, что именно его работа вызвала возрождение логических исследований в Британии. 2.2. Уильям Гамильтон: кантианскаяреакция Наиболее резкую критику новации Уэтли вызвали у Гамильтона. В своей рецензии, опубликованной в «Эдинбургском обозрении», он упоминает десять трудов по логике, опубликованных между 1826 и 1832 гг., но основное внимание уделяет «Элементам.» Уэтли. Гамильтон был последовательным кантианцем, по крайней мере, поскольку речь идёт о логике, и в целом, глубоким знатоком немецкой философии. Вместе с тем он обладал фантастической эрудицией в истории логики. Признавая его заслуги в возрождении интереса к логике, в содержательном отношении Гамильтон подвергает разрушительной критике все его основные тезисы. Категорическое несогласие Гамильтона вызывает уже понимание предмета логики, провозглашённое Уэтли. Будучи верным кантианцем, он не может согласиться с производимой Уэтли подменой анализа законов мышления рассмотрением процесса рассуждения. В частности, он никак не может смириться с принижением роли других форм мышления: «В том, что д-р Уэтли делает процесс рассуждения не только главным, но адекватным объектом, мы видим весьма ограниченную концепцию этой науки. простые представления (apprehension) и суждения рассматриваются не сами по себе как конституентные элементы мышления, а как нечто, подчиненное аргументации. При таком понимании логика превращается в силлогистику». Он пытается намекнуть, что подобные взгляды оппонента объясняются тем, что тот банально не владеет материалом: «Это мнение разделялось некоторыми арабскими и латинскими схоластами, у них оно было заимствовано Оксфордским Крэканторпом и воспринято Валлисом; аот Валлиса перешло к Уэтли. Но. это мнение отвергалось. громадным большинством даже перипатетических диалектиков. Уэтли не привёл ни одного довода, который бы заставил нас усомниться в нашем убеждении, что законы мышления, а не законы рассуждения образуют адекватный объект этой науки» [11. С. 136]. Подобные пространные исторические экскурсы с упоминанием множества мнений и описанием процесса их распространения и модификации от Аристотеля до современности автор рецензии предпринимает по поводу каждого разбираемого положения Уэтли, в дальнейшем мы не будем их приводить. Между делом он не преминул указать, что обзор истории логики у самого Уэтли — «тощий и не более чем воспроизводит нищету истори-ческихпознанийОлдрича» [11. С. 140]. Таким образом, критические аргументы Гамильтона сводятся, во-первых, к тому, что взгляды Уэтли не вписываются в философию Вольфа и Канта, которую эдинбургский профессор считал высшим достижением философии логики; во-вторых, Уэтли, в силу слабой эрудиции, отклоняется от «мэйнст-рима» всемирно-исторического развития логики, либо следуя худшим образцам эпохи упадка логики, либо производя противоречивую «отсебятину». Следует признать, что с точки зрения предшествующей истории логики, критика Гамильтона справедлива. Ни Аристотель, ни средневековые схоласты, ни Вольф и Кант не рассматривали логику ни как «исследование операций рассуждения», ни как «занятую исключительно языком». Тем не менее именно эти аспекты логики Уэтли оказались созвучными новым тенденциям в развитии не только логики, но и исследований кембриджских алгебраистов. Поэтому с точки зрения последующей истории логики критика Гамильтона оказалась консервативной и неэффективной. 2.3. Дж.С. Милль: логика и язык Помещение языка в фокус логических исследований закономерно привело к тому, что вопросы о связи лингвистических сущностей с предметом рассуждения стали неотъемлемой частью логики. Поэтому, хотя основания современной логической семантики заложены Готтлобом Фреге, концептуальный аппарат был вполне сформирован в трудах британских логиков XIX века. Именно это в значительной мере объясняет, почему семантические идеи Фреге стали столь популярны именно в англоязычной философии. Джон Стюарт Милль (1806-1873) вошёл в историю логики как адепт индуктивной методологии. Вместе с тем его основной труд «Система логики» (1843) состоит из двух томов, и только второй посвящён индуктивным методам. Первый же том рассматривает проблемы традиционной логики, и то, как Милль решал эти проблемы, позволило Уильяму Уэвеллу, соратнику и предшественнику Милля в развитии индуктивной методологии, заметить, что «Система логики» — произведение последователя Уэтли. Действительно, в споре Уэтли и Гамильтона о предмете логики, т.е. занимается ли она рассуждением или формами мышления, взгляды Милля заметно ближе к первому. Больше того, Милль способствует тому, что рассуждение начинает пониматься более гибко. Если Уэтли и другие авторы ассоциировали рассуждение с категорическим силлогизмом, Милль намерен представить индуктивное умозаключение как другой способ рассуждения. Поэтому он предлагает более широкое толкование этого термина: «Рассуждать — значит выводить любое утверждение из утверждений, уже принятых» [12. С. 10]. По его мнению, в первую очередь «логика есть наука об операциях рассудка, служащих для оценки доказательств: наука о процессе восхождения от истин известных к неизвестным». Что касается других традиционных разделов логики, Милль предоставляет им право на существование в рамках этой науки с оговоркой: «Насколько они содействуют этому процессу» [12. С.18; 13. С.13]. Фактически Милль окончательно закрепил возрожденную Уэтли номиналистическую тенденцию, сделав лингвистические соображения фундаментальным атрибутом английской логической традиции XIX и даже XX века. Действительно, язык он связывает с существом логики заметно теснее, чем любой немецкий автор. Настолько тесно, что, например, Пётр Лавров, автор предисловия и комментариев к русскому изданию «Системы логики», не удержался от следующего примечания: «Несмотря на все достоинства книги Милля, нельзя не сознаться, что он иногда смешивает вещи, которых не смешает ни один немецкий писатель по логике, даже второстепенный. Так, во всем последующем, он смешивает грамматический элемент предложения с логическим элементом суждения. Употребляя постоянно одно и то же вы -ражение (proposition), Милль, очевидно, имеет в виду то связь словесных форм мысли, то самую мысль»27 [13. С. 23]. Основная предпосылка теории именования Милля состоит в том, что имена предназначены для обозначения предметов, но не идей. Исходя из этого, он рассматривает виды имен на основе способа обозначения ими своих предметов (signification). При этом большинство дистинкций имеет достаточно тра-диционный характер. К немногим исключениям относится деление на абсолютные и коннотативные, на котором нельзя не остановить внимание. Как таковое, это деление тоже не было изобретением Милля. Его проводил и Уэтли, который заимствовал это у Олдрича, его можно обнаружить в логике Пор-Рояля, у средневековых авторов-номиналистов. Однако до Милля эта классификация носила характер, производный от грамматики. Попросту говоря, имена существительные, как правило, объявлялись денотативными (или абсолютными), а имена прилагательные — коннотативными. Претензий на теорию значения в этом не содержалось. Сначала Милль делит имена на коннотирующие и не-коннотирующие. Имена, не имеющие коннотации, указывают на предмет или качество непосредственно, не подразумевая при этом какого-либо атрибута обозначаемого предмета. Примерами таких имен могут служить «Иван», «Волга», «Англия». Кон-нотативные же имена не только обозначают предмет, но и подразумевают некий атрибут. Так, имя «белый» обозначает любой белый предмет, но при этом также подразумевает, или коннотирует, атрибут белизны. Коннотирующие имена могут прилагаться в качестве предикатов к любым предметам, именем которых они являются. Милль говорит, что такие имена имеют «два вида сигнифика-ции»: имя «человек» прямо и непосредственно указывает на предметы, т.е. де-нотирует их, но косвенно подразумевает (imply), вовлекает те признаки, которые содержатся в понятии человека, т.е. коннотирует их. К коннотативным отноКант И. Критика чистого разума // Собрание сочинений в 8 томах. М., 1994. T.3.
Кант И. Логика. Пособие к лекциям // Иммануил Кант. Трактаты. СПб.: Наука, 2006.
Fries J.F. System der Logik. Heidelberg, 1811.
Herbart J.F. Hauptpunkte der Logik // Saemmtliche Werke. Lepzig, 1850. Bd. 1.
Herbart J.F. Lehrbuch zur Einleitung in die Philosophie // Saemmtliche Werke. Lepzig, 1850. Bd. 1.
Drobisch M.W. Neue Darstellung der Logik. 3 aufl., Leipzig, 1863 (1-е изд. 1836).
Trendelenburg A. Logische Untersuchungen. 2 aufl., Leipzig, 1862.
AldrichH. Artis Logicae Compendium. Oxford, 1961.
Whately R. Elements of logic. From the 8th London ed. revised, N.Y., Harper & Brothers, 1855. 396 p.
Уэтли Р. Основания логики. СПб.: Изд. А.В. Заленскаго, 1873. 547 с.
Hamilton W. Logic. The recent English Treatises on that Science // Hamilton W. Discussions on Philosophy and Literature, Education and University reform. N.Y.: Harper & Brothers, 1861. P. 120-173.
MillJ.S. System of Logic, 8th ed. N.Y.: Harper & Brothers, 1882. 1156 p.
Милль Дж.С. Система логики, в двух томах. СПб.: Издание М.О. Вольфа, 1865. Т. 1. 553 с.
Grattan-Guinness I. The Search for Mathematical Roots, 1870-1940. Princeton UP, 2000. 690 p.
De Morgan A. Formal Logic, or the calculus of inference, necessary and probable. London: Taylor and Walton, 1847. 336 p.
Simons P. Philosophy and Logic in Central Europe from Bolzano to Tarski. Dordrecht, Boston, London: Kluwer AP, 1992.
Bolzano B. Wissenschaftlehre. Lpz, 1929-1931.
Больцано Б. Учение о науке. СПб., 2003.
Zimmerman R. Formale Logik (Philosophische Propadeutik fur obergymnasien. Zweite Abtheilung). Vienna, 1853.
Zimmerman R. Philosophische Propadeutik. Vienna, 1860.
Brentano F. Psychologie vom empirischen Standpunkt. Leipzig, 1911.
Hofler A., Meinong A. Philosophische Propadeutik. Erster Theil: Logik. Vienna, 1890.
Chernoskutov Yu.Yu. Logic and object theory in 19th century: from Bolzano to Frege» // Logical Investigations. Moscow, 2013. V.19. P. 10-22.
Логика формальная и диалектическая — Новости и политика как она есть! — ЖЖ
Различают логику формальную и диалектическую. Основателем традиционной формальной логики является, как известно, Аристотель. Термин «диалектическая логика» был введен в науку немецким философом, объективным идеалистом Г. Гегелем (1770 — 1831), впервые на идеалистической основе изложил основные законы и принципы диалектической логики как учения об общем развитии абсолютного духа.
Диалектическая логика — высшая степень в развитии логической науки, но она не отменяет и не поглощает формальную логику, последнюю не следует рассматривать как пройденный этап.
Диалектическая логика, как и формальная, изучает мышление, но с другой стороны и другими методами. Формальная логика — это логика, изучающая структуру мышления, исследует законы строения нашего мнения. Она призвана дать ответ, какой должна быть структура мысли, чтобы она была истинной и правильно воспроизводила действительность. Диалектическая логика исследует то, как в абстрактном мышлении, познает истину, действуют общие законы диалектики. Диалектическая логика изучает природу логических форм, их познавательную суть, раскрывает связь форм и законов мышления с законами объективного мира. Формальная логика исследует структуру готовых, сложившихся логических форм, не интересуясь их генетическими связями и взаимопереход, диалектическая же логика изучает формы мышления в их связях, переходах, в развитии, движении.
Ограниченность формальной логики состоит в том, что соблюдение одних только его законов для познания недостаточно, а не в том, будто она применяется только для познания каких-то элементарных связей и отношений, а при исследовании сложных явлений и связей Ее законы будто не действуют. В процессе познания на ступени абстрактного мышления имеет место постоянное сочетание двух моментов — формального соблюдения в каждом акте мысли и диалектического направления мысли в целом. И формальная, и диалектическая логика действуют повсюду, при познании любых объектов, как простых, так и сложных, при познании как относительно неподвижных предметов, так и предметов, движущихся меняются.
Не существует какой-то особой области элементарных отношений, которые бы узнавались с помощью только формальной логики, а диалектическая логика в них была бы неприменима, как не существует и такой области познания, где мышление подлежит только законам диалектической логики и где необязательно соблюдения требований формальной логики . Там, где соблюдаются законы формальной логики, действительно диалектическое мышление становится невозможным, там диалектика подменяется софистикой и эклектикой. Формальная логика обеспечивает определенность, ясность, последовательность мышления, то, без чего мышление как логический процесс по существу невозможно.
Сложным является вопрос о соотносительность формальной и математической логики. Существуют различные точки зрения. Одни считают, что современной формальной логикой является математическая логика и одной из других (общая, традиционная, классическая), кроме математической, в наши дни не существует. Математическая логика, возникла из потребностей математики, как ветвь традиционной логики, вобрала все ценное, достигнутое последней, и является новым, высшим этапом развития формальной логики.
Другие исходят из того, что существует общая формальная логика и логика математическая, что это хоть и близкие, но разные науки и их нельзя отождествлять. Каждая из этих наук имеет свой предмет, свои задачи и методы. Сторонники этого взгляда считают, что математическая логика не охватывает всех проблем формальной логики, поэтому она не может быть сведенной к математической логики, подменена ней.
Некоторые ученые относят математическую логику к математике и считают ее логике в собственном смысле.
Большинство современных логиков признают первую точку зрения, считают, что формальной логикой на современном этапе развития логической науки является математическая (символическая) логика. Приведем высказывания по этому вопросу отдельных авторов. Б. Рассел, например, отмечает: «Основное положение … состоит в том, что математика и логика тождественны, и я никогда не видел ни одного повода к изменению этой точки зрения» 3.
Этой же точки зрения придерживается и Г. Клаус. Он отмечает, что «существует только одна логика, изъятие математической логики из состава формальной логики невозможно и любая такая попытка связана с полным отрицанием современной логики — все устойчивое, все ценное, имеющееся в традиционной логике, находит себе место в современной логике и именно с ее помощью может быть понят лучше и глубже «4.
Дж. Шенфильд, наоборот, считает, что «логика изучает те типы умозаключений, которыми пользуется математика» 6. Такой же точки зрения придерживается и Б. Мендельсон: «Глубокие и опустошительные результаты Гегеля, Тарского, Рассела, Клини и многих других были богатой наградой за вложенную труд и завоевали для математической логики положения независимой ветви математики». Подобного взгляда на математическую логику придерживается и Р. Л. Гудстеин: «Математическая логика имеет своей целью выражение и систематизацию логических процессов, которые употребляются в математическом рассуждении, а также разъяснения математических понятий. Сама она является ветвью математики, которая использует математическую символику и технику … «7. «Предметом логики как философской науки, — отмечает Б. Фогараши, — является не только математическое, а все человеческое мышление. Но логика имеет математические основы, а математика — логические» 8.
Мышление человека не сводится и не может быть сведено к математическому мышлению, а значит, и логика как наука о мышлении, не может быть сведена к математической логике.
Интересно знать:
А вот если вам нужна пластиковая тара тогда самые выгодные предложения вы найдете на сайте aqua-solutions.ru
примеров логических рассуждений | Приемный совет юридической школы
Журналист заявляет, что фармацевтические компании имеют как потребность в прибыли для поддержки будущих исследований, так и моральное обязательство предоставлять лекарства тем, кто больше всего в них нуждается и не может их себе позволить. Чтобы сбалансировать эти требования, они приняли практику продажи лекарств по более низким ценам в более бедных странах. Вывод журналиста — такая практика неоправданна. В подтверждение этого утверждения журналист указывает, что разные люди в одной и той же стране имеют разные платежеспособности, но это соображение само по себе не означает, что политика фармацевтической компании необоснованна.В вопросе предлагается выбрать принцип, который больше всего поможет оправдать рассуждения журналиста.
Принцип, изложенный в ответе (C), связывает вопрос о том, заслуживает ли особого внимания личные, а не социальные потребности. В практике фармацевтических компаний особое внимание уделяется характеристикам общества, а не личным потребностям. В результате, согласно этому принципу, практика имеет тенденцию отрицать особое внимание к тем, кто этого заслуживает (более бедным гражданам более богатых стран), уделяя особое внимание тем, кто этого не заслуживает (гражданам среднего класса из более бедных стран) .Таким образом, практика не соответствует обязательству фармацевтических компаний уделять особое внимание тем, кто больше всего нуждается в лекарствах и не может их себе позволить, и, уделяя незаслуженное особое внимание, не может обеспечить доход, который можно было бы использовать для поддержки новых лекарств. исследования наркотиков. Таким образом, принцип, указанный в пункте (C), является убедительным подтверждением аргументации журналиста о том, что практика фармацевтических компаний неоправданна. Таким образом, (C) — правильный ответ.
Принцип, изложенный в ответе (A), применяется к уравновешиванию внимания, заслуживаемого больными и здоровыми людьми.Однако практика фармацевтических компаний и аргументы журналиста против такой практики касаются только больных (то есть людей, нуждающихся в лекарствах). В результате ответ (А) не имеет отношения к рассуждениям журналиста.
Принцип, изложенный в (B), требует, чтобы богатые учреждения использовали часть своих ресурсов для помощи нуждающимся. Это, как правило, подтверждает моральный долг фармацевтических компаний предоставлять лекарства тем, кто в них нуждается, но не может их себе позволить. Однако этот принцип не поддерживает аргументацию журналиста, который утверждает, что ценовая политика фармацевтических компаний не оправдывается этим моральным императивом.
Принцип, изложенный в (D), о том, что люди в богатых странах не должны иметь лучший доступ к медицинскому обслуживанию, чем в более бедных странах, является принципом, который имеет тенденцию поддерживать практику компаний, потому что практика компаний имеет тенденцию уменьшить неравенство в сфере здравоохранения между богатыми и бедными странами. По этой причине (D) фактически противоречит рассуждениям журналиста.
Принцип, изложенный в (E), касается того, является ли неравное распределение медицинской помощи или неравное распределение богатства более несправедливым.Однако это другой вопрос, чем тот, которым занимается журналист. Таким образом, ответ (E) не имеет отношения к рассуждениям журналиста.
Это был простой вопрос, основанный на количестве испытуемых, которые правильно ответили на него, когда он появился в LSAT.
философия логики | Определение, проблемы и факты
Природа и разновидности логики
Относительно легко заметить некоторый порядок в приведенных выше объяснениях. Некоторые характеристики на самом деле тесно связаны друг с другом.Когда говорят, что логика, например, изучает законы мышления, эти законы не могут быть эмпирическими (или наблюдаемыми) закономерностями реального человеческого мышления, как это изучает психология; они должны быть законами правильного мышления, которые не зависят от психологических особенностей мыслителя. Более того, существует параллелизм между правильным мышлением и достоверной аргументацией: достоверная аргументация может рассматриваться как выражение правильного мышления, а последнее — как интернализация первого.В смысле этого параллелизма законы правильного мышления будут соответствовать законам правильной аргументации. В свою очередь, характерной чертой последних является то, что они не зависят от каких-либо конкретных фактов. Всякий раз, когда аргумент, который берет аргументацию от p к q , действителен, он должен иметь силу независимо от того, что он знает или во что верит по предмету p и q . Однако единственный другой источник уверенности в связи между p и q , по-видимому, состоит из значений терминов, содержащихся в предложениях p и q .Те же самые значения сделают предложение «Если p , то q » истинным независимо от всех случайных фактов. В более общем смысле, можно обоснованно утверждать от p к q тогда и только тогда, когда импликация «Если p , то q » логически верна — т. Е. истинна в силу значений слов, встречающихся в p и q , независимо от фактов.
Логика, таким образом, может быть охарактеризована как изучение истин, полностью основанное на значениях содержащихся в них терминов.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасЧтобы приспособить определенные традиционные идеи в рамках этой формулировки, рассматриваемые значения, возможно, следует понимать как воплощающие понимание сущности сущностей, обозначаемых терминами, а не просто кодификацию обычного языкового использования.
Следующее предложение (от Аристотеля), например, является простой логической истиной: «Если зрение — это восприятие, то объекты зрения — это объекты восприятия.Его истина может быть постигнута, не придерживаясь каких-либо мнений относительно того, каковы, на самом деле, отношения между зрением и восприятием. Что необходимо, так это просто понимание того, что подразумевается под такими терминами, как «если-то», «есть» и «есть», и понимание того, что «объект чего-то» выражает некую связь.
Логическая истинность типового предложения Аристотеля отражается в том факте, что «объекты зрения являются объектами восприятия» можно обоснованно вывести из «зрение есть восприятие».
Тем не менее, эта характеристика не дает ответа на многие вопросы.Противопоставление фактов и отношений между значениями, на которые опирались в характеристике, подверглось сомнению, вместе с самим понятием значения. Даже если оба будут приняты, остается значительное противоречие между более широким и более узким пониманием логики. Согласно более широкой интерпретации, все истины, зависящие только от значений, принадлежат логике. Именно в этом смысле слово логика следует понимать в таких обозначениях, как «эпистемическая логика» (логика познания), «доксастическая логика» (логика веры), «деонтическая логика» (логика норм), «логика. науки »,« индуктивной логики »и т. д.Согласно более узкой концепции, логические истины достигаются (или сохраняются) на основании определенных конкретных терминов, часто называемых логическими константами. Можно ли дать им внутреннюю характеристику или их можно указать только путем перечисления — это спорный вопрос. Однако по общему мнению, они включают (1) такие пропозициональные связки, как «не», «и», «или» и «если – то» и (2) так называемые кванторы «(∃ x ). ) »(Который можно читать:« По крайней мере, для одного человека назовите его x , это правда ») и« (∀ x ) »(« Для каждого человека назовите его x , это правда что»).Фиктивная буква x здесь называется связанной (индивидуальной) переменной. Предполагается, что его значения являются членами некоторого фиксированного класса сущностей, называемых индивидами, класса, который по-разному известен как вселенная дискурса, вселенная, предполагаемая в интерпретации, или область индивидов. Считается, что его члены количественно выражаются в «( x )» или «( x )». Более того, (3) концепция идентичности (выражаемая знаком =) и (4) некоторое понятие предикации (индивидуум, обладающий свойством или связью между несколькими индивидами) принадлежат логике.Формы, которые принимает изучение этих логических констант, более подробно описаны в логике статьи, в которой также объясняются различные виды логической записи. Здесь дается только очертание области логики.
Когда изучаются только термины в (1), эта область называется логикой высказываний. Когда рассматриваются (1), (2) и (4), поле является центральной областью логики, которая также известна как логика первого порядка, теория квантификации, низшее исчисление предикатов, низшее функциональное исчисление или элементарная логика.Если подчеркивается отсутствие (3), добавляется эпитет «без идентичности», в отличие от логики первого порядка с идентичностью, в которую также включено (3).
Пограничные случаи между логическими и нелогическими константами следующие (среди прочего): (1) Количественная оценка более высокого порядка, что означает количественную оценку не по индивидуумам, принадлежащим к данному универсуму дискурса, как в логике первого порядка, но также по множествам особей и наборов из n — индивидуумов. (В качестве альтернативы, свойства и отношения, которые определяют эти наборы, могут быть количественно определены.) Это приводит к логике второго порядка. Процесс можно повторить. Количественная оценка наборов таких наборов (или n — наборов таких наборов или свойств и отношений таких наборов), которые рассматриваются в логике второго порядка, порождает логику третьего порядка; и все логики конечного порядка вместе образуют (простую) теорию (конечных) типов. (2) Отношение принадлежности, выражаемое символом, может быть перенесено на логику первого порядка; это дает начало теории множеств. (3) Могут быть добавлены понятия (логической) необходимости и (логической) возможности.
Это более узкое чувство логики связано с влиятельной идеей логической формы. В любом предложении все нелогические термины могут быть заменены переменными соответствующего типа, сохраняя неизменными только логические константы. В результате получается формула, отображающая логическую форму предложения. Если формула приводит к истинному предложению для любой замены интерпретируемых терминов (соответствующего логического типа) для переменных, формула и предложение считаются логически истинными (в более узком смысле выражения).
Как аргументировать распространенные заблуждения
В этой статье описаны некоторые наиболее распространенные способы, которыми аргументы могут пойти наперекосяк.
Распространенные заблуждения целесообразно разделить на три категории: заблуждения о релевантности, заблуждения о неприемлемых предпосылках и формальные заблуждения. Многие из этих заблуждений носят латинские названия, возможно, потому, что средневековые философы особенно интересовались неформальной логикой. Вам не нужно знать латинские имена: важно уметь распознавать заблуждения.Ошибки релевантности
Ошибки релевантности дают основания полагать, что утверждение или вывод, которые при рассмотрении оказываются на самом деле не основанием для каких-либо подобных действий.1. «Кто ты такой, чтобы говорить?», Или «Ты тоже», или заблуждение Tu Quoque
- Отказ от аргумента, потому что человек, который его продвигает, не может практиковать то, что он или она проповедует.
Врач: Вам следует бросить курить. Это серьезный риск для здоровья.
Пациент: Смотри, кто говорит! Я уйду, когда ты уйдешь.
Подобные ответы, вероятно, звучат знакомо. Но неспособность врача позаботиться о собственном здоровье не имеет отношения к аргументу, основанному на заботе о здоровье пациента, о том, что пациентка должна бросить курить.
2. Заблуждение отвлекающего маневра.
- Спорщик пытается отвлечь свою аудиторию, поднимая не относящийся к делу вопрос, а затем утверждает, что первоначальный вопрос был эффективно решен с помощью не относящегося к делу отвлечения.
В наши дни много говорят о необходимости исключить пестициды из наших фруктов и овощей.Но многие из этих продуктов необходимы для нашего здоровья. Морковь — отличный источник витамина А, брокколи богата железом, а апельсины и грейпфруты содержат много витамина С.
Планы по устранению или сокращению пестицидов, вероятно, не влекут за собой прекращение производства обычных овощей: предположение, что они do — это неуместный отвлекающий маневр.
3. Заблуждение Соломенного человека.
- Кто-то искажает или карикатурно изображает аргументы или взгляды оппонента, а затем атакует ослабленную версию, а не реальный аргумент.
Маргарет: «Мы должны что-то делать с парниковыми газами. Правительству следует повысить стандарты эффективности использования топлива для транспортных средств, чтобы сократить количество выбросов CO2, которые мы выбрасываем в течение следующих 20 лет ».
Роджер: «Решение Маргарет было бы катастрофой. Это убило бы экономику. Как люди могли бы работать без машин? »
Роджер утверждает, что Маргарет предлагает меры по устранению автомобилей. Маргарет не сказала ничего подобного. Это соломинка.
Положительное послание от Strawman: важность благотворительности.
Показывает, что соломенная версия позиции, против которой мы выступаем, может выиграть споры, но вряд ли приведет нас к истине. Если мы сможем показать, что даже самая сильная версия позиции, против которой мы выступаем, ошибочна, мы сможем добиться прогресса.
Итак, хорошее логическое и критическое мышление ведет к принципу благотворительности: когда вы представляете аргумент, с которым вы не согласны и пытаетесь оценить его, важно представить этот аргумент таким образом, чтобы он был достаточно верен аргументу, как он есть. Сделано создателями и максимально прочно.
4. Ad Hominem или заблуждение «на человека».
- Отклонение чьего-либо аргумента путем нападения на человека, а не оценки его аргумента по существу.
«Уважаемый редактор! Текущая кампания против совмещения пьянства с вождением автомобиля терроризирует законопослушных людей. Многие законопослушные люди сокращают потребление алкоголя, потому что боятся, что их поймают на случайной проверке дыхания. Но исследования показывают, что средний уровень алкоголя в крови водителя, попавшего в аварию со смертельным исходом, более чем в два раза превышает установленный законом предел.Текущая кампания против вождения в нетрезвом виде не позволяет достичь того, что должно быть нашим главным приоритетом; получить на дороге заядлых и заядлых пьющих ». Дуглас Майерс. Генеральный директор Dominion Breweries.
«Уважаемый редактор, вчера я прочитал письмо Дуга Майера, но он является генеральным директором крупной пивоваренной компании! Он кровно заинтересован в поддержании роста продаж алкоголя, а кампания против вождения в нетрезвом виде грозит сокращением продаж алкоголя. Мы не должны обращать внимания на его взгляды на вождение в нетрезвом виде ».
Но если Майер привел аргументы в пользу своей точки зрения, мы должны оценивать их, как и любой другой аргумент — верны ли они? сильный? звук? убедительно? (мы объясним эти термины в курсе) — вместо того, чтобы списывать их со счетов из-за фактов о нем.
Иногда, однако, позиция одного из аргументов может быть причиной для более тщательного изучения их аргументов, чем мы могли бы в противном случае.
Следующее не кажется ложным:
«Бертон Векслер, представитель Американской ассоциации производителей табака, утверждал, что нет достоверных научных доказательств того, что курение сигарет вызывает рак.Учитывая очевидную предвзятость Векслера в этом вопросе, к его аргументам следует относиться с осторожностью ».
5. Ошибочное обращение к властям.
- Полагаться на мнение очевидных (в отличие от подлинных) авторитетов для установления истинности утверждения или аргумента.
Ричард Лонг, уважаемый новозеландский новозеландский на пенсии, участвовал в рекламных кампаниях Hanover Finance. Долго не имел финансовой экспертизы.
Читатели новостей выглядят хорошо информированными, но по сути они ведущие.Их хорошо знают, потому что о них говорят в новостях, а не потому, что они знают об инвестициях. Если мы полагаемся на одобрение читателя новостей, чтобы решить, какому инвестиционному фонду мы должны доверять, мы будем принимать претензию без достаточных доказательств. Это было бы ошибочным обращением к власти.
Обращение к авторитету также противоречит основному принципу хорошего логического и критического мышления, который призывает нас брать на себя ответственность за оценку оснований для наших убеждений. Принятие убеждения только потому, что кто-то просто сказал нам, что это правда, — это способ избежать хорошего логического и критического мышления.
Иногда, однако, хорошее логическое и критическое мышление само заставляет нас полагаться на настоящие авторитеты. Если я не могу самостоятельно оценить вариант инвестирования, я могу решить, что мне следует довериться совету настоящего инвестиционного консультанта. Это не означает отказ от логического и критического мышления: это рассуждения по вопросу, косвенно связанному с вопросом, который я пытаюсь решить.
Когда я думаю о том, следует ли мне полагаться на настоящего авторитета, я должен рассмотреть следующие вопросы:
Является ли авторитет подлинным авторитетом: являются ли они экспертами?
Дают ли они советы в тех областях, в которых они являются подлинным авторитетом? (Мы должны слушать актеров об актерских играх, а не столько об инвестициях или медицине).
Существует ли широкий консенсус среди властей в этом районе? В противном случае мы не должны принимать решение верить X только потому, что авторитетный источник утверждает, что X истинен, поскольку другие подлинные авторитеты говорят, что X не соответствует действительности.
Говорит ли власть искренне (они могут поддерживать, потому что им за это платят) и свободны ли они от явной предвзятости?
Только если ответ на все четыре вопроса — «да», мы должны принимать претензию, потому что ее одобряет орган, и даже в этом случае мы должны делать это только в том случае, если мы не в состоянии оценить доказательства для претензии сами.
6. Ошибка композиции.
- Утверждая, что то, что верно для частей, должно быть истинным для всего. (Все части объекта O обладают свойством P. Следовательно, O обладает свойством P.)
Игроки в регби Ма’а Нону, Джером Кайно и Чарльз Пиату — все великие игроки. В 2012 году все они играли за «Оклендский блюз». Таким образом, «Оклендские блюз» 2012 года были отличной командой.
К сожалению, для Тима, многострадального фаната блюза, вывод этого аргумента был ложным, хотя посылки были верны.
И, показывая, что известные философы не застрахованы:
«Не следует ли нам предполагать, что точно так же, как глаз, рука, ступня и в целом каждая часть тела явно выполняет свои собственные функции, человек тоже имеет какая-то функция сверх функции его частей? » Аристотель, Нихомахова этика
7. Ошибка разделения.
- Утверждая, что то, что верно для целого, должно быть верно и для частей. (Противоположность ошибочности композиции: объект O обладает свойством P.Следовательно, все части объекта O обладают свойством P.)
Мужчины в среднем выше женщин. Поэтому Тим выше Марии Шараповой.
Тим должен быть выше 188 см, чтобы быть выше Шараповой: это не так.
8. Эквокация.
- Ключевое слово используется в двух или более смыслах в одном и том же аргументе, и очевидный успех аргумента зависит от изменения значения.
Любой закон может быть отменен надлежащим судебным органом.Закон всемирного тяготения — это закон. Следовательно, закон всемирного тяготения может быть отменен надлежащим юридическим органом.
Когда два смысла «закона» (законы, регулирующие поведение человека в сравнении с единообразием природы) становятся явными, становится очевидным, что первая посылка не имеет отношения к делу, следовательно, аргумент ошибочен.
И, показывая, что известные философы снова не застрахованы, мы видим, как Джон Стюарт Милль утверждает, что счастье желательно:
«Единственное доказательство того, что объект видим, — это то, что люди его действительно видят.Единственное доказательство того, что звук слышен, — это то, что люди его слышат … Точно так же, как я понимаю, единственное доказательство, которое можно представить, что что-либо желательно, — это то, что люди действительно этого хотят … [T] его факт , у нас есть не только все доказательства, которые допускает случай, но и все, что можно потребовать, что счастье — это благо. Джон Стюарт Милль, утилитаризм.
Но «желаемый» используется в этом отрывке двумя разными способами, чтобы означать «может быть желанным» (точно так же, как «видимый» означает «видимый») и «достойный быть желанным».
9. Апелляция к популярности.
- Утверждение, что утверждение должно быть правдой, потому что многие люди верят ему.
10 главных причин, по которым Библия истинна, в Essential Bible Blog:
Причина 8. Принятие лидером. Большинство величайших лидеров и мыслителей в истории подтвердили истинность и влияние Библии.
Причина 9. Глобальное влияние. Библия оказала большее влияние на законы, искусство, этику, музыку и литературу мировой цивилизации, чем любая другая книга в истории.
Возможно, Библия верна, но тот факт, что многие люди считают, что это так, не имеет отношения к тому, правда это или нет. Мы должны исследовать и оценивать их причины верить в это, а не принимать простой факт, что они верят в это, как причину для этого.
Но… иногда консенсус среди должным образом информированных людей может быть довольно хорошим руководством к истинности утверждения: посмотрите обстоятельства, при которых обращение к властям может не быть ошибочным.
10. Апелляция к традициям.
- Как призывы к популярности, за исключением того, что они обращаются к тому, как долго во что-то верили, а не к количеству людей, которые этому верили
Люди верили в астрологию очень давно, следовательно, это должно быть правда.
Но все возражения против аргументов, основанных на мнении большинства, применимы и здесь.
11. Апелляция к незнанию: Argumentum Ad Ignorantiam.
- Сторонник утверждает, что утверждение должно быть истинным, потому что никто не доказал его ложность, или что утверждение должно быть ложным, потому что никто не доказал его истинность.
Примечание : Когда мы описываем кого-то как невежественного, мы часто подразумеваем это как оскорбление. Здесь мы используем его для описания ситуации, в которой мы чего-то не знаем (не знаем). В этом смысле самые умные из нас очень многого не знают. (Мы не хотим двусмысленности в использовании термина «невежественный»).
На других планетах должна быть разумная жизнь: никто не доказал, что ее нет.
На других планетах нет разумной жизни: никто не доказал, что она есть.
Обе претензии предполагают, что отсутствие доказательств в пользу (или против) претензии является веской причиной полагать, что претензия является ложной (или истинной). Незнание — в смысле отсутствия знаний — является частью доказательства заключения. Но в целом сам факт того, что утверждение еще не доказано, не является достаточным основанием для того, чтобы считать это утверждение ложным.
Однако есть ли какие-нибудь не ошибочные призывы к невежеству?
a) Если квалифицированные исследователи использовали хорошо продуманные методы для поиска чего-либо в течение долгого времени, но безуспешно, и это то, что люди должны быть в состоянии найти, то тот факт, что они не нашли это, может представляют собой некоторое свидетельство того, что его не существует.
b) Некоторые практики (например, закон — см. Неделю 6) требуют, чтобы мы отклоняли иск до тех пор, пока не будет соблюден определенный стандарт доказывания: например, презумпция невиновности обвиняемых до тех пор, пока их вина не будет доказана вне разумных сомнений.
12. Обращение к эмоциям — например, жалость, привязанность.
- Спорщик пытается вызвать чувство жалости или сострадания, когда такие чувства не имеют логического отношения к выводу спора.
От студента к лектору: Я знаю, что пропустил большую часть лекций и все свои уроки.Но моя семья будет очень расстроена, если я провалю этот курс. Не можете найти еще несколько отметок?
Дочь: Можно ли завести щенка?
Отец: №
Дочь: Если бы ты меня любила, мы бы получили щенка.
Это было бы призывом к эмоциям, в данном случае любви. Обратите внимание, что настойчивый ребенок может продолжить:
Дочь: вырастет щенок и защитит нас. Мы не можем завести щенка?
Отец: №
Дочь: Если ты хочешь уберечь нас, ты бы получил щенка! Тебе на нас наплевать!
Это был бы соломенный человек, не предполагаемый отцом и не связанный с его действительным взглядом, и нападающий на это.Умение определять распространенные заблуждения может быть очень полезным в домашних условиях.
Помните, есть три вида заблуждений. Обрисованные до сих пор заблуждения релевантности представляют собой попытку ввести посылки, которые не имеют отношения к заключению.
Заблуждения о неприемлемых предпосылках
Заблуждения о неприемлемых предпосылках — попытка ввести посылки, которые, хотя и могут иметь отношение к делу, не подтверждают вывод аргумента.
13. Вопрос напрашивается.
- В философии, в отличие от многих других областей, «задавать вопрос» не означает «поднимать вопрос, на который необходимо ответить».В философии, когда кто-то задает вопрос, они формулируют или принимают в качестве предпосылки именно то, что они пытаются доказать в качестве заключения.
Артур: Бог существует.
Барбара: Откуда ты знаешь?
Артур: Потому что так сказано в Библии.
Варвара: Как узнать, что Библия истинна?
Артур: Потому что Библия богодухновенна. Все, что там сказано, правда.
Библия могла быть богодухновенной, только если бы Бог существовал. Таким образом, обращение Артура к Библии для доказательства существования Бога предполагает именно то, что он пытается доказать.
14. Ложная дилемма или ложная дихотомия.
- Происходит, когда аргумент представляет два варианта и создает впечатление, что только один из них может быть истинным, а не оба, и что других возможных вариантов нет.
Либо Шекспир написал все приписываемые ему пьесы, либо Бэкон. Есть веские основания полагать, что Шекспир написал не все пьесы, приписываемые ему. Поэтому Бэкон написал все пьесы, приписываемые Шекспиру.
Возможно, что Шекспир не написал все приписываемые ему пьесы, но это не значит, что Бэкон написал: есть и другие возможности.
В случае Шекспира / Бэкона ложная дилемма была явной (либо Шекспир написал все пьесы…, либо Бэкон сделал), но часто дилемма подразумевается.
Если я буду проводить всю неделю на вечеринках, у меня не будет времени на учебу, и я проиграю.
Если я потрачу на обучение всю неделю, я буду чрезмерно подготовлен и напряжен, и я проиграю.
Так что я все равно проиграю. С таким же успехом я мог бы провести неделю на вечеринках.
Здесь дилемма не сформулирована — «Единственный вариант — потратить всю неделю на обучение или провести всю неделю на вечеринках» — и однажды заявил, что это определенно неправдоподобно: студент может потратить часть недели на обучение, а часть недели устраивать вечеринки?
15.Ошибка точки принятия решения или парадокс Сорита.
- Иногда условия, которые делают использование термина уместным, варьируются в зависимости от континуума, и нет резкого разделения между обстоятельствами, в которых термин применяется правильно, и теми, в которых это не так.
Если аргумент утверждает, что, поскольку мы не можем определить точную отсечку или точку принятия решения, мы не можем провести различие между правильным и неправильным использованием этого термина, они утверждают ошибочно.
Одно зерно пшеницы не может быть кучей.Предположим, что это делает 1 миллион. Убери одну. Конечно, у нас все еще есть куча: если миллион составляет кучу, наверняка 999 999 тоже. Одно зерно не может превратить кучу в кучу. Убери еще одну. Конечно, у нас все еще есть куча: если 999 999, то наверняка и 999 998 тоже. Одно зерно… и т. Д. Убери другое. Наверняка у нас еще куча…. и т. д. и т. д.
Но если одно зерно не имеет значения, то кажется, что мы будем вынуждены сделать вывод, что 1 зерно действительно составляет кучу. Но это означает, что мы вообще не можем говорить о кучах пшеницы: мы не знаем, когда мы можем описать собрание пшеничных зерен как кучу, а когда — нет.
При зачатии эмбрион — это не человек. При рождении младенец — это личность. Не существует произвольного способа точно определить, когда эмбрион стал человеком. Следовательно, между эмбрионом и младенцем при рождении нет моральной разницы.
Но мы можем отличить лысых людей от не лысых, между кучей и не кучей, эмбрионами и младенцами, даже если мы не можем точно сказать, когда что-то перестало быть одним и стало другим.
16. Заблуждение о скользком спуске.
- Аргументы говорят, что не следует делать невинно выглядящий первый шаг, потому что после того, как он был сделан, будет невозможно не сделать следующий, следующий и так далее, пока вы не окажетесь в положении, которое вам не нужно быть внутри.
Не берите кредитную карту. Если вы это сделаете, у вас возникнет соблазн потратить деньги, которых у вас нет. Тогда вы исчерпаете свою карту. Тогда у вас будут настоящие долги. Вам придется начать играть в азартные игры в надежде на крупный выигрыш.Но обычно вы проигрываете. Тогда вам придется украсть деньги, чтобы покрыть убытки. Тогда ваш партнер оставит вас. И вы не сможете кормить собаку, и она умрет. И было бы плохо, если бы собака умерла. Значит, вам не нужна кредитная карта.
Аргументы о скользком спуске ошибочны, если можно остановиться на одном из шагов: нельзя ли получить кредитную карту с максимальной суммой, или проявить немного контроля, или заставить местное общество защиты животных помочь мне кормить собака?
17.Поспешные обобщения.
- Аргуэр делает общий вывод на основе смещенной или слишком малой выборки.
Самая старая женщина в мире, Жанна Кальман (122 года, 164 дня) курила до 110 лет. Поэтому курение не так уж плохо для вас.
Эндрю Уэйкфилд утверждал, что показал корреляцию между вакциной MMR, расстройствами кишечника и аутизмом, но — среди других недостатков — его исследование было сосредоточено на детях, которые, как он утверждал, уже страдали от вакцины.
Утверждение о том, что курение сопряжено с серьезными рисками для здоровья, не опровергается одним случаем, и в исследованиях, делающих выводы на уровне всего населения, необходимо привлекать репрезентативные группы исследователей.
18. Ошибочные аналогии.
- Заключение аргумента зависит от сравнения двух (или более) вещей, которые на самом деле не похожи в соответствующих отношениях, или без указания того, чем они отличаются и почему это имеет значение или не имеет значения. (См. Рассуждение по аналогии на неделе 6).
Мне нужна новая машина. Все мои последние три машины были надежными, синего цвета. Итак, я собираюсь купить синюю машину.
Письмо редактору после сообщения о том, что кого-то не пустили в медицинскую клинику, работающую в нерабочее время, потому что она не могла оплатить лечение своего лихорадочного, рвотного ребенка:
«Почему люди обращаются за лечением в частные клиники» недостаточно средств для покрытия комиссий? Идут ли эти же люди на заправочную станцию, заправляются ли они, выкидывают 5 долларов в окно и говорят: «Я вернусь с остальными позже», или, может быть, после ужина однажды вечером платят за еду и обещают вернуться на следующей неделе , месяц или год платить за вино? Думаю, нет.Ответ прост — не ходите в частные клиники ».
Аналогичны ли посещения поликлиники в нерабочее время больного ребенка посещению заправочной станции или ресторана?
19. И… Заблуждение!
- Ошибочность вывода о том, что только потому, что аргумент содержит ошибку, его вывод должен быть ложным.
Боб сказал мне, что я не должен воровать, потому что все знают, что воровство — это плохо, но я сразу понял, что этот аргумент содержит ошибку популярности, поэтому я пришел к выводу, что украсть яблоко — нормально.
Вывод аргумента может быть верным, даже если аргумент содержит ошибку. Обнаружение заблуждения просто означает, что аргумент должен искать другие, более веские причины в поддержку своего вывода.
Формальные заблуждения
Третий вид заблуждений — это формальные заблуждения. Некоторые аргументы ошибочны не из-за их содержания — из-за того, что они говорят, — а из-за их формы или структуры. Любой аргумент с этими формами или структурами будет недействительным, независимо от того, какой контент мы в них вкладываем.
Патрик расскажет немного больше о стандартных формах или структурах аргументов в течение недель 2-4. Наиболее знакомые версии содержат некоторое количество предпосылок, за которыми следует вывод, и если они верны (Патрик расскажет об этом в неделя 3) истинность посылок гарантирует истинность заключения.
Однако есть несколько распространенных форм аргументов, которые очень похожи на действительные версии, но не являются действительными. Здесь мы просто собираемся выявить две формальные ошибки, которые появятся позже в ходе курса.
20. Утверждая следствие.
Предположим, у меня есть сторожевой пес, Брут, и я уверен, что он лает, если злоумышленник войдет в мой дом.
Я могу рассуждать так:
\ (\ begin {array} {ll} \ text {P1} & \ text {Если есть злоумышленник, то Брут лает.} \\ \ text {P2} & \ text {Брут не лаял.} \\ & \ text {Следовательно,} \\ \ text {C} & \ text {Злоумышленника нет.} \ end {array} \)
Верно: если это правда что Брут будет лаять, если есть незваный гость, а если Брут не лаял, то не может быть незваного гостя.
Если посылки верны, то и вывод должен быть верным.
Но что, если я рассужу так:
\ (\ begin {array} {ll} \ text {P1} & \ text {Если есть злоумышленник, то Брут залает.} \\ \ text {P2} & \ text {Брут рявкнул.} \\ & \ text {Следовательно,} \\ \ text {C} & \ text {Злоумышленник.} \ end {array} \)
Это неверно. Почему? Что ж, посылка может быть верной, но первая посылка не говорит о том, что Брут будет лаять тогда и только тогда, когда есть незваный гость.
Первая посылка может быть верной — то есть может случиться так, что Брут будет лаять, если есть незваный гость, даже если Брут иногда лает и по другим причинам.
Обратите внимание, что здесь нельзя ответить: «О, грабитель мог накормить Брута транквилизированным стейком. Вот почему он не лаял. Это грабитель! » Это отвергает первую предпосылку (если есть злоумышленник, Брут лает), и мы видим, что произойдет, если посылки верны. Итак, здесь, если посылки верны, должен следовать вывод.
21. Отрицание предшествующего.
Предположим, я слышу лай и рассуждаю так:
\ (\ begin {array} {ll} \ text {P1} & \ text {Если он лает, значит, это собака.} \\ \ text {P2} & \ text {Он лает.} \\ & \ text {Следовательно,} \\ \ text {C} & \ text {Это собака.} \ end {array} \)
Верно. Если посылки верны — если правда, что если она лает, то это собака, и она лает, — то вывод тоже должен быть верным.
Но что, если я рассужу так:
Это неверно. Первая посылка гласит, что если что-то лает, то это собака (т. Е. Лают только собаки), но не говорится, что лают все собаки. Таким образом, мы не можем быть уверены, что вывод этого второго аргумента верен, даже если предпосылки верны. Может быть правдой то, что что-то не лает (т. Е. Антецедент ложен или отрицается, как говорится во второй посылке). , но это собака.\ (\ begin {array} {ll} \ text {P1} & \ text {Если он лает, значит, это собака.} \\ \ text {P2} & \ text {Это не лай.} \\ & \ text {Следовательно,} \\ \ text {C} & \ text {Это не собака.} \ end {array} \)
© Тим Дэр, Оклендский университет
Философия математики и ее логика: Введение
У. Аспрей и П. Китчер (редакторы) [1988], История и философия современной математики , Миннесотские исследования в философии науки 11, Миннеаполис, Университет Миннесоты. Широкий спектр статей, большинство из которых черпают философские морали из исторических исследований. Найдите этот ресурс:
Azzouni, J. [1994], Метафизические мифы, математическая практика , Кембридж, Cambridge University Press.Свежий философский взгляд. Найдите этот ресурс:
Balaguer, M. [1998], Платонизм и антиплатонизм в математике , Oxford, Oxford University Press. Отчет о реализме в онтологии и его соперниках. Найдите этот ресурс:
Benacerraf, P. [1965], «Какие числа не могут быть», Philosophical Review 74 , 47–73; перепечатано в Benacerraf and Putnam [1983], 272–294. Одна из наиболее цитируемых работ в данной области; утверждает, что числа не являются объектами, и вводит элиминативный структурализм.Найдите этот ресурс:
Бенасерраф П. и Х. Патнэм (редакторы) [1983], Философия математики , второе издание, Кембридж, Издательство Кембриджского университета. Обширный сборник, содержащий многие из центральных статей. Найдите этот ресурс:
Bernays, P. [1935], «Sur le platonisme dans les mathématiques», L’Enseignement mathématique 34 , 52–69; переведено как «Платонизм в математике» в Benacerraf and Putnam [1983], 258–271. Найдите этот ресурс:
Boolos, G.[1987], «Непротиворечивость основ арифметики Фреге », в О бытии и высказывании : Очерки Ричарда Картрайта , под редакцией Джудит Джарвис Томпсон, Кембридж, Массачусетс, MIT Press, 3–20; перепечатано в Hart [1996], 185–202. Найдите этот ресурс:
Boolos, G. [1997], «Является ли принцип Юма аналитичным?», в Language, Think and logic , под редакцией Ричарда Хека младшего. , Oxford, Oxford University Press, 245–261. Критика требований неологизма относительно статуса принципов абстракции.Найдите этот ресурс:
Brouwer, L.E.J. [1912], Intuitionisme en Formalisme , Gronigen, Noordhoof; переведено как «Интуиционизм и формализм» в Benacerraf and Putnam [1983], 77–89. Найдите этот ресурс:
Brouwer, L.E.J. [1949], «Сознание, философия и математика», в Benacerraf and Putnam [1983], 90–96. Найдите этот ресурс:
Burgess, J. [1983], «Почему я не номиналист», Notre Dame Журнал формальной логики 24 , 93–105. Ранняя критика номинализма.Найдите этот ресурс:
Берджесс, Дж. И Дж. Розен [1997], Предмет без объекта: Стратегии номиналистической интерпретации математики , Нью-Йорк, Oxford University Press. Обширная артикуляция и критика номинализма. Найдите этот ресурс:
Chihara, C. [1990], Конструируемость и математическое существование , Oxford, Oxford University Press. Защита модального взгляда на математику и резкая критика нескольких конкурирующих взглядов. Найдите этот ресурс:
(п.26) Коффа А. [1982], «Кант, Больцано и появление логицизма», Journal of Philosophy 79 , 679–689. Найдите этот ресурс:
Коффа А. [1991], Семантическая традиция из От Канта до Карнапа, , Кембридж, Издательство Кембриджского университета. Найдите этот ресурс:
Коливан, М. [2001], Незаменимость математики, , Нью-Йорк, Oxford University Press. Разработка и защита аргумента о необходимости онтологического реализма. Найдите этот ресурс:
Curry, H.[1958], Очерк формалистической философии математики , Амстердам, издательство North Holland Publishing Company. Найдите этот ресурс:
Даммет М. [1973], «Философские основы интуиционистской логики», в Даммете [1978], 215–247; перепечатано в Benacerraf and Putnam [1983], 97–129, и Hart [1996], 63–94. Влиятельная защита интуиционизма. Найдите этот ресурс:
Dummett, M. [1977], Elements of intuitionism , Oxford, Clarendon Press. Подробное введение и защита интуиционистской математики.Найдите этот ресурс:
Даммет М. [1978], Правда и другие загадки , Кембридж, Массачусетс, Издательство Гарвардского университета. Сборник основных статей Даммета по метафизике и философии языка. Найдите этот ресурс:
Field, H. [1980], Science without numbers , Princeton, New Jersey, Princeton University Press. Широко цитируемая защита фикционализма, попытка опровергнуть аргумент о незаменимости. Найдите этот ресурс:
Field, H.[1984], «Является ли математическое знание просто логическим?», The Philosophical Review 93, , 509–552; перепечатано (с добавленным приложением) в Field [1989], 79–124, и в Hart [1996], 235–271. Найдите этот ресурс:
Field, H. [1989], Реализм, математика и модальность , Oxford , Блэквелл. Отпечатки статей Филда о художественной литературе. Найдите этот ресурс:
Frege, G. [1884], Die Grundlagen der Arithmetik , Breslau, Koebner; Основы арифметики , перевод Дж.Остин, второе издание, Нью-Йорк, Харпер, 1960. Классическая формулировка и защита логицизма. Найдите этот ресурс:
Frege, G. [1893], Grundgesetze der Arithmetik , vol. 1, Йена, Х. Похле; перепечатано Hildesheim, Olms, 1966. Более техническое развитие логицизма Фреге. Найдите этот ресурс:
Gödel, K. [1944], «Математическая логика Рассела», Benacerraf and Putnam [1983], 447–469. Часто цитируемая защита реализма в онтологии и реализма в истинностной ценности. Найдите этот ресурс:
Gödel, K.[1951], «Некоторые основные теоремы об основах математики и их следствия», в его Собрании сочинений , т. 3, Oxford, Oxford University Press, 1995, 304–323. Найдите этот ресурс:
Gödel, K. [1964], «Что такое проблема континуума Кантора?», Benacerraf and Putnam [1983], 470–485. Часто цитируемая защита реализма в онтологии и реализма в истинностной ценности. Найдите этот ресурс:
Хейл, Боб [1987], Абстрактные объекты , Оксфорд, Бэзил Блэквелл. Подробное развитие неологизма в поддержку Райта [1983].Найдите этот ресурс:
Хейл, Боб [2000a], «Реальные числа по абстракции», Philosophia Mathematica, 3-я сер., 8 , 100–123. Найдите этот ресурс:
Хейл, Боб [2000b], «Абстракция и множество. теория », Notre Dame Journal of Formal Logic 41 , 379–398. Найдите этот ресурс:
Hart, WD (редактор) [1996], Философия математики , Oxford, Oxford University Press. Сборник статей, впервые опубликованных в другом месте. Найдите этот ресурс:
Hellman, G.[1989], Математика без чисел , Oxford, Oxford University Press. Артикуляция и защита модального структурализма. Найдите этот ресурс:
(стр.27) Гейтинг, А. [1930], «Die formalen Regeln der intuitionistischen Logik», Sitzungsberichte der Preussischen Akademie der Wissesschaften, Physikalisch ‐ Mathematische Klasse , 42–56. Разрабатывает дедуктивную систему и семантику для интуиционистской математики. Найдите этот ресурс:
Heyting, A. [1956], Интуиционизм: введение , Амстердам, Северная Голландия.Читаемый отчет об интуиционизме. Найдите этот ресурс:
Hodes, H. [1984], «Логицизм и онтологические обязательства арифметики», Journal of Philosophy 81 (13), 123–149. Другой примерно логицизм Фреге. Найдите этот ресурс:
Китчер П. [1983], Природа математического знания , Нью-Йорк, Oxford University Press. Формулировка конструктивистской эпистемологии и детальная атака на тезис о том, что математическое знание априорно. Найдите этот ресурс:
Lakatos, I.(редактор) [1967], Проблемы философии математики , Амстердам, издательство North Holland Publishing Company. Содержит множество важных статей крупных философов и логиков. Найдите этот ресурс:
Лакатос, I. [1976], Доказательства и опровержения, , под редакцией Дж. Уорролла и Э. Захара, Кембридж, Cambridge University Press. Часто цитируемое исследование, которое является атакой рационалистической эпистемологии математики. Найдите этот ресурс:
MacLane, S. [1986], Mathematics: Form and function , New York, Springer-Verlag.Философский отчет влиятельного математика. Найдите этот ресурс:
Мэдди П. [1990], Реализм в математике , Oxford, Oxford University Press. Артикуляция и защита реализма в отношении множеств. Найдите этот ресурс:
Мэдди П. [1997], Натурализм в математике , Oxford, Clarendon Press. Четкое описание натурализма в отношении математики и ее связи с традиционными философскими проблемами. Найдите этот ресурс:
Malament, D. [1982], Review of Field [1980], Journal of Philosophy 19, , 523–534.Найдите этот ресурс:
Парсонс, К. [1983], Математика в философии , Итака, Нью-Йорк, Cornell University Press. Сборник важных работ Парсонса по философии математики. Найдите этот ресурс:
Parsons, C. [1990], «Структуралистский взгляд на математические объекты», Synthèse 84 , 303–346; перепечатано в Hart [1996], 272–309. Найдите этот ресурс:
Posy, C. [1984], «Кантовский математический реализм», The Monist 67, , 115–134.Сравнение кантовской философии математики с интуиционизмом. Найдите этот ресурс:
Putnam, H. [1971], Philosophy of logic , New York, Harper Torchbooks. Источник аргумента о необходимости онтологического реализма. Найдите этот ресурс:
Putnam, H. [1980], «Модели и реальность», Journal of Symbolic Logic 45, , 464–482; перепечатано в Benacerraf and Putnam [1983], 421–444. Найдите этот ресурс:
Quine, W.V.O. [1951], «Две догмы эмпиризма», The Philosophical Review 60, , 20–43; перепечатано в Hart [1996], 31–51.Влиятельный источник атаки на аналитическое / синтетическое различие. Найдите этот ресурс:
Quine, W.V.O. [1960], Слово и объект , Кембридж, Массачусетс, MIT Press. Найдите этот ресурс:
Quine, W.V.O. [1981], Theories and things , Cambridge, Massachusetts, Harvard University Press. Найдите этот ресурс:
Resnik, M. [1980], Frege and the философия математики , Ithaca, New York, Cornell University Press. Экзегетическое исследование Фреге и введение в философию математики.Найдите этот ресурс:
Резник, М. [1985], «Насколько номиналистичен номинализм Хартри Филда?», Philosophical Studies 47 , 163–181. Критика Филда [1980]. Найдите этот ресурс:
Resnik, M. [1997], Математика как наука о моделях , Oxford, Oxford University Press. Полная формулировка структурализма реалистического стиля. Найдите этот ресурс:
(стр.28) Ширн, М. (редактор) [1998], Философия математики сегодня, , Oxford, Clarendon Press.Материалы конференции по философии математики, состоявшейся в Мюнхене в 1993 г .; освещение большинства актуальных вопросов. Найдите этот ресурс:
Шапиро С. [1983], «Консервативность и неполнота», Journal of Philosophy 80 , 521–531; перепечатано в Hart [1996], 225–234. Критика Филда [1980]. Найдите этот ресурс:
Шапиро С. (редактор) [1996], Математический структурализм , Philosophia Mathematica 3rd ser., 4 . Спецвыпуск, посвященный структурализму; содержит статьи Бенасеррафа, Хейла, Хеллмана, Маклейна, Резника и Шапиро.Найдите этот ресурс:
Шапиро С. [1997], Философия математики: структура и онтология , Нью-Йорк, Oxford University Press. Обширная артикуляция и защита структурализма. Найдите этот ресурс:
Shapiro, S. [1998], «Неполнота, механизм и оптимизм», Bulletin of Symbolic Logic 4 , 273–302. Найдите этот ресурс:
Shapiro, С. [2000a], «Фреге встречается с Дедекиндом: неологичистская трактовка реального анализа», Notre Dame Journal of Formal Logic 41, (4), 335–364.Найдите этот ресурс:
Shapiro, S. [2000b], Размышляя о математике: философия математики , Oxford, Oxford University Press. Популяризация и учебник по философии математики. Найдите этот ресурс:
Шапиро, С. [2003a], «Пролегомен любой будущей неологицистской теории множеств: абстракция и неопределенная расширяемость», British Journal for the Philosophy of Science 54 , 59–91. Найдите этот ресурс:
Шапиро, С. [2003b], «Философия математики», в Философия науки сегодня , под редакцией Питера Кларка и Кэтрин Хоули, Оксфорд, Oxford University Press, 181–200 .Найдите этот ресурс:
Skolem, T. [1922], «Einige Bemerkungen zur axiomatischen Begründung der Mengenlehre», in Matematikerkongressen i Helsingfors den 4–7 Juli 1922 , Helsinki, Akademiska Bokhan2–232–21; переведено как «Некоторые замечания по аксиоматизированной теории множеств» в van Heijenoort [1967], 291–301. Найдите этот ресурс:
Skolem, T. [1941], «Sur la portée du théorème de Löwenheim – Skolem», в Les Entretiens de Zurich, 6–9 декабря 1938 г., , под редакцией Ф. Гонсета, Цюрих, Лиман, 1941, 25–52.Найдите этот ресурс:
Steiner, M. [1975], Mathematical knowledge , Ithaca, New York, Cornell University Press. Формулировка некоторых эпистемологических вопросов; защита реализма. Найдите этот ресурс:
Tennant, N. [1987], Anti-realism and logic , Oxford, Clarendon Press. Артикуляция антиреализма в истинностной ценности, реализма в онтологии; защищает интуиционистскую логику релевантности от классической логики. Найдите этот ресурс:
Tennant, N. [1997], Укрощение истинного , Oxford, Oxford University Press.Подробная защита глобального семантического антиреализма. Найдите этот ресурс:
Van Heijenoort, J. (редактор) [1967], From Frege to Gödel , Cambridge, Massachusetts, Harvard University Press. Сборник многих важных статей по логике на рубеже двадцатого века. Найдите этот ресурс:
Webb, J. [1980], Механизм, ментализм и метаматематика: эссе о финитизме , Dordrecht, D. Reidel.Find этот ресурс:
Whitehead, AN, and B.Рассел [1910], Principia Mathematica , vol. 1, Кембридж, Cambridge University Press. Найдите этот ресурс:
Wright, C. [1983], Концепция чисел как объектов Фреге , Абердин, Шотландия, Aberdeen University Press. Возрождение логицизма Фреге. Найдите этот ресурс:
логических заблуждений и искусство спора
логических заблуждений и искусство споров Содержание:Введение
Это руководство по использованию логических заблуждений в дебатах.И когда я говорю «использую», Я не имею в виду просто указать на них, когда противники спорят их — Я имею в виду преднамеренное принятие их на себя или поиск способов трансформации ложные аргументы в совершенно хорошие.Дебаты, к счастью или нет, являются упражнением в убеждении, остроумии и риторике, не просто логика. В формате дебатов, ограничивающем выступление каждого участника дебатов. время, просто неразумно ожидать каждого предложения или вывода точно и строго следовать из четкого набора изложенных предпосылок в самом начале.Вместо этого участники дебатов должны свести воедино различные факты, идеи и ценности, которые разделяют или которых можно убедить принять, и затем покажите, что эти идеи более или менее правдоподобно приводят к заключению. Логика — полезный инструмент в этом процессе, но это не единственный инструмент — в конце концов, «правдоподобие» — это довольно субъективный вопрос, который не следует строгие логические правила. В конечном итоге судья в раунде дебатов должен решить: позиция какой стороны более правдоподобна в свете приведенных аргументов — и судья должен выбрать одну из этих сторон, даже если логика одно только говорит о том, что «мы не знаем» — это ответ на поставленный вопрос.
Кроме того, давайте будем честными: дебаты — это не просто поиск истины, это
также около побед. Если вы думаете, что ошибочный аргумент может исчезнуть
убедив судью проголосовать за вас, у вас все получится, верно?
Уловка не в том, чтобы попасться.
Во-вторых, и это, возможно, более важно, указать на логическую ошибку.
способ убрать аргумент из дискуссии , а не просто ослабить
Это. В большинстве случаев участник спора отвечает на аргумент, просто заявляя
контраргумент, показывающий, почему исходный аргумент не так уж и важен
по сравнению с другими проблемами, или не следует воспринимать всерьез, или что-то в этом роде.
Такой ответ хорош, за исключением того, что исходный аргумент все еще
остается в дискуссии, хотя и в менее убедительной форме, и оппозиция
может риторически оскорблять, говоря, почему это важно после
все.С другой стороны, если вы можете показать, что исходный аргумент на самом деле
совершает логическую ошибку, вы ставите оппозицию в позицию оправдания
почему их исходным аргументом следует считать у всех . Если они
не может придумать чертовски вескую причину, тогда аргумент фактически удаляется
из раунда.
Следовательно, недостаточно просто указать на логическую ошибку и двигаться дальше; есть искусство указывать на логические заблуждения в вашей оппозиции аргументы. Вот несколько стратегий, которые я нашел полезными, чтобы указать логические заблуждения эффективным способом:
- Назовите название логической ошибки, желательно на латинском и английском языках, и убедитесь, что вы используете фразу «логическая ошибка».«Почему? Потому что это важно убедить всех, что это не просто контраргумент, который вы вы делаете, и вы не просто навешиваете ярлык на точку зрения оппозиции как на «ошибочную» для риторического эффекта. Указание латинского названия заблуждения помогает, потому что некоторые люди просто не уверены, что что-то ошибочное, если только Аристотель или какой-то другой авторитет назвал это одним. Скажите что-нибудь вроде: «Оппозиция указывает, что избиратели поддержали X с большим отрывом в прошлогоднем референдум.Но это всего лишь логическая ошибка argumentsum. ad populum , апелляция к общественному мнению! »
- Расскажите всем, что означает ошибка и почему она неверна. Но будь осторожен — это надо делать без педантизма. Вы должны указать значение заблуждения, как будто вы повторяете то, что считаете разумным судья уже знает. Чтобы продолжить приведенный выше пример, скажите: «Это не имеет значения. сколько людей согласны с вами, это не значит, что это обязательно правильный .» Итак, теперь вы определили для всех, что ошибочно в аргументе ad populum.
- Приведите действительно очевидный пример того, почему заблуждение неверно. Предпочтительно, пример также должен быть неблагоприятной аналогией для оппозиции предложение. Таким образом: «В прошлом веке большинство людей в некоторых государствах считали рабство было приемлемо, но это не сделало его так! »
- Наконец, укажите, почему логическая ошибка имеет значение для раунда дебатов.»Этот ошибочный аргумент следует исключить из дискуссии. означает, что единственным оставшимся аргументом оппозиции в пользу X является …. «
список логических заблуждений Приведенное ниже не является исчерпывающим списком всех известных логических заблуждений. Это также не задумано как строгий философский трактат по логическим рассуждениям.(Если это то, что вы ищете, обратите внимание на следующие отличные веб-ресурсы: Логическая страница Atheist Web, или Сан Миссия университета Хосе: критическая страница; Я в долгу перед этими страницами за то, что напомнил мне о ряде заблуждений, о которых я забыл.) Я составил список заблуждений, которые должны быть знакомы участникам дебатов. с — либо для указания на них в аргументах других, либо для использования и защищая их по-своему.
Argumentum ad antiquitatem (аргумент в пользу древности или традиции). Это знакомый аргумент, что какая-то политика, поведение или практика являются правильными или приемлемыми потому что «так всегда делалось». Это чрезвычайно популярный ошибочность раундов дебатов; например, «Каждая великая цивилизация в истории предоставил государственные дотации на искусство и культуру! »Но это не оправдать продолжение политики.
Поскольку argumentum ad antiquitatem легко опровергнуть простым указывая на это, в целом этого следует избегать.Но если вы должны сделать такой аргумент — возможно потому, что ничего лучше не придумаешь — вы можете, по крайней мере, сделать его более приемлемым, предоставив причина, по которой обычно следует уважать традиции. Например, вы можете привести эволюционный аргумент в пользу того, что преобладание определенного практика в существующих обществах свидетельствует о том, что общества, которые не смогли усыновить его были отсеяны естественным отбором. Этот аргумент слабый, но лучше, чем одно заблуждение.
Argumentum ad hominem (аргумент направлен на человека). Это ошибка атаки персонажа или мотивы человека, высказавшего идею, а не саму идею. Самый очевидный пример этого заблуждения — когда один из участников спора клевещет на характер другого участника дебатов (например, «Члены оппозиции — пара фашистов! »), но на самом деле это не так уж и часто. проявление argumentum ad hominem атакует источник информация — например, ответ на цитату Ричарда Никсона на тему свободной торговли с Китаем, сказав: «Мы все знаем, что Никсон был лжец и мошенник, так почему мы должны верить всему, что он говорит? » Argumentum ad hominem также возникает, когда чьи-то аргументы игнорируются просто потому что они могут извлечь выгоду из политики, которую они защищают, например, Билл Гейтс выступает против антимонопольного законодательства, богатые люди выступают за снижение налогов, белые люди выступают против позитивных действий, меньшинства выступают за позитивные действия и т. д.Во всех этих случаях возникает актуальный вопрос: не то, кто выдвигает аргумент, а то, верен ли аргумент.
Использовать ошибку argumentum ad hominem — всегда дурной тон. Но бывают случаи, когда это не совсем заблуждение, например, когда нужно оценить истинность фактических утверждений (в отличие от строк аргументов или заявлений о ценности), сделанные заинтересованными сторонами. Если кто-то имеет стимул врать о чем-то , тогда это было бы наивно без вопросов принимать его утверждения по этому поводу.Это также можно переформулировать множество аргументов ad hominem , чтобы перенаправить их в сторону идей, а не людей, например, заменив «Мои оппоненты фашисты »с« аргументами моих оппонентов фашистскими ».
Argumentum ad ignorantiam (аргумент незнанию). Это ошибочное предположение верно просто потому, что это не было доказано как ложное. Например, кто-то может возразить, что глобальное потепление, безусловно, происходит, потому что никто не убедительно продемонстрировал, что это не так.Но не сумев доказать глобальный Теория потепления ложна — это не то же самое, что доказать ее истинность.
Действительно ли argumentum ad ignorantiam ошибочна в решающей степени зависит от бремени доказывания. В американском зале суда, где бремя доказывания лежит на обвинении, это было бы ошибочным обвинение утверждало, что «у обвиняемого нет алиби, поэтому он должен был совершить преступление «. Но это было бы совершенно справедливо для защита аргументирует: «Обвинение не доказало, что обвиняемый совершил преступление, поэтому вы должны признать его невиновным.»Оба заявления иметь форму argumentum ad ignorantiam ; разница в том Бремя доказательства.
Во время дебатов команда авторов в раунде дебатов обычно (но не всегда) предполагается, что несет бремя доказывания, что означает, что если команда не может доказать предложение к удовлетворению судьи, возражение побеждает. В некотором смысле версия команды соперника считается верной, пока не будет доказано. ложный. Но бремя доказывания иногда можно переложить; например, в некоторые формы дебатов, команда авторов может переложить бремя доказывания противоположной команде, представив дело prima facie , которое, при отсутствии опровержения достаточно, чтобы подтвердить предложение.Тем не менее, большая нагрузка обычно лежит на группе авторов, которая означает, что только оппозиция может обвинить argumentum ad ignorantiam относительно доказательства утверждения.
Argumentum ad logicam (аргумент к логике). Это ошибка предположения, что что-то не так. просто потому, что доказательство или аргумент, который кто-то предложил для этого, недействителен; это рассуждение ошибочно, потому что может быть другое доказательство или аргумент что успешно поддерживает предложение.Это заблуждение часто появляется в контексте соломинки мужской аргумент.
Это еще один случай, в котором бремя доказывания определяет, это на самом деле заблуждение или нет. Если предлагающая команда не может предоставить достаточно поддержки его дела, бремя доказывания диктует, что они должны потерять обсуждение, даже если существуют другие аргументы (не представленные предложением team), которая могла бы успешно поддержать дело. Более того, это обычная практика в дебатах, когда судьи не придают значения поддерживаемому аргументом, который был признан недействительным другой командой, даже если может быть веский аргумент, который команда не смогла выдвинуть, который имел бы поддержал ту же точку зрения; это потому, что неявное бремя доказательства лежит на команде, которая подняла спор.Для дальнейшего комментария о бремени доказывания см. argumentum ad ignorantiam , выше.
Argumentum ad misericordiam (аргумент или призыв к жалости). Английский перевод в значительной степени говорит все это. Пример: «Подумайте обо всех бедных, голодающих эфиопских детях! Как можем ли мы быть настолько жестокими, чтобы не помогать им? »Проблема с таким аргументом в том, что никакие особые просьбы не могут сделать невозможное возможным, ложная правда, дорогое бесплатное и т. д.
Разумеется, указание на серьезность проблема как часть обоснования принятия предлагаемого решения. Ошибка возникает, когда другие аспекты предлагаемого решения (например, насколько это возможно, сколько это стоит, кому еще может быть нанесен вред приняв политику) игнорируются или реагируют только более страстно мольбы. Вы не должны осуждать свою оппозицию за совершение этого заблуждения. если они не полагаются на призывы к состраданию, исключая другие необходимые аргументы.Вполне допустимо использовать призыв к жалости для того, чтобы утверждают, что выгоды от предлагаемой политики больше, чем они могли бы на первый взгляд (и, следовательно, способные оправдать большие затраты).
Argumentum ad nauseam (аргумент до отвращения; т.е. повторением). Это заблуждение попытки доказать что-то, повторяя это снова и снова. Но не важно сколько раз ты что-то повторяешь, ни больше ни меньше не станет правда, чем это было в первую очередь.Конечно, это не заблуждение заявлять правду снова и снова; ошибочно ожидать повторения в одиночку, чтобы заменить реальные аргументы.
Тем не менее, это очень популярное заблуждение в дебатах, и причина: чем чаще вы что-то говорите, тем больше вероятность того, что судья это запомнит. Первое, чему вас научат в любой публике разговорный курс состоит в том, что вы должны: «Скажите им, что вы собираетесь им сказать, потом скажи им, а потом скажи им то, что ты им сказал.»К сожалению, некоторые спорщики думают, что это все, без каких-либо обоснований! Подходящее время, чтобы упомянуть argumentum ad nauseam в дебатах раунд — это когда другая команда сделала какое-то утверждение, не оправдав это, а затем повторял это снова и снова. Латинская формулировка особенно здесь приятно, так как это напоминает то, что утверждают оппозиционеры. ты хочешь сделать: рвота. «Сэр, наши оппоненты говорят нам, что наркотиков неправильны , лекарств неправильны , лекарств неправильны , снова и снова и снова.Но этот аргумент до тошноты не может и не выиграет в этих дебатах. их, потому что они не дали нам оправдания своим наглым утверждениям! »
Argumentum ad numerum (аргумент или обращение к цифрам). Это заблуждение — попытка доказать что-то, показывая, сколько людей думают, что это правда. Но не важно сколько людей верят во что-то, что не обязательно соответствует действительности или вправо. Пример: «По крайней мере 70% всех американцев поддерживают ограничения. о доступе к абортам.«Что ж, может быть, 70% американцев ошибаются!
Это заблуждение очень похоже на аргумент . ad populum , обращение к народу или к популярности. Когда различие находится между двумя, ad populum имеет узкое значение для обозначения обращение к мнению людей в непосредственной близости, возможно в надежде убедить других (например, судей) поддержать эту идею, тогда как ad numerum используется для обозначения апелляций исключительно по номеру людей, придерживающихся определенных убеждений.Отличие прекрасное, и в целом эти термины могут использоваться как синонимы в раундах дебатов. (Я обнаружил, что ad populum имеет лучший риторический эффект.)
Argumentum ad populum (аргумент или обращение к общественности). Это ошибка попытки докажите что-либо, продемонстрировав, что публика с вами согласна. Например, см. выше. Это заблуждение почти идентично argumentsum. ad numerum , подробности см.
Argumentum ad verecundiam (аргумент или обращение к власти). Это заблуждение возникает, когда кто-то пытается продемонстрировать истинность предложения, цитируя человека, который соглашается, даже если этот человек может не иметь опыта в данной области. Например, некоторые люди любят цитировать мнение Эйнштейна о политике. (он был склонен к довольно левым взглядам), как будто Эйнштейн был политическим философ, а не физик.Конечно, это не заблуждение. все полагаться на авторитеты, чей опыт относится к рассматриваемому вопросу, особенно в отношении фактических вопросов, на которые нелегко ответить непрофессионала — например, имеет смысл процитировать Стивена Хокинга на тему черных дыр.
По крайней мере, в некоторых формах дебатов, цитируя различные источники в поддержку должность не только приемлема, но и обязательна. В общем, есть нет ничего плохого в этом.Даже если у указанного человека нет опыт в этой области, он мог особенно красноречиво сказать то, что делает речь более убедительной. В общем, спорщики должен быть вызван только за совершение argumentum ad verecundiam когда (а) они полагаются на неквалифицированный источник информации о фактах без других (квалифицированных) источников подтверждения, или (б) они подразумевают, что какая-то политика должна быть правильной просто потому, что так считал такой-то и такой-то.
Циркуль в демонстрации (круговой аргумент). Круговая аргументация возникает, когда кто-то использует то, что они пытаются доказать, как часть доказательства этого. Вот один из моих любимых примеров (в упрощенном виде): «Марихуана — это незаконно в каждом штате страны. И все мы знаем, что вам не следует нарушать закон. Так как курение марихуаны незаконно, не курите травку. А поскольку вы не должны курить травку, правительство обязано остановить людей от курения, вот почему марихуана запрещена! »
Круговые аргументы часто встречаются в дебатах, но не всегда легко заметить, как в примере выше.Но они всегда незаконнорожденные, и указание на них в раунде дебатов выглядит действительно хорошо, если вы умеете Это. Лучшая стратегия указать на круговой аргумент — убедиться, что вы можете четко сформулировать доказываемое утверждение, а затем указать, где это предложение фигурирует в доказательстве. Хорошее подведение итогов: «Другими словами, они пытаются сказать нам, что X истинно, потому что X есть правда! Но им еще предстоит сказать нам , почему — это правда ».
Сложный вопрос. Сложный вопрос это вопрос, который неявно предполагает, что что-то истинно по своей конструкции, типа «Вы перестали бить свою жену?» Такой вопрос ошибочен только если предполагалось, что это правда (в данном случае, что вы избили свою жену) не установлено.
Сложные вопросы — это устоявшаяся и проверенная временем практика в спорят, хотя они редко бывают такими лысыми, как только что приведенный пример. Сложные вопросы обычно появляются при перекрестном допросе или информационных сообщениях. когда спрашивающий хочет, чтобы опрашиваемый непреднамеренно что-то признал что она могла бы не признать, если бы ее спросили прямо.Например, можно сказать: «Поскольку большинство чернокожих американцев живут в бедности, неужели вы думаю, что самопомощи в черном сообществе достаточно для решения свои проблемы? »Конечно, вступительная статья о большинстве чернокожих американцев, живущих в бедности, может не соответствовать действительности (на самом деле, это ложь), но неосторожный спорщик может не подумать достаточно быстро, чтобы заметить, что Заявление безбилетного пассажира вызывает сомнения. Это хитрая тактика, но споры иногда это подлый бизнес.Вы бы не хотели задавать такой вопрос, как это в вашей магистерской диссертации, но это может сработать в дебатах. Но будь осторожен — если вы попытаетесь быстро натянуть кого-то, кто достаточно внимателен, чтобы поймать ты будешь выглядеть глупо. «Предположение, лежащее в основе вашего вопроса, просто ложный. Большинство чернокожих не , а чернокожих живут в бедности. Получите свои факты прямо, прежде чем снова перебить меня! »
Cum hoc ergo propter hoc (с этим, значит из-за этого). Это знакомое заблуждение ошибочно принимать корреляцию за причинно-следственную связь, т. е. думать, что, поскольку два вещи происходят одновременно, одно должно быть причиной другого. Популярный Примером этой ошибки является аргумент о том, что «Президент Клинтон очень экономическая политика; просто посмотрите, как хорошо в экономике, пока он в офисе! «Проблема в том, что две вещи могут произойти одновременно время просто по совпадению (например, президент может иметь незначительное влияние на экономику, а реальной движущей силой является технологический рост), или причинная связь между одним и другим может отставать во времени (е.g., текущее состояние экономики определяется действиями предыдущих президенты), или две вещи могут быть не связаны друг с другом, но связаны к общему делу (например, сокращение штата расстроило многих избирателей, заставив их избрать нового президента незадолго до того, как экономика начала получать выгоду от сокращение).
Всегда ошибочно предполагать, что существует причинная связь между две вещи просто потому, что они сосуществуют. Но обычно рассматривается корреляция приемлемые подтверждающие доказательства для теорий , которые аргументируют причинно-следственную связь связь между двумя вещами.Например, некоторые экономические теории предполагают, что существенное сокращение дефицита федерального бюджета должно вызвать в экономике чтобы добиться большего (грубо говоря), поэтому совпадение сокращений дефицита при Клинтоне и относительное здоровье экономики можно рассматривать как свидетельство в пользу этих экономических теорий. Что это означает в раундах дебатов в том, что можно продемонстрировать корреляцию между двумя явлениями. и сказать, что одно вызвало другое , если , вы также можете придумать убедительный Причины, по которым корреляция не случайна.
Cum hoc ergo propter hoc очень похож на сообщение hoc ergo propter hoc , ниже. Эти два термина могут использоваться почти как синонимы, post hoc (как его ласково называют) — предпочтительный термин.
Dicto simpliciter (разговорный просто, т.е. широкое обобщение). Это заблуждение широкое заявление и ожидание того, что оно будет правдой в каждом конкретном случае — другими словами, стереотипы.Пример: «Женщины в среднем не так сильный, как мужчина, и менее способный носить ружье. Поэтому женщины не могут тянуть их вес в воинской части «. Проблема в том, что в широком заявлении может быть правдой (в среднем женщины действительно слабее мужчин), но это не так. обязательно верно для каждого члена рассматриваемой группы (есть некоторые женщины, которые намного сильнее среднего).
Как показывает пример, dicto simpliciter является довольно распространенным в раундах дебатов.В большинстве случаев нет необходимости вызывать оппонента оспаривать это заблуждение — достаточно указать, почему сделанные ими радикальные обобщения не подтверждают их точку зрения. С всем известно, что такое широкое обобщение, употребляя в этом случай обычно звучит снисходительно. Также важно отметить, что некоторые обобщения совершенно справедливы и применимы непосредственно ко всем индивидуальным случаев, и поэтому не допускайте ошибки dicto simpliciter (например, «Все мужчины имеют Y-хромосому», насколько мне известно, абсолютно правильно).
Природа, обращение к. Это ошибочное предположение, что все, что является «естественным» или соответствует «природе» (как-то определено) хорошо, или что все, что противоречит природе, плохо. Например, «Содомия неестественна; анальный секс не является эволюционной функцией. полового члена или ануса. Следовательно, мужеложство — это плохо ». Но помимо трудности определения того, что вообще означает «естественный», нет особой причины Предположим, что неестественное и неправильное — это одно и то же.В конце концов, носить одежда, обработка почвы и использование огня могут считаться неестественными так как никакие другие животные не делают этого, но люди делают это все время и с большой пользой.
Обращение к природе время от времени появляется в дебатах, часто в форме наивных аргументов защитников окружающей среды в пользу сохранения нетронутой дикой природы или ресурсы. Аргумент очень слабый, и его всегда следует опровергать. Однако его можно усилить, показав, почему, по крайней мере в конкретных случаях, может быть (возможно, неопределенная) польза от сохранения природы как Это.Типичный экологический аргумент в этом направлении состоит в том, что люди являются частью сложной биологической системы, очень чувствительной к ударам, и поэтому для людей опасно заниматься деятельностью, которая может повредить систему способами, которые мы не можем предсказать. Обратите внимание, однако, что этот подход больше не апеллирует к самой природе, но к ценности человеческого выживания.
Дополнительные комментарии по этому поводу см. В натуралистическом заблуждение.
Натуралистическая ошибка. Это является ошибкой попытки сделать выводы о том, что правильно или хорошо (то есть о ценностях) только на основании фактов. Это недействительно потому что независимо от того, сколько фактов вы соберете, любые логические вывод из них будет еще одним констатацией факта, а не утверждением ценности. Если вы хотите сделать выводы о ценностях, вы должны Включите среди своих предположений (или аксиом, или предпосылок) утверждение значение. Если у вас есть аксиоматическая формулировка ценности, вы можете использовать это в сочетании с констатацией фактов, чтобы прийти к ценностным выводам.
Например, кто-то может возразить, что посылка «Это лекарство будет не дать вам умереть «сразу приводит к заключению». принять это лекарство ». Но это рассуждение неверно, потому что первое Заявление — это констатация факта, а последнее — ценностное утверждение. Чтобы прийти к выводу, что вам следует принимать лекарство, вы должны нужна как минимум еще одна посылка: «Вы должны попытаться сохранить свою жизнь как только возможно.»
Натуралистическая ошибка проявляется во многих формах. Два примера: argumentsum ad antiquitatem (говорить что-то правильно, потому что это всегда было сделано так) и апелляция природе (говорить что-то правильно, потому что это естественно). В обоих из этих заблуждений докладчик пытается сделать вывод о том, что мы должны делать или должны ценить, основываясь исключительно на том, что равно дело. Дэвид Хьюм назвал это попыткой восполнить пробел «в том, что нужно», хорошая фраза для использования в раундах дебатов, когда ваш оппонент совершает натуралистическая ошибка.
Одно тревожное следствие серьезного отношения к натуралистической ошибке состоит в том, что для достижения любых ценных выводов необходимо готовы постулировать некоторые начальные утверждения или заявления о ценности, которые будут рассматриваться как аксиомы, и которые сами по себе не могут быть оправданы чисто логические основания. К счастью, дебаты не ограничиваются чисто логические основания аргументации. Например, предположим, что у вашего оппонента есть аксиоматически утверждалось, что «все, что естественно, хорошо.»Поскольку это утверждение является аксиомой, а не выводом логического доказательства, там не может быть никакого чисто логического аргумента против этого. Но некоторые, тем не менее, уместные ответы на такое абсолютное заявление о ценности включают: (а) вопросы будь то кто-нибудь — вы, ваш судья или даже сам ваш оппонент — на самом деле считает, что «все естественное — хорошо»; (б) формулировка конкурирующей аксиоматики заявление о ценностях, например «все, что улучшает человеческую жизнь, хорошо» и принуждение судья выбирает между ними; и (c) указание на логические следствия утверждения «все естественное хорошо», которое противоречит нашим самым основные интуитивные представления о добре и зле.
Non Sequitur («Это не следует»). Это простое заблуждение, заключающееся в том, что в качестве заключения не следует строго из помещения. Например, «Расизм — это неправильно. Следовательно, нам нужны позитивные действия ». Очевидно, что есть по крайней мере один пропущенный шаг в этом аргументе, потому что ошибочность расизма не подразумевают необходимость позитивных действий без какой-либо дополнительной поддержки (например, например, «Расизм — это обычное дело», «Позитивные действия уменьшили бы расизм», «Там не являются лучшей альтернативой позитивным действиям »и т. д.).
Неудивительно, что раунды дебатов изобилуют non sequitur . Но отчасти это просто результат того, что вам приходилось работать в ограниченное время раунда дебатов, и отчасти результат использования хорошей стратегии. Дебаты команда, выступающая за позитивные действия, было бы глупо сказать в своем первом речи «Мы также считаем, что позитивные действия не ведут к расистским обратная реакция «, потому что это может дать другой стороне намек на хороший аргумент.Лучшая стратегия (обычно) — дождаться другого команда выдвигает аргумент, а затем опровергают его; таким образом, ты не тратьте время зря, опровергая аргументы, что оппозиция никогда не делал во-первых. (Эта стратегия не всегда предпочтительна, хотя, поскольку некоторые контраргументы настолько очевидны и важны, что имеет смысл решать их как можно раньше и пресекать их в зародыше.)
По этим причинам, как правило, кричать «non sequitur» — плохой тон. только потому, что ваша оппозиция не сумела предвидеть все контраргументы вы могли бы сделать.Лучшее время, чтобы указать на non sequitur , — это когда ваша оппозиция пытается построить цепочку причинно-следственных связей (A ведет к B ведет к C и т. Д.) Без обоснования каждого шага в цепочке. Для каждого шаг в цепочке, которую они не могут оправдать, укажите на non sequitur , так что к концу очевидно, что предполагаемая причинно-следственная связь незначительный и неправдоподобный.
Petitio Principii (попрошайничество вопрос). Это ошибка предположения при попытке доказать что-то, что вы пытаетесь доказать.Для всех практических целей это заблуждение неотличимо от циркулярного аргументация.
Главное, что нужно помнить об этом заблуждении, — это то, что термин «попрошайничество» вопрос «имеет очень конкретное значение. Часто можно услышать от спорщиков говоря такие вещи, как, «Они говорят, что порнография должна быть законной, потому что это форма свободного самовыражения. Но возникает вопрос, какое свободное выражение означает «. Это неправильное употребление терминологии. Что-то может вдохновить или мотивируют нас задать конкретный вопрос без попрошайничества вопрос.Вопрос был задан только в том случае, если вопрос был задан. заданный ранее в том же обсуждении, а затем делается вывод о связанный вопрос без ответа на вопрос. Если кто-нибудь сказал: «Тот факт, что мы считаем, что порнография должна быть юридическими средствами, это допустимая форма свободного выражения. И поскольку это свободное выражение, это не должно быть запрещено », , что будет напрашиваться вопрос.
Post hoc ergo propter hoc (после этого, значит из-за этого). Это заблуждение предположения, что A вызвало B просто потому, что A произошло до B. Пример: «Большинство насильников чтения порнографии, когда они были подростками, очевидно, порнография вызывает насилие по отношению к женщинам.»Вывод неверен, потому что может существовать корреляция между двумя явлениями, но ни одно из них не вызывает Другие. Часто это происходит потому, что оба явления могут быть связаны с одним и тем же причина. В приведенном примере возможно, что какой-то психологический фактор — скажем, неудовлетворенное половое влечение — может вызвать у обоих тенденцию к сексуальной насилие и стремление к порнографического материала, в этом случае порнографии не было бы истинной причиной насилия.
Post hoc ergo propter hoc почти идентичен cum hoc ergo propter hoc , которую вы должны увидеть для получения дополнительных сведений.
Отвлеченная сельдь. Это означает именно то, что вы думаете, что это означает: введение не относящихся к делу фактов или аргументов, чтобы отвлечь из рассматриваемого вопроса. Например, «Оппозиция утверждает, что благосостояние зависимость ведет к более высокому уровню преступности — но как бедные люди предполагаются? держать крышу над головой без нашей помощи? »Совершенно верно задать этот вопрос в рамках более широкой дискуссии, но представить его как ответ на аргумент о том, что благосостояние ведет к преступлению, ошибочен.(Также есть элемент объявления misericordiam в этом примере.)
Однако не будет ошибкой утверждать, что преимущества одного вида могут оправдать понесенные расходы иного рода. В приведенном примере беспокойство о предоставлении убежища бедным не опровергнет опасения по поводу преступности, но можно было бы правдоподобно утверждать, что несколько более высокий уровень преступности оправданная цена, учитывая необходимость борьбы с бедностью. Это спорный точка зрения, но она больше не ошибочная.
Термин отвлекающий маневр иногда используется в широком смысле для обозначения любого вида отвлекающей тактики, такой как представление относительно неважных аргументов это израсходует время выступления других участников дебатов и отвлечет их от более важные вопросы. Такой отвлекающий маневр — прекрасный стратегический маневр, с которым должен быть знаком каждый спорщик.
Скользкий спуск. Скользкий спуск аргумент не всегда является заблуждением. Заблуждение о скользкой дорожке — это аргумент, в котором говорится, что принятие одной политики или одно действие приведет к ряд других политик или действий, которые также предпринимаются, без отображения причинно-следственная связь между защищаемой политикой и последующей политикой .Популярный пример заблуждения о скользкой дорожке: «Если мы легализуем марихуану, следующее, что вы узнаете, мы легализуем героин, ЛСД и крэк-кокаин ». Этот скользкий склон представляет собой форму non sequitur , потому что не было объяснено, почему легализация чего-то одного приводит легализации другого. Табак и алкоголь в настоящее время легальны, и однако другие наркотики почему-то остались незаконными.
Есть множество способов превратить заблуждение о скользкой дорожке в веский (или, по крайней мере, правдоподобный) аргумент.Все, что вам нужно сделать, это предоставить немного причина почему принятие одной политики приведет к принятию другого. Например, вы можете утверждать, что легализация марихуаны побудить больше людей считать приемлемым использование психотропных препаратов, и эти люди будут поддерживать более либеральную политику в отношении наркотиков во всем доска. Альтернатива аргументу о скользкой дорожке — просто указать из того, что принципы, поддерживаемые вашей оппозицией, предполагают приемлемость некоторых других политик, поэтому, если они нам не нравятся, мы следует задаться вопросом, действительно ли мы принимаем эти принципы.Например, если предложившая группа выступала за легализацию марихуаны, говоря, что «отдельные лица должны иметь возможность делать со своим телом все, что они хотят », — оппозиция мог бы указать, что этот принцип также оправдал бы легализацию разнообразных других наркотиков — так что, если мы не поддерживаем легализацию других наркотиков, то, возможно, мы действительно не верим в этот принцип.
Соломенный человек. Это заблуждение опровержения карикатурная или крайняя версия чьего-то аргумента, а не фактический аргумент, который они сделали.Часто это заблуждение связано с добавлением слов в рот, сказав, что они привели аргументы, которых на самом деле не сделано, и в этом случае аргумент соломенного человека является завуалированной версией argumentsum Астрахань . Одним из примеров аргумента соломенного человека было бы сказать: «Мистер Джонс считает, что капитализм хорош, потому что все зарабатывают сколько угодно богатство у них есть, но это явно неверно, потому что многие люди просто наследуют их состояния «, хотя на самом деле мистер Джонс не привел аргументов в пользу» доходов » и вместо этого утверждал, скажем, что капитализм дает большинству людей стимул работать и экономить.Тот факт, что некоторые аргументы в пользу политики неверны не означает, что сама политика неверна.
В дебатах стратегическое использование соломенного человечка может быть очень эффективным. Тщательно сконструированный соломенный человек может иногда заманить ничего не подозревающего противника в защищая глупый аргумент, который в противном случае он бы не стал защищать. Но эта стратегия работает, только если соломенный человек не тоже другой из аргументов вашего оппонента, потому что действительно возмутительный соломенный человек будет признан именно таким.Не лучший соломенный человек, в на самом деле, это вообще заблуждение, а просто логическое продолжение или усиление аргумента, выдвинутого вашим оппонентом.
Tu quoque («ты тоже»). Это заблуждение защиты ошибки в рассуждениях указанием на то, что оппонент совершил ту же ошибку. Ошибка остается ошибкой, независимо от того, от того, сколько людей это делают. Например: «Они обвиняют нас в необоснованном утверждения. Но они тоже многое утверждали! »
Хотя очевидно ошибочность, tu quoque аргументы играют важную роль роль в дебатах, потому что они могут помочь установить, кто справился лучше дискуссии (оставив в стороне вопрос о том, истинно ли предложение или нет).Если обе команды задействовали объявлений hominem атакует, или обе команды подали несколько апелляций жаль, то наказывать за это одну команду вряд ли справедливо, но не другой. Кроме того, совершенно не ошибочно указать, что определенные преимущества или недостатки могут быть одинаково применимы к обеим позициям представлены в дебатах, и поэтому они не могут служить основанием для предпочтения одна позиция над другой (такие недостатки именуются «неуникальными»).В общем, использование операторов tu quoque — хороший способ убедиться, что судьи принимают решения, основываясь только на факторах, которые различают две стороны.
Эта страница переведена на белорусский! Вы можете найти переведенную версию здесь.
Вернуться к основным прениям
страница.
Вернуться к обложке
страница.
Эта страница была в последний раз изменена 29 января 2001 г.
логических карточек | Quizlet
Ошибка двусмысленности совершается, когда термин используется в двух или более разных смыслах в одном аргументе.Чтобы аргумент работал, слова должны иметь одно и то же значение каждый раз, когда они появляются в его предпосылках или заключении. Аргументы, которые переключаются между разными значениями слов, двусмысленны и поэтому не работают. Это потому, что изменение значения влечет за собой изменение предмета. Если слова в посылках и заключении означают разные вещи, тогда посылки и заключение о разных вещах, и поэтому первые не могут поддерживать второе.
Пример
(1) Церковь хотела бы поощрять теизм.
(2) Теизм — это заболевание, возникшее в результате чрезмерного употребления чая.
Следовательно:
(3) Церковь должна распространять чай более свободно.
Этот аргумент явно ошибочен, поскольку он двусмысленно относится к слову теизм. Первая посылка аргумента верна только в том случае, если теизм понимается как вера в определенный вид бога; Вторая посылка аргумента верна только в том случае, если теизм понимается в медицинском смысле.
Примеры из реального мира
(1) Христианство учит, что вера необходима для спасения.
(2) Вера иррациональна, это вера в отсутствие доказательств или вопреки им.
Следовательно:
(3) Христианство учит, что иррациональность вознаграждается.
Этот аргумент, который достаточно известен, переключает между двумя разными значениями слова «вера». Вера, которой придерживается христианство, необходима для спасения — это вера в Бога и соответствующий ответ на эту веру. Неважно, откуда пришла вера и ответ; тот, кто принимает Евангелие на основании доказательств (т.грамм. Сомневающийся Фома) по-прежнему попадает в рай, согласно христианству.
Для веры, для которой (1) истинно, (2), следовательно, ложно. Точно так же для веры, для которой верно (2), (1) ложно. Не существует единого понимания веры, согласно которому обе посылки аргумента истинны, и, следовательно, аргумент не может обосновать свой вывод.
Другой аргумент, относящийся к христианству, который время от времени всплывает, звучит так:
(1) Иисус есть Слово Божье.
(2) Библия — это Слово Божье.
Следовательно:
(3) Иисус есть Библия.
Это обычно используется для подтверждения некоторого дальнейшего вывода об авторитете Библии или чего-то подобного, но нет необходимости идти дальше, чтобы увидеть, что здесь есть проблема: фраза «Слово Божье» означает совсем другие вещи в эти две посылки, поэтому этот аргумент основан на двусмысленности.
ул.
ул.Фома Аквинский и пять путей
ул.Фома Аквинский (1225–1274), возможно, самый важный католический богослов в истории. В своем главном труде Summa Theologica, который широко считается высшим достижением средневекового систематического богословия, Фома Аквинский представил свои пять доказательств существования Бога, известных как Quinque Viae (лат. «Пять путей»). [1] Мы представим все аргументы более подробно чуть позже, а сейчас мы дадим краткое изложение всех пяти аргументов.
* Первый способ Томаса включает свидетельство движения.Тот факт, что для Фомы, каждой движущейся вещи нужен движитель, показывает, что Бог, Неподвижный Движитель, существует.
* Второй способ включает понятие действующей причины. Чтобы ряд причин и следствий, которые мы видим в мире, имел смысл, он должен иметь начало. Следовательно, Бог, Первопричина, существует.
* Третий способ отмечает, что все существующее не обязано своим существованием самому себе. Однако, если все контингентно, ничего не могло быть, так как когда-то все это могло не существовать.Чтобы объяснить все существование, должно быть Необходимое Существо, Бог.
* Четвертый способ показывает, что в вещах существуют градации, например, более благородное и менее благородное, более истинное или менее истинное. Существование таких градаций подразумевает существование Абсолютного Существа как данных для всех этих относительных градаций.
* Пятый способ утверждает, что поведение вещей в мире подразумевает Великий Дизайнер или архитектор, Бог. [2]
Таким образом, пять путей Аквинского определили Бога как Неподвижного Движителя, Первопричины, Необходимого Существа, Абсолютного Существа и Великого Создателя.
Следует отметить, что аргументы Фомы Аквинского основаны на некоторых аспектах разумного мира. Следовательно, аргументы Фомы Аквинского имеют апостериорный характер. Напротив, аргумент Ансельма основан исключительно на априорном определении Бога. [3] Пять путей Фомы Аквинского основаны, в конечном счете, на чувственном опыте. Чувственный опыт никогда не может быть безошибочным. Таким образом, сами по себе эти аргументы не могут с полной уверенностью установить существование Бога. Однако, если бы его аргументы были верными, существование Бога было бы установленным фактом наравне со многими открытиями современной науки.
Римско-католическая церковь рассматривает первые три пути Аквинского (все вместе называемые «Космологические аргументы» [a]) как неопровержимое доказательство установления существования Бога. [4] Несмотря на католическую церковь, теперь мы приступим к проверке обоснованности аргументов Фомы Аквинского.
Теперь мы увидим, как ни один из пяти способов не доказывает существование Бога:
* Первый путь: Бог, главный двигатель
* Путь второй: Бог, Первопричина
* Третий путь: Бог, необходимое существо
* Четвертый путь: Бог, Абсолютное Существо
* Пятый путь: Бог, великий конструктор
Первый путь: Бог, главный двигатель
В первом случае Бог определяется как Главный двигатель.Мы позволим Аквинскому говорить за себя, объясняя свой первый аргумент в пользу существования Бога.
Первый и наиболее очевидный способ — аргумент от движения. Несомненно и очевидно для наших чувств, что некоторые вещи в мире находятся в движении. Теперь все, что движется, движется другим, потому что ничто не может быть сдвинуто, кроме как потенциальным по отношению к тому, к чему оно движется; тогда как вещь движется постольку, поскольку она действует. Ибо движение — это не что иное, как сокращение чего-либо от потенциальности к действительности.Но ничто не может быть сведено от потенциальности к действительности, кроме как чем-то в состоянии действительности. Таким образом, то, что на самом деле горячее, как огонь, делает дерево, потенциально горячее, на самом деле горячим, но только в других отношениях. Ведь то, что на самом деле горячее, не может одновременно быть потенциально горячим: но одновременно потенциально холодным. Следовательно, невозможно, чтобы в одном и том же отношении и одним и тем же образом вещь двигалась и перемещалась; т.е. что он должен двигаться сам. Следовательно, того, кого трогают, должен двигать другой.Если то, что он перемещает, должно быть перемещено само, тогда это также должно быть перемещено другим, а то и другим снова. Но это не может продолжаться до бесконечности, потому что тогда не было бы ни первого движущегося, ни, следовательно, движущего, поскольку последующие движущиеся движутся только постольку, поскольку они движутся первым движущимся; поскольку посох движется только потому, что его перемещает рука. Следовательно, необходимо прийти к первопроходцу, которого никто не продвигает; и все понимают, что это Бог. [5]
С помощью современной физики мы можем навсегда избавиться от этого аргумента.Первый закон Ньютона гласит, что частица будет стремиться оставаться в покое или двигаться с постоянной скоростью, если к ней не применяется внешняя сила. Следовательно, движение тела (с постоянной скоростью) так же естественно, как и его состояние покоя. Первичный двигатель вообще не нужен.
Физика Фомы Аквинского была, конечно же, основана на теории Аристотеля, который утверждает, что естественное состояние любого тела — находиться в состоянии покоя. Кроме того, эксперименты физиков А.А. Майкельсона (1852-1931) и Э.Морли (1838-1923) в 1881 году (и снова в 1887 году) показал, что во Вселенной не существует стандартной и абсолютной системы отсчета. Альберт Эйнштейн (1879-1955) использовал вывод этого эксперимента как один из своих постулатов в своей специальной теории относительности. Этот эксперимент и теория Эйнштейна показали, что абсолютного движения не существует. Все скорости могут быть даны только относительно чего-то еще, ни одна из которых не является абсолютной ссылкой. Это, конечно, делает идею первичного двигателя абсолютной ерундой!
Есть еще одно, более традиционное возражение против первого способа.Фундаментальный принцип этого аргумента состоит в том, что все, что инициирует изменения, должно быть каким-то образом инициировано само. Следовательно, этот принцип должен применяться и к первичному двигателю. Нет никакой логической причины, по которой мы должны прекратить применение этого принципа на этом этапе. Это возражение убедительно. Поскольку аргумент начинается с наблюдения (что есть движение) и фундаментального принципа (что каждая движущаяся вещь приводится в движение другим, уже движущимся), который, по крайней мере в философии Томаса, кажется справедливым.Тем не менее, он постулировал существование «Неподвижного двигателя», что нарушает основную предпосылку аргумента. Раздражающий (для верующих) вопрос скептически настроенного ребенка подводит итог основной проблемы первого способа: если Бог создал мир, кто создал Бога? [6]
Вернуться к началу
Второй путь: Бог, первая причина
Во втором случае Бог определяется как Первопричина, как уточняет Фома Аквинский:
Второй путь исходит из природы действующей причины. [B] В мире чувственных вещей мы находим порядок действенных причин.Неизвестен случай (да и вообще он невозможен), в котором вещь оказалась бы действующей причиной сама по себе; ибо так было бы до самого себя, что невозможно. Итак, в действенных причинах невозможно идти до бесконечности, потому что во всех действующих причинах, следующих по порядку, первая является причиной промежуточной причины, а промежуточная причина является причиной исходной причины, независимо от того, несколько ли промежуточных причин. или только один. Убрать причину — значит убрать следствие.Следовательно, если среди действующих причин нет первопричины, не будет ни конечной, ни какой-либо промежуточной причины. Но если в действенных причинах можно идти до бесконечности, не будет ни первой действенной причины, ни конечного следствия, ни каких-либо промежуточных действенных причин; все это явно ложно. Поэтому необходимо признать первую действенную причину, которую все называют Богом. [7]
Второй вариант выглядит логически понятным и якобы убедительным.К сожалению, для верующего, этот аргумент содержит ряд недостатков, которые позволили полностью разрушить его философами Дэвидом Юмом (1711–1776) и Иммануилом Кантом (1724–1804).
Юм записал свою критику всех основных философских аргументов в пользу существования Бога в своей посмертно опубликованной книге «Диалоги о естественной религии» (1779). Первым Юм высказал фундаментальное предположение второго пути, согласно которому каждое событие должно иметь причину. Юм утверждал, что, когда мы говорим о причине, мы имеем в виду объяснение события.Если это так, то в лучшем случае остается предположение, что каждое событие должно иметь причину; поскольку никто никогда не давал объяснений каждому произошедшему событию.
Во-вторых, Юм показал, что на самом деле мы наблюдаем определенные события, следующие одно за другим. Мы называем более раннюю причину «причиной», а следующую сразу после нее — «следствием». Теперь, в этой последовательности событий, одно за другим, почему мы не можем продолжать отслеживать события бесконечно вперед или назад? [8] На самом деле, нет никакой логической причины, почему мы не можем.Возьмем, например, серию целых чисел 1,2,3 … и так далее. Мы можем видеть, что эта последовательность никогда не закончится, потому что для каждого числа n есть большее число n + 1. Точно так же мы можем проследить число назад 1,0, -1, -2 … и так далее. У этой последовательности тоже нет конца, потому что для каждого отрицательного числа -n существует большее отрицательное число -n-1. С этой точки зрения «первопричина» имеет такое же значение, как и «наибольшее положительное число»! [9] Как правильно указал Юм:
В такой цепочке или последовательности объектов каждая часть вызвана тем, что ей предшествовало, и причинами, которые следуют за ней.В чем же тогда трудность? Но вы говорите, что целому нужна причина. Я отвечаю, что объединение этих частей в единое целое, как и объединение нескольких отдельных графств в одно царство или нескольких отдельных членов в одно тело, осуществляется просто произвольным действием разума и не влияет на природу мира. вещи. Показал ли я вам конкретные причины каждого человека в совокупности из двадцати частиц материи, я бы подумал, что было бы очень неразумным, если бы вы впоследствии спросили меня, что было причиной всех двадцати.Это достаточно объяснено при объяснении причины возникновения деталей. [10]
Юм говорит здесь о том, что наблюдаемая последовательность событий не требует начала, поскольку мы можем представить ее возвращение в бесконечность. Вся цепочка причин и следствий также не нуждается в объяснении, поскольку это просто действие нашего разума, пытающегося структурировать наш опыт. *
Более того, Юм утверждал, что даже если аргумент верен, то есть что есть первая причина, он не установил бы существование Бога.Во-первых, почему бы первопричиной не быть сама вселенная, а не Бог. Если утверждать, что вселенная тоже должна быть вызвана, то то же самое можно сказать и о Боге. Если затем утверждать, что Бог «беспричинен», то то же самое можно сказать и о вселенной. [11]
Заняв место с того места, где остановился Юм, Кант продолжил битье над хрупкими основаниями аргумента о первопричине. Кант указывал, что принцип существования причины для каждого события применим, насколько нам известно, только к миру нашего чувственного опыта.В Аргументе Первопричины этот принцип вырывается из нашего чувственного опыта, чтобы объяснить что-то, что, как предполагается, выходит за его пределы. Эта процедура, согласно Канту, является как необоснованной, так и незаконной, поскольку нет никаких оснований предполагать, что принцип причинности справедлив в применении ко всему космосу.
В аргументе есть еще один недостаток. Кант указывал, что не существует рационального способа узнать, что мы достигли истоков причин и объяснений.То, что мы считаем первопричиной, также может быть связано с нашим незнанием причины и ее объяснения. Другими словами, когда мы можем быть уверены, что достигли первопричины? Не существует метода, с помощью которого мы могли бы воскликнуть: «Ага! Это первая причина!» Кант пришел к выводу, что эти проблемы возникают из-за фундаментального недостатка использования принципа за пределами его допустимого диапазона приложений. [12]
Современные философы дополнили и уточнили аргументы Юма и Канта. Они указывают, что второй способ, или аргумент первопричины, содержит элементарную логическую ошибку: обращение квантификатора.Привести пример легко: предположим, что у каждого игрока баскетбольной команды есть жена; затем совершается ошибка переворота квантификатора, когда этот факт расширяется до утверждения, что у самой баскетбольной команды есть жена! Это то, как аргументирует первую причину: поскольку каждая причинная серия должна иметь первую причину, аргумент утверждает, что должна быть первая причина для всех таких серий. Таким образом, ошибочность аргумента очевидна. [13]
Современная физика также показала, что основная предпосылка аргумента Первопричины, что каждое событие должно иметь причину, ложна.Явление радиоактивности — один из примеров беспричинного события. Хотя можно предсказать период полураспада радиоактивных материалов, то есть сколько времени потребуется для распада половины исходного образца, точный момент распада отдельного атома предсказать невозможно. Распад отдельного атома — пример беспричинного события. Богословы пытались решить эту проблему, говоря, что теист отрицает, что что-либо «просто происходит»; Бог направляет и вызывает момент распада, хотя у него нет физической причины.Но эта защита явно круговая. Ибо теологи используют вывод аргумента о первопричине (что Бог является первопричиной вещей), чтобы обеспечить обоснованность одной из его предпосылок (что каждое событие должно иметь причину). Прекрасный пример заблуждения petitio Principii (принцип попрошайничества). [14] Следовательно, второй способ неубедителен по следующим причинам: он предполагает, что все последовательности должны быть конечными, когда у нас нет логических оснований для этого; у нас нет способа определить, какая именно причина является первой; он совершает логическую ошибку обращения квантора; и, наконец, фундаментальное предположение о том, что каждое событие должно иметь причину, не соответствует действительности современной физикой.Аргумент Первопричины, второй путь Фомы Аквинского, показал направление первого, оба они недействительны как доказательства существования Бога.
Вернуться к началу
Третий путь: Бог, необходимое существо
В-третьих, Бог определяется как Необходимое Существо. Фома Аквинский:
Третий путь исходит из возможности и необходимости и работает таким образом. Мы находим в природе вещи, которые могут быть и не быть, поскольку обнаруживается, что они порождаются и искажаются, и, следовательно, они могут быть или не быть.Но невозможно, чтобы они существовали всегда, потому что то, чего не может быть, когда-то не существует. Следовательно, если всего не может быть, тогда когда-то ничего не существовало. Если бы это было правдой, даже сейчас ничего не существовало бы, потому что то, что не существует, начинает существовать только через что-то уже существующее. Следовательно, если когда-то ничего не существовало, невозможно, чтобы что-либо начало существовать; таким образом, даже сейчас ничего не существовало бы — что абсурдно.Следовательно, не все существа просто возможны, но должно существовать нечто, существование чего необходимо. Но каждая необходимая вещь либо вызвана другой необходимостью, либо нет. Теперь невозможно перейти к бесконечности в необходимых вещах, необходимость которых вызвана другим, как уже было доказано в отношении действующих причин. Следовательно, мы не можем не допустить существования одного существа, имеющего в себе собственную необходимость и не получающего ее от другого, а скорее вызывающего у других их необходимость.Все люди говорят об этом как о Боге. [15]
Как и в случае с двумя другими способами, здесь есть фундаментальная ошибка в аргументации Аквинского. Отмечается, что вывод космологического аргумента [c] состоит в том, что существует существо, которое обязано своим существованием только себе и ничему другому. Но следует помнить, что одна из основных предпосылок аргументации состоит в том, что не существует существа, которое обязано своим существованием самому себе. Это открыто противоречит окончательному выводу, в котором говорится, что Бог — это существо, которое обязано своим существованием самому себе.Таким образом, третий способ допускает элементарную логическую ошибку.
Были попытки изменить предпосылку, чтобы сказать, что никакое конечное существо само не обязано своим существованием и что, начиная с Бога, быть бесконечным, обязано своим существованием самому себе. Но в основном это говорит о том, что ни одно существо не обязано своим существованием самому себе, кроме Бога, тем самым совершая ошибку petitio Principii; ведь заключение уже предполагается в одном из его помещений. [16]
Слово «необходимый» может использоваться в двух разных смыслах: логическом и эмпирическом.В случае, когда «необходимо» используется в логическом смысле, утверждение «Бог существует» может означать только то, что существование Бога нельзя отрицать без противоречий. Все это сводится к утверждению, что «Бог существует» по определению. Но теперь мы вернулись к онтологическому аргументу, который, как мы показали, неверен. [17] Теперь, если «необходимо» используется в эмпирическом смысле, говоря, что нам нужен Бог как необходимая причина для всего остального, мы возвращаемся к аргументу первопричины. И это, как мы показали, ошибочно.[18]
Пожалуй, наиболее красноречивой критикой этого аргумента является критика Дэвида Юма в его «Диалогах». Сначала Юм указал, что термин «необходимое существование» не имеет логической убежденности чисто логических или математических аргументов:
Предполагается, что Божество является необходимым существующим существом; и эту необходимость его существования пытаются объяснить, утверждая, что, если бы мы знали его сущность или природу, мы бы считали невозможным, чтобы он не существовал, как если бы дважды два не было четырьмя.Но очевидно, что этого никогда не произойдет, пока наши способности остаются такими же, как и сейчас. Для нас все еще будет возможно в любое время представить несуществование того, что мы формально представляли существующим; и ум не может лежать в необходимости предполагать, что какой-либо объект всегда остается в существовании, точно так же, как мы находимся в необходимости всегда мыслить дважды два как четыре. Слова, следовательно, «необходимое существование» не имеют значения, или это одно и то же, ни одно из которых не является непротиворечивым.[19]
Затем Юм утверждал, и это важный момент, если Бог существует обязательно из-за какого-то неизвестного атрибута, почему сама вселенная не должна иметь такой атрибут, чтобы сделать его существование необходимым. Ведь, конечно, даже сегодня ни у кого нет наглости сказать, что мы знаем о вселенной все, чтобы сказать иначе:
Но, кроме того, почему никакая материальная вселенная не может быть неизбежно существующим существом, согласно этому мнимому объяснению необходимости? Мы не смеем утверждать, что знаем все качества материи; и насколько мы можем определить, он может содержать некоторые качества, которые, как мы осмеливались знать, заставили бы его несуществование показаться таким же большим противоречием, как дважды два к пяти.Я нахожу только один аргумент, используемый для доказательства того, что материальный мир не обязательно существует; и этот аргумент выводится из случайности как в материи, так и в форме мира. «Любая частица материи, — говорится, — может быть задумана как аннигилирующая, и любая форма может быть воспринята как изменяемая. Следовательно, такое уничтожение или изменение не является невозможным». Но кажется большим пристрастием не осознавать, что тот же аргумент в равной степени распространяется и на Божество, насколько мы имеем какое-либо представление о нем, и что разум может, по крайней мере, вообразить его несуществующим или его атрибуты неизменными; и никакая причина не может быть объяснена, почему эти качества не могут принадлежать материи.Поскольку они совершенно неизвестны и непостижимы, их несовместимость с ним никогда не может быть доказана.
Теперь мы можем подытожить различные проблемы Третьего пути: аргумент в его основной форме является круговым, поскольку он предполагает заключение в одной из своих предпосылок; термин «необходимое существо», если его использовать в эмпирическом смысле, сводится ко второму пути, который, как уже было показано, ошибочен, если его использовать в логическом смысле, он сводится к онтологическому аргументу, еще одному аргументу, уже отвергнутому как несостоятельный; и, наконец, даже если мы должны допустить наличие необходимой сущности, почему бы ей не быть самой вселенной ?.В целом космологические аргументы не могут продемонстрировать существование Бога.
Вернуться к началу
Четвертый путь: Бог, Абсолютное Существо
В четвертом способе Бог определяется как Абсолютное Существо, которое используется как мерило для измерения всех качеств:
Четвертый способ взят из градации, которую можно найти в вещах. Среди существ есть более и менее добрые, истинные, благородные и тому подобное. Но в большей или меньшей степени говорится о разных вещах в зависимости от того, насколько они по-разному напоминают что-то максимальное, поскольку вещь считается более горячей в зависимости от того, насколько она больше похожа на то, что является самым горячим; так что есть что-то самое истинное, что-то лучшее, что-то самое благородное и, следовательно, что-то самое существенное, потому что величайшие в истине вещи величайшие в бытии…. Максимум в любом роде является причиной всего в этом роде, как огонь, который есть максимум тепла, является причиной всего горячего, как сказано в той же книге. Следовательно, должно быть что-то, что является для всех существ причиной их бытия, добра и любого другого совершенства; и это мы называем Богом. [20]
Этот аргумент является самым слабым из пяти путей Фомы Аквинского. Во-первых, хотя можно признать, что необходимо применить какой-то критерий, прежде чем мы сможем говорить в терминах «больше» или «меньше», но нет абсолютно никаких причин, по которым этот критерий должен быть абсолютным.Это особенно верно в свете наших сегодняшних знаний.
Ценности, такие как «хорошие», «истинные» и «благородные», на самом деле меняются в разных культурах и в разные исторические периоды. Например, в западных обществах полигамия считается преступлением, следовательно, считается «плохим» или «неблагородным». Тем не менее в мусульманских странах полигамия не запрещена и фактически при определенных обстоятельствах, когда многие мужчины погибают на войне, например, она активно поощряется. В древнем конфуцианстве многоженство нигде не запрещено.Таким образом, в этих обществах полигамия является общепринятой формой супружеских отношений.
Поэтому большинство социальных стандартов и норм субъективны. Оценить многие социальные нормы в иерархическом смысле просто невозможно. Отсутствие четкой градации в этом смысле опровергает Четвертый путь. [21]
Вернуться к началу
Пятый путь: Бог, великий конструктор
В пятом способе Бог определяется как руководитель всех действий и процессов:
Пятый путь взят из управления миром.Мы видим, что вещам недостает знания, таким как естественные тела, которые действуют ради цели, и это видно из того, что они действуют всегда или почти всегда одинаково, чтобы получить наилучший результат. Отсюда ясно, что они достигают своей цели не случайно, а намеренно. То, чему недостает знания, не может двигаться к цели, если этим не руководит кто-то, наделенный знанием и разумом; как стрелка направлена лучником. Следовательно, существует какое-то разумное существо, которым все естественное направлено к своему концу; и это существо мы называем Богом.[22]
Пятый способ утверждает, что неодушевленные предметы и процессы, по-видимому, действуют для достижения наилучшего результата. Это показывает, что этим процессом должно руководить разумное существо. Но что это значит, когда мы говорим, что процессы стремятся к «лучшему результату»?
В качестве примера, безусловно, состояние окружающей среды на этой планете кажется «лучшим результатом» для живущих на ней существ. Но как мы узнаем, что это не просто случайность (для нас)? В конце концов, на других планетах Солнечной системы есть окружающая среда, которая, насколько нам известно, неспособна поддерживать какую-либо форму жизни.«Показатель успеха» — один из девяти для формирования среды, поддерживающей жизнь. Этот показатель будет еще ниже, если мы будем рассматривать спутники планет как миры-кандидаты. С этой точки зрения среда, поддерживающая жизнь, действительно выглядит случайным явлением. Более того, жизнь развивалась, чтобы адаптироваться к окружающей среде, а не наоборот. Таким образом, невозможно утверждать, что неодушевленные предметы или процессы всегда движутся к «наилучшему результату».
Фундаментальная посылка Пятого Пути о том, что неодушевленные предметы и процессы действуют с разумной целью, несостоятельна.[23]
Вернуться к началу
Примечания
а. Первые три пути Аквинского называются космологическими аргументами, потому что каждый аргумент начинается с того, что существует космос или мир, которому, кажется, нужно что-то для объяснения.
б. Термин действующая причина был использован Томасом, потому что он находился под влиянием философии Аристотеля. Согласно Аристотелю, чтобы иметь адекватное понимание чего-либо, нам нужно знать четыре типа причин: конечную причину, формальную причину, материальную причину и действующую причину.В качестве примера рассмотрим перо. Его конечная причина — функция пера, оно используется для письма. Его формальная причина — это его форма или форма, которая позволяет ему выполнять свою конечную причину (например, его длинная тонкая форма, позволяющая держать его в руке). Материальная причина относится к фактическому материалу, из которого он изготовлен, поскольку, очевидно, материал должен быть достаточно сильным, чтобы человеческая рука держала его, не сгибая, он должен быть непроницаемым для чернил и т. д. Действующей причиной является движение или действие, которое начинает или создает его, поэтому, если это редкая ручка, мастер из Швейцарии это действенная причина.
Когда мы говорим сегодня о научных причинах, мы говорим в основном о том, что Аристотель назвал эффективными причинами. Таким образом, я отказался от прилагательного в моем последующем обсуждении причины.
c. Хотя термин «космологический аргумент» используется для обозначения первых трех путей Аквинского, он также используется специально для обозначения третьего пути.
.
Список литературы
1. Benet, The Reader’s Encyclopedia: p42
.
Ливингстон, Словарь христианской церкви: p512
Миллер, Бог и разум: стр. 43
Росс, Философия религии: стр.29,
.
2.Миллер, Бог и разум: стр. 44
3. Там же: p44
.
4. Popkin & Stroll, Philosophy: Made Simple: стр. 153,
.
5. Джонс, История западной философии: II. Средневековый разум: стр. 217,
.
6. Льюис, Философия религии: стр. 159,
.
7. Джонс, История западной философии: II. Средневековый разум: стр. 217,
.
8. Popkin & Stroll, Philosophy: Made Simple: стр. 153,
.
9. Джонс, История западной философии: II. Средневековый разум: стр. 219-220,
.
10.Алстон и Брандт, Проблемы философии: стр.145
11. Popkin & Stroll, Philosophy: Made Simple: стр. 154
.
12. Там же: p154
.
13. Росс, Философия религии: стр. 33
.
14. Хепберн, Христианство и Парадокс: p161-165
15. Джонс, История западной философии: II. Средневековый разум: стр. 217-218,
.
16. Хепберн, Христианство и Парадокс: p166
17.
