Как-то все это так » конгруэнтно»… Хрен его знает, Шо это такое, но, чуЙствую, что именно так и есть! ( А что это такое ) ?:flushed::face_with_monocle::stuck_out_tongue_winking_eye::wink: — Обсуждай
Как-то все это так » конгруэнтно»… Хрен его знает, Шо это такое, но, чуЙствую, что именно так и есть! ( А что это такое ) ?:flushed::face_with_monocle::stuck_out_tongue_winking_eye::wink: — ОбсуждайМарина Марина
Как-то все это так » конгруэнтно»… Хрен его знает, Шо это такое, но, чуЙствую, что именно так и есть! ( А что это такое ) ?хрен
404
33
3
Ответы
ПД
Путь Домой
Ого! Выплыло словечко неожиданно!! Ладно)) так слово конгруэнтно заменяем словом монопенисаульно. И все становиться понятно. И легко. Без пояснений.
)) Мне так кажется. Во всяком случае))
0
Трансцедентально! Ажжж подпрыгнула, пока это слово написала..))
1
ПД
Путь Домой
))) а я в осадок выпала, когда слушала лекцию «Немецкая трансцедентально-критическая философия.» Особенно, когда услышала название лекции в аудитории))
1
Марина Марина
НичЁсеее…0
1
ПД
Путь Домой
Да нормально.)) Выжить удалось))
1
Марина Марина
1
Аксакал-Хан-Паша
Конгруэ́нтность в широком смысле — равенство, адекватность друг другу различных экземпляров чего-либо или согласованность элементов системы между собой.
..
0
Марина Марина
1
Андрон Шрайбикус
согласованность информации, одновременно передаваемой человеком; самосогласованность его личности
0
Марина Марина
1
Масяня
Подобие… В психологии — конгруэнтность это соответствие мыслей и действий… Как то так.
0
Марина Марина
1
MК
M К
Что ты чуйствуешь, формальность которой по лучшему сценарию событий модно пренебречь?
0
Марина Марина
)) соразмерность элементов.
1
MК
M К
1
Марина Марина
1
ШХ
Шагарьян Хайретдинов
геометрия 7 класс. Мы то учили признаки подобия. А им начали говорить о конгруэнтности
0
Марина Марина
1
СС
Странный Субъект …
Со школы припоминаю -конгруэнтность фигур , вроде как одинаковость их.
0
Марина Марина
1
Ел
Елена
В психологии это соответствие мыслей по отношению к действиям
0
Ел
Елена
Я и вижу))) слезами умылась!
1
СL
Света Life
То сквозь слезы))))))))))
1
Марина Марина
Веселые такие. )) и
1
СL
Света Life
С праздником !!!
1
Марина Марина
1
АМ
Анатолий Муйтуев
Повторите геометрию за 8 класс о треугольниках.
..
0
Марина Марина
ПобЁгла…
1
АМ
Анатолий Муйтуев
Удачи!
1
Марина Марина
Не подведу! )
1
АМ
Анатолий Муйтуев
1
Колючка-Это Я)))
Вам повезло,значит собеседники правдивые
0
Марина Марина
И это хорошо.
1
Bc
Bcyjdfz
Соразмерность, соответствие. Чуйствуй дальше.
0
Марина Марина
Всенепременно.
1
Bc
Bcyjdfz
Ага
1
Марина Марина
1
Bc
Bcyjdfz
1
РМ
Рафидин Меджидов
Ну,Марина,расскажите,что сие значит
0
Марина Марина
Согласованность и соразмерность элементофффф.
.))
1
РМ
Рафидин Меджидов
Уяснил.
1
Марина Марина
1
РМ
Рафидин Меджидов
Как вот.?
1
Марина Марина
Что?
1
Виктор Конобрий
Что-то похожее на «совместимо»
0
Марина Марина
Ессст-нно.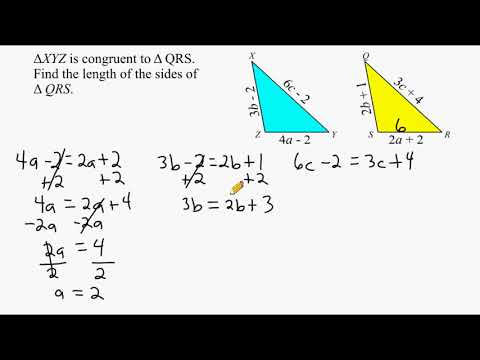
0
1
Nikola Mahkov
-не русское-не принимаем!—
0
Марина Марина
С чего бы это?)
1
Nikola Mahkov
-хватает и русских определений—
1
Марина Марина
1
AT
Aleksandr Tarnovsky
А «всё это так» — это шо? )))
0
Марина Марина
Это как-то » сыграй мне туманно».
..
1
AT
Aleksandr Tarnovsky
Конгруэнтные Ёжики в тумане… )))
1
Марина Марина
И Лошадка…)
1
AT
Aleksandr Tarnovsky
Ну таки и Сова, и Собака, иии… Эхо Тумана! )))
1
Марина Марина
)
1
Се
Сергей
сравнительное подобие-)
0
Марина Марина
1
СL
Света Life
Вроде.
равенство)))))))))))
0
СL
Света Life
Та ты у нас вообще—УНИКУМ. И жнец. и швец, и на дуде игрец !!!
1
Андрей Берзенин
Неееет… На дуде не могу, только на ф- но)))) Да и швея из меня ещё та)))
1
СL
Света Life
Тю ! Было бы желание !!!)))))))))))
1
Андрей Берзенин
))))
1
СL
Света Life
1
Pavel Arefyev
женщина! Зачем это Вам?
0
Марина Марина
пАтАмуШтА.
1
Pavel Arefyev
маладес!
1
Марина Марина
1
Вадим Осипов
Какая чуЙствительная!
0
Марина Марина
ффффся такая. )
1
Вадим Осипов
Видимо!
1
Марина Марина
1
Вадим Осипов
1
Вл
Владимир
Надо глянуть в НЕТ
0
Марина Марина
1
Вл
Владимир
1
Следующая страница
Конгруэнтность — Insch.
RuМы объясним, что такое конгруэнтность и чем она отличается от когерентности. А также его значение в геометрии и в праве
Конгруэнтность подразумевает логическое отношение удобства
Что такое конгруэнтность?
Мы говорим о конгруэнтности для обозначения чего-то, что имеет некоторую логическую связь со своим окружением или с другим конкретным референтом, подобно тому, что выражается существительными convenience и coherence, которые часто используются как синонимы
Слово ‘конгруэнтность’ происходит от латинского congruentia, слова, образованного голосами con (вместе с) и gruere (совпадать), хотя эта этимология несколько неопределенна, поскольку сохранились только записи глагола gruere, в которых он ассоциируется с криком журавля или имитацией звука журавля, что не имеет особого смысла в данном контексте
В любом случае, точное понятие конгруэнтности обычно определяется контекстом , в котором оно используется. Например, в праве конгруэнтность – это соответствие, когда есть соответствие между решением суда и требованиями сторон, участвующих в судебном процессе
Но значение слова меняется в сфере религии , с другой стороны, где оно выражает способность Бога действовать, не противореча свободной воле человека , и так далее в других областях знания
Вам может быть полезно: Текстовая связность
Конгруэнтность и когерентность
Хотя они часто используются как синонимы, эти два термина – когерентность и конгруэнтность – не имеют одинакового точного значения во всех контекстах. Оба выражают логическое отношение между двумя референтами, но различаются более или менее тонким образом: когерентность подразумевает логическое отношение соответствия, а конгруэнтность – логическое отношение удобства
Это означает, что нечто связное – это нечто, что следует той же логике , что является частью того же образа мышления или что представляется единым, согласным с самим собой. Например, политик, придерживающийся консервативных взглядов, может голосовать против изменений, предлагаемых прогрессивными секторами. Он последовательный, потому что его теория (его идеология) и его практика (его политические решения) последовательны
С другой стороны, нечто является конгруэнтным, если оно соответствует его желаниям, удобствам или стремлениям
В том же примере, если консервативный политик имеет большие надежды на избрание президентом, для него будет конгруэнтно голосовать за изменения, исходящие от прогрессивных секторов, т.е. его соперников, если это означает лучшие и более четкие шансы на получение необходимой поддержки для прихода к власти.
Его стремления (быть избранным) и его действия (заручиться поддержкой не подозревающих об этом людей) совпадают
Конгруэнтность в геометрии
математике , в частности в геометрии, термин конгруэнтность используется для обозначения отношения между двумя геометрическими фигурами , имеющими одинаковые размеры и одинаковую форму, независимо от их пространственной ориентации, вращения или отражения, т.е. когда между ними существует отношение изометрии
Так, в евклидовой геометрии конгруэнтность означает арифметическую и алгебраическую эквивалентность математических выражений двух фигур . Тогда как в аналитической геометрии требуется, чтобы евклидово расстояние между любой парой точек одной фигуры в декартовой системе координат было равно расстоянию между точками второй фигуры
Например, два угла конгруэнтны, если при повороте на 180° относительно их вершины они точно совпадают друг с другом
Конгруэнтность и подобие треугольников
Два треугольника конгруэнтны, если между ними существует отношение изометрии, которое математически выражается следующим образом: ?ABC≅?DEF (то есть: треугольник ABC конгруэнтен треугольнику DEF).
Это может произойти в любом из следующих случаев:
- Дело AAL или ALA. Два треугольника конгруэнтны, если у них два равных угла и сторона между ними, поскольку, зная два угла треугольника, мы можем определить третий.
Дело ALA
дело AAL
- дело ЛАЛ. Два треугольника конгруэнтны, если у них равны две заданные стороны и угол, в котором они соприкасаются.
- дело ЛЛЛ. Два треугольника конгруэнтны, если их три стороны равны.
- дело LLA. Два треугольника конгруэнтны, если они имеют две равные стороны и равные углы, противоположные этим сторонам. Но сначала мы должны узнать, является ли треугольник правильным или его углы тупые.
Принцип конгруэнтности
процессуальном праве максима, которая требует от судьи в любом судебном процессе делать выводы , которые конгруэнтны, то есть согласуются с заявлениями сторон в жалобе и с фактами, зафиксированными в жалобе, известна как принцип конгруэнтности
Это означает, что судья должен принять решение в рамках стремлений сторон в споре , не вовлекая причины, не относящиеся к рассматриваемому делу, и не превышая объем помощи, запрашиваемой истцом.
Это означает, что судья должен действовать в рамках параметров, продиктованных самим делом
Однако, в зависимости от правовой базы каждой страны, существуют специфические вопросы, в которых принцип согласованности может представлять исключения, например, семейные дела или когда необходимо обеспечить особую защиту одной из сторон
За ним следует: Гармония
Что такое Конгруэнтность? Определение, примеры, факты
Значение конгруэнтности
Если две фигуры можно расположить точно друг над другом, они называются конгруэнтными фигурами.
Если вы положите один ломтик хлеба на другой, вы обнаружите, что оба ломтика имеют одинаковую форму и размер.
Термин «конгруэнтный» означает в точности одинаковую форму и размер. Эта форма и размер должны оставаться одинаковыми, даже когда мы переворачиваем, поворачиваем или вращаем фигуры.
Примеры конгруэнтных фигур
Две бабочки, которые имеют одинаковую форму и размер
Два конфеты, которые представляют равную форму и размер
Два кирпичи Lego, которые представляют равную форму и размер
Символ конгресса
.
символом — ‘ ≅ ‘
Поскольку конгруэнтность объектов подразумевает одинаковую форму и размер; символ конгруэнтности состоит из двух символов, расположенных один над другим. Есть символ тильда « » , что означает сходство по форме, и «=» , что означает равенство по размеру.
Следовательно, конгруэнтность представлена символом ‘ ≅ ‘
Если два объекта A и B конгруэнтны друг другу, мы запишем это как: A ≅ B
Congruent Line Segments 004 Поскольку конгруэнтность подразумевает одинаковую форму и размер, отрезки будут конгруэнтны, если их форма и размер одинаковы.
Внимательно посмотрите на изображение выше.
Поскольку AB и PQ являются отрезками прямой, они имеют одинаковую форму. Длина отрезка AB равна 5 см и PQ также равна 5 см. Следовательно, длины обоих отрезков равны друг другу.
Итак, если две или более прямых равны по длине, говорят, что они конгруэнтны друг другу.
Следовательно, отрезки AB и PQ конгруэнтны друг другу.
Следовательно, он будет представлен в виде отрезка AB ≅ отрезка PQ.
Конгруэнтные углы
На приведенной выше диаграмме ∠ ABC = 40 °, , тогда как ∠ PQR = 40 °.
Если мы наложим или перекроем ∠ ABC на ∠ PQR, мы обнаружим, что оба угла конгруэнтны друг другу.
Согласно правилу, два угла равны, если меры обоих углов равны друг другу.
Следовательно, ∠ ABC ≅ ∠ PQR
Конгруэнтные окружности
На приведенной выше диаграмме радиус окружности A представлен радиусом OR, тогда как радиус окружности B представлен OP.
Оба круга имеют одинаковую форму и одинаковый размер, так как длина радиусов OR и OP равна 2 см каждый.
Согласно условию конгруэнтности, если радиусы двух окружностей равны по длине, то обе окружности конгруэнтны друг другу. Это также означает, что оба круга можно легко разместить друг над другом.
Таким образом, окружность A конгруэнтна окружности B и может быть записана как окружность A ≅ окружность B.
Конгруэнтные треугольники
стороны и углы должны быть равны.
Заметим, что:
Сторона AC = EG, AB = EF и BC = FG,
и ∠ A = ∠ E, ∠ B = ∠ F и ∠ C = ∠ G
Следовательно, ABC ≅ 900 EFG .
Всякий раз, когда два или более треугольника конгруэнтны, их соответствующие стороны и углы также конгруэнтны в соответствии с правилом соответствующих частей конгруэнтных треугольников (CPCT),
Разница между конгруэнтными рисунками и аналогичными рисунками
. Значительная разница между конгруэнтными рисунками и аналогичными рисунками состоит в том, что:
Конгресс фиг. | Аналогичные рисунки | 9999Похожие рисунки | 9999. углы и длины соответствующих сторон равны между собой. | На двух похожих фигурах формы выглядят одинаково. Это потому, что соответствующие углы равны. Однако длины соответствующих сторон не равны друг другу. |
Согласно приведенной выше диаграмме, конгруэнтные фигуры представлены ABC и DEF, тогда как аналогичные фигуры представлены MNO и XYZ
Что касается конгруэнтных фигур, EF,
∠ A = ∠ D, ∠ B = ∠ E и ∠ C = ∠ F
Следовательно, ABC ≅ DEF, так как соответствующие углы и длины соответствующих сторон равны друг другу.
Принимая во внимание, что в отношении аналогичных фигур.
Равны только углы, которые равны ∠ M = ∠ X, ∠ N = ∠ Y и ∠ O = ∠ Z.
Длины соответствующих сторон не равны друг другу.
Следовательно, MNO и XYZ подобны друг другу.
Однако они не конгруэнтны друг другу.
Решенные примеры
Пример 1. Два угла ∠ ABC и ∠ XYZ равны друг другу?
Решение:
Мера ∠ ABC = 40° и ∠ XYZ = 60°.
По правилу два угла равны, если величины обоих углов равны друг другу.
Мера ∠ ABC не равна мере ∠ XYZ.
Следовательно, ∠ ABC не конгруэнтно ∠ XYZ.
Пример 2: Два треугольника MNO и XYZ равны. Укажите соответствующие стороны и углы, которые будут равны.
Решение:
Дано, ∆MNO ≅ ∆XYZ
Согласно CPCT все три соответствующие стороны и углы конгруэнтных треугольников ∆MNO и ∆XYZ будут равны друг другу.
Следовательно,
MN = XY
NO = YZ
MO = XZ
также,
TM = ♂ x, T = потряно ниже фигуры похожи или конгруэнтны друг другу?
На приведенной выше диаграмме длина радиуса OL равна 2 см, тогда как OM равна 1 см.
Чтобы две окружности были конгруэнтны друг другу, длина радиуса обеих окружностей должна быть равна друг другу.
Следовательно, обе окружности подобны друг другу, но не конгруэнтны друг другу.
Заключение
Мы понимаем, что одинаковые формы и размеры называются конгруэнтными в геометрии. В конгруэнтных фигурах форма и размер должны оставаться одинаковыми, когда мы переворачиваем, поворачиваем или даже вращаем фигуры. И в конгруэнтной форме две фигуры могут быть размещены друг над другом.
С помощью SplashLearn ваш ребенок может в увлекательной форме изучить эту главу с помощью решенных примеров. SplashLearn является лучшей и самой надежной платформой для каждого ребенка, чтобы укрепить основы математики вашего ребенка. Эта образовательная онлайн-платформа делает обучение легким и увлекательным для вашего ребенка.
CTA
Вы ищете образовательную и развлекательную онлайн-платформу? Вы хотите, чтобы ваш ребенок изучал и практиковал математику, развлекаясь? Тогда не ждите слишком долго!
Зарегистрируйтесь в SplashLearn и повысьте уверенность своего ребенка в изучении математики.
Практические задачи
1 Найдите неверный ответ в случае двух конгруэнтных фигур.Конгруэнтные фигуры равны по размеру Конгруэнтны фигуры могут накладываться друг на друга Конгруэнтны фигуры не равны по форме Конгруэнтны фигуры можно поворачивать Правильный ответ: Конгруэнтны фигуры не равны по форме 2 В случае двух конгруэнтных треугольников △ABC и △MNO, если угол A равен 55°, какова мера угла M, когда он соответствует углу A?65° 55° 40° Ничего из вышеперечисленного Правильный ответ: 55° 3 Если △ABC ≅ △PQR, то какой угол будет равен ∠ R?∠B ∠C ∠A Ничего из вышеперечисленного Правильный ответ: ∠C |
Если △ABC ≅ △PQR, то угол C будет равен соответствующему углу R.Часто задаваемые вопросы
Когда можно сказать, что две фигуры равны?
Две фигуры можно назвать конгруэнтными, если они имеют одинаковую форму и одинаковый размер.
Могут ли конгруэнтные фигуры быть разных размеров?
Нет, конгруэнтные фигуры не могут иметь разные размеры. Вместо этого фигуры называются конгруэнтными, если они имеют одинаковую форму и одинаковый размер. Фигуры одинаковой формы и разных размеров называются подобными.
Все ли конгруэнтные фигуры подобны?
Да, все конгруэнтные фигуры подобны.
Могут ли конгруэнтные формы или фигуры быть зеркальными отображениями?
Да, конгруэнтные фигуры можно рассматривать как зеркальные отражения, поскольку они имеют одинаковую форму и одинаковый размер.
Имеют ли конгруэнтные круги одинаковый диаметр?
Известно, что две окружности конгруэнтны, если их радиусы равны друг другу.
Длина диаметра в два раза больше радиуса. Следовательно, конгруэнтные окружности имеют одинаковый диаметр.
Могут ли звезды быть конгруэнтными?
Две звезды можно считать конгруэнтными только в том случае, если они обе имеют одинаковую форму и размер, даже если их перевернуть, повернуть или наложить друг на друга.
Что такое конгруэнтный угол? (Примеры вопросов)
ОбзорТранскриптПрактика
Конгруэнтные углы часто используются в мире архитектуры, строительства, дизайна и искусства. Равные углы имеют одинаковую угловую меру. Например, правильный пятиугольник имеет пять сторон и пять углов, каждый из которых равен 108 градусам. Независимо от размера или масштаба правильного многоугольника, углы всегда будут конгруэнтными.
Существует множество правил, позволяющих определить, равны ли углы или нет. Например, если два треугольника подобны, их соответствующие углы будут равны. Это означает, что углы, находящиеся в одном и том же совпадающем положении, будут иметь одинаковый угол.
Еще один распространенный тест на соответствие углов требует набора параллельных прямых и поперечной линии, пересекающей набор параллельных прямых. Например, прямые a и b параллельны, а прямая l является секущей, пересекающей параллельные прямые. Когда возникает такая ситуация, образуется несколько конгруэнтных углов. В этом сценарии образуются четыре основных типа конгруэнтных углов: альтернативные внутренние углы, альтернативные внешние углы, соответствующие углы и вертикальные углы.
Альтернативные внутренние углы расположены между двумя параллельными линиями, но на разных сторонах поперечной. В этом конкретном примере конгруэнтными альтернативными внутренними углами будут ∠2 и ∠6, а также ∠7 и ∠3.
Аналогично, Альтернативные внешние углы расположены снаружи параллельных линий и на противоположных сторонах поперечных. ∠5 и ∠1 конгруэнтны, а также ∠4 и ∠8.
Соответствующие углы расположены на одной стороне поперечной и в аналогичном месте.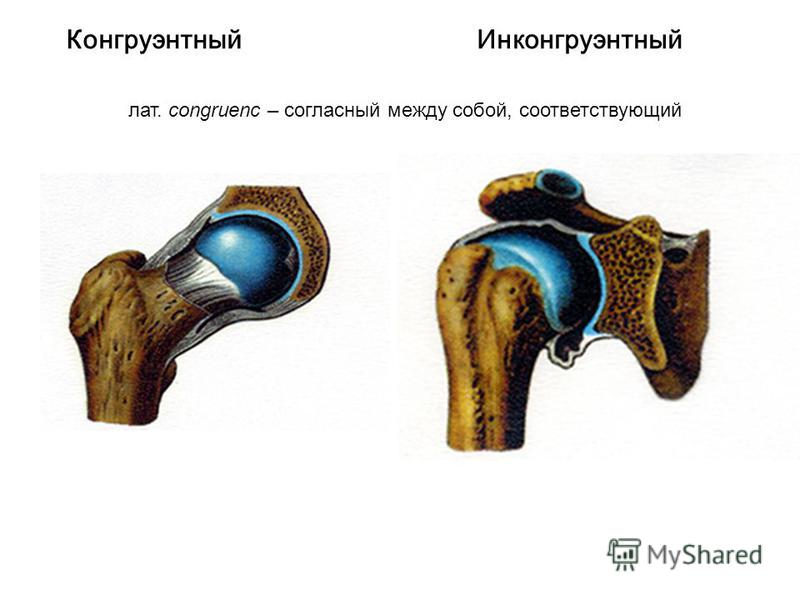
Например, ∠4 и ∠6 — соответствующие углы, поэтому они равны. Другие пары соответствующих углов включают ∠3 и ∠5, ∠1 и ∠7, а также ∠2 и ∠8.
Вертикальные углы образованы углами, противоположными друг другу. Например, ∠1 и ∠3, ∠7 и ∠5, ∠4 и ∠2, ∠6 и ∠8 — все пары равных углов. Вертикальные углы или противоположные углы обычно используются в качестве доказательства конгруэнтности.
Другая категория конгруэнтных углов связана с конгруэнтностью треугольника. Правила конгруэнтности треугольников используются, чтобы доказать, конгруэнтны два треугольника или нет. Эти правила учитывают длины сторон и углы треугольников, чтобы определить конгруэнтность. Четыре критерия используются для определения конгруэнтности треугольников, и они имеют удобные названия.
Например:
S-S-S относится к двум треугольникам, все стороны которых имеют одинаковую длину. Если это так, то все соответствующие меры углов также будут конгруэнтны.
S-A-S относится к двум треугольникам, у которых две конгруэнтные стороны и один конгруэнтный угол между ними. Если это так, то все соответствующие углы будут равны.
Аналогично, A-S-A говорит нам, что два треугольника имеют два конгруэнтных угла и одну конгруэнтную длину стороны между ними. Опять же, если это так, то все соответствующие углы будут равны.
Наконец, A-A-S относится к двум треугольникам, которые имеют два соответствующих конгруэнтных угла с соответствующей конгруэнтной длиной стороны. Это говорит нам о том, что все соответствующие углы будут равны.
Конгруэнтные углы обычно используются при изучении геометрии и во многих реальных профессиях. Строители, инженеры, строители и художники регулярно используют конгруэнтные углы. Определение конгруэнтности углов является важным навыком, который помогает заложить основу для изучения геометрии.
Углы окружают нас повсюду. Они используются инженерами, архитекторами и художниками для поиска творческих решений специализированных проблем и создания красивых светильников и произведений искусства.
Много раз углы, представленные в формах и пересекающихся линиях, имеют отношения друг к другу, которые мы можем использовать для определения их меры. Одним из таких отношений является конгруэнтность.
Если мы говорим, что два угла конгруэнтны , мы имеем в виду, что они имеют одинаковую меру в градусах. Например, предположим, что мы построили квадратную комнату, где все углы равны 9 углам.0°. Все четыре его угла будут иметь конгруэнтные углы, потому что все они имеют одинаковую меру.
Точно так же мы знаем, что в равнобедренном треугольнике два угла имеют одинаковую меру. Следовательно, эти два угла равны. Чтобы обозначить, что некоторые углы конгруэнтны друг другу, мы обычно рисуем дугу в углах.
Конгруэнтные углы действительно начинают появляться, когда мы наблюдаем пересечения прямых линий. Например, если одна прямая пересекает другую, как показано, мы можем видеть, что создаются пары конгруэнтных углов, противоположных друг другу.
Поскольку обе линии прямые, углы на каждой стороне в основном зеркальны, так что красные углы конгруэнтны, а синие углы конгруэнтны. Мы называем эти углы вертикальными углами.
Также полезно отметить, что, поскольку линии прямые, два смежных угла вместе образуют прямой угол в 180°. Это свойство пригодится, когда вам нужно найти недостающие углы.
Давайте рассмотрим пример. Если угол A равен 40°, каковы размеры углов B , C и D ? Поскольку обе пересекающиеся прямые прямые, мы знаем, что противоположные углы A и C конгруэнтны. Поэтому C также должны быть 40°. Точно так же углы B и D равны. Их размеры можно определить, используя тот факт, что A + B должны равняться 180°.
\(A+B=180°\)
\(40°+B=180°\)
\(B=140°\)
Итак, B и D должны иметь 90 меры 140°.
Что происходит, когда мы наблюдаем две параллельные линии, которые пересекает третья линия?
Рассмотрим параллельные прямые p и q и пересекающую их поперечную линию t .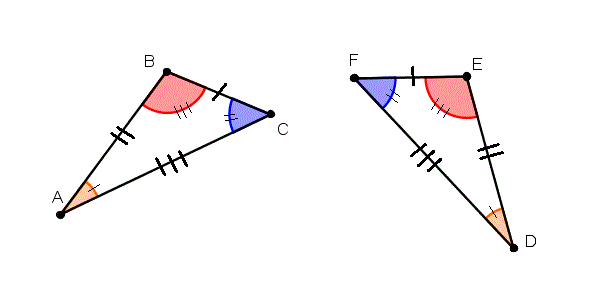
Теперь мы наблюдаем два пересечения и всего восемь углов.
При внимательном рассмотрении этих перекрестков видно, что они идентичны друг другу. Поскольку p и q параллельны, их пересечения с t образуют конгруэнтные углы. Таким образом, конгруэнтны не только углы 1 и 3, но и углы 5 и 7 также включены в это же соответствие. Точно так же равны углы 2, 4, 6 и 8.
Существует четыре классификации типов конгруэнтных углов, представленных в этом сценарии: вертикальные углы, соответствующие углы, альтернативные внешние углы и альтернативные внутренние углы.
Вертикальные углы — это углы, которые противоположны друг другу в одной точке пересечения. Это похоже на то, что мы наблюдали в предыдущем примере. Здесь мы видим, что углы 1 и 3 снова равны, и поскольку они лежат друг напротив друга в одном и том же пересечении, они классифицируются как вертикальные углы. Точно так же пары углов 2 и 4, 5 и 7, 6 и 8 являются парами вертикальных углов.
Соответствующие углы представляют собой пары углов, находящихся в одинаковом относительном положении пересечения каждой параллельной прямой и поперечной.
Соответствующие углы равны между собой. Например, углы 2 и 6 являются соответствующими углами, потому что они оба появляются справа от t и над параллельными прямыми. Значит, это равные углы. Другими парами соответствующих углов в этом примере являются углы 1 и 5, 3 и 7, 4 и 8.
Альтернативные внешние углы представляют собой пары углов, которые появляются на внешней стороне параллельных прямых и на противоположных сторонах поперечной. Альтернативные внешние углы равны друг другу. Углы 1 и 7 являются противоположными внешними углами и, следовательно, равны друг другу. Углы 2 и 8 также являются альтернативными внешними углами, что делает их конгруэнтными друг другу.
Аналогично, альтернативные внутренние углы представляют собой пары углов, которые появляются внутри параллельных прямых и на противоположных сторонах поперечной. Альтернативные внутренние углы конгруэнтны друг другу. Здесь это будут пары 3 и 5, 4 и 6.
Мы обсудили, что два или более угла конгруэнтны, если они имеют одну и ту же угловую меру, и мы рассмотрели несколько геометрических приложений конгруэнтных углов.
Эти идеи помогают строителям, плотникам и инженерам добиваться совершенства в своей работе при проектировании инструментов, объектов и зданий. Потратьте некоторое время, чтобы самостоятельно решить некоторые примеры задач, и вскоре вы увидите конгруэнтные углы в окружающем вас мире!
Надеюсь, это видео было полезным. Спасибо за просмотр и удачной учебы!
Вопрос №1:
Углы 1 и 2 — соответствующие углы. Если угол 2 равен 67°, то чему равен угол 1?
164 °
24 °
344 °
67 °
Покажите ответ
Ответ:
Когда две параллельные линии вырезаны трансверами, то же самое, что на той же побочной стороне. и в соответствующих углах будут конгруэнтными. Углы 1 и 2 равны, поэтому оба имеют угловую меру 67°.
Скрыть ответ
Вопрос №2:
Прямая r – это секущая, пересекающая две параллельные прямые s и t .
Перечислите все углы, равные углу 6.
∠8, ∠3 и ∠2
∠8, ∠4 и ∠2
∠2
∠59 20 ∠2 и 0 Показать ответ
Ответ:
∠8 конгруэнтно ∠6, потому что они вертикальные или противоположные углы.
∠2 конгруэнтно ∠6, потому что они являются соответствующими углами (на одной стороне поперечной и в соответствующих углах).
∠4 конгруэнтно ∠6, потому что они представляют собой альтернативные внутренние углы (альтернативные стороны поперечной и между двумя параллельными прямыми).
Скрыть ответ
Вопрос №3:
Если следующие неправильные четырехугольники равны, угол C должен быть равен какому другому углу?
∠Е
∠Ф
∠G
∠H
Показать ответ
Ответ:
Соответствующие углы конгруэнтны для конгруэнтных многоугольников.
Секрет согласуется с секрет
секрета строит пешеходную дорожку, пересекающую пару железнодорожных путей. Пешеходная дорожка представлена поперечной буквой t на изображении ниже. Железнодорожные пути представлены параллельными линиями l и m. Если город хочет, чтобы пешеходная дорожка пересекала рельсы под углом 135° (угол 1), каковы будут значения углов 2, 3 и 4?
∠2 = 45° ∠3 = 135° ∠4 = 45°
∠2 = 45° ∠3 = 45° ∠4 = 135°
∠2 = 145° ∠3 = 44° 45°
∠2 = 180° ∠3 = 45° ∠4 = 45°
Показать ответ
Ответ:
∠1 и ∠4 равны, потому что они являются вертикальными углами. Если ∠1 равно 135°, то ∠2 должно быть равно 45°, потому что их сумма должна быть 180°, чтобы образовать прямую линию. Теперь, когда мы знаем, что ∠2 равно 45°, мы также знаем, что ∠3 равно 45°, потому что это вертикальные углы.
Скрыть ответ
Вопрос №5:
У Келси есть прямоугольный сад, который она хочет разделить на две равные части по диагонали.
