Корреляционные связи: Корреляция, корреляционная зависимость

Корреляционная связь, ее признаки, виды. Коэффициент корреляции, определение, свойства, методы вычисления. Метод корреляции рядов Пирсона. Метод корреляции рангов Спирмена.

Многие явления в медицине, так же как в природе и обществе, взаимо­связаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различ­ными явлениями и дать обобщающую характеристику. Различают 2 формы проявления связей между явлениями: функциональную и корреляционную.

Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует строго определенное значение другой. Например, радиусу круга соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силой тяжести и временем падения. Функциональная связь характерна для физико-химических процессов.

Корреляционная связь — это такая связь, когда одной и той же величи­не одного признака соответствует несколько значений другого взаимосвязанно­го с ним признака. Врачи и биологи хорошо знакомы с этим видом связи: при одинаковой температуре у различных людей наблюдаются индивидуальные ко­лебания частоты пульса; при одинаковом росте отмечаются различные колеба­ния масс тела.

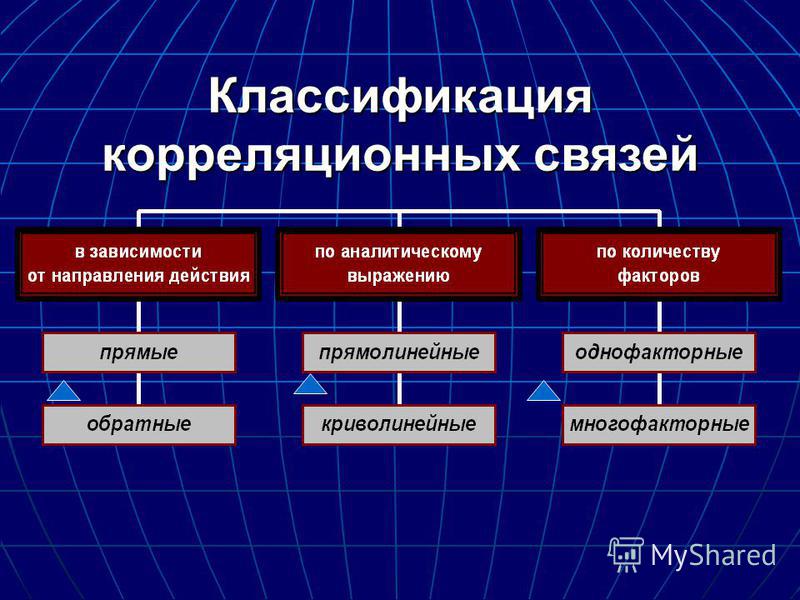
По форме корреляционная связь:

Прямолинейная связь — равномерные изменения одного признака со­ответствуют равномерным изменениям второго признака при незначительных отклонениях.

Криволинейная связь — равномерные изменения одного признака, со­ответствуют неравномерным изменениям второго признака, причем неравно­мерность имеет определенную закономерность. Общая тенденция в определен­ном моменте изменяет свос направление, дает изгиб.

Направление связи:

Прямая связь (положительная) — если с увеличением одного признака второй также уве­личивается или с уменьшением одного признака другой тоже уменьшается. Обратная связь (отрицательная) — когда с увеличением одного признака, другой, корре­ляционно связанный с ним признак, уменьшается.

Под силой связи следует понимать степень корреляции (степень сопря­женности между признаками).

Измерение силы связи и определение ее направления осуществляется пу­тем вычисления коэффициента корреляции. Существуют следующие методы вычисления коэффициента корреляции: рядов, рангов, путем составления корреляционной решетки.

Степень связи	Величина коэффициента корреляции
	При прямой связи (+)	При обратной связи (-)
Связь отсутствует	0	0
Связь малая (слабая)	от 0 до + 0,29	от 0 до -0,29
Связь средняя (умеренная)	от 0,3 до + 0,69	от -0,3 до -0,69
Связь большая (сильная)	от 0,7 до+0,99	от -0,7 до -0,99
Связь полная	+1	-1

Коэффициент корреляции рядов (r_xy) (Пирсона):

r_xy = , гдеd = V- M.

Для оценки достоверности коэффициента корреляции вычисляется средняя ошибка коэффициента корреляции:

m_r = – при числе наблюдений более 100;

m_r = – при числе наблюдений от 30 до 100;

m_r = – при числе наблюдений менее 30.

Для оценки величины полученной ошибки следует использовать крите­рий достоверности (t).

t =

Значение критерия (t) оценивается по специальной таблице Стьюдента. Если полученное значение t больше табличного для выбранного уровня дове­рия и числа степеней свободы, то коэффициент корреляции считается досто­верным.

Ко­эффициент корреляции рангов () (Спирмена):

Коэффициент корреляции рангов относится к непарамегрическим критериям. Он используется при необходимости получения быстрого результата, при малом числе наблюдений, а также в тех случаях, когда изучаемые признаки не имеют точных количественных значений или носят описательный характер. Этот метод основан на определении ранга (места) каждого из значений ряда.

= 1 – , гдеd — раз­ность между ранговыми номерами; n — число парных членов в коррелируемых рядах

Вычисления проводятся по следующему алгоритму:

1) Определить ранги по значению каждой величины ряда. (1,2,3,4…) Если первый ряд (x) ранжируется от меньшего значения к большему, то второй ряд (у) сле­дует ранжировать в том же порядке.

2) Определить разность рангов каждой пары ряда (х) и ряда (у): (d_xy)= (x) — (у). Они в сумме с учетом знаков равны нулю.

3) Возвести в квадрат полученные разности и суммировать их.

4) Рассчитать коэффициент корреляции рангов по формуле.

Прежде чем судить о степени связи между изучаемыми признаками, не­обходимо оценить достоверность коэффициента корреляции рангов.

t =

Полученное значение критерия t оценивается по таблице t-критерия Стьюдента для числа степеней свободы n’ = n-2. Коэффициент корреляции незначим, если рассчитанное значение меньше табличного.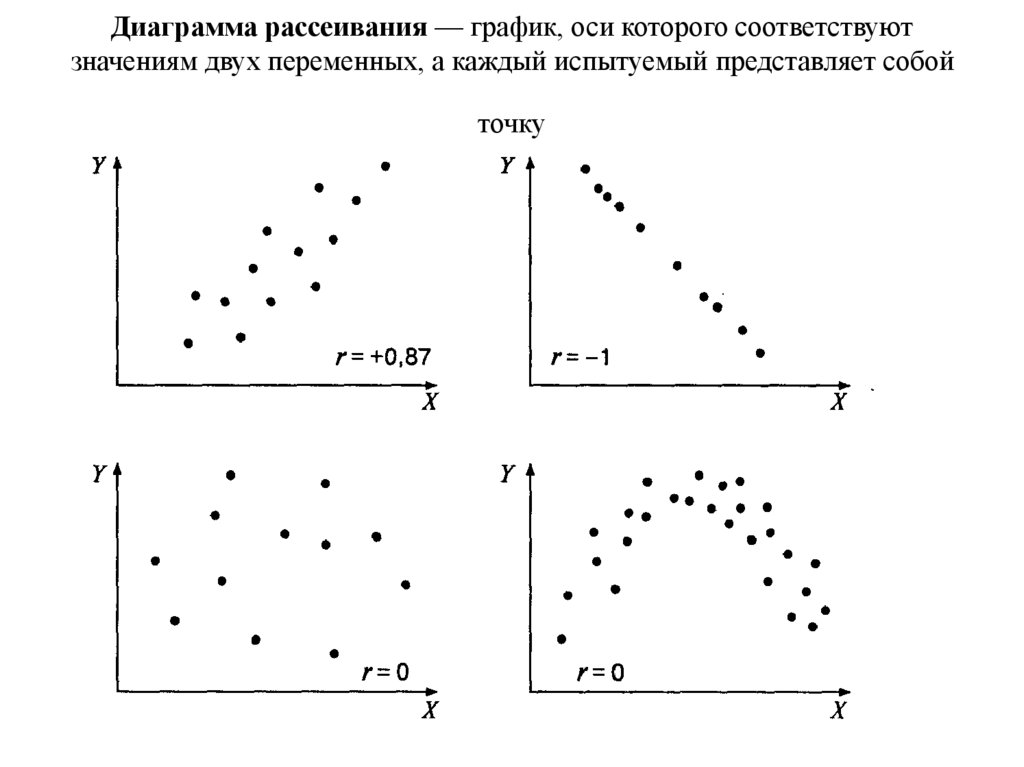

Корреляционные связи многолетних колебаний месячного и годового стока в бассейне реки Урал | Васильев

1. Андреянов В. Г. Внутригодовое распределение речного стока. Л.: Гидрометеоиздат, 1960. 327 с.

2. Андреянов В.Г. Методические указания по расчетам внутригодового распределения стока при строительном проектировании. Л.: Гидрометеоиздат, 1970. 77 с.

3. Андреянов В.Г. Некоторые уточнения и упрощения методики расчетов календарного внутригодового распределения речного стока применительно к требованиям строительного проектирования // Труды ГГИ. Л.: Гидрометеоиздат, 1966. Вып. 134. С. 80-114.

4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. М.: Мир, 1989. 540 с.

5. Болгов М.В., Филиппова И.А. Пороговые стохастические модели минимального стока // Метеорология и гидрология. 2006. № 3. С. 88-94.

6. Борщ С.В., Христофоров А.В. Гидрометеорологические прогнозы // Труды ГМЦ России. 2015. № 355. С. 48-100.

7. Васильев Д.Ю., Бабков О.К., Давлиев И. Р., Семенов В.А., Христодуло О.И. Пространственно-временная структура колебаний приземной температуры на Южном Урале // Оптика атмосферы и океана. 2018. Т. 31. № 4. С. 294-302.

8. Васильев Д.Ю., Бабков О.К., Кочеткова Е.С., Семенов В.А. Вейвлет и кросс-вейвлет анализ сумм атмосферных осадков и приповерхностной температуры на Европейской территории России // Изв. РАН. Сер. геогр. 2017. № 6. С. 63-77.

9. Васильев Д.Ю., Великанов Н.В., Водопьянов В.В., Красногорская Н.Н., Семенов В.А., Христодуло О.И. Связь аномалий яркостной температуры нижней тропосферы с климатическими индексами на примере Южного Урала // Исслед. Земли из космоса. 2019. № 2. С. 14-28.

10. Васильев Д.Ю., Гавра Н.К., Кочеткова Е.С., Ферапонтов Ю.И. Корреляции сумм атмосферных осадков со средними и максимальными расходами воды весеннего половодья в бассейне реки Белая // Метеорология и гидрология. 2013. № 5. С. 351-358.

11. Васильев Д.Ю., Лукманов Р.Л., Ферапонтов Ю.И., Чувыров А.Н. Цикличность гидрометеорологических характеристик на примере Башкирии // ДАН. 2012. Т. 447. № 3. С. 331-334.

12. Васильев Д.Ю., Павлейчик В.М., Семенов В.А., Сиво-хип Ж.Т., Чибилев А.А. Многолетний режим температуры воздуха и атмосферных осадков на территории Южного Урала // ДАН. 2018. Т. 478. № 2. С. 245-249. https://doi.org/10.7868/S0869565218050201

13. Васильев Д.Ю., Сивохип Ж.Т., Чибилев А.А. Динамика климата и внутривековые колебания стока в бассейне реки Урал // ДАН. 2016. Т. 469. № 1. С. 710-715.

14. Васильев Д.Ю., Ферапонтов Ю.И. Тренды в колебаниях приземной температуры воздуха на примере Башкирии // Изв. РАН. Сер. геогр. 2015. № 1. С. 77-86.

15. Васильев Д.Ю., Водопьянов В.В, Зайцева Г.С., Закир-зянов Ш.И., Семенов В.А., Сивохип Ж. Т., Чибилев А.А. Модель долгосрочного прогноза весеннего стока на примере реки Белая // ДАН. 2019. Т. 486. № 6. С. 723-726. https://doi.org/10.31857/S0869-56524866723-726

16. Водные ресурсы России и их использование / под ред. И.А. Шикломанова. СПб.: изд-во ГГИ, 2008. 600 с.

17. Гельфанд И. М., Фомин С. В. Вариационное исчисление. М.: Физматлит, 1961. 228 с.

18. Добровольский С. Г. Проблема глобального потепления и изменения стока российских рек // Водные ресурсы. 2007. Т. 34. № 6. С. 643-655.

19. Долгов С.В., Коронкевич Н.И. Особенности реакции рек Русской равнины на изменение температуры воздуха // Изв. РАН. Сер. геогр. 2012. № 6. С. 55-62.

20. Картвелишвили Н.А. Стохастическая гидрология. Л.: Гидрометеоиздат, 1975. 162 с.

21. Коронкевич Н.И., Барабанова Е.А., Зайцева И.С. Влияние изменения годовых значений температуры воздуха и осадков на сток рек Русской равнины // Изв. РАН. Сер. геогр. 2007. № 5. С. 64-70.

22. Мякишева Н.В., Гоюй Ч. Ритмика годовой цикличности гидрологических процессов в районах с интенсивной хозяйственной деятельностью // Вестн. СПбГУ. Сер. 7. 2011. Вып. 1. С. 98-106.

23. Мякишева Н.В., Трапезников Ю.А. Авторегрессионная модель межгодовой изменчивости гидрометеорологических процессов // Вероятностный анализ и моделирование океанологических процессов. Л.: Гидрометеоиздат, 1984. С. 31-39.

24. Музылев С.В., Привальский В.Е., Раткович Д.Я. Стохастические модели в инженерной гидрологии. М.: Наука, 1982. 184 с.

25. Раткович Д.Я. Многолетние колебания речного стока: закономерности и регулирование. Л.: Гид-рометеоиздат, 1976. 255 с.

26. Раткович Д.Я., Болгов М.В. Стохастические модели колебаний составляющих водного баланса речного бассейна. М.: ИВП РАН, 1997. 261 с.

27. Рожков В.А. Теория и методы статистического оценивания вероятностных характеристик случайных величин и функций с гидрометеорологическими примерами. СПб.: Гидрометеоиздат, 2001. 340 с.

28. Румянцев В.А., Трапезников Ю.А. Стохастические модели гидрологических процессов. СПб.: Наука, 2008. 152 с.

29. Сванидзе Г.Г. Математическое моделирование гидрологических рядов. Л.: Гидрометеоиздат, 1977. 293 с.

30. Свидетельство о государственной регистрации программы для ЭВМ 2018661796. РФ. Реализация метода периодически коррелируемого случайного процесса, на примере стока реки / ред.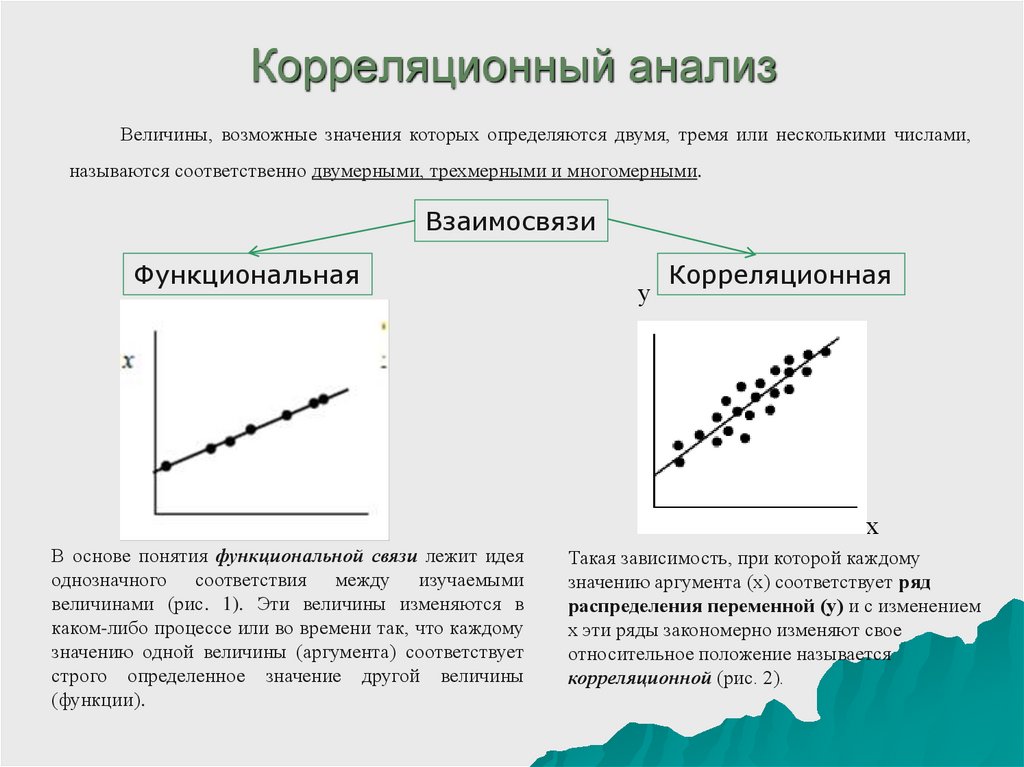 Д.Ю. Васильев, В.В. Водопьянов, Ш.Н. Закирзянов; правообладатель Уфимск. гос. авиац. техн. ун-т. № 2018618838; заявл. 17.08.2018.; зарегистр. 18.09.2018.

31. Чибилев А.А. Река Урал. Л.: Гидрометеоиздат, 1987. 168 с.

32. Hao Z, Singh V.P. Entropy-copula method for singlesite monthly streamflow simulation // Wat. Res. 2012. V. 48. W06604. https://doi.org/10.1029/2011WR011419

33. Ricker Dennis W Echo Signal Processing. Springer, 2003. 240 p.

34. Salvadori G., Michele C.D. Multivariate multiparameter extreme value models and return periods: a copula approach // Wat. Res. 2010. V. 46. W10501. https://doi.org/10.1029/2009WR009040

35. Torrence C., Campo G.P. A practical guide to wavelet analysis // Bull. Amer. Met. Soc. 1998. V. 79. P. 61-78.

36. Wen X., Tang G, Wang S, Hnang J. Comparison of global mean temperature series // Advances in Climate Change Res. 2011. V. 2. № 4. P. 187-192.

Корреляция | Введение в статистику

Что такое корреляция?

Корреляция — это статистическая мера, выражающая степень линейной зависимости двух переменных (что означает, что они изменяются вместе с постоянной скоростью). Это распространенный инструмент для описания простых отношений без утверждения о причине и следствии.

Как измеряется корреляция?

Коэффициент корреляции выборки r количественно определяет силу связи. Корреляции также проверяются на статистическую значимость.

Каковы некоторые ограничения корреляционного анализа?

Корреляция не может учитывать наличие или влияние других переменных помимо двух исследуемых. Важно отметить, что корреляция не говорит нам о причине и следствии. Корреляция также не может точно описать криволинейные отношения.

Корреляции описывают совместное перемещение данных

Корреляции полезны для описания простых взаимосвязей между данными. Например, представьте, что вы просматриваете набор данных кемпингов в горном парке. Вы хотите знать, существует ли связь между высотой кемпинга (насколько высоко он находится в горах) и средней высокой температурой летом.

Для каждого отдельного кемпинга у вас есть два показателя: высота над уровнем моря и температура. Когда вы сравниваете эти две переменные в своей выборке с корреляцией, вы можете найти линейную зависимость: по мере увеличения высоты температура падает. Они отрицательно коррелированы .

Что означают числа корреляции?

Мы описываем корреляции с безразмерной мерой, называемой коэффициентом корреляции, который находится в диапазоне от -1 до +1 и обозначается как r . Статистическая значимость указана с p-значением. Поэтому корреляции обычно записываются двумя ключевыми числами: r =  и p = .

• Чем ближе r к нулю, тем слабее линейная зависимость.
• Положительные значения r указывают на положительную корреляцию, когда значения обеих переменных имеют тенденцию к совместному увеличению.
• Отрицательные значения r указывают на отрицательную корреляцию, когда значения одной переменной имеют тенденцию к увеличению, когда значения другой переменной уменьшаются.
• Значение p свидетельствует о том, что мы можем обоснованно заключить, что коэффициент корреляции населения, вероятно, отличен от нуля, основываясь на том, что мы наблюдаем в выборке.
• «Бесединичная мера» означает, что корреляции существуют в своей собственной шкале: в нашем примере число, указанное для r , не находится в той же шкале, что и высота над уровнем моря или температура. Это отличается от других сводных статистических данных. Например, среднее значение измерений высоты находится в том же масштабе, что и его переменная.

Что такое р-значение?

Значение p — это мера вероятности, используемая для проверки гипотез.

Указывает на вероятность получения данных, которые мы видим, при отсутствии эффекта — другими словами, в случае нулевой гипотезы. Для наших данных кемпинга это будет гипотеза об отсутствии линейной зависимости между высотой над уровнем моря и температурой. Когда значение p используется для описания результата как статистически значимого, это означает, что оно падает ниже заранее определенного порога (например, p < 0,05 или p < 0,01), после чего мы отклоняем нулевую гипотезу в пользу альтернативная гипотеза (для данных о наших кемпингах существует связь между высотой над уровнем моря и температурой).

Как только мы получили значительную корреляцию, мы также можем посмотреть на ее силу. Совершенная положительная корреляция имеет значение 1, а совершенная отрицательная корреляция имеет значение -1. Но в реальном мире мы никогда не ожидали бы увидеть идеальную корреляцию, если только одна переменная на самом деле не является прокси-мерой для другой. На самом деле, вид идеального числа корреляции может предупредить вас об ошибке в ваших данных! Например, если вы случайно записали расстояние от уровня моря для каждого лагеря вместо температуры, это будет идеально коррелировать с высотой над уровнем моря.

Другой полезной информацией является N, или количество наблюдений. Как и в большинстве статистических тестов, знание размера выборки помогает нам оценить силу нашей выборки и то, насколько хорошо она представляет генеральную совокупность. Например, если мы измерили высоту и температуру только для пяти кемпингов, а в парке две тысячи кемпингов, мы хотели бы добавить в нашу выборку больше кемпингов.

Визуализация корреляций с диаграммами рассеяния

Вернемся к нашему примеру сверху: по мере увеличения высоты кемпинга температура падает. Мы можем посмотреть на это непосредственно с помощью диаграммы рассеяния. Представьте, что мы нанесли данные о нашем кемпинге:

• Каждая точка на графике представляет один кемпинг, который мы можем расположить по осям x и y по его высоте и высокой температуре в летнее время.
• Коэффициент корреляции ( r ) также иллюстрирует нашу диаграмму рассеяния. Он говорит нам в числовом выражении, насколько близки точки, отображаемые на диаграмме рассеяния, к линейной зависимости. Более сильные отношения или большие значения r означают отношения, в которых точки очень близки к линии, которую мы подогнали к данным.

А как насчет более сложных отношений?

Диаграммы рассеяния также полезны для определения того, есть ли в наших данных что-либо, что может нарушить точную корреляцию, например необычные закономерности, такие как криволинейные отношения или экстремальные выбросы.

Корреляции не могут точно отображать криволинейные отношения. В криволинейной связи переменные коррелируют в заданном направлении до определенной точки, где связь меняется.

Например, представьте, что мы посмотрели на высоту нашего кемпинга и на то, как высоко отдыхающие в среднем оценивают каждый кемпинг. Возможно, поначалу высота над уровнем моря и рейтинг кемпинга положительно коррелируют, потому что с более высоких кемпингов открывается лучший вид на парк. Но в какой-то момент более высокие высоты начинают отрицательно коррелировать с рейтингом кемпинга, потому что ночью отдыхающим становится холодно!

Мы можем получить еще больше информации, добавив заштрихованные эллипсы плотности к нашей диаграмме рассеивания. Эллипс плотности иллюстрирует самую плотную область точек на диаграмме рассеяния, что, в свою очередь, помогает нам увидеть силу и направление корреляции.

Эллипсы плотности могут быть разных размеров. Одним из распространенных вариантов изучения корреляции является эллипс с плотностью 95 %, который охватывает примерно 95 % самых плотных наблюдений.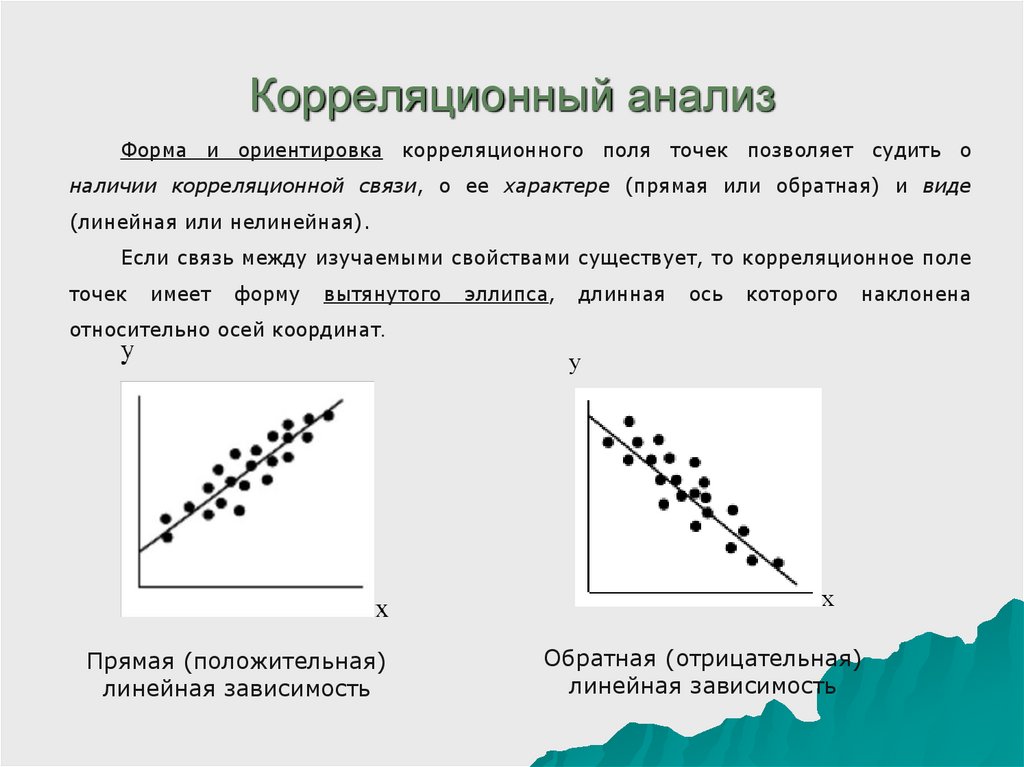 Если две переменные движутся вместе, например, высота над уровнем моря и температура в наших кемпингах, мы ожидаем, что этот эллипс плотности будет отражать форму линии. И мы видим, что в криволинейной зависимости эллипс плотности выглядит круглым: корреляция не даст нам осмысленного описания этой зависимости.

11. Корреляция и регрессия

Слово корреляция используется в повседневной жизни для обозначения той или иной формы ассоциации. Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными. Мы также предполагаем, что связь является линейной, что одна переменная увеличивается или уменьшается на фиксированную величину при увеличении или уменьшении на единицу другой. Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для обобщения ассоциации.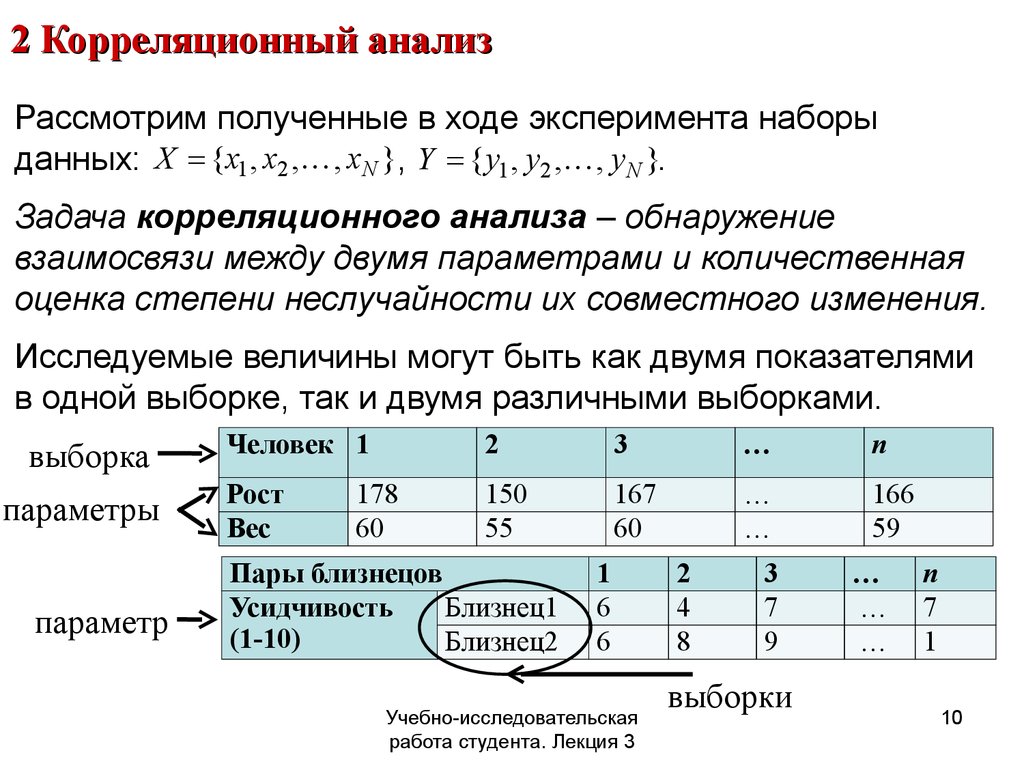

Коэффициент корреляции

Степень ассоциации измеряется коэффициентом корреляции, обозначаемым r. Его иногда называют коэффициентом корреляции Пирсона по имени его создателя, и он является мерой линейной связи. Если кривая линия необходима для выражения взаимосвязи, необходимо использовать другие, более сложные меры корреляции.

Коэффициент корреляции измеряется по шкале, которая варьируется от + 1 через 0 до – 1. Полная корреляция между двумя переменными выражается либо + 1, либо -1. Когда одна переменная увеличивается по мере увеличения другой, корреляция положительна; когда одно уменьшается по мере увеличения другого, оно отрицательно. Полное отсутствие корреляции представлено цифрой 0. На рис. 11.1 приведены некоторые графические представления корреляции.

Рисунок 11.1 Проиллюстрированная корреляция.

Просмотр данных: диаграммы рассеяния

Когда исследователь собрал две серии наблюдений и хочет увидеть, есть ли между ними взаимосвязь, он должен сначала построить диаграмму рассеяния. Вертикальная шкала представляет собой один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой состоит из временной шкалы или какой-либо классификации наблюдений, обычно результаты экспериментов помещают на вертикальную ось. Они представляют собой так называемую «зависимую переменную». «Независимая переменная», такая как время, рост или какая-либо другая наблюдаемая классификация, измеряется вдоль горизонтальной оси или базовой линии.

Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит. Эта путаница является триумфом здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может упоминаться или не упоминаться. Разумно, например, думать о росте детей как о зависимости от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смолы и выходом никотина в некоторых марках сигарет».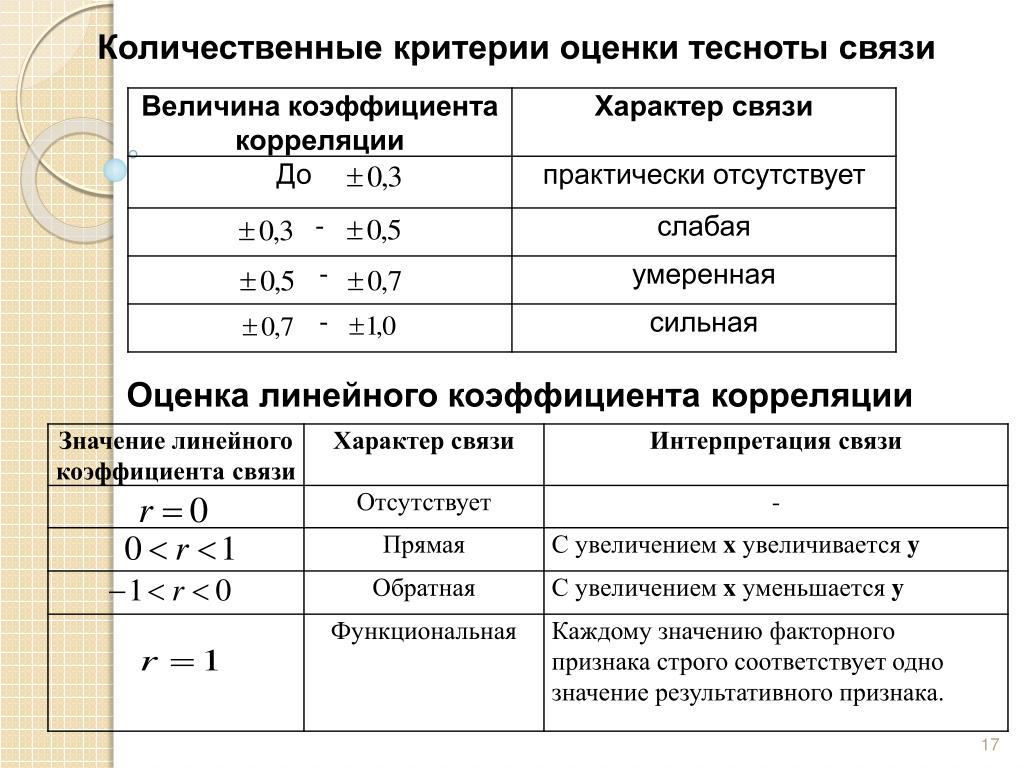 в смоле: оба изменяются параллельно с каким-то другим фактором или факторами в составе сигарет. Урожайность одного, по-видимому, не «зависит» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы рассеяния нанесен. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в основу. В качестве еще одного примера, график ежемесячных смертей от болезней сердца и ежемесячных продаж мороженого будет показывать отрицательную связь. Однако вряд ли употребление мороженого защищает от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно с температурой окружающей среды.

Расчет коэффициента корреляции

Детский регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) у 15 детей. Данные приведены в таблице 11.1, а диаграмма рассеяния показана на рисунке 11.2. Каждая точка представляет одного ребенка и находится в точке, соответствующей измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Регистратор теперь проверяет шаблон, чтобы увидеть, кажется ли вероятным, что область, покрытая точками, находится в центре прямой линии или необходима изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общий тренд точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.

При построении точечной диаграммы (рис. 11.2), чтобы показать высоту и анатомические мертвые зоны легких у 15 детей, педиатр разместил цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно располагать наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных четко идентифицируется как независимая. Соответствующие цифры для зависимой переменной затем могут быть исследованы по отношению к возрастающему ряду для независимой переменной. Таким образом, мы получаем ту же картину, но в числовом виде, как показано на диаграмме рассеяния.

Рис. 11.2. Диаграмма рассеивания соотношения роста и анатомического мертвого пространства легких у 15 детей.

Коэффициент корреляции рассчитывается следующим образом, где x представляет значения независимой переменной (в данном случае рост), а y представляет значения зависимой переменной (в данном случае анатомическое мертвое пространство). Используемая формула:

, которая может быть равна:

Процедура расчета

Найдите среднее значение и стандартное отклонение x, как описано в

Найдите среднее значение и стандартное отклонение y:

Вычтите 1 из n и умножьте на SD(x) и SD(y), (n – 1)SD(x)SD(y)

Получим знаменатель формулы. (Не забудьте выйти из режима «Stat».)

Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения вместе и сохраните их.

110 x 44 = Мин.

116 x 31 = M+

и т. д.

Сохраняет в памяти. Вычесть

MR – 15 x 144,6 x 66,93 (5426,6)

Наконец, разделите числитель на знаменатель.

г = 5426,6/6412,0609 = 0,846.

Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка. Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Между двумя коррелирующими переменными может быть или не быть причинно-следственной связи. Более того, если и есть связь, то она может быть косвенной.

Часть вариации одной из переменных (измеряемая ее дисперсией) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть как вызванная неопределенными (часто «случайными») причинами. Часть, обусловленная зависимостью одной переменной от другой, измеряется Rho. Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства приходится на рост ребенка. Если мы хотим обозначить силу ассоциации, для абсолютных значений r, 0-0,19считается очень слабой, 0,2-0,39 — слабой, 0,40-0,59 — умеренной, 0,6-0,79 — сильной и 0,8-1 — очень сильной корреляцией, но это довольно условные пределы, и следует учитывать контекст результатов.

Тест значимости

Чтобы проверить, является ли связь просто очевидной и могла ли она возникнуть случайно, используйте тест t в следующем расчете:

2 степени свободы.

Например, коэффициент корреляции для этих данных равен 0,846.

Число пар наблюдений было 15. Применяя уравнение 11.1, мы имеем:

Вводя таблицу B при 15 – 2 = 13 степенях свободы, мы находим, что при t = 5,72, P < 0,001, поэтому коэффициент корреляции можно считать как весьма значительное. Таким образом (как сразу видно из графика рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла бы случайно.

Допущения, лежащие в основе этого теста:

1. Обе переменные имеют правдоподобное нормальное распределение.
2. Между ними существует линейная зависимость.
3. Нулевая гипотеза состоит в том, что между ними нет связи.

Тест не следует использовать для сравнения двух методов измерения одного и того же количества, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом, по-видимому, является распространенной ошибкой, когда важный результат интерпретируется как означающий, что один метод эквивалентен другому. Причины широко обсуждались(2), но стоит напомнить, что значимый результат мало что говорит нам о силе взаимосвязи. Из формулы должно быть понятно, что даже при очень слабой связи (скажем, r = 0,1) мы получили бы значимый результат при достаточно большой выборке (скажем, n более 1000).

Ранговая корреляция Спирмена

На графике данных могут быть обнаружены отдаленные точки от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции.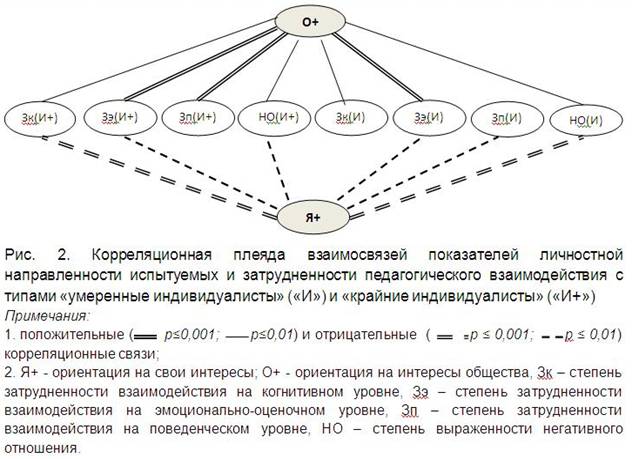 В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура, по Спирмену, заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.

Это приводит к простой формуле ранговой корреляции Спирмена, Rho.

где d — разница рангов двух переменных для данного индивидуума. Таким образом, мы можем вывести таблицу 11.2 из данных таблицы 11.1.

Отсюда получаем, что

В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена может быть проверен на значимость с использованием приведенного ранее t-критерия.

Уравнение регрессии

Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда одно изменяется на определенную величину, другое изменяется в среднем на определенную величину. Например, у описанных ранее детей больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x независимую переменную, это отношение описывается как регрессия y на x.

Связь может быть представлена ​​простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (этот термин является исторической аномалией) просто означает, что среднее значение у является «функцией» от х, то есть изменяется вместе с х.

Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, является ли корреляция положительной или отрицательной. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо. Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если таковые имеются. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две характеристики линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние над базовой линией; второй — его наклон. Они выражаются в следующих уравнение регрессии :

С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной. Параметры α и β должны быть оценены по данным. Параметр означает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину изменения y для единичного увеличения x. Таким образом, он представляет собой степень наклона линии вверх или вниз.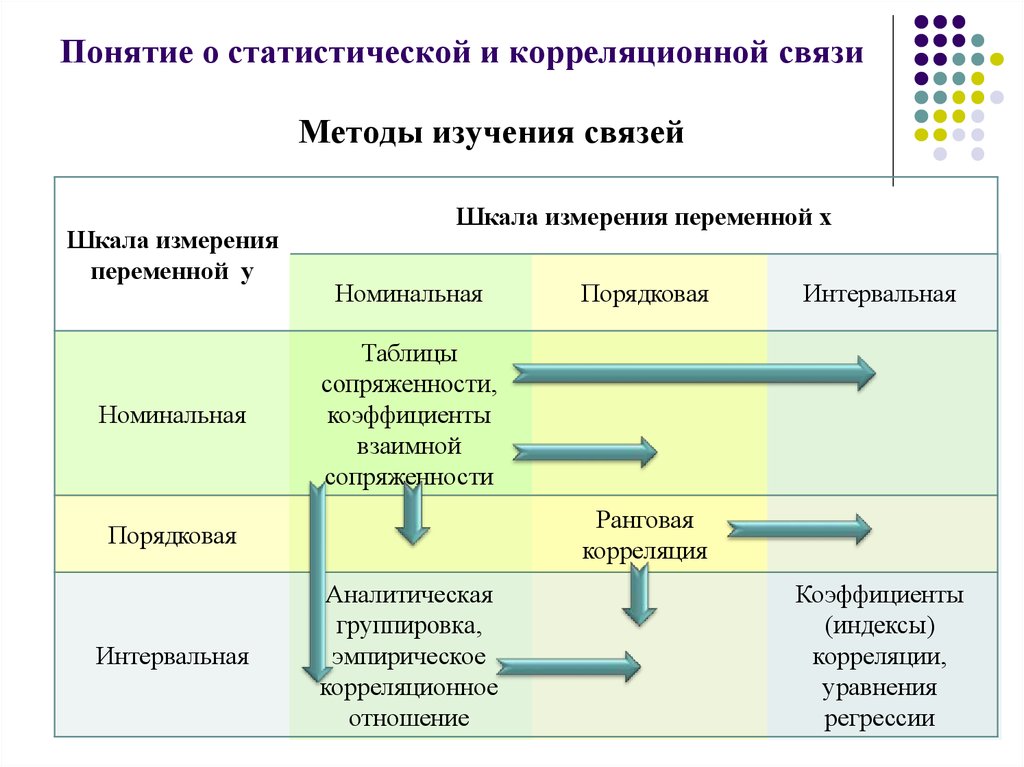

Уравнение регрессии часто бывает более полезным, чем коэффициент корреляции. Это позволяет нам предсказывать y по x и дает нам лучшее представление о взаимосвязи между двумя переменными. Если для конкретного значения x, x i уравнение регрессии предсказывает значение y fit , ошибка предсказания равна . Можно легко показать, что любая прямая линия, проходящая через средние значения x и y, даст общую ошибку предсказания, равную нулю, поскольку положительные и отрицательные члены точно сокращаются. Чтобы удалить отрицательные знаки, мы возводим в квадрат различия и уравнение регрессии, выбранное для минимизации суммы квадратов ошибок прогнозирования. Мы обозначаем выборочные оценки альфа и бета как a и b. Можно показать, что единственная прямая, минимизирующая оценку методом наименьших квадратов, задается как

и

можно показать, что

полезно, потому что мы рассчитали все компоненты уравнения (11.2) при расчете коэффициента корреляции.

Расчет коэффициента корреляции по данным таблицы 11.2 дал следующее:

Применяя эти цифры к формулам для коэффициентов регрессии, имеем:

Следовательно, в этом случае уравнение регрессии у на х становится

Это означает, что в среднем на каждое увеличение роста на 1 см увеличение анатомического мертвого пространства составляет 1,033 мл по диапазону измерений составил .

Линия, представляющая уравнение, показана наложенной на диаграмму рассеяния данных на рисунке 11.2. Чтобы нарисовать линию, нужно взять три значения x, одно в левой части точечной диаграммы, одно в середине и одно справа, и подставить их в уравнение следующим образом:

Если x = 110 , y = (1,033 x 110) – 82,4 = 31,2

Если x = 140, y = (1,033 x 140) – 82,4 = 62,2

Если x = 170, y = (1,033 x 170) – 82,4 = 93.2

Хотя для определения линии достаточно двух точек, для проверки лучше использовать три точки. Нанеся их на точечную диаграмму, мы просто проводим через них линию.

Рис. 11.3 Линия регрессии, проведенная на диаграмме рассеивания относительно роста и легочного анатомического мертвого пространства у 15 детей Можно показать, что это алгебраически равно

Нам уже нужно передать все термины в этом выражении. Таким образом, квадратный корень из . Знаменатель (11.3) равен 72,4680. Таким образом, SE(b) = 13,08445/72,4680 = 0,18055.

Мы можем проверить, значительно ли наклон отличается от нуля, с помощью:

t = b/SE(b) = 1,033/0,18055 = 5,72.

Опять же, здесь n – 2 = 15 – 2 = 13 степеней свободы. Предположения, определяющие этот тест, следующие:

1. Ошибки прогнозирования приблизительно нормально распределены. Обратите внимание, что это не означает, что переменные x или y должны иметь нормальное распределение.
2. Что связь между двумя переменными является линейной.
3. То, что разброс точек вокруг линии приблизительно постоянен – мы бы не хотели, чтобы изменчивость зависимой переменной росла по мере увеличения независимой переменной. Если это так, попробуйте логарифмировать обе переменные x и y.

Обратите внимание, что критерий значимости для наклона дает точно такое же значение P, что и критерий значимости для коэффициента корреляции. Хотя эти два теста выводятся по-разному, они алгебраически эквивалентны, что интуитивно понятно.

Мы можем получить 95% доверительный интервал для b из

, где tстатистика имеет 13 степеней свободы и равна 2,160.

Таким образом, 95% доверительный интервал равен

l,033 – 2,160 x 0,18055 до l,033 + 2,160 x 0,18055 = 0,643 до 1,422.

Линии регрессии дают нам полезную информацию о данных, из которых они получены. Они показывают, как одна переменная в среднем меняется с другой, и их можно использовать, чтобы выяснить, какой, вероятно, будет одна переменная, когда мы знаем другую — при условии, что мы задаем этот вопрос в рамках диаграммы рассеяния. Проецировать линию с любого конца — экстраполировать — всегда рискованно, потому что соотношение между x и y может измениться или может существовать какая-то точка отсечки.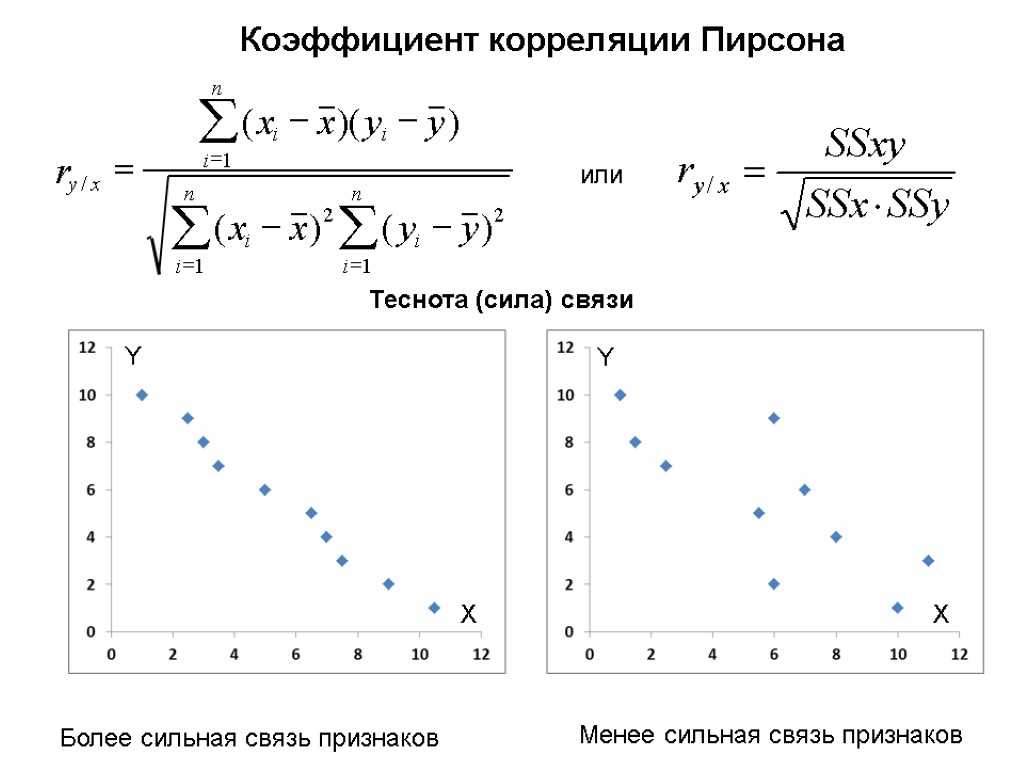 Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия между, скажем, возрастом 5 и 10 лет, но спроецировать ее до возраста 30 лет. явно приведет к ошибке. Компьютерные пакеты часто выдают результат уравнения регрессии без предупреждения о том, что это может быть совершенно бессмысленно. Рассмотрим регресс артериального давления в зависимости от возраста у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что указывает на повышение артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных младенцев мужского пола!

Более продвинутые методы

Возможно использование более одной независимой переменной – в таком случае метод известен как множественная регрессия. (3,4) Это наиболее универсальный из статистических методов, который можно использовать во многих ситуациях. Примеры включают в себя: разрешить использование более одного предиктора, возраста и роста в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимая переменная может быть исходом после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но вероятно, повлияет на результат.

Общие вопросы

Если две переменные коррелированы, связаны ли они причинно-следственной связью?

Распространенной ошибкой является путаница корреляции и причинно-следственной связи. Все, что показывает корреляция, это то, что две переменные связаны. Может быть третья переменная, смешанная переменная, которая связана с ними обоими. Например, ежемесячная смертность от утопления и ежемесячная продажа мороженого имеют положительную корреляцию, но никто не скажет, что эта связь была причинно-следственной!

Как проверить предположения, лежащие в основе линейной регрессии?

Во-первых, всегда смотрите на точечную диаграмму и спрашивайте, является ли она линейной? Получив уравнение регрессии, вычислите остатки.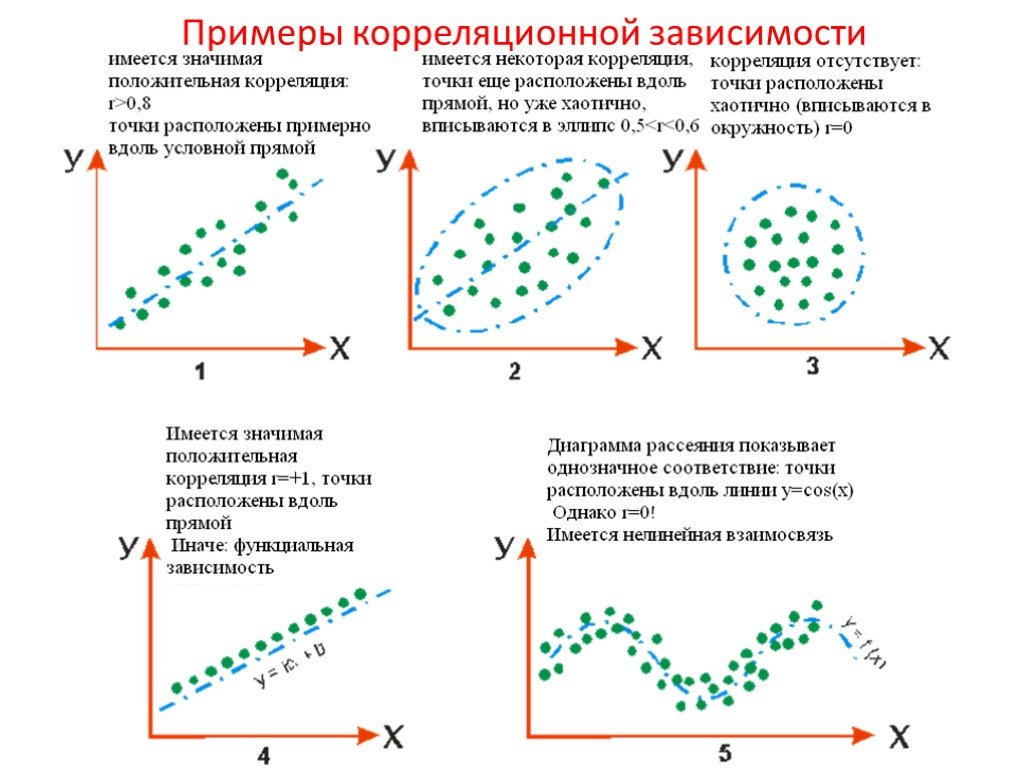 Гистограмма покажет отклонения от нормальности, а график сравнения покажет, увеличиваются ли остатки в размере по мере увеличения.

Ссылки

1. Рассел М.А.Х., Коул П.Ю., Айдл М.С., Адамс Л. Выход угарного газа из сигарет и их связь с выходом никотина и типом фильтра. БМЖ 1975; 3:713.
2. Бланд Дж. М., Альтман Д. Г. Статистические методы оценки соответствия между двумя методами клинических измерений. Ланцет 1986; я: 307-10.
3. Браун Р.А., Суонсон-Бек Дж. Медицинская статистика на персональных компьютерах, 2-е изд. London: BMJ Publishing Group, 1993.
4. Armitage P, Berry G. In: Статистические методы в медицинских исследованиях, 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 312–41.

Упражнения

11.1 Было проведено исследование посещаемости больниц людьми из 16 различных географических районов за фиксированный период времени. Расстояние центра от больницы каждого района измерялось в милях. Результаты были следующими:

(1) 21%, 6,8; (2) 12%, 10,3; (3) 30%, 1,7; (4) 8%, 14,2; (5) 10%, 8,8; (6) 26%, 5,8; (7) 42%, 2,1; (8) 31%, 3,3; (9) 21%, 4,3; (10) 15%, 9,0; (11) 19%, 3,2; (12) 6%, 12,7; (13) 18%, 8,2; (14) 12%, 7,0; (15) 23%, 5,1; (16) 34%, 4.