Корреляционный анализ | Диплом по психологии
Корреляционный анализ — один из главных методов статистической обработки результатов исследований в области психологии, биологии, медицины и т.д. — всех тех наук, которые изучают то, что уже существует в природе, а человек пытается понять, каким же закономерностям оно подчиняется.
Метод корреляционного анализа позволяет обнаружить линейные (прямые и обратные) связи между двумя переменными.
Что такое линейная связь? Говоря доступным языком, это связь между двумя измеряемыми переменными, которую можно обозначить словами «чем больше одно, тем больше другое» (прямая связь) или «чем больше одно, тем меньше другое» (обратная связь).
Простой пример прямой связи — это связь между возрастом и ростом детей. Всем нам хорошо известно, что связь между возрастом и ростом детей такова: чем больше возраст, тем больше (выше) рост. У маленького по возрасту ребенка — маленький рост, у ребенка побольше — рост повыше, а у большого ребенка — совсем большой рост, практически как у взрослого.
Для наглядности находим на просторах интернета соответствующую таблицу, отражающую связь между возрастом и ростом детей:
| Возраст детей (лет) | Средний рост детей (см) | Возраст детей (лет) | Средний рост детей (см) |
|---|---|---|---|
| 0 | 50 | 8 | 125 |
| 1 | 74 | 9 | 129 |
| 2 | 86 | 10 | 135 |
| 3 | 93 | 11 | 140 |
| 4 | 100 | 12 | 145 |
| 5 | 106 | 13 | 150 |
| 6 | 114 | 14 | 157 |
| 7 | 119 | 15 | 160 |
Поскольку таблица нужна только для примера, не будем зацикливаться на вопросе о том, насколько она достоверна. Удовлетворимся тем фактом, что данные в таблице похожи на настоящие.
Для еще большей наглядности построим график: шкала Х отражает возраст ребенка в годах, шкала Y — рост ребенка в сантиметрах.
И в таблице, и на графике хорошо видно, что по мере увеличения одного показателя (возраст детей) увеличиваются и значения второго показателя (рост детей). Об этом же нам говорит и собственный опыт: все мы знаем, что дети с возрастом становятся выше. Чем больше возраст ребенка, тем выше его рост. Это и есть прямая связь между двумя переменными (в данном случае — возрастом и ростом).
Какие еще простые примеры прямой связи можно привести из жизни? Чем больше книг читает человек, тем более начитанным он становится. Чем более высокооплачиваемой является работа, тем больше желающих на нее устроиться. Чем активнее мы используем свои холодильники, тем шире наши лица. Чем дальше в лес, тем больше дров. Ну и так далее. Увеличивается одно — увеличивается другое.
Бывает и наоборот: увеличивается одно — уменьшается другое. Чем чаще ребенка ругают, тем ниже его самооценка. Чем в большей мере наше внимание сконцентрировано на чем-то одном, тем меньше мы замечаем другое.
«Чем меньше женщину мы любим, тем легче нравимся мы ей». Тише едешь — дальше будешь. Это обратная связь между двумя переменными.
Прямая связь и обратная связь — это две разновидности линейной связи между переменными. Именно такие связи выявляет корреляционный анализ.
На практике далеко не всегда ответ настолько очевиден, как в случае связи между возрастом и ростом детей. Очень часто встречаются случаи, когда невозможно навскидку с уверенностью сказать, существует линейная связь между двумя переменными или нет. Поэтому ученые математики придумали способ достоверно определять ее наличие или отсутствие — корреляционный анализ. А мы этим способом пользуемся в своих исследованиях.
Нам не нужно помнить формулы наизусть и уметь их выводить — это задача математиков. Наша задача — правильное применение корреляционного анализа в своих исследованиях, правильный расчет коэффициентов корреляции в компьютерных программах и верная интерпретация результатов корреляционного анализа.
Понятие непараметрических корреляций и их применение в психологии *
Современная психология строится не только на классических принципах и теориях. В настоящее время в целях оптимизации научного процесса, обработки данных и правильной постановке диагноза, решения проблем эксперты все чаще используют математические и статистические способы исследований.
Одним из наиболее распространенных статистических методов, применяемых в психологии, является корреляция.
Что это такое?
Корреляция представляет собой некую функцию, которая позволяет установить взаимосвязь отдельных элементов, проследить их зависимость друг от друга, направление «движения».
Функции корреляцииКорреляционный анализ позволяет проверить некую гипотезу посредством расчета специальных коэффициентов «корреляции». Фактически этот метод позволяет грамотно перевести информацию в математический вид и проследить за объектами исследования «статистически».
Корреляционный анализ позволяет проследить динамику «разнополых» величин, несвязных между собой элементов и определить важность и значимость каждого из них, выявить зависимости и тенденции.
Использование корреляции в психологической науке специфично. Здесь важно, чтобы все исследуемые показатели были согласованными и между ними прослеживалась зримая взаимосвязь (например, причина-следствие).
Корреляция фактически демонстрирует, насколько тесная взаимосвязь между изучаемыми элементами.
Особенности корреляции в психологическом исследовании
Корреляционный анализ в психологии призван продемонстрировать зависимость объектов исследования друг от друга, степень их воздействия друг на друга и характер воздействия.
Применение корреляционного анализаКорреляция считается положительной, если с изменением одного параметра в ту же сторону изменяется второй (например, х увеличивается, за ним растет и у).
Корреляция считается отрицательной, если с изменением одного параметра, другой ухудшается (уменьшается).
При проведении корреляционного анализа исследователю необходимо установить определенные границы, которые будут свидетельствовать о той или иной динамике, результате.
Сделать это можно на основе общепризнанных статистических или психологических стандартов, законов, или по аналогии с похожими научными работами.
Перед тем, как приступить к коррелированию данных, необходимо перевести и имеющиеся данные в математический вид. Далее важно определить, какая методика корреляции допустима в данном случае, возможность ее применения. К числу наиболее популярных способов исследования при помощи коррелирования в психологической науке относят корреляция Спирмена, корреляция Кендэла и пр.
Пример использования корреляции в психологической науке
Попробуем рассмотреть возможности коррелирования данных на конкретном примере. Допустим, психолог желает узнать, влияет ли уровень интеллекта на удовлетворенность от семейной жизни. В нашем случае данные для анализа будут случайными.
Для начала определим «дано» нашей задачи: в исследовании примет участие 10 человек. Каждый из них будет в браке около 5 лет. Все участники исследования пройдут тестирование на определение уровня интеллекта, а затем определят степень удовлетворения от семейной жизни по 10 бальной шкале.
В данном случае возможно получение следующих результатов:
Вариант №1.
Пример положительной корреляцииВ этом случае, чем выше степень удовлетворения от брака (ранг), тем выше уровень интеллекта. Здесь прослеживается прямая зависимость между указанными параметрами, а значит корреляция – положительная. Если рассчитать показатель корреляции, то он получится 0,976. Значение близко к 1, что свидетельствует о тесной связи уровня IQ и удовлетворения от семейной жизни.
Вариант №2.
Пример отрицательной корреляцииВ данном случае наблюдается обратная пропорциональность: при росте уровня удовлетворенности от семейной жизни уровень интеллекта уменьшается. Это свидетельствует об отрицательной корреляции ее значение составит -1. Результаты такого анализа можно интерпретировать: чем ниже уровень интеллекта, тем выше уровень удовлетворенности от брака и наоборот.
Вариант №3.
Нет четкой последовательности.
Пример не зависящих друг от друга показателейЕсли в полученных данных невозможно проследить «очевидную взаимосвязь» между элементами, то необходимо рассчитать коэффициент корреляции.
В нашем случае он составит -0,103. Показатель близится к 0, а значит, параметры слабо зависимы. Уровень удовлетворенности от семейной жизни не зависит или почти не зависит от интеллекта человека. Уловить взаимосвязь в данном случае невозможно.
Эксперты образовательного центра Дисхелп готовы помочь в проведении корреляционного анализа в психологическом исследовании. У нас трудятся ведущие педагоги лучших Вузов страны, кандидаты и доктора психологических и иных наук, практикующие специалисты. Мы гарантируем высокое качество работ, конфиденциальность данных и индивидуальный подход каждому клиенту! Оформи заявку можно здесь и сейчас.
Корреляции | Психология | tutor2u
Психологи не одиноки в своем использовании корреляций, фактически многие дисциплины будут использовать этот метод. Корреляция проверяет, связаны ли два набора чисел ; другими словами, соответствуют ли два набора чисел некоторым образом.
В случае психологии анализируемые числа относятся к поведению (или переменным, которые могут повлиять на поведение), но на самом деле можно проверить любые две переменные, дающие количественные данные, чтобы установить, существует ли корреляция.
Каждый из двух наборов чисел представляет ко-переменную . После сбора данных для каждой из сопутствующих переменных они могут быть нанесены на диаграмму рассеяния и/или подвергнуты статистическому анализу для получения коэффициента корреляции .
Диаграммы рассеяния и коэффициенты показывают силу связи между двумя переменными , которая подчеркивает степень соответствия двух переменных.
Связь между двумя переменными всегда дает коэффициент от 1 до -1.
Коэффициенты со знаком минус перед ними подчеркивают отрицательную корреляцию , что означает, что при увеличении одного набора чисел другой набор уменьшается или при уменьшении одного набора увеличивается другой, поэтому тренд данных одной переменной противоположен Другой.
Напротив, положительные коэффициенты указывают на то, что оба набора данных демонстрируют одну и ту же тенденцию, поэтому при увеличении одного набора данных увеличивается и другой набор данных или при уменьшении одного набора те же тенденции наблюдаются во втором наборе данных
Эксперименты против корреляций
Наиболее фундаментальное различие между экспериментами и корреляциями заключается в том, что эксперименты оценивают влияние одной переменной (IV) на другую измеряемую переменную (DV).
Это требует, чтобы данные были дискретными или отдельными, и измерялось влияние этого на что-то еще.
Напротив, корреляции не используют дискретные отдельные условия, вместо этого они оценивают степень взаимосвязи между двумя совместно встречающимися переменными, которые связаны между собой.
Например, если психолог заинтересован в исследовании стресса и болезни, он может вычислить показатели стресса и заболевания для 20 участников и оценить, как эти два набора чисел соотносятся друг с другом, приняв, таким образом, корреляционный метод. Однако это можно было бы превратить в эксперимент, если бы исследователь выделил 10 участников с низкими показателями стресса (например, 10/50 или меньше) и 10 участников с высокими показателями стресса (например, 40/50 или более). Теперь есть два условия: одно для низкого стресса и одно для высокого стресса. Если бы исследователь должен был взять баллы за болезнь для всех 20 участников и сравнить участников с низким уровнем стресса и участников с высоким уровнем стресса, это было бы экспериментальной оценкой влияния стресса на болезнь.
Сильные стороны корреляций
Корреляции очень полезны в качестве метода предварительного исследования , позволяя исследователям идентифицировать связь, которую можно исследовать в дальнейшем посредством более контролируемого исследования.
Может использоваться для исследования тем, которые являются деликатными/в противном случае было бы неэтично, поскольку не требуется преднамеренного манипулирования переменными.
Ограничения корреляций
Корреляции только идентифицируют ссылку; они не определяют, какая переменная вызывает какую. Может присутствовать третья переменная, которая влияет на одну из сопутствующих переменных, которая не рассматривается.
Например. стресс может привести к курению/употреблению алкоголя, что приводит к болезни, поэтому существует косвенная связь между стрессом и болезнью.
10. Корреляция и регрессия. Статистика для начинающих психологов
Перейти к содержимому
Эта глава знаменует собой большой отход от методов логического вывода, которым мы научились до сих пор.
Здесь мы будем рассматривать отношения между двумя числовыми переменными, а не анализировать различия между средними значениями двух или более экспериментальных групп.
используется для проверки направления и силы связи между двумя числовыми переменными. Мы увидим, как диаграммы рассеяния можно использовать для построения графика переменной X относительно переменной Y для обнаружения линейных отношений. Наклон линейной зависимости может быть положительным или отрицательным, что выявляет систематические закономерности в том, как две переменные соотносятся друг с другом. Мы также рассмотрим теорию корреляционного анализа, включая некоторые предостережения относительно интерпретации результатов 
Позже в этой главе мы построим , что позволит нам предсказывать будущее по прошлому.
Точно так же, как столбчатая диаграмма полезна для визуального изучения различий между средними значениями, диаграмма рассеяния позволяет нам визуализировать закономерность, представляющую взаимосвязь между двумя числовыми переменными, X и Y.
Если линия тренда, которая лучше всего отображает линейный паттерн на точечной диаграмме, имеет восходящий наклон, мы считаем это положительной направленностью.
Чтобы выяснить, существует ли положительная корреляция, вы можете спросить себя: «Могут ли те, у кого высокие баллы по одной переменной, получить высокие баллы по другой?» Здесь мы видим пример: какова связь между кошачьим дружелюбием и количеством полученных царапин? Как видите, когда уровень дружелюбия к кошкам высок, получаемые объятия также высоки. Налицо четкая положительная линия тренда. В этом есть смысл — люди могут с большей вероятностью предложить объятия кошке, которая их просит.
Нисходящий наклон указывает на отрицательную направленность. Чтобы выяснить, существует ли отрицательная корреляция, вы можете спросить себя: «Могут ли те, у кого высокие баллы по одной переменной, иметь низкие баллы по другой?» Вот пример: какая связь между кошачьей отчужденностью и количеством полученных царапин? Налицо четкая отрицательная линия тренда. Это имеет логичный смысл, потому что люди с меньшей вероятностью будут обниматься с кошкой, которая держится особняком.
Когда мы смотрим на точечную диаграмму, мы хотим задать себе два вопроса: один о очевидной силе связи между переменными, а другой — о направлении связи. Давайте взглянем на несколько примеров.
На графике A), если мы спросим: «Связаны ли переменные X и Y сильно или слабо?» Мы бы сказали, сильно связанные. Это связано с тем, что точки на диаграмме рассеяния находятся на идеальной линии. Расстояние между точками и линией тренда отсутствует. Это совершенная корреляция .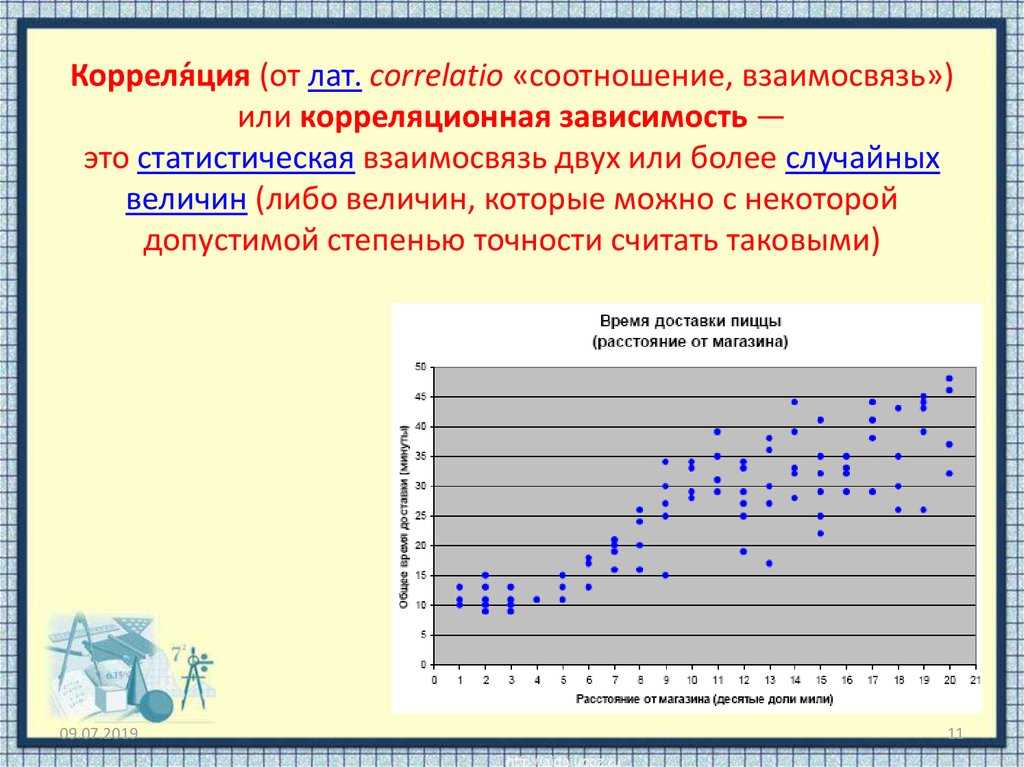
Если мы спросим: «Наклон линии тренда положительный или отрицательный?» Мы бы сказали, что она имеет отрицательный наклон. По мере того, как баллы по переменной X увеличиваются, баллы по переменной Y делают обратное — они уменьшаются. Мы могли бы ожидать такой зависимости, если бы построили график зависимости скорости от времени. Чем быстрее что-то делается, тем меньше времени требуется. В следующем примере, график B), если мы спросим: «Связаны ли переменные X и Y сильно или слабо?» Мы бы сказали слабо связанные. Четкого линейного тренда, который можно было бы различить визуально, нет — он просто выглядит как случайный разброс точек. Без линии тренда вопрос о направленности не имеет значения. это корреляция близка к нулю, поэтому она не является ни положительной, ни отрицательной как направленная связь. Если мы посмотрим на пример C), сила не такая совершенная, как в первом примере, но точки не будут сильно удалены от линии тренда, проходящей через них, так что это будет довольно сильная корреляция .
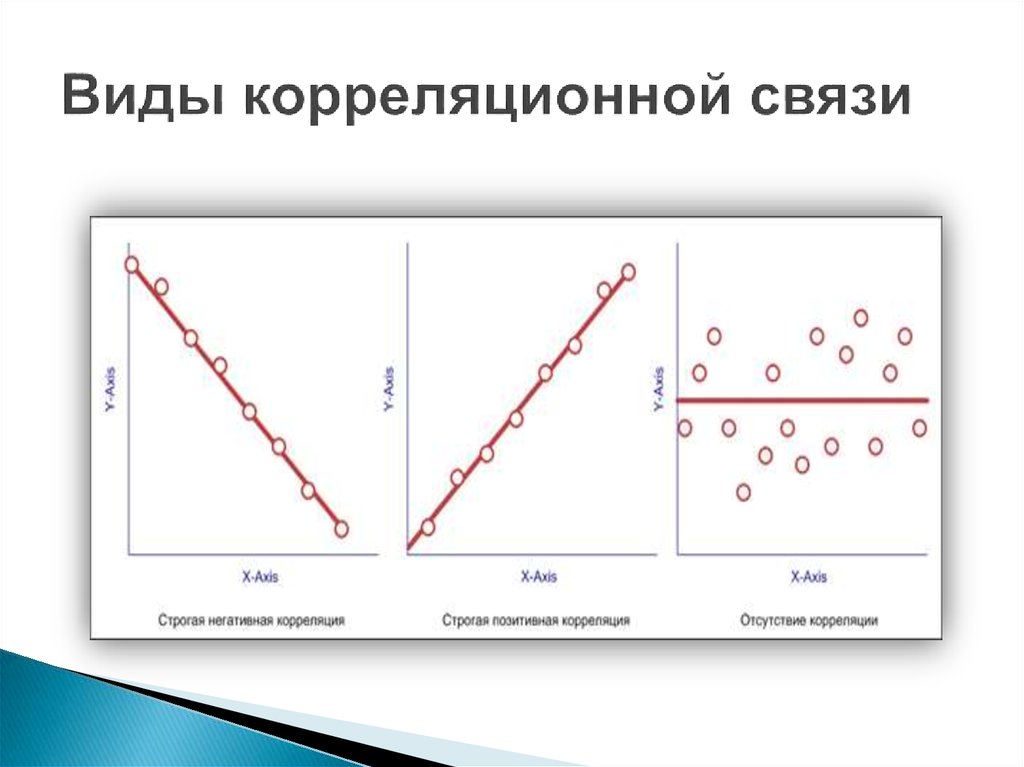По мере того как баллы по переменной X растут, растут и баллы по переменной Y, что делает эту корреляцию положительной
Корреляционный анализ пытается ответить на вопрос «насколько тесно связаны две переменные». Это очень полезный аналитический подход, когда у нас есть две числовые переменные, и мы хотим проанализировать закономерности их взаимного изменения. Однако корреляционный анализ имеет ограничения, о которых крайне важно знать.
Во-первых, корреляционный метод, который мы рассмотрим в этом курсе, способен обнаруживать только линейные отношения. Паттерны с изгибом не будут захвачены 9Мы будем использовать формулу корреляции 0003 .
Во-вторых, корреляция делает , а не равной причинно-следственной связи.
Например, если мы измерим потребление мороженого, а также смертность от утопления в выборку дней в течение года, мы можем определить, что между двумя переменными существует сильная положительная связь. Потребление мороженого и смерть от утопления, по-видимому, тесно связаны между собой. Но вызывает ли потребление мороженого смерть от утопления? Это кажется немного надуманным. Может ли быть другое объяснение закономерности? Существует ли третья переменная, которая могла бы фактически объяснить тенденции каждой из двух измеряемых здесь переменных? Что может заставить людей потреблять больше мороженого, а также подвергать себя большему риску утонуть? Может теплая погода? Если бы мы сопоставили умеренность с мороженым и смертью от утопления, увидели бы мы положительную корреляцию между каждым из них? Скорее всего.
Так как же узнать, существует ли истинная причинно-следственная связь между двумя переменными? Чтобы сделать причинно-следственные выводы, мы должны использовать экспериментальный план. Две основные особенности дизайна экспериментальных исследований устраняют логические ошибки, связанные с корреляции . Во-первых, в эксперименте используется случайное назначение участников условиям, потому что это контролирует посторонние переменные, такие как третья переменная температуры в этом примере. И, во-вторых, эксперимент манипулирует независимой переменной, чтобы установить причину, а затем измерить последствия.
Настоящий эксперимент требует следующих элементов для контроля посторонних переменных и установления причинно-следственной направленности:
- случайное назначение участников условиям (или рандомизация порядка условий в планах повторных измерений)
- манипулирование независимой переменной
В нашем исследовании мороженого и утопления, как мы могли превратить его в эксперимент, чтобы сделать выводы о причинно-следственных связях? Сначала нам нужно было бы случайным образом распределить наших участников в экспериментальную и контрольную группы. Не должно быть систематической предвзятости в отношении того, кому дают мороженое, а кому нет. Во-вторых, нам пришлось бы манипулировать независимой переменной — нам нужно было бы, чтобы участники экспериментальной группы ели мороженое. Затем мы помещали всех участников в воду одинаковой температуры и смотрели, сколько из них утонет. Мы рассчитали бы среднее количество случаев утопления в группе, поедающей мороженое, по сравнению с контрольной группой, и провели t-тест или дисперсионный анализ, чтобы выяснить, значительно ли они отличаются друг от друга.
Конечно, вы можете подумать: «А этично ли это?» По крайней мере, я надеюсь, что вы так думаете. Конечно нет! Было бы бессмысленно позволять людям тонуть только для того, чтобы ответить на этот эмпирический вопрос. Собственно, именно поэтому существует корреляция .
«Herp Derp :D» от O hai :3 лицензируется в соответствии с CC BY 2.0Часто практические или этические ограничения делают эксперимент непомерно трудным или невозможным. Если мы ограничимся корреляционными методов в конкретном исследовании, мы просто не можем делать выводы о причинно-следственных связях.
Итак, главная мысль этого урока — не уподобляться этому парню.
Итак, как нам вычислить корреляцию ? Что ж, аналогично ANOVA, мы можем рассматривать этот процесс концептуально как разделение дисперсии. Но на этот раз хорошей дисперсией считается ковариация . Это систематическая дисперсия, которая является общей для обеих переменных X и Y.
Как только мы найдем r , другой статистический показатель, предоставляющий полезную информацию, будет . р 2 — доля изменчивости одной переменной, которую можно объяснить связью с другой переменной. Обратите внимание на этот факт, потому что доля изменчивости, объясняемая корреляцией , является очень полезным показателем.
Теперь мы можем рассмотреть, какую форму примет проверка гипотезы в контексте корреляционного плана исследования. Такая проверка гипотез задает вопрос: «Насколько маловероятно, что корреляция 9Коэффициент 0004 на самом деле равен нулю?»
На шаге 1, чтобы сохранить гипотезу в форме, аналогичной той, что мы делали раньше, мы можем идентифицировать популяции определенным образом.
Население 1 будет состоять из «людей, подобных тем, что включены в выборку», а население 2 будет состоять из «людей, у которых нет связи между переменными». Таким образом, исследовательская гипотеза может быть сформулирована следующим образом: «Корреляция для популяции 1 [больше/меньше/отличается] от корреляции для популяции 2. Нулевая гипотеза может быть такой: «Корреляция для популяции 1 такая же, как и для корреляция для населения 2».
На шаге 2 нам нужно найти характеристики распределения сравнения, и в этом случае нам нужен коэффициент корреляции r , который может принимать значения от -1 до 1. Значение r , равное 0, указывает на отсутствие корреляция между двумя измеряемыми переменными. r из 1 является идеальной положительной корреляцией , а r из -1 является идеальной отрицательной корреляцией. Большинство корреляций в реальной жизни ближе к 0, чем к 1 или -1.
В этой формуле коэффициента корреляции используются Z-баллы, что является отличным способом просмотреть эти стандартизированные баллы, рассмотренные в предыдущей главе. Напомним, что
, где
Для каждой переменной X и Y мы должны вычислить среднее значение и стандартное отклонение переменной, чтобы каждый балл можно было преобразовать в Z-баллы. Только после этого их можно перемножить и затем просуммировать в формуле r .
Как только мы вычислим значение r для корреляции , мы можем проверить статистическую значимость этого значения на основе того, насколько оно экстремально в распределении t. r , равный 0, помещается в центр распределения t в качестве среднего распределения сравнения, а положительные и отрицательные единицы помещаются в любой конец распределения.
Чем дальше мы попадаем в соответствующий хвост, тем выше наши шансы отвергнуть нулевую гипотезу о нулевой корреляции.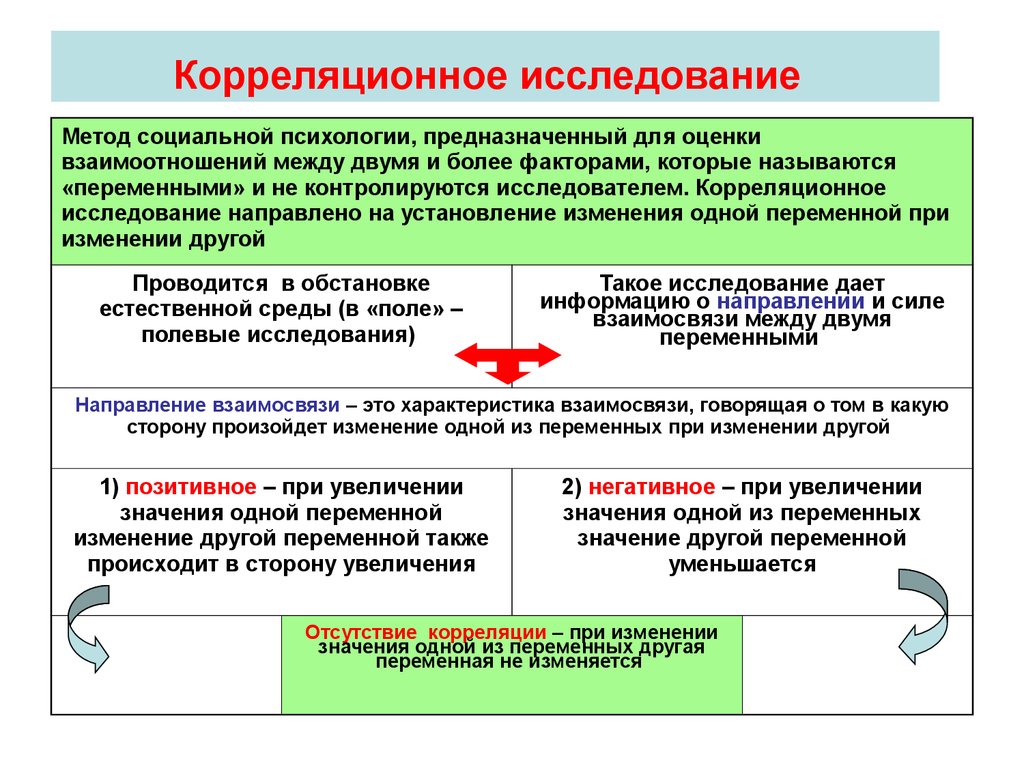
Плохая новость в том, что мы вернулись к t-критерию, а это значит, что нам нужно подумать о направленности. Хорошая новость в том, что это отличная возможность освежить в памяти то, как работает t-тест.
На шаге 3 мы находим пороговую оценку, используя таблицы t. Для корреляции степеней свободы будет N -2, где N — количество людей в выборке. Это так, потому что у нас есть две измеряемые (числовые) переменные, каждая из которых имеет N -1 баллов, которые могут свободно изменяться.
На шаге 4 t-критерий рассчитывается как r , деленное на S r , где S r количественно определяет необъяснимую изменчивость.
Шаг 5 — это решение: мы отклоняем нулевую гипотезу, если результат t-критерия попадает в заштрихованный хвост за пределы отсечки.
Мы могли бы выразить результаты проверки гипотезы о взаимосвязи между доходом и оценками следующим образом:
«Мы обнаружили значительную положительную корреляцию между доходом семьи и средним уровнем успеваемости учащихся (r = 0,65, t 11 = 2,97, p < 0,05)».
Обратите внимание, что наша интерпретация , а не мы обнаружили, что более высокий доход семьи приводит к более высокому среднему баллу. Почему бы и нет? Что ж, как мы уже говорили ранее, причинно-следственные выводы требуют экспериментального дизайна. Чтобы сделать такой вывод о взаимосвязи между семейным доходом и средними оценками учащихся, нам нужно было бы случайным образом распределить учащихся по уровням семейного дохода, богатым или бедным, а затем измерить влияние этих манипуляций на их оценки. Как и в нашем примере с утоплением, это кажется не только сложным с точки зрения логистики, но и довольно неэтичным. Итак, мы ограничены корреляция здесь по какой-то причине, и поэтому нам просто нужно охарактеризовать наши результаты как взаимосвязь или закономерность, а не формулировку причины и следствия.
Когда мы поместили последнюю ветвь в наше дерево решений, теперь у нас есть поток решений для ситуации отсутствия независимых переменных.
Если обе переменные являются числовыми, вы должны использовать корреляцию, чтобы проверить их взаимосвязь.
В следующей части главы мы рассмотрим статистический метод регрессии 9.0004 . Регрессия позволяет нам расширить результаты корреляции , чтобы предсказать будущее из прошлого.
После того, как мы рассчитали корреляцию , регрессия позволяет нам предсказать, как человек будет работать с одной переменной, основываясь на его результатах по другой переменной. В примере корреляции между доходом и оценками регрессия позволила бы нам увидеть, какой уровень оценки будет достигнут человеком с уровнем семейного дохода, который фактически не был собран в нашем наборе данных. Мы также можем определить уровень дохода на основе заданного уровня обучения.
Линия регрессии — это линия на нашем графике рассеяния, которую можно описать уравнением. Уравнение состоит из двух компонентов: наклона и точки пересечения.
Наклон показывает, на сколько единиц вверх (или вниз) идет линия для каждой единицы. Перехват говорит, где линия попадает на ось Y.
Линия регрессии — это линия, которая «наиболее соответствует» собранным нами точкам данных. Математически это линия, которая минимизирует квадраты отклонений (то есть ошибки) отдельных точек от линии.
Чтобы найти уравнение для линии регрессии , вы можете вычислить наклон b , а затем разделить a , используя показанные формулы.
Для каждого человека найти отклонение показателя Х от среднего.*
Для каждого человека найти отклонение показателя Y от среднего.*
Для каждого человека умножьте отклонение X на соответствующее отклонение Y
Сложите продукты из шага 3 для всех лиц.
Разделите эту сумму на SS x .*
*Эти вычисления уже должны быть выполнены для корреляции.
После вычисления a и b мы можем подставить эти числа в линейное уравнение регрессии .
Здесь я покажу вам уравнение линии регрессии для примера зависимости дохода нашей семьи от оценок.
b равно 0,11, что означает, что на каждую единицу семейного дохода линия поднимается на 0,11 единицы средней оценки. a равно 77,96, что означает, что линия пересекает ось Y на высоте 77,96.
Уравнение линии позволяет нам построить точную линию регрессии на графике рассеяния. Чтобы построить линию регрессии, выберите два значения X, которые находятся на нижнем и верхнем концах шкалы. Подставьте их в линейное уравнение, чтобы найти соответствующие значения Y на линии.
Используя линию регрессии, вы можете предсказать значение X по значениям Y и значения Y по значениям X. Это означает, что даже если в вашем наборе данных не было никого с семейным доходом 105, вы можете вычислить, какой была бы средняя оценка учащегося, если бы у него был такой семейный доход.
Точно так же, если бы в вашем наборе данных не было никого со средней оценкой 75, вы можете выяснить, каким был бы доход их семьи, если бы у них была такая оценка. Обратите внимание, что это всего лишь прогнозы. Они несовершенны и не учитывают другие факторы или индивидуальную изменчивость.
Здесь мы попробуем предсказать среднюю оценку (Y) для учащегося, чей семейный доход равен 200. Для этого мы подставим 200 вместо X в уравнение линии регрессии (как показано здесь).
Результат — оценка 100,55. Конечно, получить средний балл выше 100% невозможно (по крайней мере, во многих учебных заведениях). В этом случае наш прогноз показывает «эффект потолка». Это означает, что существует максимальная средняя оценка, которую мы достигнем, прежде чем достигнем максимального семейного дохода. Следовательно, линейное уравнение регрессии становится бесполезным, если доход семьи составляет около 190.
Теперь мы можем попробовать спрогнозировать доход семьи (Y) для учащегося со средним баллом 60 (X).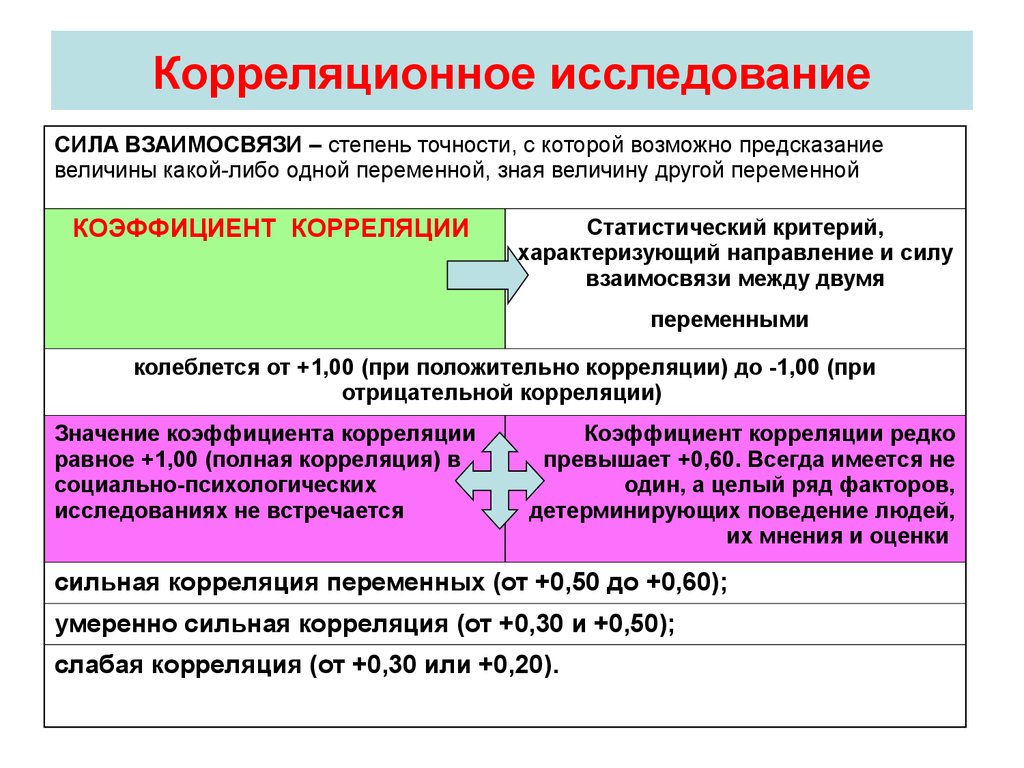
Чтобы сделать это, вы должны подставить 60 вместо Y в уравнение, а затем найти X.
Обратите внимание: чтобы изменить уравнение для решения X, сначала нужно переместить точку пересечения (a) на:
Затем нужно разделить на наклон:
Теперь вы готовы решить для X: -159. Результатом нахождения X для Y из 60 является отрицательный доход! Это, конечно, невозможно (или очень маловероятно). Здесь мы можем увидеть эффект пола.
Это означает, что существует минимальный семейный доход, которого мы достигнем, прежде чем достигнем минимального класса. Таким образом, линия регрессии становится бесполезной ниже средней оценки 77,96 (пересечение Y). Эффекты пола и потолка являются общими проблемами для регрессии , и вы должны следить за этими проблемами при использовании этого метода. Мы видим, что 9Линия регрессии 0003 для этого конкретного набора данных полезна для прогнозирования средней оценки 80-100 и диапазона уровня дохода 0-190.
Разумеется, предсказания не идеальны. Регрессия позволяет прогнозировать одну переменную по другой переменной. Как мы видим на наших диаграммах рассеяния, не каждая реальная точка данных находится точно на линии регрессии. Фактическая точка данных может отличаться. Почему это? Потому что, если только это не идеальная корреляция , некоторая изменчивость реальных данных не учитывается уравнением регрессии. Мы можем оценить, насколько точны наши предсказания, взглянув на r в квадрате . r 2 — доля дисперсии одной переменной, объясняемая ее связью с другой переменной. Остальное – сумма, которая не учтена.
Точно так же, как мы можем включить несколько факторов в ANOVA, мы также можем включить несколько прогностических переменных в регрессию . Мы не будем пытаться сделать это в этом курсе, но если вы пройдете более продвинутый курс статистики, вы увидите, что чем больше переменных вы включите, каждая из которых объясняет часть изменчивости критериальной переменной, тем более точной станет ваша регрессионная модель.
Здесь мы используем только одну прогностическую переменную, и наше r 2 , вероятно, не соответствует 100% объясненной дисперсии. Таким образом, в этом случае мы можем ожидать, что наша регрессия будет лишь умеренно точной.
В этой главе вы познакомились со статистическими методами корреляции и регрессии . Мы увидели, как мы можем обнаружить и описать силу и направление взаимосвязи между двумя числовыми переменными, а также запустить проверку гипотезы, чтобы выяснить, значительно ли корреляция отличается от нуля. Наконец, мы увидели, что регрессия может генерировать линейную модель, позволяющую прогнозировать одну переменную по другой. Ключевое напоминание: корреляция делает , а не равной причинно-следственной связи. Эти методы подходят для планов исследования, которые не соответствуют требованиям дизайна эксперимента, и поэтому наши выводы относительно статистических данных должны избегать причинно-следственных формулировок.
