Моделирование – процесс построения моделей для исследования и изучения объектов, процессов, явлений.
| Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: АрхеологияБиология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человекаПриготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления | Задание № 1. Программа-набор команд, выполняющихся процессором автоматически в определенной последовательности. Суть программного принципа работы компьютера является управление аппаратными средствами. Задание № 2. Модель -некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Моделирование – процесс построения моделей для исследования и изучения объектов, процессов, явлений. Примеры моделей процессов: модель развития вселенной, экономических процессов, экологических процессов. Задание № 3.
Модели | Кукла | Глобус | игрушка | письменный | ||||||
| фотография | Географический атлас | сувенир | журнальный | ||||||||
| манекен | карта | Опытный образец | рабочий | ||||||||
| робот | Макет местности | тренажёр | кухонный |
Задание № 4.
Математическая модель
Астрономическая модель
Физическая модель
Задание № 5
| Жизненная ситуация | Моделируемый объект | Цель моделирования | Моделируемые характеристики | Модель |
| Чтобы объяснить сестренке движение Земли вокруг своей оси, девочка принесла глобус | Земной шар | Объяснение Изучение | Форма земли и ее движение вокруг своей оси | Глобус |
| Мальчик рисует своему приятелю схему дороги к его дому | Дорога | Правильный путь дороги к дому | Длина дороги, преграды, перекрёстки | Карта |
| Объясняя движение Земли вокруг солнца, девочка носит глобус по комнате вокруг настольной лампы | Земной шар | Объяснение | движение Земли вокруг солнца | Глобус |
| На конкурс по благоустройству центральной улицы города архитекторы сдают свои рисунки | Центральная улица | Моделирование улицы | Объяснение построения дороги | рисунок |
| Для подготовки организма к перегрузкам в полете пилоты тренируются на центрифуге | Подготовка к полёту в космос | Понять готов ли человек для полёта в космос | повышения устойчивости организма к факторам космического полета | Центрифуга |
| Готовя к игре футбольную команду, тренер на макете футбольного поля передвигает фигурки, обозначающие игроков | Футбольное поле | Объяснение тактики | Объяснение тактики игрокам | макет |
Задание № 6.
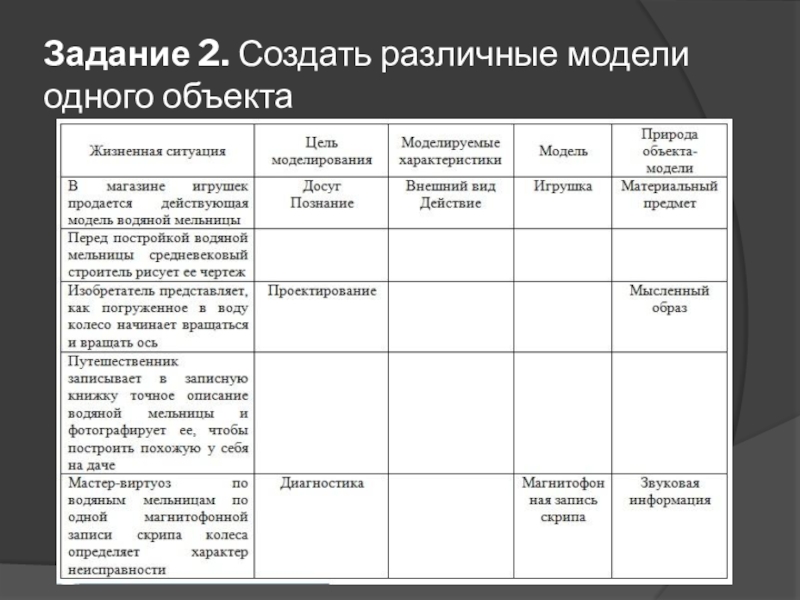
| Жизненная ситуация | Цель моделирования | Моделируемые характеристики | Модель | Природа объекта-модели |
| В магазине игрушек продается действующая модель водяной мельницы | Досуг Познание | Внешний вид Действие | Игрушка | Материальный предмет |
| Перед постройкой водяной мельницы средневековый строитель рисует ее чертеж | Изучение проектирования | Действие и особенности | Водяная мельница | Изображение |
| Изобретатель представляет, как погруженное в воду колесо начинает вращаться и вращать ось | Проектирование | Знания физики | Опыт | Мысленный образ |
| Путешественник записывает в записную книжку точное описание водяной мельницы и фотографирует ее, чтобы построить похожую у себя на даче | Копирование | Описание внешнего вида мельницы | Фотография | Информационная модель |
| Мастер-виртуоз по водяным мельницам по одной магнитофонной записи скрипа колеса определяет характер неисправности | Диагностика | Неисправность | Магнитофонная запись скрипа | Звуковая информация |
Задание № 7.
| Фамилия | Имя | Рост | Любимый учебный предмет | Хобби | Фоторобот | |
| Антоневич | Анастасия | рисование | ||||
| Буйнова | Алина | |||||
| Ершов | Николай | Пение, танцы, разговаривать, рисование | ||||
| Смирнова | Юлия | |||||
| Мордвинов | Михаил | музыка |
Задание № 8.
На нижнем уровне находятся программы базовой системы ввода-вывода (BIOS). В момент включения компьютера эти программы выполняют проверку оборудования и обеспечивают простейшее взаимодействие с клавиатурой и монитором — клавиатура способна реагировать на нажатие некоторых клавиш, а на мониторе отображается информация о ходе запуска компьютера. Взаимодействие с человеком у программ этого уровня крайне ограниченно и возможно только в первые секунды после запуска компьютера.
7. Функции программного обеспечения для работы с файлами:
— обеспечения всех типовых действий с файлами;
— гарантирование корректности данных размещенных в файле;
— оптимизация временных характеристик работы с файлами;
— поддержка различных внешних носителей;
— исключение или минимизация потерь данных;
—
— обеспечение коллективного использования файлов в многопользовательской системе.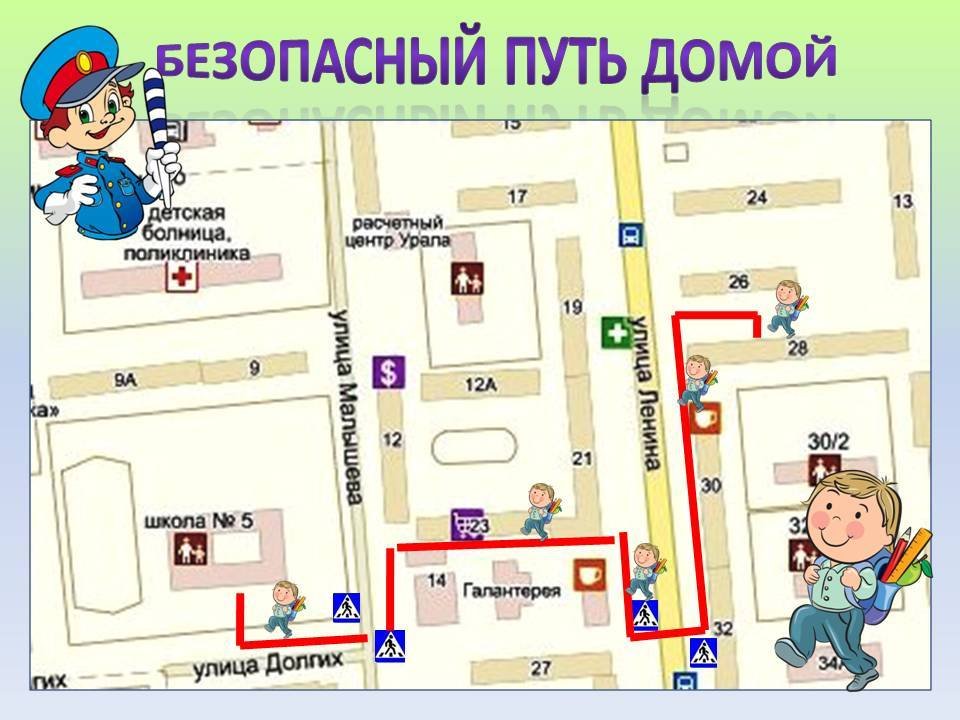
Задание № 9. Вывод о проделанной практической работе: В ходе практической работы я узнала что такое модель, моделирование, принцип работы компьютера и применение компьютерных моделей в различных ситуациях.
Задание № 1. Программа-набор команд, выполняющихся процессором автоматически в определенной последовательности. Суть программного принципа работы компьютера является управление аппаратными средствами.
Задание № 2. Модель -некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.
Моделирование – процесс построения моделей для исследования и изучения объектов, процессов, явлений.
Примеры моделей процессов: модель развития вселенной, экономических процессов, экологических процессов.
Задание № 3.
| обьект | Человек | Земля | Автомобиль | Стол |
Модели
Задание № 4.
Математическая модель
Астрономическая модель
Физическая модель
Задание № 5
| Жизненная ситуация | Моделируемый объект | Цель моделирования | Моделируемые характеристики | Модель |
| Чтобы объяснить сестренке движение Земли вокруг своей оси, девочка принесла глобус | Земной шар | Объяснение Изучение | Форма земли и ее движение вокруг своей оси | Глобус |
| Мальчик рисует своему приятелю схему дороги к его дому | Дорога | Правильный путь дороги к дому | Длина дороги, преграды, перекрёстки | Карта |
| Объясняя движение Земли вокруг солнца, девочка носит глобус по комнате вокруг настольной лампы | Земной шар | Объяснение | движение Земли вокруг солнца | Глобус |
| На конкурс по благоустройству центральной улицы города архитекторы сдают свои рисунки | Центральная улица | Моделирование улицы | Объяснение построения дороги | рисунок |
| Для подготовки организма к перегрузкам в полете пилоты тренируются на центрифуге | Подготовка к полёту в космос | Понять готов ли человек для полёта в космос | повышения устойчивости организма к факторам космического полета | Центрифуга |
| Готовя к игре футбольную команду, тренер на макете футбольного поля передвигает фигурки, обозначающие игроков | Футбольное поле | Объяснение тактики | Объяснение тактики игрокам | макет |
Задание № 6.
| Жизненная ситуация | Цель моделирования | Моделируемые характеристики | Модель | Природа объекта-модели |
| В магазине игрушек продается действующая модель водяной мельницы | Досуг Познание | Внешний вид Действие | Игрушка | Материальный предмет |
| Перед постройкой водяной мельницы средневековый строитель рисует ее чертеж | Изучение проектирования | Действие и особенности | Водяная мельница | Изображение |
| Изобретатель представляет, как погруженное в воду колесо начинает вращаться и вращать ось | Проектирование | Знания физики | Опыт | Мысленный образ |
| Путешественник записывает в записную книжку точное описание водяной мельницы и фотографирует ее, чтобы построить похожую у себя на даче | Копирование | Описание внешнего вида мельницы | Фотография | Информационная модель |
| Мастер-виртуоз по водяным мельницам по одной магнитофонной записи скрипа колеса определяет характер неисправности | Диагностика | Неисправность | Магнитофонная запись скрипа | Звуковая информация |
Задание № 7.
| Фамилия | Имя | Рост | Вес | Любимый учебный предмет | Хобби | Фоторобот |
| Антоневич | Анастасия | рисование | ||||
| Буйнова | Алина | |||||
| Ершов | Николай | Пение, танцы, разговаривать, рисование | ||||
| Смирнова | Юлия | |||||
| Мордвинов | Михаил | музыка |
Задание № 8.
Читайте также:
Организация работы процедурного кабинетаСтатус республик в составе РФ
Понятие финансов, их функции и особенности
Сущность демографической политии
Последнее изменение этой страницы: 2020-12-19; просмотров: 6488; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.157.157 (0.013 с.)
Информатика: 9 КЛАСС
9 КЛАСС
9 КЛАСС
Рабочую тетрадь 9 класса можно скачать здесь РТ9
Урок №4, 5 (12.10.16/28.09.16 и 05.10.16) Графические информационные модели. Табличные информационные модели.
Д/З: п.1.3, — читать, отвечать на вопросы, выполнить № 6 с.
 26, №7 с.36 учебник, РТ № 43, 48
26, №7 с.36 учебник, РТ № 43, 48Презентация Графические информационные модели
Презентация Табличные информационные модели
интерактивный задачник, раздел «Графические модели» (119308)
http://sc.edu.ru/catalog/res/1b72afbc-9200-485a-a051-68a64aed7bdc/?interface=catalog
инструмент разработки и анализа родословных «Живая Родословная» (145555)
http://sc.edu.ru/catalog/res/f6c85ff7-9567-4b28-b441-b270d163899c/?interface=catalog
демонстрация «Примеры табличных моделей» (119417)
http://sc.edu.ru/catalog/res/d68b2443-11a2-4f03-b3e4-16c46b195125/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog
кроссворд по теме: «Информационное моделирование» (119349)
http://sc.edu.ru/catalog/res/56c53f18-9ddc-4727-a879-3a8537348bb3/?interface=catalog
тренировочный тест к главе 2 «Информационное моделирование» (119338)
http://sc.edu.ru/catalog/res/11e166df-bce0-47e6-8279-8729c7b2e67c/?interface=catalog Урок №3 (21.09.16) Знаковые модели.
 Словесные и математические модели. Компьютерные математические модели.
Словесные и математические модели. Компьютерные математические модели.Д/З: п.1.2, — читать, отвечать на вопросы, выполнить № 5, 6. РТ № 28
Дополнительное задание: подготовить презентацию по одной из следующих тем: «Разнообразие моделей, изучаемых в школе», «примеры использования компьютерных моделей»
Презентация к уроку
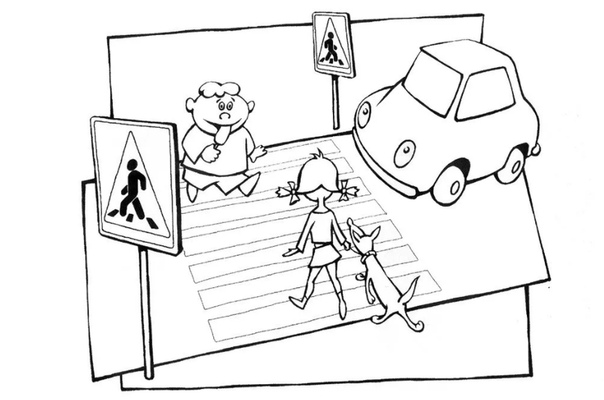
Определите для следующих ситуаций
Ситуация | Моделируемый объект | Цель моделирования | Форму модели | Моделируемые характеристики | Модель |
Чтобы объяснить сестренке движение Земли вокруг своей оси, девочка принесла глобус | Земной шар | Объяснение, изучение | натурная | Форма Земли и её движение вокруг оси | Глобус |
Мальчик рисует своему приятелю схему дороги к его дому | |||||
Семья готовится к перестановке мебели. | |||||
На конкурс по благоустройству центральной улицы города архитекторы сдают свои рисунки | |||||
Для подготовки организма к перегрузкам в полёте, пилоты тренируются на центрифуге | |||||
Для съемок фильма о средневековье в павильоне создают макет улицы старого города | |||||
В витрине магазина стоят манекены в модной одежде |
 09.16) Моделирование как метод познания. Виды
информационных моделей (словесное описание, таблица, график, диаграмма,
формула, чертёж, граф, дерево, список и др.) и их назначение.
09.16) Моделирование как метод познания. Виды
информационных моделей (словесное описание, таблица, график, диаграмма,
формула, чертёж, граф, дерево, список и др.) и их назначение. Д/З: п.1.1, — читать, отвечать на вопросы, выучить конспект, выполнить по учебнику № 5, 6; РТ №23
Презентация к уроку
Урок №1 (07.09.16) Цели изучения курса информатики. Техника безопасности и организация рабочего места. Д/З: учебник 9 класса: введение (стр.3-4), Рабочая тетрадь № 1 — 19.
Главная страница
Подписаться на: Сообщения (Atom)
2.2 Скорость и скорость — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Вычислять среднюю скорость объекта
- Соотнесите перемещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:- (B) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (Б) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Основные термины раздела
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителей
Поддержка учителей
В этом разделе учащиеся будут применять полученные знания о расстоянии и перемещении к понятиям скорости и скорости.
[BL][OL] Прежде чем учащиеся прочитают этот раздел, попросите их привести примеры того, как они слышали употребление слова «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто взаимозаменяемы в повседневной жизни, но их научные определения различны. Скажите студентам, что они узнают об этих различиях, когда будут читать этот раздел.
[AL] Объясните учащимся, что скорость, как и перемещение, является векторной величиной. Попросите их предположить, чем скорость отличается от скорости. После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Что такое пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, называется его скоростью. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, поскольку имеет величину, но не направление. Поскольку скорость — это скорость, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение во времени ΔtΔt движения как разницу между временем окончания и временем начала
Δt=tf−t0.Δt=tf−t0.
Единицей времени в СИ является секунда (с), а единицей скорости в СИ является метр в секунду (м/с), но иногда километры в час (км/ч), мили в час (миль/ч) или другие единицы скорости.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость v avg — это пройденное расстояние, деленное на время, в течение которого происходит движение.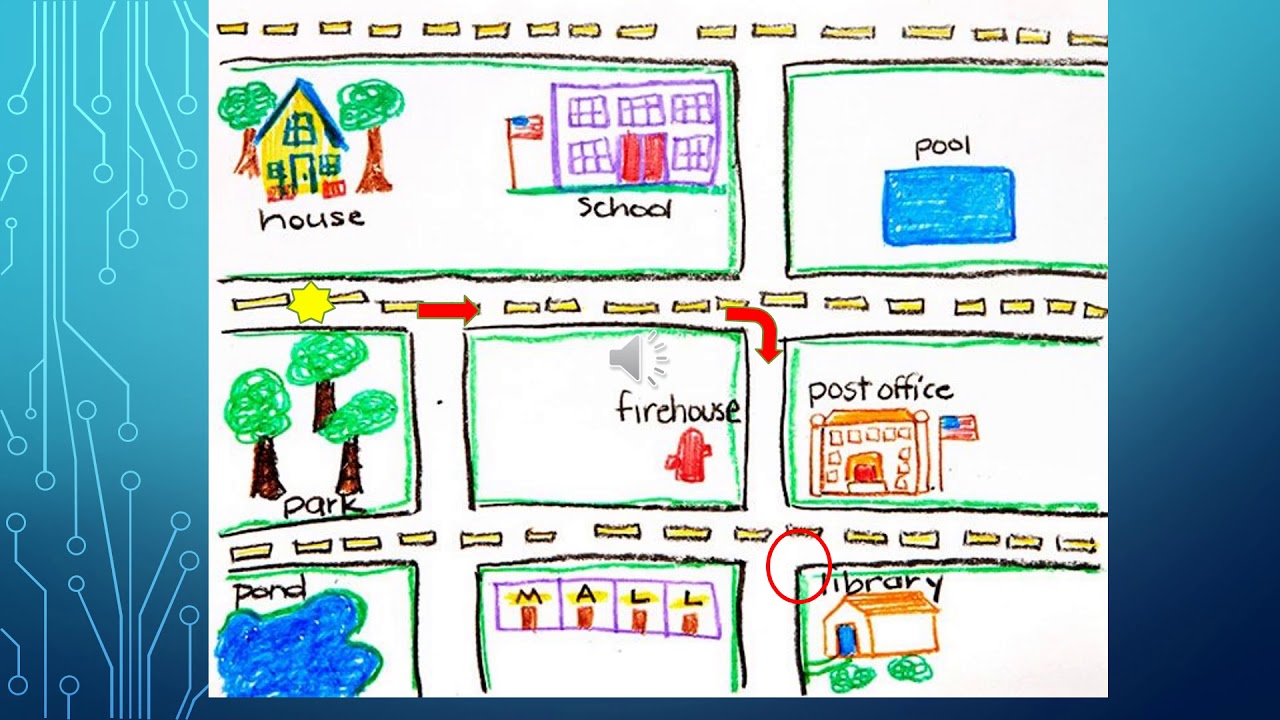
vavg=distancetimevavg=distancetime
Вы, конечно, можете изменить уравнение, чтобы решить либо расстояние, либо время
время = distancevavg.time = distancevavg.
расстояние = срч × времярасстояние = срч × время
Предположим, например, что автомобиль проезжает 150 километров за 3,2 часа. Его средняя скорость за поездку
ср=расстояние/время=150 км3,2 ч=47 км/ч. ср=расстояние/время=150 км3,2 ч=47 км/ч.
Скорость автомобиля может увеличиваться и уменьшаться во много раз за 3,2-часовую поездку. Однако его скорость в конкретный момент времени является его мгновенной скоростью. Спидометр автомобиля описывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL][AL] Предупредите учащихся, что средняя скорость не всегда является средним значением начальной и конечной скоростей объекта. Например, предположим, что автомобиль проехал расстояние 100 км. Первые 50 км он едет со скоростью 30 км/ч, а вторые 50 км – со скоростью 60 км/ч. Его средняя скорость будет равна расстоянию /(интервал времени) = (100 км)/[(50 км)/(30 км/ч) + (50 км)/(60 км/ч)] = 40 км/ч. Если бы автомобиль проехал одинаковое время 30 км и 60 км, а не равное расстояние на этих скоростях, его средняя скорость была бы 45 км/ч.
Его средняя скорость будет равна расстоянию /(интервал времени) = (100 км)/[(50 км)/(30 км/ч) + (50 км)/(60 км/ч)] = 40 км/ч. Если бы автомобиль проехал одинаковое время 30 км и 60 км, а не равное расстояние на этих скоростях, его средняя скорость была бы 45 км/ч.
[BL][OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» в повседневном языке часто называются просто скоростью. Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передать идеи.
Рисунок 2,8 За 30-минутную поездку туда и обратно до магазина общее пройденное расстояние составляет 6 км. Средняя скорость 12 км/ч. Перемещение для кругового рейса равно нулю, потому что нет чистого изменения положения.
Рабочий пример
Вычисление средней скорости
Мрамор катится на 5,2 м за 1,8 с. Какова была средняя скорость шарика?
Стратегия
Мы знаем расстояние, которое проходит шарик, 5,2 м, и интервал времени, 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg=distancetime=5,2 м1,8 с=2,9 м/svavg=distancetime=5,2 м1,8 с=2,9 м/с отвечать. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды равно 2,5 м/с. Поскольку 2,5 м/с близко к 2,9м/с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
9.Питчер бросает бейсбольный мяч с насыпи питчера на домашнюю тарелку за 0,46 с. Расстояние 18,4 м. Какова была средняя скорость бейсбольного мяча?
- 40 м/с
- — 40 м/с
- 0,03 м/с
- 8,5 м/с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м/с. Расстояние между домами 205 м. Сколько времени заняла у нее поездка?
146 с
0,01 с
2,50 мин
287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость равна смещению, деленному на время, в течение которого происходит смещение.
Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость равна смещению, деленному на время, в течение которого происходит смещение.
vavg=displacementtime=ΔdΔt=df−d0tf−t0vavg=displacementtime=ΔdΔt=df−d0tf−t0
Скорость, как и скорость, измеряется в единицах СИ в метрах в секунду (м/с), но поскольку это вектор, вы также должен включать направление. Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели со смещением и расстоянием в предыдущем разделе, изменения направления во временном интервале оказывают большее влияние на скорость и скорость.
Предположим, что пассажир двигается к задней части самолета со средней скоростью –4 м/с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или дал задний ход, прежде чем он добрался до задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты пути за более короткие интервалы времени, такие как те, что показаны на рис. 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, то есть скорость в определенный момент времени. Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рисунок 2,9 На диаграмме показана более подробная запись пассажира самолета, направляющегося к задней части самолета, с указанием меньших сегментов его поездки.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой. Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, значит, ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю.
Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, значит, ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю.
Смотреть физику
Вычисление средней скорости или скорости
В этом видео рассматриваются векторы и скаляры, а также описывается, как рассчитать среднюю скорость и среднюю скорость, когда известны перемещение и изменение во времени. В видео также рассматривается, как преобразовать км/ч в м/с.
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление.
 Перемещение является примером скалярной величины, а время — примером векторной величины.
Перемещение является примером скалярной величины, а время — примером векторной величины.Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление. Время — пример скалярной величины, а перемещение — пример векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина. Перемещение является примером скалярной величины, а время — примером векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина.
 Время — пример скалярной величины, а перемещение — пример векторной величины.
Время — пример скалярной величины, а перемещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
В этом видео хорошо видна разница между векторами и скалярами. Студент знакомится с идеей использования «s» для обозначения перемещения, которое вы можете поощрять или не поощрять. Прежде чем учащиеся посмотрят видео, обратите внимание на то, что преподаватель использует s→s→ для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является распространенным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часов и секунд. Напомните учащимся, что в своей работе они должны использовать сокращения h для обозначения часов и s для обозначения секунд.
Рабочий пример
Вычисление средней скорости
Студент переместился на 304 м на север за 180 с.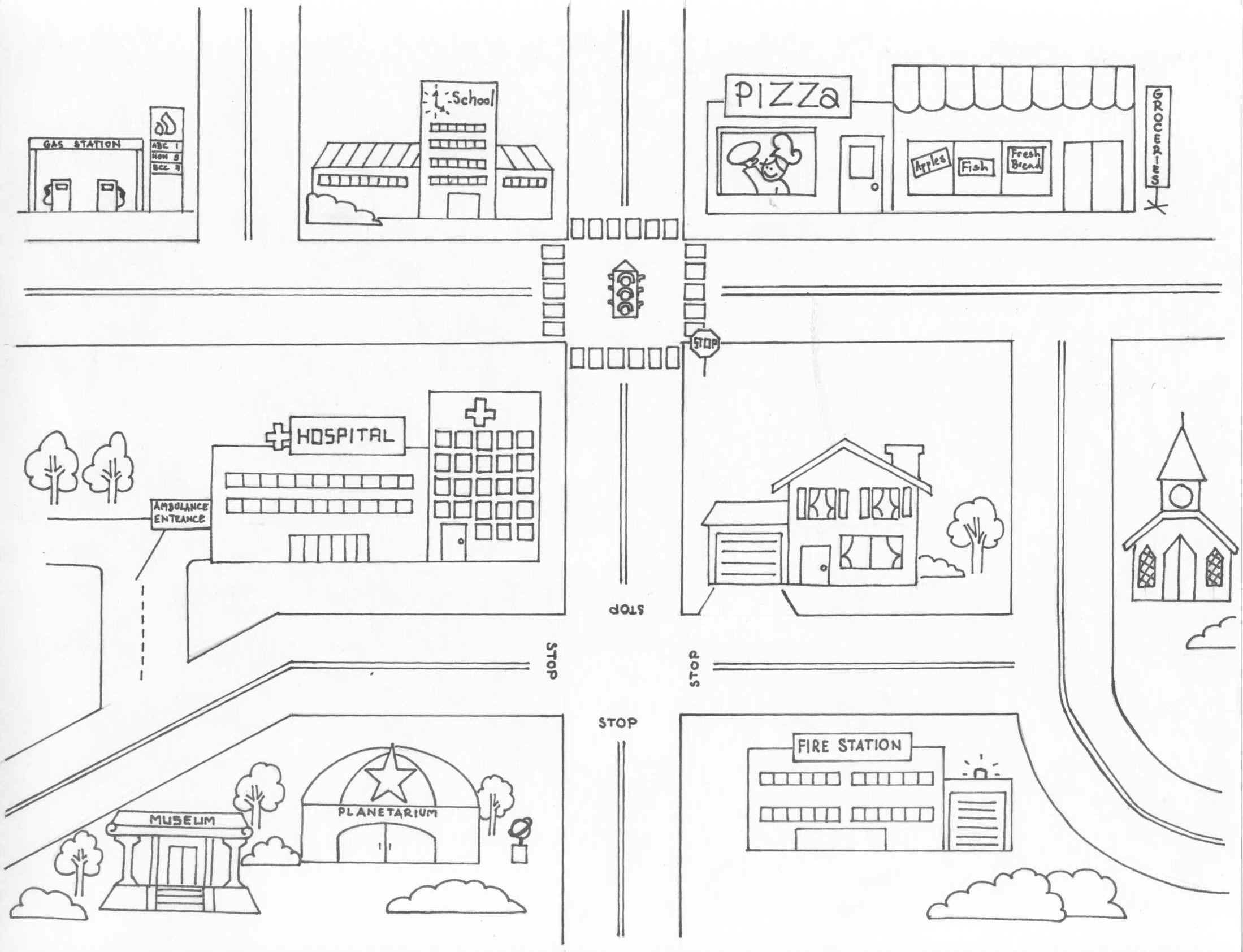 Какова была средняя скорость студента?
Какова была средняя скорость студента?
Стратегия
Мы знаем, что смещение 304 м на север и время 180 с. Для решения задачи можно использовать формулу средней скорости.
Решение
ср=ΔdΔt=304 м180 с=1,7 м/с север vср=ΔdΔt=304 м180 с=1,7 м/с север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны указать в ответе не только величину, но и направление. Обратите внимание, однако, что направление можно опустить до конца, чтобы не загромождать задачу. Обратите внимание на значащие цифры в задаче. Расстояние 304 м имеет три значащих цифры, а временной интервал 180 с — только две, поэтому частное должно иметь только две значащие цифры.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d представляет собой расстояние и перемещение. Точно так же v представляет скорость, а v представляет скорость. Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Векторы иногда представляются маленькими стрелками над переменной.
Векторы иногда представляются маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте это задание, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые учащиеся склонны включать много цифр в свои окончательные расчеты. Они ошибочно полагают, что повышают точность своего ответа, записывая многие из цифр, показанных на калькуляторе. Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда использовать одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бежит трусцой со средней скоростью 2,4 м/с на восток. Каково ее водоизмещение через 46 секунд?
Каково ее водоизмещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м/с на восток, а временной интервал равен 46 секундам. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м истср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м восток2.2
Обсуждение
Ответ примерно 110 м на восток, что является разумным смещением для чуть менее минуты бега трусцой. Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя экспоненциальную запись, потому что хотели, чтобы было ясно, что мы использовали только две значащие цифры.
Советы для успеха
Анализ размерностей — хороший способ определить, правильно ли вы решили задачу. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают по разные стороны от знака равенства. В рабочем примере у вас есть
м = (м/с)(с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица измерения сокращается, оставляя только m и, конечно же, m = m.
Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица измерения сокращается, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны перемещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени потребуется ему, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м/с на запад?
Стратегия
Мы знаем, что перемещение Филиппа составляет 428 м к западу, а его средняя скорость — 1,7 м/с к западу. Мы можем рассчитать время, необходимое для поездки, изменив уравнение средней скорости.
Раствор
ср=ΔdΔtΔt=Δdср=428 м1,7 м/с=2,5×102 срср=ΔdΔtΔt=Δdср=428 м1,7 м/с=2,5×102 с2,3
Обсуждение
И снова мы пришлось использовать научную запись, потому что ответ мог иметь только две значащие цифры. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
11.Дальнобойщик едет по прямому шоссе 0,25 ч со смещением 16 км на юг. Какова средняя скорость дальнобойщика?
4 км/ч на север
4 км/ч на юг
64 км/ч север
64 км/ч на юг
Птица перелетает со средней скоростью 7,5 м/с на восток с одной ветки на другую за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м/с на восток в течение 3,5 с к другой ветке. Каково полное перемещение птицы от исходной точки?
Каково полное перемещение птицы от исходной точки?
- 42 м на запад
- 6 м на запад
- 6 м на восток
- 42 м на восток
Виртуальная физика
Ходячий человек
В этой симуляции вы будете наводить курсор на человека и перемещать его сначала в одном направлении, а затем в противоположном. Держите вкладку Introduction активной. Вы можете использовать вкладку Charts после того, как узнаете о построении графиков движения позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. На данный момент игнорируйте поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость отрицательной. Затем посмотрите, можете ли вы сделать наоборот.
Проверка захвата
Какая ситуация правильно описывает ситуацию, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек уходит от 0 слева от 0
- Человек уходит от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать во многих уроках. На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Это также может показать, что когда смещение отрицательно, скорость может быть как положительной, так и отрицательной. Позже его можно использовать, чтобы показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется, чтобы вы удерживали учащихся на уровне 9.0081 Введение табл. Вкладку Charts можно использовать после того, как учащиеся узнают о построении графиков движения позже в этой главе.
На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Это также может показать, что когда смещение отрицательно, скорость может быть как положительной, так и отрицательной. Позже его можно использовать, чтобы показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется, чтобы вы удерживали учащихся на уровне 9.0081 Введение табл. Вкладку Charts можно использовать после того, как учащиеся узнают о построении графиков движения позже в этой главе.
Проверьте свое понимание
13.Два бегуна, движущиеся по одной и той же прямой дорожке, начинают и заканчивают свой бег в одно и то же время. На полпути они имеют разные мгновенные скорости. Могут ли их средние скорости за весь путь быть одинаковыми?
Да, потому что средняя скорость зависит от чистого или полного водоизмещения.

Да, потому что средняя скорость зависит от общего пройденного пути.
Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
Нет, потому что мгновенные скорости бегунов должны оставаться одинаковыми в средней точке, но могут различаться в других точках.
Если разделить общее расстояние, пройденное за автомобильную поездку (определенное по одометру), на время в пути, вычисляете ли вы среднюю скорость или величину средней скорости и при каких обстоятельствах эти две величины такой же?
- Средняя скорость.
 Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление. - Средняя скорость. Оба одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. Оба одинаковы, когда автомобиль не меняет своего направления.
Может ли средняя скорость быть отрицательной?
Да, если чистый водоизмещение отрицательное.
Да, если направление объекта меняется во время движения.
Нет, потому что средняя скорость описывает только величину, а не направление движения.

Нет, потому что средняя скорость описывает величину только в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте Проверьте свое понимание вопроса для оценки достижений учащихся по разделам целей обучения. Если учащиеся борются с определенной задачей, тест «Проверка вашего понимания» поможет определить, что именно, и направит учащихся к соответствующему содержанию. Элементы оценки в TUTOR позволят вам переоценить.
Третий закон движения Ньютона
Третий закон движения НьютонаДомашнее задание
Глава 5; Третий закон Ньютона
Домашнее задание: Упр. 6, 8, 11, 12, 13, 14, 17, 19, 23, 24, 25, 28, 32; Пб 1, 2, 3,
6
6, 8, 11, 12, 13, 14, 17, 19, 23, 24, 25, 28, 32; Пб 1, 2, 3,
6
Пример 5.6 Когда вы роняете резиновый мяч на пол, он почти отскакивает от него. на свою первоначальную высоту. Что заставляет мяч отскакивать?
Пол воздействует на мяч восходящей силой, которая останавливается. шары и придают ему ускорение вверх.
Эта восходящая сила от пола заставит мяч деформироваться или измениться. форму, пока он находится в контакте с полом.
Пример 5.8 Два груза по 100 Н прикреплены к пружинным весам, как показано на рисунке. Показывает ли шкала ноль, 100 Н или 200 Н — или какое-то другое значение?
Шкала показывает натяжение в струне.
Напряжение в струна 100 Н. Это сила, которую должна прилагать струна от 90 175 до 90 176 на любом из 100-Н грузиков на обоих концах струны.
Ничто не движется, ничто не ускоряется, поэтому чистая сила на пружине ноль. Аналогично, чистая сила на любой 100-н гирь также равна нулю. Но это другой вопрос. Весна шкала не измеряет чистая сила . Весенняя шкала просто измеряет напряжение , магнитуду усилие, действующее на струну.
Пример 5.11 Почему на педали велосипеда можно прикладывать большее усилие если потянуть за руль?
Затем руль тянет вниз на вас, как будто кто-то толкали вниз на ваши плечи. Это позволяет вам проявлять больше вниз усилие на педалях
Пример 5.12 Замедляется ли бейсбольная бита при ударе по мячу?
Конечно.
Когда бита воздействует на бейсбольный мяч, мяч также оказывает силу на летучую мышь — в противоположном направлении.
Пример 5.13 Почему альпинист тянет веревку вниз, чтобы двигаться вверх?
Когда альпинист тянет вниз по веревке, веревка тянет вверх на альпинист. Это еще один хороший пример третьего закона Ньютона или Закон действия и противодействия.
Пример 5.14 Вы вручную толкаете тяжелую машину. Автомобиль, в свою очередь, отталкивает с противоположной, но равной силой на вас. Разве это не означает, что силы отменяются? друг друга, что делает ускорение невозможным?
Чтобы «отменить друг друга», две силы должны были бы воздействовать на одно и то же объект. Силы действия-противодействия, о которых мы говорим с помощью третьего закона Ньютона — или силы в этом вопросе — действуют на различных предметов.
Пример 5.17 Предположим, что две тележки, одна из которых вдвое массивнее другой, летят друг от друга, когда сжатая пружина, соединяющая их, освобождается. Как быстро более тяжелый ролик тележки по сравнению с более легкой тележкой?
Согласно третьему закону Ньютона силы, действующие на эти две массы, должны быть равны (и в разные стороны). По Ньютону секунд Закон, F = m a, мы находим a = F / m. Это означает ускорение вдвое более массивного корзина будет половина ускорение другой.
Пример 5.19 Если грузовик Mack и Honda Civic столкнулись лоб в лоб, на какое транспортное средство сила удара больше? Какое транспортное средство испытывает большее ускорение?
сила будет той же на двух транспортных средствах, согласно третьему закону Ньютона.
Это означает, что Civic , с гораздо меньшей массы, испытает гораздо большее ускорение, согласно второму закону Ньютона.
Упр. 5.23 Рассмотрим перетягивание каната на гладком полу между мальчиками в носки и девушки в обуви на резиновой подошве. Почему девушки побеждают?
Девочки могут прикладывать большее усилие в своих туфлях на резиновой подошве, чтобы они Выиграет.
Упр. 5.24 Два человека равной массы пытаются перетянуть канат 12-метровой канат, стоя на гладком льду. Когда они тянут веревку, каждый скользить друг к другу. Как соотносятся их ускорения и насколько каждый человек скользит перед встречей?
Сила на каждом будет одинаковой, поэтому они всегда будут иметь одинаковое ускорение. — и поэтому они имеют одинаковую скорость и пройдут одинаковое расстояние. Таким образом, они встретятся посередине, поэтому каждому придется пройти 6 м.
Пример 5.28 Когда сумма двух векторов равна нулю, как они должны быть связаны?
Они должны быть равны по модулю и ровно противоположны по направление.
Пример 5.32 Если вы стоите в автобусе, который движется с постоянной скоростью и бросьте мяч из вытянутой руки, вы увидите его траекторию как вертикальную прямая линия. Каким покажется путь другу, стоящему на боку дорога?
Друг у дороги увидит горизонтальную составляющую ее движения. Он/она может описать это, сказав, что оно движется по «дуге» или вдоль «изогнутый путь». Внимательное наблюдение показало бы, что он движется вдоль «параболический путь». Мы поговорим об этом подробнее в следующей главе. по нелинейному движению.
Pb 5.1 Боксер пробивает лист бумаги в воздухе и выносит его из
отдых до скорости 25 м/с за 0,05 с. Если масса бумаги 0,003 кг.
(то есть 3 грамма), с какой силой на него действует боксер?
Если масса бумаги 0,003 кг.
(то есть 3 грамма), с какой силой на него действует боксер?
F = м а
А какое ускорение, а?
а = в / т
а = (25 м/с) / (0,05 с)
а = 500 м/с/с
а = 500 м/с
Pb 5.2 Если вы стоите у стены на скейтборде без трения и толкните стену с силой 30 Н, с какой силой стена давит на вас? Если ваш масса 60 кг, каково ваше ускорение?
Из третьего закона Ньютона мы знаем, что стена реагирует на , отталкиваясь от нее. вы с силой 30 Н.
Ф = 30 Н
Из второго закона Ньютона мы можем вычислить ускорение, которое производит
F =
мАа = Ф/м
а = (30 Н) / (60 кг)
а = 0,5 м/с 2
Pb 5. 3 Если капли дождя падают вертикально со скоростью 3 м/с, а вы
двигаясь со скоростью 4 м/с, как быстро они ударяют вас по лицу?
3 Если капли дождя падают вертикально со скоростью 3 м/с, а вы
двигаясь со скоростью 4 м/с, как быстро они ударяют вас по лицу?
Для этого нам понадобится диаграмма сложения векторов. Пока капли дождя падают вниз со скоростью 3 м/с, они также кажутся движущимися горизонтально со скоростью 4 м/с, потому что вы бежите горизонтально со скоростью 4 м/с. Мы будем рисовать векторы (или стрелки) для представления этих скоростей,
Вы можете начать с рисования вектора скорости 3 м/с сначала вниз, а затем, в конце этого вектора, начать 4 м/с горизонтальный вектор. Результирующий вектор — это вектор, который вы рисуете, который начинается где ваша диаграмма началась и заканчивается там, где закончилась ваша диаграмма.
Или вы можете подумать о том, чтобы начать рисовать горизонтальную скорость 4 м/с.
сначала вектор, а затем, в конце этого вектора, начните движение вниз со скоростью 3 м/с. вектор скорости. Результирующий вектор — это вектор, который вы рисуете, который начинается где ваша диаграмма началась и заканчивается там, где закончилась ваша диаграмма.
Для всех этих диаграмм сложения векторов результирующее , векторная сумма этих двух скоростей равна 5 м / с под углом 37 градусов. от горизонтали.
Pb 5.6 Каноэ плывет со скоростью 4 км/ч прямо по реке, которая течет со скоростью 3 км/ч, как показано на рисунке.
(a) Какова результирующая скорость каноэ относительно берега?
Для этого требуется другая диаграмма сложения векторов. Это очень сильно как предыдущий!
Для любой из этих векторных диаграмм чистый результат результат , векторная сумма этих скоростей такова, что каноэ движется по реке на скорости 5 км/ч под углом 37 градусов к югу от востока или 53 градуса к востоку от юга (или 37 градусов, как показано на диаграмме).
(b) Примерно в каком направлении следует грести на каноэ добраться до пункта назначения через реку?
Конечно, для этого потребуется еще одна диаграмма сложения векторов. Но этот веселее. Мы хотим результирующий должен быть горизонтальным (или восток). Мы знаем, как быстро может двигаться каноэ (это 4 км/ч), но мы не знаем направление . На в каком направлении нужно ли нам грести на каноэ со скоростью 4 км/ч, чтобы, когда река течет вниз (или на юг) при скорости 3 км/ч результирующая скорость будет горизонтальной (или восток)?
Типичные вопросы с несколькими вариантами ответов:
1. Силы действия-противодействия, с которыми мы сталкиваемся в третьем законе Ньютона
Силы действия-противодействия, с которыми мы сталкиваемся в третьем законе Ньютона
а) всегда компенсируют друг друга.
б) всегда действуют на разные объекты.
в) всегда совпадают с силами трения и опоры.
d) могут быть перпендикулярны друг другу.
2. Применяется третий закон Ньютона
а) только к объектам в состоянии покоя (например, толкание стены)
b) на пары объектов, из которых хотя бы один должен находиться в состоянии покоя (например, удар по стена с движущимся мячом)
c) любым двум взаимодействующим объектам
г) только к парам объектов, у которых один значительно массивнее другого.
3. Третий закон Ньютона равен
.а) частный случай второго закона Ньютона.
б) частный случай первого закона Ньютона.
c) не зависит от других законов движения Ньютона.
d) применяется только тогда, когда сопротивлением воздуха можно пренебречь.
4. Результат двух векторов равен
.а) меньший из двух векторов.
б) среднее значение двух векторов.
c) векторная сумма двух векторов.
г) больший из двух векторов.
5. Можно добавлять векторы
а) как обычные числа.
б) путем умножения их величин.
c) путем вычитания их величин и умножения их единиц.
г) путем построения диаграммы сложения векторов.
Типичные вопросы с несколькими вариантами ответов и ответами:
1. Силы действия-противодействия, с которыми мы сталкиваемся в третьем законе Ньютона
а) всегда компенсируют друг друга.
б) всегда действуют на разные объекты.

в) всегда совпадают с силами трения и опоры.
d) могут быть перпендикулярны друг другу.
2. Применяется третий закон Ньютона
а) только к объектам в состоянии покоя (например, толкание стены)
b) на пары объектов, из которых хотя бы один должен находиться в состоянии покоя (например, удар по стена с движущимся мячом)
в) любым двум взаимодействующим объектам
г) только к парам объектов, у которых один значительно массивнее другого.
3. Третий закон Ньютона равен
.а) частный случай второго закона Ньютона.
б) частный случай первого закона Ньютона.
в) не зависит от других законов движения Ньютона.
d) применяется только тогда, когда сопротивлением воздуха можно пренебречь.
4. Результат двух векторов равен
.а) меньший из двух векторов.

 Все правила по сольфеджио
Все правила по сольфеджио Папа вырезал бумажные фигурки по форме мебели и двигает их по плану квартиры
Папа вырезал бумажные фигурки по форме мебели и двигает их по плану квартиры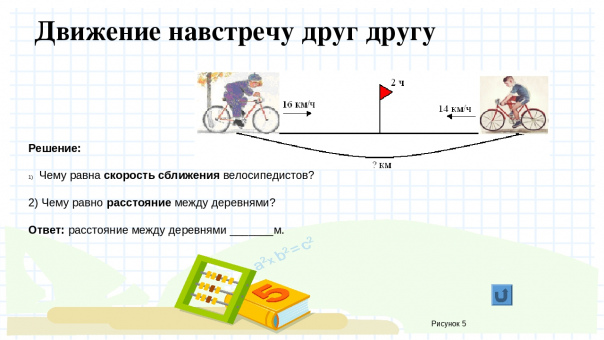 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент: Перемещение является примером скалярной величины, а время — примером векторной величины.
Перемещение является примером скалярной величины, а время — примером векторной величины. Время — пример скалярной величины, а перемещение — пример векторной величины.
Время — пример скалярной величины, а перемещение — пример векторной величины.
 Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
 Напряжение в
струна 100 Н. Это сила, которую должна прилагать струна
от 90 175 до 90 176 на любом из 100-Н грузиков на обоих концах струны.
Напряжение в
струна 100 Н. Это сила, которую должна прилагать струна
от 90 175 до 90 176 на любом из 100-Н грузиков на обоих концах струны. Когда бита воздействует на бейсбольный мяч, мяч также
оказывает силу на летучую мышь — в противоположном направлении.
Когда бита воздействует на бейсбольный мяч, мяч также
оказывает силу на летучую мышь — в противоположном направлении.
 Это означает, что Civic , с
гораздо меньшей массы, испытает гораздо большее ускорение,
согласно второму закону Ньютона.
Это означает, что Civic , с
гораздо меньшей массы, испытает гораздо большее ускорение,
согласно второму закону Ньютона.
 сначала вектор, а затем, в конце этого вектора, начните движение вниз со скоростью 3 м/с.
вектор скорости. Результирующий вектор — это вектор, который вы рисуете, который начинается
где ваша диаграмма началась и заканчивается там, где закончилась ваша диаграмма.
сначала вектор, а затем, в конце этого вектора, начните движение вниз со скоростью 3 м/с.
вектор скорости. Результирующий вектор — это вектор, который вы рисуете, который начинается
где ваша диаграмма началась и заканчивается там, где закончилась ваша диаграмма.