Измерение площади с помощью палетки
Тема. Измерение площади фигуры с помощью палетки.
Цель. Познакомить детей со способом нахождения площади фигур различной формы с помощью палетки, закрепить умение решать текстовые задачи изученных видов, переводить одни единицы площади в другие, работать с геометрическими фигурами. Развивать логическое мышление учащихся, умение точно и обоснованно аргументировать. Воспитать интерес к предмету, любознательность, дружеское отношение к одноклассникам в совместной работе.
1.Организация начала урока.
Чтобы спорилось нужное дело
Чтобы в жизни не знать неудач,
В мир математики отправимся смело
В мир примеров и разных задач.
2. Актуализация опорных знаний.
Запишем число, классная работа
А сейчас мы проведём арифметический диктант.
Математический диктант
Найти частное чисел: 96 и 3. Выразить: 9см 34мм=…мм Число 78000 увеличить в 10 раз. Найти произведение чисел: 16 и 5. . Записать число: три тысячи пять. 32 увеличить в 4 раза. Найти сумму чисел: 57 и 38. 26000 уменьшить в 100 раз.
Найти произведение чисел: 16 и 5. . Записать число: три тысячи пять. 32 увеличить в 4 раза. Найти сумму чисел: 57 и 38. 26000 уменьшить в 100 раз.
32 934 780000 80 3005 128 95 260
Проверка на слайде Самопроверка Оценивание детьми
Устный счет на слайде с поверкой
3 см2 = 300 мм2 5 дм2 =50000 мм2
8 м2 = 800 дм2 = 70000
4 = 400 9км2 =9000000м2
2.Сообщние темы и цели урока слайд
С какими единицами мы сейчас работали? О чем пойдет речь на уроке?
Вспомним всё, что мы знаем о площади Слайд с таблицей
1 Слово Площадь
А что такое площадь одним словом ? (величина) Начинаем заполнять таблицу
-Давайте вспомним, в каких единицах измеряется площадь?Начинаем с малых
По какой формуле находим площадь прямоугольника?
По какой формуле находим площадь квадрата?
Какие действия можем выполнять с площадями?
Что осталось незаполненным? Значит, на уроке мы узнаем что-то новое, то, чего мы ещё не знаем о площади
3. Работа над новым материалом
Работа над новым материалом
— В математике множество различных фигур. Что вы видете?(Слайд )
Рассмотрите геометрические фигуры. Назовите их.
Какие работы умеем выполнять с геометрическими фигурами? (умеем находить площадь и периметр , измерять длину и ширину).
На какие группы можно разделить эти фигуры? (многоугольники и фигуры без углов)
Среди данных фигур выберите те, площадь которых умеете находить?
– Повторим еще раз как находим площадь квадрата, прямоугольника? По формулам
Слайд прямоугольник со сторонами 5см и 4см. Найдите площадь.
Квадрат со стороной 3см. Найдите площадь.
По вариантам. Запишите в тетрадь решение и ответ
Проверка по 1 ученику (Слайд ответы )
Слайд– А что делать с остальными фигурами?.Как вычислить их площадь ?Почему не смогли? Какая проблема? (не знаем, как найти площадь фигуры неопределенной формы)А что же нам делать, если нужно найти площадь остальных фигур? (Предложение учащихся)
Как узнать?Для этого нам поможет учебник .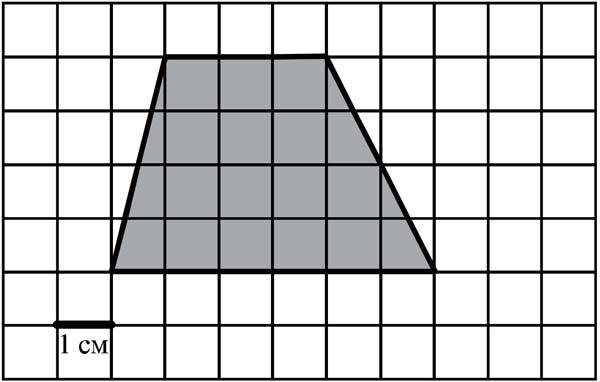 Открыли и читаем объяснение вверху
Открыли и читаем объяснение вверху
Какая тема урока? Цель урока? Чему должны научиться?
На ваших столах лежат конверты. Достаньте из них прозрачную плёнку. Внимательно рассмотрите её. Это – палетка. Расскажите, как она выглядит.
Палетка — прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры.
— Рассмотрите вашу палетку, чему равна её сторона. Измерили (Слайд 10) (1 кв. см)
– Итак, наша палетка разделена на одинаковые квадратные сантиметры.
Скажите, как измерить площадь таких фигур с помощью палетки?. (Ответы детей)
Слайд плана измерения палеткой.
Работа в парах. На партах по 2 фигуры. Дети измеряют площадь палеткой по алгоритму и записывают в тетрадь решение.
ФИЗКУЛЬТМИНУТКА
– Сосчитайте, какова площадь ваших фигур.Как вы думаете ответ будет точный? Почему?
4.Работа по учебнику
191- работа в парах
192-задача на оценку на доске
Всего-128 стр.
1 д.-? 4 часть
2д.-? несколько
Осталось-63 стр.
128:4=32
32+63=95
128-95=33
Ответ:
193-задача на доске
Было- Осталось продали
Яб.-380 295
Гр.-180 106
380-295=95
180-106=74
95-74=21
Ответ:
Самостоятельная работа.Взаимопроверка
5.итог урока
Что такое палетка?
Для чего нужна палетка? (для измерения площади сложных геометрических фигур)
Как измеряют палеткой?
На какие квадраты делятся палетки?
В жизни где можно применить палетку?
«Измерение площадей плоских фигур произвольной формы: нестандартные методы»
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Шихалиев Р.М. 1
1МБОУ «СОШ №3 г. Тосно»
Неизвестный Е. В. 1
В. 1
1МБОУ «СОШ №3 г. Тосно»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Работа посвящена исследованию и сравнению методов измерения площадей фигур произвольной формы.
Актуальность и практическая значимость исследования.
В школьном курсе математики мы в основном имеем дело с многоугольниками. С проблемой вычисления площади фигур я столкнулся при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которых мы не рассматривали на уроках математики. Ведь до 8 класса мы знакомимся только с формулами для вычисления площади квадрата, прямоугольника и прямоугольного треугольника. Так как на уроке мы обычно выполняем решение в тетради, то я обратил внимание, что вычислить площадь того же квадрата помогают клетки, изображенные в тетради.
Гипотеза: площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.
Цель работы: исследовать различные способы вычисления площадей фигур, сравнить полученные результаты.
Задачи исследования:
изучить литературу по исследуемой теме;
отобрать интересную и понятную информацию для исследования;
найти различные методы и приёмы вычисления площади фигур на клетчатой бумаге.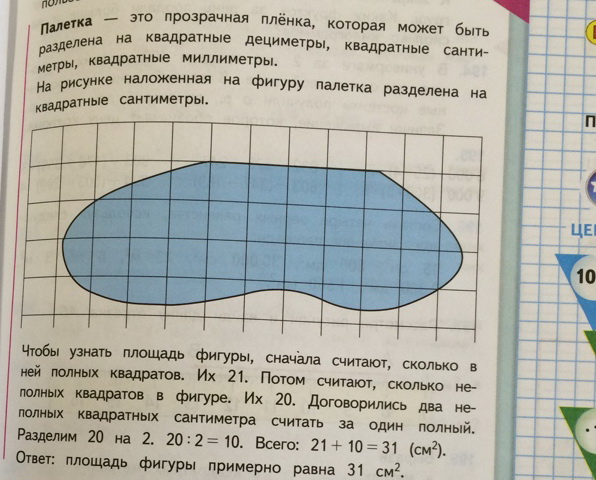
изучение методов нахождения площади с помощью взвешивания.
измерение с помощью методов взвешивания площадей контрольных фигур: прямоугольника, квадрата, выявление погрешностей измерения
провести сравнительный анализ «плюсов» и «минусов» найденных способов.
провести эксперимент в 8В классе об выявлении математических знаний у учащихся при вычислении площади фигур;
Поиск интересных задач на нахождение площади фигуры.
проанализировать и систематизировать полученную информацию.
Объектом исследования являются методы измерения площади фигур произвольной формы:
1) метод взвешивания;
2) использование клетчатой бумаги;
3) применение точных формул.
Предметом исследования является площадь фигур произвольной формы.
Из истории возникновения понятия «Площадь».
В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д.
Мы говорим: площадь квартиры, площадь садового участка и т.д.
Позже возникла потребность в измерении и сравнении разнообразных «фигур» (н.п. земельных участков). Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади.
Вавилоняне, так же как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.
Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.
Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.
Способы вычисления площади фигуры на клетчатой бумаге.
При изучении вычисления площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке — пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.
Рис. 1. фотография рыбацкой сетки
1. фотография рыбацкой сетки
Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления. [1, с.36]
Три способа вычисления площади выпуклого многоугольника.
Разбиение. Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Тогда площадь фигуры можно сосчитать по формуле:
Sф = S1 + S2 + S3 = 10 + 1 + 12 = 23.
Дополнение до прямоугольника. Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:
Sф = Sпр — (S1 + S2) = 36 — (1 + 12) = 23.
Формула Пика. Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 — 1, где В — количество внутренних узлов, а Г — количество узлов на границе многоугольника.
Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так S = В + Г/2 — 1, где В — количество внутренних узлов, а Г — количество узлов на границе многоугольника.
Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге.
Используя рисунок В= 17, Г = 14, получаем
S = 17 + 14/2 — 1 = 23.
Вычисляя площадь выпуклого многоугольника тремя способами, я получил один и тот же результат.
Три способа вычисления площади невыпуклого многоугольника.
Способ разбиенияне подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Дополнение до прямоугольника.
Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры
Sф = S — (S1 + S2 + S3 + S4) = 42 — (6 + 2 + 1 + 1) = 16 — 10 = 6.
ФормулаПика.
При подсчете внутренних узлов многоугольника и узлов, лежащих на границе получим, что
В = 5; Г = 4; S = 5 + 4/2 — 1 = 6.
И опять я получил один и тот же результат.
Вычисление площади кольца по формуле Пика.
А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.
Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.
Вычислим площадь кольца с помощью формулы Пика:
В = 32, Г = 8, S= 32 + 4 — 1 = 35.
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.
S = πR2 — πr2 = 3* 16 — 3*4 = 48 — 12 = 36.
Округлим теперь π до десятых:
S = πR2 — πr2 = 3,1* 16 — 3,1*4 = 49,6 — 12,4 = 37,2.
А если округлить число π до сотых, то получим:
S = πR2 — πr2 = 3,14* 16 — 3,14*4 = 50, 24 — 12,56 = 37,68.
Сравнив результаты можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников. [2, с.17], [4]
Метод взвешивания
Метод измерения вспомогательной величины придуман еще в древности и заключается в измерении массы плоской копии измеряемой фигуры. Если толщина листа, из которого изготовлены взвешиваемая фигура, постоянна, то масса фигуры прямо пропорциональна ее площади. Нужно нанести на плотную бумагу квадрат, площадь которого S0 точно известна, вырезать его и определить на весах его массу m0. На такую же бумагу перенести фигуру с искомой площадью S. Вырезать фигуру и определите её массу m. Затем, пользуясь правилом пропорции – S/S0 = m/m0, вычислить искомую площадь.
Тогда
Вычисление площади клинового листа
Для решения задачи была взят фотография кленового листа (рис. 2).
Рисунок 2. Фотография листа клена
1Разбиение.
Окантовка листа была перенесена на лист бумаги и была разбита (разрезана) на прямоугольники и (или) прямоугольные треугольники. (Рисунок 3).
Рисунок 3. Разбиение листа клена на прямоугольники и прямоугольные треугольники
После чего произведен расчет площади каждого прямоугольника и прямоугольного треугольника в см2
|
7,56 |
||
Тогда общая площадь листа будет равна:
Sобщая = S1+S2+…+S54
см2
2. Дополнение до прямоугольника.
Дополнение до прямоугольника.
Окантовка листа была перенесена на лист бумаги и была дополнена до прямоугольника. (Рисунок 4).
Рисунок 4. Дополнение листа клена на прямоугольника
После чего произведен расчет площади общего прямоугольника и каждого прямоугольника и прямоугольного треугольника в см2
Общий прямоугольник имеет размеры 18,2 см на 15 см, т. Е. его площадь прямоугольника составляет S=18,2∙15=273 см2
Sобщая= S – (S1+S2+…+S42)
см2
3Формула Пика.
Окантовка листа была перенесена на миллиметровую бумагу. (Рисунок 5).
Рисунок 5. Разбиение листа клена на узлы
В (внутренние точки) =13353 шт.
Г (граничные точки) = 725 шт.
Тогда по формуле S = В + Г/2 – 1
S=13353+362,5-1=13714,5мм2=137,145 см2
4. Метод взвешивания
Метод взвешивания
Для проведения взвешивания взяли лист бумаги SvetoCopy. По ее плотности определили вес бумаги при помощи таблицы и путем взвешивания. Результаты сошлись. Вес одного листа бумаги А4 =5г. Размеры листа А4 равны 210х297мм, т.е. площадь одного листа равна S0 = 623,7 см2
Рис. 6. Фотография оборотной стороны упаковки бумаги SvetoCopy
Рис. 7. Таблицы дляболее точного измерения массы листа по его плотности.
Для определения погрешности вычислений вырезали в качестве эталонов несколько геометрических фигур (прямоугольник (эталон 1) и квадрат (эталон 2)), площадь которых можно сравнить вычислив ее по формуле.
Прямоугольник имеет размеры: 7см на 5 см, а квадрат: 5см на 5см.
S0 = 623,7 см2
т0= 5000мг
|
Наименование образца |
Площадь по формуле, см2 |
Взвешивание |
Погрешность измерения ∆ |
|
|
Масса, мг |
Площадь, см2 |
|||
|
эталон 1 |
35 |
250 |
31,185 |
1,908 |
|
эталон 2 |
25 |
150 |
18,711 |
3,145 |
|
Лист А4 |
623,7 |
5000 |
623,7 |
0 |
|
Лист клена |
— |
1100 |
137,214 |
2,526 |
Количественной характеристикой точности является погрешность измерения. Если известно точное значение некоторой величины и ее приближенное значение x, то предельной абсолютной погрешностью приближенного значения называется величина , а предельной относительной погрешностью – величина . Однако на практике точные значения измеряемой величины неизвестны, а приближенное значение заключено в некоторых пределах: . В этом случае считают, что .
Если известно точное значение некоторой величины и ее приближенное значение x, то предельной абсолютной погрешностью приближенного значения называется величина , а предельной относительной погрешностью – величина . Однако на практике точные значения измеряемой величины неизвестны, а приближенное значение заключено в некоторых пределах: . В этом случае считают, что .
Таким образом после взвешивания величина площади листа клена составляет 137,214 см2 с погрешностью измерения 2,53 см2
Рис. 8. Фотографии опреденения массы листа
Сравнительный анализ способов нахождения площади многоугольника на клетчатой бумаге.
1. Разбиение.
Этот способ прост в подсчёте площадей фигур, которые разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. К ним относятся выпуклые многоугольники.
К минусам можно отнести то, что в использовании этого способа приходится производить множество действий, а так же невозможность подсчёта площади фигур, которые не разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
2. Дополнение до прямоугольника.
Этот способ так же прост в подсчёте при вычислении площади при небольшом количестве фигур, площадь которых необходимо отнять.
Минусы этого способа — сложность подсчёта площади многоугольников необычной
формы, большое количество фигур, площадь которых необходимо отнять, а так же невозможность подсчёта площади фигур, не относящихся к многоугольникам.
3. Формула Пика.
К плюсам я отнес то, что легко вычисляется площадь многоугольника с необычной формой, в отличие от предыдущих способов, краткость формулы, а так же возможность вычисления приближенного значения площади местности по карте, представив ее в виде многоугольника, перенеся ее на клетку.
Минусами этого способа считаю сложность вычисления площади фигуры с большим количеством узлов, а так же, если в фигуре есть «спорные» узлы (узлы, лежащие близко к стороне многоугольника). Вычисляя площадь фигур, не относящихся к многоугольникам, результат получается не точным.
4. Метод взвешивания.
К минусам я отнес, что можно вычислить площадь фигуры с помощью весов с большой погрешностью измерения и большей продолжительности времени измерения
Заключение
Изучив различные источники, выяснилось, что существует различные способы вычисления фигур по клеткам, но для меня были интересны и понятны три: разбиение, дополнение до прямоугольника и вычисления по формуле Пика.
Моя гипотеза – о том, что если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми, частично подтвердилась. Рассмотрев все три способа, я пришел к выводу, что не для всякой фигуры можно приметить каждый из них. У каждого из них есть свои плюсы и минусы.
Все три способа можно применить только для выпуклых многоугольников, перенеся их на клетчатую поверхность.
Формула Пика интересна своей простотой. И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.
И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.
Как показал метод взвешивания является пригодным для приближенного нахождения площадей фигур сложной формы.
Список литературы и Интернет-ресурсов
Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
История математики с древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича., издательство Наука., М., 1970г
Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
https://ege.sdamgia.ru/
http://www.pppa.ru/additional/01geodesy/06/02topo.php
http://ru.wikihow.comhttp://knowledge.allbest.ru/mathematics/3c0b65635b3bd68b4c43b89521306d27_0.html
http://argonavt.narod.ru/Kenpark.html
Приложение 1
Опрос сверстников о знании ими способов вычисления площадей плоских фигур
|
Анкета
Умеете ли вы определять площадь не стандартного многоугольника?
Если да, то как? (определите площади следующих фигур)
А можете ли вы определить площадь нестандартной фигуры (например, площадь лужи). |
Результаты опроса
1 вопрос:
Рис. 9. Гистограмма ответов на 1 вопрос
2. вопрос:
Рис. 10. Гистограмма ответов на 2 вопрос
Вывод по 1 и 2 вопросу: практически 70% респондентов не владеют знаниями вычисления площади многоугольника, если он не стандартной формы.
3 вопрос:
Рис. 11. Гистограмма ответов на 3 вопрос
После проведения анкетирования я показал как измерить площадь лужи при помощи палетки (использовал видео с сайта «математические этюды»)
Рис. 12. Фотографии моего рассказа одноклассникам о измерении площади лужи при помощи палетки
Приложение 2
Работы одноклассников по вычислению площади собственной ладони по формуле Пика
Рис. 13. Фотографии работ одноклассников по вычислению площади собственной ладони по формуле Пика
Просмотров работы: 4616
Как вычислить площадь фигуры.
 Как найти площадь прямоугольника
Как найти площадь прямоугольника Важные замечания!
1. Если вместо формул вы видите абракадабру, очистите кеш. Как это сделать в браузере написано здесь:
2. Прежде чем начать читать статью, обратите внимание на наш навигатор по самому полезному ресурсу по
Как найти площадь цифр на бумаге в клетку:
Проиллюстрируйте первым способом.
Пусть нужно найти площадь такой трапеции построенной на листе в клетке
Просто считаем клетки и видим, что в нашем случае и. Подставляем в формулу:
Вроде даже прямоугольное и, но чему равно, а чему равно? Как узнать? Воспользуемся обоими способами для полной ясности.
I путь.
Второй способ (открою секрет — этот способ лучше!)
Нам нужно окружить нашу фигуру прямоугольником. Вот так:
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко вычисляются на листе в клетку!
Здесь мы их посчитаем, а потом просто вычтем из всего прямоугольника.
Почему так лучше? потому что работает и для самых хитрых фигур.
Окружаем прямоугольником и снова получаем одну нужную, но сложную область и много ненужных, но простых.
А теперь, чтобы найти площадь, просто найдем площадь прямоугольника и отнимем от нее оставшуюся площадь фигур на клетчатой бумаге.
КВАДРАТ ЦИФР НА БУМАГЕ В КЛЕТКУ. СВОДНАЯ И ОСНОВНАЯ ФОРМУЛА
Алгоритм нахождения площади фигур на клетчатой бумаге:
Способ 1: (полезно для стандартных фигур: треугольник, трапеция и т.д.)
- Путем подсчета клеток и применения простых теорем, найти те стороны, высоты, диагонали, которые требуются для применения формулы площади.
- Подставить найденные значения в уравнение площади.
Способ 2: (очень удобен для сложных фигур, но неплох для простых)
- Завершите нужную фигуру прямоугольником.
- Найдите площадь всех получившихся дополнительных фигур и площадь самого прямоугольника.

- Вычесть сумму площадей всех лишних фигур из площади прямоугольника.
Ну вот и закончилась тема. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны что-то освоить самостоятельно. А если вы дочитали до конца, то вы в 5%!
Теперь самое главное.
Вы разобрались с теорией по этой теме. И, повторюсь, это… это просто супер! Вы уже лучше, чем подавляющее большинство ваших сверстников.
Проблема в том, что этого может не хватить…
Для чего?
За успешную сдачу ЕГЭ, за поступление в институт на бюджет и, ГЛАВНОЕ, пожизненно.
Не буду вас ни в чем убеждать, скажу только одно…
Люди, получившие хорошее образование, зарабатывают гораздо больше, чем те, кто его не получил. Это статистика.
Но не это главное.
Главное, что они БОЛЬШЕ СЧАСТЛИВЫ (есть такие исследования). Может быть, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю. ..
..
Но подумайте сами…
Что нужно, чтобы быть уверенным, что лучше других сдашь экзамен и в конечном счете будешь… счастливее?
НАБИРАЙТЕ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене теорию не спросят.
Вам понадобится решать задачи вовремя .
И, если ты их не разгадал (МНОГО!), то обязательно где-нибудь совершишь глупую ошибку или просто не успеешь.
Это как в спорте — нужно повторять много раз, чтобы точно выиграть.
Найди коллекцию где хочешь обязательно с решениями, подробный разбор и решай, решай, решай!
Вы можете использовать наши задачи (не обязательно) и мы их обязательно рекомендуем.
Для того, чтобы получить помощь с помощью наших заданий, вам необходимо помочь продлить жизнь учебнику YouClever, который вы сейчас читаете.
Как? Есть два варианта:
- Разблокировать доступ ко всем скрытым задачам в этой статье —
- Разблокировать доступ ко всем скрытым заданиям во всех 99 статьях туториала — Купить учебник — 499 рублей
Да, у нас есть 99 таких статей в учебнике и доступ ко всем заданиям и всем скрытым текстам в них можно открыть сразу.
Доступ ко всем скрытым заданиям предоставляется на все время существования сайта.
В заключение…
Если вам не нравятся наши задачи, найдите другие. Только не останавливайтесь на теории.
«Понял» и «Я умею решать» — совершенно разные навыки. Вам нужны оба.
Найди проблемы и реши их!
Площади геометрических фигур представляют собой числовые значения, характеризующие их размеры в двумерном пространстве. Это значение может быть измерено в системных и несистемных единицах измерения. Так, например, внесистемной единицей площади является сотня, гектар. Это тот случай, когда измеряемая поверхность представляет собой участок земли. Системной единицей площади является квадрат длины. В системе СИ принято считать, что единицей площади плоской поверхности является квадратный метр. В СГС единица площади выражается в квадратных сантиметрах.
Геометрия и формулы площади неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основано именно на их применении. Для многих фигур выведено несколько вариантов, по которым рассчитываются их квадратные размеры. На основании данных из постановки задачи мы можем определить наиболее простой способ ее решения. Это облегчает расчет и сводит к минимуму вероятность ошибки расчета. Для этого рассмотрим основную площадь фигур в геометрии.
Для многих фигур выведено несколько вариантов, по которым рассчитываются их квадратные размеры. На основании данных из постановки задачи мы можем определить наиболее простой способ ее решения. Это облегчает расчет и сводит к минимуму вероятность ошибки расчета. Для этого рассмотрим основную площадь фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими способами:
1) Площадь треугольника вычисляется из основания а и высоты h. Основание – это сторона фигуры, на которую опущена высота. Тогда площадь треугольника равна:
2) Точно так же вычисляется площадь прямоугольного треугольника, если основанием считать гипотенузу. Если же за основание взять катет, то площадь прямоугольного треугольника будет равна произведению катетов пополам.
На этом формулы вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a, b и синусоидальную функцию угла γ между a и b. Значение синуса находится в таблицах. Его также можно найти с помощью калькулятора. Тогда площадь треугольника равна:
Его также можно найти с помощью калькулятора. Тогда площадь треугольника равна:
По этому равенству также можно убедиться, что площадь прямоугольного треугольника определяется через длины катетов. Поскольку угол γ является прямым углом, площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, в котором сторона а известна по условию или ее длина может быть найдена при решении. Больше о фигуре в задаче по геометрии ничего не известно. Тогда как найти площадь при этом условии? В этом случае применяется формула площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать размеры сторон, имеющих общую вершину? Выражение для расчета:
Если вы хотите использовать длины диагоналей для вычисления площади прямоугольника, то вам нужна функция синуса угла, образованного при их пересечении. Формула площади прямоугольника:
Квадрат
Площадь квадрата определяется как вторая степень длины стороны:
Доказательство следует из определения, что прямоугольник называется квадратом. Все стороны, образующие квадрат, имеют одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к умножению одной на другую, т. е. ко второй степени стороны. И формула вычисления площади квадрата примет нужный вид.
Все стороны, образующие квадрат, имеют одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к умножению одной на другую, т. е. ко второй степени стороны. И формула вычисления площади квадрата примет нужный вид.
Площадь квадрата можно найти и другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной круг? Для вычисления площади используются формулы:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если высота неизвестна, то как найти площадь параллелограмма? Есть еще один способ расчета. Требуется определенное значение, которое примет тригонометрическая функция угла, образованного соседними сторонами, а также их длины.
Формулы площади параллелограмма:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических операций с диагоналями. Доказательство основано на том факте, что диагональные отрезки d1 и d2 пересекаются под прямым углом. Таблица синусов показывает, что для прямого угла эта функция равна единице. Следовательно, площадь ромба вычисляется так:
Доказательство основано на том факте, что диагональные отрезки d1 и d2 пересекаются под прямым углом. Таблица синусов показывает, что для прямого угла эта функция равна единице. Следовательно, площадь ромба вычисляется так:
Площадь ромба можно найти и другим способом. Это также нетрудно доказать, учитывая, что его стороны одинаковы по длине. Затем подставьте их произведение в аналогичное выражение для параллелограмма. Ведь частный случай именно этой фигуры – ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяется так:
Трапеция
Как найти площадь трапеции через основания (а и б), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не получится. Поскольку это значение содержит выражение для расчета:
Точно так же можно рассчитать площадь прямоугольной трапеции. При этом учитывается, что в прямоугольной трапеции совмещены понятия высоты и стороны. Поэтому для прямоугольной трапеции нужно указывать длину стороны вместо высоты.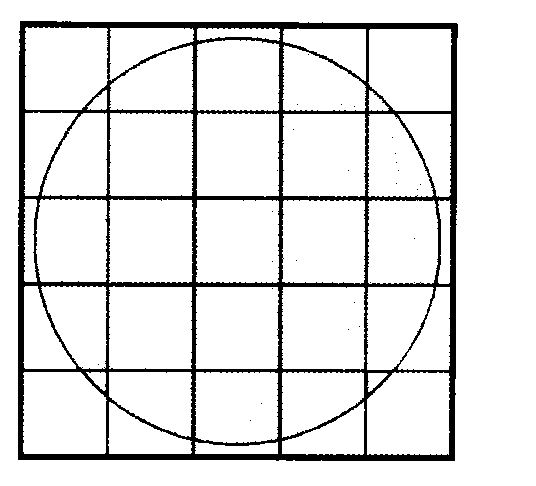
Цилиндр и параллелепипед
Рассмотрим, что нужно для расчета поверхности всего цилиндра. Площадь этой фигуры – это пара окружностей, называемых основаниями, и боковая поверхность. Окружности, образующие окружности, имеют длину радиуса, равную r. Для площади цилиндра происходит следующий расчет:
Как найти площадь параллелепипеда, состоящего из трех пар граней? Его измерения соответствуют конкретной паре. Грани, находящиеся напротив, имеют одинаковые параметры. Сначала найдите S(1), S(2), S(3) — квадратные размеры неравных граней. Тогда площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Также они ограничивают площадь кольца. При этом обе формулы расчета учитывают размеры каждой окружности. Первый, вычисляющий площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешними и внутренними. Во втором выражении площадь кольца рассчитывается с использованием большего диаметра D и меньшего диаметра d. Таким образом, площадь кольца по известным радиусам вычисляется следующим образом:
Таким образом, площадь кольца по известным радиусам вычисляется следующим образом:
Площадь кольца, используя длины диаметров, определяется следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого неверна? Общей формулы площади таких фигур не существует. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, то как в этом случае найти площадь поверхности? Здесь используют метод, не требующий приблизительного измерения фигуры. Делают так: если находят точки, попадающие в угол ячейки или имеющие целочисленные координаты, то учитываются только они. Чтобы затем узнать, чему равна площадь, воспользуйтесь формулой, доказанной Пиком. Необходимо сложить количество точек, находящихся внутри ломаной с половиной лежащих на ней точек, и вычесть единицу, т.е. вычисляется так:
где C, D — количество точек, расположенных внутри и на всей полилинии соответственно.
С таким понятием, как площадь, нам приходится сталкиваться в нашей жизни каждый день. Так, например, при строительстве дома его необходимо знать, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Без этого определения не обойтись даже ремонт в квартире. Поэтому вопрос, как найти площадь прямоугольника, возникает у нас очень часто и важен не только для школьников.
Так, например, при строительстве дома его необходимо знать, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Без этого определения не обойтись даже ремонт в квартире. Поэтому вопрос, как найти площадь прямоугольника, возникает у нас очень часто и важен не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура с равными противоположными сторонами и углами по 90 градусов. Для обозначения области в математике используется английская буква S. Измеряется в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попробуем дать развернутый ответ на вопрос, как найти площадь прямоугольника. Есть несколько способов определить это значение. Чаще всего мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник шириной b и длиной k. Чтобы вычислить площадь данного прямоугольника, умножьте ширину на длину. Все это можно представить в виде формулы, которая будет выглядеть так: S = b*k.
Теперь давайте рассмотрим этот метод на конкретном примере. Необходимо определить площадь садового участка шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в математике, приходится определять площадь другими способами, так как во многих случаях мы не знаем ни длины, ни ширины прямоугольника. В то же время известны и другие величины. Как найти площадь прямоугольника в этом случае?
- Если мы знаем длину диагонали и один из углов, составляющих диагональ с любой стороной прямоугольника, то в этом случае нам нужно запомнить площадь. Ведь если разобраться, прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определенному значению. Сначала нужно определить косинус угла. Умножьте полученное значение на длину диагонали. В результате получаем длину одной из сторон прямоугольника. Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.

В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d — длина диагонали
- Другой способ определения площади прямоугольника проходит через вписанную в него окружность. Это применимо, если прямоугольник является квадратом. Чтобы воспользоваться этим методом, нужно знать Как вычислить площадь прямоугольника таким способом? Конечно, по формуле. Мы не будем это доказывать. А выглядит это так: S = 4 * r2, где r — радиус.
Бывает, что вместо радиуса мы знаем диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2, где d — диаметр.
- Если известна одна из сторон и периметр, то как в этом случае узнать площадь прямоугольника? Для этого нужно произвести ряд простых расчетов. Как известно, противоположные стороны прямоугольника равны, поэтому из значения периметра необходимо вычесть известную длину, умноженную на два. Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника.
 В форме формулы это будет выглядеть так:
В форме формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видите, площадь прямоугольника можно определить разными способами. Все зависит от того, какие величины мы знаем до рассмотрения этого вопроса. Конечно, новейшие вычислительные методы в жизни практически не встречаются, но для решения многих задач в школе они могут пригодиться. Возможно, эта статья будет полезна для решения ваших проблем.
Существует бесконечное множество плоских фигур различной формы, как правильной, так и неправильной. Общим свойством всех фигур является то, что любая из них имеет площадь. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Это значение всегда выражается как положительное число. Единицей измерения является площадь квадрата, сторона которого равна единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она делится, на площадь одного квадрата.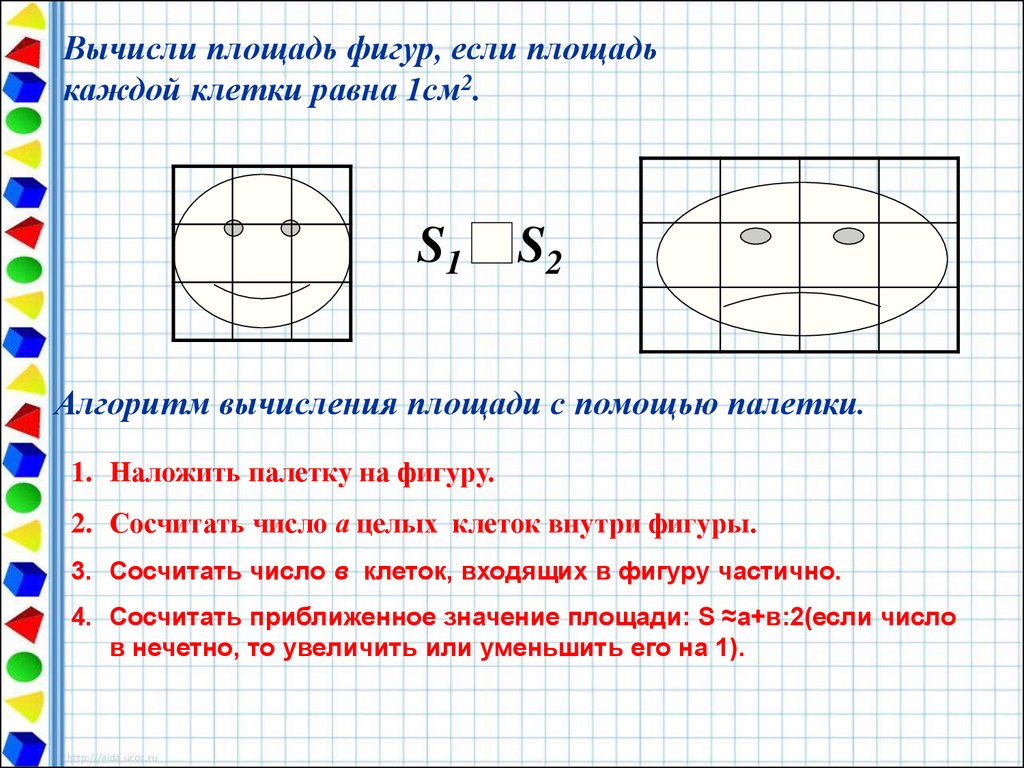
Другие определения этого понятия следующие:
1. Площади простых фигур – скалярные положительные величины, удовлетворяющие условиям:
Равные фигуры имеют равные площади;
Если фигура делится на части (простые фигуры), то ее площадь равна сумме площадей этих фигур;
Квадрат с единицей измерения стороны служит единицей площади.
2. Площади фигур сложной формы (многоугольников) – положительные величины со следующими свойствами:
Равные многоугольники имеют одинаковую площадь;
Если многоугольник состоит из нескольких других многоугольников, его площадь равна сумме площадей последних. Это правило верно для непересекающихся полигонов.
В качестве аксиомы принято утверждение, что площади фигур (многоугольников) являются положительными величинами.
Определение площади круга дано отдельно как величина, к которой стремится площадь данного круга, вписанного в круг, — несмотря на то, что число его сторон стремится к бесконечности.
Площади фигур неправильной формы (произвольных фигур) не имеют определения, определяются только способы их вычисления.
Расчет площадей уже в древности был важной практической задачей при определении размеров земельных участков. Правила вычисления площадей на несколько сотен лет были сформулированы греческими учеными и изложены в «Началах» Евклида в виде теорем. Интересно, что правила определения площадей простых фигур в них такие же, как и в настоящее время. Области с криволинейным контуром вычислялись с помощью предельного перехода.
Вычисление площадей простых прямоугольников, квадратов), знакомое всем со школы, довольно просто. Не обязательно даже запоминать формулы, содержащие буквенные обозначения площадей фигур. Просто запомните несколько простых правил:
2. Площадь прямоугольника вычисляется путем умножения его длины на ширину. При этом необходимо, чтобы длина и ширина были выражены в одних и тех же единицах измерения.
3. Вычисляем площадь сложной фигуры, разделив ее на несколько простых и сложив полученные площади.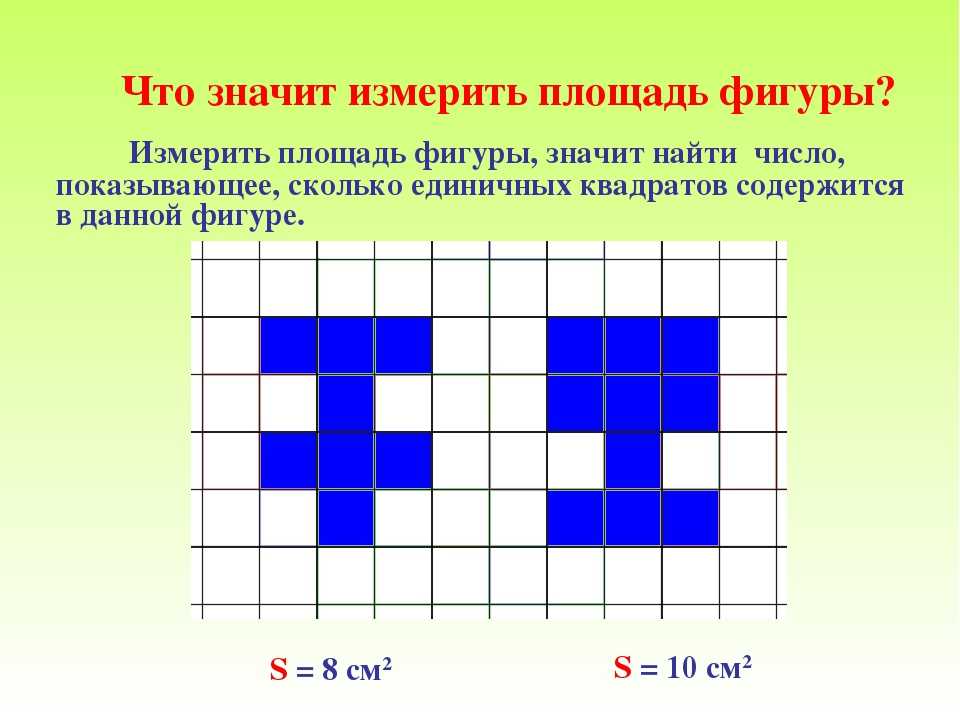
4. Диагональ прямоугольника делит его на два треугольника, площади которых равны и равны половине его площади.
5. Площадь треугольника вычисляется как половина произведения его высоты на основание.
6. Площадь круга равна произведению квадрата радиуса на известное число «π».
7. Площадь параллелограмма вычисляется как произведение смежных сторон на синус угла, лежащего между ними.
8. Площадь ромба равна ½ результата умножения диагоналей на синус внутреннего угла.
9. Площадь трапеции находится путем умножения ее высоты на длину средней линии, которая равна среднему арифметическому оснований. Другой вариант определения площади трапеции – умножение ее диагоналей и синуса лежащего между ними угла.
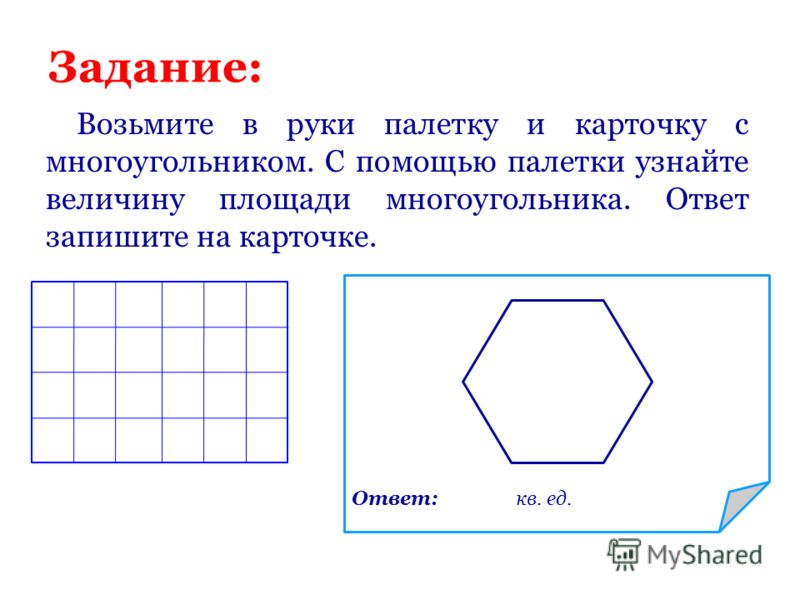
Для наглядности детям в начальной школе часто дают задания: найти площадь фигуры, начерченной на бумаге, с помощью палитры или листа прозрачной бумаги, разделенного на клетки. Такой лист бумаги накладывается на измеряемую фигуру, подсчитывается количество полных клеток (единиц площади), вписывающихся в ее контур, затем количество неполных, которое делится пополам.
Нахождение площади разных фигур. Как рассчитать и обозначить площадь. Сбор и использование личной информации
Существует бесконечное множество плоских фигур самых разных форм, как правильных, так и неправильных. Общим свойством всех фигур является то, что любая из них имеет площадь. Площади фигур — это размеры части плоскости, занимаемой этими фигурами, выраженные в конкретных единицах. Это значение всегда выражается как положительное число. Единицей измерения является площадь квадрата, сторона которого равна единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она делится, на площадь одного квадрата.
Другие определения этого понятия следующие:
1. Площади простых фигур – скалярные положительные величины, удовлетворяющие условиям:
Равные фигуры имеют равные площади;
Если фигура делится на части (простые фигуры), то ее площадь равна сумме площадей этих фигур;
Квадрат со стороной в единицу измерения служит единицей площади.
2. Площади фигур сложной формы (многоугольников) – положительные величины со следующими свойствами:
Равные многоугольники имеют одинаковую площадь;
Если многоугольник составлен из нескольких других многоугольников, его площадь равна сумме площадей последних. Это правило верно для непересекающихся полигонов.
В качестве аксиомы принято, что площади фигур (многоугольников) являются положительными величинами.
Определение площади круга дано отдельно как величина, к которой стремится площадь данного круга, вписанного в круг, — несмотря на то, что число его сторон стремится к бесконечности.
Площади неправильной формы (произвольные формы) не определяются, определяются только методы их расчета.
Расчет площадей уже в древности был важной практической задачей при определении размеров земельных участков. Правила вычисления площадей на несколько сотен лет были сформулированы греческими учеными и изложены в «Началах» Евклида в виде теорем.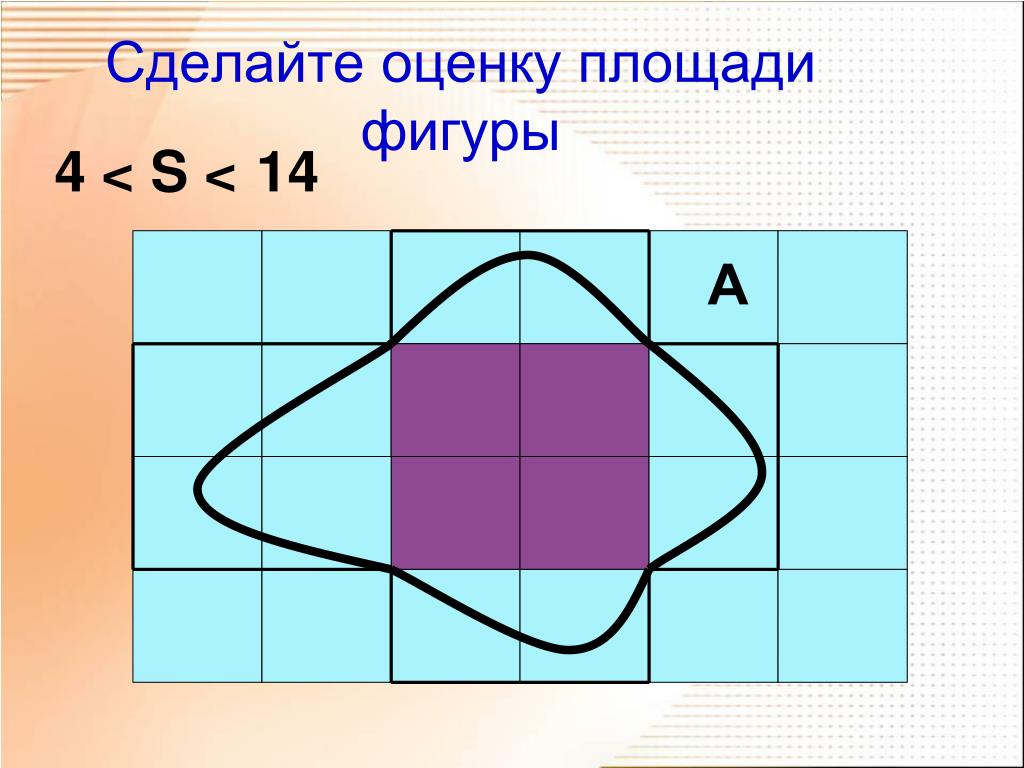 Интересно, что правила определения площадей простых фигур в них такие же, как и в настоящее время. Области с искривленным контуром рассчитывались с помощью предельного перехода.
Интересно, что правила определения площадей простых фигур в них такие же, как и в настоящее время. Области с искривленным контуром рассчитывались с помощью предельного перехода.
Вычисление площадей простого прямоугольника, квадрата), знакомое всем со школы, довольно просто. Не обязательно даже запоминать формулы площадей фигур, содержащих буквенные обозначения. Достаточно запомнить несколько простых правил:
2. Площадь прямоугольника вычисляется путем умножения его длины на ширину. При этом необходимо, чтобы длина и ширина были выражены в одних и тех же единицах измерения.
3. Площадь сложной фигуры вычисляется путем деления ее на несколько простых и сложения полученных площадей.
4. Диагональ прямоугольника делит его на два треугольника, площади которых равны и равны половине его площади.
5. Площадь треугольника вычисляется как половина произведения его высоты на основание.
6. Площадь круга равна произведению квадрата радиуса и всем известного числа «π».
7. Площадь параллелограмма вычисляется как произведение прилежащих сторон на синус угла, лежащего между ними.
8. Площадь ромба равна ½ результата умножения диагоналей на синус внутреннего угла.
9. Площадь трапеции находится путем умножения ее высоты на длину средней линии, которая равна среднему арифметическому оснований. Другой вариант определения площади трапеции — умножение ее диагоналей и синуса угла, лежащего между ними.
Для наглядности детям в начальной школе часто дают задания: найти площадь фигуры, начерченной на бумаге, с помощью палитры или листа прозрачной бумаги, разрезанного на клетки. Такой лист бумаги накладывается на измеряемую фигуру, подсчитывается количество полных клеток (единиц площади), вписывающихся в ее контур, затем количество неполных клеток, которое уменьшается вдвое.
Инструкции
Это удобно, если ваша фигура представляет собой многоугольник. Вы всегда можете разбить его на конечное число, и вам нужно только запомнить одну формулу — площадь треугольника. Итак, треугольник — это половина произведения длины его стороны на длину высоты, проведенной к этой самой стороне. Суммируя площади отдельных треугольников, в которые по вашей воле трансформировался более сложный, вы узнаете искомый результат.
Итак, треугольник — это половина произведения длины его стороны на длину высоты, проведенной к этой самой стороне. Суммируя площади отдельных треугольников, в которые по вашей воле трансформировался более сложный, вы узнаете искомый результат.
Сложнее решить задачу с определением площади произвольной фигуры. Такая фигура может иметь не только, но и криволинейные границы. Есть способы грубого расчета. Простой.
Во-первых, вы можете использовать палитру. Это прозрачный инструмент с нанесенной на его поверхность сеткой квадратов или треугольников с известной площадью. Помещая палитру на фигуру, которую вы ищете, вы пересчитываете количество ваших единиц измерения, которые перекрывают изображение. Соединяйте между собой не полностью замкнутые единицы измерения, дополняя их в уме до завершения. Далее, умножая площадь одной формы палитры на число, которое было рассчитано, вы узнаете примерную площадь вашей произвольной формы. Понятно, что чем чаще сетка применяется к вашей палитре, тем точнее ваш результат. 2*α/360. Для каждой меньшей части вашей фигуры вы определяете площадь и получаете общий результат, складывая полученные значения.
2*α/360. Для каждой меньшей части вашей фигуры вы определяете площадь и получаете общий результат, складывая полученные значения.
Третий способ сложнее, но для кого-то точнее, проще. Площадь любой фигуры можно определить с помощью интегрального исчисления. Определенный интеграл функции показывает площадь от графика функции до оси абсцисс. Площадь, заключенная между двумя графиками, может быть определена путем вычитания определенного интеграла с меньшим значением из интеграла в тех же границах, но с большим значением. Для использования этого метода удобно свою произвольную фигуру перевести в систему координат, а затем определить их функции и действовать методами высшей математики, в которые мы здесь и сейчас углубляться не будем.
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация означает данные, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы отправляете запрос на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. д.
Как мы используем вашу личную информацию:
- Собираемая нами личная информация позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.

- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, постановлением суда, в судебном порядке и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои Персональные данные. Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим общественно важным причинам.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему третьему лицу — правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Уважение к вашей конфиденциальности на уровне компании
Для того, чтобы убедиться, что ваша личная информация находится в безопасности, мы доводим до наших сотрудников правила конфиденциальности и безопасности, строго следим за выполнением мер конфиденциальности.
Если вы планируете делать ремонт самостоятельно, то вам потребуется составить смету на строительные и отделочные материалы. Для этого вам потребуется рассчитать площадь помещения, в котором вы планируете проводить ремонтные работы. Главный помощник в этом – специально разработанная формула. Площадь помещения, а именно его расчет, позволит вам значительно сэкономить на строительных материалах и направить высвободившиеся финансовые средства в более нужное русло.
Геометрическая форма помещения
Формула расчета площади помещения напрямую зависит от его формы. Наиболее типичными для отечественных построек являются прямоугольные и квадратные помещения. Однако при перепланировке стандартная форма может быть искажена. Номера:
Номера:
- Прямоугольные.
- Квадрат.
- Сложная конфигурация (например, круглая).
- С нишами и выступами.
Каждый из них имеет свои расчетные характеристики, но, как правило, используется одна и та же формула. Площадь комнаты любой формы и размера, так или иначе, поддается расчету.
Прямоугольная или квадратная комната
Чтобы вычислить площадь прямоугольной или квадратной комнаты, достаточно вспомнить школьные уроки геометрии. Поэтому вам не составит труда определить площадь комнаты. Формула расчета:
S комнат = А*В, где
А — длина комнаты.
B — ширина комнаты.
Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить максимально точный расчет, стоит измерить стену с двух сторон. Если значения не сходятся, возьмите за основу среднее значение полученных данных. Но помните, что в любых расчетах есть свои погрешности, поэтому материал следует приобретать с запасом.
Помещение сложной конфигурации
Если ваше помещение не подходит под определение «типовое», т.е. имеет форму круга, треугольника, многоугольника, то вам может понадобиться другая формула для расчетов. Можно попробовать условно разделить площадь комнаты с такой характеристикой на прямоугольные элементы и произвести расчеты стандартным способом. Если у вас нет такой возможности, то воспользуйтесь следующими способами:
- Формула нахождения площади круга:
S комнаты = π * R 2 , где
R — радиус комнаты.
- Формула нахождения площади треугольника:
S комнат = √ (P (P — A) x (P — B) x (P — C)), где
P — полупериметр треугольника.
А, В, С — длины его сторон.
Отсюда Р=А+В+С/2
Если в процессе расчета у вас возникли трудности, то лучше не мучить себя и обратиться к профессионалам.
Зона помещения с выступами и нишами
Часто стены украшают декоративными элементами в виде всевозможных ниш или выступов. Также их наличие может быть связано с необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет должен производиться поэтапно. Те. сначала находят площадь плоского участка стены, а затем к ней прибавляют площадь ниши или уступа.
Также их наличие может быть связано с необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет должен производиться поэтапно. Те. сначала находят площадь плоского участка стены, а затем к ней прибавляют площадь ниши или уступа.
Площадь стен находится по формуле:
S стен = Р х С, где
Р — периметр
С — высота
Также необходимо учитывать наличие окон и дверей. Их площадь необходимо вычесть из полученного значения.
Комната с многоуровневым потолком
Многоярусный потолок не так усложняет расчеты, как кажется на первый взгляд. Если он имеет простую конструкцию, то расчеты можно производить по принципу нахождения площади стен, осложненных нишами и выступами.
Однако, если в конструкции вашего потолка есть дугообразные и волнообразные элементы, то его площадь целесообразнее определять по площади пола. Для этого требуется:
- Найдите размеры всех прямых участков стены.

- Найдите площадь пола.
- Умножьте длину и высоту вертикальных секций.
- Добавьте полученное значение к площади пола.
Пошаговая инструкция по определению общей
площади помещения
- Освободите комнату от ненужных вещей. В процессе замеров вам потребуется свободный доступ ко всем зонам вашей комнаты, поэтому нужно избавиться от всего, что может этому помешать.
- Визуально разделите комнату на правильные и неправильные зоны. Если ваша комната строго квадратная или прямоугольная, то этот шаг можно пропустить.
- Сделать произвольную планировку комнаты. Этот чертеж нужен для того, чтобы все данные всегда были у вас под рукой. Также он не даст вам возможности запутаться в многочисленных измерениях.
- Измерения необходимо проводить несколько раз. Это важное правило, позволяющее избежать просчетов. Также, если вы используете, убедитесь, что луч ровно лежит на поверхности стены.
- Найдите общую площадь комнаты.
 Формула общей площади комнаты заключается в нахождении суммы всех площадей отдельных участков комнаты. Те. S общ = S стен + S пола + S потолка
Формула общей площади комнаты заключается в нахождении суммы всех площадей отдельных участков комнаты. Те. S общ = S стен + S пола + S потолка
Как найти площадь фигуры?
Знание и умение вычислять площади различной формы необходимо не только для решения простых геометрических задач. Без этих знаний не обойтись при составлении или проверке сметы на ремонт помещения, расчете количества необходимых расходных материалов. Итак, давайте разберемся, как найти площади разной формы.
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Площадь выражается количеством заключенных в ней квадратных единиц.
Для расчета площади основных геометрических фигур необходимо использовать правильную формулу.
Площадь треугольника
Легенда:
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенного на эту сторону, деленное пополам: S = (a h ) / 2
- Если известны a, b, c, то искомая площадь вычисляется по формуле Герона: квадратный корень, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √ (р (р — а) (р — b) (р — с)).

- Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S = (a b sin γ) / 2
- Если известны a, b, c, R, то искомая площадь определяется как произведение длин всех сторон треугольника на четыре радиуса описанной окружности: S = (a b c) / 4R
- Если p, r известны, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной окружности: S = p r
Площадь
Легенда:
- Если сторона известна, то площадь этой фигуры определяется как квадрат длины ее стороны: S = a 2
- Если известно d, то площадь квадрата определяется как половина квадрата длины его диагонали: S = d 2/2
Площадь прямоугольника
Легенда:
- S — определенная площадь,
- а, б — длины сторон прямоугольника.
- Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S = a b
- Если длины сторон неизвестны, то площадь прямоугольника надо разделить на треугольники.
 В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
Площадь параллелограмма
Легенда:
- S — необходимая площадь,
- а, б — длины сторон,
- h — длина высоты этого параллелограмма,
- d1, d2 — длины двух диагоналей,
- α угол между сторонами,
- γ — угол между диагоналями.
- Если известны a, h, то искомая площадь определяется путем умножения длин стороны и высоты, опущенной на эту сторону: S = a h
- Если известны a, b, α, то площадь параллелограмма определяется путем умножения длин сторон параллелограмма на значение синуса угла между этими сторонами: S = a b sin α
- Если известны d 1 , d 2 , γ, то площадь параллелограмма определяется как половина произведения длин диагоналей на значение синуса угла между этими диагоналями: S = (d 1 d 2 sinγ) / 2
Площадь ромба
Легенда:
- S необходимая площадь,
- а — длина стороны,
- h — высота длина,
- α — меньший угол между двумя сторонами,
- d1, d2 — длины двух диагоналей.

- Если известны a, h, то площадь ромба определяется путем умножения длины стороны на длину высоты, которая опущена на эту сторону: S = a h
- Если известны a, α, то площадь ромба определяется умножением квадрата длины стороны на синус угла между сторонами: S = a 2 sin α
- Если d 1 и d 2 известны, то искомая площадь определяется как половина произведения длин диагоналей ромба: S = (d 1 d 2) / 2
Площадь трапеции
Легенда:
- Если известны a, b, c, d, то искомая площадь определяется по формуле: S = (a + b) / 2 * √.
- При известных a, b, h искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S = (a + b) / 2 h
Площадь выпуклого четырехугольника
Легенда:
- Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника на синус угла между этими диагоналями: S = (d 1 d 2 sin α) / 2
- При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S = p r
- Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разности полупериметра и длины каждой стороны за вычетом произведения из длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a ) (p — b) (p — c) (p — d) — abcd cos 2 ( (α + β) / 2)
Площадь круга
Легенда:
Если известно r, то искомая площадь определяется как произведение числа π на квадрат радиуса: S = π r 2
Если известно d, то площадь круга определяется как произведение π на квадрат диаметра, деленное на четыре: S = (π d 2) / 4
Площадь сложной фигуры
Сложный можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность площадей составляющих. Рассмотрим, например, кольцо.
Площадь сложной фигуры определяется как сумма или разность площадей составляющих. Рассмотрим, например, кольцо.
Обозначение:
- S — площадь кольца,
- R, r — радиусы внешней и внутренней окружностей соответственно,
- D, d — диаметры наружной и внутренней окружностей соответственно.
Для того чтобы найти площадь кольца, необходимо из площади большего круга вычесть меньший круг. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).
Таким образом, если R и r известны, то площадь кольца определяется как разность квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S = π (R 2 -р 2).
Если D и d известны, то площадь кольца определяют как четверть разности квадратов диаметров наружной и внутренней окружностей, умноженной на число пи: S = (1/ 4) (D 2 -d 2) π.
Площадь заполненной фигуры
Предположим, что внутри одного квадрата (А) находится другой (В) (меньшего размера), и нам нужно найти заполненную полость между фигурами «А» и «В».

 И если да, то как?
И если да, то как?
 В форме формулы это будет выглядеть так:
В форме формулы это будет выглядеть так: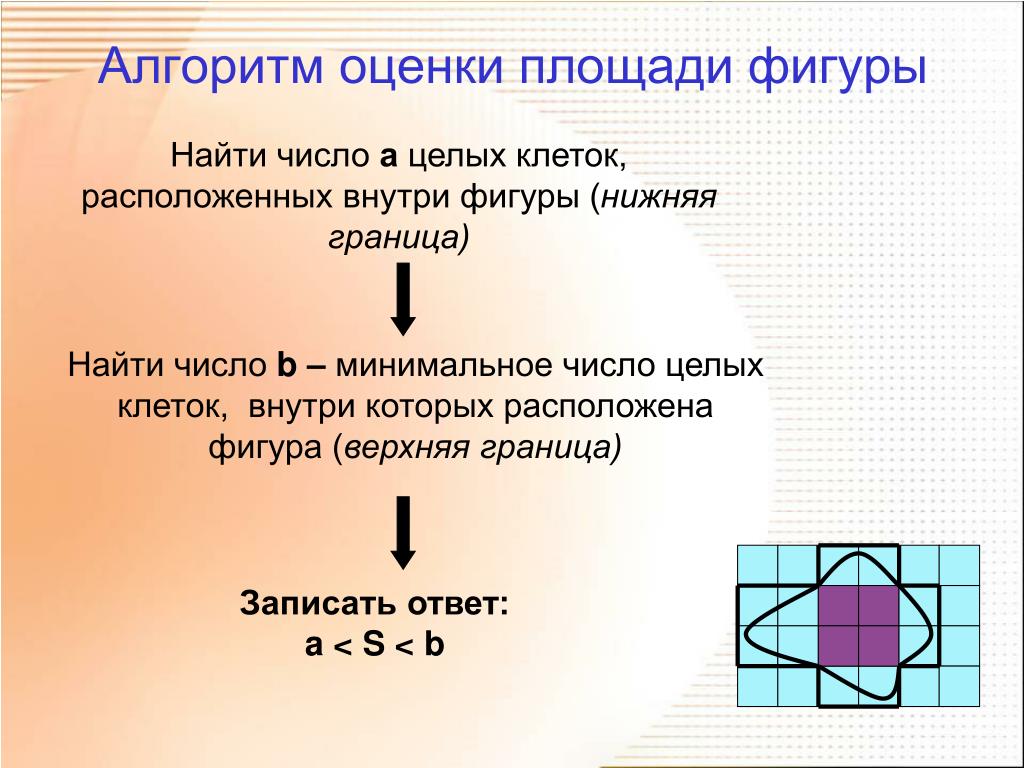

 Формула общей площади комнаты заключается в нахождении суммы всех площадей отдельных участков комнаты. Те. S общ = S стен + S пола + S потолка
Формула общей площади комнаты заключается в нахождении суммы всех площадей отдельных участков комнаты. Те. S общ = S стен + S пола + S потолка
 В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.