Измерение площади фигуры с помощью палетки
Урок 20. Математика и игры 3–4 классы
В этом видеоуроке мы расскажем, что представляет из себя палетка, какие бывают палетки. Научимся находить площадь фигуры с помощью палетки.
Конспект урока «Измерение площади фигуры с помощью палетки»
В повседневной жизни людям часто приходится находить площадь комнаты, площадь окна в комнате, площадь садового участка, площадь поля.
Так, например, площадь комнаты надо знать, чтобы купить необходимое количество краски для покраски пола в этой комнате. Чтобы найти площадь комнаты, надо её длину умножить на ширину. Ведь пол комнаты обычно имеет форму прямоугольника.
Таким же образом можно найти площадь грядки в огороде, так как она представляет собой прямоугольник.
А
вот как, например, найти площадь лужи? Ведь её границы имеют неправильную форму
– это не прямоугольник, не квадрат и даже не круг.
Сейчас мы поговорим о том, как найти площадь любой, даже самой искривлённой фигуры.
Посмотрите на эту прозрачную пластинку или плёнку с разлиновкой в клеточку, которая называется палеткой. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры, квадратные дециметры.
Давайте найдём площадь вот такой фигуры.
Итак, возьмём палетку, которая разделена на квадратные сантиметры. Следует отметить, что в школе чаще всего пользуются именно такими палетками.
Накладываем эту палетку на нашу фигуру так, чтобы, если это возможно, хотя бы одна сторона совместилась с линией разлиновки палетки. У нашей фигуры удалось совместить даже не одну, а две стороны. И уголки верхней и нижней сторон фигуры совпадают с уголками клеточек палетки.
Сначала
считаем, сколько всего целых квадратов, то есть квадратных сантиметров,
укладывается в данной фигуре. Их 40.
Теперь считаем все оставшиеся кусочки. Их 12.
Каждые 2 таких кусочка принято засчитывать за 1 полный квадратик. Поэтому количество таких кусочков надо разделить на 2.
Далее к 40 прибавляем частное 12 и 2. Получаем 46. Так как палетка разделена на квадратные сантиметры, то площадь фигуры примерно равна 46 квадратным сантиметрам.
40 + 12 : 2 = 46 (см2)
Примерно, потому что с помощью палетки площадь фигуры вряд ли можно точно определить. Ведь 2 кусочка редко могут идеально заменить целый квадратик.
А сейчас давайте найдём с помощью палетки площадь вот такой фигуры.
Эта фигура напоминает лужу и здесь уже совместить линии фигуры с разметкой палетки не получится. Снова воспользуемся палеткой, которая разделена на квадратные сантиметры. Накладываем её на данную фигуру и считаем целые квадратики. Их 28.
Теперь считаем кусочки. Их 30.
Снова повторим, что 2 таких кусочка принято
засчитывать за один полный квадратик, поэтому их количество надо разделить на 2.
К 28 прибавим частное 30 и 2. Получим, что площадь рассматриваемой фигуры примерно равна 43 квадратным сантиметрам.
28 + 30 : 2 = 43 (см2)
Далее найдём площадь вот такой фигуры.
Накладываем на неё палетку. В первую очередь считаем, сколько целых квадратиков укладывается в этой фигуре. Их 26. Теперь считаем кусочки. Их 21.
Обратите внимание, что в данном случае количество кусочков – нечётное число. В таком случае на 2 надо делить ближайшее чётное число, которое больше данного на один, ведь всё равно с помощью палетки точно найти площадь фигуры невозможно. А вот почему берём чётное число, которое больше данного, вы узнаете в пятом классе. То есть надо 22 разделить на 2.
Таким образом, чтобы найти площадь фигуры, к 26 прибавим частное 22 и 2. Получим, что площадь примерно равна 37 квадратным сантиметрам.
26 + 22 : 2 = 37 (см2)
И найдём площадь ещё одной фигуры – треугольника.
Накладываем
на него палетку.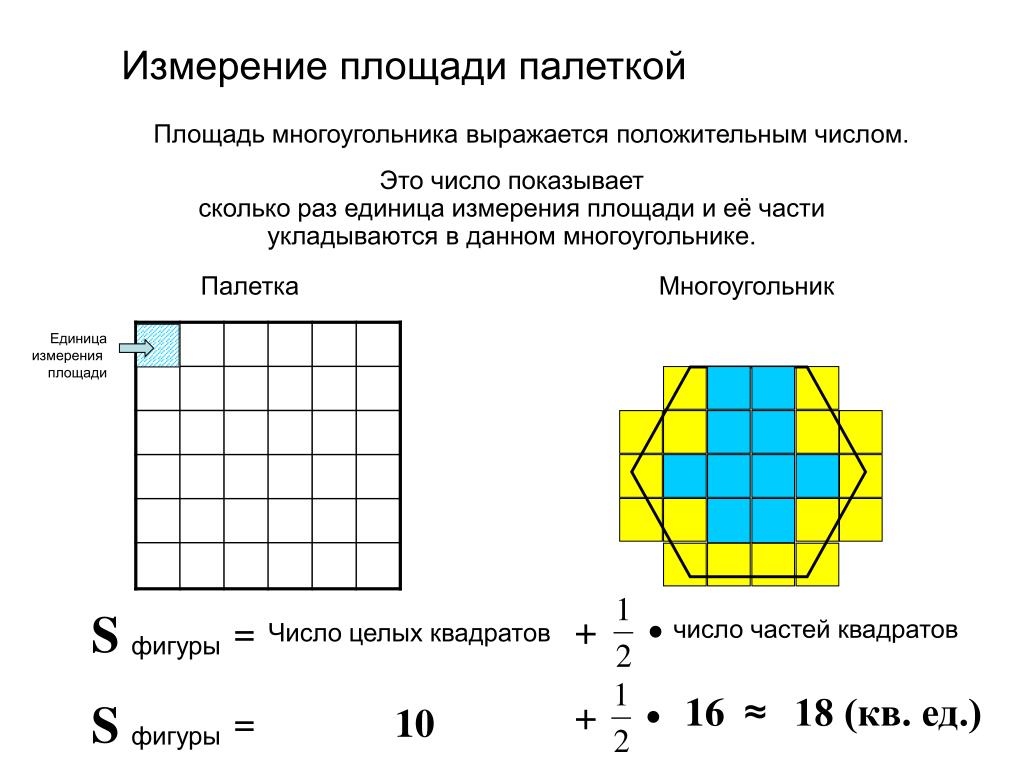
Здесь удаётся с разметкой палетки совместить одну из сторон. Я
думаю, вы уже догадались, что если удастся совместить одну из сторон фигуры с
разметкой палетки, и углы фигуры совместятся с уголками квадратиков, то
останется меньше кусочков, и измерение будет более точным.
Сначала считаем целые квадратики. Их 21. Затем считаем кусочки. Их 18.
Прибавим к 21 частное 18 и 2 и получим, что площадь треугольника примерно равна 30 квадратным сантиметрам.
21 + 18 : 2 = 30 (см2)
Итак, повторим, как мы определяем площадь фигуры с помощью палетки.
Предыдущий урок 19 Задачи с геометрическим содержанием
Следующий урок 21 Задачи на нахождение площади сложных фигур
Получите полный комплект видеоуроков, тестов и презентаций Математика и игры 3–4 классы
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
| Этапы урока | Формируемые умения | Деятельность учителя | Деятельность обучающихся |
I. Мотивация к учебной
деятельности. |
Умение мобилизовать волевую сферу для учебной деятельности. | Приветствует учащихся, проверяет
готовность класса и оборудования, эмоционально
настраивает на учебную деятельность. Прозвенел
уже звонок, Слайд 3. |
Слушают учителя. Демонстрируют готовность к уроку, готовят рабочее место к уроку. |
| II. Актуализация знаний. | Владеют способами выполнения заданий
творческого и поискового характера, логическими
действиями, базовыми предметными понятиями. |
1. Выполните действия в задании
“Цепочка”. Слайд 4. 2. Составьте четыре верных равенства, используя данные значения: 15 см 2, 800 дм 2, 30 000 см 2, 23м 2, 8 м 2, 3 м 2, 2300 дм 2, 1500 мм 2. Слайды 5-6. — Что вы располагали в порядке возрастания? — Какими знаниями вы уже владеете в рамках этой темы? |
Выполняют задания.
Отвечают на вопросы. |
| III. Фиксирование затруднений в пробном учебном действии. | Принимать и сохранять учебную задачу,
участвовать в обсуждении учебных проблем; точно
выражать свои мысли; ориентироваться в своей
системе знаний – отличают новое от уже
известного. |
1. Вычислите площадь фигур. Слайд 7-9. 2. Почему не смогли найти площадь последней фигуры? |
Выполняют задания.
Отвечают на вопросы. |
| IV. Выявление причины затруднения. | Принимать и сохранять учебную задачу, участвовать в обсуждении учебных проблем; точно выражать свои мысли. | — Какая проблема? — Определим тему урока — Какова цель нашего урока? Слайд 10. |
-Не знаем, как найди площадь фигуры
неопределённой формы. -Узнать, как находить площадь фигур неопределённой формы. |
| V. Построение проекта выхода из затруднения. | Принимать цель деятельности,
работать по предложенному плану; сохранять учебную задачу; контролировать и оценивать свои действия и их результаты; производить коррекцию на основе содержательной оценки; анализировать объект, выделяя существенные признаки, делать умозаключения; работать с информационными источниками; договариваться в процессе решения задачи,
точно выражать свои мысли, владеть диалогической
речью. |
— Как вы находили площадь
прямоугольника, когда ещё не знали формулу его
площади? — Как можно узнать площадь криволинейной фигуры с помощью мерки? |
— Мы измеряли площадь прямоугольника с
помощью мерки.
— Разбить на мерки. |
| — Что будете делать, когда разобьёте фигуру на мерки, чтобы узнать площадь фигуры? | — Посчитаем количество мерок в фигуре. Работа в группах. Представители от групп записывают свои ответы на доске. Ответы оказываются разными. |
||
| — Почему ответы оказались разными? | — Мы не считали нецелые мерки. | ||
| — Что же делать с неполными мерками,
ребята? Как их считать? — Да, в математике
договорились считать всё количество неполных
мерок и делить на 2. |
— Складывать по две мерки. | ||
| — Посчитайте ещё раз количество полных
мерок. Неполных мерок. -Скольким квадратным меркам равна площадь фигуры? — Подумайте, удобно ли каждый раз размечать фигуру на мерки? |
Работают в группах. Представители от групп называют ответы. Все сверяют со своими ответами. |
||
| — Чтобы ускорить работу, люди придумали
приспособление для определения площади фигур. (Учитель
раздает детям прозрачные пленки, расчерченные на
квадратные сантиметры, и карточки с фигурами.) - Откройте учебники на стр.43 и прочитайте, как оно называется. Слайд 11. — Проговорите алгоритм нахождения площади фигуры неопределённой формы с помощью палетки. Слайд 12. — Найдите с помощью палетки площадь фигуры. |
Палетка — прозрачная пленка,
разделенная на одинаковые квадраты. - Накладываем палетку на фигуру. Считаем количество полных квадратов. Считаем количество неполных квадратов и делим пополам. Складываем результаты. Выполняют задание. |
||
| VI. Физкультминутка. | Снять усталость и напряжение, выработать четкие координированные действия во взаимосвязи с речью. | Проговаривает слова физкультминутки. | Выполняют соответствующие движения. |
| VII. Первичное закрепление с проговариванием во внешней речи. | Владеют способами выполнения заданий
поискового характера, логическими действиями,
базовыми предметными понятиями. Принимают и сохраняют учебную задачу. Проявляют готовность слушать друг друга. |
— Найдите с помощью палетки площадь
фигуры. Стр.43 № 191 (зелёная фигура) |
Работа по учебнику (с комментированием) |
| VIII.Самостоятельная работа с самопроверкой по эталону. | Владеют способами выполнения заданий
поискового характера, логическими действиями,
базовыми предметными понятиями. Принимают и сохраняют учебную задачу. |
-Найдите самостоятельно с помощью
палетки площадь фигуры. Стр.43 № 191 (красная фигура). Слайд 14. |
Самостоятельная работа с самопроверкой. |
| IX. Включение в систему знаний и повторения. | Владеют способами выполнения заданий
поискового характера, логическими действиями,
базовыми предметными понятиями. About the Author Related Posts |
Слайд
13.