Урок 22. площадь прямоугольника — Математика — 3 класс
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки.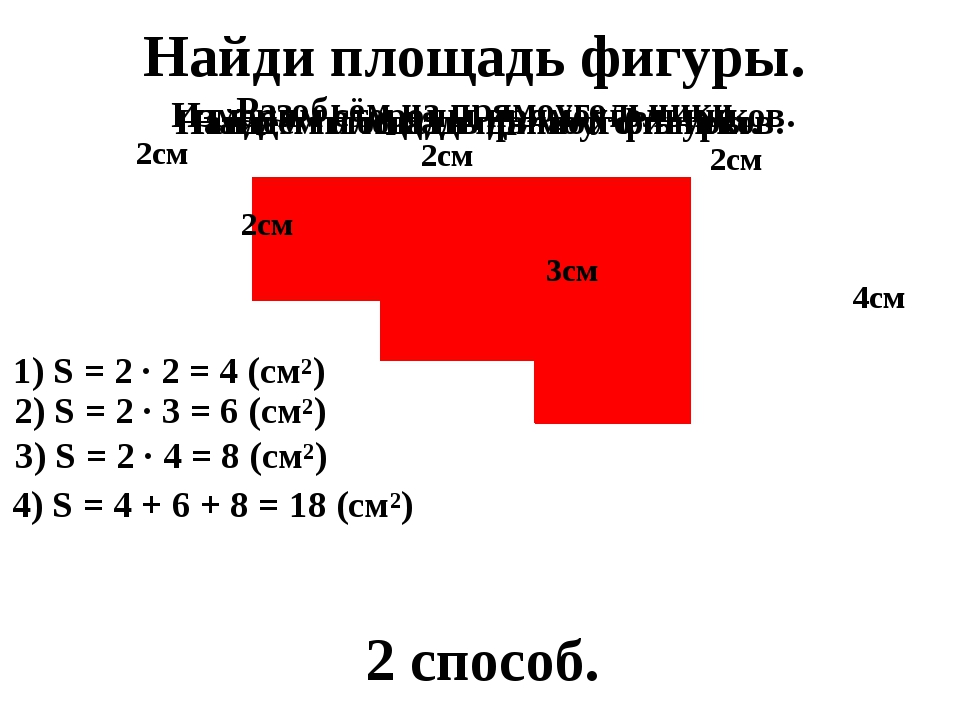
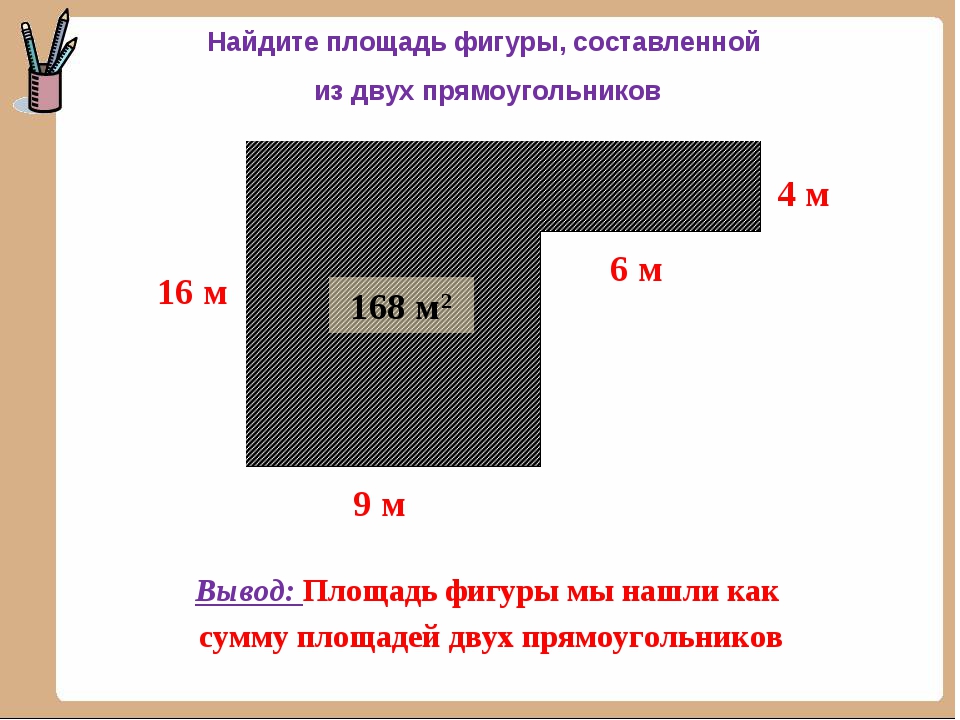
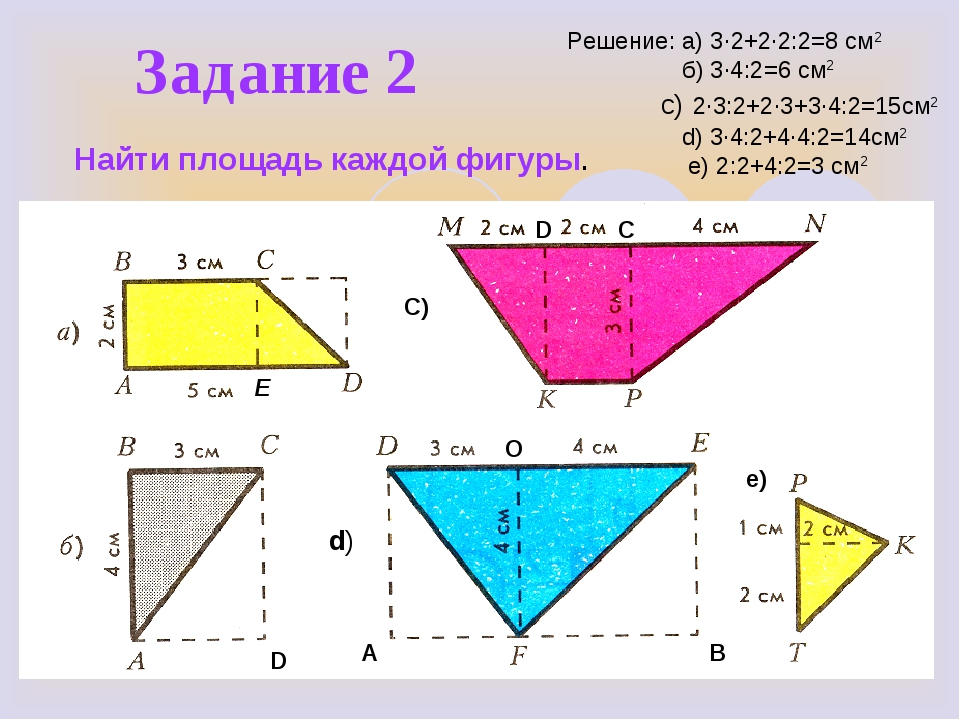
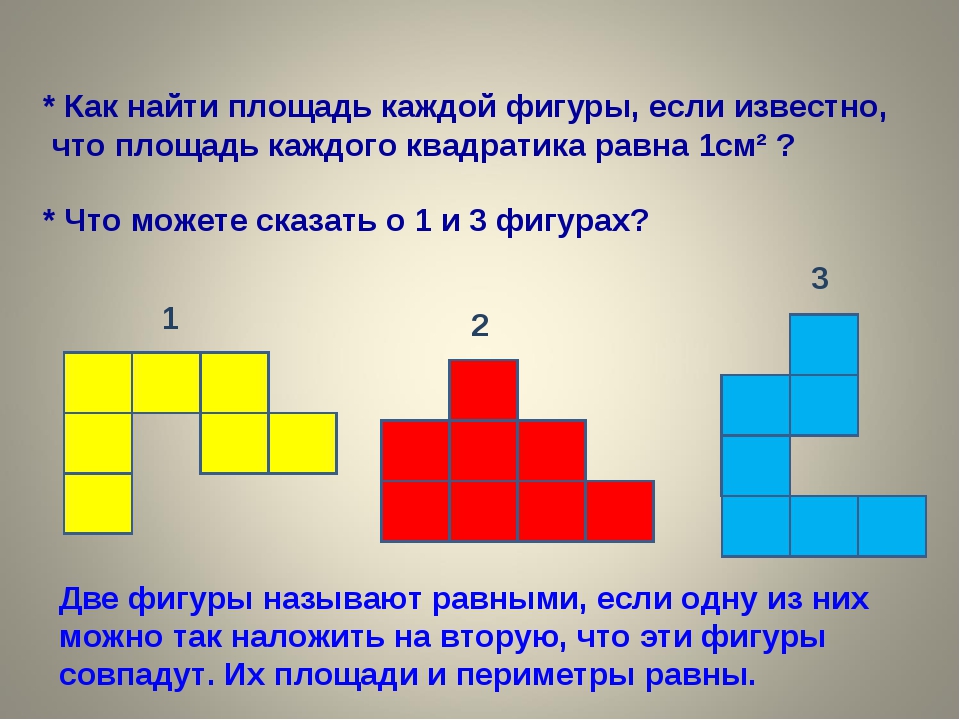
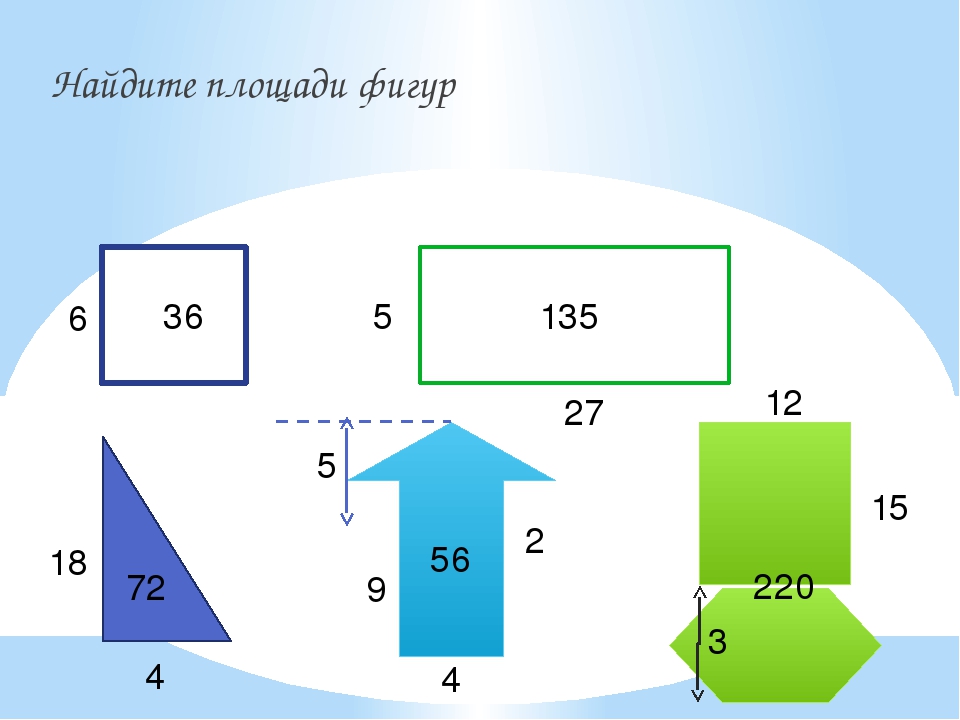
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
Правильный ответ:
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ:32см2.
Нахождение площади фигуры, прямоугольника. Математика, 3 класс: уроки, тесты, задания.
| 1. |
Площадь квадрата
Сложность: лёгкое |
1 |
2.
|
Площадь прямоугольника
Сложность: лёгкое |
1 |
| 3. |
Найди сторону прямоугольника, зная его площадь
Сложность: лёгкое |
1 |
| 4. |
Найди площадь квадрата, зная его периметр
Сложность: среднее |
2 |
5.
|
Найди периметр прямоугольника, зная его площадь
Сложность: среднее |
2 |
| 6. |
У какой клумбы больше площадь?
|
2 |
| 7. |
Площадь незакрашенной части прямоугольника
Сложность: среднее |
2 |
8.
|
Изменится ли периметр и площадь клумбы
Сложность: сложное |
3 |
| 9. |
Площадь дорожки в саду
Сложность: сложное |
3 |
| 10. |
Сравни площади квадратов
Сложность: сложное |
3 |
3 класс, периметр и площадь прямоугольника
Дата публикации: .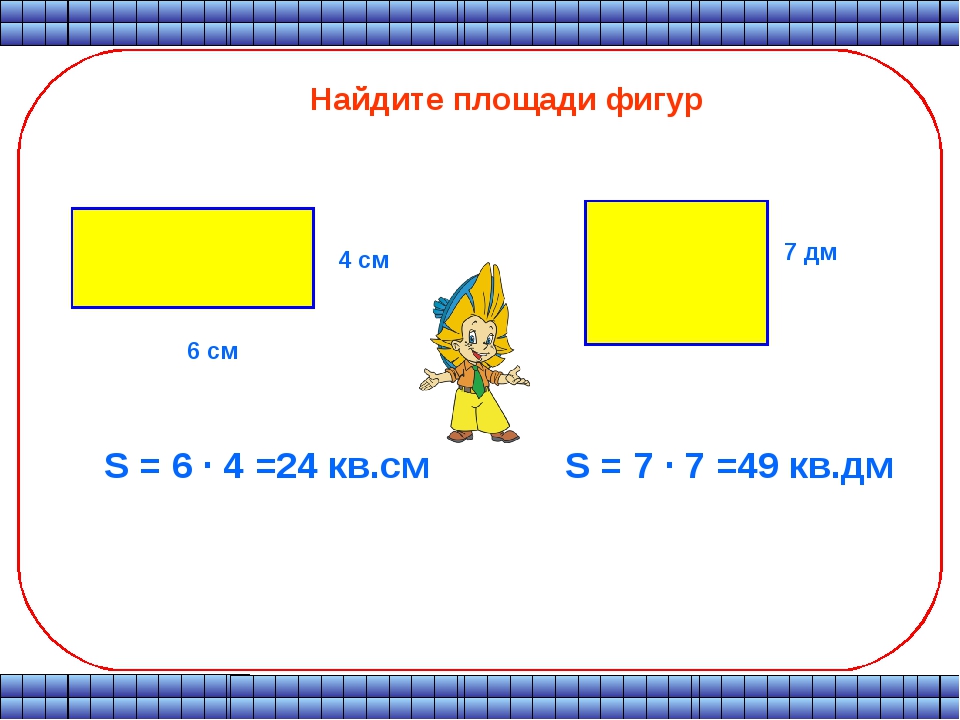
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
PABCD = 2 * (AB + BС)
3. Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
PABCD= 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
PABCD = 4 * AB
3. Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Ответ: 14 см2.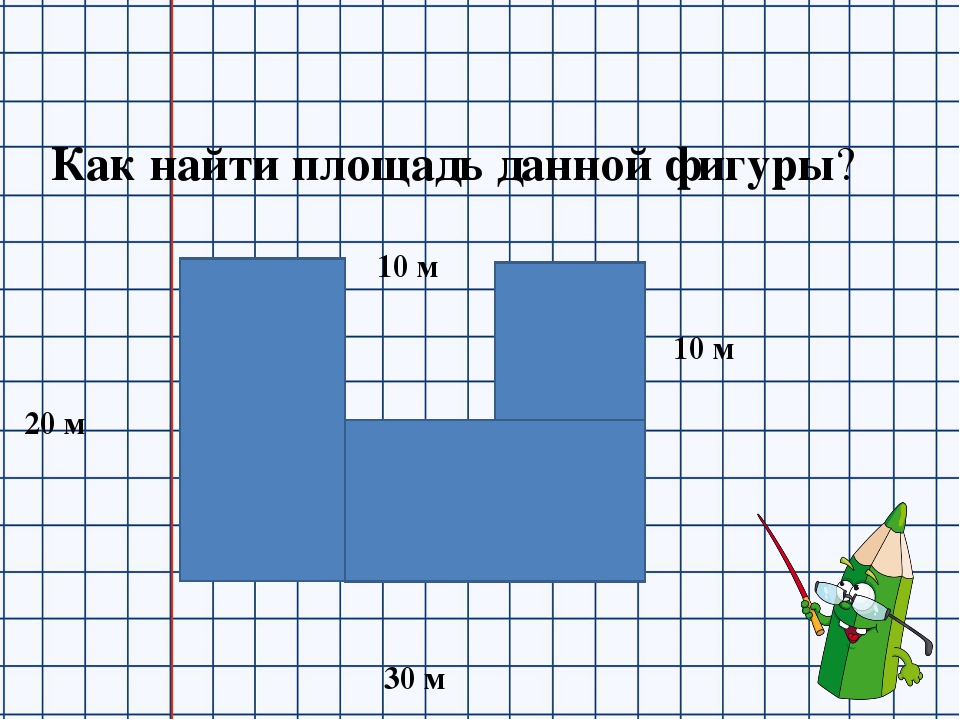
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см2
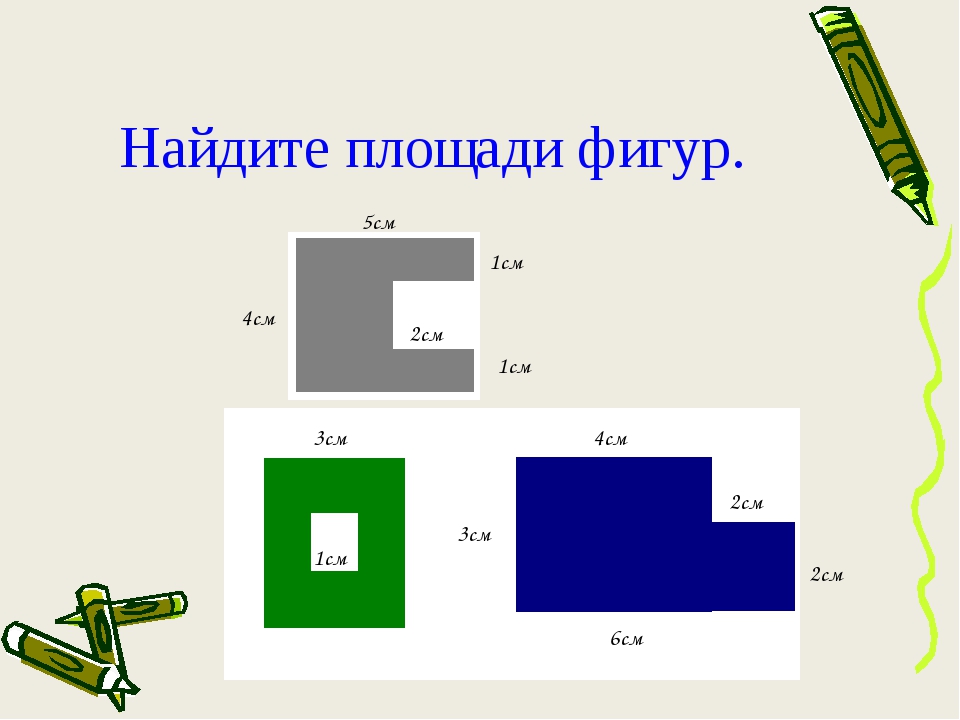
Ответ: 64 см2.Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
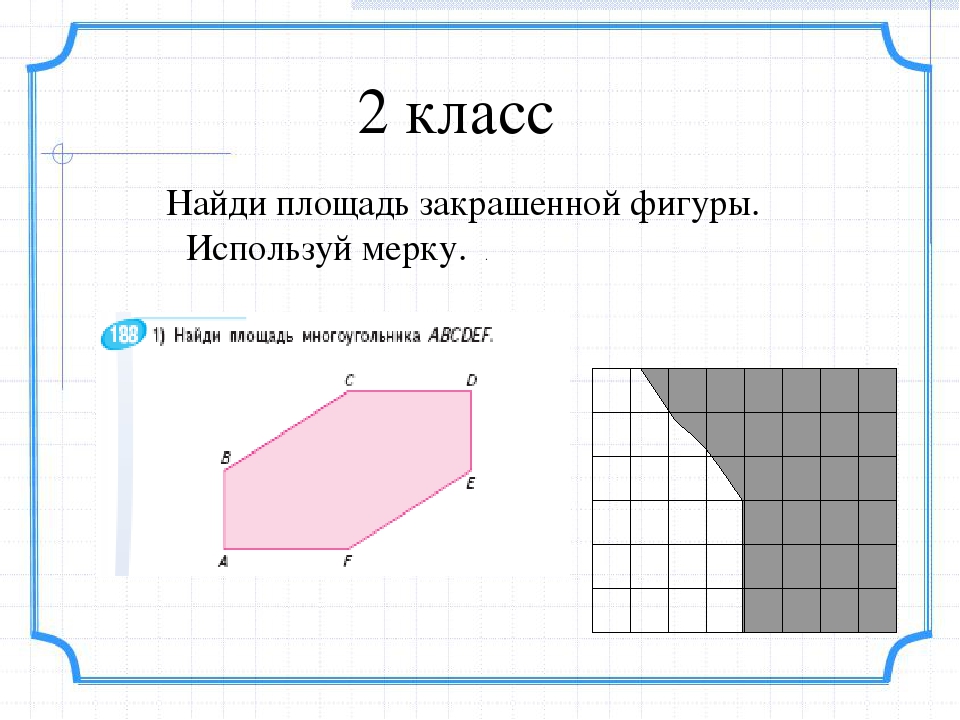
Как найти площадь фигуры? Ответ на webmath.ru
Содержание:
Определения
Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.
Определение
Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.
Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.
Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.
Если фигура имеет площадь, то она называется квадрируемой.
Формулы площади основных геометрических фигур
Площадь треугольника
Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. {2}$$
{2}$$
Читать дальше: формула площади круга и примеры решений →
Площадь квадрата
Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть
Читать дальше: формула площади квадрата и примеры решений →
Площадь прямоугольника
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть
Читать дальше: формула площади прямоугольника и примеры решений →
Площадь параллелограмма
Чтобы найти площадь параллелограмма, нужно найти произведение стороны $a$ параллелограмма на высоту , проведенную к этой стороне, то есть
Читать дальше: формулы площади параллелограмма и примеры решений →
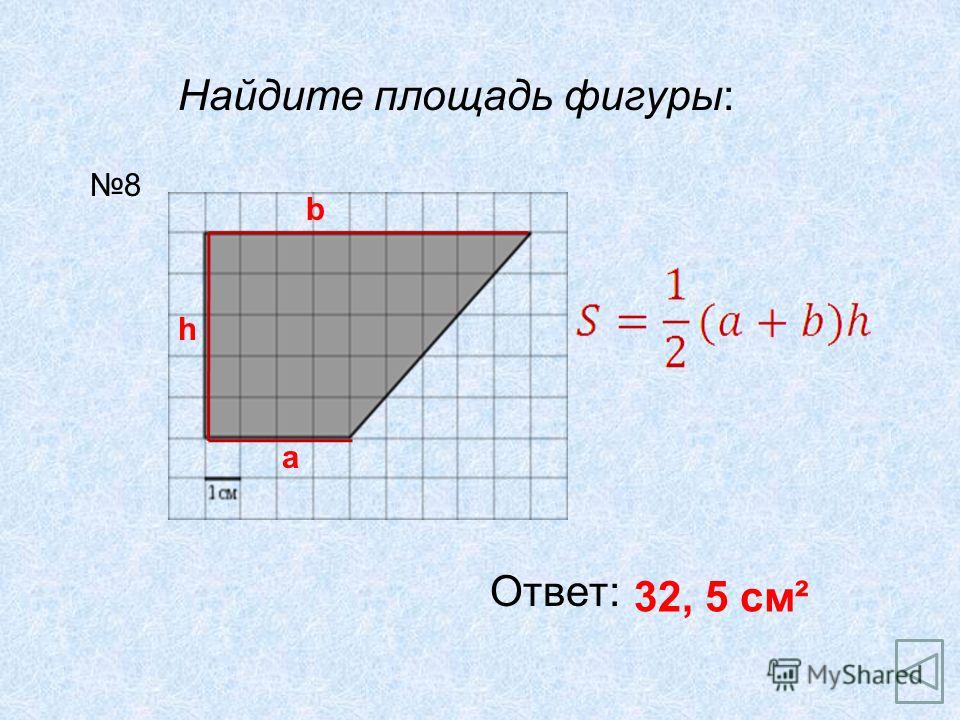
Площадь трапеции
Чтобы найти площадь трапеции, нужно длину средней линии умножить на длину высоты , опущенной к основанию:
Читать дальше: формулы площади трапеции и примеры решений →
Площадь ромба
Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:
Читать дальше: формулы площади ромба и примеры решений →
Площадь эллипса
Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число $\pi$, то есть
Читать дальше: формула площади эллипса и примеры решений →
«Площади фигур». 3-й класс
Тип урока: урок комплексного применения знаний и умений
Цель урока: создавать условия для формирования умения решать задачи на нахождение площади фигур через совершенствование вычислительных навыков, знакомство со старинными мерами длины и площади, развитие логического мышления учащихся, кругозора, трудолюбия и аккуратности.
Задачи урока:
Образовательные:
- формировать целостный взгляд на мир средствами
междисциплинарных связей на уроке;
ориентировать на разнообразие способов решения
задач и выбор наиболее рациональных из них;
отрабатывать навыки решения задач с применением
известных формул.

Развивающие:
- развивать творческую и мыслительную деятельность учащихся через решение геометрических заданий; формировать навыки самостоятельной и коллективной работы.
Воспитательные:
- прививать учащимся интерес к предмету через решение задач; формировать умение ясно и четко излагать свои мысли, правильно и рационально решать геометрические задачи; воспитывать веру в свои силы.
Методы: практический, частично-поисковый.
Организация пространства: работа фронтальная, групповая, индивидуальная, в парах (учащиеся располагаются за столами по 4 человека).
Оборудование: модели единиц площади (1см2, 1дм2, 1м2) на стенах класса, модели сложных фигур на листах А2, индивидуальные листы, презентация, листы А4, фломастеры.
Личностные УУД: осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Регулятивные УУД: определять и формулировать цель на уроке с помощью учителя; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.
Коммуникативные УУД: развивать коммуникативные навыки работы в группе.
Познавательные УУД: ориентироваться в своей системе знаний; понимать информацию, представленную в схематичной, модельной форме; выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; самостоятельно создавать способы решения проблем творческого и поискового характера.
Планируемые результаты:
Метапредметные
- использовать знаково-символические средства
представления информации для создания способов
решения практических задач.

Предметные результаты
- Уметь вычислять площади простых и сложных фигур разными способами;
- Уметь использовать наглядные модели (план, чертеж, схема), отражающие отношения между предметами для решения задач;
- Овладеть основами пространственного воображения, измерения, наглядного представления периметра и площади фигур.
Ход урока
I. Организационный момент
Учитель:
— Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В мир математики отправимся смело,
В мир примеров и разных задач.
А девизом нашего урока будут слова: (Хором.)Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно! (Слайд 2.)
II. Актуализация знаний учащихся
Учитель:
— Перед Вами древнерусская деревня. (Слайд 3.)
(Читает ученик.) Полторы тысячи лет прошло с тех пор, как на берегу реки на большой лесной равнине поселились славяне. Свое поселение они обнесли частоколом, высотой в целую сажень. Длина деревни достигала одной версты. В домах древних славян пол был углублен в землю почти на целый аршин. В углу находилась сложенная из камня печь - она обогревала дом, на ней же готовили еду. Вход в избу закрывала дверь толщиной в вершок.
— О каких величинах Вы услышали?
— Их использовали наши предки. Ребята познакомят с ними. (Слайды 4 — 9.) (Сообщения учащихся о старинных единицах длины и показ.)
1) Вершок – длина фаланги указательного пальца, мера длины, равная примерно 4-5 см.
2) Пядь — мера длины, равная расстоянию между
концами вытянутых пальцев – большого и
указательного.
3) Локоть – расстояние от концов пальцев до локтя согнутой руки.
4) При торговле с восточными народами стали применять аршин. В нем укладывается 16 вершков. Это примерно 71см. Первоначально “аршин” обозначал длину человеческого шага.
5) В Древней Руси применялись косая сажень – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки; маховая сажень – расстояние между концами пальцев разведенных в стороны рук.
6) Для измерения больших расстояний на Руси использовали версту.
Учитель:
— Сегодня мы пользуемся современными терминами, обозначающими меры длины. Где могут встретиться “локти”, “аршины”, “пяди”?
— Часто в своей речи мы используем пословицы, но, не зная толкования слова “пядь”, вряд ли бы сумели мы разобраться в значении выражений “Семи пядей во лбу”, “На свой аршин мерит”.
III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Подготовка: участник № 1 складывает лист формата А4 так, чтобы он разделился на 8 частей.
Учитель:
— Участники, по очереди запишите современные единицы, которые используем на уроках математики. № 1, разрежьте лист на отдельные листочки. Разделите листочки на группы. Назовите их. (Единицы длины и единицы площади.)
| см | дм | м | мм |
| см2 | дм2 | м2 | км |
— № 2, переверните листочки с единицами площади, перемешайте и раздайте их участникам своей группы.
— № 1, 3, 4, посмотрите на листочек и выберите, к
какой модели сейчас отправитесь.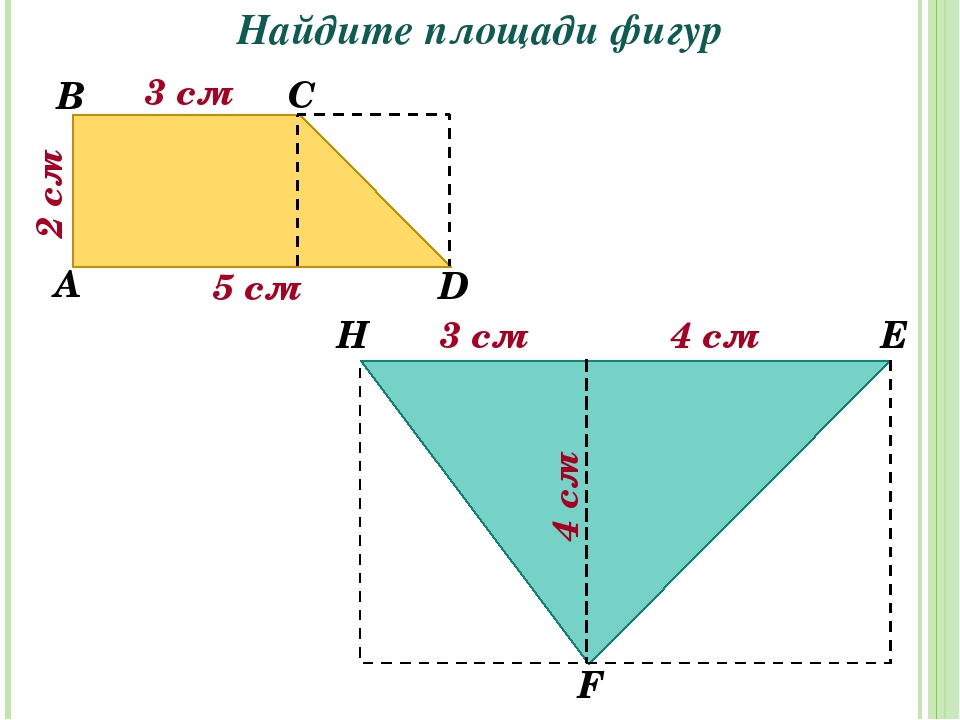 (Участники №
1,3,4 групп получают листочки с записью единиц
площади и отправляются к выбранным моделям: 1см2,
1дм2, 1м2, представленных на
стенах класса.)
(Участники №
1,3,4 групп получают листочки с записью единиц
площади и отправляются к выбранным моделям: 1см2,
1дм2, 1м2, представленных на
стенах класса.)
— Обсудите в группах, почему выбрали эту модель. Обсуждение и представление выбранной модели:
1) 1см2 — очень маленький, но играет важную роль в математике. Это квадрат со стороной 1см;
2) 1 дм2 — квадрат со стороной 1дм или 10см. В нем содержится 100 см2;
3) 1 м2 в 100 раз больше 1дм2 и в 10000 раз больше 1см2.
— Назовите одним словом. (Единицы площади.)
— Для измерения площади у русского народа были свои особые мерки: “копна”, “выть”, “соха”, “обжа”, “десятина”. От древних землемеров нам досталось только слово “площадь”.
— № 2, образуйте группу. Назовите ее. (Современные единицы длины.)
— Сформулируйте тему урока. Чему будем учиться?
— Еще 4-5 тысяч лет назад жители древнего города Вавилон умели определять площадь. Какая фигура служила эталоном при измерении площади?
— Квадрат, благодаря своим замечательным свойствам. Знаете их? Выясните в группах. (Обсуждение и обмен мнениями: 1) Равные стороны; 2) Прямые углы; 3) Совершенная форма; 4) Легко строить.)
— В Древнем Китае мерой площади была другая фигура. Догадайтесь, какая.
— Почему на уроке по нахождению площади фигур присутствуют единицы длины?
IV. Первичное закрепление в знакомой ситуации
а) Типовые задания
Устный счет “Калькулятор площади”. (Слайд 10 .)
Решение задач и объединение учащихся в группы в зависимости от ответа.
1. Длина прямоугольника 6см, ширина 2см. Чему равна третья часть площади прямоугольника?
2. Площадь коридора 18м2.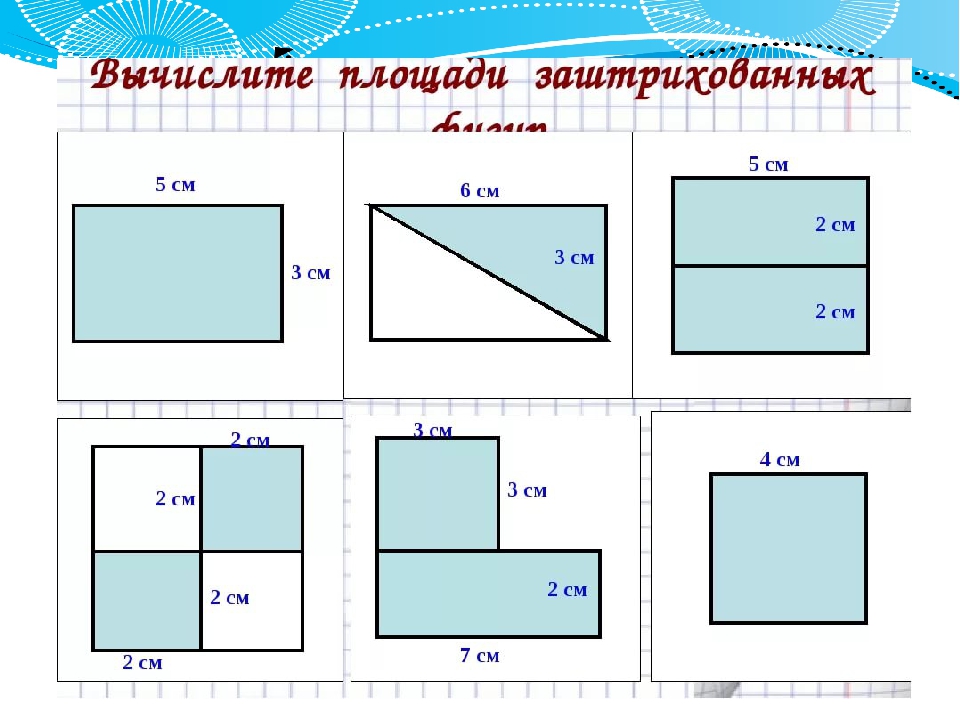 Вычислите ширину,
если длина 9м.
Вычислите ширину,
если длина 9м.
3. Найдите площадь прямоугольника, ширина которого 2см, и она в 3 раза меньше его длины.
4. Площадь фундамента дома квадратной формы 64м2. Чему равна сторона фундамента?
5. Найдите площадь прямоугольника, одна сторона которого 6см, другая – на 2см короче.
6. Во сколько раз площадь зала, равная 27м2, больше площади комнаты, равной 9м2?
Игра “Математическое лото”. (Слайд 11.)
Правила игры: 1 – придумать, 2 – решить, 3 – оценить.
Подготовка: участник № 3 складывает лист формата А4 так, чтобы он разделился на 8 частей. Получается таблица:
| a (длина) | ? | ||
| b (ширина) | ? | ||
| P (периметр) | ? | ? | |
| Ѕ (площадь) | ? | ? |
1. Составление задач. Передача листа-таблицы по команде для решения другой группе (по часовой стрелке).
2. Решение задач (заполнение таблицы). Передача листа-таблицы по команде для проверки следующей группе.
3. Проверка и оценка решения.
б) конструктивные задания (в измененной ситуации)
Учитель:
— Внимание на экран! (Слайд 12.)
Запишите, какими способами Вы найдете площади
этих фигур.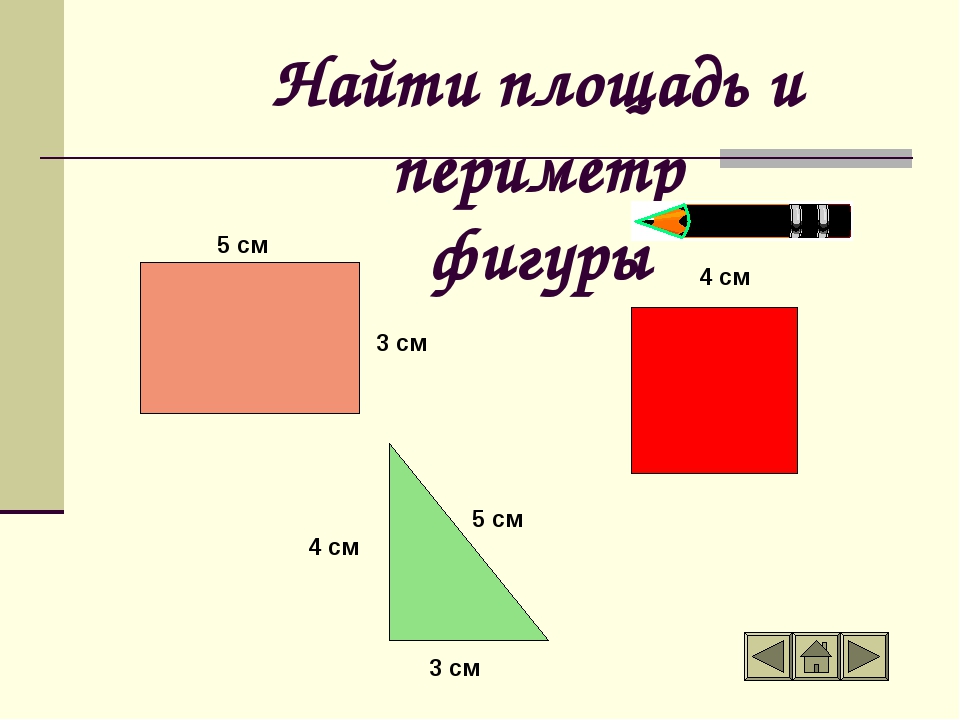
— По сигналу встаньте, найдите пару и расскажите о своих способах. Если у Вас есть этот способ, поставьте “+”, если нет, дополните свой список. Запись известных способов:
1) Пользуясь формулой;
2) Палеткой;
3) Дополнить до прямоугольника или квадрата;
4) Разбить на квадратные мерки;
5) Разделить на отдельные квадраты и прямоугольники и найти их площади;
6) Из площади большой фигуры вычесть площадь маленькой фигуры.
— Расскажите в группе по одному способу, начиная с участника № 1. (Сбор информации, обмен знаниями и дополнение списка ответов в паре при перемещении по классу; обмен информацией в своей группе.)
— Подчеркните нерациональные способы. Почему Вы считаете их нерациональными? Покажите рациональные способы.
V. Физкультминутка
Учащиеся делятся на группы, получают карточки (“татарский танец”, “русская плясовая”, “полька”, “марш”), исполняют танцевальные движения под музыку.
VI. Творческое применение и добывание знаний в новой ситуации
а) Вычисление площади сложной фигуры на листе формата А2, представление работы групп.
б) Индивидуальная работа с планом классной комнаты, проверка ответов с партнером по плечу. (Слайд 13.)
в) Практическая работа по измерению площади, занимаемой группой, высказывание ответов.
VII. Информация о домашнем задании, инструктаж
1) Решите разноуровневые задания на карточке (Приложение);
2) Найдите площадь одной из комнат Вашей квартиры.
VIII. Итог урока
Учащиеся отвечают на вопросы:
- Что такое площадь?
- Как измерить площадь?
- Назовите единицы площади.
- По какой формуле находят площадь прямоугольника, квадрата?
- Какие площади у равных фигур?
- Какое свойство площади знаете?
- Людям каких профессий необходимо знание площади?
- Где Вы можете применить знания площади?
Проверка: зажигается звезда. (Слайд 14.)
(Слайд 14.)
Учитель:
— Послушайте притчу.
Шёл мудрец и встретил трех работников. “Что ты сегодня делал?” — спросил он каждого. Первый ответил: “Я целый день таскал ненавистные камни”. Второй ответил: “Я немного устал, но добросовестно выполнял свою работу”. Третий ответил: “Работа принесла мне радость и большое удовлетворение”.
— Кто из вас на уроке был первым работником, вторым работником, третьим работником? Очень хорошо, что работа на этом уроке принесла вам радость, вы открыли новые знания.
— Что для Вас было новым?
Использованная литература.
1. Федеральный государственный образовательный стандарт начального общего образования. Москва, 2010 г.
2. Концепция духовно-нравственного развития и воспитания личности гражданина России.
3. Овчинникова М.В. Методика изучения темы “Величины” на уроках математики в начальных классах: Методические рекомендации для студентов факультета “Начальное обучение. Дошкольное воспитание”. Ялта: ЦОП “Надежда”, 2000.
4. Райкина Т.Н. Математика. 3 класс. В 2 ч. Саратов: Лицей, 2009.
5. Жильцова Т.В., Обухова А.А. Поурочные разработки по наглядной геометрии: 1-4 класс. М.: ВАКО, 2004.
Конспект урока «Площадь прямоугольника». 3 класс
|
Название этапа урока |
Содержание этапа |
Деятельность учителя |
Деятельность учащихся |
Формы работы |
Результат (формируемые УУД) |
|
I. |
Ребята, на каждом уроке вы стремитесь сделать для себя открытие, получить новые знания. Вот и сегодня мы постараемся углубить математические знания, узнать новое. С маленькой удачи начинается большой успех. Улыбнитесь и пожелайте друг другу удачи. В добрый путь за знаниями! |
Организует актуализацию требований к ученику со стороны учебной деятельности. |
Дети желают друг другу удачи.
|
Коллективная |
Личностные: самоопределение Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
|
II . Актуализация знаний и фиксация затруднения в детальности.(5-6 мин.)
|
Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета: Устный счет. 1.Найдите в каждом ряду числа, которые не являются результатом табличного умножения. — 6,18,17,12, 41 24,30,16,11,28 2) Игра “ Кто быстрее” (дети друг другу задают примеры на умножение)
3)В городском сквере 2 ряда лип, по 8деревьев в каждом ряду и ещё 7 берёз. 4)Какие фигуры изображены на доске? (треугольник, круг, прямоугольник, ромб, овал) — Среди данных фигур найдите прямоугольники. Докажите свой выбор. |
Создаёт условия для возникновения у учеников внутренней потребности включения в учебную деятельность.
Показывает фигуры, просит их назвать.
|
Дети устно отвечают на вопросы, показывают карточки с верным ответом; друг другу задают примеры на умножение
Называют номер фигуры и доказывают свой выбор.
|
Коллективная, индивидуальная |
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Познавательные: логические – анализ объектов с целью выделения признаков. |
|
III. Постановка учебной задачи (2 – 3 мин) |
Задача на нахождение площади. В группах предлагает посчитать площадь прямоугольника. (Раздают карточки с чертежом прямоугольника/7на3/ расчерченного на квадратные см)
— Проблема: как найти площадь, не расчерчивая каждый раз на квадратные сантиметры? — Сформулируйте тему урока. — Какую цель вы поставите для себя на сегодняшнем уроке?
|
Предлагает найти площадь прямоуголь ника посчитав квадраты. Предлагает сравнить свои ответы с эталоном (слайд) |
Подсчитывают квадратные сантиметры-21см.
Ответ детей: Сегодня мы научимся находить площадь прямоугольника и использовать знания при решении задач. |
Коллективная, групповая |
Регулятивные: целеполагание;
Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение – формулирование познавательной цели. |
|
IV. Построение проекта выхода из затруднения (10 – 11 мин)
|
-Каким способом вы производили подсчёт квадратных см в прямоугольнике? — Какое математическое действие помогло вам узнать количество квадратных см в прямоугольнике?(умножение) Что обозначает число 7? (длина) 3?(ширина).Каким образом получите искомое вами число -21? (7*3=21) Делают вывод: S = длину х ширину. — Откройте учебники, сравните свои выводы с эталоном (чтение правила на стр. 54) Сформулируйте вывод: как найти площадь? Сформулируйте вывод: как найти площадь? |
Предлагает сформулировать правило нахождения S.
Предлагает ещё раз сформулировать правило нахождения S
|
Находят площадь. Формулировка правила. Проверка по эталону (слайд)
|
|
Коммуникативные: постановка вопросов; Познавательные: самостоятельное выделение – формулирование познавательной цели;
Регулятивные: планирование, прогнозирование; Познавательные: моделирование; Логические – решение проблемы, построение логической цепи рассуждений, доказательство; Коммуникативные – инициативное сотрудничество в поиске и выборе информации. |
|
Физкультминутка.
|
«Мы чертёжники».
-Начертите глазами луч (на стене найдите точку и отправьте луч далеко сквозь окно), кончиком носа — окружность, правой рукой- прямой угол, а левой- острый! Чертите аккуратно! Левой ногой — квадрат, а правой прямоугольник. Сформулируйте вывод: для чего необходимо выполнять физкультминутку? «Чтобы отдохнуть и расти здоровыми». |
Показывает движения, как образец. |
Дети выполняют соответствующие движения.
|
Индивидуальная |
Личностные: самоопределение |
|
V. Первичное закрепление во внешней речи (4 – 5 мин) |
Решение задачи по учебнику стр.55 № 3 Решим задачу: — Начертите в тетрадях прямоугольник длина которого 9см, а ширина — 2см. Найдите его площадь.( Выполняется задание с комментированием). — Какими еще могут быть длины сторон прямоугольника с такой площадью? (3 и 6) Сформулируйте вывод: как найти площадь?
|
Предлагает выполнить задания по учебнику.
Предлагает ещё раз сформулировать правило нахождения S
|
Решают типовые задания с проговариванием алгоритма вслух. Взаимопроверка в парах Ребята делают предположения и обосновывают свои ответы. |
Парная, индивидуальная |
Регулятивные: контроль, оценка, коррекция; Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач; рефлексия способов и условий действия; Коммуникативные: управление поведением партнера – контроль, коррекция, оценка действий партнера. |
|
VI. Самостоятельная работа с самопроверкой (4 – 5 мин) |
Предлагаю вам побыть в роли строителей. Нам необходимо для классной комнаты закупить напольное покрытие.Выполнив необходимые измерения и пользуясь математическими знаниями узнайте, сколько квадратных метров покрытия вы закупите? (Дети работают в группах). |
Предлагает побыть в роли строителей. |
Самостоятельное решение в тетради. Проверка с эталона. (слайд) |
Групповая |
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Личностные: самоопределение. |
|
VII.
|
Приготовьте веер с цифрами. Определите площадь фигур. Кто из ребят правильно выполнил задание? |
Координирует работу учащихся. |
Высказывают свое мнение, аргументируют. |
фронтальная |
Познавательные: анализировать и выделять существенную информацию из текста. |
|
VIII. Рефлексия деятельности (итог урока) (2 – 3 мин) |
— Какую цель мы ставили в начале урока, достигли мы ее? Расскажите по схеме, чему научились. Я знаю ….. Я запомнил…. Я смог …
|
Предлагает вопросы для рефлексии. |
Подводят итог своей работы на уроке, делают выводы. |
Индивидуальная |
Регулятивные: контроль, коррекция. Личностные: самоопределение. |
|
|
Домашнее задание. 1. стр.55, №4,6. 2.Творческое задание. Придумать задачу на нахождение площади прямоугольника для своего друга.
|
Предлагает выбрать задания для домашней работы |
Обсуждение и запись задания в дневник.
|
Индивидуальная |
Регулятивные: коррекция. Личностные: самоопределение. |
Математика 3 класс Нахождение площади фигуры | План-конспект урока по математике (3 класс) по теме:
Урок математики 3 класс.
Тема: ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА.
Тип урока: урок изучения нового и первичного закрепления новых знаний
Цели урока:
- Обеспечить усвоение детьми способа нахождения площади прямоугольника.
- Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.
Задачи урока:
Образовательные:
- Вывести правило вычисления площади прямоугольника.
- Актуализировать знания о признаках и свойствах геометрических фигур.
- Закреплять умение решать задачи на приведение к единице, записывая условие в таблицу.
- Способствовать совершенствованию вычислительных навыков.
Развивающие:
- Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).
- Развитие умения анализировать и находить пути решения поднимаемой проблемы.
- Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)
Воспитательные:
- Содействовать повышению интереса к чтению книг.

- Формировать навыки самоанализа.
Технологии: игровая, информационно-компьютерная, развивающая, образовательная (выбор оптимальной модели обучения для данных конкретных условий).
Методы: словесные, наглядные, деятельностные, практические, (выполнение учащимися практических действий)
Оборудование:
- Презентация Рower Point.
- Вееры с цифрами 25 штук,
- Конверты (по 1 шт. на парту) 15 штук.
- Палетки 15 штук.
- Прямоугольник 2см х6см 15штук.
- Карточки – помогайки: 1 см2, Sпр.=а х в,
единицы длины, таблица умножения, порядок действий.
- Текст задачи 15 штук.
- Мартышка 1 штука.
- Корзина 1 штука.
- Бананы (жёлтые и зелёные) по 2 штуки 25 штук.
Ход урока.
- Организационный момент.
- Самоопределение.
- Поднимите руки те, кто из вас любит сказки?
Сегодня к нам на урок придут герои одной очень известной сказки. А чтобы узнать автора этой сказки — надо разгадать кроссворд.
- Устный счёт.
А) Отгадайте кроссворд.
Возьмите в руки вееры, показывайте только одни ответы:
- Сколько раз по 4 содержится в 12 (три)
- На сколько надо разделить 49, чтобы получить 7 ( на семь)
- 36 уменьши в 6 раз (шесть)
- 53 уменьши на 48 (пять)
- 4 увеличь в 2 раза (восемь)
- Кто автор этой сказки? (Григорий Остер)
- Кто догадался, как называется сказка?
(«38 попугаев»)
Б) Геометрический материал.
- Какого героя вы видите на экране? (Удава)
Он принёс вам следующее задание. Рассмотрите фигуры.
- Какая из данных фигур лишняя? (треугольник)
- Почему? (все остальные – четырехугольники)
- Теперь какая фигура лишняя? (№1 – не прямые углы),
- У какой из этих фигур все стороны равны? (квадрат)
- Как называется данная фигура? (прямоугольник)
- Какие свойства прямоугольника вы знаете? (4 угла, 4 стороны, углы прямые, противоположные стороны равны
В) Единицы измерения величин.
Какие единицы измерения длины вы знаете? (см, мм, дм, м)
Герои мультфильма решили поиграть. Чтобы узнать кому какой мяч достался, расставим величины в порядке возрастания. (мм, см, дм, м)
Г) Вырази. Герои сказки принесли для вас ещё интересное задание:
- Толщина кожи слона составляет 2 см 5 мм. Сколько это будет мм? (25мм)
- У некоторых обезьян хвост может быть длиннее их тела. Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см)
- Длина обычного удава в природе 3 м. Сколько это дм? (30 дм)
- Длина тела самых мелких попугайчиков не более 1 дм. Сколько это см? (10 см)
4. Подводящий диалог.
Д) Найди пару. Обезьяна, Попугай и Слонёнок не могут справиться с заданием. Давайте им поможем.
Рассмотрите фигуры.
- Что общего у этих фигур? (Фигуры разбиты на равные квадраты, эти фигуры прямоугольники)
- Какая из данных записей подходит к первому прямоугольнику?(3х4)
Фигура №1.
- Сколько квадратов в первом столбце?(3)
- Сколько квадратов в строке?(4)
- Сколько раз по 3 взяли? (4)
- Докажите. (3 квадрата в одном столбце и 4 квадрата в строке)
- Чему равно произведение? Покажите ответ на веерах.
- Что такое 12 в этом прямоугольнике? (количество одинаковых квадратов в прямоугольнике)
- Какая запись подходит ко второй фигуре? (2 х 3). Чему равно произведение? (6)
- Какая запись подходит к третьей фигуре? (2 х 5). Чему равно произведение? (10)
- Если мы будем знать площадь каждого из этих квадратиков, что мы сможем узнать? (площадь прямоугольника)
- Кто догадался, какая тема сегодняшнего урока? («Нахождение площади прямоугольника»)
- Определение темы.
Сегодня мы должны научиться находить площадь прямоугольника удобным и быстрым способом.
- Зачем нам надо уметь находить площадь прямоугольника? (поклеить обои, покрасить пол, поклеить потолок).
- Какие единицы площади вы знаете? (см2)
- Что значит квадратный сантиметр? (площадь квадрата, сторона которого 1 см)
- Открытие новых знаний.
- Практическая работа в парах.
Откройте конверты, достаньте прямоугольник и палетку. ( Прямоугольник 2см на 6 см)
- Наложите палетку и посчитайте сколько квадратных см укладывается в прямоугольнике? (12 см2 )
- Сколько полос с квадратами в прямоугольнике? (2 полосы)
- Сколько квадратов в каждой полосе? (6)
- Как узнать сколько всего квадратов? (по 2 взяли 6 раз, т.е 2х6)
- Что такое 6 см в прямоугольнике? (длина)
- Что такое 2 см? (ширина)
- Как нашли площадь? (длину умножили на ширину)
Записываем в тетрадь. 1 ученик на доске.
№1.
6 х 2 = 12 (см2)
Ответ: 12 см2.
- А Слонёнок нашёл площадь этого прямоугольника вот так: по 2 взял 6 раз.
- Как вы думаете можно ли таким способом найти площадь прямоугольника?
- Какой вывод можно сделать? Как найти площадь? (длину умножить на ширину или ширину умножить на длину)
- Нахождение площади (формула)
Если длина прямоугольника а, ширина в.
- Как узнать площадь прямоугольника?
В математике принято площадь обозначать буквой S. И сегодня вы сами вывели формулу нахождения площади прямоугольника.
Давайте проверим. Откройте учебник с.54, прочитайте правило.
Для нахождения площади прямоугольника достаточно измерить его длину и ширину в см и полученные числа перемножить. Площадь прямоугольника будет выражена в квадратных см.
Формулу записываем в тетрадь.
- Физ. минутка
Под музыку из мультфильма.
- Первичное закрепление материала.

№ 3 (1) Прочитайте задание. Начертите прямоугольник, длина которого 9 см, а ширина 2 см.
- Найдите площадь прямоугольника , пользуясь формулой.
- Запишите решение в тетрадь (один ученик диктует).
9 х 2 = 18 (см2)
Ответ: 18 см2.
А обезьяна нашла площадь по-другому. Прочитайте 2 х 9=18 (см2 )
- Как вы думаете, правильно ли она нашла площадь ?
- Решение задачи.
- Что больше всего любят есть обезьяны? (бананы). Обезьянка приготовила для вас задачу.
20 кг бананов разложили в 4 одинаковых ящика. Сколько потребуется таких ящиков, чтобы разложить 30кг бананов.
- Что известно в задаче? ( 20 кг бананов разложили в 4 одинаковых ящика)
- Что такое 20кг? (общая масса)
- Сколько было ящиков? (4)
- Что известно про ящики? (одинаковые)
- Нам известна масса 1 ящика? (нет)
- Что надо узнать в задаче? (сколько потребуется ящиков, чтобы разложить 30 кг бананов)
- Что такое 30 кг? (общая масса)
- Количество ящиков? (не знаем, но все ящики одинаковые)
- Каким действием найти массу одного ящика? (делением)
- Каким действием можно узнать количество ящиков, чтобы разложить 30 кг бананов? (делением)
Запишите решение самостоятельно.
Проверка с доской.
- Самостоятельная работа с. 73 №5
1в. – 1 строчка
2в. – 2 строчка
2 ученика за доской – потом проверяют.
- Поднимите руки, кто решил примеры без ошибок?
- Кто допустил ошибки?
- Итог урока.
- Что нового узнали на уроке? (как вычислить площадь прямоугольника)
- Как найти площадь прямоугольника? (надо длину умножить на ширину)
- Кто написал сказку «38 попугаев»? (Григорий Остер)
Он написал ещё много увлекательных книг: «Середина сосиски», «Книга о вкусной и здоровой пище людоеда», «Вредные советы и другие истории», которые я рекомендую вам прочитать.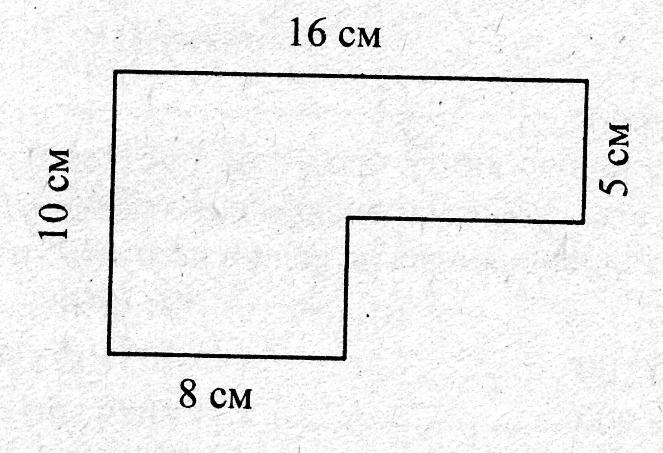
- Домашнее задание
с. 55 № 4, 7. Правило с. 73 наизусть.
- Рефлексия.
Герои сказки прощаются с нами.
Кому было сегодня на уроке легко и интересно положите в корзину Обезьяны жёлтый банан, а кому было трудно – зелёный.
Урок окончен!
областей прямоугольников и квадратов — математика для 3-го класса
Как найти площадь прямоугольников и квадратов
Прямоугольники и квадраты — две наиболее распространенные формы.
Можете ли вы представить себе прямоугольник? 000
Вот несколько примеров прямоугольных объектов:
Можете ли вы думать о квадратных объектах?
Вот несколько квадратных объектов:
В этом уроке мы научимся находить область прямоугольников и квадратов.
Давайте рассмотрим
Площадь — это пространство, которое занимает форма или объект.
Посмотрите на эту фигуру.
Сколько квадратов покрывает этот зеленый прямоугольник?
Занимает 6 квадратов.
Его площадь составляет 6 квадратных единиц .
Мы используем единиц площади , чтобы точно знать, как измеряется форма.
Например, если каждый квадрат в приведенной выше сетке равен 1 квадратному метру, то площадь зеленого прямоугольника составляет 6 квадратных метров .
Совет: Мы можем записать 6 квадратных метров как 6 m² . Это читается как «6 квадратных метров » .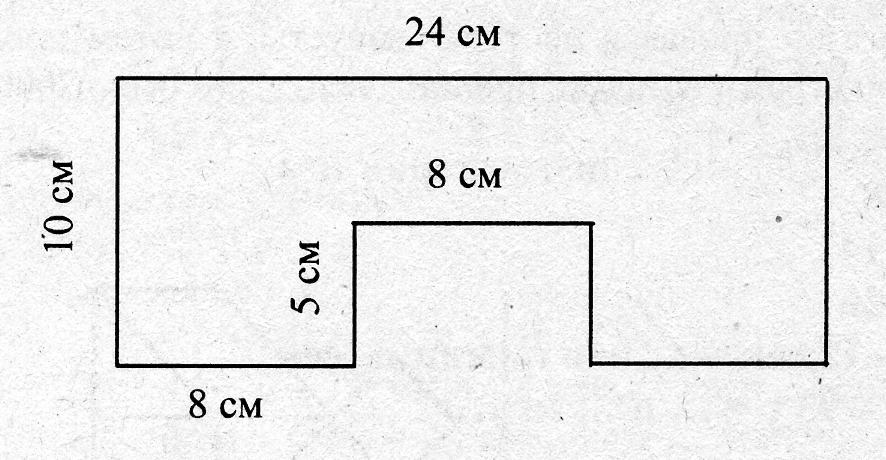
Обратите внимание на маленькую цифру 2, написанную в верхней правой части m. Это действительно важно.
Площадь прямоугольника
Чтобы узнать площадь прямоугольника, мы подсчитываем количество квадратов, которые он покрывает.
Другой способ — умножить на на длину сторон .
В прямоугольнике противоположных сторон равны .
Длина сторон, идущих от слева направо , называется шириной .
Длина сторон, идущих от сверху вниз , называется высотой или длиной .
Чтобы найти площадь прямоугольника , умножьте ширину на высоту.
ширина x высота = площадь
Давайте воспользуемся этой формулой, чтобы найти ширину зеленого прямоугольника.
Сначала , знайте ширину и высоту.
Ширина составляет 3 квадратных единицы, а высота составляет 2 квадратных единицы.
Теперь умножьте ширины на высоту.
3 x 2 = 6 квадратных единиц
✅ Если 1 квадратная единица равна 1 квадратному метру, то 6 квадратных единиц равны 6 квадратным метрам (6 м²).
Это тот же ответ, который мы получили, когда подсчитали каждый квадрат. 000
Площадь Квадрата
У квадрата 4 равные стороны.
Это означает, что длина сторон одинакова.
Чтобы найти площадь квадрата , умножьте на длину одной стороны на себя.
Какая площадь у этого квадрата?
Длина каждой стороны 3.
3 x 3 = 9 квадратных единиц
Площадь квадрата 9 кв.
✅ Если 1 квадратная единица равна 1 сантиметру, то 9 квадратных единиц равны 9 квадратному сантиметру (9 см²).
Отличная работа! 000
Без сетейЕсли нет сеток с квадратами, чтобы помочь вам, вы все равно можете вычислить площадь фигуры.
Чтобы найти площадь прямоугольника , умножьте на :
длина ширины x длина высоты = площадь
Чтобы найти площадь квадрата , умножьте на :
длина любой стороны сама по себе
Попрактикуемся на примерах!
Найдите площадь этого прямоугольника:
Мы видим, что ширина 10 дюймов, а высота 6 дюймов.
Мы умножаем этих двух чисел вместе.
10 x 6 = 60
✅ Площадь этого прямоугольника составляет 60 квадратных дюймов (или 60 кв.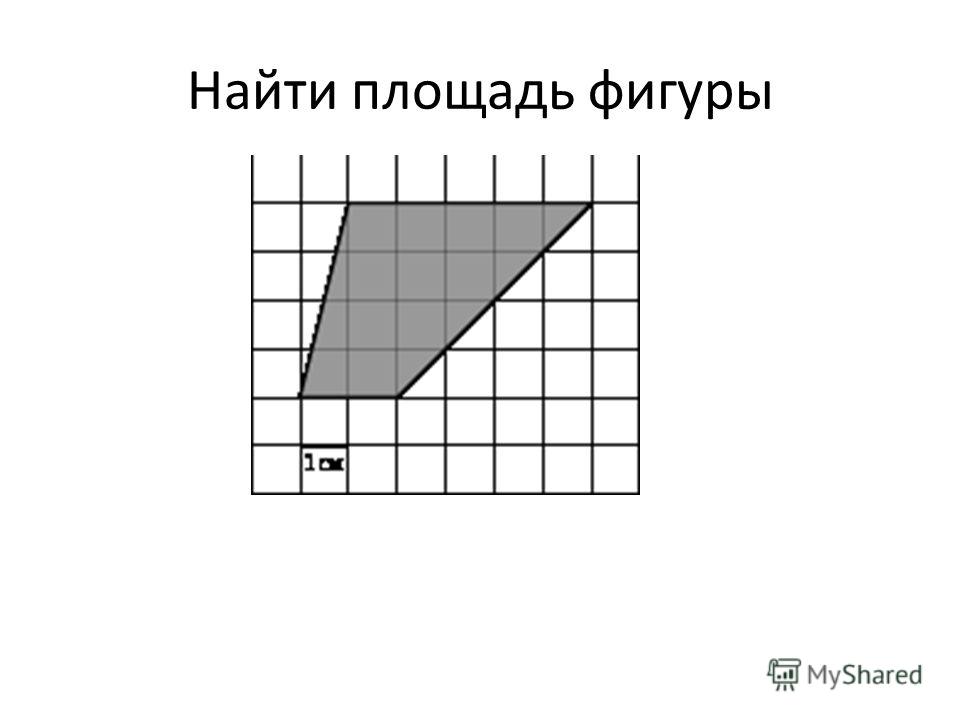 Дюймов) .
Дюймов) .
😃 Обязательно укажите после числа, указав единицу площади .
Какова площадь этого квадрата?
Длина одной стороны 4 фута.
Давайте умножим на себя.
4 фута x 4 фута = 16 квадратных футов
✅ Площадь этого квадрата составляет 16 квадратных футов или 16 футов².
Отличная работа! 000
Смотри и учись
Теперь попробуйте выполнить практические упражнения. 000
областей сложных фигур — математика для 3-го класса
Как найти область сложных фигур
На последних уроках вы научились определять площадь прямоугольников и квадратов.
В этом уроке вы узнаете, как найти площадь сложных фигур.
Сложные фигуры — это фигуры, которые не являются ни квадратами, ни прямоугольниками.
Их еще называют неправильными формами. 000
Площадь сложных фигур
Как узнать площадь этого парка?
Чтобы найти область сложной формы , начните с , разделив ее на меньшие, правильные формы , такие как квадрат и прямоугольник.
Как мы можем это разделить?
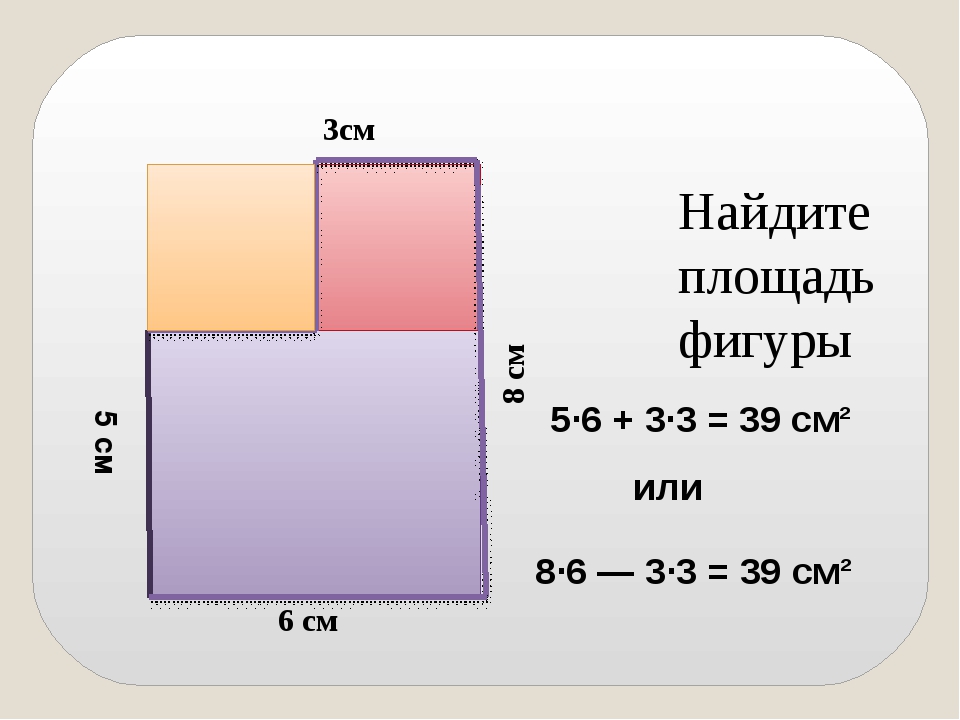
Вы поняли! Мы можем разделить эту фигуру на прямоугольник и квадрат.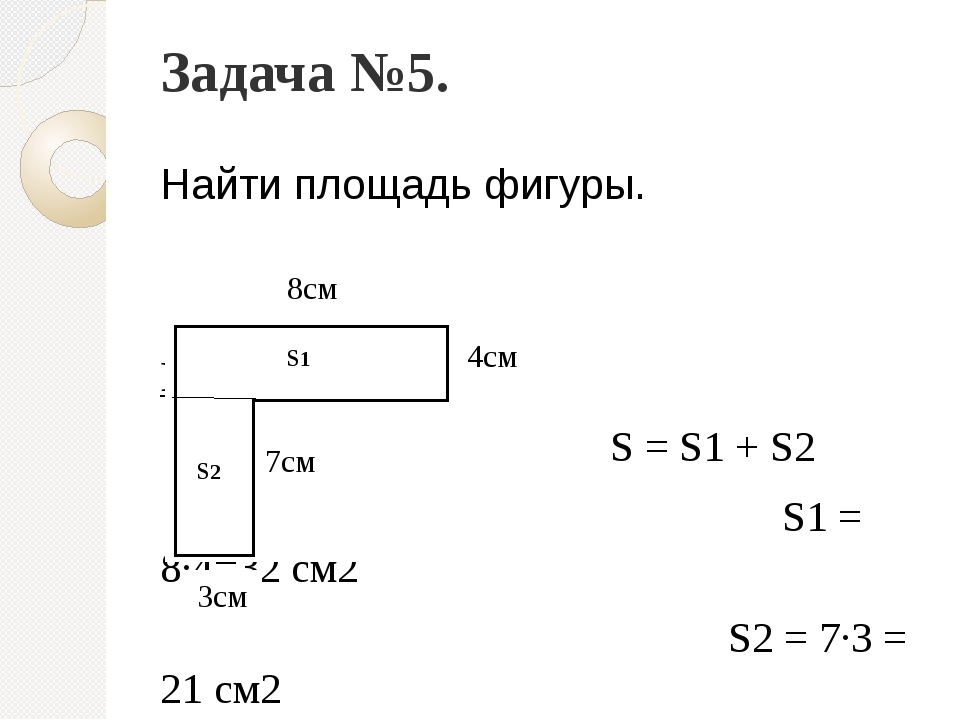 000
000
👆 7 км и 2 км были вычеркнуты , потому что они больше не применяют к новым формам.
— Форма верха представляет собой прямоугольник . Ширина 2 км, длина 7 км.
— Форма основания представляет собой квадрат . Длина всех его сторон 5 км каждая.
👉 Давайте сначала найдем площадь прямоугольника .
2 x 7 = 14
Прямоугольник имеет площадь 14 км² (квадратных километров).
👉 Затем находим площадь квадрата.
5 x 5 = 25
Площадь квадрата составляет 25 км² (квадратных километров).
👉 Теперь мы складываем две области, , чтобы получить площадь всего парка.
14 + 25 = 39
✅ Площадь парка составляет 39 квадратных километров ( или 39 км²).
Пример 2: Площадь плавательного бассейна
Какова площадь этого бассейна? 000
Сначала , вам нужно выяснить, как разделить его на .
— Один из способов — разделить его на 3 прямоугольника.
— Другой способ — разделить его на 2 прямоугольника.
Какой способ сделать проще? 000
Да, второй! Потому что нам нужно иметь дело только с двумя формами.
Давайте найдем таким образом территорию бассейна. 000
Посмотрите на размеры двух прямоугольников:
Совет : Мы не знали длину длинной стороны второго прямоугольника, поэтому нам пришлось прибавить длины сторон, которые мы знали.
Чтобы найти площадь первого прямоугольника , умножьте 8 м на 9 м:
8 x 9 = 72 м²
Чтобы найти площадь второго прямоугольника , умножьте 16 м на 6 м:
6 x 16 = 96 м²
Теперь мы складываем две области вместе:
72 + 96 = 168 м²
✅ Площадь бассейна 168 квадратных метров ( или 168 м²).
Смотри и учись
Теперь попробуйте выполнить практические упражнения. 000
Как рассчитать площадь | Помощь с математикой
Расчетная зонаПлощадь измеряется в квадратах (или квадратных единицах).
Сколько квадратов в этом прямоугольнике?
Мы можем сосчитать квадраты или взять длину и ширину и использовать умножение. Прямоугольник выше имеет площадь 15 квадратных единиц.
Площадь прямоугольника = длина x ширина
Примеры расчета площади прямоугольника
Единицы измерения площади Измеряем площадь квадратами. Мы используем квадраты разного размера в зависимости от того, насколько велика или мала площадь.
Мы используем квадраты разного размера в зависимости от того, насколько велика или мала площадь.
| Пример | Длина стороны квадратов | Блок |
| Размер ногтя на большом пальце | Миллиметр | мм 2 |
| Размер листка бумаги | Сантиметр | см 2 |
| Размер комнаты | Метр | м 2 |
| Размер города | Километр | км 2 |
| Не забывайте крошечный 2 |
| Мы пишем размеры квадрата с помощью маленького 2 рядом с единицей. Мы пишем mm 2 , cm 2 , m 2 , km 2 , cm 2 Мы можем сказать «63 миллиметра в квадрате» или «63 квадратных миллиметра» |
Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5 000 квадратных метров было бы гораздо проще сказать, написать и визуализировать.
Вероятно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары — все это единицы, используемые для измерения площади.
Дополнительные примеры расчета площади
Площадь квадратаДлина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.
| Площадь = длина x длина Площадь = 6 см x 6 см = 36 см 2 |
Площадь круга = πr 2
, где r — радиус круга, а π — отношение длины окружности к ее диаметру.
π (произносится как «пирог» и часто пишется как «пи») — бесконечная десятичная дробь с общим приближением 3,14159. Вы можете узнать больше о Pi здесь
Пример расчета площади круга| Площадь = πr 2 Площадь = 3,14159 x (4 см) 2 Площадь = 3,14159 x 16 см 2 Площадь = 50,27 см 2 Ответ округлен до 2 десятичных знаков |
Возьмите круг, разделите его на сектора одинакового размера и переставьте их, как показано ниже.Обратите внимание, как по мере уменьшения размеров секторов форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти секторы и насколько они могут напоминать прямоугольник при расположении.
Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, переконфигурированный как прямоугольник, имеет площадь, которая приблизительно равна πr x r или πr 2
Перестановка секторов круга Перестановка секторов круга — начинает выглядеть как прямоугольник Площадь сложных формВо многих случаях для вычисления общей площади требуется вычисление нескольких площадей с последующим сложением, вычитанием или какой-либо другой комбинацией операций для поиска требуемой площади.
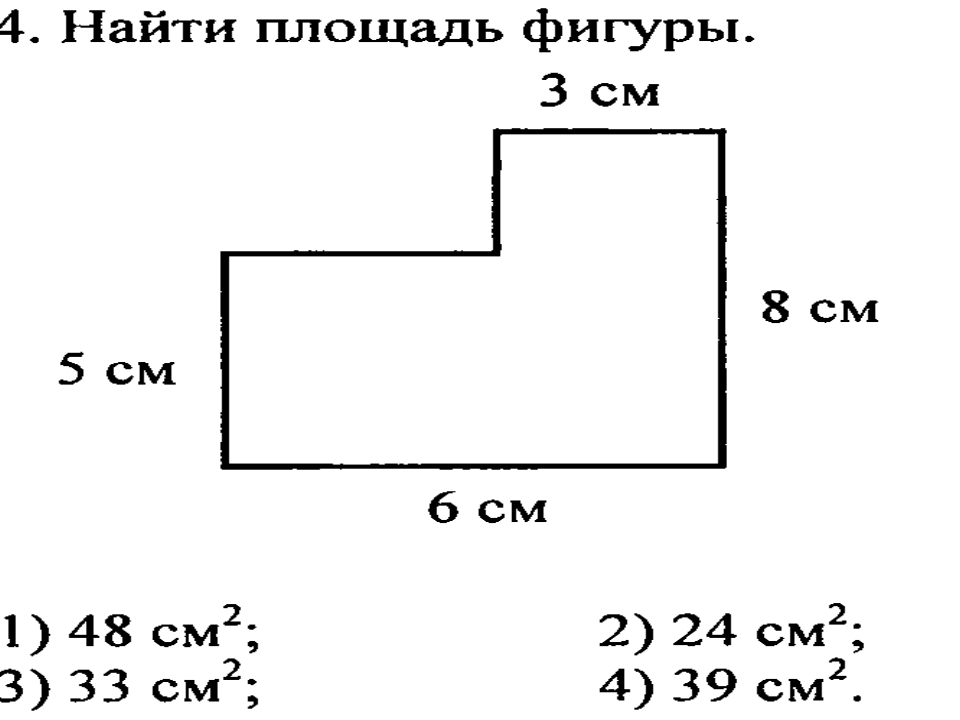
Примечание. В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до ближайшей сотой.
Пример: простые составные формы Пример вычисления площади ниже относительно прост. Фигуру можно рассматривать как треугольник в сочетании с прямоугольником.
Фигуру можно рассматривать как треугольник в сочетании с прямоугольником.
| Площадь треугольной части: ½ x основание x высота ½ x 9 x 4 = 18 Площадь прямоугольной части: Общая площадь = 18 + 54 = 72 |
В приведенном выше примере показано общее требование при работе с составными формами — поиск размеров, которые не показаны.Обучая своих детей, при необходимости помогайте им найти эти «недостающие» измерения. Ниже приведен еще один пример.
Определение размеров| Каковы размеры маленькой прямоугольной детали? Ширина? 12-7-2 = 3 Высота? 8–6 = 2 |
В примере ниже фигура выглядит как прямоугольник с вырезанным треугольником.
| Площадь прямоугольной части: ширина x высота 5 x 6 = 30 Площадь треугольной части: Общая площадь = 30 — 4,50 = 25,50 |
Пример ниже аналогичен приведенному выше, хотя, поскольку у нас есть полукруг, нам нужно вычислить долю (половину) площади круга. Обратите внимание, что в этом примере показан диаметр, а не радиус.
| Площадь треугольной части: ½ x основание x высота ½ x 6 x 6 = 18 Площадь полукруглой части: Общая площадь = 18 — 3,53 = 14,47 |
Обычно используется более одного способа вычисления окончательной площади. В приведенных ниже примерах фигуру можно рассматривать как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
В приведенных ниже примерах фигуру можно рассматривать как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
Распечатайте приведенные ниже рабочие листы и используйте их для практики при обучении своих детей.
Здесь вы найдете другие распечатанные геометрические рабочие листы.
Рабочие листы
Добро пожаловать на страницу рабочих листов Math Salamanders Area.
На этой странице есть ссылки на все наши рабочие листы с областями, включая области прямоугольников, треугольников и четырехугольников.
Эти листы предназначены для детей от 3-х классов и старше.
Эта страница содержит ссылки на другие веб-страницы математики, где вы найдете ряд занятий и ресурсов.
Если вы не можете найти то, что ищете, попробуйте выполнить поиск на сайте с помощью окна поиска Google вверху каждой страницы.
На этой веб-странице вы найдете ссылки на все наши конкретные страницы рабочих листов.
У нас есть ряд различных рабочих листов по площади, включая область прямоугольников, прямоугольных треугольников и четырехугольников.
Существует также распечатываемая страница формул для определения площади различных 2-мерных фигур.
Попробуйте приложение, разработанное компанией PhET Interactive Simulations из Университета Колорадо.
Это отличный способ исследовать территорию и периметр в увлекательной и увлекательной форме.
Мы также создали несколько задач, которые можно использовать вместе с приложением.
На нашей странице поддержки для печати есть формулы для площади обычных 2-мерных фигур.
Листы здесь включают поиск области прямоугольников, а также области прямолинейных форм.
Прямолинейные фигуры — это фигуры, состоящие из нескольких прямоугольников.
У нас есть широкий выбор листов для учеников от 3-го класса и выше.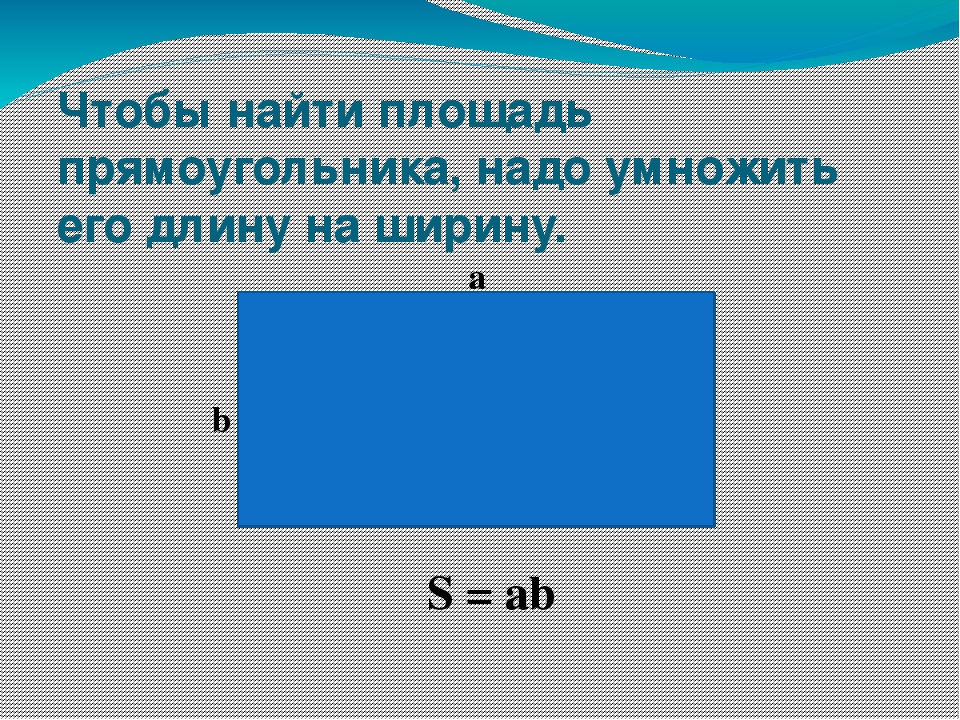
Листы здесь включают определение площади и периметров прямоугольников и прямолинейных форм.
Прямолинейные фигуры — это фигуры, состоящие из нескольких прямоугольников.
У нас есть некоторая поддержка, а также широкий выбор листов, подходящих для учащихся от 3-го класса и выше.
Существуют проблемы с площадью и периметром, а также проблемы с более длинной областью и периметром.
Этот раздел содержит рабочие листы по области для 5-го и 6-го классов.
Основное внимание уделяется вычислению площади прямоугольных треугольников.
Использование этих листов поможет вашему ребенку:
- умеют рассчитать площадь треугольника;
- выучите формулы для вычисления площади треугольников.
Этот раздел содержит рабочие листы по области для 5-го и 6-го классов.
Основное внимание уделяется вычислению площадей различных четырехугольников.
Использование этих листов поможет вашему ребенку:
- умеют вычислять площадь ряда четырехугольников.
- выучите формулы для вычисления площади определенных типов четырехугольника.
Узнайте, как рассчитать площадь круга, и ознакомьтесь с некоторыми рабочими примерами.
Существует ряд рабочих листов, которые помогут вам отработать этот навык, а также некоторые задачи со словами, чтобы увидеть, сможете ли вы применить его.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Вот наша подборка бесплатных распечатываемых листов периметра для 3-го и 4-го классов.
Все листы отсортированы от самого простого к самому сложному.
Использование этих листов поможет вашему ребенку:
- проработать периметр ряда прямоугольников;
- найдите периметр прямолинейной формы.
Все листы в этом разделе поддерживают тесты элементарной математики.
Вот наша подборка рабочих листов по геометрии для 4-го класса.
Использование этих листов поможет вам:
- классифицируют углы — острый, тупой, прямой, рефлекторный, прямой;
- классифицируют треугольники — острые, тупые, правые;
- измерять углы с помощью транспортира;
- знает, что углы в треугольнике составляют в сумме 180 °
- постройте и запишите координаты в первом квадранте.

Все листы в этом разделе поддерживают тесты по элементарной математике.
Вот наш ассортимент рабочих листов.
Использование этих листов поможет вашему ребенку:
- знать, что такое объем и как его найти;
- найти объем фигур, считая кубики;
- найти объем прямоугольной призмы;
- решение основных задач, связанных с объемом
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Что такое площадь? — Определение, факты и пример
Area Games
AreaИспользуйте единичные квадраты, чтобы понять концепцию площади и найти площадь для различных двухмерных форм.
охватывает Common Core Curriculum 3.MD.7Играть сейчасПосмотреть все игры по геометрии >>Учитесь с полной программой обучения математике K-5
Что такое область? В геометрии площадь можно определить как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.Площадь приведенных ниже квадратов со стороной 1 сантиметр каждый будет измеряться в квадратных сантиметрах (см²).
Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).
Слово «площадь» происходит от латинского «площадь», что означает «свободный участок ровной поверхности».Происхождение далее привело к неправильному получению площади как «определенного количества пространства, заключенного в пределах набора границ».
Мы часто находим площадь пола комнаты, чтобы определить размер покупаемого ковра. Покрытие пола плиткой, покрытие стен краской или обоями или строительство бассейна — другие примеры, где площадь вычисляется.
Обычные простые формы и многоугольники имеют свои собственные формулы для вычисления площади. Вот как вычисляется площадь обычных двухмерных или двумерных фигур:| Двумерные геометрические формы: |
| Название формы: | Изображение формы: | Формула площади: |
| Круг | Площадь = πr², где r радиус. | |
| Треугольник | Площадь = bh, где b — основание, А h — высота. | |
| Квадрат | Площадь = l × l, где l — длина каждой стороны. | |
| Прямоугольник | Площадь = д × ш, где l длина и w — ширина. | |
| Параллелограмм | Площадь = b × h, где b — основание, и h — высота по перпендикуляру. | |
| Трапеция | Площадь = (a + b) h, , где a и b — длины параллельных сторон, и h — высота по перпендикуляру. |
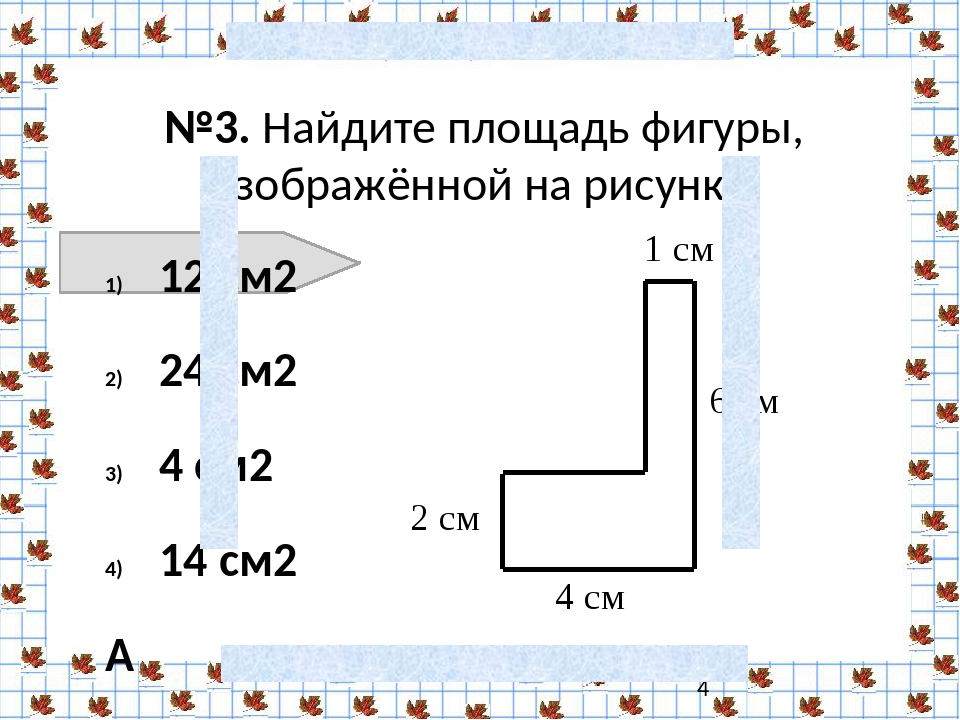
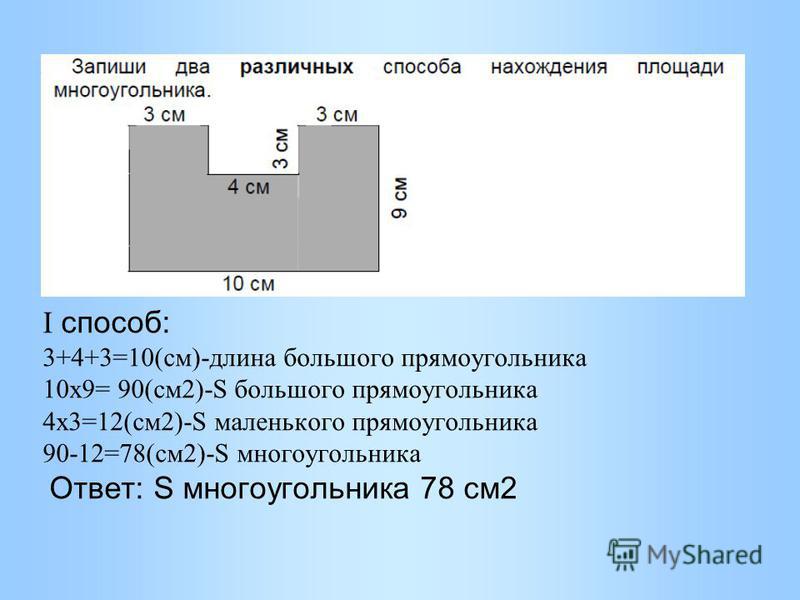
В реальной жизни не каждую плоскую фигуру можно однозначно классифицировать как прямоугольник, квадрат или треугольник. Чтобы найти площадь составной фигуры, состоящей из более чем одной фигуры, нам нужно найти сумму площадей обеих или всех фигур, образующих составную фигуру.
Площадь внешней поверхности твердой или трехмерной формы называется площадью поверхности. Например, прямоугольная призма имеет 6 прямоугольных оснований и боковые грани. Итак, общая площадь поверхности — это сумма площадей всех 6 прямоугольников.
Интересные факты
|
Для посадки овощей в саду,
Найдите площадь поля — все внутри.
Умножьте его длину на ширину,
И вот формула площади, которую вы применили!
Давайте сделаем это!Вместо того, чтобы раздавать своим детям рабочие листы по математике, вовлекайте их в проекты по благоустройству дома. Сообщите им о комнате, которую вы собираетесь покрасить. Попросите их подсчитать общую площадь стен, чтобы узнать, сколько требуется краски.
Обсудите, чем все стены в комнате могут отличаться друг от друга, и, таким образом, проведение общих измерений с последующим вычитанием площади двери, окон или книжных полок поможет в оценке необходимого количества краски.
Вы также можете попросить рассмотреть возможность определения общей площади подарка, который они упаковывают, чтобы определить необходимое количество оберточной бумаги.
Сопутствующий математический словарьМатематика для 3-го класса — Блок 4: Область
Сводка по агрегату
В Блоке 4 учащиеся понимают площадь как объем двумерного пространства, занимаемого фигурой, и связывают это со своей работой с умножением в Блоках 2 и 3.
В младших классах учащиеся могут неформально сравнивать площадь, видя, какая из двух фигур занимает больше места. Во 2 классе учащиеся разделили прямоугольник на строки и столбцы квадратов одинакового размера и посчитали их общее количество, включая подсчет пропусков и повторное сложение, чтобы сделать это более эффективно (2.G.2, 2.OA .4).
Учащиеся начинают свою работу в этом модуле, развивая понимание площади как атрибута плоских фигур (3.MD.5) и измеряя ее, считая единичные квадраты (3.MD.6). После обширной работы по развитию пространственного структурирования студентов ученики подключают площадь к операции умножения длины и ширины фигуры (3.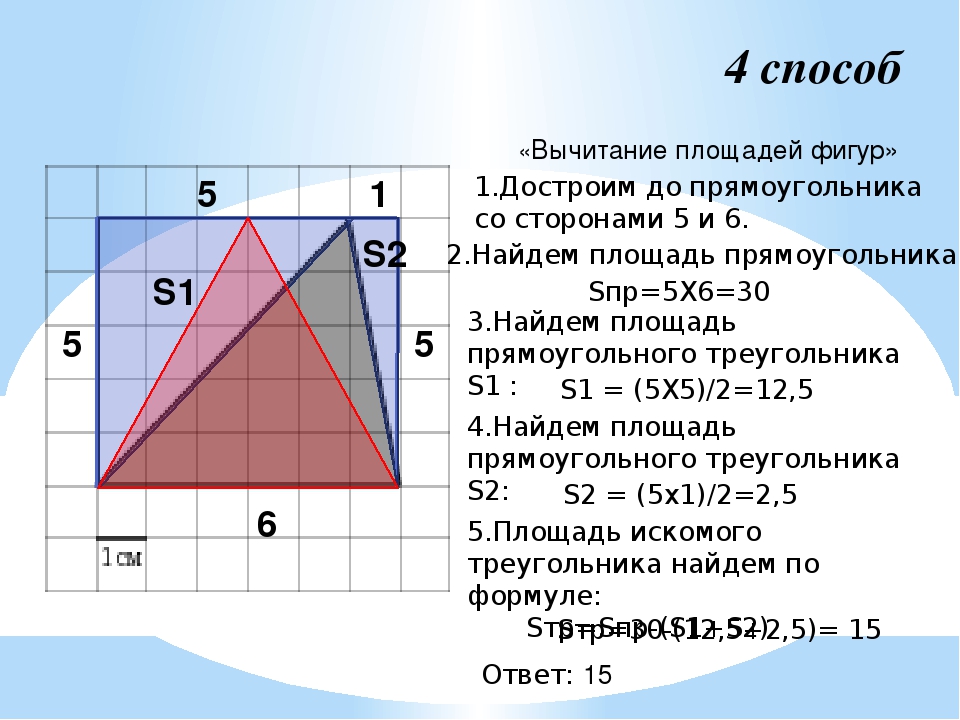 MD.7a, b). Наконец, учащиеся связывают меру площади как с умножением, так и с площадью, видя на конкретных примерах, что площадь прямоугольника с целочисленными длинами сторон $$ a $$ и $$ b + c $$ является суммой $$ a \ times b $$ и $$ a \ times c $$ (3.MD.7c) и, используя более общую идею, что площадь является аддитивной, найти площадь составных фигур (3.MD.7d). Таким образом, модуль служит способом связать темы и размышления между модулями, обеспечивая согласованность между работой с умножением и делением в модулях 2 и 3 (3.OA) с работой над областью в этом модуле (3.MD.C) .
MD.7a, b). Наконец, учащиеся связывают меру площади как с умножением, так и с площадью, видя на конкретных примерах, что площадь прямоугольника с целочисленными длинами сторон $$ a $$ и $$ b + c $$ является суммой $$ a \ times b $$ и $$ a \ times c $$ (3.MD.7c) и, используя более общую идею, что площадь является аддитивной, найти площадь составных фигур (3.MD.7d). Таким образом, модуль служит способом связать темы и размышления между модулями, обеспечивая согласованность между работой с умножением и делением в модулях 2 и 3 (3.OA) с работой над областью в этом модуле (3.MD.C) .
Студенты будут глубоко заниматься многими математическими практиками в этом модуле. Например, студенты «используют стратегии для поиска продуктов и коэффициентов, основанные на свойствах операций; например, чтобы найти [площадь прямоугольника путем умножения] $$ 4 \ times 7 $$, они могут распознать, что $$ 7 = 5 + 2 $$, и вычислить $$ 4 \ times 5 + 4 \ times 2 $$.Это пример видения и использования структуры (МР.7). Такие процессы рассуждения сводятся к кратким аргументам, которые студенты могут построить и критиковать (MP.3) »(PARCC Model Content Frameworks for Mathetmatics, стр. 16). Кроме того, учащиеся используют физические плитки, линейки, чтобы связать длины сторон с физическими плитками, а позже в модуле — свойства самих операций, чтобы найти площадь прямоугольника (МР.5). Кроме того, «чтобы построить от пространственного структурирования к пониманию количества единиц площади как произведения количества единиц в строке и количества строк, студенты могут рисовать прямоугольные массивы квадратов и учиться определять количество квадратов в каждой строке с помощью все более изощренные стратегии, такие как пропуск числа в каждой строке и, в конечном итоге, умножение числа в каждой строке на количество строк (MP.8) »(GM Progression, стр. 17).
В будущих классах учащиеся будут полагаться на понимание площади для решения все более сложных задач, касающихся площади, периметра, площади поверхности и объема (4.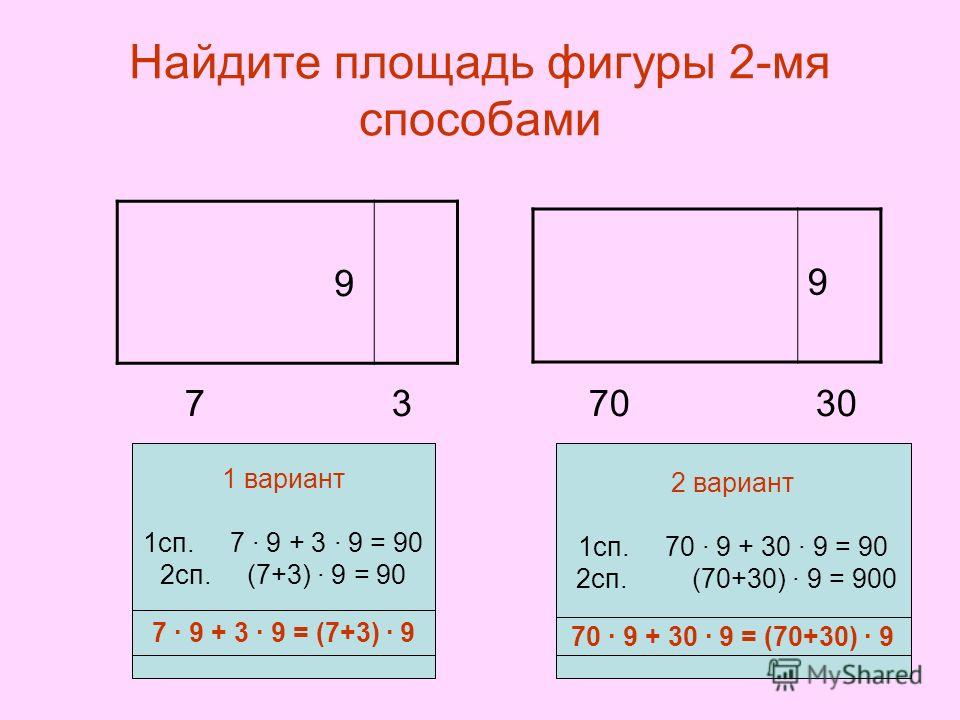 MD.3, 5.MD.3–5, 6.G.1–4 ). Студенты также будут использовать это понимание вне своего изучения геометрии, например, в задачах многозначного умножения в 4 классе (4.NBT.5), умножении дробей в 5 классе (5.NF.4) и даже в задачах полиномиального умножения в алгебре. (A.APR.1) полагаются на модель площади.
MD.3, 5.MD.3–5, 6.G.1–4 ). Студенты также будут использовать это понимание вне своего изучения геометрии, например, в задачах многозначного умножения в 4 классе (4.NBT.5), умножении дробей в 5 классе (5.NF.4) и даже в задачах полиномиального умножения в алгебре. (A.APR.1) полагаются на модель площади.
Темп: 16 учебных дней (13 уроков, 2 гибких дня, 1 контрольный день)
Чтобы узнать, как изменить темп обучения на 2020-2021 учебный год в связи с закрытием школ, см. Наши Рекомендуемые корректировки объема и очередности для 3-го класса.
Что такое площадь?
Площадь — это размер поверхности!
Пример:
У всех этих фигур одинаковая площадь 9:
.Это помогает представить , сколько краски покроет форму.
Площадь простых форм
Существуют специальные формулы для определенных форм:
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = ш × в
ш = ширина
в = высота
Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :
Площадь = 5 × 3 = 15
Узнайте больше в Area of Plane Shapes.
Площадь по счету квадратов
Мы также можем нанести фигуру на сетку и подсчитать количество квадратов:
Прямоугольник имеет площадь 15
Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь будет 15 м 2 (15 квадратных метров)
Квадратный метр vs Квадратный метр
Базовая единица площади в метрической системе — квадратный метр , который представляет собой квадрат с 1 метром на каждой стороне:
1 квадратный метр
Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:
Существуют также «квадратные мм», «квадратные см» и т. Д., Подробнее см. В метрической зоне.
Д., Подробнее см. В метрической зоне.
Приблизительная площадь по подсчету квадратов
Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.
В одну сторону:
- больше чем половина квадрата считается как 1
- меньше чем половина квадрата считается как 0
Как это:
Этот пятиугольник имеет площадь примерно 17
Или мы можем сосчитать один квадрат, когда
областей складываются в .Пример: Здесь область, отмеченная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):
Этот круг имеет площадь примерно 14
Но лучше всего использовать формулу (когда это возможно):
Пример: круг имеет радиус 2,1 метра:
Формула:
Площадь = π × r 2
Где:
Радиус 2.1м , итого:
Площадь = 3,1416 … × (2,1 м) 2
= 3,1416 … × (2,1 м × 2,1 м)
= 13,854 … м 2
Итак, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)
Область сложных форм
Иногда мы можем разбить фигуру на две или более простые формы:
Пример: Какова площадь этой фигуры?
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B
Площадь = 400 м 2 + 140 м 2
Площадь = 540м 2
Площадь путем сложения треугольников
Мы также можем разбить фигуру на треугольники:
Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:
Затем вычислите каждую площадь
(используя Area = ½b × h) и сложите их все.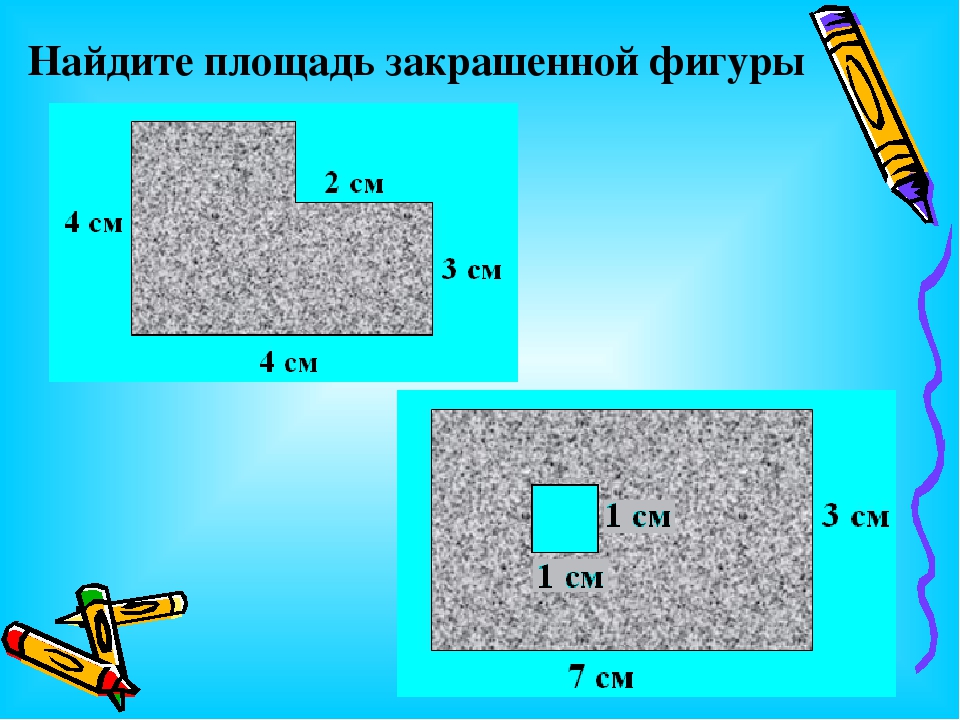

 Самоопределение к деятельности (1 – 2 мин)
Самоопределение к деятельности (1 – 2 мин)
 Сколько всего деревьев в сквере?
Сколько всего деревьев в сквере?


 Включение в систему знаний и повторение (4 – 5 мин)
Включение в систему знаний и повторение (4 – 5 мин)