Урок математики «Измерение площадей криволинейных фигур. Палетка». 4-й класс
Оборудование. Учебник Э.И.Александровой (изд-во ВИТА-ПРЕСС), на каждого ученика листочки четырёх цветов, листочки с четырьмя вариантами заданий, непрозрачные конверты с палетками из целлофана, два больших демонстрационных листа с рисунками 2 и 3, 6 листов для работы (по количеству групп) с фигурой на рисунке 2, 12 листов с фигурой на рисунке 3.
Тема. Измерение площадей криволинейных фигур. Палетка.
Цели.
Образовательная: познакомить с способом измерения площадей криволинейных фигур; с устройством для измерения площадей — палеткой; закреплять умение находить площади прямолинейных фигур.
Развивающая: развивать внимание, наблюдательность, умение рассуждать, обобщать и делать выводы.
Воспитательная: воспитывать умение общаться,
аккуратность, внимательность.
1. Учебная ситуация успеха
Учитель. Чем мы занимались на вчерашнем уроке?
Ученики. Находили площади и периметры фигур.
Учитель. Как найти площадь геометрической фигуры?
Ученики. Площадь прямоугольника и треугольника находят по формуле. Если это не прямоугольник и не треугольник, то сначала многоугольник надо разбить или достроить до фигур, площади которых мы уже знаем как находить.
Учитель. Я предлагаю вам выполнить эти задания. Здесь 4 варианта заданий. Посмотрите на них и выберите себе любое. Все 4 варианта лежат у вас на партах.
На доске четыре варианта заданий. Каждое записано своим цветом. У детей на партах кроме карточек с фигурами четырёх цветов, квадраты соответствующих цветов.
На доске
Дети, решив задание, поднимают карточку с
соответствующим заданию цветом. По цвету они
находят группу, сверяют решение, выбирают одного
представителя от группы, который записывает
решение на доске.
Учитель. Ребята, научились мы находить площади геометрических фигур?
Ученики. Да.
2. Постановка учебной задачи
Учитель. А теперь найдите площадь этой фигуры.
Показывает и вывешивает на доску
Ученики молчат.
Учитель. Почему вы не можете выполнить задание?
Ученики. Это не прямоугольник и не треугольник. Это не многоугольник.
Учитель. Чем эта фигура отличаются от нам известных фигур, многоугольников?
Ученики. Непонятно, где длина, ширина. Нет углов. Фигуры некрасивые, какие-то кривые.
Учитель. Да, все многоугольники состоят из прямых линий. Поэтому их называют прямолинейными фигурами. А из каких линий состоят эти фигуры?
Как бы вы их назвали?
Ученики. Кривые.
Учитель. В математике такие фигуры называют криволинейными.
Учитель. Чем же мы будем заниматься сегодня на уроке?
Ученики. Учиться находить площади
криволинейных фигур.
Учиться находить площади
криволинейных фигур.
Учитель фиксирует проблему на доске:
S = ?
3. Поиск решения поставленной задачи
Учитель. Как же мы будем решать эту задачу? Как вы находили площадь прямоугольника, когда ещё не знали формулу его площади?
Ученики. Мы измеряли площадь прямоугольника с помощью мерки.
Учитель. А для криволинейной фигуры такой способ можно попробовать?
Ученики. Да.
Учитель. Как можно узнать площадь криволинейной фигуры с помощью мерки в одну клетку?
Ученики. Разбить на мерки, продолжив линии клеток-мерок.
Учитель. Что будете делать, когда разобьёте фигуру на мерки, чтобы узнать площадь фигуры?
Ученики. Посчитаем количество мерок в фигуре.
Учитель. Работаем в группах.
Представители от групп записывают свои ответы на доске. Ответы оказываются разными.
Учитель. Почему ответы оказались разными? Наши ребята не умеют считать?
Группа, у которой количество мерок меньше,
объясняют: “Мы не считали нецелые мерки”.
Учитель. Правильно будет вообще не считать неполные мерки?
Ученики. Нет.
Учитель. А считать половинку как полную мерку-квадрат можно?
Ученики. Нет.
Учитель. Что же делать с неполными мерками, ребята? Как их считать?
Ученики. Складывать по две мерки.
Учитель. Да, в математике договорились считать всё количество неполных мерок и делить на 2.
Учитель. Посчитайте ещё раз количество полных мерок. Неполных мерок.
Ученики работают в группах.
Учитель. Скольким квадратным меркам равна площадь фигуры?
Представители от групп называют ответы. Все сверяют со своими ответами.
4. Моделирование
Учитель. Что мы сейчас нашли?
Ученики. Мы узнали площадь криволинейной фигуры.
Учитель. Давайте вспомним, как мы это делали.
Дети говорят, учитель записывает на доске.
1. Разбить на мерки.
1. Посчитать полные мерки.
2. Посчитать неполные мерки и разделить на 2.
3. Сложить.
Учитель. Так можно найти площадь только этой криволинейной фигуры?
Ученики. Можно найти площадь и другой фигуры.Учитель. Как записать, чтобы было понятно, что таким способом можно воспользоваться для вычисления площади любой криволинейной фигуры?
Как обозначить полные мерки? Неполные мерки?
Дети предлагают разные варианты. Учитель сообщает, что в математике договорились полные мерки обозначать буквой n, а неполные мерки буквой m.
Учитель. Кто закончит запись So = ?
На доске появляется запись: So = n + m : 2
Физминутка
5. Рефлексия
Учитель. Откройте учебники на стр. 61. Найдите №
88. Работая в парах, узнайте площади криволинейных
фигур: 1 ряд – площадь первой фигуры, 2 ряд –
площадь второй фигуры, 3 ряд – площадь третьей
фигуры.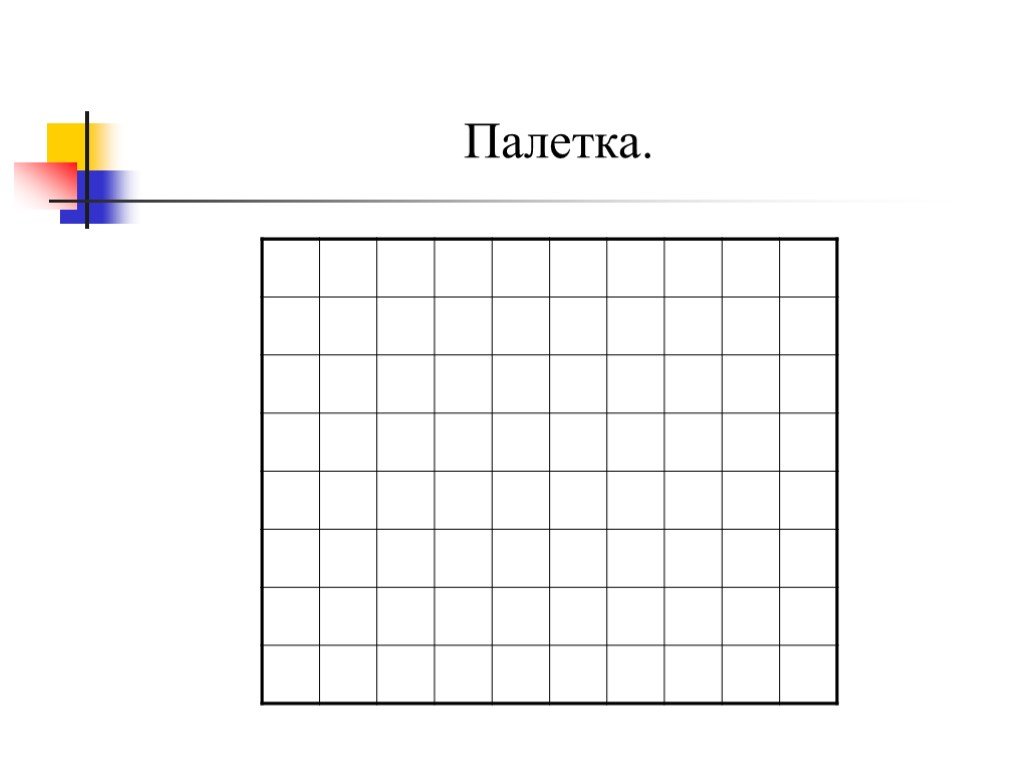
Проверка
Представители от пар, выполнивших задание первыми, записывают на доске ответы. Остальные сравнивают свои ответы с их записями.
Учитель. По какой формуле вы находили площадь криволинейной фигуры?
Ученики. S = n + m : 2
Учитель. При таком способе нахождения площади (путём разбиения фигуры на мерки-квадраты) измерения получаются неточными.
Какие единицы измерения площадей вы знаете?
Ученики. Кв.см, кв.мм, кв.м, кв.км.
Учитель. Откройте учебник на с. 62 , № 89.
Одну и ту же фигуру измеряли сначала в кв.см, потом в кв. мм
Как вы думаете, в каком случае измерения выполнены более точно: в кв. см или в кв.мм?
Ученики. Более точно измерили квадратными мм .
6. Конкретизация способа нахождения площади криволинейной фигуры
Учитель. Мы научились измерять площади криволинейных фигур, разбивая их на клетки – мерки.
А сейчас посмотрите вот на эту фигуру:
Надо узнать площадь этой фигуры с помощью мерки
в 1 кв. см.
см.
Чем отличается данное задание от предыдущего?
Ученики. Нет клеточек, по которым можно провести линии мерок.
Учитель. Да, здесь нет сетки из квадратов. Как же узнать, сколько полных и неполных кв. см поместилось в данной фигуре?
Все задумались и молчат. Один ученик предлагает свою версию – накинуть сверху какую-нибудь сетку из квадратиков.
Учитель. Да, можно изготовить специальное устройство (показываю). Это палетка.
Достаньте из конверта палетку. Кто догадался, как её сделали?
Ученики. Расчертили на квадраты со стороной в 1 см.
Учитель. А как ей пользоваться?
Ученики. Наложить на фигуру и посчитать количество клеток.
Посчитайте в парах площадь этой криволинейной фигуры.
Учитель. Выполните задание в учебнике № 90.Каждый самостоятельно.
Проверка.
Три первых ученика, выполнивших задание, выходят к доске и записывают свои ответы
Класс сверяет ответы.
7. Д\з.
Учитель. Дома вам надо найти площади фигур из № 91. Что вам для этого понадобится?
Ученики. Палетка.
Учитель. Кто сможет сделать её сам?
Как это сделать?
Думаю, что все справятся с этой работой.
Если вы увидите фигуру, площадь которой можно найти другим способом, то вычислите площадь такой фигуры двумя способами: с помощью палетки и без неё.
8. Итоговая рефлексия
Учитель. Какую задачу решали на уроке?
Ученики. Учились находить площадь криволинейной фигуры.
Учитель. Кто сможет дома рассказать родителям ,как найти площадь криволинейной фигуры?
Как это сделать?
Учитель. А как вы думаете, чем мы будем заниматься на следующих уроках?
Ученики. Будем решать задачи на нахождение площадей фигур.
Будем находить новые формулы для нахождения площадей фигур.
Учитель. Да, на следующих уроках мы будем
использовать полученные знания в решении задач.
Палетка.Измерение площади с помощью палетки.
Данный урок имеет место в разделе программы «Величины». Соответствует требованиям ФГОС.
При проектировании урока учтены индивидуальные особенности класса. Этапы урока выдержаны. Материал носит научно- практический характер. Соответствует возрастным нормам и требованиям рабочей программы. Осуществляется тесная связь теории с практикой. На уроке развивается познавательная активность, связная речь, память, внимание, фантазия и воображение. Подводятся итоги деятельности, рефлексия.
Актуализация знаний представлена через задаваемые вопросы учителем и рассказ учениками. Детям предлагается задание для осмысления уже имеющихся знаний и выявления области незнания. Через использование приёма «Линейка знаний» дети фиксируют свои изначальные знания по теме.
Просмотр содержимого документа
«Палетка.Измерение площади с помощью палетки.»
Урок 27
Палетка. Измерение площади фигуры с помощью палетки
Измерение площади фигуры с помощью палетки
Цель деятельности учителя | Способствовать развитию умений находить площадь фигур различной формы с помощью палетки, решать текстовые задачи изученных видов, переводить одни единицы площади в другие, работать с геометрическими фигурами, соблюдать порядок выполнения действий в числовых выражениях со скобками и без скобок |
Тип урока | Освоение новых знаний и способов действий |
Планируемые | Предметные (объем освоения и уровень владения компетенциями): научатся находить площадь фигур различной формы Метапредметные (компоненты культурно-компетентностного опыта/приобретенная компетентность): овладеют способностью понимать учебную задачу урока, отвечать на вопросы, обобщать собственные представления; слушают собеседника и ведут диалог, оценивают свои достижения на уроке; умеют вступать в речевое общение, пользоваться учебником. Личностные: проявляют интерес к расширению знаний, к выполнению заданий, предложенных в учебнике или учителем |
методы и формы | Формы: фронтальная, индивидуальная. Методы: словесный, наглядный, практический |
Образовательные | 1. Математика. 3–4 классы : поурочные планы по программе «Школа России». – Волгоград : Учитель, 2012. – 1 электрон. опт. диск (CD-ROM). 2. http://rusfolder.com/32474579 3. |
Оборудование | Интерактивная доска (экран), компьютер, проектор |
Основные понятия и термины | Палетка |
Этапы | Деятельность учителя | Деятельность | Формируемые умения | |||||||||
I. Орг-т (мотивация) | Приветствует учащихся, проверяет готовность класса и оборудования, эмоционально настраивает на учебную деятельность. Прозвенел звонок. Начался урок. Мы пришли сюда учиться, Не лениться, а трудиться. Работаем старательно, Слушаем внимательно. | Слушают учителя. | К – планируют учебное сотрудничество с учителем и сверстниками. Л – понимают и принимают значение знаний для человека; проявляют интерес к изучаемому предмету | |||||||||
II. Актуализация знаний | Устный счет: См. приложение 1 | Выполняют задания. | П – владеют способами выполнения заданий творческого и поискового характера, логическими действиями, базовыми предметными понятиями; самостоятельно находят необходимую информацию и используют знаково-символические средства для ее представления, для построения моделей изучаемых объектов Р – принимают и сохраняют цели и задачи учебной деятельности; самостоятельно планируют К – умеют слушать друг друга, строить понятные для партнера по коммуникации речевые высказывания, задают вопросы с целью получения необходимой для решения проблемы; могут работать в коллективе, уважают мнения других участников образовательного процесса; Л – осознают свои возможности в учении | |||||||||
III.Сообщение темы, цели урока | Озвучивает тему и цель урока. См. приложение 2 -Давайте найдем площадь изображенной фигуры. Для этого разобьём фигуры на три прямоугольника. -Измерим стороны верхнего прямоугольника? Длина 5 см, ширина 2 см. -Как найти площадь прямоугольника? Умножаем длину на ширину. S=a*b S=5*2=10 кв. -Нижний прямоугольник имеет размеры как и верхний. Значит, площадь нижнего прямоугольника равна 10кв.см. Измеряем стороны центрального прямоугольника.(3 и 4 см) S=3*4= 12 кв.см. S=10+10+12=32 кв.см. Возьмем овал. Как же найти площадь овала? На партах у учеников тоже овалы. Ученики предлагают свои варианты: 1) приблизительно считаем длину и ширину при помощи линейки; 2) площадь — это квадраты, берём тетрадный лист в клетку. -Назовите тему урока. -Чем будем заниматься сегодня на уроке? | Слушают учителя и отвечают на вопросы. | ||||||||||
IV. Изучение нового материала | – Мы умеем находить площадь прямоугольников. А как же можно найти площадь других фигур? Для приблизительного определения площадей фигур используется палетка. Палетка – это прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры. – Палетку накладывают на фигуру, площадь которой надо измерить, тогда фигура будет как бы разбита на квадратные единицы. – Откройте учебник на странице 43. Там вы видите рисунок, где на фигуру наложили палетку. Палетка здесь разбита на квадратные сантиметры, как в данном случае на рисунке. Здесь получились полные и неполные квадратные сантиметры. Площадь фигуры в таких случаях находят так: сначала находят число полных квадратных сантиметров в фигуре. Сосчитайте, сколько их? – А теперь сосчитайте, сколько в фигуре неполных квадратных сантиметров. – Договорились, что два неполных квадратных сантиметра считать за один полный. Разделим 20 на 2. 20 : 2 = 10. Значит, всего: 21 + 10 = 31 (см2). – Прочитайте еще раз объяснение, которое дано в учебнике на странице 43 | Слушают учителя. – В фигуре их 21. – В фигуре 20 неполных квадратных сантиметров. Читают | ||||||||||
V. | № 191 (под руководством учителя). Полных квадратов -6 Неполных-16 16:2=8 6+8=14кв.см. Полных-5 Неполных-14 14:2=7 5+7=12 кв.см. | |||||||||||
Физкультминутка | ||||||||||||
VI. Практическая деятельность | № 193.
1) 380 – 295 = 85 (кг) – продали яблок. 2) 180 – 106 = 74 (кг) – продали груш. 3) 85 – 74 = 11 (кг). Ответ: на 11 кг яблок продали больше. № 196 15 кв. 23кв.см=2300кв.дм 800кв.дм=8кв.м 30000кв.см=3кв.м №198 7км=7000м 8км060м=8060м 90см005=90.005м 40км305м=40305м 7кв.км=7000000кв.м 1600кв.дм=160000кв.м 240000кв.см=24кв.м 28500кв.дм=285кв.дм Тест см. приложение 3 | Записывают краткую запись и решение задачи. Выполняют самостоятельно (с последующей проверкой). Выполняют задания. | П – проводят анализ; осуществляют моделирование и преобразование моделей разных типов (схемы, знаки и т. д.), построение логической цепи рассуждений, доказательство. Р – осуществляют контроль; оценку, волевуюсаморегуляцию в ситуации затруднения. К – контролируют свои действия и соотносят их ченные правила общения. Л – осуществляют смыслообразование; осознают ответственность за общее дело | |||||||||
VII. Итоги урока. Рефлексия | – Чем занимались на уроке? – Что изучили нового на уроке? – Какие задания понравились? – Какие вызвали затруднения? – Как оцениваете свою работу на уроке? Задания на рефлексию с диска | Отвечают на вопросы | П – ориентируются в своей системе знаний – отличают новое от уже известного. Р – оценивают собственную деятельность на уроке. Л – проявляют познавательный интерес к предмету | |||||||||
VIII. Домашнее задание | С. 44, № 195 | Задают уточняющие вопросы | Р – принимают и сохраняют учебную задачу, осуществляют поиск средств для ее выполнения | |||||||||
Приложение 1
Математический диктант | ||
1. | В одном автобусе 70 пассажиров, а в другом — 80 пассажиров. Сколько пассажиров в этих двух автобусах? | 150 |
2. | Какое число надо разделить на четыре, чтобы получить 50? | 100 |
3. | Какое число надо умножить на восемь, чтобы получить 240? | 30 |
4. | Какое число надо разделить на 300, чтобы получилось 6? | 1800 |
5. | В выражении 900:20 число 900 является делителем? | — |
6. | В 1 кв.км = 1000000кв. | + |
7. | Число 574 увеличьте в 1000 раз. | 574000 |
8. | Напишите число, следующее за числом 898 999. | 899000 |
9. | Из какого числа надо вычесть 1, чтобы получить 1000? | 1001 |
10. | Длина участка 30 м, ширина 20 м. Половина площади участка занята под картофель, а остальная — под свёклу. Какая площадь занята свёклой? | (30*20):2=300 |
Приложение 2
Набор математических плакатовBOHO DESERT NEUTRALS | Цветовая палитра Boho
Ваш класс будет красиво смотреться в тренде с этим потрясающим ассортиментом современных плакатов и дисплеев Boho Desert Neutral Math.
Сделанный так, чтобы идеально сочетаться с моими коллекциями декора для классной комнаты BOHO VIBES & EARTHY RAINBOW , нейтральные пустынные тона и минималистичный дизайн, несомненно, повысят качество обучения вашего ученика, не создавая чрезмерно стимулирующей классной среды.
В комплект входят 13 плакатов.0006
- Плакаты 3D Shapes
- Плакаты 2D Shape
- Плакаты стратегии сложения
- Плакаты стратегии вычитания
- Плакаты дробей
- Плакаты разрядности
- Разрядное значение и отображение десятичных знаков
- Плакаты с математическими операциями
- Плакаты с измерениями
- Число Строка
- Таблицы умножения Плакаты
- Отображение цифр с пропуском счета
- Плакаты с номерами десяти кадров
******************************* ************************************************
Нравится матчи матчи?
Ознакомьтесь с остальной частью моей коллекции декора для классной комнаты Boho Vibes:
- Набор декоративной отделки Boho Vibes
- Набор наклеек для классной комнаты Boho Vibes
- Плакаты Boho Vibes Alphabet 900 14
- Наклейки для часов Boho Vibes
**** ******************************************************* *******************
Оставайтесь на связи!
Будьте первыми, кто увидит мои последние ресурсы и подарки!
Нажмите здесь, чтобы следить за моим магазином
******************************************* *********************************
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Это загружаемый цифровой файл к которым вы можете получить доступ сразу после покупки.
Чтобы открыть файлы, на вашем компьютере должна быть установлена программа PDF Reader , например Adobe Acrobat. Чтобы отредактировать файлы, к которым у вас должен быть доступ Microsoft PowerPoint . Вы можете получить доступ к бесплатной пробной версии здесь.
Пожалуйста, убедитесь, что ваше программное обеспечение обновлено, чтобы избежать проблем с совместимостью.
ЕСТЬ ТЕХНИЧЕСКАЯ ПРОБЛЕМА?
Если у вас возникли трудности с загрузкой или открытием математических плакатов на нейтральную тему пустыни Бохо, убедитесь, что вы распаковали все папки и просмотрели каждый файл, прежде чем связываться с ним. Для этого: — щелкните правой кнопкой мыши заархивированную папку — и выберите «распаковать».
Пожалуйста, ознакомьтесь с разделом часто задаваемых вопросов учителей, платящих учителям, если у вас возникнут какие-либо другие технические проблемы. Пожалуйста, свяжитесь с support@teacherspayteachers.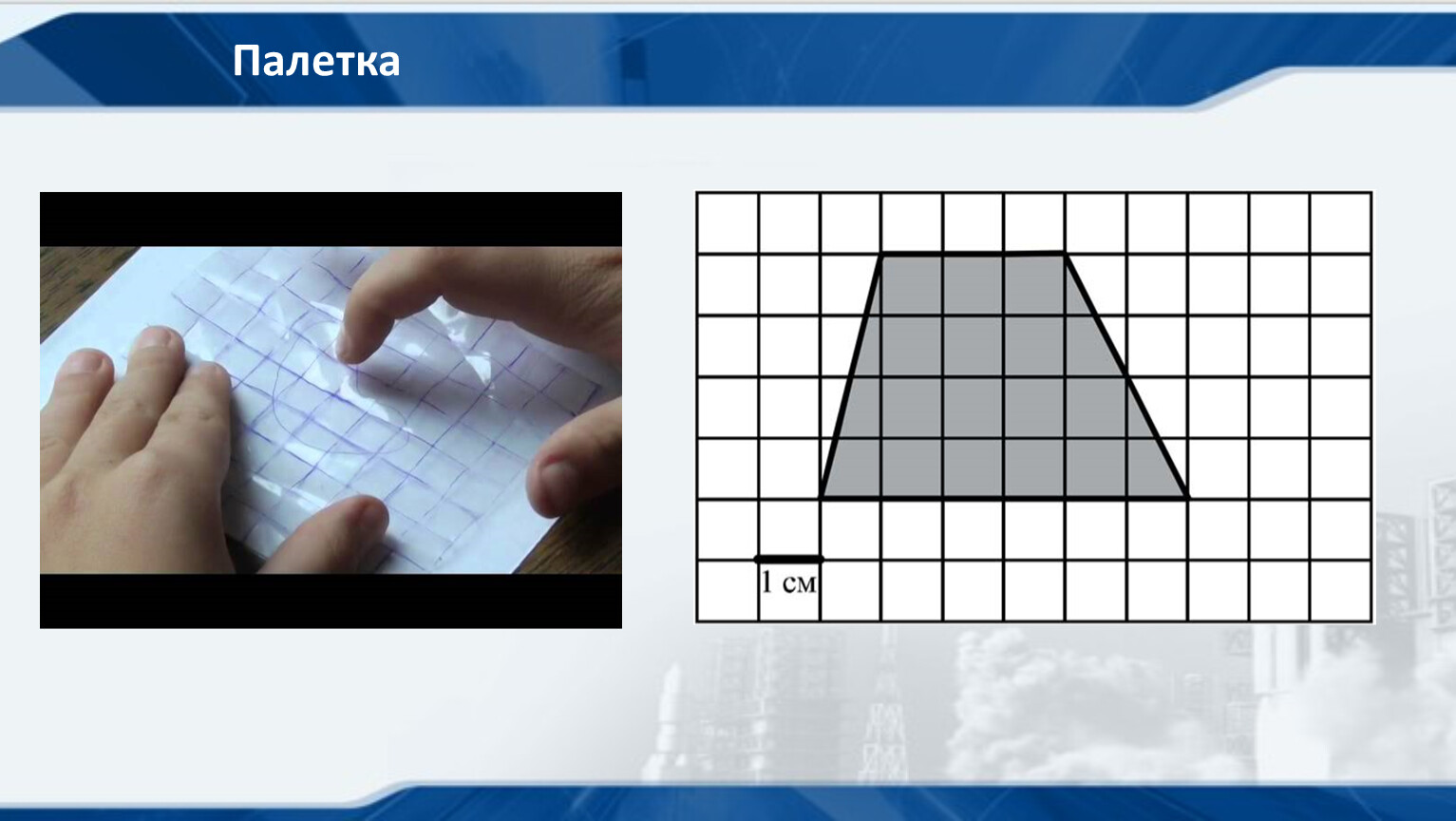 com
com
УСЛОВИЯ ИСПОЛЬЗОВАНИЯ
Покупка этого ресурса дает покупателю право воспроизводить страницы в ограниченном количестве только для использования в одном классе или домашней школе.
Копирование для друга, другого сотрудника, всей школы или в коммерческих целях без покупки дополнительной лицензии строго запрещено.
Копирование любой части этого ресурса и размещение его в Интернете в любой форме (даже на личном или классном веб-сайте/школьном сервере) является нарушением Закона об авторском праве в цифровую эпоху (DMCA).
Copyright © Chantelle Jacobs
Miss Jacobs Little Learners Pty Ltd
WWW.MISSJACOBSLITTLELEARNERS.COM
Блог | Facebook | Пинтерест | Инстаграм | Электронная почта
Узнайте, как работает математика теории цвета. Понятия и советы. | by Subarna Creative
Опубликовано в·
Чтение: 4 мин.·
5 февраля 2022 г. Математические советы по теории цвета для дизайнеров Я рад написать о математике по теории цвета. Теория цвета — обширная тема. Итак, я решил изучить его и поделиться готовыми советами по теории цвета для дизайнеров. Но я также сначала объясню концепции. Наслаждайся чтением.
Теория цвета — обширная тема. Итак, я решил изучить его и поделиться готовыми советами по теории цвета для дизайнеров. Но я также сначала объясню концепции. Наслаждайся чтением.
Дизайнеры используют цветовые схемы RGB и CMYK для смешивания цветов. Один предназначен для отображения на компьютерах, другой — для печатных СМИ. Давайте поймем их обоих.
теория цвета rgb объясняетRGB означает красный, зеленый, синий.
В ЖК-дисплеях, ЭЛТ, камерах и сканерах используется цветовая схема RGB.
Мы используем его для создания файлов таких форматов, как JPEG, PNG и GIF.
Мы используем их для создания логотипов, веб-сайтов, социальных сетей, рекламы и т. д.
Вы смешиваете свет, чтобы смешивать цвета. Это похоже на то, когда вы светите факелами двух разных цветов в одном и том же месте.
При сложении трех цветов получается белый цвет в центре. Это связано с тем, что цветовая схема RGB является аддитивной моделью.
Вы добавляете красный, зеленый и синий в разных пропорциях, чтобы получить различные цвета.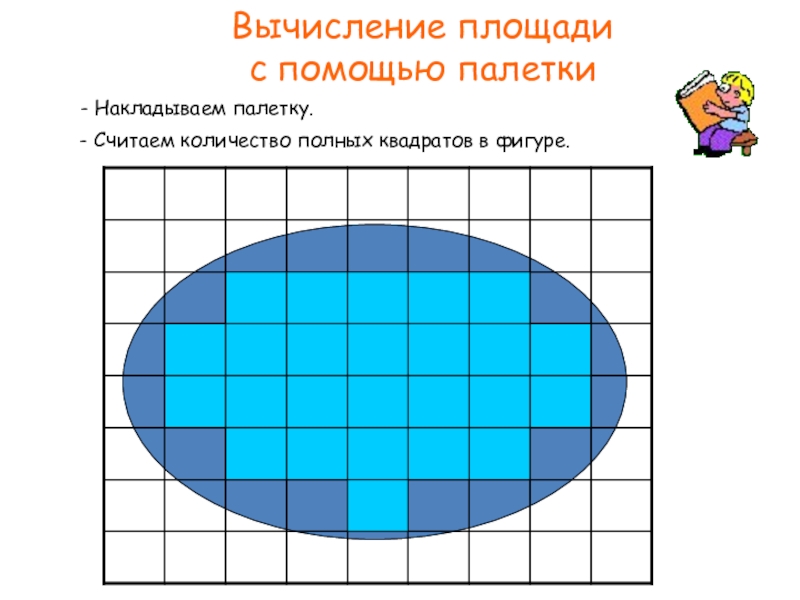 Черный означает отсутствие цветов.
Черный означает отсутствие цветов.
CMYK означает голубой, пурпурный, желтый и ключевой (черный)
В печатных СМИ мы используем цветовую схему CMYK.
Мы используем его для создания файлов в таких форматах, как PDF и EPS.
Мы используем их для изготовления визитных карточек, брошюр, канцелярских товаров и т. д.
Вы добавляете цвет к белой бумаге, чтобы вычесть цвета из белого цвета.
При вычитании трех цветов получается черный (ключевой) цвет в центре. Это потому, что цветовая схема CMYK является субтрактивной моделью.
Вы продолжаете вычитать цвета из черного, чтобы получить цвет. Белый означает отсутствие цветов.
теория цвета rgb против теории цвета колеса cmykcolorЦветовое колесо составляет 360 градусов. Вы можете применить следующие формулы, чтобы найти эти цветовые схемы:
Цветовая схема №1. Монохроматические цвета
Монохроматическая цветовая схема означает использование только одного цвета для всего дизайна. Выберите любой оттенок и примените его различные значения. Вот монохромная картина. Он основан на концепции оттенка, насыщенности и яркости.
Выберите любой оттенок и примените его различные значения. Вот монохромная картина. Он основан на концепции оттенка, насыщенности и яркости.
Цветовая схема №2. Дополнительные цвета
Когда два цвета отстоят друг от друга на 180 градусов на цветовом круге, они являются дополнительными цветами.
цветовой круг теория цветов дополнительные цветаЦветовая схема №3. Триадные цвета
Цветовой круг Теория цветов Триадные цветаНарисуйте равносторонний треугольник на цветовом круге. Вы найдете триадные цвета.
Или выберите любой цвет. Затем выберите цвет на расстоянии 120 градусов друг от друга.
И найдите цвет, отстоящий на 240 градусов от первого цвета.
У вас три цвета в цветовой триаде.
Цветовая схема №4. Четырехцветные цвета
Нарисуйте квадрат на цветовом круге, чтобы найти тетрадные цвета.
Или выберите любой цвет.
цветовой круг Теория цветов тетрадные цвета Поиск цветов на 90, 180 и 270 градусов относительно этого цвета соответственно.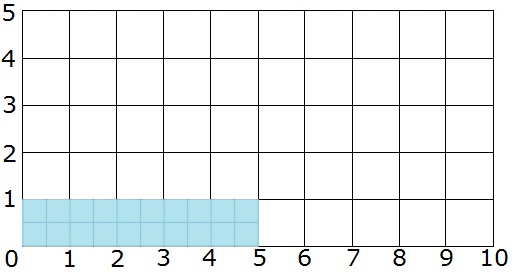


 http://www.proshkolu.ru/user/Ligiya/file/2383648
http://www.proshkolu.ru/user/Ligiya/file/2383648

 см.
см.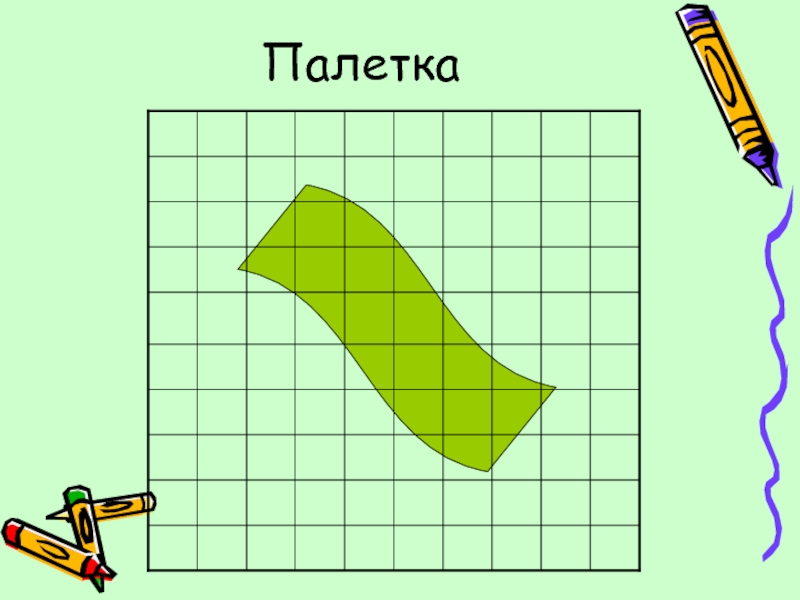
 Первичное закрепление
Первичное закрепление см=1500кв. мм
см=1500кв. мм

 м?
м?