Правило минус плюс минус: Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

• Альфашкола
• Статьи
• Сложение и вычитание отрицательных чисел

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами.  Существуют определенные правила для знаков при сложении и вычитании:

• Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

• Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\)     \(7,1+(-7,1)=0\)

• При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

• Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

• Также не стоит забывать минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

 

1.  \(4+(-5)\)
2.  \(-36+15\)
3. \((-17)+(-45)\)
4. \(-9+(-1)\)

 

Решение:

 

1.  \(4+(-5)=4-5=-1\)
2.  \(-36+15=-21\)
3. \((-17)+(-45)\) \(=-17-45=-62\)
4. \(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

1. \(3-(-6)\)
2.  \(-16-35\)
3. \(-27-(-5)\)
4.  \(-94-(-61)\)

Решение:

1.  \(3-(-6)=3+6=9\)
2. \(-16-35=-51\)
3.  \(-27-(-5)=-27+5=-22\)
4.  \(-94-(-61)=-94+61=-33\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ольга Яновна Савинова

Репетитор по математике

Стаж (лет)

Образование:

Гродненский государственный университет имени Янки Купалы

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Алла Алексеевна Кандыба

Репетитор по математике

Стаж (лет)

Образование:

Полтавский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Андрей Алексеевич Тарасов

Репетитор по математике

Стаж (лет)

Образование:

Новосибирский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ЕГЭ по математике (базовый уровень)
• Подготовка к ОГЭ по математике
• Репетитор по алгебре
• Репетитор по химии для подготовки к ЕГЭ
• Репетитор для подготовки к ЕГЭ по физике
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Репетитор по грамматике русского языка
• ВПР по физике
• Репетитор по географии для подготовки к ОГЭ
• Программирование Pascal

Похожие статьи

• Пропорция в математике
• Десятичные дроби
• Свойства корней
• Теорема Пифагора
• НИУ ВШЭ: Факультет Психологии
• РУДН: факультет Психологии (отзывы,проходной балл, стоимость обучения)
• Решаем профильный ЕГЭ.
  Простейшие текстовые задачи
• Задачи на исследование функций

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Плюс минус

Плюс минус

      Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.

      Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.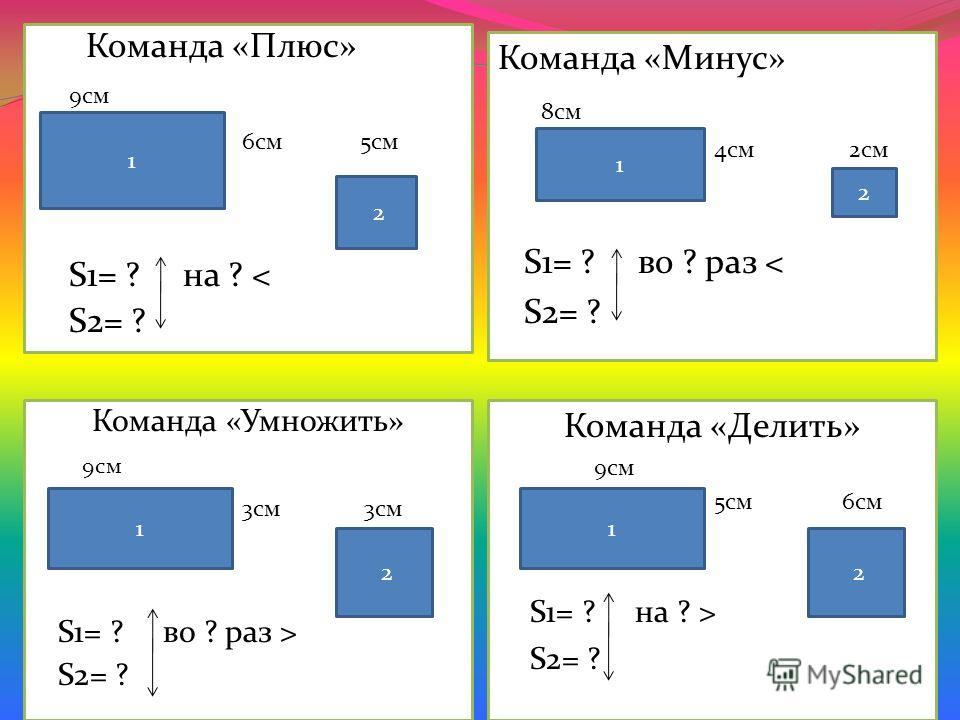

      При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.

      В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.

      При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.

      Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа.

При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.

ВОПРОС — ОТВЕТ

«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».

«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке

(-6) : (-3) = +2

Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:

(-6) : (-3) = 2

«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.

      13 ноября 2009 года — 22 сентября 2019 года.

© 2006 — 2021 Николай Хижняк. Все права защищены.

Сложение и вычитание положительных и отрицательных чисел

Числа могут быть положительными или отрицательными

Это номер строки:

Отрицательные числа (-)	Положительные числа (+)

«-» — отрицательный знак.	«+» — положительный знак

Отсутствие знака означает положительный результат

Если число имеет без знака , это обычно означает, что это положительное число .

Пример: 5 на самом деле +5

Играй!

На числовой прямой положительный идет вправо, а отрицательный — влево.

Попробуйте использовать ползунки ниже и посмотрите, что произойдет:

числа/изображения/номер-линия-add.js?sub=n

Воздушные шары и гири

Давайте представим числа как шарики (положительные) и веса (отрицательные):

К этой корзине привязаны воздушные шары и грузы:

• Воздушные шары подтягиваются ( положительный )
• И гири тянутся вниз ( отрицательный )

Добавление положительного числа

Добавление положительных чисел — это простое сложение.

 

Мы можем добавить воздушные шары (мы добавляем положительное значение )

корзина поднимается вверх (положительный результат)

Пример: 2 + 3 = 5

на самом деле говорит

«Положительное 2 плюс положительное 3 равно положительному 5»

Мы могли бы записать это как (+2) + (+3) = (+5)

Вычитание положительного числа

Вычитание положительных чисел — это простое вычитание.

Мы можем забрать воздушные шары (мы вычитаем положительное значение )

корзина тянется вниз (негатив)

Пример: 6 − 3 = 3

на самом деле говорит

«Положительные 6 минус Положительные 3 равно Положительным 3»

Мы могли бы записать это как (+6) — (+3) = (+3)

Добавление отрицательного числа

Теперь давайте посмотрим, как выглядит сложение и вычитание отрицательных чисел:

Мы можем добавить веса (мы добавляем отрицательные значения )

корзина тянется вниз (негатив)

Пример: 6 + (−3) = 3

на самом деле означает

«Положительные 6 плюс отрицательные 3 равны положительным 3»

 

Мы могли бы записать это как (+6) + (−3) = (+3)

Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного значения) или добавление веса (добавление отрицательного значения) приводит к тому, что корзина опускается.

Таким образом, они имеют одинаковый результат :

• (+6) — (+3) = (+3)
• (+6) + (-3) = (+3)

Другими словами вычитание положительного равносильно добавлению отрицательного .

Вычитание отрицательного числа

Наконец, мы можем убрать веса (мы вычитаем отрицательные значения)

корзина поднимается вверх (положительный результат)

Пример: чему равно 6 − (−3) ?

6−(−3) = 6 + 3 = 9

Да, действительно! Вычитание минуса – это то же самое, что добавление!

Два минуса дают плюс

Что мы нашли?

Добавление положительного числа — это простое сложение…

Добавление положительного Добавление

 

Положительное и отрицательное вместе…

Вычитание положительного
или
Добавление отрицательного
равно
Вычитание

Пример: Сколько будет 6 − (+3) ?

6−(+3) = 6 − 3 = 3

Пример: Сколько будет 5 + (−7) ?

5+(-7) = 5 — 7 = -2

 

Вычитание отрицательного значения.

..

Вычитание минуса аналогично Сложение

Пример. Сколько будет 14 − (−4) ?

14−(−4) = 14 + 4 = 18

Правила:

Все это можно поместить в два правила :

	Правило				Пример
+(+)	Два одинаковых знака становятся положительным знаком				3+(+2) = 3 + 2 = 5
−(−)					6−(−3) = 6 + 3 = 9
+(-)	Два разных знака становятся отрицательным знаком				7+(−2) = 7 − 2 = 5
−(+)					8−(+2) = 8 − 2 = 6

Они «подобны знакам», когда они похожи друг на друга (другими словами: одинаковы).

 

Итак, все, что вам нужно запомнить, это:

Два подобных знака становятся положительным знаком

Два непохожих знака становятся отрицательным знаком

Пример: Что такое 5+(−2) ?

+(-) — это в отличие от знаков (они не одинаковы), поэтому они становятся отрицательным знаком .

5+(−2) = 5 − 2 = 3

Пример: чему равно 25−(−4) ?

−(−) равно подобен знаку , поэтому они становятся положительным знаком .

25−(−4) = 25+4 = 29

Стартовый отрицательный

Что, если мы начнем с отрицательного числа?

Использование числовой линии может помочь:

Пример: чему равно −3+(+2) ?

+(+) — это , как знак, поэтому они становятся положительным знаком .

-3+(+2) = -3 + 2

Начните с -3 на числовой прямой,
сдвиньте вперед 2, и вы окажетесь на -1

−3+(+2) = −3 + 2 = −1

Пример: чему равно −3+(−2) ?

+(-) это в отличие от знаков, поэтому они становятся отрицательным знаком .

-3+(-2) = -3 — 2

Начните с -3 на числовой прямой,
переместитесь назад на 2, и вы окажетесь на -5

-3+(-2) = — 3 − 2 = −5

А теперь поиграй!

Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха!

Объяснение здравого смысла

И есть объяснение «здравого смысла»:

Если я скажу «Ешь!» Я призываю вас есть (положительно)

Если я скажу «Не есть!» Я говорю обратное (отрицательно).

Теперь, если я скажу: « НЕ НЕ ешьте!», я говорю, что не ем. хочу, чтобы вы голодали, поэтому я снова говорю: «Ешьте!» (положительно).

Итак, два минуса дают плюс, и если вас это устраивает, то вы сделали!

 

Другое объяснение здравого смысла

Друг +, враг —

+ + ⇒ +		друг друга мой друг
+ — ⇒ —		друг врага мой враг
— + ⇒ —		враг друга мой враг
− − ⇒ +		враг врага мой друг

Пример банка

Пример: В прошлом году банк по ошибке списал с вашего счета 10 долларов, и они хотят это исправить.

Итак, банк должен забрать минус 10 долларов .

Предположим, что ваш текущий баланс составляет 80 долларов США, поэтому у вас будет:

80 долларов США − (− 10 долларов США) = 80 долларов США + 10 долларов США = 90 долларов США

Таким образом, вы получите долларов США на 10 дополнительных на вашем счету.

Длинный пример, который может вам понравиться

Очки союзника

Элли может быть озорной или милой. Итак, родители Элли сказали

«Если ты будешь хорошим, мы добавим 3 балла (+3).
Если ты будешь непослушным, мы уменьшим 3 балла (−3).
Когда ты наберешь 30 баллов, ты получишь игрушку.»

 

Союзник начинает день с 9 очками:		9
Мама Элли обнаруживает пролитое молоко:		9 − 3 = 6
Потом папа признается, что пролил молоко и пишет «отменить». Как нам «отменить» минус 3? Мы добавляем 3 обратно!
Мама считает:		6 − (−3) = 6 + 3 = 9

Таким образом, когда мы вычитаем отрицательное значение, мы получаем
очков (то есть то же самое, что и сложение очков).

Таким образом, вычитание отрицательного числа равно . Сложение

.

 

Несколько дней спустя. У Элли 12 очков.
Мама добавляет 3 балла, потому что в комнате Элли чисто.		12 + 3 = 15
Папа говорит: «Я убрал эту комнату» и пишет «отменить» на графике. Мама считает:		15 − (+3) = 12
Папа видит, как Элли расчесывает собаку. Пишет «+3» на графике. Мама считает:		12 + (+3) = 15
Элли бросает камень в окно. Папа пишет «-3» на графике. Мама считает:		15 + (−3) = 12

См.: как « 15 − (+3) », так и « 15 + (−3) » дают 12.

Итак:

Не имеет значения, вычитаете ли вы положительные очки
или добавляете отрицательные очки,
вы все равно теряете очки.

Итак, вычитание положительного
или
Добавление отрицательного
равно
Вычитание

 

Попробуйте эти упражнения…

Теперь попробуйте этот рабочий лист и посмотрите, как у вас получится.

А также попробуйте эти вопросы:

11715, 11716, 11717, 11718, 11719, 11720, 11721, 3445, 3446

Основные правила для положительных и отрицательных чисел

• Описание

  Правила для добавления и вычитания двух чисел положительных и отрицательных

• Источник

  , созданные Karina goto For Yourdictionary

• . YourDictionary 

Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.

При использовании положительных и отрицательных чисел используются правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.

Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.

Реклама

Дополнение: одинаковые знаки, добавьте числа

Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:

• 1 + 1 = 2
• 51 + 32 = 83
• -14 + (-6) = -20
• -196 + (-71) = -267

Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.

Сложение: разные знаки, вычитание чисел

Если вы складываете положительные и отрицательные числа вместе, вычтите меньшее число из большего и используйте знак из большего числа. Например:

• 6 + (-5) = 1
• -17 + 22 = 5
• -100 + 54 = -45
• 299 + (-1) = 298

Как видите, сложение числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.

Реклама

Вычитание: Переключиться на сложение

Вычитание положительных и отрицательных чисел означает, что вы складываете противоположные числа или добавите обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:

• -3 — (+5) становится -3 + (-5) = -8
• 9 — (-7) становится 9 + (+7) = 16
• -14 — (+8) становится -14 + (-8) = -22
• 25 — (-90) становится 25 + (+90) = 115

Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно превращайте их в положительные знаки. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.

Умножение и деление: один и тот же знак, положительный результат

Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:

• 8 x 4 = 32
• (-8) x (-4) = 32
• 10 x 9 = 90
• (-10) x (-9) = 90

То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:

• 12 ÷ 6 = 2
• -12 ÷ (-6) = 2
• 100 ÷ 5 = 20
• -100 ÷ (-5) = 20

числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.

Реклама

• Описание

  Правила для умножения и деления двух чисел положительные и отрицательные

• Источник

  Созданы Karina goto для yourdictionary

• . Умножение и деление: обратный знак, отрицательный результат

  При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:

  • 6 х (-7) = -42
  • -7 х 6 = -42
  • 12 х (-11) = -132
  • -11 х 12 = -132

  Во всех этих случаях вам сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
  

  Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки подряд. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:

  • 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
  • 9 + (-8) = 1 (+- не являются знаками, поэтому уравнение представляет собой вычитание)
  • 11 — (+13) = 2 (-+ не похожи на знаки, поэтому уравнение представляет собой вычитание)
  • 15 — (-10) = 25 (— похожи на знаки, поэтому уравнение представляет собой сложение)

  Этот метод следует те же правила, что и выше, но они могут помочь вам решить проблему быстрее, если вы предпочитаете работать над знаками заранее.