примеры и вычисление функции потерь
Линейная регрессия (Linear regression) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.
Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала простым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.
Применение линейной регрессии
Предположим, нам задан набор из 7 точек (таблица ниже).
Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:
Попробуем несколько случайных кандидатов:
Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.
Функция потерь — метод наименьших квадратов
Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y(х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.
Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.
Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.
Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.
Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Если мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.
Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.
Больше размерностей
Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:
f(x) = b+w_1*x_1 + … + w_n*x_n
Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:
f(x) = b*1+w_1*x_1 + … + w_n*x_n
Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.
Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.
Проклятие нелинейности
Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.
Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).
Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.
Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.
Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.
Примеры линейной регрессии
Если вы считаете регрессионное моделирование недоступным для понимания, или если у вас были проблемы с алгеброй в старшей школе, то эта статья для вас. Конечно, всем остальным она тоже не повредит.
Загрузить программу ВІ
Демонстрации решений
Оглавление
Если вы считаете регрессионное моделирование недоступным для понимания, или если у вас были проблемы с алгеброй в старшей школе, то эта статья для вас. Конечно, всем остальным она тоже не повредит.
Конечно, всем остальным она тоже не повредит.Представьте, что вам дали базу данных, содержащую возраст и доход каждого жителя определенного района. Ваш начальник хочет, чтобы вы использовали эти данные, чтобы создать модель, предсказывающую доход человека на основании его возраста. И вот вы звоните с просьбой о срочной статистической помощи некоему Доктору Иванову из Информационных Систем. Удача вам сопутствует – доктор на связи. Док Иванов мудро удостоверяется, что среди данных нет аномальных значений, способных исказить анализ. Затем он колдует над данными и добросовестно представляет вам математическую модель: «Умножьте возраст в годах на 971.4, приплюсуйте 1536.2 и получите годовой доход в долларах. Вот ваша оптимальная модель».
Вы как следует благодарите Доктора Иванова и спешите подготовить отчет своему начальнику. Вы используете формулу, чтобы построить график с доходом по вертикальной оси и возрастом по горизонтальной, и восхищаетесь простотой, с которой это правило связывает возраст и доход.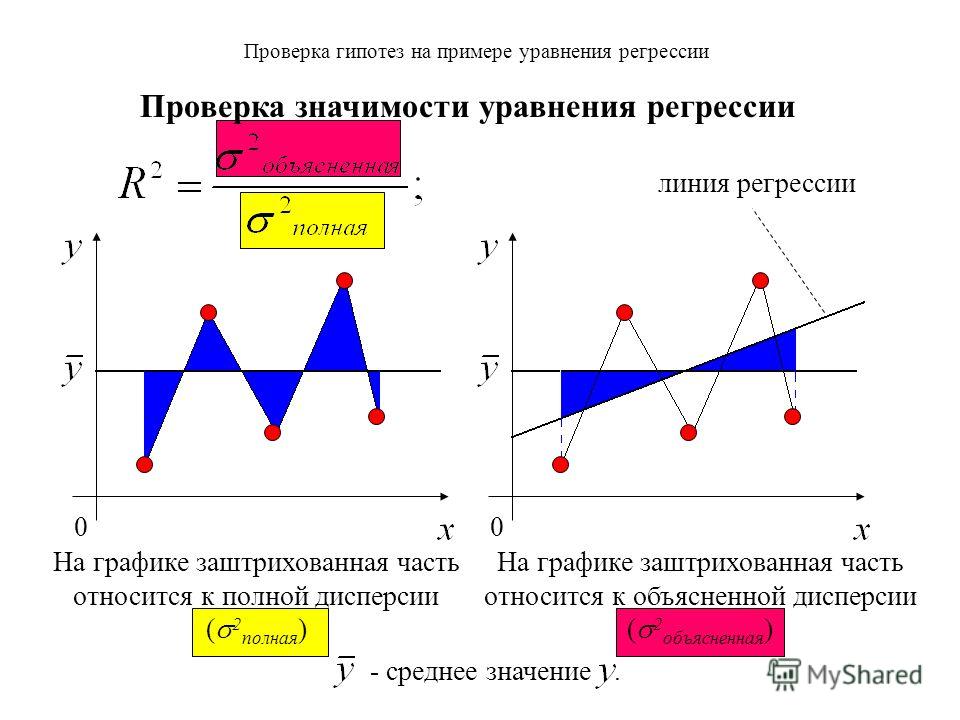 Это прямая линия – и к тому же, оптимальная. Но ее блеск чуть меркнет, когда вы замечаете, что по этой модели доход 18-летних составляет $19,021 (этим юнцам следовало бы делать домашние задания, а не грести такие суммы!) И он исчезает окончательно, когда вы видите, что предполагаемый доход 70-летних составляет $69,534, и каждый последующий год жизни добавляет автоматический бонус в $971 (и вряд ли за счет надбавок к государственной пенсии).
Это прямая линия – и к тому же, оптимальная. Но ее блеск чуть меркнет, когда вы замечаете, что по этой модели доход 18-летних составляет $19,021 (этим юнцам следовало бы делать домашние задания, а не грести такие суммы!) И он исчезает окончательно, когда вы видите, что предполагаемый доход 70-летних составляет $69,534, и каждый последующий год жизни добавляет автоматический бонус в $971 (и вряд ли за счет надбавок к государственной пенсии).
Так почему же формула доктора Иванова выглядит подозрительной? Потому что она плохая. Но как модель может быть плохой, когда она «оптимальна»? Она будет оптимальна только в том случае, если Иванов сделал правильное предположение о ее форме. Он предположил, что правильная форма модели – это прямая линия. Компьютер сделал свою часть работы, выбрав наиболее подходящую прямую линию из всех возможных с помощью применения многоуважаемой техники, созданной еще Карлом Гауссом (1777-1855).
Уловка-22
Если вам кажется, что здесь есть Уловка-22, то вы правы. Если бы вы знали верную форму модели с самого начала, вам бы не понадобился Доктор Иванов. Док тоже не знал, какая форма является верной, так что из-за своей занятости он выбрал самое простое и предположил, что это прямая линия. Уравнение прямой линии выглядело научным, по крайней мере, в тот момент, но по сути научным не являлось. Прямые линии зачастую отражают невероятные физические законы в науке и инженерии, и нет никаких оснований полагать, что они применимы к экономическим ситуациям. Алгебраическая формула, и впрямь, проста и удобна, но кому нужно простое описание плохой модели?
Если бы вы знали верную форму модели с самого начала, вам бы не понадобился Доктор Иванов. Док тоже не знал, какая форма является верной, так что из-за своей занятости он выбрал самое простое и предположил, что это прямая линия. Уравнение прямой линии выглядело научным, по крайней мере, в тот момент, но по сути научным не являлось. Прямые линии зачастую отражают невероятные физические законы в науке и инженерии, и нет никаких оснований полагать, что они применимы к экономическим ситуациям. Алгебраическая формула, и впрямь, проста и удобна, но кому нужно простое описание плохой модели?
Действительно ли объединенные силы математики и процессора Pentiumвытянули именно то, что было нужно, из данных? Вот и нет. То, что сделал Док, случается слишком часто, потому что всегда есть искушение бездумно применить повсеместно используемый инструмент, называемый линейной регрессией.
Линейная регрессия
Формула, которую дал вам Док, умножает возраст на 971.4 и добавляет 1536. 2 к результату. Он получил 971.4 и 1536.2 с помощью компьютерной программы линейной регрессии, которая выполнила все трудоемкие вычисления, чтобы найти эти числа. Данные числа определяют конкретную прямую, на которую ложатся исходные данные.
2 к результату. Он получил 971.4 и 1536.2 с помощью компьютерной программы линейной регрессии, которая выполнила все трудоемкие вычисления, чтобы найти эти числа. Данные числа определяют конкретную прямую, на которую ложатся исходные данные.
Линейная регрессия – это математический метод оценивания некоего количественного значения (например, суммы в долларах), посредством «взвешивания» одного или нескольких прогнозирующих параметров, таких как возраст, число детей, средний счет в боулинге и так далее. Он был разработан задолго до цифровых компьютеров, и его вечная слава обусловлена привлекательностью для академических исследований.
Если предположить, что линейная регрессия была единственным моделирующим инструментом в арсенале Дока, то мы можем увидеть, как его созданная из подручных средств модель появилась на свет. Подобные инструменты делают допущение, что прямая линия является правильной формой, определяющей отношение каждого из прогнозирующих параметров к искомому количественному показателю. Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Доход = 1007.8*Возраст -752.35*Число детей +933.6
Звездочка – знак умножения.Влияние нашей новой переменной «число детей», тоже линейное. Это происходит потому, что предполагаемый доход прямолинейно уменьшается на $752.35 за каждого дополнительного ребенка. Мы используем эту формулу, показывающую отношение возраста и числа детей к доходу, чтобы проиллюстрировать то, что важно знать о числах, предоставляемых линейной регрессией.
1) Довольно часто, некорректно полагают, что 1007.8 – это «вес» возраста, а -752.35 – «вес» числа детей. Если бы возраст выражался в месяцах, а не в годах, то новый «вес» был бы разделен на 12 лишь для того, чтобы отразить изменение шкалы. Таким образом, величина «веса» не является мерой важности прогнозирующего параметра, к которому он относится.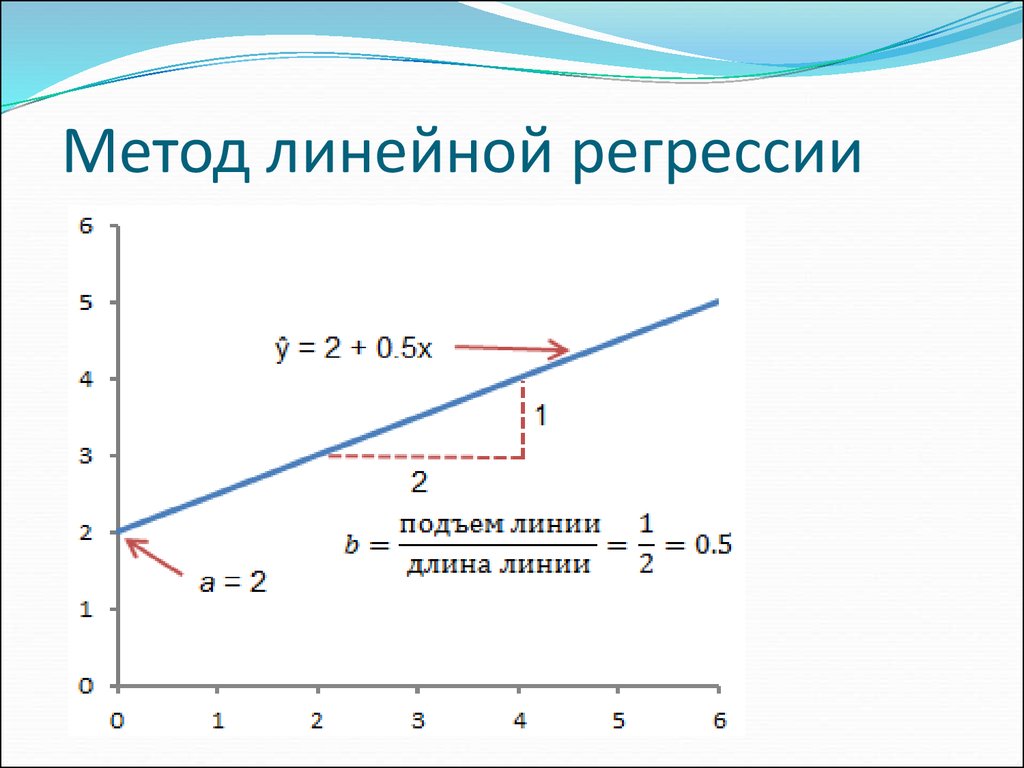 Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Единственное предназначение коэффициентов и, в сущности, всех чисел (технически, значений параметров), производимых регрессией – это сделать так, чтобы формула хорошо сходилась с исходными данными.
2) Обратите внимание, что коэффициент (-752.35), множитель числа детей, имеет отрицательно значение. В реальности это вовсе не означает, что если число детей растет, то предполагаемый доход обязательно уменьшается. Знак перед коэффициентом будет достоверно указывать направление только в том случае, когда он является единственным прогнозирующим параметром. Если имеется два и более прогнозирующих параметра, и между ними существует корреляция, то вполне вероятно, что один параметр будет иметь положительный коэффициент, а другой – отрицательный, вопреки здравому смыслу. Для нашего примера, на самом деле, если бы число детей было бы единственным прогнозирующим параметром, то тогда коэффициент перед ними оказался бы положительным. Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
3) Последний параметр регрессии, константа +933.6 существует для того, чтобы удостоверится, что если каждый параметр принимает среднее значение, то результирующий предполагаемый доход тоже окажется средним. Линейная регрессия всегда так работает. Допустим, средний возраст равен 45.67, а среднее число детей – 1.41. Мы можем подставить эти значения в формулу следующим образом:
1007.8*45.67 -752.35*1.41 +933.56 = 45899
И 45899 – действительно, средний доход в исходных данных. После того как коэффициенты умножены на свои соответствующие параметры и просуммированы, в итоге всегда останется добавить эту константу (даже если она равна нулю).
Математический подвиг
До этого момента мы говорили о том, как линейная регрессия делает допущение о линейности отношений, и о том, как интерпретировать параметры, которые она находит. Но что делать, если отношения не линейны? Вы можете, не задумываясь, подставить данные в линейную регрессию, но то, что вы получите, будет линейным округлением для верной формы. Чем больше верная форма отличается от прямой линии, тем менее точным будет результат.
Но что делать, если отношения не линейны? Вы можете, не задумываясь, подставить данные в линейную регрессию, но то, что вы получите, будет линейным округлением для верной формы. Чем больше верная форма отличается от прямой линии, тем менее точным будет результат.
Из-за того, что процедура линейной регрессии выбита в граните классики, ответственность за выпрямление данных в нечто напоминающее прямую линию ложится на сознательного пользователя. Технический термин для выпрямления – это «трансформирование». Из своих предпочтений Док Иванов, скорее всего, использует что-то математическое, чтобы выполнять трансформирование. Например, если между возрастом и доходом не существует линейных отношений, возможно, они существуют между квадратным корнем возраста и доходом. Нет ничего волшебного в квадратном корне. Это всего лишь одна из множества математических функций, которая может использоваться в попытке трансформировать возраст во что-то новое, что будет более сопоставимо с линейной регрессией. Пара трансформаций тут и там может оказаться делом веселым и интересным, но что если вам приходится иметь дело с сотней потенциальных прогнозирующих параметров?
Пара трансформаций тут и там может оказаться делом веселым и интересным, но что если вам приходится иметь дело с сотней потенциальных прогнозирующих параметров?
Книга 1995 года, адресованная индустрии прямого маркетинга, говорит о трансформировании следующее [наши комментарии – в квадратных скобках]:
«…довольно просто взглянуть на диаграмму рассеяния [точечный график, в котором горизонтальная ось – прогнозирующие параметры, а вертикальная – прогнозируемые] для определения, являются ли отношения линейными, или же они должны быть выпрямлены с помощью какой-либо трансформации».
Предыдущее утверждение верно, если рассматривается небольшое число параметров, и отношения настолько сильны, что очевидны при первом взгляде. Но если слабые отношения погребены под грудой из 50,000 параметров, тогда бы и Шерлок Холмс, вооруженный своей лупой, их бы не нашел. Другой подход с такой же сложностью – это построить график с ошибками («погрешностью») линейной модели, чтобы обнаружить очевидные закономерности упущенной информации.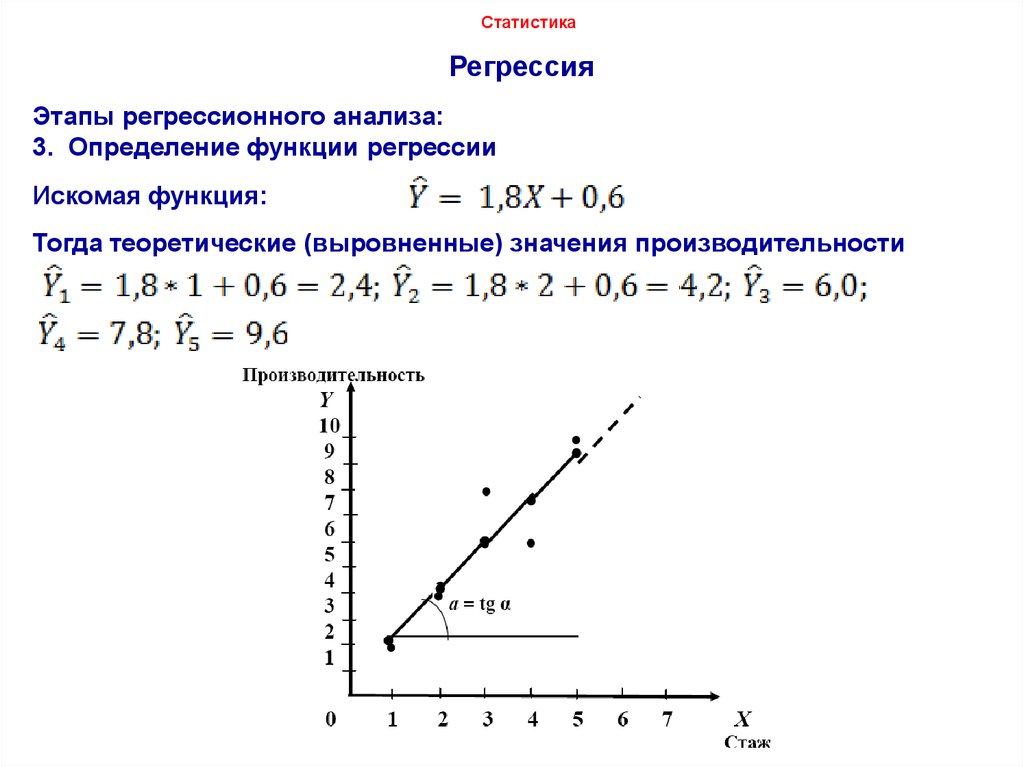 Недавно была продемонстрирована работа очень медленной (но упорной) компьютерной программы, которая испытывает одно уравнение трансформации за другим, усердно строя графики каждой найденной формулы на экране. Вы буквально можете оставить эту штуку работать всю ночь. Столь фанатичную преданность аналитическим функциям сложно оправдать, потому что пользователь, тот, кто платит по счетам, без сомнений, не обладает способностью интуитивно интерпретировать любую из них.
Недавно была продемонстрирована работа очень медленной (но упорной) компьютерной программы, которая испытывает одно уравнение трансформации за другим, усердно строя графики каждой найденной формулы на экране. Вы буквально можете оставить эту штуку работать всю ночь. Столь фанатичную преданность аналитическим функциям сложно оправдать, потому что пользователь, тот, кто платит по счетам, без сомнений, не обладает способностью интуитивно интерпретировать любую из них.
Давайте вернемся к изначальной проблеме предсказания дохода на основе возраста. Чтобы проиллюстрировать нашу позицию, давайте предположим, что следующая героическая модель наиболее соответствует вашим данным:
Доход = 46001 -exp(0.01355*(Возраст-46)**2)
Спорим, что она не вызовет у вашего начальника теплых и нежных чувств. У этого уравнения нет никакого смысла, кроме того, что эта гладкая кривая больше соответствует вашим данным, чем прямая линия. Можно найти еще более экзотичные уравнения, которые будут еще лучше соответствовать данным.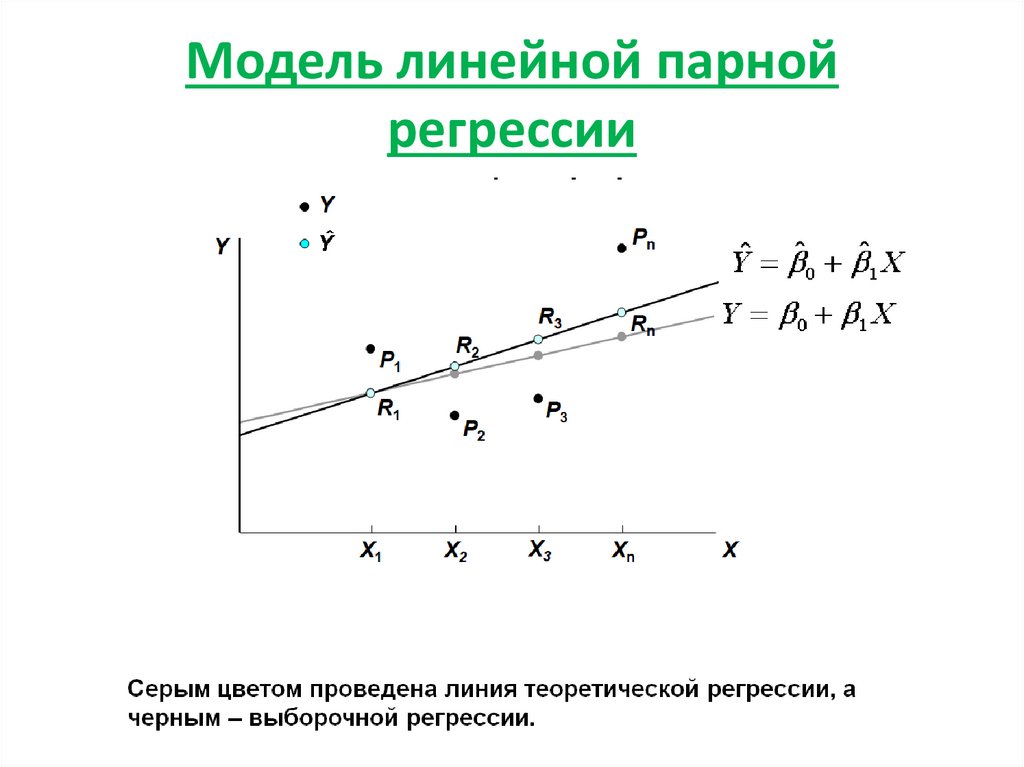 Но эти упражнения по поиску наиболее соответствующей кривой не только лишены всякого смысла, но и полученная в результате кривая может подойти чересчур хорошо, внушив ложную уверенность в том, что было совершено некое научное достижение.
Но эти упражнения по поиску наиболее соответствующей кривой не только лишены всякого смысла, но и полученная в результате кривая может подойти чересчур хорошо, внушив ложную уверенность в том, что было совершено некое научное достижение.
Повседневный подвиг
Давайте начнем с того, что такое модель и что ей не является. Модель – это просто набор правил, который позволит вам оттолкнуться от того, что вы уже знаете, и предсказать то, что вы желаете узнать. Возвращаясь к нашей исходной гипотетической проблеме. Вы хотите оттолкнуться от того, что вы уже знаете (возраст), и предсказать то, что вы хотите узнать (доход). Здесь, разумеется, будут возникать ошибки, но вы хотели бы в среднем оказываться правым, при этом постоянно не завышая и не занижая оценку дохода для возрастных диапазонов. Нужен набор правил, который точно описывает отношения между возрастом и доходом, и будет действительно моделью.
Начать вам лучше с составления собственной табличной модели со следующими строчками:
| Возраст | Доход |
|---|---|
| 18-22 | $7,500 |
| 23-33 | $25,000 |
| 34-44 | $38,000 |
| 45-55 | $58,000 |
| 56-60 | $30,000 |
| 61 и больше | $21,000 |
По крайней мере, эта таблица отражает реальность, в которой студенты и пенсионеры в среднем получают меньше остальных.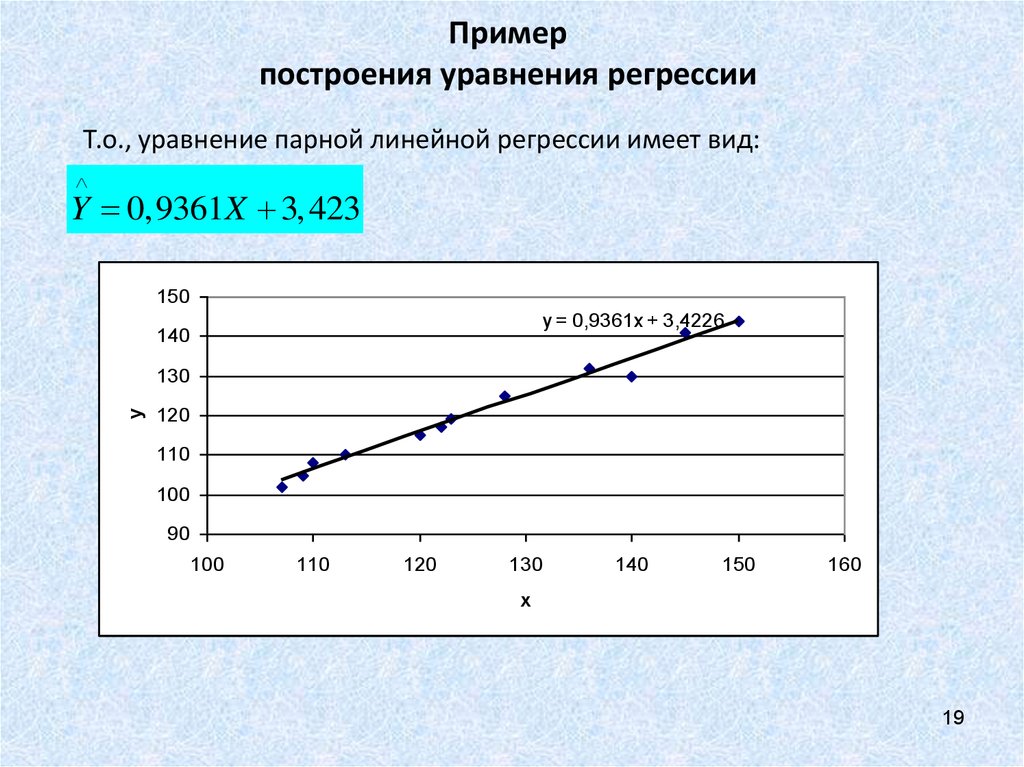 Это может быть не алгебраично и не оптимально, но это модель и, к тому же, хорошая и нелинейная. Существует естественная разница между линейной моделью Дока и вашей прагматичной таблицей. Уравнение Дока «глобально»: это означает, что оно делает оценки для любого возраста от нуля до бесконечности. Если из-за ошибки ввода или программирования, в формулу будет подставлено значение возраста 999, то она радостно определит предполагаемый доход как $971,965. Помните, что многие математические формулы безжалостно проецируются в прекрасное далеко, если в них подставляют значения прогнозирующего параметра абсурдно далекие от их разумных пределов. Не всегда легко найти математические выражения, которые подстраиваются под данные в рамках разумного диапазона.
Это может быть не алгебраично и не оптимально, но это модель и, к тому же, хорошая и нелинейная. Существует естественная разница между линейной моделью Дока и вашей прагматичной таблицей. Уравнение Дока «глобально»: это означает, что оно делает оценки для любого возраста от нуля до бесконечности. Если из-за ошибки ввода или программирования, в формулу будет подставлено значение возраста 999, то она радостно определит предполагаемый доход как $971,965. Помните, что многие математические формулы безжалостно проецируются в прекрасное далеко, если в них подставляют значения прогнозирующего параметра абсурдно далекие от их разумных пределов. Не всегда легко найти математические выражения, которые подстраиваются под данные в рамках разумного диапазона.
Ко всей этой затее с трансформированием есть более практичный подход. Его можно осуществить на основе таблицы, в которой доход для диапазона возрастов 56-60 превосходил бы доход для диапазона 18-22 примерно в четыре раза – лучше или хуже группируя разные диапазоны возрастов и наблюдая, как изменяется средний доход. Такая компьютерная процедура называется локальным сглаживаем. При локальном сглаживании предполагается, что прогнозируя, скажем, доход для 35-, 34- и 36-летних мы получим значение, схожее со значением дохода для 35-летних, и таким образом, это значение будет обладать почти одним с ним весом при округлении. Доходы для 18-летних или 70-летних не будут иметь ничего общего с доходом 35-летних, и поэтому получат нулевой вес при взвешивании. Более разумно использовать компьютер для нахождения этой локальной информации, чем пускаться в охоту за формой (математической функцией), которая по счастливой случайности будет иметь изгибы в нужных местах.
Такая компьютерная процедура называется локальным сглаживаем. При локальном сглаживании предполагается, что прогнозируя, скажем, доход для 35-, 34- и 36-летних мы получим значение, схожее со значением дохода для 35-летних, и таким образом, это значение будет обладать почти одним с ним весом при округлении. Доходы для 18-летних или 70-летних не будут иметь ничего общего с доходом 35-летних, и поэтому получат нулевой вес при взвешивании. Более разумно использовать компьютер для нахождения этой локальной информации, чем пускаться в охоту за формой (математической функцией), которая по счастливой случайности будет иметь изгибы в нужных местах.
Прогнозирующие параметры
Линейная регрессия делает допущение, что прогнозирующие параметры что-то измеряют. Предположим, у нас есть прогнозирующий параметр – семейное положение, и он кодируется так: 1 = состоит в браке, 2 = не состоит в браке, 3 = разведен(а), 4 = вдова(ец). Эти четыре числовых кода ничего не измеряют; они произвольно выбраны, чтобы обозначать категории. Пользователю линейной регрессии приходится обходить эту проблему с помощью создания дополнительных прогнозирующих параметров, называемых вспомогательными переменными. Мы не станем в это углубляться, но рекомендуем вам учесть, что это другой неудобный аспект попытки приспособиться к допущениям линейной регрессии. Мы не завидуем тем, кому приходится иметь дело с дюжиной потенциальных прогнозирующих параметров, которые требуют применения уловки с трансформацией или же со вспомогательными переменными.
Пользователю линейной регрессии приходится обходить эту проблему с помощью создания дополнительных прогнозирующих параметров, называемых вспомогательными переменными. Мы не станем в это углубляться, но рекомендуем вам учесть, что это другой неудобный аспект попытки приспособиться к допущениям линейной регрессии. Мы не завидуем тем, кому приходится иметь дело с дюжиной потенциальных прогнозирующих параметров, которые требуют применения уловки с трансформацией или же со вспомогательными переменными.
Значима ли модель?
В оценке того, насколько модель хороша, только одна вещь имеет значение – насколько хорошо модель делает предположения на основе данных, которых никогда не встречала. Всегда придерживайте некоторые данные в стороне в процессе моделирования как раз на этот случай. Когда значения внешних данных отсортированы от меньшего к большему, очевидна ли разница между возможностями и рисками? Сравнение различий между нижними 10 процентами значений и верхними 10 процентами – это распространенная проверка качества модели. Нет ничего особенного в группировке по десяткам. Общее правило – сделать группы настолько маленькими, насколько возможно, чтобы при этом сохранялась закономерность ступенчатого различия между группами. Если градация сохраняется, а результаты, полученные на основе данных, не входящих в выборку, выглядят хорошо, то модель значима. Точка.
Нет ничего особенного в группировке по десяткам. Общее правило – сделать группы настолько маленькими, насколько возможно, чтобы при этом сохранялась закономерность ступенчатого различия между группами. Если градация сохраняется, а результаты, полученные на основе данных, не входящих в выборку, выглядят хорошо, то модель значима. Точка.
Повседневный семантический смысл слова «значимый» – это «имеющий смысл» или «важный». Статистическое значение слова – это оценка того, является ли отхождение от гипотезы достаточно большим, чтобы обоснованно считаться не случайным. «Значимость» в статистическом смысле не имеет ничего общего с тем, является ли результат хорошим или плохим, а означает, что результат является не случайным.
Охраняя храм
Если вы посмотрите на линейную регрессию с точки зрения математики, то она прекрасна. Если вы взгляните на нее как на инструмент моделирования и оценки, то у нее обнаружится множество недостатков. Чтобы приблизится к математическому храму, вам потребуется жрец, который знает, как манипулировать данными, чтобы они соответствовали линейному канону, говорит о F-тестах и делает такого рода предупреждения (все та же книга):
«…нам следует не забывать тот факт, что финальная модель регрессии может быть применена к клиентскому файлу, содержащему миллионы имен, и что чем сложнее модель, тем больше трудностей она может вызывать у программистов, которые не являются специалистами по статистике и у которых может не оказаться программных инструментов, необходимых для работы с логарифмами и оценки базы данных».
Это невероятное заявление! После всей суеты вокруг модели, может оказаться, что у бедного программиста нет необходимых инструментов, чтобы с ней работать!
Заключение
Можно еще многое сказать о линейной регрессии. В статье представлены наиболее практичные советы, потому что регрессия находится повсюду и обладает такой богатой историей, что она будет использоваться еще долго. Линейная регрессия – это наследие тех дней, когда компьютеров не существовало, и нужен эксперт, чтобы грамотно ей воспользоваться. Это контрпродуктивно и дорого. Программное обеспечение должно помогать людям. Если вы действительно знаете, чего хотите, вы можете выполнить это в компьютерной программе. Современные компьютерно-ориентированные методы могут позаботиться о тех ограничениях линейной регрессии, которые требуют затратных услуг эксперта, вроде выявления аномальных значений, проведения трансформаций и манипуляций с категориями. Когда дело касается предсказаний, они тоже могут выполняться с помощью компьютерных программ, используя в основе данные, использованные при создании модели.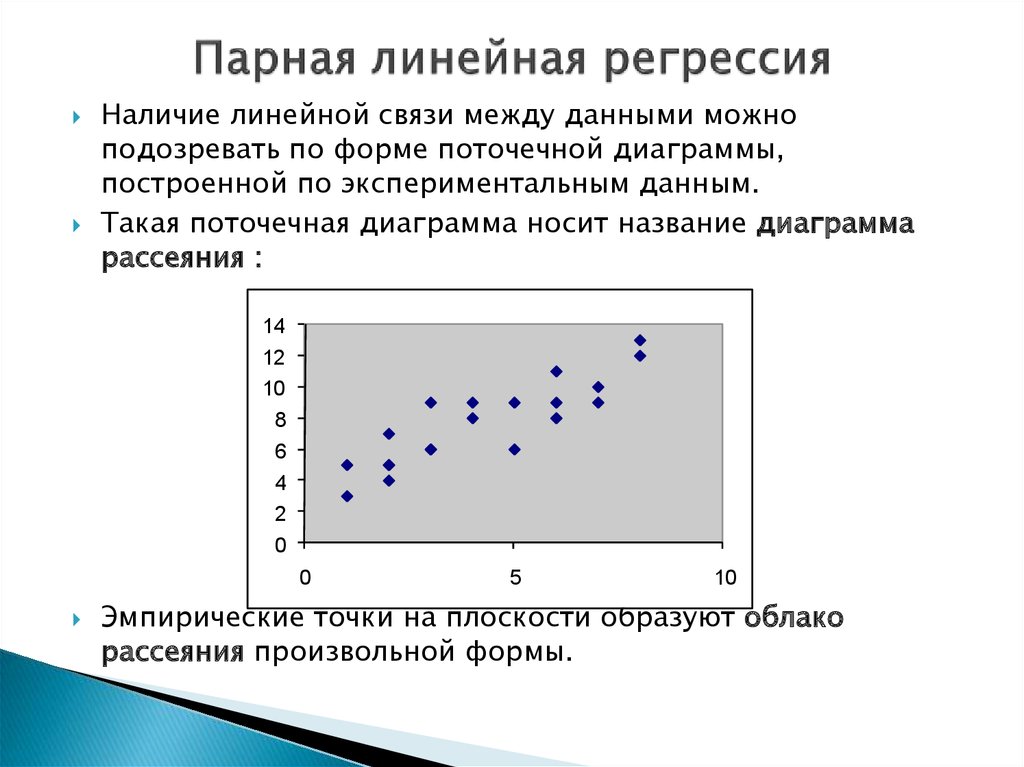
Оригинал статьи www.quirks.com
Перевод статьи Агентство маркетинговых исследований FDFgroup
Почитать еще
Скользкий склон безудержной семантики
Недавняя статья под названием «Спящее будущее визуализации данных? Фотография »расширяет определение визуализации данных до нового предела.
Data mining средства обнаружения данных могут создавать ценность для бизнеса?
Мы живем во время, когда данные вокруг нас. В эпоху цифровых технологий те, кто может выжать
Что такое гипер-персонализация? Преимущества, структура и примеры
Представьте себе сценарий встречи с кем-то много раз: Представьте, что человек узнает ваше имя, ваши
Введение в анализ временных рядов
Хотя для анализа данных используются все многочисленные передовые инструменты и методы, такие как наука о
Визуализация данных и виртуальная реальность
Время от времени кто-то заявляет, что визуализация данных может быть улучшена при просмотре в виртуальной
Структурированные и неструктурированные данные
Из-за всей шумихи вокруг больших данных и способов их использования компаниями вы можете спросить: «Какие
Что может сделать машинное обучение для вашего бизнеса прямо сейчас?
Этим вопросом задается множество бизнес-лидеров, поскольку ежедневно новшества в сфере ИИ и машинного обучения расширяют
История развития моделей данных
Итак, прыгайте на борт и наслаждайтесь путешествиями во времени наших попыток справиться с временностью в
Информационный шум
Чтобы тщательно, точно и четко информировать, мы должны определить предполагаемый сигнал, а затем усилить его,
Читайте о всех решениях
Какие бы задачи перед Вами не стояли, мы сможем предложить лучшие инструменты и решения
Смотреть
Проиграть видео
Презентация аналитической платформы Tibco Spotfire
Проиграть видео
Отличительные особенности Tibco Spotfire 10X
Проиграть видео
Как аналитика данных помогает менеджерам компании
защитный механизм, примеры регрессии в психологии
Регрессия – это такой способ защиты, когда психика прибегает к возврату в детское состояние с целью понижения тревоги или разрешения конфликта. Соответственно детская модель поведения оказывается незрелой, менее эффективной, затрудняет адаптацию. При этом у окружающих она часто вызывает состояние родителя, бессознательное желание опекать будь-то более слабую или ущербную личность. Однако механизм регрессии включается не лишь в межличностном взаимодействии, человек может активировать его также наедине с собой, во внутренней психологической реальности, ведь детская модель поведения кажется ему более безопасной и успокаивающей.
Соответственно детская модель поведения оказывается незрелой, менее эффективной, затрудняет адаптацию. При этом у окружающих она часто вызывает состояние родителя, бессознательное желание опекать будь-то более слабую или ущербную личность. Однако механизм регрессии включается не лишь в межличностном взаимодействии, человек может активировать его также наедине с собой, во внутренней психологической реальности, ведь детская модель поведения кажется ему более безопасной и успокаивающей.
Что такое регрессия в психологии
Регрессия есть возвращение к своим более ранним формам поведения. Она происходит оттого, что нынешним, зрелым поведением человек не имеет возможности добиться желаемых целей. Например, девушка не может убедить своего мужчину в действительности какого-то факта. Что выбирает она? Часто это слезы, и плач, которые не являются рациональным способом в разрешении ситуации, это тот способ, которым она пользовалась в детстве, дабы привлечь внимание и добиться желаемого.
Спортсмены, занимающиеся боевыми искусствами и изучающие множество приемов в зале, выходя на ринг, используют лишь несколько приемов регрессии, что происходит из-за фрустрации, стресса, в котором человеку свойственно возвращаться к наиболее эффективным ранним формам поведения, которые его никогда не подводили. Хотя их эффективность – очень спорный вопрос, на деле было бы уместнее использовать другие формы поведения. Но есть навыки, какие содержатся в основе психики, как говорят, «на подкорке», вернуться к которым легко, и это происходит бессознательно. Проблему это не решает, но временно успокаивает человека, снижает уровень его тревоги.
Каждый сохраняет из детства воспоминания о приятных моментах, легком разрешении проблем и хоть раз задумывался, чтобы вернуться в детство. Личности же, что используют регрессию как доминирующий механизм защиты, когда она становится стратегией жизни, называются инфантильными, такая длительная регрессия в психологии это синоним инфантилизма.
Регрессия как явление была описана впервые Фрейдом. Регрессия по Фрейду есть отказ от прогрессивного движения желания в сторону действий, возврат к образам или галлюцинациям. Также регрессия по Фрейду находит себя в сновидениях и неврозах, в каких он рассматривал возврат к архаическим формам жизни как индивидуальным, так и филогенетическим.
Регрессия по Фрейду есть отказ от прогрессивного движения желания в сторону действий, возврат к образам или галлюцинациям. Также регрессия по Фрейду находит себя в сновидениях и неврозах, в каких он рассматривал возврат к архаическим формам жизни как индивидуальным, так и филогенетическим.
Регрессия – защитный механизм
Регрессия в психологии это механизм защиты, развивающийся при слабости Я личности, именно к регрессии чаще всего прибегает личность незрелая, поскольку этот способ ей ближе остальных и не требует никаких дополнительных усилий.
В регрессии человек стремится к бессознательному воссоединению, полному комфорту и удовлетворению потребностей, какое он получал от матери. Отсутствие необходимости прилагать усилия, пробуя новые стратегии проведения, при недостатке энергии и инертности личности делает регрессию доступным и простым способом приспособления. Другой вопрос уже, что адаптация затрудняется и в итоге оказывается неполной. Построить зрелые отношения с окружающими при доминирующей регрессивной защите, инфантилизме, становится невозможным. Взаимодействие выстраивается только в случае наличия у партнера дополняющей стратегии, активного состояния родителя, отношения тогда скорее напоминают детско-родительский симбиоз.
Взаимодействие выстраивается только в случае наличия у партнера дополняющей стратегии, активного состояния родителя, отношения тогда скорее напоминают детско-родительский симбиоз.
Более сильная, стеническая личность прибегает к регрессии, только когда остальные механизмы защиты оказались неэффективными, наступило состояние фрустрации. Регрессия в таком случае чаще всего частичная и непродолжительная, возвратившись к детским формам удовлетворения потребностей и получив желаемую разрядку, снизив напряжение, личность возвращается к другим видам защит. Потому, определив, что регрессия длительное время доминирует в арсенале защит, следует направить внимание на развитие личности, признав ее незрелость. В характере при этом преобладают такие черты, как зависимость от окружающих и их мнения, несамостоятельность, легкая внушаемость и поддавание влиянию других, отсутствие глубоких стабильных интересов, быстрая смена настроений, плаксивость, обидчивость, неумение доводить начатое до конца, безответственность и страх будущего. В крайних случаях это может выразиться в тунеядстве, злоупотреблении алкоголем, зависимости от наркотических препаратов.
В крайних случаях это может выразиться в тунеядстве, злоупотреблении алкоголем, зависимости от наркотических препаратов.
Регрессия в психологии – примеры
Частым примером регрессии как отката назад, в прошлое, к более ранним своим паттернам, является поведение старшего ребенка при рождении младшего. Старшему становится тяжело вынести то, что появился еще один объект для родительской любви, и он начинает плакать и капризничать, как несколько лет назад, может начать лезть в коляску, брать одежду, соску и погремушки младшего, есть его еду, гулить, ползать, изображая из себя малыша. Часто даже появляется возврат к непроизвольному мочеиспусканию. Это помогает ему справиться с напряжением, обидой и ревностью, появившимися в связи с конкуренцией, «предательством» родителей, привлечь к себе внимание, чтобы его полюбили так же, как малыша. Более старшему ребенку в данной ситуации кажется, что о нем забыли, хотя в том же возрасте ему уделяли обычно такое же количество внимания.
Регулярные детские болезни также могут говорить о потребности в родительском внимании, при нежелании идти в сад или школу быстро появляются симптомы простуды, а в запущенных ситуациях развиваются и серьезные хронические болезни, имеющие психосоматическую природу.
То же может происходить и с взрослым человеком, когда он заболевает. Невысокая температура переживается уже как серьезная, тяжелая болезнь, что может бессознательно демонстрироваться окружающим, чтобы получить ту полноту заботы и внимания, какую взрослый помнит из детства. Это то, что в психологии рассматривается как получение вторичной выгоды.
Здесь может иметь место и соматизация, когда и сама болезнь наступает по причине потребности снизить психическое напряжение, словно вернуться в детство и передохнуть. Если действительной причиной болезни была регрессия, то излечение становится очень сложным, усилия докторов часто не приносят нужных результатов, болезнь может менять свои формы или даже переходить в другую, проявляя высокую резистентность к различным врачебным вмешательствам, развивается ипохондрия. Своевременная успешная диагностика психологической причины болезни позволяет не только идти в верном направлении к излечению, но и сохраняет действительное физическое здоровье пациента.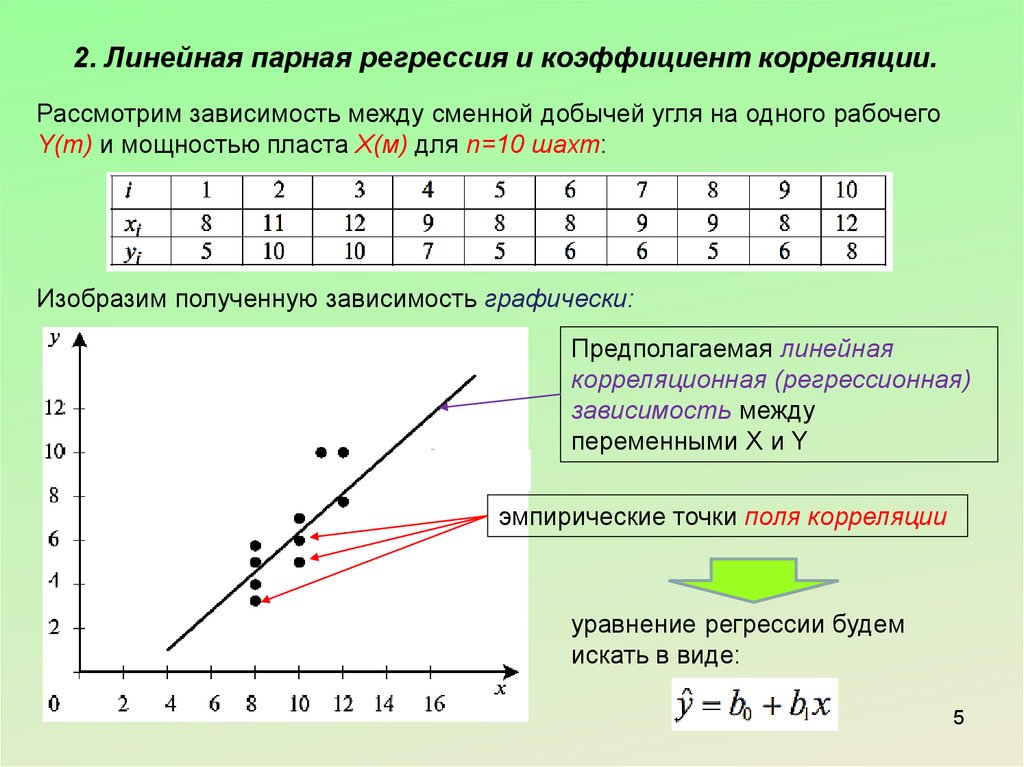
В других случаях уставший взрослый человек может начать хныкать как ребенок, топнуть ногой или обидеться, невесть на кого, развернуться и уйти. Сюда относятся и несдержанность в эмоциях, какую часто прощают детям, бунт против авторитетов, хаотичное поведение, любовь к быстрой и неосторожной езде на машине, не задумываясь о последствиях. В ситуациях перегрузки практически каждый испытывал желание закутаться в одеяло, есть конфеты и смотреть мультики. Некоторые взрослые на всю жизнь сохраняют любовь к детской мультипликации, носят одежду в ребяческом стиле, играют в игры. Компьютерная зависимость также связана с регрессивным уходом от взрослой реальности в детский мир на экране, к которому человек привык еще будучи ребенком.
Примеры регрессии в психологии. Психологи часто наблюдают регрессию у своих клиентов на консультации. Как только психолог с клиентом подходят к сверхважному для последнего вопроса, в котором нужно принять решение – клиент часто не выносит этой эмоциональной перегрузки и начинает дурачиться: накручивать волосы на нос, снимать и играть кольцом, крутиться на кресле, шутить. Регресс в детское поведение оттаскивает человека назад, чтобы снизить критический уровень напряжения, и психолог должен отследить это и проработать с клиентом.
Регресс в детское поведение оттаскивает человека назад, чтобы снизить критический уровень напряжения, и психолог должен отследить это и проработать с клиентом.
Регрессивный откат в детство свойственен практически всем людям в ситуации, когда желаемое можно получить от кого-то из близких. Так ребенок начинает выпрашивать конфеты у матери более детским голосом, капризничая и давя на жалость. Также может поступать и жена, прося у мужа, например, купить ей платье, бессознательно активируя в себе поведение маленькой девочки. А муж может проситься на рыбалку с друзьями, обещая свое хорошее поведение, словно мальчишка.
Склонность к мистике часто также является регрессивной защитой, когда человек не желает разбираться в реальных причинах происходящего, что потребует от него усилий и ответственности в разрешении проблемы, а, к примеру, оправдывает сложности наложенной порчей или родовым проклятием.
Регрессивность часто находит выражение в откате к более ранним психосексуальным формам развития, что связано с возникновением неврозов. В случае регрессии либидо в полном объеме генитальность замещается прегенитальными способами проявления сексуальности, откуда развивается анально-садистичные или инцестуозные наклонности, бисексуальность, нарциссизм.
В случае регрессии либидо в полном объеме генитальность замещается прегенитальными способами проявления сексуальности, откуда развивается анально-садистичные или инцестуозные наклонности, бисексуальность, нарциссизм.
К механизмам регрессии часто прибегают маркетологи, создавая в рекламе предпосылки для эмоционального возвращения в детские ощущения полного комфорта, тотальной продуманности и контроля производителем своего продукта, приобретя который человек может, словно погрузиться в идеальную реальность.
Автор: Практический психолог Ведмеш Н.А.
Спикер Медико-психологического центра «ПсихоМед»
примеры и вычисление функции потерь — Общие дети, г. Воронеж
Содержание
примеры и вычисление функции потерь
Линейная регрессия (Linear regression) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.
Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала простым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.
Применение линейной регрессии
Предположим, нам задан набор из 7 точек (таблица ниже).
Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:
Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.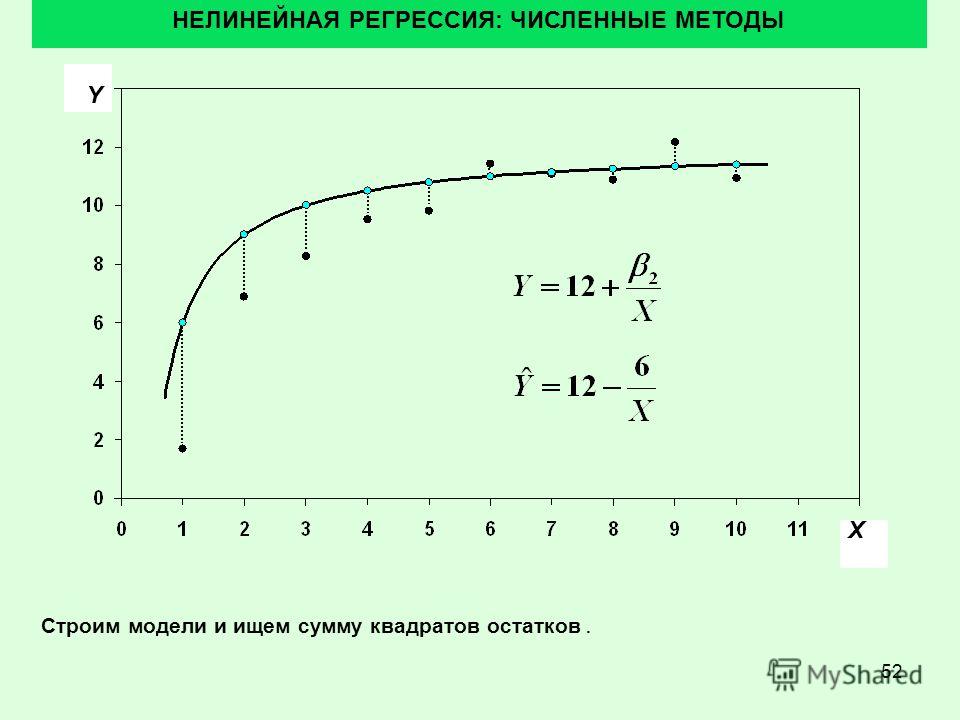
Функция потерь — метод наименьших квадратов
Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y(х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.
Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.
Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.
Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.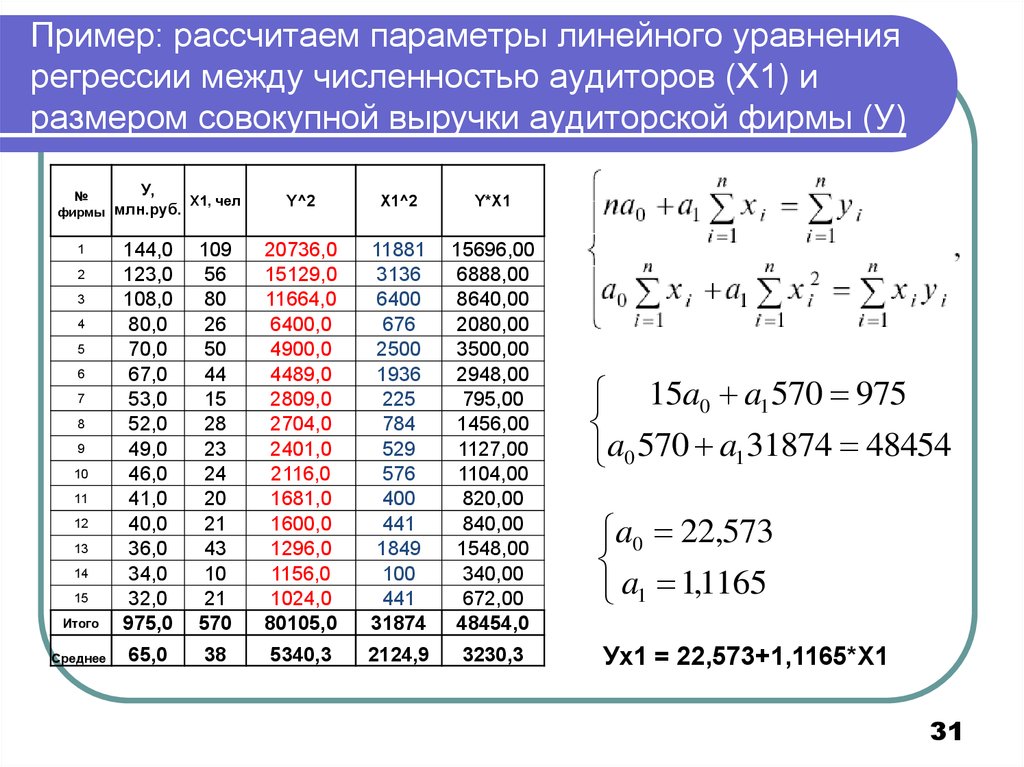
Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.
Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Если мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.
Больше размерностей
Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:
f(x) = b+w_1*x_1 + … + w_n*x_n
Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:
Другими словами:
f(x) = b*1+w_1*x_1 + … + w_n*x_n
Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.
Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.
Проклятие нелинейности
Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.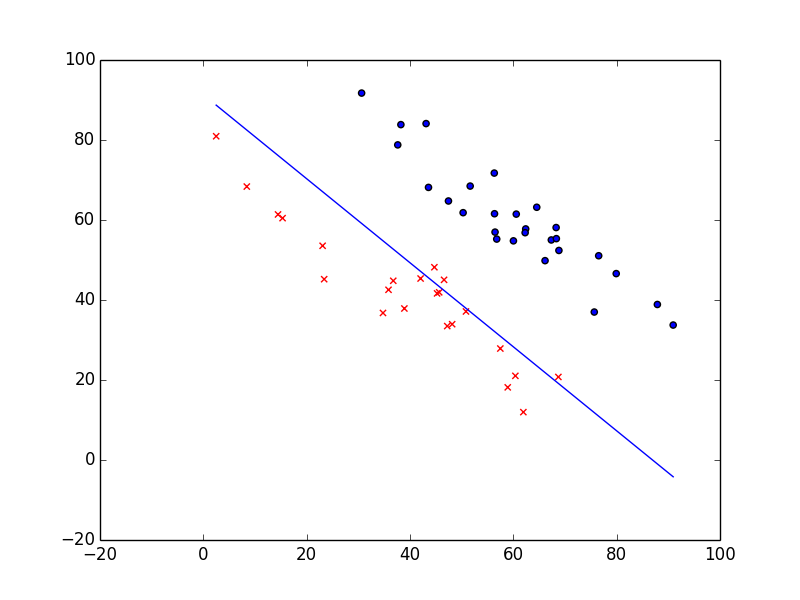
Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).
Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.
Минимум функции
Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.
Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.
Парная линейная регрессия. Задачи регрессионного анализа
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимостиy = f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено,
что при каждом определённом значении x существует сколько-то (n) значений переменной
y, то зависимость средних арифметических значений y от x и является регрессией
в статистическом понимании.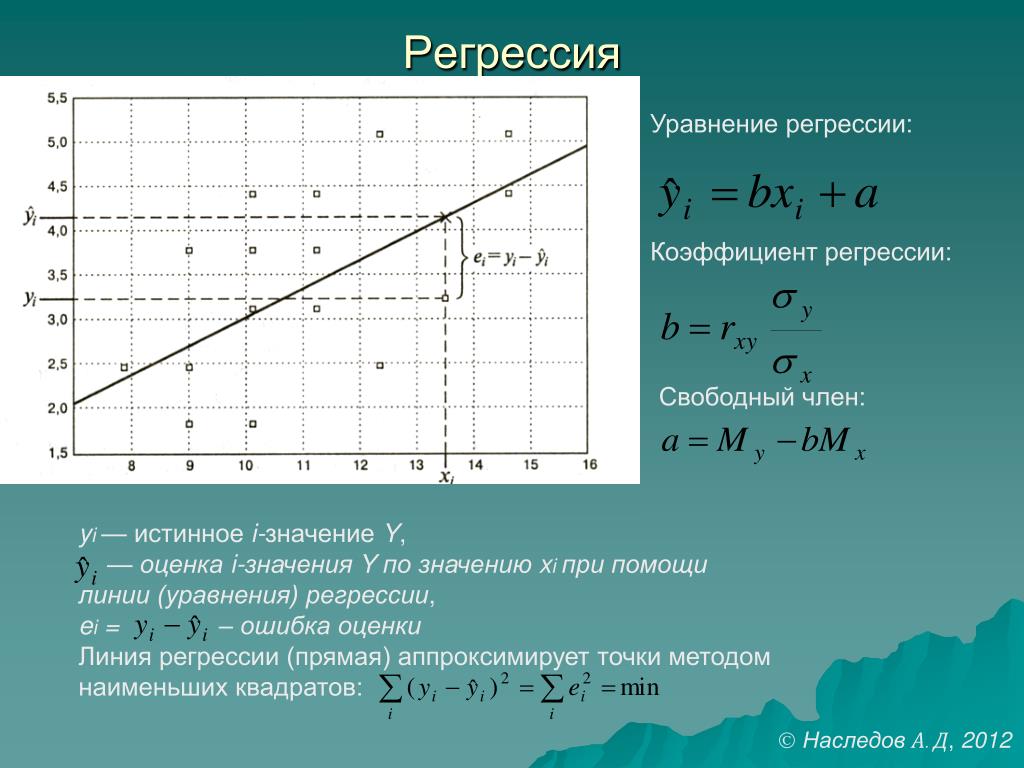
Если установленная зависимость может быть записана в виде уравнения прямой
y = ax + b,
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости
были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади
кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором
приближении к прямой, хотя и не на самой прямой.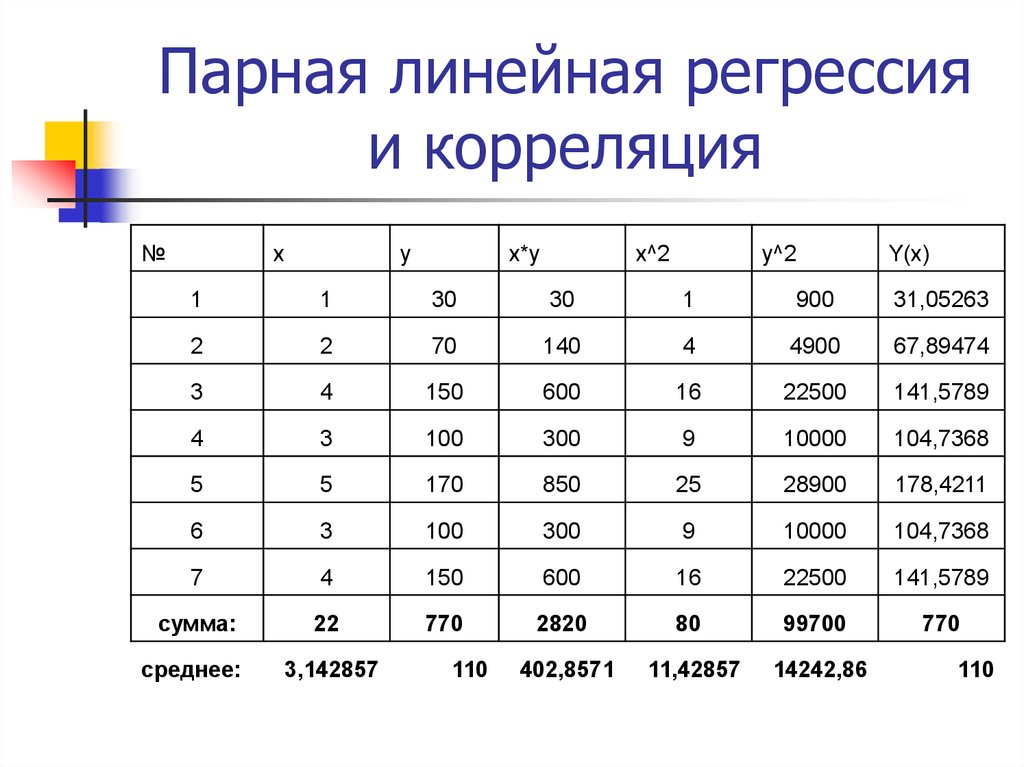 Если точки корреляционной диаграммы соединить ломанной
линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то
полученная прямая будет прямой теоретической регрессии. На рисунке ниже
она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
Если точки корреляционной диаграммы соединить ломанной
линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то
полученная прямая будет прямой теоретической регрессии. На рисунке ниже
она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
где
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
или
где
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Определение коэффициентов уравнения парной линейной регрессии
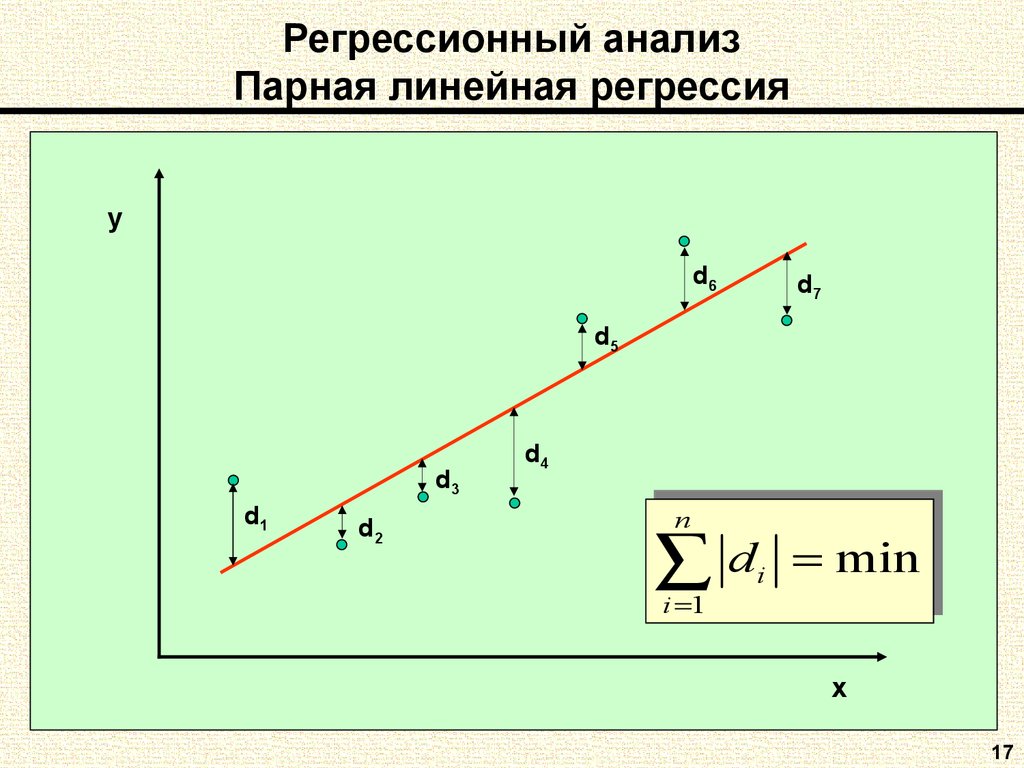
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Правильное решение и ответ.
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
где
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,
—
сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует
рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
Правильное решение и ответ.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
где
—
остатки — разности между реальными значениями зависимой переменной и значениями,
оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593, SSE = 10 459,587, SSR = 53 311,007.
Можем убедиться, что выполняется закономерность SSR = SST — SSE:
63770,593-10459,587=53311,007.
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной
регресии.
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода)
описывается уравнением парной линейной регрессии .
Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при
увеличении дохода на 5000 у. е. Меняется ли потребление, если доход не меняется?
е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии xi = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. yi = 17036,4662.
Подставляем в уравнение парной линейной регрессии xi = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. yi = 4161,9662.
Если доход не меняется, то xi = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям
независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не
влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы,
то есть линейной зависимости Y от X нет.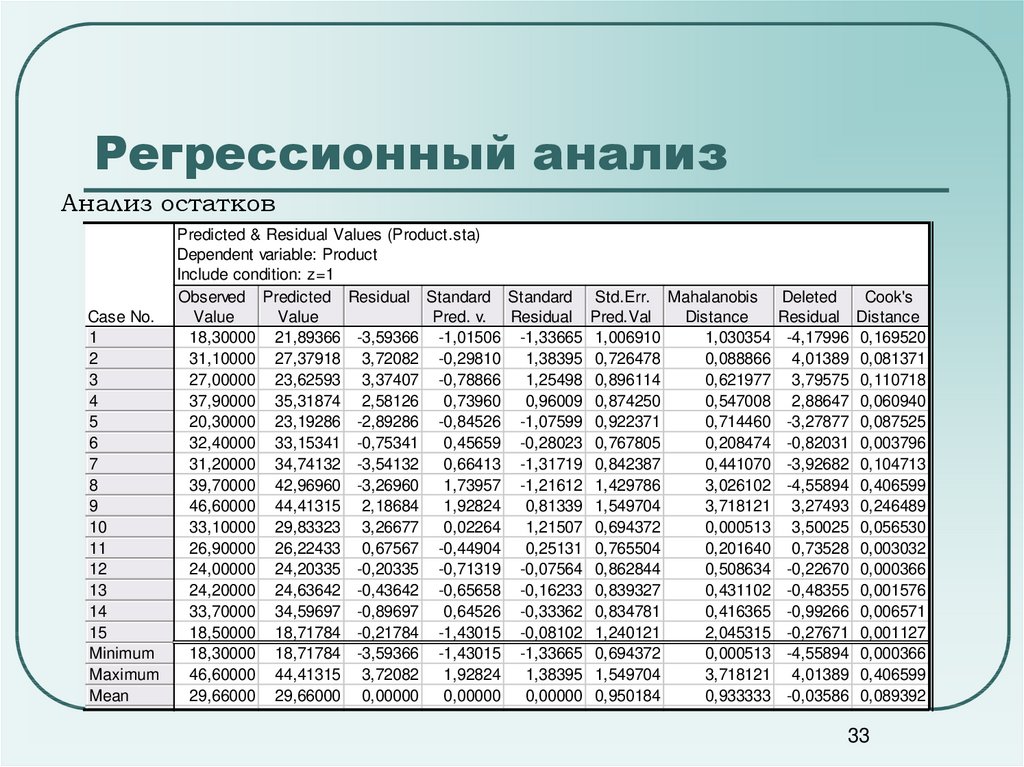
Нулевую гипотезу
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2,
где — стандартная погрешность коэффициента направления прямой линейной регресии b1.
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном
потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и
проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.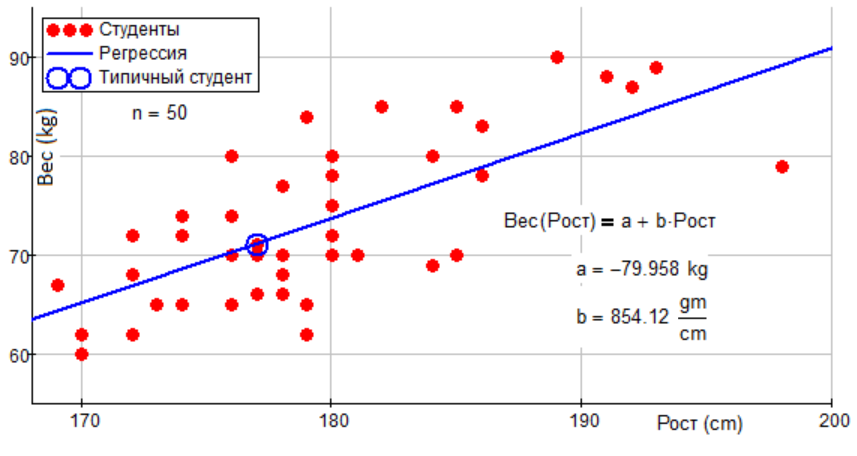
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b1:
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
Всё по теме «Математическая статистика»
Линейная регрессия на Python: объясняем на пальцах
Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!
Регрессия ищет отношения между переменными.
Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.
Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.
Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.
Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.
Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.
Зависимые данные называются зависимыми переменными, выходами или ответами.
Независимые данные называются независимыми переменными, входами или предсказателями.
Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.
Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.
Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.
Где она вообще нужна?
Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.
Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.
Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.
Постановка проблемы
Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.
Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.
Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.
Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.
Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.
Простая линейная регрессия
Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.
А вот и она:
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.
Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.
Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.
Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).
Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.
Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.
Пакеты Python для линейной регрессии
NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.
Незнакомы с NumPy? Начните с официального гайда.
Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.
Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.
Простая линейная регрессия со scikit-learn
Начнём с простейшего случая линейной регрессии.
Следуйте пяти шагам реализации линейной регрессии:
- Импортируйте необходимые пакеты и классы.
- Предоставьте данные для работы и преобразования.
- Создайте модель регрессии и приспособьте к существующим данным.

- Проверьте результаты совмещения и удовлетворительность модели.
- Примените модель для прогнозов.
Это общие шаги для большинства подходов и реализаций регрессии.
Шаг 1: Импортируйте пакеты и классы
Первым шагом импортируем пакет NumPy и класс LinearRegressionиз sklearn.linear_model:
import numpy as np from sklearn.linear_model import LinearRegression
Теперь у вас есть весь функционал для реализации линейной регрессии.
Фундаментальный тип данных NumPy – это тип массива numpy.ndarray. Далее под массивом подразумеваются все экземпляры типа numpy.ndarray.
Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.
Шаг 2 : Предоставьте данные
Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.) или похожими объектами. Вот простейший способ предоставления данных регрессии: ndarray
ndarray
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([5, 20, 14, 32, 22, 38])
Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape()на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).
Вот как x и y выглядят теперь:
>>> print(x) [[ 5] [15] [25] [35] [45] [55]] >>> print(y) [ 5 20 14 32 22 38]
Шаг 3: Создайте модель
На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.
Давайте сделаем экземпляр класса LinearRegression, который представит модель регрессии:
model = LinearRegression()
Эта операция создаёт переменную model в качестве экземпляра LinearRegression. Вы можете предоставить несколько опциональных параметров классу
Вы можете предоставить несколько опциональных параметров классу LinearRegression:
- fit_intercept – логический (
Trueпо умолчанию) параметр, который решает, вычислять отрезок b₀ (True) или рассматривать его как равный нулю (False). - normalize – логический (
Falseпо умолчанию) параметр, который решает, нормализовать входные переменные (True) или нет (False). - copy_X – логический (
Trueпо умолчанию) параметр, который решает, копировать (True) или перезаписывать входные переменные (False). - n_jobs – целое или
None(по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях.Noneозначает отсутствие процессов, при -1 используются все доступные процессоры.
Наш пример использует состояния параметров по умолчанию.
Пришло время задействовать model. Сначала вызовите .fit() на model:
model.fit(x, y)
С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model. Поэтому можно заменить две последние операции на:
model = LinearRegression().fit(x, y)
Эта операция короче и делает то же, что и две предыдущие.
Шаг 4: Получите результаты
После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.
Вы можете получить определения (R²) с помощью .score(), вызванной на model:
>>> r_sq = model.score(x, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0. 715875613747954
715875613747954
.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².
model содержит атрибуты .intercept_, который представляет собой коэффициент, и b₀ с .coef_, которые представляют b₁:
>>> print('intercept:', model.intercept_)
intercept: 5.633333333333329
>>> print('slope:', model.coef_)
slope: [0.54]Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.
Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.
Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:
>>> new_model = LinearRegression().fit(x, y.reshape((-1, 1))) >>> print('intercept:', new_model.intercept_) intercept: [5.63333333] >>> print('slope:', new_model.coef_) slope: [[0.54]]
Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.
Шаг 5: Предскажите ответ
Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.
Получите предсказанный ответ, используя .predict():
>>> y_pred = model.predict(x)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333]Применяя .predict(), вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.
Вот почти идентичный способ предсказать ответ:
>>> y_pred = model.intercept_ + model.coef_ * x >>> print('predicted response:', y_pred, sep='\n') predicted response: [[ 8.33333333] [13.73333333] [19.13333333] [24.53333333] [29.93333333] [35.33333333]]
В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.
Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.
Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1), x.flatten() или x.ravel() при умножении с помощью model.coef_.
На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:
>>> x_new = np.arange(5).reshape((-1, 1)) >>> print(x_new) [[0] [1] [2] [3] [4]] >>> y_new = model.predict(x_new) >>> print(y_new) [5.63333333 6.17333333 6.71333333 7.25333333 7.79333333]
Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new. Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.
О LinearRegression вы узнаете больше из официальной документации.
Теперь у вас есть своя модель линейной регрессии!
Источник
Нравится Data Science? Другие материалы по теме:
Логистическая регрессия и ROC-анализ — математический аппарат
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,\, x_2, \,\dots, \, x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.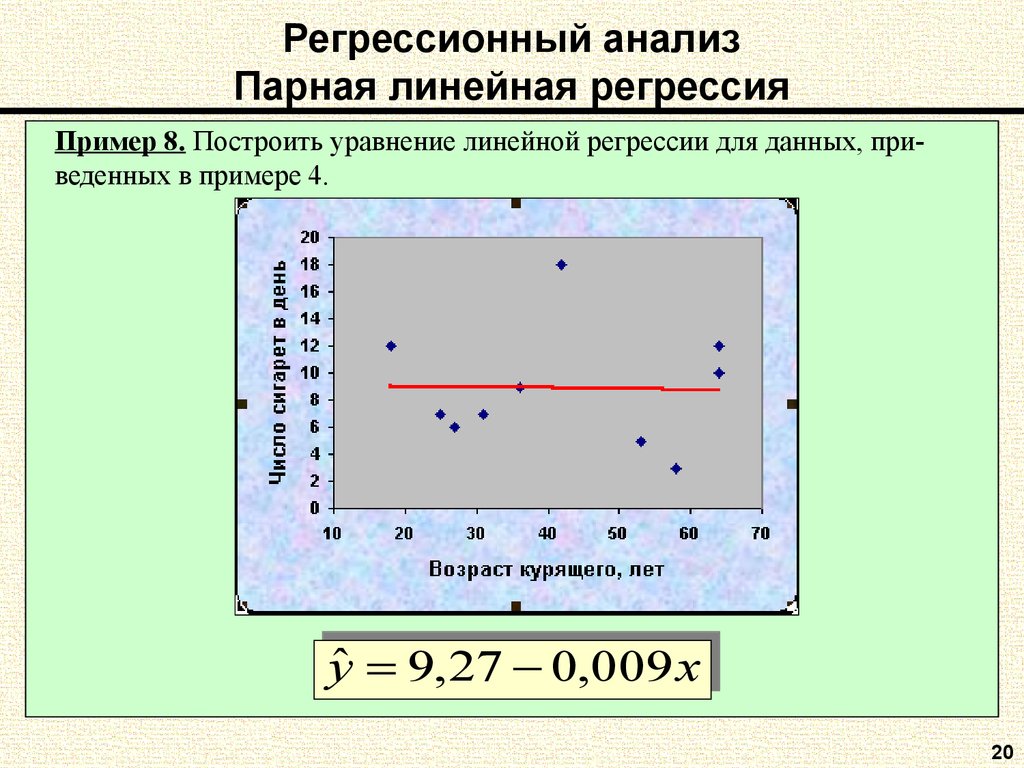 е.:
е.:
y = a\,+\,b_1\,x_1\,+\,b_2\,x_2\,+\,\dots\,+\,b_n\,x_n
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Однако здесь возникает проблема: множественная регрессия не «знает», что переменная отклика бинарна по своей природе. Это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи. Таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения (логит-преобразование):
P = \frac{1}{1+\,e^{-y}}
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):
Рис. 1 — Логистическая кривая
Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:
P’ = \log_e \Bigl(\frac{P}{1-P}\Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия.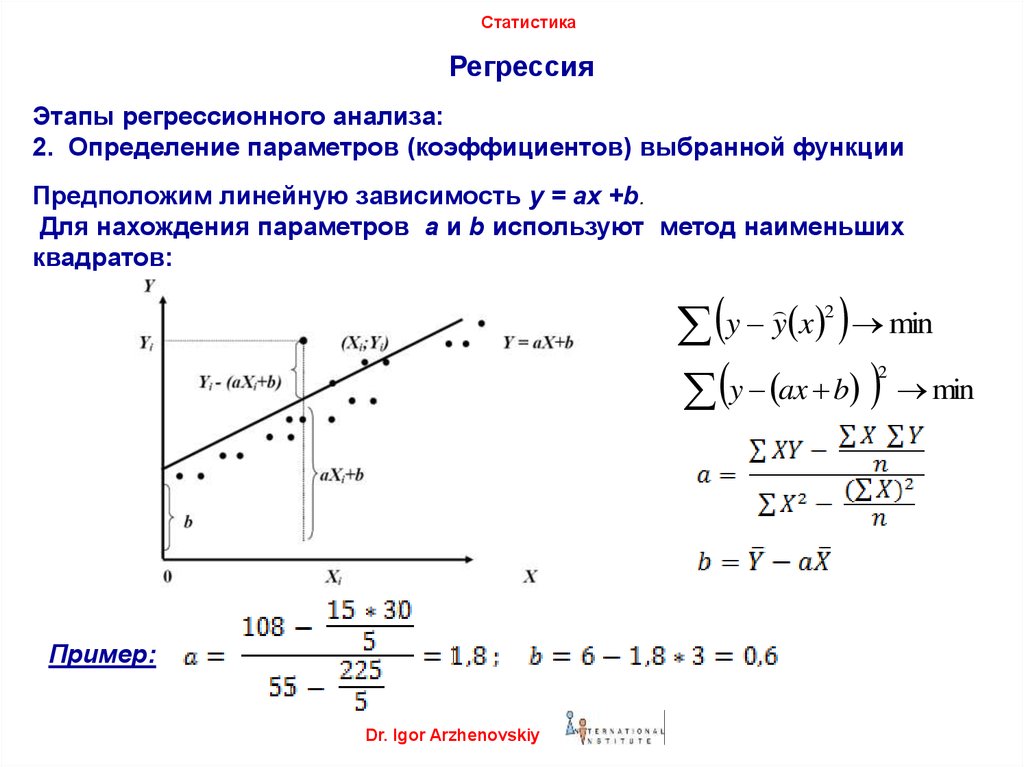 Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L\,(Y_1,\,Y_2,\,\dots,\,Y_k;\,\theta) = p\,(Y_1;\, \theta)\cdot\dots\cdotp\,p\,(Y_k;\,\theta)
Согласно методу максимального правдоподобия в качестве оценки неизвестного параметра принимается такое значение \theta=\theta(Y_1,…,Y_k), которое максимизирует функцию L.
Нахождение оценки упрощается, если максимизировать не саму функцию L, а натуральный логарифм ln(L), поскольку максимум обеих функций достигается при одном и том же значении \theta:
L\,*\,(Y;\,\theta) = \ln\,(L\,(Y;\,\theta)\,) \rightarrow \max
В случае бинарной независимой переменной, которую мы имеем в логистической регрессии, выкладки можно продолжить следующим образом. Обозначим через P_i вероятность появления единицы: P_i=Prob(Y_i=1). Эта вероятность будет зависеть от X_iW, где X_i — строка матрицы регрессоров, W — вектор коэффициентов регрессии:
P_i = F\,(X_i W),\, F(z) = \frac{1}{1+\,e^{-z}}
Логарифмическая функция правдоподобия равна:
L^* = \sum_{i \epsilon\ I_1}ln{P_i(W)} + \sum_{i \epsilon\ I_0}ln{(1-P_i(W))} = \sum_{i=1}^{k} [Y_i \ln {P_i (W)}+(1-Y_i)\ln {(1 — P_i(W))}]
где I_0, I_1— множества наблюдений, для которых Y_i=0 и Y_i=1 соответственно. {-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t
{-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
- TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
- TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
- FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
- FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
- Доля истинно положительных примеров (True Positives Rate): TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
- Доля ложно положительных примеров (False Positives Rate): FPR = \frac{FP}{TN\,+\,FP}\,\cdot\,100 \,\%
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
S_e = TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
S_p = \frac{TN}{TN\,+\,FP}\,\cdot\,100 \,\%
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.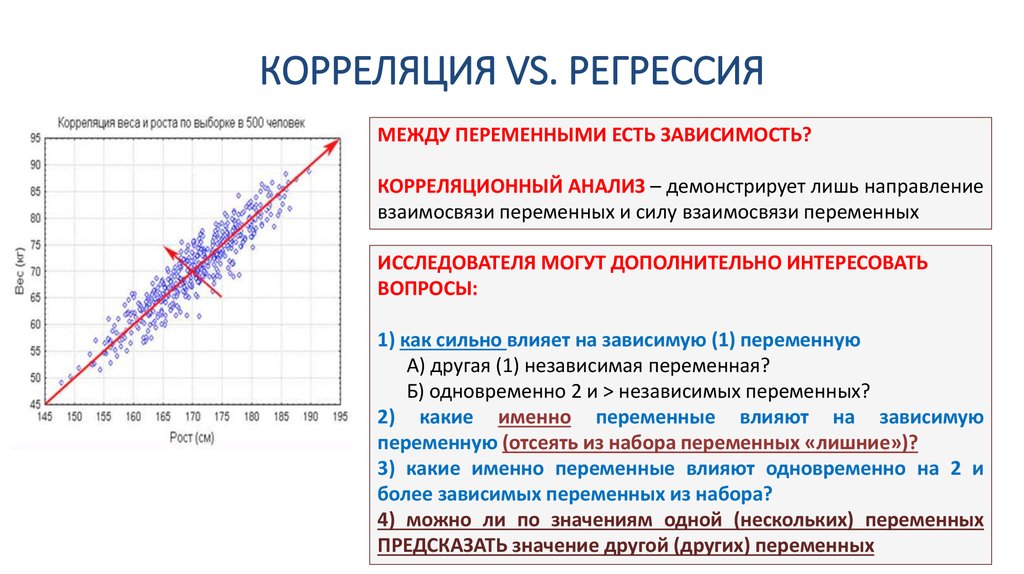
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
- Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.
ROC-кривая получается следующим образом:
Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp.
 В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.
Канонический алгоритм построения ROC-кривой
Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.
- t=min
- повторять
- FP=TP=0
- для всех примеров i принадлежит L {
- если f[i]>=t тогда // этот пример находится за порогом
- если i положительный пример тогда
- { TP=TP+1 }
- иначе // это отрицательный пример
- { FP=FP+1 }
- }
- Se=TP/P*100
- point=FP/N // расчет (100 минус Sp)
- Добавить точку (point, Se) в ROC-кривую
- t=t+d_x
- пока (t>max)
В результате вырисовывается некоторая кривая (рис. 2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.
2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac{X_{i+1}\,+\,X_i}{2}\Bigr]\,\cdot \,(Y_{i+1}\,-\, Y_i)
Рис. 5 — Площадь под ROC-кривой
С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель.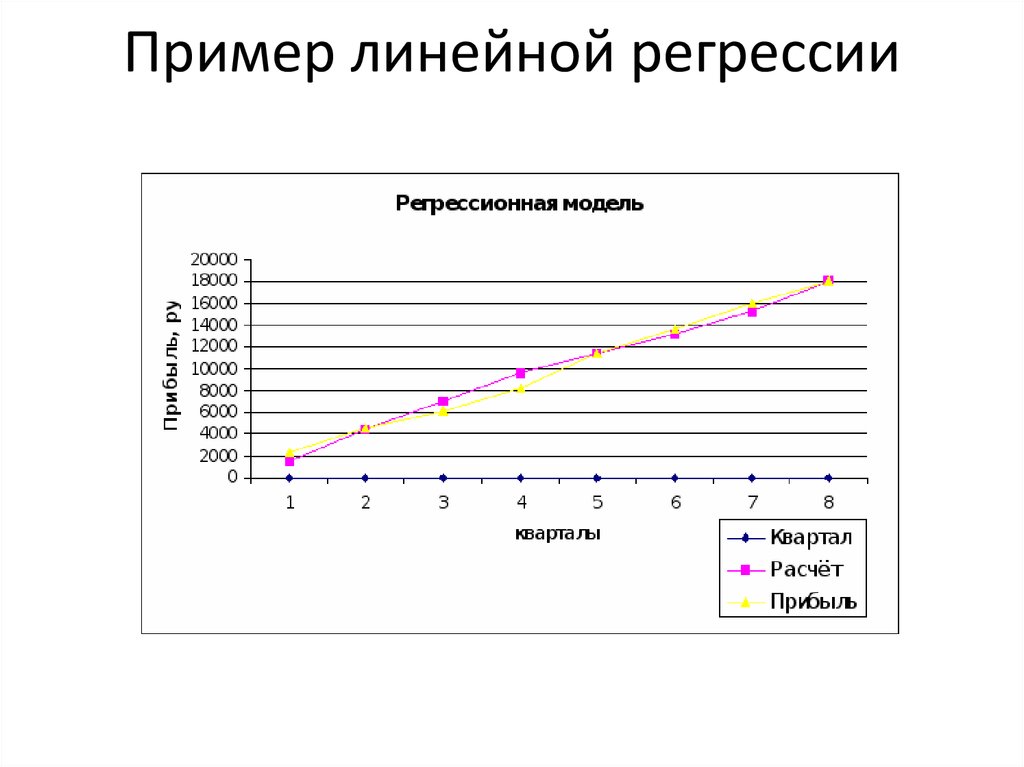 Однако следует знать, что:
Однако следует знать, что:
- показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
- AUC не содержит никакой информации о чувствительности и специфичности модели.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:
Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
Критериями выбора порога отсечения могут выступать:
- Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
- Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cutt\underline{\,\,\,}off_o = \max_k (Se_k\,+\,Sp_k)
- Требование баланса между чувствительностью и специфичностью, т.е. когда Se \approx Sp: Cutt\underline{\,\,\,}off_o = \min_k \,\bigl |Se_k\,-\,Sp_k \bigr |
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Литература
- Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
- Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
- Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
- Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.
Другие материалы по теме:
Применение логистической регрессии в медицине и скоринге
Machine learning в Loginom на примере задачи c Kaggle
Линейная Регрессия Пример Из Реальной Жизни
Я изучаю машинное обучение (линейную регрессию) у проф. Лекция Эндрю. Слушая, когда использовать нормальное уравнение против градиентного спуска, он говорит, что когда число наших функций очень велико(например, 10E6), то нужно использовать градиентный спуск. Мне все понятно, но интересно, может ли кто-нибудь привести мне примеры из реальной жизни, где мы используем такое огромное количество функций?
Мне все понятно, но интересно, может ли кто-нибудь привести мне примеры из реальной жизни, где мы используем такое огромное количество функций?
machine-learning
linear-regression
Поделиться Источник Nusrat 20 апреля 2014 в 21:18
2 ответа
- Адаптивная линейная регрессия
Допустим, у меня есть набор выборок, который состоит из нестационарного стохастического процесса с равномерным распределением вероятностей (гауссовым). Мне нужна адаптивная линейная регрессия по набору выборок. В принципе, я хочу, чтобы строка ‘best-fit’ вела себя определенным образом. У меня есть…
- Контролируемое обучение линейная регрессия
Меня смущает, как работает линейная регрессия в контролируемом обучении. Теперь я хочу сгенерировать оценочную функцию для настольной игры с использованием линейной регрессии, поэтому мне нужны как входные, так и выходные данные.
 Входные данные — это мое условие платы, и мне нужно соответствующее…
Входные данные — это мое условие платы, и мне нужно соответствующее…
1
Список наборов данных, имеющих большое количество атрибутов :-
1. Ссылка на набор данных о ежедневных и спортивных мероприятиях
2. Ссылка на набор данных объявлений фермы
3. Ссылка на набор данных Arcene
4. Пакет слов Ссылка на набор данных
Выше приведены реальные примеры наборов данных, имеющих большие значения no. атрибутов.
Поделиться Devavrata 21 апреля 2014 в 18:58
1
Например, в классификации текста (например, фильтрация спама email) мы можем использовать в качестве функций униграммы (мешок слов), биграммы, триграммы. В зависимости от размера набора данных количество объектов может быть очень большим.
Поделиться NLPer 21 апреля 2014 в 02:33
Похожие вопросы:
какая функция keypress() применима в реальной жизни
Я делаю пример перемещения следующей статьи, используя keypress() из codeacademy об интерактивных веб-сайтах, и это так трудно получить доступ на веб-сайте, нажмите клавишу один раз, когда он…
Линейная регрессия в MATLAB
Как я мог бы сделать линейную регрессию с несколькими значениями, равными на x с MATLAB? Теперь пример с минимальными данными (не те данные, которые я использую) : y = [1,2,3,4,5,6,7,8,9,10]; x =…
Пример из реальной жизни, когда использовать OUTER / CROSS APPLY в SQL
Я смотрел CROSS / OUTER APPLY с коллегой, и мы изо всех сил пытаемся найти реальные примеры того, где их можно использовать. Я потратил довольно много времени, глядя на то, когда я должен…
Я потратил довольно много времени, глядя на то, когда я должен…
Адаптивная линейная регрессия
Допустим, у меня есть набор выборок, который состоит из нестационарного стохастического процесса с равномерным распределением вероятностей (гауссовым). Мне нужна адаптивная линейная регрессия по…
Контролируемое обучение линейная регрессия
Меня смущает, как работает линейная регрессия в контролируемом обучении. Теперь я хочу сгенерировать оценочную функцию для настольной игры с использованием линейной регрессии, поэтому мне нужны как…
Линейная регрессия против точности производительности случайного леса
Если набор данных содержит объекты, некоторые из которых являются категориальными переменными,а некоторые-непрерывными переменными, дерево решений лучше, чем линейная регрессия, поскольку деревья…
Линейная регрессия через эллипс показывает неожиданное поведение
Я рисую эллипс 2D на пустом изображении.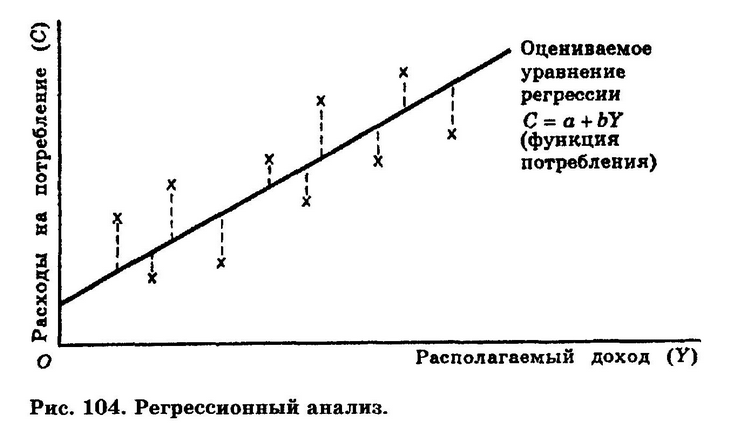 Теперь я хочу провести линию через эллипс, чтобы получить главную ось. Зная, что существует множество вариантов (PCA, моменты изображения и т. д.), Я думал,…
Теперь я хочу провести линию через эллипс, чтобы получить главную ось. Зная, что существует множество вариантов (PCA, моменты изображения и т. д.), Я думал,…
Реальный пример из жизни, чтобы сбросить значение autoincrement в mysql
Хочу знать сценарий, в котором нам нужно сбросить значение автоинкремента в базе данных. Если это возможно (пример из реальной жизни, который я ищу).
Примеры из реальной жизни балансировщика сетевой нагрузки?
Даже после долгих поисков в Google я не смог найти простого ответа на этот вопрос. Все, что я смог найти, это балансировщик нагрузки уровня 4, который может обрабатывать миллионы запросов в секунду,…
Линейная регрессия — неверный вывод
У меня есть база данных из двух columns[A, B], где A-входная переменная, а B-целевая переменная. Все значения выражены в целых числах. Мой код: X.shape >>(2540, 1) y.shape >>(2540, 1)…
Простые регрессионные модели в Python by Oleg Nagornyy
Регуляризация линейных моделей
Переобучение
Регуляризация — это метод для уменьшения степени переобучения модели, а значит, прежде чем мы разберемся, что такое регуляризация, нужно понять суть переобучения (overfitting).
Переобучение дает неплавные кривые прогнозирования, т. е. «нерегулярные». Такие плохие сложные кривые прогнозирования обычно характеризуются весовыми значениями, которые имеют очень большие или очень малые величины. Поэтому один из способов уменьшить степень переобучения состоит в том, чтобы не допускать очень малых или больших весовых значений для модели. В этом и заключается суть регуляризации.
Проблема многомерности: Bias-variance trade-off
https://elitedatascience.com/wp-content/uploads/2017/06/Bias-vs.-Variance-v5.png
Линейная регрессия с большим числом предикторов – комплексная модель и характеризуется:
- Достаточно высоким смещением
- Высокой дисперсией
Чем больше предикторов, тем больше риск переобучения модели. Переобучение также связано с размером коэфициентов.
Переобучение – ситуация, в которой обучающая ошибка продолжает снижаться с повышением сложности модели, а тестовая ошибка растет.
Как с этим бороться?
- Отбор наилучших предикторов
- Снижение размерности предикторов
- Регуляризация
Регуляризация — это способ уменьшить сложность модели чтобы предотвратить переобучение или исправить некорректно поставленную задачу. Обычно это достигается добавлением некоторой априорной информации к условию задачи.
Обычно это достигается добавлением некоторой априорной информации к условию задачи.
В данном случае суть регуляризации состит в том, что мы создаём модель со всеми предикторами, а потом искуственно уменьшаем размер коэффициентов, прибавляя некоторую величину к ошибке.
Ошибка — это то, что минимизируется обучением с помощью одного из примерно десятка численных методов вроде градиентного спуска (gradient descent), итерационного алгоритма Ньютона-Рафсона (iterative Newton-Raphson), L-BFGS, обратного распространения ошибок (back-propagation) и оптимизации роя (swarm optimization).
Чтобы величины весовых значений модели не становились большими, процесс регуляризации штрафует весовые значения добавляя их в вычисление ошибки. Если весовые значения включаются в общую ошибку, которая минимизируется, тогда меньшие весовые значения будут давать меньшие значения ошибки. L1-регуляризация штрафует весовые значения добавлением суммы их абсолютных значений к ошибке.
L2-регуляризация выполняет аналогичную операцию добавлением суммы их квадратов к ошибке. m \left| w_j \right|L(X,y,w)=2n1i=1∑n(xiTw−yi)2+λj=1∑m∣∣∣∣wj∣∣∣∣
m \left| w_j \right|L(X,y,w)=2n1i=1∑n(xiTw−yi)2+λj=1∑m∣∣∣∣wj∣∣∣∣
Чем меньше λ\lambdaλ, тем выше дисперсия и ниже смещение.
Чем больше λ\lambdaλ, тем ниже дисперсия и выше смещение.
Взяв производную от этой функции, мы получим формулу, которая не имеет аналитического решения, т.е. МНК не подходит. Следовательно, необходимо использовать градиентный спуск.
Лассо регрессия (Least absolute shrinkage and selection operator)
Очень похожа на ридж регрессию. В ней штраф — это сумма модулей значений коэффициентов.
В чем сила ридж и лассо?
• Ридж регрессия снижает размер коэффициентов, а лассо сокращает многие до 0
• Это позволяет снизить размерность (ридж) и выбрать важные предикторы (лассо)
• Работает, когда p > n, где p — число предикторов
• Работает, когда много коллинеарных предикторов
• Обязательно надо делать шкалирование и центрирование, иначе предикторы с высоким стандартным отклонением будут сильно штравоваться.
ElasticNet — комбинация L1 и L2 регуляризации в разных пропорциях.
Примеры линейной регрессии
Формула, которую дал вам Док, умножает возраст на 971.4 и добавляет 1536.2 к результату. Он получил 971.4 и 1536.2 с помощью компьютерной программы линейной регрессии, которая выполнила все трудоемкие вычисления, чтобы найти эти числа. Данные числа определяют конкретную прямую, на которую ложатся исходные данные.
Линейная регрессия – это математический метод оценивания некоего количественного значения (например, суммы в долларах), посредством «взвешивания» одного или нескольких прогнозирующих параметров, таких как возраст, число детей, средний счет в боулинге и так далее. Он был разработан задолго до цифровых компьютеров, и его вечная слава обусловлена привлекательностью для академических исследований.
Если предположить, что линейная регрессия была единственным моделирующим инструментом в арсенале Дока, то мы можем увидеть, как его созданная из подручных средств модель появилась на свет. Подобные инструменты делают допущение, что прямая линия является правильной формой, определяющей отношение каждого из прогнозирующих параметров к искомому количественному показателю. Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Подобные инструменты делают допущение, что прямая линия является правильной формой, определяющей отношение каждого из прогнозирующих параметров к искомому количественному показателю. Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Доход = 1007.8*Возраст -752.35*Число детей +933.6
Звездочка – знак умножения.Влияние нашей новой переменной «число детей», тоже линейное. Это происходит потому, что предполагаемый доход прямолинейно уменьшается на $752.35 за каждого дополнительного ребенка. Мы используем эту формулу, показывающую отношение возраста и числа детей к доходу, чтобы проиллюстрировать то, что важно знать о числах, предоставляемых линейной регрессией.
1) Довольно часто, некорректно полагают, что 1007.8 – это «вес» возраста, а -752.35 – «вес» числа детей. Если бы возраст выражался в месяцах, а не в годах, то новый «вес» был бы разделен на 12 лишь для того, чтобы отразить изменение шкалы. Таким образом, величина «веса» не является мерой важности прогнозирующего параметра, к которому он относится. Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Таким образом, величина «веса» не является мерой важности прогнозирующего параметра, к которому он относится. Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Единственное предназначение коэффициентов и, в сущности, всех чисел (технически, значений параметров), производимых регрессией – это сделать так, чтобы формула хорошо сходилась с исходными данными.
2) Обратите внимание, что коэффициент (-752.35), множитель числа детей, имеет отрицательно значение. В реальности это вовсе не означает, что если число детей растет, то предполагаемый доход обязательно уменьшается. Знак перед коэффициентом будет достоверно указывать направление только в том случае, когда он является единственным прогнозирующим параметром. Если имеется два и более прогнозирующих параметра, и между ними существует корреляция, то вполне вероятно, что один параметр будет иметь положительный коэффициент, а другой – отрицательный, вопреки здравому смыслу. Для нашего примера, на самом деле, если бы число детей было бы единственным прогнозирующим параметром, то тогда коэффициент перед ними оказался бы положительным. Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
Для нашего примера, на самом деле, если бы число детей было бы единственным прогнозирующим параметром, то тогда коэффициент перед ними оказался бы положительным. Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
3) Последний параметр регрессии, константа +933.6 существует для того, чтобы удостоверится, что если каждый параметр принимает среднее значение, то результирующий предполагаемый доход тоже окажется средним. Линейная регрессия всегда так работает. Допустим, средний возраст равен 45.67, а среднее число детей – 1.41. Мы можем подставить эти значения в формулу следующим образом:
1007.8*45.67 -752.35*1.41 +933.56 = 45899
И 45899 – действительно, средний доход в исходных данных. После того как коэффициенты умножены на свои соответствующие параметры и просуммированы, в итоге всегда останется добавить эту константу (даже если она равна нулю).
Пошаговых статей, видео, простых определений
Вероятность и статистика> Регрессионный анализ
График простой линейной регрессии для количества осадков.
Регрессионный анализ — это способ найти тенденции в данных. Например, вы можете предположить, что существует связь между тем, сколько вы едите и сколько вы весите; регрессионный анализ может помочь вам количественно оценить это.
Посмотрите видео для краткого обзора:
Не можете посмотреть видео? Кликните сюда.
Регрессионный анализ предоставит вам уравнение для графика, чтобы вы могли делать прогнозы относительно ваших данных. Например, если вы прибавляли в весе в течение последних нескольких лет, он может предсказать, сколько вы будете весить через десять лет, если продолжите набирать вес с той же скоростью. Он также предоставит вам множество статистических данных (включая значение p и коэффициент корреляции), чтобы узнать, насколько точна ваша модель. Большинство курсов по элементарной статистике охватывают самые базовые методы, такие как построение диаграмм рассеяния и выполнение линейной регрессии. Однако вы можете встретить более сложные методы, такие как множественная регрессия.
Однако вы можете встретить более сложные методы, такие как множественная регрессия.
В комплекте:
- Введение в регрессионный анализ
- Множественный регрессионный анализ
- Переоснащение и как этого избежать
- Статьи по теме
Технологии:
- Регрессия в Minitab
В статистике трудно смотреть на набор случайных чисел в таблице и пытаться разобраться в этом. Например, глобальное потепление может снизить среднее количество снегопадов в вашем городе, и вас просят предсказать, сколько снега, по вашему мнению, выпадет в этом году.Глядя на следующую таблицу, вы можете предположить, что где-то около 10-20 дюймов. Это хорошее предположение, но вы можете сделать лучше, используя регрессию.
По сути, регрессия — это «лучшее предположение» при использовании набора данных для того или иного прогноза. Это подгонка набора точек к графику. Существует целый ряд инструментов, которые могут запускать регрессию для вас, включая Excel, который я использовал здесь, чтобы помочь разобраться в данных о снегопадах:
Просто взглянув на линию регрессии, проходящую через данные, вы можете точно настроить все, что вам нужно. угадай немного.Вы можете видеть, что первоначальное предположение (около 20 дюймов) было неверным. В 2015 году линия будет составлять от 5 до 10 дюймов! Это может быть «достаточно хорошо», но регрессия также дает вам полезное уравнение, которое для этого графика выглядит следующим образом:
угадай немного.Вы можете видеть, что первоначальное предположение (около 20 дюймов) было неверным. В 2015 году линия будет составлять от 5 до 10 дюймов! Это может быть «достаточно хорошо», но регрессия также дает вам полезное уравнение, которое для этого графика выглядит следующим образом:
y = -2,2923x + 4624,4.
Это означает, что вы можете подставить значение x (год) и получить довольно хорошую оценку количества снегопадов для любого года. Например, 2005 год:
y = -2,2923 (2005) + 4624,4 = 28,3385 дюйма, что довольно близко к фактическому значению в 30 дюймов для этого года.
Лучше всего то, что вы можете использовать уравнение для прогнозов. Например, сколько снега выпадет в 2017 году?
y = 2,2923 (2017) + 4624,4 = 0,8 дюйма.
Регрессия также дает значение R в квадрате, которое для этого графика составляет 0,702. Этот номер говорит вам, насколько хороша ваша модель. Значения варьируются от 0 до 1, где 0 — ужасная модель, а 1 — идеальная модель. Как вы, вероятно, видите, 0. 7 — довольно приличная модель, поэтому вы можете быть достаточно уверены в своих прогнозах погоды!
7 — довольно приличная модель, поэтому вы можете быть достаточно уверены в своих прогнозах погоды!
В начало
Множественный регрессионный анализ используется для проверки наличия статистически значимой связи между наборами переменных.Он используется для поиска тенденций в этих наборах данных.
Анализ множественной регрессии — это почти , то же самое, что и простая линейная регрессия. Единственная разница между простой линейной регрессией и множественной регрессией заключается в количестве предикторов (переменных «x»), используемых в регрессии.
- Простой регрессионный анализ использует одну переменную x для каждой зависимой переменной «y». Например: (x 1 , Y 1 ).
- Множественная регрессия использует несколько переменных «x» для каждой независимой переменной: (x1) 1 , (x2) 1 , (x3) 1 , Y 1 ).
В линейной регрессии с одной переменной вы должны ввести одну зависимую переменную (например, «продажи») против независимой переменной (например, «прибыль»). Но вас может заинтересовать, как различных типов продаж влияют на регрессию. Вы можете настроить свой X 1 как один тип продаж, свой X 2 как другой тип продаж и так далее.
Но вас может заинтересовать, как различных типов продаж влияют на регрессию. Вы можете настроить свой X 1 как один тип продаж, свой X 2 как другой тип продаж и так далее.
Когда использовать множественный регрессионный анализ.
Обычной линейной регрессии обычно недостаточно, чтобы учесть все реальные факторы, влияющие на результат.Например, на следующем графике показано сравнение одной переменной (количества врачей) с другой переменной (ожидаемая продолжительность жизни женщин).
Изображение: Колумбийский университет
Из этого графика может показаться, что существует взаимосвязь между ожидаемой продолжительностью жизни женщин и количеством врачей в населении. На самом деле, это, вероятно, правда, и можно сказать, что это простое решение: увеличить количество врачей среди населения, чтобы увеличить продолжительность жизни. Но на самом деле вам придется учитывать другие факторы, например, вероятность того, что у врачей в сельской местности может быть меньше образования или опыта. Или, возможно, у них нет доступа к медицинским учреждениям, таким как травматологические центры.
Или, возможно, у них нет доступа к медицинским учреждениям, таким как травматологические центры.
Добавление этих дополнительных факторов заставит вас добавить дополнительные зависимые переменные в регрессионный анализ и создать модель множественного регрессионного анализа.
Вывод множественного регрессионного анализа.
Регрессионный анализ всегда выполняется в программном обеспечении, таком как Excel или SPSS. Выходные данные различаются в зависимости от того, сколько переменных у вас есть, но по сути это тот же тип выходных данных, который вы найдете в простой линейной регрессии.И еще кое-что:
.
- Простая регрессия: Y = b 0 + b 1 x.
- Множественная регрессия: Y = b 0 + b 1 x1 + b 0 + b 1 x2… b 0 … b 1 xn.
Вывод будет включать сводку, аналогичную сводке для простой линейной регрессии, которая включает:
Эти статистические данные помогут вам выяснить, насколько хорошо регрессионная модель соответствует данным. Таблица ANOVA в выходных данных даст вам p-значение и f-статистику.
Таблица ANOVA в выходных данных даст вам p-значение и f-статистику.
Минимальный размер выборки
«Ответ на вопрос о размере выборки, по-видимому, частично зависит от целей
исследователя, исследуемых вопросов исследования и типа используемой модели
. Хотя есть несколько исследовательских статей и учебников, дающих
рекомендаций по минимальному размеру выборки для множественной регрессии, немногие согласны с
относительно того, насколько большой является достаточно большим, и не многие обращаются к прогнозирующей стороне MLR ». ~ Грегори Т.Кнофчинский
Если вы заинтересованы в нахождении точных значений квадрата коэффициента множественной корреляции, минимизации
сокращения квадрата коэффициента множественной корреляции или преследуете другую конкретную цель, статью Грегори Кнофчински стоит прочитать, и в ней есть множество ссылок для дальнейшего изучения. Тем не менее, многие люди просто хотят запустить MLS, чтобы получить общее представление о тенденциях, и им не нужны очень конкретные оценки. В этом случае вы можете использовать практическое правило .В литературе широко говорится, что в вашей выборке должно быть более 100 наименований. Хотя иногда этого достаточно, вы будете в большей безопасности, если у вас будет не менее 200 наблюдений или еще лучше — более 400.
В этом случае вы можете использовать практическое правило .В литературе широко говорится, что в вашей выборке должно быть более 100 наименований. Хотя иногда этого достаточно, вы будете в большей безопасности, если у вас будет не менее 200 наблюдений или еще лучше — более 400.
В начало
Переоснащение может привести к плохой модели ваших данных.
Переобучение — это когда ваша модель слишком сложна для ваших данных. — это происходит, когда размер вашей выборки слишком мал. Если вы поместите достаточно переменных-предикторов в свою регрессионную модель, вы почти всегда получите модель, которая выглядит значимой.
Хотя переоборудованная модель может очень хорошо соответствовать особенностям ваших данных, она не подойдет для дополнительных тестовых выборок или для всей генеральной совокупности.
p-значений модели, R-квадрат и коэффициенты регрессии могут вводить в заблуждение. По сути, вы слишком многого требуете от небольшого набора данных.
Как избежать переобучения
При линейном моделировании (включая множественную регрессию) у вас должно быть не менее 10-15 наблюдений для каждого члена, который вы пытаетесь оценить. Если меньше, то вы рискуете переобучить свою модель.
«Условия» включают:
Хотя это эмпирическое правило является общепринятым, Грин (1991) идет дальше и предлагает, чтобы минимальный размер выборки для любой регрессии был 50, с дополнительными 8 наблюдениями на член. Например, если у вас есть одна взаимодействующая переменная и три переменные-предикторы, вам понадобится около 45-60 элементов в вашей выборке, чтобы избежать переобучения, или 50 + 3 (8) = 74 элемента, согласно Грину.
Исключения
Из эмпирического правила «10-15» есть исключения. В их числе:
- При наличии мультиколлинеарности в ваших данных или при небольшом размере эффекта. В таком случае вам нужно будет включить больше терминов (хотя, к сожалению, нет практического правила, сколько терминов добавить!).

- Если вы используете логистическую регрессию или модели выживания, возможно, вам удастся обойтись всего лишь с 10 наблюдениями на один предиктор, если у вас нет экстремальных вероятностей событий, небольших размеров эффекта или переменных-предикторов с усеченными диапазонами.(Педуцци и др.)
Как обнаружить и избежать переобучения
Самый простой способ избежать переобучения — увеличить размер выборки за счет сбора большего количества данных. Если вы не можете этого сделать, второй вариант — уменьшить количество предикторов в вашей модели, комбинируя или исключая их. Факторный анализ — это один из методов, который вы можете использовать для определения связанных предикторов, которые могут быть кандидатами для объединения.
1. Перекрестная проверка
Используйте перекрестную проверку для обнаружения переобучения: это разбивает ваши данные, обобщает вашу модель и выбирает модель, которая работает лучше всего. Одна из форм перекрестной проверки — предсказанных R-квадратов . Большинство хороших статистических программ будет включать эту статистику, которая рассчитывается следующим образом:
Одна из форм перекрестной проверки — предсказанных R-квадратов . Большинство хороших статистических программ будет включать эту статистику, которая рассчитывается следующим образом:
- Удаление одного наблюдения из ваших данных,
- Оценка уравнения регрессии для каждой итерации,
- Использование уравнения регрессии для прогнозирования удаленного наблюдения.
Перекрестная проверка не является волшебным лекарством для небольших наборов данных, и иногда четкая модель не может быть идентифицирована даже при адекватном размере выборки.
2. Усадка и повторная выборка
Методы сжатия и повторной выборки (например, этот R-модуль) могут помочь вам определить, насколько хорошо ваша модель может соответствовать новому образцу.
3. Автоматизированные методы
Автоматизированную пошаговую регрессию не следует использовать как дополнительное решение для небольших наборов данных. По данным Бабяка (2004),
«Проблем с автоматическим отбором, проводимым таким очень типичным способом, настолько много, что было бы трудно каталогизировать их все [в журнальной статье].
”
Бабяк также рекомендует избегать одномерного предварительного тестирования или скрининга («скрытый вариант автоматического выбора»), дихотомии непрерывных переменных — что может значительно увеличить количество ошибок типа I или многократного тестирования смешивающих переменных (хотя это может быть нормально, если используется разумно).
Список литературы
Книги:
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Линдстром, Д. (2010). Краткое изложение статистики Шаума, второе издание (Schaum’s Easy Outlines), 2-е издание.McGraw-Hill Education
Журнальные статьи:
- Бабяк, М.А., (2004). «То, что вы видите, может быть не тем, что вы получаете: краткое, нетехническое введение в переоснащение в моделях регрессионного типа». Психосоматическая медицина. 2004 май-июнь; 66 (3): 411-21.
- Грин С.Б., (1991) «Сколько испытуемых требуется для проведения регрессионного анализа?» Многомерное исследование поведения 26: 499–510.

- Peduzzi P.N., et. al (1995). «Важность событий для каждой независимой переменной в многомерном анализе, II: точность и точность оценок регрессии.» Журнал клинической эпидемиологии 48: 1503–10.
- Peduzzi P.N., et. al (1996). «Имитационное исследование количества событий на переменную в логистическом регрессионном анализе». Журнал клинической эпидемиологии 49: 1373–9.
В начало
Посетите наш канал YouTube, чтобы увидеть сотни видеороликов по элементарной статистике, включая регрессионный анализ с использованием различных инструментов, таких как Excel и TI-83.
- Аддитивная модель и мультипликативная модель
- Как построить диаграмму рассеяния.
- Как рассчитать коэффициенты корреляции Пирсона.
- Как вычислить значение теста линейной регрессии.
- Тест Чоу для разделенных наборов данных
- Выбор вперед
- Что такое кригинг?
- Как найти уравнение линейной регрессии.

- Как найти точку пересечения наклона регрессии.
- Как найти наклон линейной регрессии.
- Как найти стандартную ошибку наклона регрессии.
- Mallows ’Cp
- Коэффициент достоверности: что это такое и как его найти.
- Квадратичная регрессия.
- Регрессия четвертого порядка
- Пошаговая регрессия
- Нестандартизованный коэффициент
- Далее: : Слабые инструменты
Интересный факт: Знаете ли вы, что регрессия предназначена не только для создания линий тренда. Это также отличный способ найти n-й член квадратичной последовательности.
В начало
Определения
- ANCOVA.
- Допущения и условия регресса.
- Бета / Стандартизированные коэффициенты.
- Что такое бета-вес?
- Билинейная регрессия
- Тест Бреуша-Пагана-Годфри
- Расстояние повара.
- Что такое ковариата?
- Регрессия Кокса.

- Данные о бестрендовом движении.
- Экзогенность.
- Алгоритм Гаусса-Ньютона.
- Что такое общая линейная модель?
- Что такое обобщенная линейная модель?
- Что такое тест Хаусмана?
- Что такое гомоскедастичность?
- Влиятельные данные.
- Что такое инструментальная переменная?
- Отсутствие посадки
- Регрессия Лассо.
- Алгоритм Левенберга – Марквардта
- Какая линия лучше всего подходит?
- Что такое логистическая регрессия?
- Что такое расстояние Махаланобиса? Модель
- Неверная спецификация.
- Полиномиальная логистическая регрессия.
- Что такое нелинейная регрессия?
- Упорядоченная логит / упорядоченная логистическая регрессия
- Что такое регрессия методом наименьших квадратов?
- Переоборудование.
- Экономные модели.
- Что такое коэффициент корреляции Пирсона?
- Регрессия Пуассона.

- Пробит Модель.
- Что такое интервал прогнозирования?
- Что такое регуляризация?
- Регулярные наименьшие квадраты.
- Регуляризованная регрессия
- Что такое относительный вес?
- Что такое остаточные участки?
- Обратная причинность.
- Регрессия хребта
- Среднеквадратичная ошибка.
- Полупараметрические модели
- Смещение одновременности.
- Модель одновременных уравнений.
- Что такое ложная корреляция?
- Модель структурных уравнений
- Каковы интервалы допуска?
- Анализ тенденций
- Параметр настройки
- Что такое взвешенная регрессия наименьших квадратов?
- Y Hat объяснил.
В начало
Посмотрите видео для шагов:
Не можете посмотреть видео? Кликните сюда.
Регрессия — это подгонка данных к линии (Minitab также может выполнять другие типы регрессии, например квадратичную регрессию). Когда вы обнаружите регрессию в Minitab, вы получите диаграмму разброса ваших данных вместе с линией наилучшего соответствия, плюс Minitab предоставит вам:
Когда вы обнаружите регрессию в Minitab, вы получите диаграмму разброса ваших данных вместе с линией наилучшего соответствия, плюс Minitab предоставит вам:
- Стандартная ошибка (насколько точки данных отклоняются от среднего).
- R в квадрате: значение от 0 до 1, которое показывает, насколько хорошо ваши точки данных соответствуют модели.
- Скорректированный R 2 (корректирует R 2 с учетом точек данных, которые не соответствуют модели).
Регрессия в Minitab занимает всего пару щелчков мышью на панели инструментов и доступна через меню Stat.
Пример вопроса : Найдите регрессию в Minitab для следующего набора точек данных, которые сравнивают калории, потребляемые в день, и вес:
Калорий, потребляемых ежедневно (вес в фунтах): 2800 (140), 2810 (143), 2805 (144) , 2705 (145), 3000 (155), 2500 (130), 2400 (121), 2100 (100), 2000 (99), 2350 (120), 2400 (121), 3000 (155).
Шаг 1: Введите данные в два столбца в Minitab .
Шаг 2: Щелкните «Stat», затем щелкните «Regression», а затем щелкните «Fitted Line Plot».”
Регрессия в выборе Minitab.
Шаг 3: Щелкните имя переменной для зависимого значения в левом окне. Для этого типового вопроса мы хотим знать, влияет ли потребление калорий на вес , поэтому калории являются независимой переменной (Y), а вес — зависимой переменной (X). Щелкните «Калории», а затем «Выбрать».
Шаг 4: Повторите шаг 3 для зависимой переменной X , веса.
Выбор переменных для регрессии Minitab.
Шаг 5: Нажмите «ОК». Minitab создаст линейный график регрессии в отдельном окне.
Шаг 4: Прочтите результаты. Помимо создания графика регрессии, Minitab предоставит вам значения для S, R-sq и R-sq (adj) в верхнем правом углу окна подобранного линейного графика.
с = стандартная ошибка.
R-Sq = Коэффициент детерминации
R-Sq (adj) = Скорректированный коэффициент детерминации (Скорректированный R в квадрате).
Вот и все!
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Линейная регрессия: простые шаги, видео. Найти уравнение, коэффициент, наклон
Состав:
Что такое простая линейная регрессия?
Как найти уравнение линейной регрессии:
- Как найти уравнение линейной регрессии вручную .
- Найдите уравнение линейной регрессии в Excel .
- TI83 Линейная регрессия.
- TI 89 Линейная регрессия
Поиск сопутствующих товаров:
- Как найти коэффициент регрессии.

- Найдите наклон линейной регрессии.
- Найдите значение теста линейной регрессии.
Кредитное плечо:
- Кредитное плечо в линейной регрессии.
Наверх
Посмотрите видео для краткого введения в линейную регрессию:
Не можете посмотреть видео? Кликните сюда.
Если вы только начинаете изучать регрессионный анализ, простой линейный метод — это первый тип регрессии, с которым вы столкнетесь в классе статистики.
Линейная регрессия — это наиболее широко используемый статистический метод ; это способ смоделировать отношения между двумя наборами переменных. В результате получается уравнение линейной регрессии, которое можно использовать для прогнозирования данных.
Большинство программных пакетов и калькуляторов могут рассчитывать линейную регрессию. Например:
Вы также можете найти линейную регрессию вручную.
Перед тем, как приступить к расчетам, вы всегда должны строить диаграмму рассеяния, чтобы увидеть, подходят ли ваши данные примерно к линии. Почему? Потому что регрессия будет всегда даст вам уравнение, и это может не иметь никакого смысла, если ваши данные следуют экспоненциальной модели. Если вы знаете, что взаимосвязь нелинейна, но не знаете точно, что это за взаимосвязь, одним из решений является использование моделей линейных базисных функций, которые популярны в машинном обучении.
Почему? Потому что регрессия будет всегда даст вам уравнение, и это может не иметь никакого смысла, если ваши данные следуют экспоненциальной модели. Если вы знаете, что взаимосвязь нелинейна, но не знаете точно, что это за взаимосвязь, одним из решений является использование моделей линейных базисных функций, которые популярны в машинном обучении.
Этимология
«Линейный» означает линию.Слово Регрессия пришло от ученого XIX века сэра Фрэнсиса Гальтона, который ввел термин «регрессия к посредственности» (на современном языке это регрессия к среднему. Он использовал этот термин для описания феномена того, как природа стремится к смягчать лишние физические черты из поколения в поколение (например, чрезмерный рост).
Зачем нужны линейные отношения?
С линейными отношениями, то есть линиями, легче работать, и большинство явлений естественно связаны линейно.Если переменные не связаны линейно с , тогда некоторые математические вычисления могут преобразовать эту связь в линейную, чтобы исследователю (то есть вам) было легче понять.
Что такое простая линейная регрессия?
Вы, вероятно, знакомы с построением линейных графиков с одной осью X и одной осью Y. Переменная X иногда называется независимой переменной, а переменная Y — зависимой переменной. Простая линейная регрессия отображает одну независимую переменную X против одной зависимой переменной Y.Технически в регрессионном анализе независимая переменная обычно называется переменной-предиктором, а зависимая переменная — переменной критерия. Однако многие люди просто называют их независимыми и зависимыми переменными. Более продвинутые методы регрессии (например, множественная регрессия) используют несколько независимых переменных.
Регрессионный анализ может дать линейных или нелинейных графиков. Линейная регрессия — это когда отношения между вашими переменными можно описать прямой линией.Нелинейные регрессии образуют изогнутые линии. ( ** )
Простая линейная регрессия для количества осадков за год.
Регрессионный анализ почти всегда выполняется компьютерной программой, поскольку выполнение уравнений вручную требует очень много времени.
** Поскольку это вводная статья, я сделал ее простой. Но на самом деле существует важное техническое различие между линейным и нелинейным, которое станет еще более важным, если вы продолжите изучать регрессию.Подробнее см. В статье о нелинейной регрессии.
К началу
Регрессионный анализ используется для поиска уравнений, соответствующих данным. Получив уравнение регрессии, мы можем использовать модель для прогнозов. Один из видов регрессионного анализа — это линейный анализ. Когда коэффициент корреляции показывает, что данные, вероятно, могут предсказать будущие результаты, а диаграмма разброса данных выглядит как прямая линия, вы можете использовать простую линейную регрессию, чтобы найти прогностическую функцию.Если вы помните из элементарной алгебры, уравнение для прямой: y = mx + b . В этой статье показано, как получить данные, рассчитать линейную регрессию и найти уравнение y ’= a + bx . Примечание : Если вы берете статистику AP, вы можете увидеть уравнение, записанное как b 0 + b 1 x, что одно и то же (вы просто используете переменные b 0 + b 1 вместо a + b.
Примечание : Если вы берете статистику AP, вы можете увидеть уравнение, записанное как b 0 + b 1 x, что одно и то же (вы просто используете переменные b 0 + b 1 вместо a + b.
Посмотрите видео или прочтите приведенные ниже инструкции, чтобы вручную найти уравнение линейной регрессии.
Не можете посмотреть видео? Кликните сюда.
Все еще не уверены? Посмотрите репетиторов на Chegg.com. Ваши первые 30 минут бесплатно!
Уравнение линейной регрессии
Линейная регрессия — это способ моделирования взаимосвязи между двумя переменными. Вы также можете узнать это уравнение как формулу наклона . Уравнение имеет вид Y = a + bX, где Y — зависимая переменная (то есть переменная, которая идет по оси Y), X — независимая переменная (т. Е.е. он нанесен на ось X), b — наклон линии, а a — точка пересечения с y.
Первый шаг в поиске уравнения линейной регрессии — определить, существует ли связь между двумя переменными. Это часто является суждением исследователя. Вам также понадобится список ваших данных в формате x-y (т. Е. Два столбца данных — независимые и зависимые переменные).
Это часто является суждением исследователя. Вам также понадобится список ваших данных в формате x-y (т. Е. Два столбца данных — независимые и зависимые переменные).
Предупреждения:
- Тот факт, что две переменные связаны, не означает, что одна вызывает другую.Например, хотя существует взаимосвязь между высокими баллами GRE и лучшей успеваемостью в аспирантуре, это не означает, что высокие баллы GRE приводят к хорошей успеваемости в аспирантуре.
- Если вы попытаетесь найти уравнение линейной регрессии для набора данных (особенно с помощью автоматизированной программы, такой как Excel или TI-83), вы, , найдете его , но это не обязательно означает, что уравнение является подходящим. подходит для ваших данных. Один из методов состоит в том, чтобы сначала построить диаграмму рассеяния, чтобы увидеть, соответствуют ли данные примерно линии , прежде чем вы попытаетесь найти уравнение линейной регрессии.
Как найти уравнение линейной регрессии: шаги
Шаг 1: Составьте диаграмму своих данных, заполняя столбцы так же, как если бы вы заполняли диаграмму, если бы вы находили коэффициент корреляции Пирсона.
| Тема | Возраст x | Уровень глюкозы у | xy | x 2 | y 2 | 1 | 43 | 99 | 4257 | 1849 | 9801 |
|---|---|---|---|---|---|
| 2 | 21 | 65 | 1365 | 441 | 4225 | 3 | 25 | 79 | 1975 | 625 | 6241 |
| 4 | 42 | 75 | 3150 | 1764 | 5625 | 5 | 57 | 87 | 4959 | 3249 | 7569 |
| 6 | 59 | 81 | 4779 | 3481 | 6561 |
| Σ | 247 | 486 | 20485 | 11409 | 40022 |
Из приведенной выше таблицы Σx = 247, Σy = 486, Σxy = 20485, Σx2 = 11409, Σy2 = 40022.n — размер выборки (в нашем случае 6).
Шаг 2: Используйте следующие уравнения, чтобы найти a и b.
a = 65,1416
b = ,385225
Щелкните здесь, чтобы получить простые пошаговые инструкции по решению этой формулы.
Найдите :
- ((486 × 11,409) — ((247 × 20,485)) / 6 (11,409) — 247 2 )
- 484979/7445
- = 65,14
Найти b :
- (6 (20,485) — (247 × 486)) / (6 (11409) — 247 2 )
- (122 910 — 120 042) / 68 454 — 247 2
- 2 868/7 445
- = .385225
Шаг 3: Вставьте значения в уравнение .
y ’= a + bx
y’ = 65,14 + 0,385225x
Вот как найти уравнение линейной регрессии вручную!
Понравилось объяснение? Ознакомьтесь со Справочником по статистике практического мошенничества, в котором есть еще сотни пошаговых решений, подобных этому!
* Обратите внимание на , что этот пример имеет низкий коэффициент корреляции и поэтому не годится для предсказания чего-либо.
К началу
Посмотрите видео или прочтите следующие шаги:
Уравнение линейной регрессии Microsoft Excel: шаги
Шаг 1: Установите Data Analysis Toolpak , если он еще не установлен. Для получения инструкций по загрузке пакета инструментов анализа данных щелкните здесь.
Шаг 2: Введите данные в два столбца в Excel. Например, введите данные «x» в столбец A и данные «y» в столбец b. Не оставляйте пустых ячеек между записями.
Шаг 3: Щелкните вкладку «Анализ данных» на панели инструментов Excel.
Шаг 4: Нажмите «регрессия» во всплывающем окне, а затем нажмите «ОК».
Всплывающее окно «Анализ данных» имеет множество параметров, включая линейную регрессию.
Шаг 5: Выберите входной диапазон Y. Вы можете сделать это двумя способами: либо выбрать данные на листе, либо ввести расположение данных в поле «Введите диапазон Y». Например, если ваши данные Y находятся в диапазоне от A2 до A10, введите «A2: A10» в поле «Диапазон ввода Y».
Шаг 6: Выберите входной диапазон X , выбрав данные на листе или введя расположение данных в поле «Входной диапазон X».
Шаг 7: Выберите место, куда вы хотите поместить выходной диапазон , выбрав пустую область на листе или введя местоположение, куда вы хотите поместить ваши данные в поле «Диапазон вывода».
Шаг 8: Нажмите «ОК». Excel рассчитает линейную регрессию и заполнит ваш рабочий лист результатами.
Совет: информация об уравнении линейной регрессии дается в последнем выходном наборе (столбец коэффициентов). Первая запись в строке «Перехват» — «а» (точка пересечения по оси Y), а первая запись в столбце «X» — «b» (наклон).
Вернуться к началу
Посмотрите видео для шагов:
Не можете посмотреть видео? Кликните сюда.
Две линии линейной регрессии.
TI 83 Линейная регрессия: обзор
Линейная регрессия утомительна и подвержена ошибкам, когда выполняется вручную, но вы можете выполнить линейную регрессию за время, необходимое для ввода нескольких переменных в список. Линейная регрессия даст вам разумный результат, только если ваши данные выглядят как линия на диаграмме рассеяния, поэтому, прежде чем вы найдете уравнение для линии линейной регрессии , вы можете сначала просмотреть данные на диаграмме рассеяния. См. Эту статью, чтобы узнать, как построить диаграмму рассеяния на TI 83.
Линейная регрессия даст вам разумный результат, только если ваши данные выглядят как линия на диаграмме рассеяния, поэтому, прежде чем вы найдете уравнение для линии линейной регрессии , вы можете сначала просмотреть данные на диаграмме рассеяния. См. Эту статью, чтобы узнать, как построить диаграмму рассеяния на TI 83.
TI 83 Линейная регрессия: шаги
Пример задачи: Найдите уравнение линейной регрессии (вида y = ax + b) для значений x 1, 2, 3, 4, 5 и значений y 3, 9, 27, 64 и 102.
Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы открыть экран списков. Если у вас уже есть данные в L1 или L2, очистите данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. Повторите для L2.
Шаг 2: Введите переменные x по очереди. Следуйте за каждым числом, нажимая клавишу ENTER. Для нашего списка вы должны ввести:
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER
Шаг 3: Используйте клавиши со стрелками для перехода к следующему столбцу L2.
Шаг 4: Введите переменные y по очереди. Следуйте за каждым числом, нажимая клавишу ввода. Для нашего списка вы должны ввести:
3 ENTER
9 ENTER
27 ENTER
64 ENTER
102 ENTER
Шаг 5: Нажмите кнопку STAT, затем с помощью клавиши прокрутки выделите «CALC».
Шаг 6: Нажмите 4, чтобы выбрать «LinReg (ax + b)». Нажмите ENTER, а затем снова ENTER. TI 83 вернет переменные, необходимые для уравнения. Просто вставьте указанные переменные (a, b) в уравнение линейной регрессии (y = ax + b).Для приведенных выше данных это y = 25,3x — 34,9 .
Вот как выполнить линейную регрессию TI 83!
Вернуться к началу
Помните из алгебры, что наклон — это «m» в формуле y = mx + b .
В формуле линейной регрессии наклон равен a в уравнении y ’= b + ax .
В основном это одно и то же. Итак, если вас попросят найти наклон линейной регрессии, все, что вам нужно сделать, это найти b так же, как вы нашли бы m .
Вычислить линейную регрессию вручную, мягко говоря, непросто. Есть лот суммирования (это символ Σ, что означает сложение). Основные шаги приведены ниже, или вы можете посмотреть видео в начале этой статьи. В видео гораздо больше подробно рассказывается о том, как проводить суммирование. Поиск уравнения также даст вам наклон. Если вы не хотите определять уклон вручную (или если вы хотите проверить свою работу), вы также можете использовать Excel.
Как найти наклон линейной регрессии: шаги
Шаг 1: Найдите следующие данные из предоставленной информации: Σx, Σy, Σxy, Σx 2 , Σy 2 .Если вы не помните, как получить эти переменные из данных, прочтите эту статью о том, как найти коэффициент корреляции Пирсона. Выполните указанные здесь шаги, чтобы создать таблицу и найти Σx, Σy, Σxy, Σx 2 и Σy 2 .
Шаг 2: Вставьте данные в формулу b (нет необходимости находить a ).
Если формулы пугают вас, вы можете найти более подробные инструкции о том, как работать с формулой, здесь: Как найти уравнение линейной регрессии: обзор.
Как найти наклон регрессии в Excel 2013
Подпишитесь на наш канал Youtube, чтобы получить больше советов и рекомендаций по статистике.
Вернуться к началу
Коэффициент регрессии — это то же самое, что наклон линии уравнения регрессии . Уравнение для коэффициента регрессии, которое вы найдете в тесте AP Statistics: B 1 = b 1 = Σ [(x i — x) (y i — y)] / Σ [ (x i — x) 2 ].«Y» в этом уравнении — это среднее значение y, а «x» — среднее значение x.
Вы можете найти коэффициент регрессии вручную (как указано в разделе вверху этой страницы).
Однако вам не нужно рассчитывать коэффициент регрессии вручную в тесте AP — вы воспользуетесь калькулятором TI-83. Почему? Вычисление линейной регрессии вручную занимает очень много времени (дайте себе около 30 минут, чтобы провести расчеты и проверить их), и из-за огромного количества вычислений , которое вы должны выполнить, очень высока вероятность того, что вы сделаете математические ошибки. Когда вы найдете уравнение линейной регрессии на TI83, вы получите коэффициент регрессии как часть ответа.
Когда вы найдете уравнение линейной регрессии на TI83, вы получите коэффициент регрессии как часть ответа.
Пример задачи : Найдите коэффициент регрессии для следующего набора данных:
x: 1, 2, 3, 4, 5.
y: 3, 9, 27, 64, 102.
Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы войти в СПИСКИ. Вам может потребоваться очистить данные, если у вас уже есть числа в L1 или L2. Чтобы очистить данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. При необходимости повторите для L2.
Шаг 2: Введите свои x-данные в список. Нажимайте клавишу ENTER после каждого ввода.
1 ВВОД
2 ВВОД
3 ВВОД
4 ВВОД
5 ВВОД
Шаг 3: Прокрутите до следующего столбца L2 с помощью клавиш со стрелками в верхнем правом углу клавиатуры.
Шаг 4: Введите y-данные:
3 ENTER
9 ENTER
27 ENTER
64 ENTER
102 ENTER
Шаг 5: Нажмите кнопку STAT, затем выделите «CALC. ”Нажмите ENTER
”Нажмите ENTER
Шаг 6: Нажмите 4, чтобы выбрать «LinReg (ax + b)». Нажмите Ввод. TI 83 вернет переменные, необходимые для уравнения линейной регрессии. Искомое значение> коэффициент регрессии> равно b, что составляет 25,3 для этого набора данных.
Вот и все!
Вернуться к началу
Две линии линейной регрессии.
Значения теста линейной регрессии используются в простой линейной регрессии точно так же, как значения теста (например, z-оценка или T-статистика) используются при проверке гипотез.Вместо работы с z-таблицей вы будете работать с таблицей t-распределения. Значение теста линейной регрессии сравнивается со статистикой теста, чтобы помочь вам поддержать или отклонить нулевую гипотезу.
Значение теста линейной регрессии: шаги
Пример вопроса : Для набора данных с размером выборки 8 и r = 0,454 найдите значение теста линейной регрессии.
Примечание : r — коэффициент корреляции.
Шаг 1: Найдите r, коэффициент корреляции, , если он еще не был указан вам в вопросе.В этом случае дается r (r = 0,0454). Не знаете, как найти r? См .: Коэффициент корреляции, чтобы узнать, как найти r.
Шаг 2: Используйте следующую формулу для вычисления тестового значения ( n — размер выборки):
Как решить формулу:
- Замените переменные своими числами:
T = .454√ ((8 — 2) / (1 — [. 454] 2 ))- Вычтем 2 из n:
8-2 = 6 - Квадрат r:
.454 × 0,454 = 0,206116 - Вычесть шаг (3) из 1:
1 — .206116 = .793884 - Разделите шаг (2) на шаг (4):
6 / .793884 = 7,557779 - Извлеките квадратный корень из шага (5):
√7,557779 = 2,744
- Умножьте r на шаг (6):
. 454 × 2,744 = 1,24811026
- Вычтем 2 из n:
Значение теста линейной регрессии, T = 1,24811026
Вот и все!
Нахождение тестовой статистики
Значение теста линейной регрессии бесполезно, если вам не с чем его сравнивать. Сравните свое значение со статистикой теста. Статистика теста также представляет собой t-показатель (t), определяемый следующим уравнением:
Сравните свое значение со статистикой теста. Статистика теста также представляет собой t-показатель (t), определяемый следующим уравнением:
t = наклон линии регрессии выборки / стандартная ошибка наклона.
См .: Как найти наклон линейной регрессии / Как найти стандартную ошибку наклона (TI-83).
Вы можете найти рабочий пример расчета значения теста линейной регрессии (с альфа-уровнем) здесь: Коэффициенты корреляции.
Вернуться к началу
Точки данных с кредитным плечом могут перемещать линию линейной регрессии.Они склонны быть выбросами. Выброс — это точка с очень высоким или очень низким значением.
Очки влияния
Если оценки параметров (стандартное отклонение выборки, дисперсия и т. Д.) Значительно изменяются при удалении выброса, эта точка данных называется влиятельным наблюдением .
Чем больше точка данных отличается от среднего других значений x, тем больше у нее рычагов . Чем больше кредитное плечо у точки, тем выше вероятность того, что точка будет влиять на (т. е. это может изменить оценки параметров).
е. это может изменить оценки параметров).
Кредитное плечо в линейной регрессии: как оно влияет на графики
В линейной регрессии влиятельная точка (выброс) будет пытаться подтянуть линию линейной регрессии к себе. На графике ниже показано, что происходит с линией линейной регрессии при включении выброса A:
Две линии линейной регрессии. Влиятельная точка A включена в верхнюю строку, но не в нижнюю.
Выбросы с крайними значениями X (значения, не попадающие в диапазон других точек данных) имеют больше возможностей для линейной регрессии, чем точки с меньшими экстремальными значениями x.Другими словами, экстремальных выбросов значения x сдвинут линию на больше, чем менее экстремальные значения.
На следующем графике показана точка данных за пределами диапазона других значений. Значения варьируются от 0 до примерно 70 000. Эта одна точка имеет значение x около 80 000, что выходит за пределы диапазона. Это влияет на линию регрессии намного больше, чем на точку на первом изображении выше, которая находилась внутри диапазона других значений.
Исключительный показатель с высоким долгом. Точка сместила график еще больше, потому что она выходит за пределы диапазона других значений.
Как правило, выбросы, значения которых близки к среднему значению x, будут иметь меньшее влияние, чем выбросы, по направлению к краям диапазона. Выбросы со значениями x за пределами диапазона будут иметь больший рычаг. Значения, которые являются крайними по оси Y (по сравнению с другими значениями), будут иметь большее влияние, чем значения, близкие к другим значениям Y.
Нравится видео? Подпишитесь на наш канал Youtube.
Связь с аффинным преобразованием
Линейная регрессия бесконечно связана с аффинным преобразованием.Формула y ′ = b + ax на самом деле не является линейной… это аффинная функция, которая определяется как линейная функция плюс преобразование. Так что это действительно следует называть аффинной регрессией, а не линейной!
Список литературы
Эдвардс, А. Л. Введение в линейную регрессию и корреляцию. Сан-Франциско, Калифорния: У. Х. Фриман, 1976.
Сан-Франциско, Калифорния: У. Х. Фриман, 1976.
Эдвардс, А. Л. Множественная регрессия и анализ дисперсии и ковариации. Сан-Франциско, Калифорния: У. Х. Фриман, 1979.
. ————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Коэффициент детерминации (R в квадрате): определение, расчет
Содержание :
Коэффициент детерминации (R в квадрате)
Коэффициент детерминации R 2 используется для анализа того, как различия в одной переменной могут быть объяснены разницей во второй переменной.Например, , когда человек забеременеет, имеет прямое отношение к тому, когда он рожает.
Более конкретно, R-квадрат дает вам процентное изменение y, объясняемое переменными x. Диапазон составляет от 0 до 1 (т.е. от 0% до 100% вариации y можно объяснить переменными x).
Посмотрите это видео, чтобы ознакомиться с кратким определением r в квадрате и узнать, как его найти:
Не можете посмотреть видео? Кликните сюда.
Коэффициент детерминации R 2 аналогичен коэффициенту корреляции , R.Формула коэффициента корреляции покажет вам, насколько сильна линейная связь между двумя переменными. R в квадрате — это квадрат коэффициента корреляции, r (отсюда и термин r в квадрате).
Нахождение R в квадрате / Коэффициент детерминации
Нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Шаг 1: Найдите коэффициент корреляции r (он может быть указан вам в вопросе). Пример, r = 0.543 .
Шаг 2: Возведите коэффициент корреляции в квадрат.
0,543 2 = ,295
Шаг 3: Преобразуйте коэффициент корреляции в проценты .
,295 = 29,5%
Вот и все!
Значение коэффициента детерминации
Коэффициент детерминации можно представить как процент. Это дает вам представление о том, сколько точек данных попадает в результаты линии, образованной уравнением регрессии.Чем выше коэффициент, тем больший процент точек проходит линия при построении точек данных и линии. Если коэффициент равен 0,80, то 80% точек должны попадать в линию регрессии. Значения 1 или 0 будут означать, что линия регрессии представляет все или никакие данные соответственно. Более высокий коэффициент является показателем лучшего соответствия наблюдениям.
CoD может быть отрицательным , хотя обычно это означает, что ваша модель плохо подходит для ваших данных.Он также может стать отрицательным, если вы не установили перехват.
Полезность R
2
Полезность R 2 заключается в его способности находить вероятность будущих событий, попадающих в пределы прогнозируемых результатов. Идея состоит в том, что если добавить больше выборок, коэффициент будет показывать вероятность падения новой точки на линии.
Идея состоит в том, что если добавить больше выборок, коэффициент будет показывать вероятность падения новой точки на линии.
Даже если существует сильная связь между двумя переменными, определение не доказывает причинно-следственную связь. Например, исследование дней рождения может показать, что большое количество дней рождения происходит в течение одного или двух месяцев.Это не означает, что беременность наступает по прошествии времени или смене времен года.
Синтаксис
Коэффициент детерминации обычно записывается как R 2 _p. «P» указывает количество столбцов данных, что полезно при сравнении R 2 различных наборов данных.
В начало
Что такое скорректированный коэффициент детерминации?
Скорректированный коэффициент детерминации (скорректированный R-квадрат) — это поправка для коэффициента детерминации, которая учитывает числа переменных в наборе данных. Он также наказывает вас за очки, не соответствующие модели.
Возможно, вы знаете, что небольшое количество значений в наборе данных (слишком маленький размер выборки) может привести к недостоверной статистике, но вы можете не знать, что слишком много точек данных также может привести к проблемам. Каждый раз, когда вы добавляете точку данных в регрессионный анализ, R 2 будет увеличиваться. R 2 никогда не уменьшается. Следовательно, чем больше очков вы добавите, тем лучше будет казаться, что регрессия «соответствует» вашим данным.Если ваши данные не совсем умещаются в строке, может возникнуть соблазн продолжить добавление данных, пока вы не найдете более подходящего.
Некоторые из добавленных вами баллов будут значительными (соответствовать модели), а другие — нет. R 2 не заботится о незначительных моментах. Чем больше вы добавите, тем выше коэффициент детерминации .
Скорректированный R 2 можно использовать для включения более подходящего числа переменных, что избавит вас от соблазна продолжать добавлять переменные в ваш набор данных. Скорректированный R 2 будет увеличиваться только в том случае, если новая точка данных улучшит регрессию больше, чем вы ожидаете случайно. R 2 не включает все точки данных, всегда ниже, чем R 2 и может быть отрицательным (хотя обычно положительным). Отрицательные значения вероятны, если R 2 близок к нулю — после настройки значение немного опустится ниже нуля.
Скорректированный R 2 будет увеличиваться только в том случае, если новая точка данных улучшит регрессию больше, чем вы ожидаете случайно. R 2 не включает все точки данных, всегда ниже, чем R 2 и может быть отрицательным (хотя обычно положительным). Отрицательные значения вероятны, если R 2 близок к нулю — после настройки значение немного опустится ниже нуля.
Подробнее см .: Скорректированный R-квадрат.
Посетите мой канал на Youtube, чтобы получить больше советов по статистике и помощи!
Список литературы
Гоник, Л.(1993). Мультяшный справочник по статистике. HarperPerennial.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Точечная диаграмма / Точечная диаграмма: определение, примеры, Excel / TI-83 / TI-89 / SPSS
Состав:
Что такое диаграмма рассеяния?
Графики разброса
(также называемые графиками разброса ) аналогичны линейным графикам. На линейном графике используется линия на оси X-Y для построения непрерывной функции, а на точечной диаграмме используется точек для представления отдельных фрагментов данных.В статистике эти графики полезны, чтобы увидеть, связаны ли две переменные друг с другом. Например, точечная диаграмма может предложить линейную зависимость (т. Е. Прямую линию).
Посмотрите видео, чтобы увидеть пример того, как вручную построить диаграмму рассеяния.
Не можете посмотреть видео? Кликните сюда.
Диаграмма рассеяния, предполагающая линейную зависимость.
Точечные диаграммы также называются точечными диаграммами, точечными диаграммами, точечными диаграммами и точечными диаграммами.
Корреляция в диаграммах рассеяния
Связь между переменными называется корреляцией.Корреляция — это просто еще одно слово, обозначающее «отношения». Например, ваш вес связан (коррелирован) с тем, сколько вы едите. Есть два типа корреляции: положительная корреляция и отрицательная корреляция. Если точки данных образуют линию от начала координат от низких значений x и y к высоким значениям x и y, то точки данных — это с положительной корреляцией , как на приведенном выше графике. Если график начинается с высоких значений y и продолжается до низких значений y, тогда график с отрицательной корреляцией .
Вы можете думать о положительной корреляции как о чем-то, что дает положительный результат. Например, чем больше вы тренируетесь, тем лучше ваше сердечно-сосудистое здоровье. «Положительный» не обязательно означает «хорошо»! Чем больше вы курите, тем выше вероятность рака, и чем больше вы водите машину, тем больше вероятность того, что вы попадете в автомобильную аварию.
Например, чем больше вы тренируетесь, тем лучше ваше сердечно-сосудистое здоровье. «Положительный» не обязательно означает «хорошо»! Чем больше вы курите, тем выше вероятность рака, и чем больше вы водите машину, тем больше вероятность того, что вы попадете в автомобильную аварию.
В начало
3D точечная диаграмма
Трехмерный график рассеяния — это график рассеяния с тремя осями. Например, следующий трехмерный график разброса показывает оценки учащихся по трем предметам: чтение (ось y), письмо (ось x) и математика (ось z).
Учащийся A получил 100 баллов по письму и математике и 90 по чтению, а студент B получил 50 баллов по письму, 30 по чтению и 15 по математике. Для нескольких точек довольно легко построить трехмерные графики, но как только вы начнете разбираться в более крупных наборах данных, вам захочется использовать технологии. К сожалению, в Excel нет возможности создавать эти диаграммы. Статистические программы, обычно доступные в колледжах и университетах (например, SAS), могут их создавать. Доступно довольно много бесплатных вариантов, но я рекомендую:
Доступно довольно много бесплатных вариантов, но я рекомендую:
- Plotly — это простой способ создать трехмерную диаграмму онлайн.
- Gnuplot: загружаемая программа. Легко использовать по сравнению с другими программами.
- R: Также загружаемый. Имеет довольно крутую кривую обучения, но справляется с большинством статистических вычислений. Если вам нужен общий пакет stst (в отличие от того, который просто создает диаграммы), это лучший вариант.
В начало
Что такое пузырьковая диаграмма?
Что такое пузырьковая диаграмма?
Пузырьковый график, показывающий суммы Medicare по услуге / специальности. Изображение: CMS.губ.
Пузырьковая диаграмма — это способ показать, как переменные связаны друг с другом. Она похожа на точечную диаграмму, только вместо точек пузырьки разного размера.
Пузырьковые диаграммы — хороший выбор, если ваши данные имеют 3 серии / характеристики со связанным значением; Другими словами, вам нужно:
- категория со значениями для оси x,
- — категория со значениями для оси Y, а —
- категория со значениями размеров пузырей.

Они часто используются в финансовых целях и для использования с квадрантами декартовой плоскости.
Типы пузырьковой диаграммы
В самой основной форме большие пузыри указывают на большие значения. Размещение пузыря по осям x и y дает вам информацию о том, что представляет собой пузырек. На этой диаграмме показана длина инвестиций (ось X), цена на момент покупки (ось Y) и относительный размер инвестиций на сегодняшний день.
Цветные пузырьковые диаграммы используют цвет для сортировки пузырьков по категориям. Например, я могу отсортировать свою инвестиционную диаграмму по акциям, облигациям и паевым инвестиционным фондам:
Картограмма — это пузырьковая диаграмма карты, на которой по осям x и y отложены долгота и широта.Размер пузыря может указывать на численность населения, количество нефтяных вышек, природные погодные явления или другие географические данные.
Графики иногда называют размерами:
- Двумерные диаграммы имеют только значения x и y.
 Они эквивалентны диаграмме рассеяния.
Они эквивалентны диаграмме рассеяния. - Трехмерные диаграммы имеют оси x-y и размер пузырьков.
- Четырехмерные диаграммы имеют оси x-y, размер и цвет пузырьков.
В начало
Как построить диаграмму рассеяния: обзор
Простой график рассеяния.
Диаграмма рассеяния дает вам визуальное представление о том, что происходит с вашими данными. Точечные графики похожи на линейные графики. Единственное отличие состоит в том, что на линейном графике есть непрерывная линия, а на точечной диаграмме — ряд точек. Диаграммы разброса в статистике создают основу для простой линейной регрессии , где мы берем диаграммы разброса и пытаемся создать пригодную для использования модель с помощью функций.Фактически, регрессия пытается провести черту через все эти точки.
Вернуться к началу
Сделайте точечную диаграмму вручную
Чтобы вручную создать диаграмму рассеяния, нужно выполнить всего три шага.
Постройте точечную диаграмму: шаги
Пример вопроса: создать диаграмму рассеяния для следующих данных:
| x | y |
|---|---|
| 3 | 25 |
| 4,1 | 25 |
| 5 | 30 |
| 6 | 29 |
| 6.1 | 42 |
| 6,3 | 46 |
Шаг 1: Постройте график. Обозначьте оси x и y. Выберите диапазон, который включает максимумы и минимумы из заданных данных. Например, наши значения x изменяются от 3 до 6,3, поэтому диапазон от 3 до 7 будет подходящим.
Шаг 2: Нарисуйте первую точку на графике. Наша первая точка (3,25).
Шаг 3: . Нарисуйте оставшиеся точки на графике.
Вот и все!
В начало
Как построить диаграмму рассеяния в Excel
В этом разделе я расскажу, как создать диаграмму рассеяния в Excel, а также расскажу о некоторых дополнительных параметрах, таких как форматирование диаграммы, добавление меток и добавление линии тренда (уравнение линейной регрессии).
Посмотрите видео по шагам в Excel 365. Вы найдете более старую версию (2007–2013) ниже шагов:
Если вы не можете посмотреть видео, нажмите здесь.
Ступеньки
Шаг 1. Введите данные в два столбца (прокрутите вниз до второго примера, чтобы увидеть несколько снимков экрана).
Шаг 2: Нажмите «Вставить», затем нажмите «Разброс».
Шаг 3: Выберите тип участка. Например, щелкните первый значок (разброс только с маркерами).
Форматирование
Удалить легенду.
Шаг 1. Щелкните легенду правой кнопкой мыши и нажмите «Удалить».
Очистить белое пространство
Иногда ваши маркеры будут сгруппированы вверху или внизу справа на графике.Вот как избавиться от этого пробела, отформатировав горизонтальную и вертикальную оси.
Шаг 1. Щелкните вкладку «Макет», затем щелкните «Оси».
Шаг 2: Щелкните «Первичный горизонтальный», затем нажмите «Дополнительные основные горизонтальные параметры».
Шаг 3: Щелкните переключатель «Фиксированное значение» и затем введите значение, в котором должна начинаться горизонтальная ось. Нажмите «Закрыть».
Шаг 4: Повторите шаги с 1 по 3, выбрав «Вертикальный» вместо горизонтального.
Добавление меток диаграмм
Excel обычно добавляет ненужные метки или не учитывает нужные метки осей.Чтобы удалить ненужные ярлыки, вы можете щелкнуть и удалить. Вот как добавить ярлык:
Шаг 1. Перейдите на вкладку «Макет».
Шаг 2: Щелкните заголовки «Ось», а затем «Заголовок основной горизонтальной оси».
Шаг 3: Выберите позицию. например, вам может понадобиться заголовок под осью.
Шаг 4: Щелкните текст и введите новую этикетку.
Шаг 5: Повторите шаги с 1 по 4, выбрав «вертикальный» для вертикальной оси.
Совет . Если вам не нравится вертикальное расположение заголовка оси, щелкните правой кнопкой мыши и выберите «Формат заголовка оси.»Щелкните« Выравнивание », а затем выберите направление текста (т. Е. Горизонтальное).
Е. Горизонтальное).
Добавление линии тренда
Шаг 1: Щелкните вкладку «Макет».
Шаг 2. Щелкните «Линия тренда», а затем «Дополнительные параметры линии тренда».
Шаг 3. Щелкните «Показать уравнение в поле диаграммы», а затем нажмите «Закрыть».
Пример 2 : Создайте диаграмму разброса в Microsoft Excel, на которой будут нанесены следующие данные исследования зависимости между ростом и весом пациентов с преддиабетом:
Рост (дюймов): 72, 71,70,67,65,64 , 64,63,62,60
Вес (фунты): 180, 178,190,150,145,132,170,120,143,98
Шаг 1: Введите данные в электронную таблицу. Для правильной работы точечной диаграммы ваши данные должны быть введены в два столбца. В приведенном ниже примере показаны данные, введенные для роста (столбец A) и веса (столбец B).
Шаг 2: Выделите свои данные. Чтобы выделить данные, щелкните левой кнопкой мыши в верхнем левом углу данных и затем перетащите мышь в нижний правый угол.
Шаг 3: Нажмите кнопку «Вставить» на ленте , затем нажмите «Разброс», затем нажмите «Разброс только с маркерами». Microsoft Excel создаст диаграмму рассеяния из ваших данных и отобразит диаграмму рядом с вашими данными в электронной таблице.
Совет: Если вы хотите изменить данные (и, следовательно, ваш график), нет необходимости повторять всю процедуру. Когда вы вводите новые данные в любой из столбцов, Microsoft Excel автоматически вычисляет изменение и мгновенно отображает новый график.
В начало
Инструкции MATLAB
Используйте команду SCATTER (X, Y, S, C).
- Векторы X и Y должны быть одного размера.
- S — площадь каждого пузыря (в точках в квадрате).S может быть вектором или скаляром. Если скалярный, все маркеры будут одного размера.
- C — цвет производителя.
Точечная диаграмма в Minitab
Посмотрите видео о том, как создать диаграмму рассеяния в Minitab:
Не можете посмотреть видео? Кликните сюда.
Изображение: Penn State
Шаг 1: Введите данные в два столбца . Один столбец должен быть переменной x (независимая переменная), а второй столбец должен быть переменной y (зависимой переменной).Убедитесь, что вы поместили заголовок для ваших данных в первую строку каждого столбца — это упростит создание диаграммы рассеяния на шагах 4 и 5.
Шаг 2: Щелкните «График» на панели инструментов, а затем щелкните «График рассеяния».
Шаг 3: Щелкните «Простой» график рассеяния. В большинстве случаев это вариант, который вы будете использовать для диаграмм рассеяния в элементарной статистике. Вы можете выбрать один из других (например, диаграмму рассеяния с линиями), но вам редко понадобится их использовать.
Шаг 4: Щелкните имя вашей переменной y в левом окне, затем щелкните «Выбрать», чтобы переместить эту переменную y в поле переменной y.
Шаг 5: Щелкните имя своей переменной x в левом окне, затем щелкните «Выбрать», чтобы переместить эту переменную x в поле переменной x.
Шаг 6: Нажмите «ОК», чтобы создать диаграмму рассеяния в Minitab. График появится в отдельном окне.
Совет: Если вы хотите изменить отметки (интервал для оси x или оси y), дважды щелкните одно из чисел, чтобы открыть окно редактирования масштаба, где вы можете изменить различные параметры для вашего диаграмма рассеяния, включая отметки.
В начало
Как создать диаграмму рассеяния SPSS
В IBM SPSS Statistics есть несколько различных вариантов диаграмм рассеяния: Простое разбросание, Матричное разбросание, Простая точка, Наложение разброса и 3D-разброс. Какой тип диаграммы рассеяния вы выберете, в основном зависит от того, сколько переменных вы хотите построить:
- Простая диаграмма рассеяния отображает одну переменную относительно другой.
- Матричный точечный график отображает все возможные комбинации двух или более числовых переменных относительно друг друга
- Простой точечный график отображает одну категориальную переменную или одну непрерывную переменную.

- Наложенная диаграмма рассеяния отображает две или более пары переменных.
- 3D-диаграммы рассеяния — это трехмерные графики трех числовых переменных.
Посмотрите видео, чтобы узнать, как построить диаграмму рассеяния SPSS с помощью построителя диаграмм:
Не можете посмотреть видео? Кликните сюда.
Как создать диаграмму рассеяния SPSS с помощью диалогового меню Legacy
Шаг 1: Щелкните «Графики», , затем наведите указатель мыши на «Устаревшие диалоги», затем щелкните «Точечная диаграмма / точка».
Шаг 2: Выберите тип точечной диаграммы. В этом примере щелкните «Простой разброс».
Шаг 3: Нажмите кнопку «Определить» , чтобы открыть окно «Простая диаграмма рассеяния».
Шаг 4: Щелкните переменную, которую вы хотите отобразить на оси Y , а затем щелкните стрелку слева от поля выбора «Ось Y».
Шаг 4: Щелкните переменную, которую вы хотите отобразить на оси X , а затем щелкните стрелку слева от поля выбора «Ось X». Нажмите «ОК», чтобы построить диаграмму рассеяния.
Нажмите «ОК», чтобы построить диаграмму рассеяния.
Вот и все!
Совет: Вам не нужно выбирать метки значений по, но если вы это делаете, метки значений используются как метки точек для диаграммы рассеяния. Если вы не выберете переменную для маркировки наблюдений, выбросы и экстремумы могут быть помечены номерами наблюдений.
В начало
Точечная диаграмма на TI-89: обзор
Создание диаграммы рассеяния на TI-89 включает три этапа: доступ к редактору матрицы данных, ввод значений X и Y и последующее построение графика данных.
ТИ-89
Точечная диаграмма на TI-89: Шаги:
Пример задачи: построить диаграмму рассеяния для следующих данных: (1,6), (2,8), (3,9), (4,11) и (5,14).
Доступ к редактору матрицы данных
Шаг 1. Нажмите ПРИЛОЖЕНИЯ, затем перейдите к редактору «Данные / матрица», нажмите ENTER и затем выберите «новый».
Шаг 2: Прокрутите вниз до «Переменная» и введите желаемое имя. Например, введите «scatterone». Примечание: вам не нужно нажимать клавишу АЛЬФА для доступа к альфа-клавиатуре.Просто введите!
Например, введите «scatterone». Примечание: вам не нужно нажимать клавишу АЛЬФА для доступа к альфа-клавиатуре.Просто введите!
Шаг 3: Нажмите ENTER ENTER.
Ввод значений X и Y
Шаг 1: Введите значения X в столбец «c1». Нажимайте ENTER после каждой записи.
Для нашего списка вам нужно будет нажать:
1 ENTER
2 ENTER
3 ENTER
4 ENTER
5 ENTER
Шаг 2: Введите значения Y под столбцом «c2» (используйте клавиши со стрелками для прокрутки к верхнему краю столбца). Нажимайте ENTER после каждой записи.
Для нашего списка вам нужно будет нажать:
6 ENTER
8 ENTER
9 ENTER
11 ENTER
14 ENTER
Графическое изображение данных
Шаг 1: Нажмите F2 для настройки графика.
Шаг 2: Нажмите F1.
Шаг 3: Выберите «разброс» рядом с «типом графика»
Шаг 4. Установите флажок рядом с «типом метки»
Шаг 5: Прокрутите до поля «x» и нажмите АЛЬФА) 1, чтобы ввести «c1».
Шаг 6: Прокрутите до поля «y» и нажмите ALPHA) 2, чтобы ввести «c2».
Шаг 7: Нажмите ENTER ENTER.
Шаг 8: Нажмите ромбовидную клавишу F3, чтобы просмотреть диаграмму рассеяния.
Шаг 9: Нажмите F2, а затем 9, чтобы график рассеяния отображался в правильном окне для данных.
Вот и все!
Посетите наш канал YouTube, чтобы получить больше советов и помощи!
В начало
TI 83 Точечная диаграмма
Посмотрите видео с шагами:
Не можете посмотреть видео? Кликните сюда.
TI 83 Точечная диаграмма: обзор
Создание точечной диаграммы на графическом калькуляторе TI-83 — легкий ветерок с простым в использовании меню LIST. Чтобы построить график рассеяния TI 83 , вам понадобится набор двумерных данных. Двумерные данные — это данные, которые можно отобразить на оси XY: вам понадобится список значений «x» (например, вес) и список значений «y» (например, рост). Значения XY могут быть в двух отдельных списках или они могут быть записаны как координаты XY (x, y). Как только они у вас появятся, это так же просто, как ввести списки в калькулятор и выбрать график.
Как только они у вас появятся, это так же просто, как ввести списки в калькулятор и выбрать график.
TI 83 Точечная диаграмма: шаги
Пример задачи: Создайте диаграмму рассеяния TI 83 для следующих координат (2, 3), (4, 4), (6, 9), (8, 11) и (10, 12).
Шаг 1: Нажмите STAT, затем нажмите ENTER, чтобы открыть экран списков. Если у вас уже есть данные в L1 или L2, очистите данные: переместите курсор на L1, нажмите CLEAR, а затем ENTER. Повторите для L2.
Шаг 2: Введите переменные x по очереди. Следуйте за каждым числом, нажимая клавишу ENTER. Для нашего списка вы должны ввести:
2 ENTER
4 ENTER
6 ENTER
8 ENTER
10 ENTER
Шаг 3: Используйте клавиши со стрелками для перехода к следующему столбцу L2.
Шаг 4: Введите переменные y по очереди. Следуйте за каждым числом, нажимая клавишу ввода. Для нашего списка вы должны ввести:
3 ENTER
4 ENTER
9 ENTER
11 ENTER
12 ENTER
Шаг 5: Нажмите 2nd, затем нажмите STATPLOT (клавиша Y =).
Шаг 6: Нажмите ENTER, чтобы войти в StatPlots для Plot1.
Шаг 7: Нажмите ENTER, чтобы включить Plot1.
Шаг 8: Перейдите к следующей строке («Тип») и выделите диаграмму рассеяния (первое изображение).Нажмите Ввод.
Шаг 9: Стрелка вниз до «Xlist». Если «L1» не отображается, нажмите 2-ю и 1. Стрелку вниз до «Ylist». Если «L2» не отображается, нажмите 2-й и 2-й.
Шаг 10: Нажмите ZOOM, затем 9. На экране должна появиться диаграмма рассеяния.
Совет : Нажмите TRACE и нажимайте кнопки со стрелками вправо и влево, чтобы перемещаться от точки к точке, отображая значения XY для этих точек.
Вот как построить точечную диаграмму TI 83!
Потеряли путеводитель? Загрузите новый здесь с веб-сайта TI.
Посетите наш канал Youtube, чтобы получить дополнительную статистику, помощь и советы!
Список литературы
Бейер, У. Х. Стандартные математические таблицы CRC, 31-е изд. Бока Ратон, Флорида: CRC Press, стр. 536 и 571, 2002.
Х. Стандартные математические таблицы CRC, 31-е изд. Бока Ратон, Флорида: CRC Press, стр. 536 и 571, 2002.
Агрести А. (1990) Анализ категориальных данных. Джон Вили и сыновья, Нью-Йорк.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Регрессионный анализ — формулы, объяснения, примеры и определения
Что такое регрессионный анализ?
Регрессионный анализ — это набор статистических методов, используемых для оценки взаимосвязей между зависимой переменной и одной или несколькими независимыми переменными Независимая переменная Независимая переменная — это входные данные, предположения или драйверы, которые изменяются для оценки их влияния на зависимую переменную. (результат).. Его можно использовать для оценки силы взаимосвязи между переменными и для моделирования будущей взаимосвязи между ними.
(результат).. Его можно использовать для оценки силы взаимосвязи между переменными и для моделирования будущей взаимосвязи между ними.
Регрессионный анализ включает несколько вариантов, таких как линейный, множественный линейный и нелинейный. Наиболее распространены простые линейные и множественные линейные модели. Нелинейный регрессионный анализ обычно используется для более сложных наборов данных, в которых зависимые и независимые переменные показывают нелинейную взаимосвязь.
Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.
Регрессионный анализ — предположения линейной модели
Линейный регрессионный анализ основан на шести фундаментальных предположениях:
- Зависимые и независимые переменные показывают линейную зависимость между наклоном и точкой пересечения.
- Независимая переменная не случайна.
- Значение невязки (ошибки) равно нулю.
- Значение невязки (ошибки) постоянно для всех наблюдений.

- Значение невязки (ошибки) не коррелировано по всем наблюдениям.
- Остаточные (ошибочные) значения подчиняются нормальному распределению.
Регрессионный анализ — Простая линейная регрессия
Простая линейная регрессия — это модель, которая оценивает взаимосвязь между зависимой переменной и независимой переменной. Простая линейная модель выражается с помощью следующего уравнения:
Y = a + bX + ϵ
Где:
- Y — Зависимая переменная
- X — Независимая (объясняющая) переменная
- a — Пересечение
- b — Наклон
- ϵ — Остаточный (ошибка)
Регрессионный анализ — Множественная линейная регрессия
Множественный линейный регрессионный анализ по существу аналогичен простой линейной модели, за исключением того, что в модели используются несколько независимых переменных.Математическое представление множественной линейной регрессии:
Y = a + b
X 1 + c X 2 + d X 3 + ϵ
Где:
- Y — Зависимая переменная
- X 1 , X 2 , X 3 — Независимые (объясняющие) переменные
- a — Пересечение
- b, c, d — Наклоны
- ϵ — Невязка (ошибка)
Множественная линейная регрессия подчиняется тем же условиям, что и простая линейная модель. Однако, поскольку в множественном линейном анализе есть несколько независимых переменных, существует еще одно обязательное условие для модели:
Однако, поскольку в множественном линейном анализе есть несколько независимых переменных, существует еще одно обязательное условие для модели:
- Неколлинеарность: Независимые переменные должны показывать минимальную корреляцию друг с другом. Если независимые переменные сильно коррелированы друг с другом, будет трудно оценить истинные отношения между зависимыми и независимыми переменными.
Регрессионный анализ в финансах
Регрессионный анализ имеет несколько приложений в финансах.Например, статистический метод является фундаментальным для модели ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM) — это модель, которая описывает взаимосвязь между ожидаемой доходностью и риском ценной бумаги. Формула CAPM показывает, что доходность ценной бумаги равна безрисковой доходности плюс премия за риск на основе бета-версии этой ценной бумаги. По сути, уравнение CAPM — это модель, которая определяет взаимосвязь между ожидаемой доходностью актива и премией за рыночный риск.
Анализ также используется для прогнозирования доходности ценных бумаг на основе различных факторов или для прогнозирования эффективности бизнеса. Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!
1. Бета и CAPM
В финансах для расчета бета-бета используется регрессионный анализ. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой ее волатильности доходности относительно всего рынка. Он используется в качестве меры риска и является неотъемлемой частью модели ценообразования капитальных активов (CAPM).Компания с более высокой бета-версией имеет больший риск, а также большую ожидаемую прибыль. (волатильность доходности по отношению к рынку в целом) для акции. Это можно сделать в Excel с помощью функции наклона Функция наклона Функция наклона относится к категории статистических функций Excel. Он вернет наклон линии линейной регрессии через точки данных в известных_y и известных_x. В финансовом анализе SLOPE может быть полезен при расчете бета-версии акции. Формула = LOPE (известные_y, известные_x) Функция использует расширение.
Формула = LOPE (известные_y, известные_x) Функция использует расширение.
Скачать бесплатный бета-калькулятор CFI Калькулятор бета-версии Этот бета-калькулятор позволяет измерить волатильность доходности отдельной акции относительно всего рынка. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой ее волатильности доходности относительно всего рынка. Он используется как мера риска и является неотъемлемой частью Cap!
2. Прогнозирование доходов и расходов
При прогнозировании финансовой отчетности Финансовое прогнозирование Финансовое прогнозирование — это процесс оценки или прогнозирования того, как бизнес будет работать в будущем.В этом руководстве о том, как построить финансовый прогноз для компании, может быть полезно провести множественный регрессионный анализ, чтобы определить, как изменения в определенных допущениях или драйверах бизнеса повлияют на доходы или расходы в будущем. Например, может быть очень высокая корреляция между количеством продавцов, нанятых компанией, количеством магазинов, которыми они управляют, и доходом, который приносит бизнес.
В приведенном выше примере показано, как использовать функцию прогноза Функция прогнозирования Функция прогнозирования относится к категории статистических функций Excel.Он рассчитает или спрогнозирует для нас будущую стоимость с использованием существующих значений. В финансовом моделировании функция прогноза может быть полезна при вычислении статистической ценности сделанного прогноза. Например, если мы знаем прошлые доходы и в Excel, чтобы рассчитать доход компании на основе количества показанных объявлений.
Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!
Инструменты регрессии
Excel остается популярным инструментом для проведения базового регрессионного анализа в финансах, однако есть еще много более сложных статистических инструментов, которые можно использовать.
Python и R — мощные языки программирования, ставшие популярными для всех типов финансового моделирования, включая регрессию. Эти методы составляют основную часть науки о данных и машинного обучения, где модели обучаются обнаруживать эти отношения в данных.
Узнайте больше о регрессионном анализе, Python и машинном обучении в сертификации CFI Business Intelligence & Data Analysis.
Дополнительные ресурсы
CFI предлагает аналитика по финансовому моделированию и оценке (FMVA) ® Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по финансовому моделированию и оценке (FMVA) ® поможет вам обрести уверенность в себе. необходимость в вашей финансовой карьере.Запишитесь сегодня! программа сертификации для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы узнать больше о связанных темах, ознакомьтесь со следующими бесплатными ресурсами CFI:
- Анализ поведения затрат 10 самых важных навыков финансового моделирования и то, что требуется для хорошего финансового моделирования в Excel.Важнейшие навыки: бухгалтерский учет
- Методы прогнозированияМетоды прогнозированияЛучшие методы прогнозирования. В этой статье мы объясним четыре типа методов прогнозирования доходов, которые финансовые аналитики используют для прогнозирования будущих доходов.

- Метод High-Low Метод High-Low В учете затрат метод high-low — это метод, используемый для разделения смешанных затрат на переменные и постоянные. Хотя метод высокого-низкого
Что такое линейная регрессия? | Примеры линейной регрессии
Линейная регрессия количественно определяет взаимосвязь между одной или несколькими прогностическими переменными и одной выходной переменной . Линейная регрессия обычно используется для прогнозного анализа и моделирования. Например, его можно использовать для количественной оценки относительного влияния возраста, пола и диеты (переменные-предикторы) на рост (переменная результата). Линейная регрессия также известна как множественная регрессия , многомерная регрессия , обычная регрессия наименьших квадратов (МНК) и регрессия . В этом посте будут показаны примеры линейной регрессии, включая пример простой линейной регрессии и пример множественной линейной регрессии .
Попробуйте свою собственную линейную регрессию!
Пример простой линейной регрессии
В таблице ниже приведены некоторые данные с первых дней существования итальянской швейной компании Benetton. Каждая строка в таблице показывает продажи Benetton за год и сумму, потраченную на рекламу в этом году. В этом случае интересующий нас результат — это продажи — это то, что мы хотим спрогнозировать. Если мы используем рекламу в качестве переменной-предиктора, линейная регрессия оценивает, что Продажи = 168 + 23 Рекламы .То есть, если расходы на рекламу увеличатся на один миллион евро, то ожидается, что продажи вырастут на 23 миллиона евро, а если бы не было рекламы, мы бы ожидали, что объем продаж составит 168 миллионов евро.
Пример множественной линейной регрессии
Линейная регрессия с одной переменной-предиктором известна как простая регрессия . В реальных приложениях обычно используется более одной переменной-предиктора. Такие регрессии называются множественной регрессией . Для получения дополнительной информации ознакомьтесь с этим сообщением о том, почему вам не следует использовать множественную линейную регрессию для анализа ключевых драйверов с примерами данных для примеров множественной линейной регрессии.
Такие регрессии называются множественной регрессией . Для получения дополнительной информации ознакомьтесь с этим сообщением о том, почему вам не следует использовать множественную линейную регрессию для анализа ключевых драйверов с примерами данных для примеров множественной линейной регрессии.
Возвращаясь к примеру Benetton, мы можем включить год переменную в регрессию, что дает результат продаж = 323 + 14 рекламы + 47 лет. Интерпретация этого уравнения заключается в том, что каждый дополнительный миллион евро расходов на рекламу приведет к дополнительным 14 миллионам евро продаж, и что продажи будут расти из-за факторов, не связанных с рекламой, на 47 миллионов евро в год.
Попробуйте свою собственную линейную регрессию!
Проверка качества регрессионных моделей
Оценка регрессии — вещь относительно простая. Сложность использования регрессии — избегать использования неправильной регрессии. Ниже приведены стандартные регрессионные диагностики для более ранней регрессии.
Ниже приведены стандартные регрессионные диагностики для более ранней регрессии.
В столбце Оценка показаны значения, использованные в уравнениях ранее. Эти оценки также известны как коэффициенты , параметры и . Столбец Standard Error дает количественную оценку неопределенности оценок. Стандартная ошибка для рекламы относительно мала по сравнению с оценкой, которая говорит нам о том, что оценка является довольно точной, на что также указывает высокое значение t (, что составляет оценка / стандартное ) и небольшое p — значение. Кроме того, статистика R-Squared 0,98 очень высока, что позволяет предположить, что это хорошая модель.
Ключевым предположением линейной регрессии является то, что в анализ включены все соответствующие переменные. Мы можем увидеть важность этого предположения, посмотрев, что происходит, когда включается год . Мало того, что реклама стала намного менее важной (с пониженным коэффициентом с 23 до 14), но и увеличилась стандартная ошибка. Коэффициент больше не является статистически значимым (то есть значение p- 0,22 выше стандартного порогового значения.05). Это означает, что, хотя оценка эффекта от рекламы составляет 14, мы не можем быть уверены, что истинный эффект не равен нулю.
Мало того, что реклама стала намного менее важной (с пониженным коэффициентом с 23 до 14), но и увеличилась стандартная ошибка. Коэффициент больше не является статистически значимым (то есть значение p- 0,22 выше стандартного порогового значения.05). Это означает, что, хотя оценка эффекта от рекламы составляет 14, мы не можем быть уверены, что истинный эффект не равен нулю.
В дополнение к просмотру статистики, показанной в таблице выше, существует ряд дополнительных технических диагностических средств, которые необходимо изучить при проверке регрессионных моделей, включая проверку выбросов , факторов инфляции дисперсии , гетероскедастичности , автокорреляции , а иногда и нормальность остатков.Эта диагностика также выявляет чрезвычайно высокий коэффициент инфляции отклонения (VIF) , равный 55 для каждого из Рекламы и Года. Поскольку эти две переменные сильно коррелированы, невозможно разделить их относительные эффекты, т. Е. Они смешаны.
Е. Они смешаны.
Терминология
Переменные-предикторы
также известны как ковариаты , , независимые переменные , , регрессоры , , факторы , и особенности , среди прочего.Выходная переменная также известна как зависимая переменная и переменная ответа .
Попробуйте свою собственную линейную регрессию!
Мы надеемся, что этот пост дал вам ответ «Что такое линейная регрессия»! Узнайте больше о терминологии науки о данных в нашей серии статей «Что такое» или бесплатно исследуйте собственную линейную регрессию.
2.9 — Примеры простой линейной регрессии
Пример 1: Данные о рождаемости среди подростков и уровне бедности
Этот набор данных размером n = 51 относится к 50 штатам и округу Колумбия в США (бедность.txt). Переменные: y = коэффициент рождаемости в 2002 году на 1000 женщин в возрасте от 15 до 17 лет и x = уровень бедности, который представляет собой процент населения штата, проживающего в домохозяйствах с доходами ниже установленного федеральным уровнем бедности. (Источник данных: Mind On Statistics , 3-е издание, Utts and Heckard).
(Источник данных: Mind On Statistics , 3-е издание, Utts and Heckard).
График данных ниже (коэффициент рождаемости по вертикали) показывает в целом линейную зависимость, в среднем, с положительным наклоном. По мере увеличения уровня бедности рождаемость женщин в возрасте от 15 до 17 лет также имеет тенденцию к увеличению.
На следующем графике показана линия регрессии, наложенная на данные.
Уравнение подобранной линии регрессии приведено в верхней части графика.Уравнение действительно должно указывать, что оно предназначено для «средней» рождаемости (или «предсказанная» рождаемость тоже подойдет), потому что уравнение регрессии описывает среднее значение y как функцию одной или нескольких x-переменных. В статистической записи уравнение можно записать в виде \ (\ hat {y} = 4,267 + 1,373x \).
- Интерпретация наклона (значение = 1,373) состоит в том, что коэффициент рождаемости в возрасте от 15 до 17 лет увеличивается в среднем на 1,373 единицы на каждую единицу (один процент) увеличения уровня бедности.

- Интерпретация точки пересечения (значение = 4,267) состоит в том, что если бы существовали штаты с уровнем бедности = 0, прогнозируемое среднее значение рождаемости в возрасте от 15 до 17 лет было бы 4,267 для этих штатов. Поскольку нет штатов с уровнем бедности = 0, такая интерпретация точки пересечения не имеет практического смысла для этого примера.
На графике с линией регрессии мы также видим информацию о том, что s = 5,55057 и r 2 = 53.3%.
- Значение s примерно говорит нам о стандартном отклонении разницы между значениями y отдельных наблюдений и прогнозами y на основе линии регрессии.
- Значение r 2 может быть истолковано как означающее, что уровень бедности «объясняет» 53,3% наблюдаемой вариации средней рождаемости в штатах в возрасте от 15 до 17 лет.
Значение R 2 (прил.) (52,4%) представляет собой корректировку к R 2 в зависимости от количества x-переменных в модели (здесь только одна) и размера выборки. При наличии только одной переменной x скорректированное значение R 2 не имеет значения.
При наличии только одной переменной x скорректированное значение R 2 не имеет значения.
Пример 2: Функция легких у детей в возрасте от 6 до 10 лет
Данные взяты из n = 345 детей в возрасте от 6 до 10 лет. Переменные: y = объем форсированного выдоха (FEV), мера того, сколько воздуха кто-то может принудительно выдохнуть из легких, и x = возраст в годах. (Источник данных: данные здесь являются частью набора данных, приведенного в Kahn, Michael (2005). «Большая проблема для преподавания статистики», The Journal of Statistical Education , 13 (2).
Ниже представлен график данных с наложенной простой линией линейной регрессии.
- Расчетное уравнение регрессии: средний ОФВ = 0,01165 + 0,26721 × возраст. Например, для 8-летнего ребенка мы можем использовать уравнение, чтобы оценить, что средний ОФВ = 0,01165 + 0,26721 × (8) = 2,15.
- Интерпретация наклона состоит в том, что средний ОФВ увеличивается на 0,26721 за каждый год увеличения возраста (в наблюдаемом возрастном диапазоне).

Интересной и, возможно, важной особенностью этих данных является то, что отклонение индивидуальных значений y от линии регрессии увеличивается с возрастом.Эта особенность данных называется непостоянной дисперсией . Например, значения ОФВ у 10-летних более изменчивы, чем значения ОФВ у 6-летних. Это видно по вертикальным диапазонам данных на графике. Это может привести к проблемам с использованием простой модели линейной регрессии для этих данных, и это проблема, которую мы рассмотрим более подробно в Уроке 4.
Выше мы проанализировали только часть всего набора данных. Полный набор данных (fev_dat.txt) показан на графике ниже:
Как мы видим, диапазон возрастов теперь составляет от 3 до 19 лет, и расчетное уравнение регрессии составляет FEV = 0.43165 + 0,22204 × возраст. И наклон, и точка пересечения заметно изменились, но дисперсия все еще остается непостоянной. Это показывает, что важно знать, как вы анализируете свои данные. Если вы используете только подмножество данных, охватывающее более короткий диапазон значений предикторов, то вы можете получить результаты, заметно отличающиеся от результатов, если бы вы использовали полный набор данных.
.
Линейная регрессия на Python: объясняем на пальцах
Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!
Регрессия ищет отношения между переменными.
Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.
Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.
Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.
Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.
Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.
Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.
Зависимые данные называются зависимыми переменными, выходами или ответами.
Независимые данные называются независимыми переменными, входами или предсказателями.
Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.
Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.
Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.
Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.
Где она вообще нужна?
Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.
Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.
Постановка проблемы
Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.
Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.
Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.
Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.
Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.
Простая линейная регрессия
Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.
А вот и она:
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.
Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.
Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).
Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.
Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.
Пакеты Python для линейной регрессии
NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.
Незнакомы с NumPy? Начните с официального гайда.
Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.
Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.
Простая линейная регрессия со scikit-learn
Начнём с простейшего случая линейной регрессии.
Следуйте пяти шагам реализации линейной регрессии:
- Импортируйте необходимые пакеты и классы.
- Предоставьте данные для работы и преобразования.
- Создайте модель регрессии и приспособьте к существующим данным.
- Проверьте результаты совмещения и удовлетворительность модели.
- Примените модель для прогнозов.
Это общие шаги для большинства подходов и реализаций регрессии.
Шаг 1: Импортируйте пакеты и классы
Первым шагом импортируем пакет NumPy и класс LinearRegressionиз sklearn.linear_model:
import numpy as np from sklearn.linear_model import LinearRegression
Теперь у вас есть весь функционал для реализации линейной регрессии.
Фундаментальный тип данных NumPy – это тип массива numpy.. Далее под массивом подразумеваются все экземпляры типа  ndarray
ndarraynumpy.ndarray.
Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.
Шаг 2 : Предоставьте данные
Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray) или похожими объектами. Вот простейший способ предоставления данных регрессии:
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([5, 20, 14, 32, 22, 38])
Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape()на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).
Вот как x и y выглядят теперь:
>>> print(x) [[ 5] [15] [25] [35] [45] [55]] >>> print(y) [ 5 20 14 32 22 38]
Шаг 3: Создайте модель
На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.
Давайте сделаем экземпляр класса LinearRegression, который представит модель регрессии:
model = LinearRegression()
Эта операция создаёт переменную model в качестве экземпляра LinearRegression. Вы можете предоставить несколько опциональных параметров классу LinearRegression:
- fit_intercept – логический (
Trueпо умолчанию) параметр, который решает, вычислять отрезок b₀ (True) или рассматривать его как равный нулю (False). - normalize – логический (
Falseпо умолчанию) параметр, который решает, нормализовать входные переменные (True) или нет (False). - copy_X – логический (
Trueпо умолчанию) параметр, который решает, копировать (True) или перезаписывать входные переменные (False). - n_jobs – целое или
None(по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях.
Noneозначает отсутствие процессов, при -1 используются все доступные процессоры.
Наш пример использует состояния параметров по умолчанию.
Пришло время задействовать model. Сначала вызовите .fit() на model:
model.fit(x, y)
С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model. Поэтому можно заменить две последние операции на:
model = LinearRegression().fit(x, y)
Эта операция короче и делает то же, что и две предыдущие.
Шаг 4: Получите результаты
После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.
Вы можете получить определения (R²) с помощью .score(), вызванной на model:
>>> r_sq = model.score(x, y) >>> print('coefficient of determination:', r_sq) coefficient of determination: 0.715875613747954
.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².
model содержит атрибуты .intercept_, который представляет собой коэффициент, и b₀ с .coef_, которые представляют b₁:
>>> print('intercept:', model.intercept_)
intercept: 5.633333333333329
>>> print('slope:', model.coef_)
slope: [0.54]Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.
Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.
Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:
Тогда результаты не будут отличаться:
>>> new_model = LinearRegression().fit(x, y.reshape((-1, 1)))
>>> print('intercept:', new_model.intercept_)
intercept: [5.63333333]
>>> print('slope:', new_model.coef_)
slope: [[0.54]]Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.
Шаг 5: Предскажите ответ
Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.
Получите предсказанный ответ, используя .predict():
>>> y_pred = model.predict(x)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333]Применяя .predict(), вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.
Вот почти идентичный способ предсказать ответ:
>>> y_pred = model.intercept_ + model.coef_ * x
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[[ 8.33333333]
[13.73333333]
[19.13333333]
[24.53333333]
[29.93333333]
[35.33333333]]В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.
Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.
Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1), x.flatten() или x.ravel() при умножении с помощью model.coef_.
На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:
Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:
>>> x_new = np.arange(5).reshape((-1, 1)) >>> print(x_new) [[0] [1] [2] [3] [4]] >>> y_new = model.predict(x_new) >>> print(y_new) [5.63333333 6.17333333 6.71333333 7.25333333 7.79333333]
Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new. Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.
О LinearRegression вы узнаете больше из официальной документации.
Теперь у вас есть своя модель линейной регрессии!
Источник
Нравится Data Science? Другие материалы по теме:
- 6 советов, которые спасут специалиста Data Science
- Как изучать Data Science в 2019: ответы на частые вопросы
- Схема успешного развития data-scientist специалиста в 2019 году
Регрессионный анализ—ArcGIS Insights | Документация
Регрессионный анализ статистический аналитический метод, позволяющий вычислить предполагаемые отношения между зависимой переменной одной или несколькими независимыми переменными. Используя регрессионный анализ, вы можете моделировать отношения между выбранным переменными, а также прогнозируемыми значениями на основе модели.
Используя регрессионный анализ, вы можете моделировать отношения между выбранным переменными, а также прогнозируемыми значениями на основе модели.
Обзор регрессионного анализа
Регрессионный анализ использует выбранный метод оценки, зависимую переменную и одну или несколько независимых переменных для создания уравнения, которое оценивает значения зависимой переменной.
Модель регрессии включает выходные данные, например R2 и p-значения, по которым можно понять, насколько хорошо модель оценивает зависимую переменную.
Диаграммы, например матрица точечной диаграммы, гистограмма и точечная диаграмма, также используются в регрессионном анализе для анализа отношений и проверки допущений.
Регрессионный анализ используется для решения следующих типов проблем:
- Выявить, какая независимая переменная связана с зависимой.
- Понять отношения между зависимой и независимыми переменными.
- Предсказать неизвестные значения зависимой переменной.

Примеры
Аналитик в рамках исследования для небольшой розничной сети изучает эффективность работы различных магазинов. Он хочет выяснить, почему некоторые магазины показывают очень небольшой объем продаж. Аналитик строит модель регрессии с независимыми переменными, такими как средний возраст и средний доход жителей, проживающих вокруг магазинов, а так же расстояние до торговых центров и остановок общественного транспорта, чтобы выявить, какая именно переменная наиболее влияет на продажи.
Аналитик департамента образования исследует эффективность новой программы питания в школе. Аналитик строит модель регрессии для показателей успеваемости, используя такие независимые переменные, как размер класса, доход семьи, размер подушевого финансирования учащихся и долю учащихся, питающихся в школе. Уравнение модели используется для выявления относительного вклада каждой переменной в показатели успеваемости учебного заведения.
Аналитик неправительственной организации изучает эффект глобальных выбросов парниковых газов. Аналитик строит модель регрессии для выбросов в последнее время, зафиксированных в каждой стране, используя независимые переменные, такие как валовой внутренний продукт( ВВП), численность населения, производство электроэнергии с использованием добываемого углеводородного топлива и использование транспортных средств. Эту модель можно использовать использована для прогнозирования будущих выбросов парниковых газов на основе предполагаемых значений значений ВВП и численности населения.
Аналитик строит модель регрессии для выбросов в последнее время, зафиксированных в каждой стране, используя независимые переменные, такие как валовой внутренний продукт( ВВП), численность населения, производство электроэнергии с использованием добываемого углеводородного топлива и использование транспортных средств. Эту модель можно использовать использована для прогнозирования будущих выбросов парниковых газов на основе предполагаемых значений значений ВВП и численности населения.
Наименьшие квадраты
Регрессионный анализ в ArcGIS Insights моделируется на основе Метода наименьших квадратов (МНК).
МНК – форма множественной линейной регрессии, допускающей, что отношения между зависимыми и независимыми переменными должны моделироваться подгонкой линейного уравнения к данным наблюдений.
МНК использует следующее уравнение:
yi=β0+β1x1+β2x2+...+βnxn+ε
, где:
- yi=наблюдаемое=наблюдаемое значение независимой переменной в точке i
- β0=y-интерсепт (отрезок на координатной оси, постоянное значение)
- βn=коэффициент регрессии или уклона независимой переменной N в точке i
- xn=значение переменной N в точке i
- ε=ошибка уравнения регрессии
Допущения (Предположения)
Каждый метод регрессии имеет несколько допущений, которые должны быть выполнены для того, чтобы уравнение считалось надежным. Допущения МНК должны быть проверены при создании модели регрессии.
Допущения МНК должны быть проверены при создании модели регрессии.
Следующие допущения должны быть проверены и удовлетворены при использовании метода МНК:
- Модель должна быть линейной.
- Данные должны быть распределены произвольно.
- Независимые переменные не должны быть коллинеарны.
- Независимые переменные должны иметь незначительную погрешность измерения.
- Предполагаемая сумма невязок должна быть равна нулю.
- Невязки должны иметь равномерную вариабельность.
- Распределение невязок должно соответствовать нормальному.
- Смежные невязки не должны обнаруживать автокорреляцию.
Модель должна быть линейной.
Регрессия МНК используется только при построении линейной модели. Линейную зависимость между зависимой и независимыми переменными можно проверить используя точечную диаграмму (рассеивания). Матрица точечной диаграммы может проверить все переменные, при условии, что всего используется не более 5 переменных.
Данные должны быть распределены произвольно.
Данные, используемые в регрессионном анализе, должны быть произвольно распределены, то есть выборки данных не должны зависеть от какого-либо внешнего фактора. Произвольное распределение можно проверить, используя невязки в модели регрессии. Невязки, рассчитываемые как результат модели регрессии, не должны коррелировать при нанесении их на точечную диаграмму или матрицу точечной диаграммы вместе с независимыми переменными.
Независимые переменные не должны быть коллинеарны.
Коллинеарность — это линейная связь между независимыми переменными, которая создает избыточность в модели. В ряде случаев модель создается с коллинеарностью. Тем не менее, если одна из коллинеарных переменных зависит от другой, возможно, стоит удалить ее из модели. Оценить коллинеарность можно с помощью точечной диаграммы или матрицы точечной диаграммы независимых переменных.
Независимые переменные должны иметь незначительную погрешность измерения.

Точность модели регрессии соответствует точности входных данных. Если независимые переменные имеют большой разброс ошибок, модель нельзя считать точной. При выполнении регрессионного анализа очень важно использовать наборы данных только из известных и доверенных источников, чтобы быть уверенным в незначительности ошибок.
Предполагаемая сумма невязок должна быть равна нулю.
Невязки представляют собой разность между ожидаемыми и наблюдаемыми значениями в регрессионном анализе. Наблюдаемые значения выше кривой регрессии имеют положительное значение невязки, а значения ниже кривой регрессии – отрицательные. Кривая регрессии должны проходить через центр точек данных; соответственно сумма невязок должны стремиться к нулю. Сумму значений поля можно вычислить в суммарной таблице.
Невязки должны иметь равномерную вариабельность.
Величина вариабельности должна быть одинаковой для всех невязок. Это допущение проверяется с использованием точечной диаграммы невязок (ось y) и оцениваемых значений (ось x). Результирующая точечная диаграмма отображается как горизонтальная полоса с произвольно разбросанными точками по всей площади.
Результирующая точечная диаграмма отображается как горизонтальная полоса с произвольно разбросанными точками по всей площади.
Распределение невязок должно соответствовать нормальному.
Нормальное распределение – кривая в форме колокола – является естественным распределением, где высокая частота явления наблюдается рядом со средним значением, и по мере увеличения расстояния от среднего частота снижается. В статистическом анализе нормальное распределение часто используется как нулевая гипотеза. Если распределение невязок соответствует нормальному, линия наилучшего соответствия проходит по центру наблюдаемых точек данных, а не отклоняется, приближаясь к одним, и отклоняясь от других. Это допущение можно проверить, построив гистограмму невязок. Кривая нормального распределения может не поместиться в карточку и сдвиги и эксцессы переносятся на обратную сторону карточки гистограммы.
Смежные невязки не должны обнаруживать автокорреляцию.
Это допущение основано на хронологии данных. Если данные соответствуют хронологии, каждая точка данных должна быть независима от предыдущей или последующей точки данных. Поэтому при выполнении регрессионного анализа важно убедиться, что хронологический порядок данных соответствует нормальному ходу времени. Это допущение вычисляется с использованием теста Дарбина-Уотсона.
Если данные соответствуют хронологии, каждая точка данных должна быть независима от предыдущей или последующей точки данных. Поэтому при выполнении регрессионного анализа важно убедиться, что хронологический порядок данных соответствует нормальному ходу времени. Это допущение вычисляется с использованием теста Дарбина-Уотсона.
Тест Дарбина-Уотсона измеряет автокорреляцию невязок в модели регрессии. Критерий Дурбина-Ватсона использует шкалу от 0 до 4, где значения от 0 до 2 указывают на положительную автокорреляцию, 2 – отсутствие автокорреляции, а от 2 до 4 отрицательную автокорреляцию. То есть, чтобы соответствовать допущению об отсутствии автокорреляции невязок, необходимо получить значение, приближающееся к 2. В целом, значения между 1.5 и 2.5 считаются допустимыми, а меньше 1.5 или больше 2.5 указывают на то, что модель не соответствует утверждению об отсутствии автокорреляции.
Пригодность модели
Точность уравнения регрессии – основа регрессионного анализа. Все модели будут иметь некую ошибку, но понимание этой статистики поможет вам определить, можно ли использовать эту модель для вашего анализа, или необходимо выполнить дополнительные преобразования.
Существуют два метода проверки корректности модели регрессии: исследовательский анализ и подтверждающий анализ.
Исследовательский анализ
Исследовательский анализ – технология анализа данных с использованием разнообразных статистических и визуальных методов. В рамках исследовательского анализа вы проверяете допущения регрессии МНК и сравниваете эффективность различных независимых переменных. Исследовательский анализ позволяет вам сравнить эффективность и точность разных моделей, но не может определить, должны ли вы использовать или отклонить ту или иную модель. Исследовательский анализ необходимо проводить перед анализом подтверждения для каждой модели регрессии, возможно, несколько раз, для сравнения разных моделей.
Как часть исследовательского анализа могут быть использованы следующие диаграммы и статистические показатели:
- Точечная диаграмма (рассеяния) и матрица точечной диаграммы
- Гистограмма и анализ нормального распределения
- Уравнение регрессии и прогнозирование новых наблюдений
- Коэффициент детерминации, R2 и скорректированный R2
- Стандартная ошибка невязки
- Точечная диаграмма
Исследовательский анализ начинается, когда вы выбираете независимые переменные, и до построения модели регрессии. Так как МНК – метод линейной регрессии, основное допущение – модель должна быть линейной. Точечная диаграмма (рассеяния) и матрица точечной диаграммы могут быть использованы для анализа линейной зависимости между зависимой переменной и независимыми переменными. Матрица точечной диаграммы может отобразить до 4х независимых переменных с зависимой переменной, что позволяет сразу провести сравнение между всеми переменными. Простая диаграмма рассеяния может отобразить только две переменные: одну зависимую и одну независимую. Просмотр диаграммы рассеяния с зависимой переменной и одной независимой переменной позволяет сделать более точное допущение об отношении между переменными. Линейность можно проверить перед созданием модели регрессии, чтобы определить, какие именно независимые переменные следует использовать для создания пригодной модели.
Так как МНК – метод линейной регрессии, основное допущение – модель должна быть линейной. Точечная диаграмма (рассеяния) и матрица точечной диаграммы могут быть использованы для анализа линейной зависимости между зависимой переменной и независимыми переменными. Матрица точечной диаграммы может отобразить до 4х независимых переменных с зависимой переменной, что позволяет сразу провести сравнение между всеми переменными. Простая диаграмма рассеяния может отобразить только две переменные: одну зависимую и одну независимую. Просмотр диаграммы рассеяния с зависимой переменной и одной независимой переменной позволяет сделать более точное допущение об отношении между переменными. Линейность можно проверить перед созданием модели регрессии, чтобы определить, какие именно независимые переменные следует использовать для создания пригодной модели.
Несколько выходных статистических показателей также доступны после создания модели регрессии, к ним относятся: уравнение регрессии, значение R2 и критерий Дурбина-Ватсона. После создания модели регрессии вы должны использовать выходные показатели, а также диаграммы и таблицы для проверки остальных допущений регрессии МНК. Если ваша модель удовлетворяет допущениям, вы можете продолжить исследовательский анализ.
После создания модели регрессии вы должны использовать выходные показатели, а также диаграммы и таблицы для проверки остальных допущений регрессии МНК. Если ваша модель удовлетворяет допущениям, вы можете продолжить исследовательский анализ.
Уравнение регрессии дает возможность оценить влияние каждой независимой переменной на прогнозируемые значения, включая коэффициент регрессии для каждой независимой переменной. Можно сравнить величины уклона для определения влияния каждой независимой переменной на зависимую переменную; Чем дальше от нуля значение уклона (неважно, в положительную, или отрицательную сторону) – тем больше влияние. Уравнение регрессии также может быть использовано для прогнозирования значений зависимой переменной через вод значений каждой независимой переменной.
Коэффициент детерминации, обозначаемый как R2, измеряет, насколько хорошо уравнение регрессии моделирует фактические точки данных. Значение R2 – число в диапазоне от 0 до 1, причем, чем ближе значение к 1, тем более точная модель. Если R2 равен 1, это указывает на идеальную модель, что крайне маловероятно в реальных ситуациях, учитывая сложность взаимодействий между различными факторами и неизвестными переменными. Поэтому следует стремиться к созданию регрессионной модели с максимально возможным значением R2 , понимая, что значение не может быть равно 1.
Если R2 равен 1, это указывает на идеальную модель, что крайне маловероятно в реальных ситуациях, учитывая сложность взаимодействий между различными факторами и неизвестными переменными. Поэтому следует стремиться к созданию регрессионной модели с максимально возможным значением R2 , понимая, что значение не может быть равно 1.
При выполнении регрессионного анализа существует риск создания модели регрессии, имеющей допустимое значение R2, путем добавления независимых переменных, случайным образом показывающих хорошее соответствие. Значение Скорректированный R2, которое также должно находиться в диапазоне между 0 и 1, учитывает дополнительные независимые переменные, уменьшая роль случайности в вычислении. Скорректированный R2 нужно использовать в модели с большим количеством независимых переменных или при сравнении моделей с различным числом независимых переменных.
Стандартная ошибка невязки измеряет точность, с которой регрессионная модель может предсказывать значения с новыми данными. Меньшие значения указывают на более точную модель, соответственно при сравнении нескольких моделей, та, где это значение самое меньшее из всех – модель, в которой минимизирована стандартная ошибка невязки.
Меньшие значения указывают на более точную модель, соответственно при сравнении нескольких моделей, та, где это значение самое меньшее из всех – модель, в которой минимизирована стандартная ошибка невязки.
Точечная диаграмма может быть использована для анализа независимых переменных, с целью выявления кластеризации или выбросов, которые могут влиять на точность модели.
Анализ подтверждения
Анализ подтверждения — процесс оценки модели в сравнении с нулевой гипотезой. В регрессионном анализа нулевая гипотеза утверждает, что отношения между зависимой и независимыми переменными отсутствуют. Для модели с отсутствием отношений величина уклона равна 0. Если элементы анализа подтверждения статистически значимы — вы можете отклонить нулевую гипотезу ((другими словами, статистически подтверждается наличие отношений между зависимой и независимыми переменными).
Для определения значимости, как компонента анализа, используются следующие статистические показатели:
- F-статистика, и связанное с ней p-значение
- T-статистика, и связанное с ней p-значение
- Доверительные интервалы
F-статистика — глобальный статистический показатель, возвращаемый F-критерием, который показывает возможности прогнозирования модели через расчет коэффициентов регрессии в модели, которые значительно отличаются от 0. F-критерий анализирует комбинированное влияние независимых переменных, а не оценивает каждую в отдельности. С F-статистикой связано соответствующее p-значение, которое является мерой вероятности того, что детерминированные отношения между переменными являются случайными Так как p-значения базируются на вероятности, значения располагаются в диапазоне от 0.0 до 1.0. Небольшое p-значение, обычно 0.05 или меньше, свидетельствует о том, что в модели реально есть отношения между переменными (то есть, выявленная закономерность не является случайной) что дает нам право отвергнуть нулевую гипотезу. В этом случае, вероятность того, что отношения в модели случайны, равна 0.05, или 1 к 20. Или, вероятность того, что отношения реальны, равна 0.95, или 19 к 20.
F-критерий анализирует комбинированное влияние независимых переменных, а не оценивает каждую в отдельности. С F-статистикой связано соответствующее p-значение, которое является мерой вероятности того, что детерминированные отношения между переменными являются случайными Так как p-значения базируются на вероятности, значения располагаются в диапазоне от 0.0 до 1.0. Небольшое p-значение, обычно 0.05 или меньше, свидетельствует о том, что в модели реально есть отношения между переменными (то есть, выявленная закономерность не является случайной) что дает нам право отвергнуть нулевую гипотезу. В этом случае, вероятность того, что отношения в модели случайны, равна 0.05, или 1 к 20. Или, вероятность того, что отношения реальны, равна 0.95, или 19 к 20.
Показатель t-статистика — это локальный статистический показатель, возвращаемый t-критерием, который показывает возможности прогнозирования для каждой независимой переменной отдельно. Так же, как и F-критерий, t-критерий анализирует коэффициенты регрессии в модели, которые значительно отличаются от 0. Так как t-критерий применяется к каждой независимой переменной, модель вернет значение t-статистики для каждой независимой переменной, а не одно значение для всей модели. Каждое значение t-статистики имеет связанное с ним p-значение, которое указывает на значимость независимой переменной. Так же, как и для F-критерия, p-значение для каждого t-критерия должно быть 0.05 или менее, чтобы мы могли отвергнуть нулевую гипотезу. Если p-значение для независимой переменной больше 0.05, эту переменную не стоит включать в модель, и необходимо строить новую модель, даже если глобальное значение вероятности для исходной модели указывает на статистическую значимость.
Так как t-критерий применяется к каждой независимой переменной, модель вернет значение t-статистики для каждой независимой переменной, а не одно значение для всей модели. Каждое значение t-статистики имеет связанное с ним p-значение, которое указывает на значимость независимой переменной. Так же, как и для F-критерия, p-значение для каждого t-критерия должно быть 0.05 или менее, чтобы мы могли отвергнуть нулевую гипотезу. Если p-значение для независимой переменной больше 0.05, эту переменную не стоит включать в модель, и необходимо строить новую модель, даже если глобальное значение вероятности для исходной модели указывает на статистическую значимость.
Доверительные интервалы визуализируют коэффициенты регрессии для каждой независимой переменной и могут быть 90, 95 и 99 процентов. Поэтому доверительные интервалы можно использовать наряду с p-значениями t-критерия для оценки значимости нулевой гипотезы для каждой независимой переменной. Коэффициенты регрессии на должны быть равны 0, только в этом случае вы можете отклонить нулевую гипотезу и продолжить использовать модель. Поэтому, для каждой независимой переменной, коэффициент регрессии, и связанный с ним доверительный интервал не может перекрываться с 0. Если доверительные интервалы в 99 или 95 процентов для данной независимой переменой перекрываются с 0, эта независимая переменная не дает возможности отклонить нулевую гипотезу. Включение этой переменной в модель может негативно повлиять на общую значимость вашей модели. Если только 90-процентный доверительный интервал перекрывается с 0, эта переменная может быть включена в модель, общая статистическая значимость которой вас удовлетворяет. В идеале, доверительные интервалы для всех независимых переменных должны быть как можно дальше от 0.
Поэтому, для каждой независимой переменной, коэффициент регрессии, и связанный с ним доверительный интервал не может перекрываться с 0. Если доверительные интервалы в 99 или 95 процентов для данной независимой переменой перекрываются с 0, эта независимая переменная не дает возможности отклонить нулевую гипотезу. Включение этой переменной в модель может негативно повлиять на общую значимость вашей модели. Если только 90-процентный доверительный интервал перекрывается с 0, эта переменная может быть включена в модель, общая статистическая значимость которой вас удовлетворяет. В идеале, доверительные интервалы для всех независимых переменных должны быть как можно дальше от 0.
Другие выходные данные
Остальные выходные данные, такие как прогнозируемые значения и невязки также важны для допущений регрессии МНК. В этом разделе вы можете узнать подробнее, как эти значения вычисляются.
Ожидаемые значения
Ожидаемые значения вычисляются на основе уравнения регрессии и значений каждой независимой переменной. В идеале, ожидаемые значения должны совпадать с наблюдаемыми (реальными значениями зависимой переменной).
В идеале, ожидаемые значения должны совпадать с наблюдаемыми (реальными значениями зависимой переменной).
Ожидаемые значения, вместе с наблюдаемым значениями, используются для вычисления невязок.
Невязки
Невязки в регрессионном анализе – это различия между наблюдаемыми значениями в наборе данных и ожидаемыми значениями, вычисленными с помощью уравнения регрессии.
Невязки A и B для отношений выше вычисляются следующим образом:
невязкиA = наблюдаемыеA - ожидаемыеA невязкиA = 595 - 487.62 невязкиA = 107.38
невязкиB = наблюдаемыеB - ожидаемыеB невязкиB = 392 - 527.27 невязкиB = -135.27
Невязки используются для вычисления ошибки уравнения регрессии, а также для проверки некоторых допущений.
Отзыв по этому разделу?
Пошаговые статьи, видео, простые определения
Вероятность и статистика > Регрессионный анализ
График простой линейной регрессии для количества осадков. Регрессионный анализ — это способ найти тенденции в данных. Например, вы можете догадаться, что существует связь между тем, сколько вы едите, и тем, сколько вы весите; регрессионный анализ может помочь вам определить это количественно.
Регрессионный анализ — это способ найти тенденции в данных. Например, вы можете догадаться, что существует связь между тем, сколько вы едите, и тем, сколько вы весите; регрессионный анализ может помочь вам определить это количественно.
Посмотрите видео с кратким обзором:
Введение в регрессионный анализ
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Регрессионный анализ предоставит вам уравнение для графика, чтобы вы могли делать прогнозы относительно ваших данных. Например, если вы набирали вес в течение последних нескольких лет, он может предсказать, сколько вы будете весить через десять лет, если продолжите набирать вес с той же скоростью. Это также даст вам множество статистических данных (включая значение p и коэффициент корреляции), чтобы сказать вам, насколько точна ваша модель. Большинство курсов по элементарной статистике охватывают самые базовые методы, такие как построение точечных диаграмм и выполнение линейной регрессии. Однако вы можете столкнуться с более продвинутыми методами, такими как множественная регрессия.
Однако вы можете столкнуться с более продвинутыми методами, такими как множественная регрессия.
Содержание:
- Введение в регрессионный анализ
- Множественный регрессионный анализ
- Переоснащение и как его избежать
- Связанные статьи
Технология:
- Регрессия в Minitab
В статистике трудно смотреть на набор случайных чисел в таблице и пытаться понять это. Например, глобальное потепление может уменьшить среднее количество снегопадов в вашем городе, и вас просят предсказать, сколько снега, по вашему мнению, выпадет в этом году. Глядя на следующую таблицу, вы можете догадаться, что это где-то 10-20 дюймов. Это хорошее предположение, но вы можете сделать лучше угадать , используя регрессию.
По сути, регрессия — это «наилучшая догадка» при использовании набора данных для того, чтобы сделать какой-либо прогноз. Это подгонка набора точек к графику. Существует целый ряд инструментов, которые могут выполнить регрессию для вас, включая Excel, который я использовал здесь, чтобы помочь разобраться в этих данных о снегопаде: угадай немного. Вы можете видеть, что первоначальное предположение (20 дюймов или около того) было далеко от истины. В 2015 году линия будет где-то между 5 и 10 дюймами! Это может быть «достаточно хорошо», но регрессия также дает полезное уравнение, которое для этого графика:
Существует целый ряд инструментов, которые могут выполнить регрессию для вас, включая Excel, который я использовал здесь, чтобы помочь разобраться в этих данных о снегопаде: угадай немного. Вы можете видеть, что первоначальное предположение (20 дюймов или около того) было далеко от истины. В 2015 году линия будет где-то между 5 и 10 дюймами! Это может быть «достаточно хорошо», но регрессия также дает полезное уравнение, которое для этого графика:
г = -2,2923x + 4624,4.
Это означает, что вы можете подставить значение x (год) и получить довольно точную оценку количества снегопадов для любого года. Например, 2005 г.:
г = -2,2923 (2005 г.) + 4624,4 = 28,3385 дюймов, что довольно близко к фактическому значению 30 дюймов для этого года.
Лучше всего то, что вы можете использовать уравнение для прогнозирования. Например, сколько снега выпадет в 2017 году?
г = 2,2923 (2017) + 4624,4 = 0,8 дюйма.
Регрессия также дает значение R в квадрате, которое для этого графика равно 0,702. Это число говорит вам, насколько хороша ваша модель. Значения варьируются от 0 до 1, где 0 — ужасная модель, а 1 — идеальная модель. Как вы, вероятно, видите, 0,7 — довольно приличная модель, поэтому вы можете быть достаточно уверены в своем прогнозе погоды!
Это число говорит вам, насколько хороша ваша модель. Значения варьируются от 0 до 1, где 0 — ужасная модель, а 1 — идеальная модель. Как вы, вероятно, видите, 0,7 — довольно приличная модель, поэтому вы можете быть достаточно уверены в своем прогнозе погоды!
В начало
Множественный регрессионный анализ используется для проверки наличия статистически значимой связи между наборами переменных. Он используется для поиска тенденций в этих наборах данных.
Анализ множественной регрессии почти аналогичен простой линейной регрессии. Единственная разница между простой линейной регрессией и множественной регрессией заключается в количестве предикторов (переменных «x»), используемых в регрессии.
- Простой регрессионный анализ использует одну переменную x для каждой зависимой переменной «y». Например: (х 1 , Y 1 ).
- Множественная регрессия использует несколько переменных «x» для каждой независимой переменной: (x1) 1 , (x2) 1 , (x3) 1 , Y 1 ).

В линейной регрессии с одной переменной вы должны ввести одну зависимую переменную (т. е. «продажи») вместо независимой переменной (т. е. «прибыль»). Но вас может заинтересовать, как различных типов продаж влияют на регрессию. Вы можете установить свой X 1 как один из видов продаж, ваш X 2 как еще один тип продаж и так далее.
Когда использовать множественный регрессионный анализ.
Обычной линейной регрессии недостаточно, чтобы учесть все факторы реальной жизни, влияющие на результат. Например, на следующем графике показана зависимость одной переменной (количества врачей) от другой переменной (продолжительность жизни женщин).
Изображение: Колумбийский университет
Из этого графика может показаться, что существует зависимость между ожидаемой продолжительностью жизни женщин и количеством врачей среди населения. На самом деле, это, вероятно, правда, и можно сказать, что это простое решение: добавить больше врачей к населению, чтобы увеличить продолжительность жизни. Но реальность такова, что вам придется учитывать другие факторы, например, вероятность того, что врачи в сельской местности могут иметь меньше образования или опыта. Или, возможно, у них нет доступа к медицинским учреждениям, таким как травмпункты.
Но реальность такова, что вам придется учитывать другие факторы, например, вероятность того, что врачи в сельской местности могут иметь меньше образования или опыта. Или, возможно, у них нет доступа к медицинским учреждениям, таким как травмпункты.
Добавление этих дополнительных факторов заставит вас добавить дополнительные зависимые переменные в ваш регрессионный анализ и создать модель множественного регрессионного анализа.
Выходные данные анализа множественной регрессии.
Регрессионный анализ всегда выполняется в программном обеспечении, таком как Excel или SPSS. Выходные данные различаются в зависимости от того, сколько переменных у вас есть, но, по сути, это тот же тип выходных данных, который вы найдете в простой линейной регрессии. Просто больше:
- Простая регрессия: Y = b 0 + b 1 x.
- Множественная регрессия: Y = b 0 + b 1 x1 + b 0 + b 1 x2…b 0 …b 1 xn.

Выходные данные будут включать сводку, аналогичную сводке для простой линейной регрессии, которая включает:
- R (коэффициент множественной корреляции),
- Р в квадрате (коэффициент детерминации),
- скорректированный R-квадрат,
- Стандартная ошибка оценки.
Эти статистические данные помогут вам понять, насколько хорошо регрессионная модель соответствует данным. Таблица ANOVA на выходе даст вам p-значение и f-статистику.
Минимальный размер выборки
«Ответ на вопрос о размере выборки, по-видимому, частично зависит от целей
исследователя, решаемых вопросов исследования и типа используемой
модели. Хотя есть несколько исследовательских статей и учебников, дающих
рекомендации по минимальному размеру выборки для множественной регрессии, немногие согласны с
в отношении того, насколько большим является достаточно большой, и не многие обращаются к прогнозирующей стороне MLR».~ Грегори Т. Кнофчински
Если вы заинтересованы в поиске точных значений квадрата множественного коэффициента корреляции, минимизации усадки квадрата множественного коэффициента корреляции на
или преследуете другую конкретную цель, стоит прочитать статью Грегори Кнофчински, и ее много. ссылок для дальнейшего изучения. Тем не менее, многие люди просто хотят запустить MLS, чтобы получить общее представление о тенденциях, и им не нужны очень конкретные оценки. Если это так, вы можете использовать эмпирическое правило . В литературе широко утверждается, что в вашей выборке должно быть более 100 элементов. Хотя иногда этого достаточно, вы будете в большей безопасности, если у вас будет не менее 200 наблюдений, а еще лучше — более 400. ваша модель слишком сложна для ваших данных — это происходит, когда размер вашей выборки слишком мал. Если вы поместите в свою регрессионную модель достаточно переменных-предикторов, вы почти всегда получите модель, которая выглядит значимой.
Хотя переобученная модель может очень хорошо соответствовать особенностям ваших данных, она не будет соответствовать дополнительным тестовым образцам или генеральной совокупности.
p-значения модели, R-квадрат и коэффициенты регрессии могут вводить в заблуждение. По сути, вы слишком многого требуете от небольшого набора данных.
Как избежать переобучения
При линейном моделировании (включая множественную регрессию) у вас должно быть не менее 10-15 наблюдений для каждого термина, который вы пытаетесь оценить. Меньше этого значения, и вы рискуете переоснастить свою модель.
«Условия» включают:
- Эффекты взаимодействия,
- Полиномиальные выражения (для моделирования кривых),
- Переменные-предикторы.
Хотя это эмпирическое правило является общепринятым, Грин (1991) идет дальше и предлагает, чтобы минимальный размер выборки для любой регрессии составлял 50 с дополнительными 8 наблюдениями на терм. Например, если у вас есть одна взаимодействующая переменная и три переменные-предикторы, вам потребуется около 45-60 элементов в вашей выборке, чтобы избежать переобучения, или 50 + 3 (8) = 74 элемента в соответствии с Грином.
Например, если у вас есть одна взаимодействующая переменная и три переменные-предикторы, вам потребуется около 45-60 элементов в вашей выборке, чтобы избежать переобучения, или 50 + 3 (8) = 74 элемента в соответствии с Грином.
Исключения
Существуют исключения из эмпирического правила «10-15». К ним относятся:
- Когда в ваших данных присутствует мультиколлинеарность или размер эффекта мал. Если это так, вам нужно будет добавить больше терминов (хотя, к сожалению, нет эмпирического правила, сколько терминов нужно добавить!).
- Возможно, вам удастся обойтись всего 10 наблюдениями на предиктор, если вы используете модели логистической регрессии или выживания, если у вас нет экстремальных вероятностей событий, небольших размеров эффекта или переменных предикторов с усеченными диапазонами. (Педуцци и др.)
Как обнаружить и избежать переобучения
Самый простой способ избежать переобучения — это увеличить размер выборки путем сбора дополнительных данных. Если вы не можете этого сделать, второй вариант — уменьшить количество предикторов в вашей модели — путем их объединения или исключения. Факторный анализ — это один из методов, который вы можете использовать для выявления связанных предикторов, которые могут быть кандидатами на объединение.
Если вы не можете этого сделать, второй вариант — уменьшить количество предикторов в вашей модели — путем их объединения или исключения. Факторный анализ — это один из методов, который вы можете использовать для выявления связанных предикторов, которые могут быть кандидатами на объединение.
1. Перекрестная проверка
Использование перекрестной проверки для обнаружения переобучения: это разделяет ваши данные, обобщает вашу модель и выбирает модель, которая работает лучше всего. Одной из форм перекрестной проверки является предсказание R-квадрат . Большинство хороших статистических программ будут включать эту статистику, которая рассчитывается следующим образом:
- Удаление одного наблюдения за раз из ваших данных,
- Оценка уравнения регрессии для каждой итерации,
- Использование уравнения регрессии для прогнозирования удаленного наблюдения.
Однако перекрестная проверка не является волшебным лекарством для небольших наборов данных, и иногда четкая модель не идентифицируется даже при достаточном размере выборки.
2. Сокращение и повторная выборка
Методы сжатия и повторной выборки (например, этот R-модуль) могут помочь вам выяснить, насколько хорошо ваша модель может соответствовать новому образцу.
3. Автоматизированные методы
Автоматическую пошаговую регрессию не следует использовать в качестве решения для переобучения для небольших наборов данных. Согласно Бабяку (2004),
«Проблемы с автоматическим отбором, проводимым таким типичным образом, настолько
многочисленны, что было бы трудно каталогизировать их все [в журнальной статье]».
Бэбиак также рекомендует избегать одномерного предварительного тестирования или скрининга («разновидность замаскированного автоматического отбора»), дихотомии непрерывных переменных , которые могут значительно увеличить ошибки типа I, или многократного тестирования смешанных переменных (хотя это может быть хорошо, если использовать с умом).
Ссылки
Книги:
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
Линдстрем, Д. (2010). «Простое наброски статистики Шаума», второе издание (Простые наброски Шаума), 2-е издание. McGraw-Hill Education
Журнальные статьи:
- Бабяк, Массачусетс, (2004). «То, что вы видите, может не совпадать с тем, что вы получаете: краткое нетехническое введение в переоснащение в моделях регрессионного типа». Психосоматическая медицина. 2004 г., май-июнь; 66(3):411-21.
- Грин С.Б., (1991) «Сколько испытуемых требуется для проведения регрессионного анализа?» Многомерное исследование поведения 26:499–510.
- Peduzzi P.N., et. др. (1995). «Важность событий на независимую переменную в многопараметрическом анализе, II: точность и точность регрессионных оценок». Журнал клинической эпидемиологии 48:1503–10.
- Peduzzi P.N., et. др. (1996). «Моделирование количества событий на переменную в логистическом регрессионном анализе».
 Журнал клинической эпидемиологии 49:1373–9.
Журнал клинической эпидемиологии 49:1373–9.
Вернуться к началу
Посетите наш канал YouTube, где вы найдете сотни видеороликов об элементарной статистике, включая регрессионный анализ с использованием различных инструментов, таких как Excel и TI-83.
- Аддитивная модель и мультипликативная модель
- Как построить точечную диаграмму.
- Как рассчитать коэффициенты корреляции Пирсона.
- Как вычислить значение теста линейной регрессии.
- Тест Чоу для разделенных наборов данных
- Прямой выбор
- Что такое кригинг?
- Как найти уравнение линейной регрессии.
- Как найти точку пересечения наклона регрессии.
- Как найти наклон линейной регрессии.
- Синусоидальная регрессия: определение, пример Desmos, TI-83
- Как найти стандартную ошибку наклона регрессии.
- Мальвы Cp
- Коэффициент достоверности: что это такое и как его найти.

- Квадратичная регрессия.
- Четвертая регрессия
- Пошаговая регрессия
- Ненормированный коэффициент
- Далее: : Слабые инструменты
Забавный факт: Знаете ли вы, что регрессия предназначена не только для построения линий тренда. Это также отличный способ найти n-й член квадратичной последовательности.
Вернуться к началу
Определения
- ANCOVA.
- Допущения и условия регрессии.
- Бета-коэффициенты/стандартизированные коэффициенты.
- Что такое бета-вес?
- Билинейная регрессия
- Тест Бреуша-Пагана-Годфри
- Расстояние Кука.
- Что такое ковариата?
- Регрессия Кокса.
- Данные об удалении тренда.
- Экзогенность.
- Алгоритм Гаусса-Ньютона.
- Что такое общая линейная модель?
- Что такое обобщенная линейная модель?
- Что такое тест Хаусмана?
- Что такое гомоскедастичность?
- Влиятельные данные.

- Что такое инструментальная переменная?
- Отсутствие посадки
- Регрессия Лассо.
- Алгоритм Левенберга-Марквардта
- Какая линия лучше всего подходит?
- Что такое логистическая регрессия?
- Что такое расстояние Махаланобиса?
- Неправильная спецификация модели.
- Полиномиальная логистическая регрессия.
- Что такое нелинейная регрессия?
- Упорядоченная логит/Упорядоченная логистическая регрессия
- Что такое регрессия методом наименьших квадратов?
- Переоснащение.
- Бережливые модели.
- Что такое коэффициент корреляции Пирсона?
- Регрессия Пуассона.
- Пробит-модель.
- Что такое интервал прогнозирования?
- Что такое регуляризация?
- Регуляризованный метод наименьших квадратов.
- Регулярная регрессия
- Что такое относительные веса?
- Что такое остаточные графики?
- Обратная причинно-следственная связь.

- Регрессия хребта
- Среднеквадратическая ошибка.
- Полупараметрические модели
- Смещение одновременности.
- Модель одновременных уравнений.
- Что такое ложная корреляция?
- Модель структурных уравнений
- Что такое допустимые интервалы?
- Анализ тенденций
- Параметр настройки
- Что такое взвешенная регрессия методом наименьших квадратов?
- Y Шляпа объяснила.
Вернуться к началу
Посмотрите видео с шагами:
Как найти регрессию в minitab
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Регрессия — это подгонка данных к линии (Minitab также может выполнять другие типы регрессии, такие как квадратичная регрессия). Когда вы найдете регрессию в Minitab, вы получите точечную диаграмму ваших данных вместе с линией наилучшего соответствия, а также Minitab предоставит вам:
- Стандартная ошибка (насколько точки данных отклоняются от среднего).

- R в квадрате: значение от 0 до 1, которое говорит вам, насколько хорошо ваши точки данных соответствуют модели.
- Скорректировано R 2 (скорректировано R 2 для учета точек данных, которые не соответствуют модели).
Регрессия в Minitab выполняется всего парой щелчков на панели инструментов и доступна через меню «Статистика».
Пример вопроса : Найдите регрессию в Minitab для следующего набора точек данных, которые сравнивают количество потребляемых за день калорий с весом:
Калории, потребляемые ежедневно (вес в фунтах): 2800 (140), 2810 (143), 2805 (144), 2705 (145), 3000 (155), 2500 (130), 2400 (121), 2100 (100), 2000 (99), 2350 (120), 2400 (121), 3000 (155).
Шаг 1: Введите данные в два столбца в Minitab .
Шаг 2: Нажмите «Статистика», затем нажмите «Регрессия», а затем нажмите «Графический график с аппроксимацией».
Регрессия при выборе Minitab.
Шаг 3: Щелкните имя переменной для зависимого значения в левом окне. Для этого примера вопроса мы хотим знать, влияют ли потребляемых калорий на вес , поэтому калории являются независимой переменной (Y), а вес — зависимой переменной (X). Нажмите «Калории», а затем нажмите «Выбрать».
Шаг 4: Повторите шаг 3 для зависимой переменной X , вес.
Выбор переменных для регрессии Minitab.
Шаг 5: Нажмите «ОК». Minitab создаст линейный график регрессии в отдельном окне.
Шаг 4: Прочитать результаты. Помимо создания графика регрессии, Minitab предоставит вам значения для S, R-sq и R-sq(adj) в правом верхнем углу окна графика аппроксимированной линии.
с = стандартная ошибка.
R-Sq = коэффициент детерминации
R-Sq(adj) = скорректированный коэффициент детерминации (скорректированный R в квадрате).
Вот и все!
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Регрессионный анализ: пошаговые статьи, видео, простые определения» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/regression-analysis/
«Регрессионный анализ: пошаговые статьи, видео, простые определения» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/regression-analysis/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Regression model: Definition, Types and examples
+13236381128
+1519
+61480040096
Book a Demo
TRY A SAMPLE SURVEY
- Book demo
- Watch demo
- Pricing
- Contact
- Наши клиенты
- Истории клиентов
- Характеристики
- Ресурсы
- 17 декабря 2021 г.

ПОДЕЛИТЬСЯ СТАТЬЕЙ ПО
Содержание
Что такое регрессионная модель?
Модель регрессии определяет взаимосвязь между независимой переменной и зависимой переменной, предоставляя функцию. Формулировка регрессионного анализа помогает предсказать влияние независимой переменной на зависимую.
Пример: мы можем сказать, что возраст и рост можно описать с помощью модели линейной регрессии. Поскольку рост человека увеличивается с возрастом, они имеют линейную зависимость.
Регрессионные модели обычно используются в качестве статистического доказательства утверждений относительно повседневных фактов.
В этой статье мы более подробно рассмотрим регрессионную модель и ее типы.
Усовершенствуйте свои данные опроса с помощью Voxco Analytics.
Собирайте отзывы и раскрывайте идеи.
Подробнее
Какие существуют типы регрессионных моделей?
Существует три различных типа регрессионных моделей:
- Линейная
- Нелинейная
- Множественная
Рассмотрим их подробнее:
Модель линейной регрессии Модель линейной регрессии используется для отображения пропорций между переменными. Это означает, что зависимая переменная увеличивается/уменьшается вместе с независимой переменной.
Это означает, что зависимая переменная увеличивается/уменьшается вместе с независимой переменной.
В графическом представлении имеет прямую линию, проведенную между переменными. Даже если точки не лежат точно на прямой линии (что всегда так), мы все равно можем увидеть закономерность и понять ее смысл.
Например, с возрастом человека увеличивается и уровень глюкозы в его организме.
Модель нелинейной регрессииВ модели нелинейной регрессии график не показывает линейную прогрессию. В зависимости от того, как переменная отклика реагирует на входную переменную, линия будет подниматься или опускаться, показывая высоту или глубину эффекта переменной отклика.
Чтобы понять, что модель нелинейной регрессии лучше всего подходит для вашего сценария, обязательно изучите свои переменные и их закономерности. Если вы видите, что переменная ответа показывает не столь постоянный вывод для входной переменной, вы можете использовать нелинейную модель для своей проблемы.
Например, реакция пациента на лечение может быть хорошей или плохой в зависимости от предрасположенности его тела и силы воли.
Загрузить набор инструментов для исследования рынка
Получить руководство по тенденциям исследования рынка, руководство по онлайн-опросам, руководство по гибким исследованиям рынка и 5 шаблонов исследования рынка независимая переменная, влияющая на зависимую переменную. При прогнозировании переменной результата важно измерить, как каждая из независимых переменных движется в своей среде и как их изменения повлияют на выходную или целевую переменную.
Например, вероятность того, что учащийся не сдаст экзамен, может зависеть от различных входных переменных, таких как тяжелая работа, семейные проблемы, проблемы со здоровьем и т. д.
Что такое пошаговое регрессионное моделирование?
В отличие от вышеупомянутых типов регрессионных моделей, пошаговое регрессионное моделирование является скорее методом, используемым, когда различные входные переменные влияют на одну выходную переменную . Аналитик автоматически приступит к измерению переменной, которая напрямую коррелирует с входной переменной, и построит на ее основе модель. Остальные переменные вступают в игру, когда он решает усовершенствовать модель.
Аналитик автоматически приступит к измерению переменной, которая напрямую коррелирует с входной переменной, и построит на ее основе модель. Остальные переменные вступают в игру, когда он решает усовершенствовать модель.
Аналитик может добавлять оставшиеся входные данные один за другим в зависимости от их значимости и степени, в которой они влияют на целевую переменную.
Например, в некоторых районах выросли цены на овощи. Причиной события может быть что угодно: от стихийных бедствий до управления транспортом и цепочками поставок. Когда аналитик решит изобразить это на графике, он выберет самую очевидную причину — обильные осадки в сельскохозяйственных регионах.
После того, как модель построена, он может добавить в картину остальные влияющие входные переменные в зависимости от их появления и значимости.
Изучите все типы вопросов опроса
, возможные на Voxco
Подробнее
Управляемые данными, основанные на данных и вдохновленные данными
14 марта 2022 г. Комментариев нет
Комментариев нет
На основе данных, на основе данных и на основе данных. Подробнее »
Руководство по контрольным вопросам опроса
23 июня 2021 г. Комментариев нет
Руководство по контрольным вопросам опроса Voxco доверяют более 450 мировых брендов в более чем 40 странах Посмотрите, какие типы вопросов возможны, с помощью образца
Подробнее »
Использование t-теста
4 февраля 2022 г. Комментариев нет
Использование t-теста ПОДЕЛИТЬСЯ СТАТЬЕЙ В Поделиться на facebook Поделиться в Twitter Поделиться на linkedin Содержание T-тест — это статистический метод
Подробнее »
Извлечение данных стало проще
19 апреля 2022 г. Комментариев нет
Извлечение данных стало проще ПОДЕЛИТЬСЯ СТАТЬЕЙ В Поделиться на facebook Поделиться на Twitter Поделиться на linkedin Содержание Введение Бизнес-лидеры и предприниматели
Подробнее »
DG Solutions Ведущий игрок в области исследований в области здравоохранения и ухода за пациентами
18 июня 2020 г. Комментариев нет
Комментариев нет
D G Solutions – Как этот ветеран здравоохранения и партнер Voxco увеличили свой бизнес в 4 раза за один год! Соединения клиента DG —
Подробнее »
Стратифицированная выборка против кластерной выборки
19 августа 2021 г. Комментариев нет
Стратифицированная выборка против кластерной выборки Проведите рентабельное исследование с Voxco Закажите демонстрацию ПОДЕЛИТЬСЯ СТАТЬЕЙ В Оглавлении Что такое выборка? Выборка обследования
Подробнее »
Что такое регрессия? Определение, расчет и пример
Что такое регрессия?
Регрессия — это статистический метод, используемый в финансах, инвестициях и других дисциплинах, который пытается определить силу и характер связи между одной зависимой переменной (обычно обозначаемой Y) и рядом других переменных (известных как независимые переменные).
Линейная регрессия, также называемая простой регрессией или методом наименьших квадратов (OLS), является наиболее распространенной формой этого метода. Линейная регрессия устанавливает линейную связь между двумя переменными на основе линии наилучшего соответствия. Таким образом, линейная регрессия графически изображается с использованием прямой линии с наклоном, определяющим, как изменение одной переменной влияет на изменение другой. Y-отрезок отношения линейной регрессии представляет значение одной переменной, когда значение другой равно нулю. Существуют также модели нелинейной регрессии, но они гораздо сложнее.
Линейная регрессия устанавливает линейную связь между двумя переменными на основе линии наилучшего соответствия. Таким образом, линейная регрессия графически изображается с использованием прямой линии с наклоном, определяющим, как изменение одной переменной влияет на изменение другой. Y-отрезок отношения линейной регрессии представляет значение одной переменной, когда значение другой равно нулю. Существуют также модели нелинейной регрессии, но они гораздо сложнее.
Регрессионный анализ является мощным инструментом для выявления связей между переменными, наблюдаемыми в данных, но не может легко указать причинно-следственную связь. Он используется в нескольких контекстах в бизнесе, финансах и экономике. Например, он используется, чтобы помочь инвестиционным менеджерам оценить активы и понять взаимосвязь между такими факторами, как цены на сырьевые товары и запасы предприятий, занимающихся этими товарами.
Регрессию как статистический метод не следует путать с концепцией регрессии к среднему (возврат к среднему).
Основные выводы
- Регрессия — это статистический метод, который связывает зависимую переменную с одной или несколькими независимыми (пояснительными) переменными.
- Модель регрессии способна показать, связаны ли изменения, наблюдаемые в зависимой переменной, с изменениями в одной или нескольких независимых переменных.
- Он делает это, по существу подбирая наиболее подходящую линию и наблюдая, как данные распределяются вокруг этой линии.
- Регрессия помогает экономистам и финансовым аналитикам в различных вещах, от оценки активов до прогнозирования.
- Чтобы результаты регрессии были правильно интерпретированы, необходимо выполнить несколько допущений относительно данных и самой модели.
Регрессия
Понимание регрессии
Регрессия фиксирует корреляцию между переменными, наблюдаемыми в наборе данных, и определяет, являются ли эти корреляции статистически значимыми или нет.
Двумя основными типами регрессии являются простая линейная регрессия и множественная линейная регрессия, хотя существуют методы нелинейной регрессии для более сложных данных и анализа. Простая линейная регрессия использует одну независимую переменную для объяснения или прогнозирования результата зависимой переменной Y, в то время как множественная линейная регрессия использует две или более независимых переменных для прогнозирования результата (при сохранении всех остальных постоянными).
Простая линейная регрессия использует одну независимую переменную для объяснения или прогнозирования результата зависимой переменной Y, в то время как множественная линейная регрессия использует две или более независимых переменных для прогнозирования результата (при сохранении всех остальных постоянными).
Регрессия может помочь специалистам в области финансов и инвестиций, а также специалистам в других сферах бизнеса. Регрессия также может помочь прогнозировать продажи компании на основе погоды, предыдущих продаж, роста ВВП или других типов условий. Модель оценки капитальных активов (CAPM) — это часто используемая регрессионная модель в финансах для оценки активов и определения стоимости капитала.
Регрессия и эконометрика
Эконометрика — это набор статистических методов, используемых для анализа данных в области финансов и экономики. Примером применения эконометрики является изучение эффекта дохода с использованием наблюдаемых данных. Экономист может, например, предположить, что по мере того, как человек увеличивает свой доход, его расходы также увеличиваются.
Если данные показывают наличие такой связи, можно провести регрессионный анализ, чтобы понять силу связи между доходом и потреблением, а также выяснить, является ли эта связь статистически значимой, т. е. маловероятно, что она существует. только благодаря случайности.
Обратите внимание, что в вашем анализе может быть несколько объясняющих переменных, например, изменения ВВП и инфляции в дополнение к безработице для объяснения цен на фондовом рынке. Когда используется более одной независимой переменной, это называется множественной линейной регрессией. Это наиболее часто используемый инструмент в эконометрике.
Эконометрику иногда критикуют за то, что она слишком сильно полагается на интерпретацию результатов регрессии, не связывая ее с экономической теорией или не ища причинно-следственных механизмов. Крайне важно, чтобы результаты, обнаруженные в данных, могли быть адекватно объяснены теорией, даже если это означает разработку вашей собственной теории лежащих в основе процессов.
Расчет регрессии
В моделях линейной регрессии часто используется метод наименьших квадратов для определения линии наилучшего соответствия. Метод наименьших квадратов определяется путем минимизации суммы квадратов, созданных математической функцией. Квадрат, в свою очередь, определяется путем возведения в квадрат расстояния между точкой данных и линией регрессии или средним значением набора данных.
После завершения этого процесса (сегодня это обычно делается с помощью программного обеспечения) строится регрессионная модель. Общая форма каждого типа регрессионной модели:
Простая линейная регрессия:
Д знак равно а + б Икс + ты \begin{выровнено}&Y = a + bX + u \\\end{выровнено} Y=a+bX+u
Множественная линейная регрессия:
Д знак равно а + б 1 Икс 1 + б 2 Икс 2 + б 3 Икс 3 + . . . + б т Икс т + ты куда: Д знак равно Зависимая переменная, которую вы пытаетесь предсказать или объясните Икс знак равно Пояснительная (независимая) переменная (переменные), которой вы являетесь использование для предсказания или ассоциации с Y а знак равно Y-перехват б знак равно (бета-коэффициент) – это наклон пояснительной переменная (ы) ты знак равно Остаток регрессии или термин ошибки \begin{align}&Y = a + b_1X_1 + b_2X_2 + b_3X_3 + . .. + b_tX_t + u \\&\textbf{где:} \\&Y = \text{Зависимая переменная, которую вы пытаетесь предсказать} \\& \text{или объясните} \\&X = \text{Независимая (независимая) переменная (переменные), которую вы используете} \\&\text{используете для предсказания или связи с Y} \\&a = \text{Отрезок по оси y } \\&b = \text{(бета-коэффициент) — это наклон пояснительной} \\&\text{переменная(-и)} \\&u = \text{Невязка регрессии или член ошибки} \\\end{aligned }
Y=a+b1X1+b2X2+b3X3+…+btXt+u, где:Y=зависимая переменная, которую вы пытаетесь предсказать, объяснитеX=независимая переменная( s) вы используете, чтобы предсказать или связать с Yaa = y-interceptb = (бета-коэффициент) — это наклон независимой переменной (s) u = невязка регрессии или член ошибки
.. + b_tX_t + u \\&\textbf{где:} \\&Y = \text{Зависимая переменная, которую вы пытаетесь предсказать} \\& \text{или объясните} \\&X = \text{Независимая (независимая) переменная (переменные), которую вы используете} \\&\text{используете для предсказания или связи с Y} \\&a = \text{Отрезок по оси y } \\&b = \text{(бета-коэффициент) — это наклон пояснительной} \\&\text{переменная(-и)} \\&u = \text{Невязка регрессии или член ошибки} \\\end{aligned }
Y=a+b1X1+b2X2+b3X3+…+btXt+u, где:Y=зависимая переменная, которую вы пытаетесь предсказать, объяснитеX=независимая переменная( s) вы используете, чтобы предсказать или связать с Yaa = y-interceptb = (бета-коэффициент) — это наклон независимой переменной (s) u = невязка регрессии или член ошибки
Пример использования регрессионного анализа в финансах
Регрессия часто используется для определения того, сколько конкретных факторов, таких как цена товара, процентные ставки, конкретные отрасли или сектора, влияют на движение цены актива. Вышеупомянутый CAPM основан на регрессии и используется для прогнозирования ожидаемой доходности акций и определения стоимости капитала. Доходность акции регрессируется по сравнению с доходностью более широкого индекса, такого как S&P 500, для получения коэффициента бета для конкретной акции.
Вышеупомянутый CAPM основан на регрессии и используется для прогнозирования ожидаемой доходности акций и определения стоимости капитала. Доходность акции регрессируется по сравнению с доходностью более широкого индекса, такого как S&P 500, для получения коэффициента бета для конкретной акции.
Бета — это риск акции по отношению к рынку или индексу, который отражается в виде наклона в модели CAPM. Доходность рассматриваемой акции будет зависимой переменной Y, а независимой переменной X будет премия за рыночный риск.
Дополнительные переменные, такие как рыночная капитализация акций, коэффициенты оценки и недавняя доходность, могут быть добавлены в модель CAPM, чтобы получить более точные оценки доходности. Эти дополнительные факторы известны как факторы Фама-Френча, названные в честь профессоров, которые разработали модель множественной линейной регрессии для лучшего объяснения доходности активов.
Почему это называется регрессией?
Хотя о происхождении названия ведутся споры, описанная выше статистическая техника, скорее всего, была названа сэром Фрэнсисом Гальтоном в XIX веке «регрессией» для описания статистической характеристики биологических данных (например, роста людей в населения) регрессировать до некоторого среднего уровня. Другими словами, в то время как есть более низкие и более высокие люди, только выбросы очень высокие или низкорослые, и большинство людей группируются где-то около среднего (или «регрессируют» до) среднего.
Другими словами, в то время как есть более низкие и более высокие люди, только выбросы очень высокие или низкорослые, и большинство людей группируются где-то около среднего (или «регрессируют» до) среднего.
Какова цель регрессии?
В статистическом анализе регрессия используется для выявления связей между переменными, встречающимися в некоторых данных. Он может показать как величину такой связи, так и определить ее статистическую значимость (т. е. вероятность того, что связь является случайной). Регрессия — это мощный инструмент для статистических выводов, который также использовался, чтобы попытаться предсказать будущие результаты на основе прошлых наблюдений.
Как интерпретировать регрессионную модель?
Выходные данные регрессионной модели могут быть представлены в виде Y = 1,0 + (3,2) X 1 — 2,0 ( X 2 ) + 0,21.
Здесь мы имеем множественную линейную регрессию, которая связывает некоторую переменную Y с двумя независимыми переменными X 1 и X 2 . Мы бы интерпретировали модель как изменение значения Y в 3,2 раза при каждом изменении X на одну единицу (если X 1 увеличивается на 2, Y увеличивается на 6,4 и т. д.) при неизменности всех остальных параметров. (при прочих равных). Это означает, что контроль для X 2 , X 1 имеет эту наблюдаемую связь. Аналогичным образом, при постоянном значении X1 каждое увеличение X 2 на единицу связано с 2x уменьшением Y. Мы также можем отметить точку пересечения y со значением 1,0, что означает, что Y = 1, когда X 1 и X 2 оба равны нулю. Погрешность (остаток) равна 0,21.
Мы бы интерпретировали модель как изменение значения Y в 3,2 раза при каждом изменении X на одну единицу (если X 1 увеличивается на 2, Y увеличивается на 6,4 и т. д.) при неизменности всех остальных параметров. (при прочих равных). Это означает, что контроль для X 2 , X 1 имеет эту наблюдаемую связь. Аналогичным образом, при постоянном значении X1 каждое увеличение X 2 на единицу связано с 2x уменьшением Y. Мы также можем отметить точку пересечения y со значением 1,0, что означает, что Y = 1, когда X 1 и X 2 оба равны нулю. Погрешность (остаток) равна 0,21.
Какие допущения должны выполняться для регрессионных моделей?
Чтобы правильно интерпретировать выходные данные регрессионной модели, должны выполняться следующие основные допущения относительно процесса обработки данных, лежащего в основе того, что вы анализируете:
- Связь между переменными является линейной
- Гомоскедастичность, или что дисперсия переменных и ошибка должны оставаться постоянными
- Все объясняющие переменные независимы друг от друга
- Все переменные нормально распределены
В этом уроке мы применяем регрессионный анализ к некоторым фиктивные данные, и мы показываем, как интерпретировать результаты нашего анализа.

Примечание: Ваш браузер не поддерживает видео HTML5. Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.
Примечание: Вычисления регрессии обычно обрабатываются программным пакетом или графический калькулятор. Для этого Однако расчеты будем производить «вручную», т.к. кровавые подробности имеют воспитательное значение.
Постановка задачи
В прошлом году пять случайно выбранных учеников сдали тест на математические способности до того, как они начали свой курс статистики. Статистика У отдела три вопроса.
- Насколько хорошо уравнение регрессии соответствует данным?
Реклама
Как найти уравнение регрессии
В приведенной ниже таблице в столбце x i показаны результаты тест на выявление способностей. Аналогично столбец y i показывает статистику оценки.
 Последние два столбца показывают баллы отклонений — разницу между
оценка студента и средний балл по каждому измерению. Последние две строки показывают суммы и средние
оценки, которые мы будем использовать для проведения регрессионного анализа.
Последние два столбца показывают баллы отклонений — разницу между
оценка студента и средний балл по каждому измерению. Последние две строки показывают суммы и средние
оценки, которые мы будем использовать для проведения регрессионного анализа.Студент x i y i (x i -x) (y i -y) 1 95 85 17 8 2 85 95 7 18 3 80 70 2 -7 4 70 65 -8 -12 5 60 70 -18 -7 Sum 390 385 Mean 78 77 И для каждого учащегося нам также необходимо вычислить квадраты оценок отклонений (последние два столбца в таблице ниже).

Студент x i y i (x i -x) 2 (y i -y) 2 1 95 85 289 64 2 85 95 49 324 3 80 70 4 49 4 70 65 64 144 5 60 70 324 49 Sum 390 385 730 630 Mean 78 77 И, наконец, для каждого студента нам нужно вычислить произведение оценки отклонений (последний столбец в таблице ниже).
Студент x i y i (x i -x)(y i -y) 1 95 85 136 2 85 95 126 3 80 70 -14 4 70 65 96 5 60 70 126 Sum 390 385 470 Mean 78 77 The regression equation is a linear equation of the form: ŷ = b 0 + b 1 х .
 Провести регрессию
анализ, нам нужно решить для b 0 и b 1 .
Расчеты показаны ниже. Обратите внимание, что все наши входные данные для
регрессионный анализ исходит из трех вышеприведенных таблиц.
Провести регрессию
анализ, нам нужно решить для b 0 и b 1 .
Расчеты показаны ниже. Обратите внимание, что все наши входные данные для
регрессионный анализ исходит из трех вышеприведенных таблиц.Сначала находим коэффициент регрессии (b 1 ): — x) 2 ]
b 1 = 470/730
b 1 = 0,644
Зная значение коэффициента регрессии, мы можем решить (b7 1 ) для коэффициента регрессии наклон (b 0 ):
b 0 = y — b 1 * x
b 0 = 77 — (0,644)(78)
b 0 = 26,768
Следовательно, уравнение регрессии: ŷ = 26,768 + 0,644x .
Как использовать уравнение регрессии
Если у вас есть уравнение регрессии, использовать его несложно. Выбирать значение для независимой переменной ( x ), выполните вычисление, и у вас есть оценочное значение (ŷ) для зависимой переменной.
В нашем примере независимой переменной является балл студента на тесте способностей.
 Зависимой переменной является студент.
класс статистики. Если ученик набрал 80 баллов за способности
теста, расчетная оценка статистики (ŷ) будет:
Зависимой переменной является студент.
класс статистики. Если ученик набрал 80 баллов за способности
теста, расчетная оценка статистики (ŷ) будет:ŷ = B 0 + B 1 x
ŷ = 26,768 + 0,644x = 26,768 + 0,644 * 80
ŷ = 26,768 + 51,52 = 78,288
Warnging: 66.52 = 78,288
. не используйте значения для независимой переменной, которые находятся за пределами диапазон значений, используемых для создания уравнения. Это называется экстраполяции , и это может привести к необоснованным оценки.
В этом примере результаты теста способностей, использованные для создания уравнение регрессии варьировалось от 60 до 95. Следовательно, используйте только значения внутри этого диапазона для оценки оценок статистики. Использование значений вне этого диапазона (меньше 60 или больше 95) проблематично.
Как найти коэффициент детерминации
Всякий раз, когда вы используете уравнение регрессии, вы должны спросить, насколько хорошо уравнение соответствует данным.
 Один из способов оценить соответствие — проверить
коэффициент детерминации, который можно вычислить из
следующую формулу.
Один из способов оценить соответствие — проверить
коэффициент детерминации, который можно вычислить из
следующую формулу.R 2 = { ( 1 / N ) * Σ [ (x i — x) * (y i — y) ] / (σ x * σ y ) } 2
где N — количество наблюдения, используемые для подгонки модели, Σ — символ суммирования, x i — значение x для наблюдения i, х — среднее значение х, y i — значение y для наблюдения i, у — среднее значение у, σ x — стандартное отклонение x, а σ y — стандартное отклонение y.
Расчеты для примера задачи этого урока показаны ниже. Начнем с вычисления стандартного отклонения x (σ x ):
σ x = sqrt [ Σ ( x i — x ) 2 / N ]
σ x = sqrt ( 0,07 730/5 ) = sqrt
Далее находим стандартное отклонение y, (σ y ): ( 630/5 ) = sqrt(126) = 11,225
И, наконец, вычисляем коэффициент детерминации (R 2 ):
R 2 = { ( 1 / N ) * Σ [ (x i — x) * (y i — y) ] / (σ x * σ y ) } 2
R 2 = [(1/5) * 470 / (12,083 * 11,225)] 2R 2 = (94 / 135,632) 2 = (0,693) 2 = 0,48
9950 = (0,693) 2 = 0,489507950 = (0,693). детерминации, равной 0,48, свидетельствует о том, что около
48% разброса оценок по статистике (самый
зависимая переменная) можно объяснить
связь с оценками математических способностей (т.
независимая переменная). Это будет считаться хорошей подгонкой
к данным в том смысле, что это существенно улучшит
способность преподавателя прогнозировать успеваемость учащихся по статистике
учебный класс.
детерминации, равной 0,48, свидетельствует о том, что около
48% разброса оценок по статистике (самый
зависимая переменная) можно объяснить
связь с оценками математических способностей (т.
независимая переменная). Это будет считаться хорошей подгонкой
к данным в том смысле, что это существенно улучшит
способность преподавателя прогнозировать успеваемость учащихся по статистике
учебный класс.Последний урок Следующий урок
Учебное пособие по регрессии с примерами анализа
Регрессионный анализ математически описывает отношения между независимыми переменными и зависимой переменной. Это также позволяет вам прогнозировать среднее значение зависимой переменной, когда вы указываете значения для независимых переменных. В этом учебном пособии по регрессионному анализу я собрал большое количество статей, которые я написал о регрессионном анализе. Мой учебник поможет вам пройти через содержание регрессии в систематическом и логическом порядке.В этом учебном пособии рассматриваются многие аспекты регрессионного анализа, включая выбор правильного типа регрессионного анализа, указание наилучшей модели, интерпретацию результатов, оценку соответствия модели, создание прогнозов и проверку допущений.
 Закрываю пост примерами разных видов регрессионного анализа.
Закрываю пост примерами разных видов регрессионного анализа.Если вы изучаете регрессионный анализ, вы можете добавить это руководство в закладки!
Когда использовать регрессию и признаки качественного анализа
Прежде чем мы перейдем к учебникам по регрессии, я расскажу о нескольких общих вопросах.
Зачем вообще использовать регрессию? Какие распространенные проблемы сбивают с толку аналитиков? И как отличить высококачественный регрессионный анализ от менее тщательного исследования? Прочтите эти сообщения, чтобы узнать:
- Когда следует использовать регрессионный анализ? Узнайте, что регрессия может сделать для вас и когда вам следует ее использовать.
- Пять советов по регрессионному анализу для лучшего анализа. Эти советы помогут вам провести высококачественный регрессионный анализ.
Учебное пособие. Выбор правильного типа регрессионного анализа
Существует множество различных типов регрессионного анализа.
 Как объясняется в этих сообщениях, выбор правильной процедуры зависит от ваших данных и характера отношений.
Как объясняется в этих сообщениях, выбор правильной процедуры зависит от ваших данных и характера отношений.- Выбор правильного типа регрессионного анализа: обзор различных методов регрессии с упором на типы данных.
- Как выбрать между линейной и нелинейной регрессией: определение того, какой из них использовать, путем оценки статистических результатов.
- Разница между линейной и нелинейной моделями: Оба типа моделей могут соответствовать кривым, так в чем же разница?
Учебное пособие. Определение регрессионной модели
Выбор правильного типа регрессионного анализа — это только начало процесса. Далее необходимо указать модель. Спецификация модели — это процесс определения того, какие независимые переменные принадлежат модели и подходят ли моделирование кривизны и эффектов взаимодействия.
Спецификация модели — это итеративный процесс. Разделы интерпретации и подтверждения предположений этого руководства объясняют, как оценить вашу модель и как изменить модель на основе статистических выходных данных и графиков.

- Спецификация модели: выбор правильной регрессионной модели: я рассматриваю стандартные статистические подходы, трудности, с которыми вы можете столкнуться, и предлагаю несколько практических советов.
- Использование интеллектуального анализа данных для выбора модели регрессии может создать проблемы: такой подход к выбору модели может привести к вводящим в заблуждение результатам. Узнайте, как обнаружить и избежать этой проблемы.
- Руководство по пошаговой регрессии и регрессии наилучших подмножеств: два общих инструмента для определения переменных-кандидатов на этапах исследования построения модели.
- Переобучение моделей регрессии: слишком сложные модели могут давать вводящие в заблуждение значения R-квадрата, коэффициенты регрессии и p-значения. Узнайте, как обнаружить и избежать этой проблемы.
- Подгонка кривой с использованием линейной и нелинейной регрессии: если ваши данные не следуют прямой линии, модель должна соответствовать кривизне.
 В этом посте рассматриваются различные методы подгонки кривых.
В этом посте рассматриваются различные методы подгонки кривых. - Понимание эффектов взаимодействия: когда эффект одной переменной зависит от значения другой переменной, вам необходимо включить эффект взаимодействия в вашу модель, иначе результаты будут вводящими в заблуждение.
- Когда вам нужно стандартизировать переменные?: В определенных ситуациях стандартизация независимых переменных может выявить статистически значимые результаты.
- Вмешивающиеся переменные и отклонение от пропущенных переменных. Переменные, которые вы не включили в модель, могут повлиять на переменные, которые вы включаете.
- Прокси-переменные: хороший двойник вмешивающихся переменных: найдите способы включить ценную информацию в свои модели и избежать вмешивающихся факторов.
Учебное пособие: интерпретация результатов регрессии
После выбора типа регрессии и указания модели необходимо интерпретировать результаты. В следующем наборе сообщений объясняется, как интерпретировать результаты для различных статистических данных регрессионного анализа:
- Коэффициенты и p-значения
- Константа (пересечение с Y)
- Сравнение наклонов и констант регрессии с проверкой гипотез
- R-квадрат и качество подгонки
- Насколько высоким должен быть R-квадрат?
- Интерпретация модели с низким R-квадратом
- Скорректированный R-квадрат и прогнозируемый R-квадрат
- Стандартная ошибка регрессии (S) по сравнению с R-квадратом
- Пять причин, по которым ваш R-квадрат может быть слишком высоким: высокий R-квадрат иногда может указывать на проблему с вашей моделью.

- F-критерий общей значимости
- Определение наиболее важных независимых переменных. После выбора модели аналитики часто спрашивают: «Какая переменная является наиболее важной?»
Учебное пособие. Использование регрессии для прогнозирования
Аналитики часто используют регрессионный анализ для прогнозирования. В этом разделе руководства по регрессии вы узнаете, как делать прогнозы и оценивать их точность.
- Создание прогнозов с помощью регрессионного анализа. В этом руководстве для прогнозирования процентного содержания жира в организме используется ИМТ.
- Предсказанный R-квадрат: эта статистика оценивает, насколько хорошо модель предсказывает зависимую переменную для новых наблюдений.
- Понимание точности прогнозирования, чтобы избежать дорогостоящих ошибок: исследования показывают, что презентация влияет на количество ошибок интерпретации. Охватывает интервалы предсказания.
- Интервалы прогнозирования по сравнению с другими интервалами: Интервалы прогнозирования указывают на точность прогнозов.
 Я сравниваю интервалы предсказания с разными типами интервалов.
Я сравниваю интервалы предсказания с разными типами интервалов.
Учебное пособие: проверка допущений регрессии и устранение проблем
Как и другие статистические процедуры, регрессионный анализ имеет допущения, которым необходимо соответствовать, иначе результаты могут быть ненадежными. В регрессии вы в первую очередь проверяете предположения, оценивая остаточные графики. В сообщениях ниже объясняется, как это сделать, и представлены некоторые методы устранения проблем.
- Семь классических допущений линейной регрессии МНК
- Остаточные графики: Показывает, как должны выглядеть графики и почему они могут не выглядеть!
- Гетероскедастичность: остатки должны иметь постоянный разброс (гомоскедастичность). Показывает, как обнаружить эту проблему и различные способы ее устранения.
- Мультиколлинеарность: Сильно коррелированные независимые переменные могут быть проблематичными, но не всегда! Объясняет, как определить эту проблему и несколько способов ее решения.

Примеры различных типов регрессионного анализа
Последняя часть руководства по регрессионному анализу содержит примеры регрессионного анализа. Некоторые примеры включены в предыдущие разделы руководства. Большинство этих примеров регрессии включают наборы данных, так что вы можете попробовать сами! Кроме того, попробуйте использовать Excel для выполнения регрессионного анализа с пошаговым примером!
- Линейная регрессия с двойным логарифмическим преобразованием: моделирует взаимосвязь между массой млекопитающих и скоростью метаболизма с использованием аппроксимированного линейного графика.
- Понимание рейтинга историков президентов США с использованием регрессионных моделей: ранжирование моделей президентов США по различным предикторам.
- Моделирование взаимосвязи между ИМТ и процентным содержанием телесного жира с помощью линейной регрессии.
- Аппроксимация кривой с линейной и нелинейной регрессией.
Если вы изучаете регрессию и вам нравится подход, который я использую в своем блоге, ознакомьтесь с моей электронной книгой!
4 примера использования линейной регрессии в реальной жизни
Линейная регрессия — один из наиболее часто используемых методов в статистике.
 Он используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика.
Он используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика.Самая основная форма линейной регрессии известна как простая линейная регрессия, которая используется для количественной оценки взаимосвязи между одной переменной-предиктором и одной переменной-откликом.
Если у нас есть более одной переменной-предиктора, мы можем использовать множественную линейную регрессию, которая используется для количественной оценки взаимосвязи между несколькими переменными-предикторами и переменной ответа.
В этом руководстве представлены четыре различных примера использования линейной регрессии в реальной жизни.
Линейная регрессия Пример из реальной жизни #1Компании часто используют линейную регрессию, чтобы понять взаимосвязь между расходами на рекламу и доходами.
Например, они могут соответствовать простой модели линейной регрессии, используя расходы на рекламу в качестве переменной-предиктора и доход в качестве переменной-отклика.
 Модель регрессии примет следующий вид:
Модель регрессии примет следующий вид:доход = β 0 + β 1 (расходы на рекламу)
Коэффициент β 0 представляет общий ожидаемый доход, когда расходы на рекламу равны нулю.
Коэффициент β 1 представляет собой среднее изменение общего дохода при увеличении расходов на рекламу на одну единицу (например, на один доллар).
Если β 1 отрицательное значение, это будет означать, что большие расходы на рекламу связаны с меньшим доходом.
Если β 1 близко к нулю, это будет означать, что расходы на рекламу мало влияют на доход.
И если β 1 положительное значение, это будет означать, что чем больше расходов на рекламу, тем больше доход.
В зависимости от значения β 1 компания может принять решение о сокращении или увеличении своих расходов на рекламу.
Линейная регрессия Пример из реальной жизни #2Медицинские исследователи часто используют линейную регрессию, чтобы понять взаимосвязь между дозировкой лекарств и кровяным давлением пациентов.

Например, исследователи могут давать пациентам различные дозы определенного лекарства и наблюдать за реакцией их кровяного давления. Они могут соответствовать простой модели линейной регрессии, используя дозировку в качестве предиктора и артериальное давление в качестве переменной отклика. Модель регрессии будет иметь следующий вид:
кровяное давление = β 0 + β 1 (дозировка)
.
Коэффициент β 1 представляет собой среднее изменение артериального давления при увеличении дозы на одну единицу.
Если β 1 отрицательное значение, это будет означать, что увеличение дозы связано со снижением артериального давления.
Если β 1 близко к нулю, это будет означать, что увеличение дозы не связано с изменением артериального давления.
Если β 1 положительный результат, это будет означать, что увеличение дозы связано с повышением артериального давления.

В зависимости от значения β 1 исследователи могут решить изменить дозировку, назначаемую пациенту.
Линейная регрессия Пример из реальной жизни #3Ученые-агрономы часто используют линейную регрессию для измерения влияния удобрений и воды на урожайность сельскохозяйственных культур.
Например, ученые могут использовать разное количество удобрений и воды на разных полях и посмотреть, как это повлияет на урожайность. Они могут соответствовать модели множественной линейной регрессии, используя удобрения и воду в качестве переменных-предикторов и урожайность в качестве переменной отклика. Модель регрессии примет следующий вид:
Выход урожая = β 0 + β 1 (количество удобрений) + β 2 (количество воды)
Коэффициент β 0 . без удобрений и воды.
Коэффициент β 1 представляет собой среднее изменение урожайности при увеличении количества удобрений на одну единицу, при условии, что количество воды остается неизменным.

Коэффициент β 2 представляет собой среднее изменение урожайности при увеличении количества воды на одну единицу, при условии, что количество удобрений остается неизменным.
В зависимости от значений β 1 и β 2 ученые могут изменить количество удобрений и воды, используемых для получения максимальной урожайности.
Линейная регрессия Пример из реальной жизни #4Исследователи данных профессиональных спортивных команд часто используют линейную регрессию для измерения влияния различных режимов тренировок на результаты игроков.
Например, специалисты по данным в НБА могут проанализировать, как разное количество еженедельных занятий йогой и тяжелой атлетикой влияет на количество очков, набранных игроком. Они могут соответствовать модели множественной линейной регрессии, используя занятия йогой и занятия тяжелой атлетикой в качестве переменных-предикторов и общее количество баллов, набранных в качестве переменной отклика.
 Модель регрессии будет иметь следующий вид:
Модель регрессии будет иметь следующий вид:набранных баллов = β 0 + β 1 (занятия йогой) + β 2 (занятия тяжелой атлетикой)
Коэффициент β 0 представляет собой ожидаемое количество очков, набранных игроком, который участвует в нулевых занятиях йогой и нулевых занятиях тяжелой атлетикой.
Коэффициент β 1 представляет собой среднее изменение в баллах, набранных при увеличении количества еженедельных занятий йогой на единицу, при условии, что количество еженедельных занятий тяжелой атлетикой остается неизменным.
Коэффициент β 2 будет представлять собой среднее изменение в баллах, набранных при увеличении количества еженедельных занятий тяжелой атлетикой на единицу, при условии, что количество еженедельных занятий йогой остается неизменным.
В зависимости от значений β 1 и β 2 специалисты по обработке и анализу данных могут порекомендовать игроку более или менее еженедельно заниматься йогой и тяжелой атлетикой, чтобы максимально набрать очки.




 715875613747954
715875613747954
 fit(x, y.reshape((-1, 1)))
>>> print('intercept:', new_model.intercept_)
intercept: [5.63333333]
>>> print('slope:', new_model.coef_)
slope: [[0.54]]
fit(x, y.reshape((-1, 1)))
>>> print('intercept:', new_model.intercept_)
intercept: [5.63333333]
>>> print('slope:', new_model.coef_)
slope: [[0.54]]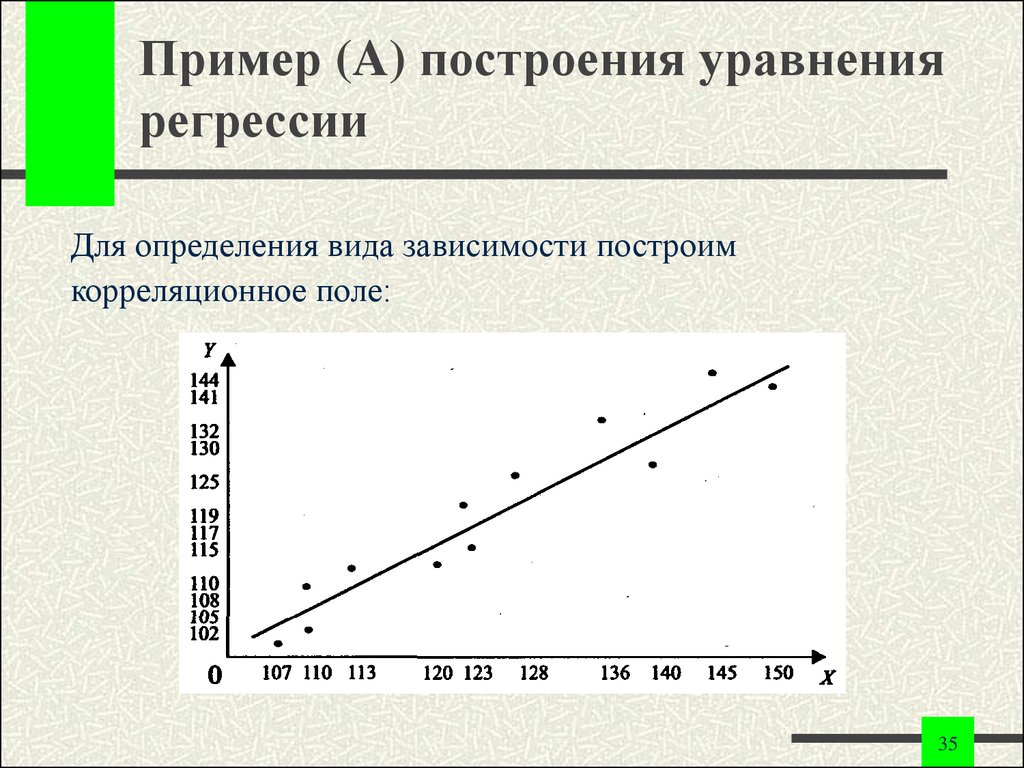 intercept_ + model.coef_ * x
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[[ 8.33333333]
[13.73333333]
[19.13333333]
[24.53333333]
[29.93333333]
[35.33333333]]
intercept_ + model.coef_ * x
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[[ 8.33333333]
[13.73333333]
[19.13333333]
[24.53333333]
[29.93333333]
[35.33333333]]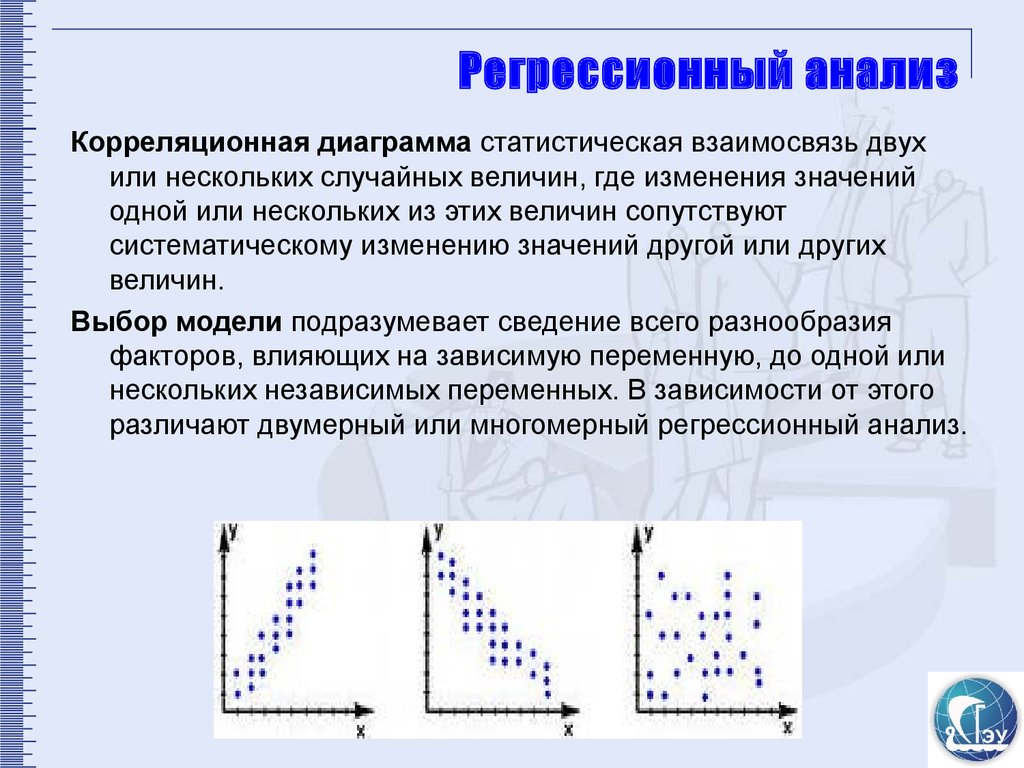 arange(5).reshape((-1, 1))
>>> print(x_new)
[[0]
[1]
[2]
[3]
[4]]
>>> y_new = model.predict(x_new)
>>> print(y_new)
[5.63333333 6.17333333 6.71333333 7.25333333 7.79333333]
arange(5).reshape((-1, 1))
>>> print(x_new)
[[0]
[1]
[2]
[3]
[4]]
>>> y_new = model.predict(x_new)
>>> print(y_new)
[5.63333333 6.17333333 6.71333333 7.25333333 7.79333333] В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
В качестве альтернативы порогом может являться каждое последующее значение примера в выборке. Входные данные — это мое условие платы, и мне нужно соответствующее…
Входные данные — это мое условие платы, и мне нужно соответствующее…