Синквейн математика: Синквейн к слову «Математика»

СИНКВЕЙН НА УРОКАХ МАТЕМАТИКИ

 

Синквейн прост в овладении и применим уже на начальной ступени обучения как самостоятельный продукт.  Синквейны полезны в качестве инструмента для синтезирования сложной информации, в качестве среза оценки понятийного и словарного багажа учащихся. Можно проанализировать лексическое богатство (или бедность) предложенных синквейнов и сделать вывод. При внешней простоте формы, синквейн — быстрый, но мощный инструмент для рефлексии.

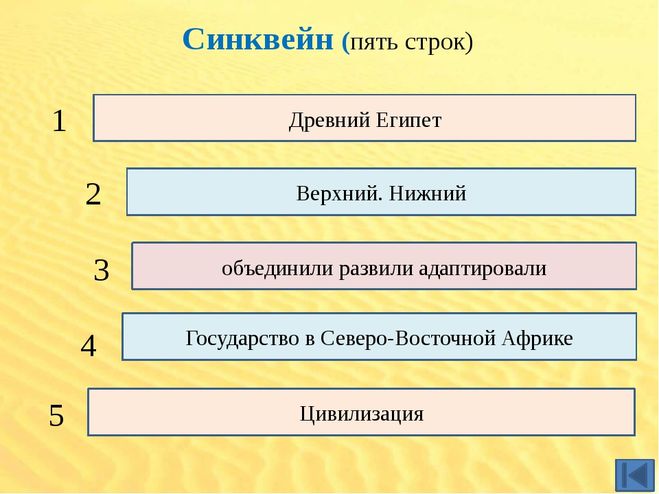
Слово «синквейн» — французское, обозначающее «пять строк». При его написании существуют определенные правила, которые в незначительной мере варьируют от автора к автору.

Правила написания  синквейна:

1 строка — заключает в себе одно слово, обычно существительное или местоимение, которое обозначает объект или предмет, о котором пойдет речь.
        2 строка — два слова, чаще всего прилагательные или причастия. Они дают описание признаков и свойств выбранного в синквейне предмета или объекта.

         3 строка — образована тремя глаголами или деепричастиями, описывающими характерные действия объекта.

4 строка — фраза из четырех слов, выражает личное отношение автора синквейна к описываемому предмету или объекту.

5 строка — одно слово, характеризующее суть предмета или объекта.

СИНКВЕЙН — приём технологии развития критического мышления, на стадии рефлексии.

СИНКВЕЙН — малая стихотворная форма, используемая для фиксации эмоциональных  оценок, описания своих текущих впечатлений, ощущений и ассоциаций.

СИНКВЕЙН — короткое литературное произведение, характеризующее предмет.

Ученики убеждаются в том, что каждый из них вполне может быть автором такого “интересного” стихотворения. Написание синквейнов целесообразно предложить как при введении в тему, так и при проведении итоговых уроков. Ученики увлеченно  работают и, обычно, к концу урока в классе уже готово несколько “стихотворных шедевров”.

Наиболее эффективные синквейны получаются при работе в парах, в группах. Это даёт возможность рассуждать ученикам и критически рассматривать ту или иную тему. Ученики пишут синквейны не только на уроках, но и дома. Дети с удовольствием красочно оформляют и иллюстрируют свои стихи.

Этот методический приём вписывается в концепцию взаимодействия и сотрудничества в образовательном процессе, расширяя арсенал парных и групповых форм деятельности. Кроме того, он требует, чтобы учащиеся слушали друг друга и извлекали из произведений товарищей идеи, которые они могут сопоставить со своими.

 

 

 

 

 

ПРИЛОЖЕНИЕ ( примеры работ учащихся 7 класса)

1.     Функция

2.     Линейная

3.     Чертим, находим

4.     Функции нужны в математике

5.     Значение

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Функция

2.  Табличная

3.   Чертим, пишем

4.  Табличный способ легкий

      5.  Зависимость

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Функция

2.  Убывающая, возрастающая

3.  Подставляем, считаем, чертим

4.  Функция играет важную роль

5.  Зависимость

 

1.  График

2.  Линейный, изогнутый

3.  Убывает, возрастает

4.  С помощью графика можно наблюдать состояние чего-то в течение времени

5.  Линия

 

 

 

1.  Треугольник

2.  Равнобедренный

3.  Доказываем, измеряем, чертим

4.  Прямой угол треугольника

5.  Фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Треугольник

2.  Равнобедренный, прямоугольный

3.  Рисуем, чертим, строим

4.  Уже изучила его

5.  Геометрическая фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.   Треугольник

2.  Прямоугольный, равнобедренный

3.  Доказываем, измеряем, чертим

4.  Прямоугольный треугольник удобно чертится

5.  Фигура

1.  Смежные углы

2.  Красивы, но не всегда равны

3.  Чертим, измеряем

4.  Сумма их равна 180⁰

5.  Теорема

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Прямые

2.  Пересекающиеся, параллельные

3.  Строим, проектируем, совмещаем

4.  Все прямые не имеют ни начала, ни конца

5.  Бесконечность

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Прямая

2.  Пересекающая, параллельная

3.  Строим, проектируем, совмещаем

4.  Все прямые не имеют, ни начала, ни конца

5.  Это бесконечность

1.  Круг

2.  Круглый

3.  Чертим, измеряем, доказываем

4.   Равноудаленный от центральной точки

5.  Простая фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Круг

2.  Кругленький, плоский

3.  Строим, кружим, измеряем

4.  Очень удобно кружится циркулем

5.  Кругляшок

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Круг

2.  Круглый, плоский

3.  Решать, чертить, использовать

4.  Конечная часть плоскости, ограниченная окружностью

5.  Только начал изучать, хорошее

6. Фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Круг

2.  Круглый, плоский

3.  Рисуем, чертим, строим

4.  Только начала его изучать

5.  Фигура

 

 

 

1.  Окружность

2.   Круглая, плоская

3.  Чертим, изучаем, рисуем

4.  ЕЕ очень легко строить

5.  Фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Окружность

2.  Бесконечность, замкнутая

3.  Вычисляем, чертим, доказываем

4.  Ее легко чертить

5.  Эта фигура состоит из всех точек плоскости

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

     1.  Окружность

2.  Круг, замкнутый

3.  Рисуем, находим, определяем

4.  Ее рисуем легко циркулем

5.  Фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1. Окружность

2.  Круглая, замкнутая

3.  Рисуем, измеряем, зарисовываем

4.  Очень легкая фигура

5.  Фигура

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

 

 

1.   Окружность

2.  Круглая, плоская

3.  Доказываем, измеряем, чертим

4.  Она очень легко чертится

5.  Фигура

 

       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Окружность

2.  Круглая, плоская

3.  Рисуем, чертим, доказываем

4.  Она легко чертится

5.  Фигура

 

 

1.  Хорда

2.  Прямая, ровная

3.  Чертим, строим, изучаем

4.  Соединяет две точки окружности

5.  Отрезок

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Хорда

2.  Небольшая, отрезок

3.  Рисуем, измеряем, ищем

4.  Находится в окружности

5.  Отрезок

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Радиус

2.  Часть, отрезок

3.   Рисуем, измеряем, проводим

4.  Радиус соединяет центр с любой точкой, лежащей на окружности

5.  Отрезок

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Радиус

2.  Небольшая, ровная

3.  Измеряем, ищем, учим

4.  Два радиуса, как один диаметр

5.  Отрезок

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

 

1.  Центр окружности

2.  Маленькая, центральная

3.  Рисуем, ставим, находим

4.  Центр окружности — это центральная точка

5.  Прямая

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.  Касательная

2.  Прямая, ровная

3.  Ищем, рисуем, измеряем

4.  Имеет с окружностью общую точку

5.  Прямая

 

*       *      *       *        *       *        *        *        *        *       *      *       *       *

1.

  Диаметр

2.  Прямой, ровный

3.  Чертим, проводим, находим

4.  Диаметр как два радиуса

5.  Прямая

Синквейн на уроках математики как средство развития творческих способностей | Творческая работа учащихся по алгебре по теме:

Синквейн на уроках математики

Синквейн (от фр. cinquains, англ. cinquain) — пятистрочная стихотворная форма, возникшая в США в начале XX века под влиянием японской поэзии.

Это стихотворение, которое состоит из пяти строчек по определенным правилам.

Правила создания синквейна:

строчка – это название темы

строчка – это определение темы в двух прилагательных или причастиях

строчка – это три глагола, показывающие действие в рамках темы.

строчка – фраза из четырех слов, оказывающая отношение автора к теме.

строчка – завершение темы, синоним первого слова, выраженный любой частью речи.

Синквейн на уроках математики позволяет не только развить творческие способности учащихся, но и помогает кратко обобщить изученное понятие или тему, выразить личное отношение к ней, то есть формирует навыки рефлексии.

Математические синквейны

Математика
Точная, красивая,

Учит, решает, развивает
Думать, решать — много знать
Важно

Математика
Занимательная, увлекательная
Cистематизирует, развивает, обогащает
Её учить – ум точить
Царица

Математика 
Развивающая, загадочная 
Мыслить, рассуждать, понимать 
Не зная математики, не знаешь ничего 
Царица наук!

Математика 
Интересная, великая 
Думать, спорить, доказывать 
В порядок ум приводит 
Гениально!

Математика
Наука точная
Сижу, пишу, учу
Волненье, напряженье
Сложно!

Математика
Точная, увлекательная,
Думать, рассуждать, решать
Ум свой развивать!
Логика!

Математика
Загадочная, интересная
Мыслю, творю, решаю
Напрягать мозги — это здорово!
Наука!

Математика
Серьёзная, занимательная
Учим, доказываем, вычисляем
Математике почёт и уважение!
Знание.

Математика
Строгая, логичная
Учит думать, считать, рассуждать.
Нам нравится наука сложная
Полезно знать!

Математика
Непознана, глубока
Увлекает, манит, забавляет
из кирпичиков — чисел мир собирает
Занимательно.

Математика
Сложная, точная
Помогает,вычисляет, развивает
Любимый предмет -ужасно интересный,
Полезно!

Математика
Сложная, весёлая.
Решаю, считаю, черчу.
Она — любимый мой урок.
Точная!

Математика
Увлекательная, познавательная
Решает, считает, рассуждает
Математика- царица наук
Восхитительно!

Математика
Точная, грамотная, умная
Учит, решает, вычитает
Школьное расписание- любимый предмет
Классно!

Математика
Занимательная, нужная
Думаем, соображаем, решаем
Мой любимый урок — математика
Обожаю!

Математика
Трудная, сложная, иногда- невозможная
стараться, не спотыкаться, думать, «вгрызаться»
С делом не знаться- дураком остаться
Надо!

 Математика
Занятная, непонятная, но всё же приятная
Не отступать, решать, считать
Маленькое дело лучше большого безделья
Работа!

Математика
Занимательная, поучительная
Решает, заставляет, считает
Учиться, учиться, учиться
Здорово!

Математика
Точная, развивающая
Учит, находит,помогает
Математика — царица!
Сила

Дробь-

Правильная, неправильная,

Делит, показывает, увлекает,

Помогает хорошо решать.

Число!

Число «пи»

Иррациональное, загадочное,

Увлекает, забавляет, измеряет.

Отношение длины к диаметру.

Загадочно!

Прямоугольник.

Важный, прямой.

Решать, доказывать, находить.

Имеет равные диагонали.

Параллелограмм.

Парабола,

Красивая, симметричная,

Строить, исследовать, находить.

График квадратичной функции.

Полезная!

Функция.

Возрастающая, убывающая.

Исследовать, решать, изучать.

Зависимость между переменной и аргументом.

Нужная.

Медиана

Важная, нужная.

Строить, чертить, находить.

Делит сторону пополам.

Полезная!

Биссектриса

Красивая, ровная.

Изображать, решать, думать.

Делит угол пополам.

Важно!

Высота

Строгая, ровная.

Доказывать, строить, вычислять.

Перпендикуляр к противоположной стороне.

Умение!

Теорема

Прямая, обратная.

Доказывать, изучать, запоминать.

Развивает логическое мышление.

Трудно!

Степень

Понятная, лёгкая.

Решать, вычислять, считать.

Произведение нескольких множителей.

Интересно!

.

Задача

Трудная, непонятная.

Думать, рассуждать, решать.

Развивает логическое мышление.

Получится!

Геометрия

Новая, важная

Доказывать, запоминать, рассуждать.

Наука о различных фигурах.

Сложная.

Как пересекаются математика и поэзия — Блог National Geographic Education

Классные идеи, Связь с текущими событиями, Главное

ИСКУССТВО

И поэзия, и математика требуют экономии и точности, и каждая точка зрения может улучшить другую. (Smithsonian)

Используйте нашу деятельность, чтобы познакомить учащихся с математикой, поэзией и природой.

Учителя, прокрутите вниз, чтобы увидеть краткий список ключевых ресурсов в нашем Инструментарии для учителей.

Поэты МНОГО считают на пальцах. Поверьте мне.
Фотография Джоди Кобб, National Geographic

Идеи для обсуждения

• Одной из основных характеристик, общих для многих форм поэзии и математики, является использование формул. Как математика использует формулы?
  • Формулы, обычно в форме уравнений, являются основным способом передачи математики. Математические формулы — это правила, описывающие отношения между переменными. Поскольку формулы стабильны, если математик знает только некоторые переменные, он часто может выяснить, какие из них отсутствуют. (Алгебра!)
    • Математические формулы обычно выражаются буквами и символами.
      • Пример: Формула a ² +b ² =c ² известна как теорема Пифагора. A и B — более короткие стороны любого прямоугольного треугольника, а C — гипотенуза треугольника или самая длинная сторона. Если математик знает любые два из этих чисел, он может найти и третье. (Геометрия!)

 

• Как поэзия использует формулы?
  • Во многих формах поэзии используются числовые формулы. Формулы обычно указывают на заданное количество слогов, которые определяют тип стихотворения или используемую поэтическую форму. Например:
    • хайку. Хайку представляет собой стихотворение из трех строк и всего 17 слогов: пять слогов в первой строке, семь во второй строке и пять в последней строке. Узнайте больше с нашей деятельностью.
    • сонет. Сонет – стихотворение из 14 строк, по 10 слогов в каждой строке. Вот 14 строк о соснах Монтерей.
    • синквейн. Стихотворение синквейн – это стихотворение из пяти строк, которые не рифмуются. Используйте наше видео, чтобы помочь учащимся составить стихотворения о синквейне.

 

Блог Джоанны Гроуни Intersections—Poetry with Mathematics включает широкий спектр стихотворений на математические темы или построенных с использованием математических правил. Попробуйте несколько с вашим классом!

• Попробуйте снежок!
  Снежок — стихотворение, в котором каждая строка увеличивается или уменьшается на одну букву, слово или слог. Вот один со слогами.

Я
не был
собирался
попробовать это, но я
хотел посмотреть, насколько
сложно будет завершить
.
Это сложно.
Дарн.

Попробуйте гео-снежок!

новейшая
ГИС
технология
использует слои и
картографию
для создания
карт.

 

• Попробуйте выдумки!
  Смоделируйте свои стихи на основе последовательности Фибоначчи: в Фибоначчи слог или буква каждой строки представляет собой сумму двух предыдущих строк: 1, 1, 2, 3, 5, 8, 13, 21 …

Я
утра
устал
писать
так много стихов
за такой короткий промежуток времени.
Пожалуйста, прочитайте этот блог и хотя бы дайте мне знать, что оно того стоит.

Попробуйте гео-фибы! Включите географический термин или понятие.

Идите
на север
, чтобы найти
Арктику,
затем продолжайте движение на запад.
Вы можете найти Северо-Западный проход
, который ускользнул от многих моряков в их эпических поисках.

 

• Попробуйте N+7!
  Возьмите словарь и свое любимое короткое стихотворение. Это тот случай, когда большой книжный словарь гораздо полезнее, чем цифровая версия. Это также отлично подходит для правописания и просмотра. (Мы используем номер American Heritage , потому что он прекрасен, и библиотека Nat Geo позволила нам проверить его, несмотря на то, что это справочник!)
• N+7 — это стихотворение, в котором каждое основное существительное заменено седьмым существительным, следующим за ним в словаре.

Резюме, Дороти Паркер
Бритвы причиняют вам боль,
Реки влажные,
Кислоты окрашивают тебя,
А наркотики вызывают судороги.
Пушки незаконны,
Петли дают,
Газ ужасно пахнет.
Ты можешь жить.

 

Резюме +7иш
Моллюски-бритвы причиняют тебе боль,
Ривьера сырая,
Ацидофильное молоко окрашивает тебя,
И друиды вызывают судороги .
Перестрелки незаконны ,
Северный народ дает ,
Раны ужасно пахнут.
Ты можешь жить.

 

Попробуйте гео+7! Замените основные существительные географическими терминами и понятиями, имеющими такое же количество слогов.

Климатические изменения,
Реки влажные
У видов есть ареалы
Мы протестовали против марок.
Оружие может быть законным,
Нам нужна энергия,
Новости могут быть ужасными.
Учи географию.

 

TEACHERS TOOLKIT

Смитсоновский институт: Как пересекаются поэзия и математика

Nat Geo: Миграция планктона/Создание хайку (хайку)0003

Nat Geo: Pining Away (sonnet)

Nat Geo: Я из: Поэма (синквейн)

Нравится:

Нравится Загрузка…

carylsue 26.04.2018 26.04.2018 искусство, английский язык, математика, национальный месяц поэзии, стихи, поэзия Искать:

Что ты читаешь?

• Когда-то списанное на смерть, Аральское море теперь полно жизни
• Лесные пожары 101: что нужно знать
• Что такое расширение на запад?
• Насколько велико сердце синего кита?
• ДНК древнего финикийца может заставить нас пересмотреть историю миграции людей

facebook.com/natgeoeducation»> Больше идей на Facebook

• @BarenieMerv @FulbrightTeach Присоединяйтесь к нам на facebook.com/natgeoeducation! 4 месяца назад
• @sharma10_jai @LindbladExp The Grosvenor Teacher Fellowship — это возможность профессионального развития для текущих п… twitter.com/i/web/status/1… 4 months назад
• В рамках празднования #GeographyAwarenessWeek мы рады объявить, что скоро будут открыты приложения для Gro… twitter.com/i/web/status/1… 4 months agore
• В эту #GeographyAwarenessWeek соберите своих друзей, семью, коллег и всех, кто находится между ними, чтобы помочь вам отпраздновать… twitter.com/i/web/status/1… 4 months agore
• @SusanJDorsey @LindbladExp @WildlifeRanger 💛🙌 5 месяцев назад

Искать в этом блоге

Искать:

Смотри первым!

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты

Подпишитесь на нашу рассылку новостей!

Покопайтесь в наших архивах

Покопайтесь в наших архивах Выберите месяц Февраль 2023 г. (2) Январь 2023 г. (1) Декабрь 2022 г. (2) Ноябрь 2022 г. (4) Октябрь 2022 г. (4) Сентябрь 2022 г. (4) Август 2022 г. (3) Июль 2022 г. (4) Июнь 2022 г. (4) Май 2022 г. ( 2) апрель 2022 г. (4) март 2022 г. (1) февраль 2022 г. (8) январь 2022 г. (8) декабрь 2021 г. (6) ноябрь 2021 г. (8) октябрь 2021 г. (7) сентябрь 2021 г. (8) август 2021 г. (6) июль 2021 г. ( 7) июнь 2021 г. (8) май 2021 г. (8) апрель 2021 г. (8) март 2021 г. (6) февраль 2021 г. (5) январь 2021 г. (1) декабрь 2020 г. (5) ноябрь 2020 г. (5) октябрь 2020 г. (8) сентябрь 2020 г. ( 9) август 2020 г. (4) июль 2020 г. (5) июнь 2020 г. (5) май 2020 г. (4) апрель 2020 г. (4) март 2020 г. (5) февраль 2020 г. (7) январь 2020 г. (7) декабрь 2019 г. (7) ноябрь 2019 г. (9) ) октябрь 2019 (11) сентябрь 2019 (7) август 2019 (7) июль 2019 (9) июнь 2019 (10) май 2019 (8) апрель 2019 (4) март 2019 (11) февраль 2019 (16) январь 2019 (12) ) Декабрь 2018 г. (9) Ноябрь 2018 г. (17) Октябрь 2018 г. (14) Сентябрь 2018 г. (9) Август 2018 г. (9) Июль 2018 г. (13) Июнь 2018 г. (22) Май 2018 г. (32) Апрель 2018 г. (31) Март 2018 г. (29)) Февраль 2018 г. (33) Январь 2018 г. (30) Декабрь 2017 г. (28) Ноябрь 2017 г. (31) Октябрь 2017 г. (40) Сентябрь 2017 г. (34) Август 2017 г. (19) Июль 2017 г. (12) Июнь 2017 г. (16) Май 2017 г. (28) ) Апрель 2017 (31) Март 2017 (33) Февраль 2017 (25) Январь 2017 (26) Декабрь 2016 (17) Ноябрь 2016 (21) Октябрь 2016 (24) Сентябрь 2016 (26) Август 2016 (19) Июль 2016 (13) ) Июнь 2016 (28) Май 2016 (40) Апрель 2016 (37) Март 2016 (39) Февраль 2016 (34) Январь 2016 (27) Декабрь 2015 (24) Ноябрь 2015 (39)) октябрь 2015 (36) сентябрь 2015 (29) август 2015 (17) июль 2015 (13) июнь 2015 (19) май 2015 (29) апрель 2015 (30) март 2015 (29) февраль 2015 (30) январь 2015 (29) ) Декабрь 2014 г. (35) Ноябрь 2014 г. (38) Октябрь 2014 г. (37) Сентябрь 2014 г. (34) Август 2014 г. (17) Июль 2014 г. (17) Июнь 2014 г. (10) Май 2014 г. (26) Апрель 2014 г. (34) Март 2014 г. (35) ) Февраль 2014 г. (27) Январь 2014 г. (24) Декабрь 2013 г. (16) Ноябрь 2013 г. (30) Октябрь 2013 г. (24) Сентябрь 2013 г. (33) Август 2013 г. (22) Июль 2013 г. (4) Июнь 2013 г. (13) Май 2013 г. (29)) Апрель 2013 г. (19) Март 2013 г. (31) Февраль 2013 г. (15) Январь 2013 г. (17) Ноябрь 2012 г. (19) Октябрь 2012 г. (11) Сентябрь 2012 г. (5) Август 2012 г. (6) Июль 2012 г. (8) Июнь 2012 г. (10) ) май 2012 (10) апрель 2012 (13) март 2012 (38) февраль 2012 (10) январь 2012 (11) декабрь 2011 (18) ноябрь 2011 (51) октябрь 2011 (17) сентябрь 2011 (14) август 2011 (2) ) июль 2011 г. (9) июнь 2011 г. (7) май 2011 г. (8) апрель 2011 г. (9) март 2011 г. (13) февраль 2011 г. (8) январь 2011 г. (10) декабрь 2010 г. (8) ноябрь 2010 г. (57) октябрь 2010 г. (10) ) сентябрь 2010 г. (12) август 2010 г. (6) июль 2010 г. (7) июнь 2010 г. (11) май 2010 г. (11) апрель 2010 г. (11) март 2010 г. (11) февраль 2010 г. (5) январь 2010 г. (2) декабрь 2009 г.(12) ноябрь 2009 г. (52) октябрь 2009 г. (12) сентябрь 2009 г. (4) август 2009 г. (14) июль 2009 г. (17) июнь 2009 г. (18) май 2009 г. (13) апрель 2009 г. (18) март 2009 г. (13) февраль 2009 г. (24) январь 2009 г. (15) декабрь 2008 г. (15) ноябрь 2008 г. (28) октябрь 2008 г. (12) сентябрь 2008 г. (16) август 2008 г. (18) июль 2008 г. (17) июнь 2008 г. (11) май 2008 г. (13) апрель 2008 г. (10) март 2008 г. (11) февраль 2008 г. (8) январь 2008 г. (8) декабрь 2007 г. (9) ноябрь 2007 г. (6) октябрь 2007 г. (6) сентябрь 2007 г. (6) август 2007 г. (6) июль 2007 г. (3) июнь 2007 г. (5) май 2007 г. (8) апрель 2007 г. (4) март 2007 г. (4) февраль 2007 г. (6) январь 2007 г. (7) декабрь 2006 г. (9)) Ноябрь 2006 г. (21) Октябрь 2006 г. (11) Сентябрь 2006 г. (7) Август 2006 г. (5) Июль 2006 г. (3) Июнь 2006 г. (3) Май 2006 г. (5)

Использование творческого письма для обучения математике

Благодаря партнерству с издательством Eye on Education, EducationWorld рада представить идею этого урока из книги «Математика на простом английском: стратегии грамотности для класса математики » от Эми Бенджамин . Книга предлагает учителям математики множество способов использовать язык, чтобы повысить способность своих учеников понимать, запоминать и применять математические термины и концепции.

Творческое письмо, хотя и делается в основном в связи с языковыми искусствами, является формой письма, которая может укрепить изучение математики. Творческое письмо, подходящее для математики, может включать стихи, рассказы и пародии. Поэзия, поскольку она имеет размер, уже имеет математическую составляющую. Здесь мы поговорим о двух формах поэзии: хайку и синквейн.

Хайку в японском стиле представляет собой небольшой нерифмованный клочок языка, состоящий из трех строк, семнадцати слогов, по схеме 5–7–5. В аутентичных хайку используется изображение природы, но в данном случае мы будем использовать концепцию математики. Мы можем использовать математический термин в качестве названия, а затем описать его в нашем хайку, или мы можем включить математический термин в хайку. Мы можем использовать математический термин буквально или метафорически.

Хайку, в названии которой используется математический термин:

Периметр
Многоугольники имеют стороны
Это идет по краям:
Сумма длин

Остаток
После деления
Это число, оставшееся после
Это не вписывается в

Синквейн — это пятистрочное нерифмованное стихотворение, строки которого соответствуют следующему шаблону:

. Строка 1:   два слога (существительное)
Строка 2: Четыре слога (два прилагательных, описывающих существительное)
Строка 3: Шесть слогов (три глагола, определяющих действия существительного)
Строка 4: Восемь слогов (полное предложение) Строка6 :  два слога (повторение существительного или синонима)

Пример математического синквейна:

. Фракции
Частичный, порционный
Разделение, нарушение, обмен
Они являются составляющими целого
штук

Возможностей для включения математических слов и понятий в творческое письмо слишком много, чтобы их перечислять, но вот еще несколько идей, которыми учащиеся могут воспользоваться, укрепляя свои знания по математике:

• мини-тайны, решение которых зависит от признания математической лжи;
• Традиционные рассказы и сказки, где математическая задача является частью рассказа;
• Пародии на тексты песен, в которых математические слова и понятия заменяют некоторые слова;
• Колонки советов, где ищут советы по математике; и,
• Смешения и сопоставления, в которых вы представляете список существительных и предложных фраз и просите учащихся соединить их таким образом, чтобы он начинался, заканчивался или находился в середине истории.