Краткое введение в Теорию Хаоса / Хабр
Все в мире целиком и полностью имеет свои причины и последствия. Возможно, эта мысль навела меня на осознание того, что все в мире взаимосвязано. Всему есть свои причины. Даже в случайности заложено движение к какой-то цели.События, кажущиеся случайными, происходят в определенной последовательности.
«Даже в хаосе есть порядок».Что в точности есть хаос? Название «Теория Хаоса» произошло благодаря тому факту, что системы, описываемые теорией, взятые по кусочкам- неупорядочены, но Теория Хаоса на самом деле заключается в том, чтобы найти скрытый порядок в кажущихся случайными данных.
Когда был открыт Хаос? Первый истинный экспериментатор в области Хаоса был метеоролог Эдвард Лоренс. В 1960 году он работал над проблемой предсказания погоды. У него была компьютерная установка с набором из 12 уравнений, моделирующих погоду (имеются ввиду воздушные потоки в атмосфере)[уточнение тут].
Однажды в 1961 году он [Эдвард Лоренс] снова захотел посмотреть особенную последовательность. Чтобы сэкономить время, он начал с середины последовательности, вместо того, чтобы сделать это сначала. Он ввел числа из распечатки и запустил программу…
Когда он вернулся часом позже, закономерность была решена по-другому. Вместо той же модели, что была прежде, была модель, отклоняющаяся в конце очень сильно, отличаясь от оригинальной (см. Рисунок 1). В конце –концов он выяснил, что произошло. Компьютер поместил в память 6 чисел после запятой. Чтобы сэкономить бумагу, он вводил только 3 числа после запятой. В оригинальном порядке было число 0.0506127, а он напечатал только 0.506.
 141)
141)По общепринятому мнению того времени это должно было сработать. Он должен был получить порядок очень близкий к оригинальному. Ученый мог посчитать себя счастливцем, получив измерения с точностью до 3 чисел после запятой. Конечно, измерить 4-ю и 5-ю цифру, используя рациональные методы, было невозможно, и это не могло повлиять на результат эксперимента. Лоренс посчитал идею неверной. Этот эффект известен как Эффект Бабочки. Разница в начальных точках двух кривых настолько мала, что сравнима с порханием крыльев бабочки [в реальной жизни].
Движение крыльев одной бабочки сегодня создает малейшие изменения состояния атмосферы. По прошествии времени атмосфера отличается от той, какой она могла бы быть. Таким образом, через месяц Торнадо, который мог обрушиться на Индонезию, не появляется. Или, если он не должен был появиться, он появляется.(Ян Стюарт, «Does God Play Dice?», Математика Хаоса, стр.141).
Этот феномен, в общем называемый Теорией Хаоса, также известен как чувствительная зависимость от начальных условий. Всего лишь маленькое изменение в начальных условиях может кардинально изменить поведение системы, рассматриваемой длительный период времени. Такая маленькая разница в измерениях может быть вызвана в эксперименте шумом, фоновым шумом или неисправностью оборудования. Этих вещей невозможно избежать даже в самой изолированной лаборатории.
Всего лишь маленькое изменение в начальных условиях может кардинально изменить поведение системы, рассматриваемой длительный период времени. Такая маленькая разница в измерениях может быть вызвана в эксперименте шумом, фоновым шумом или неисправностью оборудования. Этих вещей невозможно избежать даже в самой изолированной лаборатории.
Начиная с числа 2, в итоге может получиться результат, всецело отличающийся от результатов такой же системы с начальной цифрой 2.000001. Это просто невозможно- достигнуть такого уровня точности- просто попытайтесь измерить что-нибудь с точностью до миллионной доли дюйма!Исходя из этой идеи, Лоренс установил невозможность точного предсказания погоды. Как бы то ни было, это открытие привело Лоренса к другим аспектам того, что впоследствии стало известным как Теория Хаоса.
Лоренс начал наблюдать за простейшими системами, которые чувствительны к разнице в начальных условиях. Его первое открытие имело 12 уравнений, и он хотел его очень упростить, но чтобы оно все же имело этот атрибут[чувствительность к разнице в начальных условиях]. Он взял уравнения конвекции и сделал их неимоверно простыми. Эта система больше не имела отношения к конвекции, но имела чувствительность к разнице в начальных условиях, и на этот раз осталось всего лишь 3 уравнения. Позже было установлено, что эти уравнения описывают водоворот.
Он взял уравнения конвекции и сделал их неимоверно простыми. Эта система больше не имела отношения к конвекции, но имела чувствительность к разнице в начальных условиях, и на этот раз осталось всего лишь 3 уравнения. Позже было установлено, что эти уравнения описывают водоворот.
На поверхности вода неуклонно образует как бы обод колеса. Каждый «обод» расходится от маленького отверстия Если поток воды имеет маленькую скорость, «ободки» никогда не станут достаточно быстрыми, чтобы образовался водоворот. Вращение может продолжаться. Или, если поток настолько быстрый, что тяжелые «ободы» все время вращаются вокруг дна и поверхности, водоворот может замедлиться, остановиться и поменять направление вращения, вращаясь сначала в одну сторону, а затем в другую.
Уравнения для этой системы также казалось, показывали общую случайность поведения.Как бы то ни было, когда был построен график, он был удивлен [Лоренс]. Выходные параметры всегда оставались на кривой, образуя двойную спираль. До этого было известно только два типа порядка: постоянное состояние, в котором переменные никогда не меняются, и периодичное состояние, в котором система циклична, и неопределенно повторяется. Уравнения Лоренса были определенно упорядочены- они всегда следовали по спирали. Они никогда не останавливались на одной точке, но никогда не повторяли то же состояние, то есть не были периодичными. Он назвал полученные уравнеия аттрактором Лоренса(см. Рисунок 2).
До этого было известно только два типа порядка: постоянное состояние, в котором переменные никогда не меняются, и периодичное состояние, в котором система циклична, и неопределенно повторяется. Уравнения Лоренса были определенно упорядочены- они всегда следовали по спирали. Они никогда не останавливались на одной точке, но никогда не повторяли то же состояние, то есть не были периодичными. Он назвал полученные уравнеия аттрактором Лоренса(см. Рисунок 2).
В 1963 Лоренс опубликовал статью, описывающую его открытие. Он включил туда статью о непредсказуемости погоды и обсудил все типы уравнений, вызвавших этот тип поведения. К несчастью, единственным журналом, в котором он мог опубликовать свою статью, был метеорологический журнал, так как он был не физиком или математиком, a метеорологом. В результате открытия Лоренса не были известны до тех пор, пока не были открыты снова другими людьми. Лоренс открыл нечто революционное, и ждал, пока кто-то откроет его.
Другая система, в которой есть чувствительность к разнице в начальных условиях- бросание монетки. Есть две переменные в бросании монетки: как скоро она упадет и как быстро она вращается. Теоретически, возможно контролировать эти две переменные полностью, и контролировать- как монетка упадет. На практике невозможно контролировать абсолютно точно скорость вращения монеты и то, насколько она подлетит. Возможно только поместить эти переменные в определенном диапазоне, но невозможно контролировать их настолько, чтобы знать результат.
Схожая проблема имеет место в экологии и предсказании биологических популяций. Уравнение простое, если популяция растет определенно, но хищники и ограниченность в пище делают это уравнение неверным. Самое простое уравнение имеет вид:
next year’s population = r * this year’s population * (1 — this year’s population) [где next year’s population-популяция в следующем году, this year’s population- популяция в этом году]
В этом уравнении популяция описывается числом между 1 и 0, где 1 представляет собой максимально возможную популяцию, а 0- вымирание.
Биолог Роберт Мэй, решил выяснить, что случится с уравнением, если повышать показатель роста. При низких значениях популяция устанавливалась на каком-либо определенном значении. Для показателя равного 2.7 она устанавливалась на уровне 0.6292. Далее при увеличении показателя роста популяции«R», итоговая популяция также росла. Но затем случалось нечто странное.
Как только показатель превышал 3, линия разделялась надвое. Вместо устанавливания в каком-то определенном положении, она «прыгала» между двумя различными значениями. Она имела одно значение в одном году, и совершенно иное- в следующем. И так этот цикл повторялся постоянно. Повышение показателя роста вызывало скачки между двумя разными значениями.:origin()/pre00/7e61/th/pre/i/2012/162/0/a/chaos_theory_ii_by_faei-dk0m4k.jpg)
Как только параметр повышался далее, линия бифурцировала(раздваивалась) снова. Бифуркации происходили быстрее и быстрее, до тех пор, пока неожиданно не становились хаотичными. Устанавливая точный показатель роста невозможно предсказать поведение уравнения. Как бы то ни было, при ближайшем исследовании можно увидеть белые полоски. Посмотрев на эти полоски ближе обнаруживаем ряд маленьких окон, где через бифуркации проходит линия, перед тем, как вновь вернуться к состоянию хаоса. Эта похожесть на саму себя,- факт того, что график- точная копия его самого, спрятанного глубоко внутри.Это стало очень важным аспектом хаоса.(рисунок 3)
Рисунок 3- БифуркацияСлужащий IBM Бенуа Мандельброт был математиком, изучавшим эту самопохожесть. Одной из областей, которые он изучал, было колебание цен на хлопок. Неважно, как были проанализированы данные о ценах на хлопок, результаты не были распределенными нормально. Мандельброт в конечном счете получил все доступные данные о ценах на хлопок, вплоть до 1900 года. Когда он проанализировал данные с помощью ЭВМ, он заметил поразительный факт:число с точки зрения нормальных продаж было симметрично относительно точки зрения в масштабе. Каждая отдельная цена менялась случайно и непредсказуемо. Но расчет изменений был независим от масштабов: кривые дневных и месячных колебаний цен абсолютно совпадали. Поразительно, но проанализированные Мандельбротом изменения цен оставались постоянными на протяжении всего шумного периода 60-х, Второй Мировой и депрессии.
Когда он проанализировал данные с помощью ЭВМ, он заметил поразительный факт:число с точки зрения нормальных продаж было симметрично относительно точки зрения в масштабе. Каждая отдельная цена менялась случайно и непредсказуемо. Но расчет изменений был независим от масштабов: кривые дневных и месячных колебаний цен абсолютно совпадали. Поразительно, но проанализированные Мандельбротом изменения цен оставались постоянными на протяжении всего шумного периода 60-х, Второй Мировой и депрессии.
Мандельброт проанализировал не только цены на хлопок, но и другие явления. Одним из них была протяженность береговой линии. Карта побережья показывает множество заливов. Но как бы то ни было, при подсчете длины береговой линии будут упущены мелкие заливы, которые слишком малы, чтобы быть показанными на карте. Это подобно тому, как при прогулке по берегу мы пропускаем микроскопические промежутки между песчинками. Неважно, насколько увеличить линию побережья, будет больше видимых промежутков при приближении.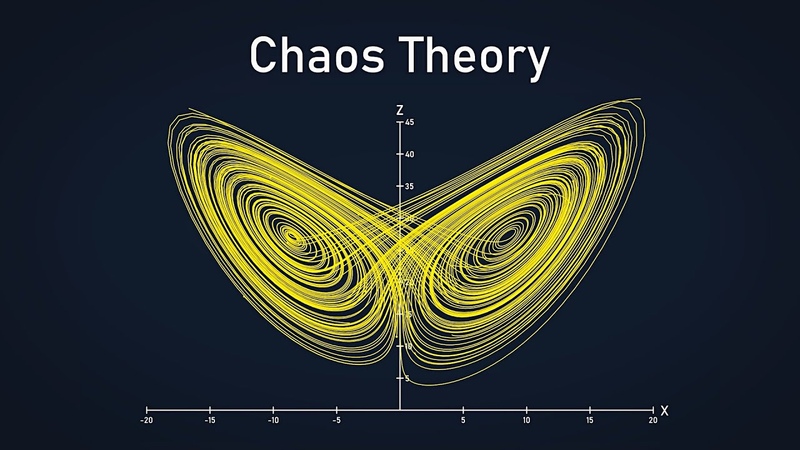
Один математик, Хельге вон Кох взл эту идею для математического конструирования, названного кривой Коха. Чтобы создать кривую Коха, представьте равносторонний треугольник. К середине каждой стороны дорисуйте еще по равностороннему треугольнику.Продолжайте добавлять новые треугольники к серединам каждой из сторон, и в результате получите кривую Коха.(см. Рисунок 4).
Приближенная кривая Коха выглядит точно так же, как и оригинал. Это другой пример самопохожести.
Кривые Коха заключают в себе интересный парадокс. Каждый раз, когда добавляется очередной треугольник, длина линии становится больше. Но как бы то ни было, внутренняя площадь[ограниченная] кривой Коха всегда остается меньше площади описанной окружности вокруг первого треугольника. То есть это линия неограниченной длины, заключенная в ограниченной области.
Чтобы разобраться в этом, математики использовали понятие фрактала. Фрактал происходит от слова дробный. Фрактальное дробление кривой Коха составляет примерно 1. 26. Фрактальное дробление невозможно придумать, но оно имеет смысл. Кривая Коха более грубая, чем гладкая кривая линия, у которой единичное дробление. Так как она грубее и более «морщинистая», она лучше занимает пространство. Как бы то ни было, она не так хороша в заполнении пространства как квадрат с двумя дроблениями, поскольку не имеет площади. Это означает, что дробление кривой Коха меньше 2.
26. Фрактальное дробление невозможно придумать, но оно имеет смысл. Кривая Коха более грубая, чем гладкая кривая линия, у которой единичное дробление. Так как она грубее и более «морщинистая», она лучше занимает пространство. Как бы то ни было, она не так хороша в заполнении пространства как квадрат с двумя дроблениями, поскольку не имеет площади. Это означает, что дробление кривой Коха меньше 2.
Под фракталом имеется ввиду любое изображение, имеющее в себе самопохожесть. Бифуркационная диаграмма уравнения популяции- фрактал. Аттрактор Лоренса- фрактал.Кривая Коха- тоже фрактал.
В это время ученые нашли трудным публиковать работы о Хаосе. С тех пор как они еще не показали его отношение к реальному миру. Большинство ученых не думали, что результаты экспериментов относительно Хаоса важны. Как результат, даже несмотря на то, что Хаос- математический феномен, большинство исследований в области Хаоса были сделаны людьми, являющимися специалистами в других областях, таких как метеорология и экология.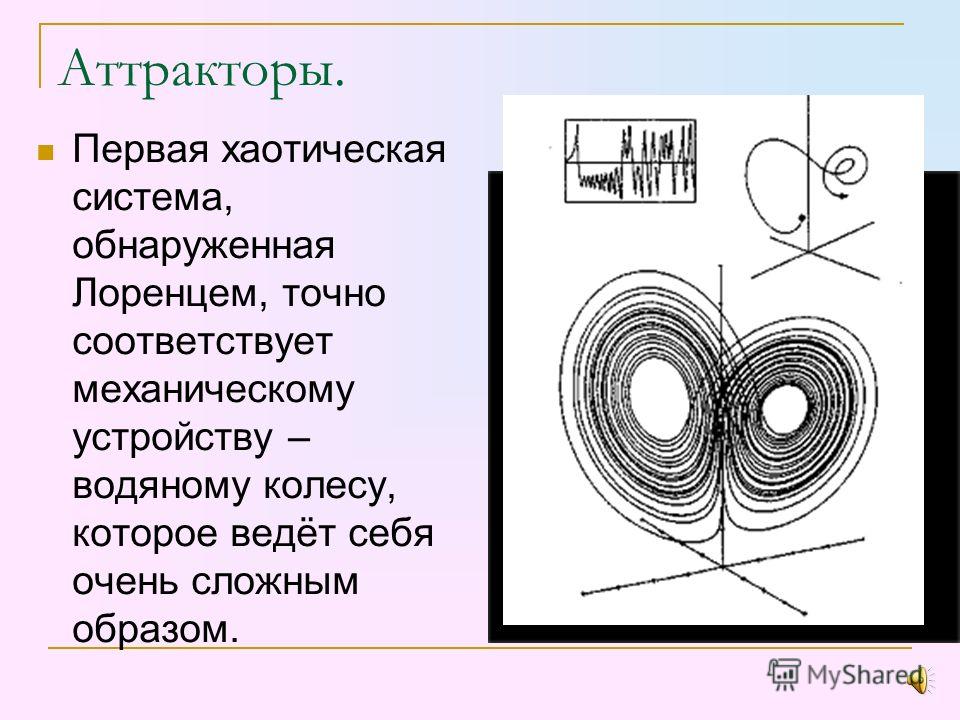 Изучение области распространения Хаоса – было хобби для ученых, работающих над проблемой, что же с этим делать.
Изучение области распространения Хаоса – было хобби для ученых, работающих над проблемой, что же с этим делать.
Позже, ученый по фамилии Фигенбаум снова исследовал диаграмму бифуркации.Он исследовал скорость наступления бифуркации. Он открыл, что она наступает при постоянном показателе. Он вычислил, что это число 4.669. другими словами, он определил точный масштаб при котором кривая бифуркации приобретает свойство самопохожести.
Уменьшенная в 4.669 раз, диаграмма выглядит как последующий регион бифуркации. Он решил посмотреть на другие уравнения чтобы увидеть, возможно ли применить фактор масштаба и к ним. К большому удивлению, фактор масштаба оказался таким же. Не только для сложных уравнений, описывающих закономерность.Закономерность была точно такой же как и у простых уравнений.Он опробовал множество функций, и они давали фактор масштабирования 4.669.
Это было революционным открытием. Он обнаружил целый класс математических функций, ведущих себя одинаково, предсказуемо. Универсальность помогла многим ученым легко анализировать уравнения хаоса. Она дала ученым первые инструменты для анализа хаотических систем. Теперь они могли использовать простые уравнения для получения результата более сложных.
Универсальность помогла многим ученым легко анализировать уравнения хаоса. Она дала ученым первые инструменты для анализа хаотических систем. Теперь они могли использовать простые уравнения для получения результата более сложных.
Многие ученые открыли уравнения, создающие фрактальные уравнения. Самое известное изображение фрактала- является и самым простым. Оно известно как уравнение Мандельброта. Уравнение простое: z=z2+c. Чтобы выяснить, является ли ваше уравнение таковым, возьмите комплексное число z. Получите его квадрат и затем добавьте число. Введите в квадрат полученный результат и добавьте число. Повторяйте далее, и если число стремится к бесконечности, это не уравнение Мандельброта.
Фрактальные структуры были замечены во многих областях реального мира. Кровь разносится по кровеносным сосудам, ветвящимся дальше и дальше, ветви дерева, структура легких, графики данных о продаже акций, и другие системы раельного мира имеют нечто общее: они все обладают самопохожестью(самоповторением).
Ученые в Университете Санта Круз нашли проявления Хаоса в водопроводном кране[то, как он капает]. Записывая падение капель из крана и периоды времени, они открыли точную скорость потока, капли не падали в то же самое время. Когда они построили графики данных, они нашли, что на самом деле капли падают с определенной закономерностью.
Человеческое сердце тоже бьется с хаотической закономерностью. Время между ударами непостоянно, оно зависит от того, насколько активен человек в данный момент, и от многих других вещей. При постоянных условиях сердцебиение все равно может ускориться. При различных условиях сердце бьется неуправляемо. Это можно назвать хаотичным сердцебиением. Анализы сердцебиения могут помочь в медицинских исследованиях найти способ установить сердцебиение в определенных рамках, вместо неконтролируемой хаотичности.
Хаос имеет применение даже в науке. Компьютерные изображения становятся более реалистичными при применении Хаоса и фракталов. Сейчас с помощью простой формулы можно создать на компьютере красивое реалистично выглядещее дерево. Вместо того, чтобы следовать нормальной закономерности, ветки деревьев могут быть созданы по формуле, которая почти, но не точно повторяет себя.
Вместо того, чтобы следовать нормальной закономерности, ветки деревьев могут быть созданы по формуле, которая почти, но не точно повторяет себя.
Также с помощью фракталов может быть создана музыка. Используя аттрактор Лоренса, Диана С. Дэбби, выпускница по специальности электронной инженерии Массачусетского Института Технологий, создала музыкальные темы. («Bach to Chaos: Chaotic Variations on a Classical Theme», Science News, Dec. 24, 1994). Путем ассоциирования музыкальных нот фрагмента музыки из Прелюдии Баха в С с координатами х аттрактора Лоренса, запустив программу на компьютере, она создала вариации на тему данного произведения. Большинство музыкантов, слышавших эти новые звуки, говорили, что вариации очень музыкальны и креативны.
UPD: Благодарю ixside. «Chaotic Variations on a Classical Theme» доступны тут.Правка: перенесено в Научно-популярное.
«Как бы вы простыми словами объяснили ребенку теорию хаоса?» — Яндекс Кью
ПопулярноеСообществаФизикаМатематика+2
Простыми словами ·49,8 KОтветить1УточнитьНадежда ШиховаМатематика
8,6 KРедактор, автор и переводчик книг по математике · 25 янв 2020 ·problemadayЧтобы понять, что такое хаос, лучше всего сравнить хаос с другими системами.
Полностью детерминированная и хорошо предсказуемая система — часы. По начальному положению минутной стрелки можно определить ее положение через час, через полчаса или через сколько хотите. Для этого не нужно следить за стрелкой. Если начальные положения стрелки не сильно отличаются, то и конечные не сильно отличаются.
Недетерминированная и непредсказуемая система — игра-бродилка, в которой ходы определяются бросанием кубика.
Игру начинают всегда в одном и том же месте. И через 10 (например) ходов каждый раз оказываются в разных местах, — предсказать это невозможно. Такая игра — случайный процесс.
- Хаос мы видим в детерминированной и непредсказуемой игре вроде пинбола.

Специальная пружинка толкает шарик, который двигается по игровому полю. Как только шарик выкатился, его путь строго определен, не случаен. Если бы получилось толкнуть шарик в том же направлении и с той же силой, он прокатился бы по тому же пути. В этом отличие от случайного процесса.
Но если хоть чуть-чуть поменять начальное направление или начальное положение шарика, — все, место финиша меняется непредсказуемо. Место финиша мы можем определить, только проследив все движение шарика шаг за шагом. В этом отличие хаотического движения от детерминированного предсказуемого движения часовой стрелки.
2 эксперта согласны
17,7 KAndrei Novikovподтверждает
6 апреля 2022В отличие о большинства ответов, которые уперлись в словарное значения слова «хаос», здесь речь идет именно о… Читать дальше
Комментировать ответ…Комментировать…Антон ТкачевФизика
1,2 KФизик-экспериментатор · 17 авг 2020
Динамический хаос по определению — это сильная зависимость от начальных условий. Прочитав ваш вопрос, я сразу вспомнил стихотворение С. Маршака «Гвоздь и подкова»
Не было гвоздя —
Подкова пропала,
Не было подковы —
Лошадь захромала,
Лошадь захромала —
Командир убит,
Конница разбита,
Армия бежит!
Враг вступает в город,
Пленных не щадя,
Оттого, что в кузнице
Не было… Читать далее
Прочитав ваш вопрос, я сразу вспомнил стихотворение С. Маршака «Гвоздь и подкова»
Не было гвоздя —
Подкова пропала,
Не было подковы —
Лошадь захромала,
Лошадь захромала —
Командир убит,
Конница разбита,
Армия бежит!
Враг вступает в город,
Пленных не щадя,
Оттого, что в кузнице
Не было… Читать далее
wmmaster
19 августа 2020Отличные примеры!
Комментировать ответ…Комментировать…Елена СелезневаОбразование
703Увлеченный учитель со стажем и опытом. Говорить могу о разном: книги, дети, философия и… · 28 авг 2021 ·public210921909Я не объясняю ребенку сакральный смысл данного слова, но использую его как синоним к слову «беспорядок» (для ребенка этого вполне достаточно). Часто, когда хочу показать ценность структурирования знаний, привожу пример. Представьте две комнаты — это склад-хранилище важных вещей. Один хаотично сваливает все вещи в кучу (лень, некогда или не умеет по-другому), а второй… Читать далее
Учитель и ученик в одном лице.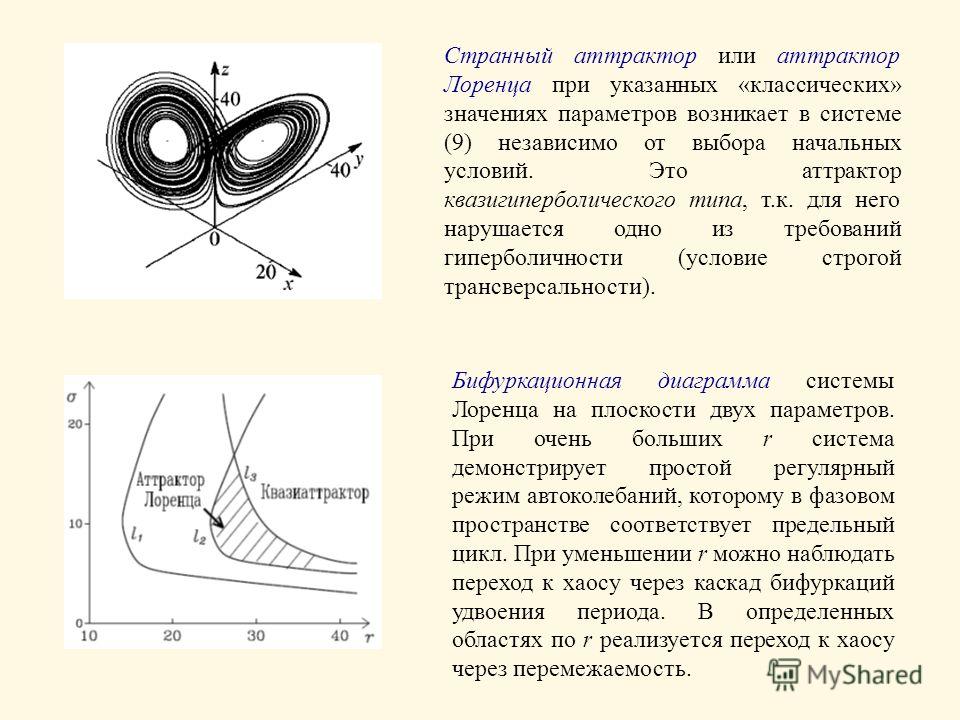 Перейти на vk.com/id645463114 Комментировать ответ…Комментировать…Виктор Палыч Шестипалов
Перейти на vk.com/id645463114 Комментировать ответ…Комментировать…Виктор Палыч ШестипаловПсихология
5,5 KБывший комментатор ЖЖ, могу не отвечать на комментарии. · 10 сент 2020
Ну здесь нужно отталкиваться от возраста ребенка и целей родителя. Для ребенка младше 3-5 лет вообще эта тема не актуальна и интересна только родителю. (Есть конечно вундеркинды, но там совсем другие советы) Для подростка до 12-14 лет «хаос» может быть актуален только с практической точки зрения — для осознания «порядка», как антагониста «хаосу». Для этой задачи я бы… Читать далее
Комментировать ответ…Комментировать…Олег ПапковПрограммирование
512Писатель. Автор мистической книги «Не упасть бы в эту яму!». И научно-фантастической — «… · 21 июн 2021
Для ребенка можно просто, достаточно объяснить.
Солдаты ходят строем — это не хаос.
А мухи вечером возле лампочки на улице летают как попало, хаотически.
С уважением, Олег. Читайте мой роман «БЕСПИЛОТНИК». Мир, как он есть.Перейти на ridero.ru/books/bespilotnik_1
Мир, как он есть.Перейти на ridero.ru/books/bespilotnik_1Филипп Золотухин
25 августа 2021Вы же занудная профессура, коллеги! Это же ребенок! Опыт — вот залог закрепления информации! Запоминайте «заклинани… Читать дальше
Комментировать ответ…Комментировать…Алексей КрутяковОбщество
1,3 Kвоенный инженер-математик на пенсии, интересы: гномоника, воспитание детей, Van-life. · 24 мар 2022 · analemma.ru
Ни одному ребенку я бы не стал объяснять теорию. Все теории в той или иной степени догматичны и «зашоривают» сознание. Вместо этого я бы пытался передать ему понимание и ощущение хаоса. Для ребенка 5-10 лет я бы использовал аналогию с мышлением. Когда ребёнок не спит, его мысли в порядке или беспорядке, то есть в путанном порядке 🙂 А когда он спит, вместо мыслей хаос… Читать далее
Стараюсь жить по истинному времени, поэтому общаюсь в offlineПерейти на analemma.ru3 эксперта не согласны
Борис Державецвозражает
6 апреля 2022Ответ не релевантен. +1
Смотри https://en.wikipedia.org/wiki/Chaos_theory
Основателями теории считаются французский… Читать дальше
+1
Смотри https://en.wikipedia.org/wiki/Chaos_theory
Основателями теории считаются французский… Читать дальше
Пенсионер, йога, политика, немного философии, религиозные темы и др. · 12 янв 2021
- Папа, что такое хаос. — Сынок, это очень просто. Берём твой ящик с игрушками и высыпаем на пол. Теперь то, что мы видим это и есть хаос. Чтобы упорядочить хаос, необходимо выбрать сценарий того, в какую игру, ты хочешь играть. Откладываем те игрушки, которые участвуют в этой игре, а остальные, возвращаем в коробку. Приблизительно так же, это и происходит в Вселенском масштабе…
Безработный философ · 21 дек 2020
Не стоит объяснять ребёнку то, что не имеет никакого отношения к действительности. Теория — это то, что «формулируется, разрабатывается и проверяется в соответствии с научным методом», то есть теория не может выходить за рамки того, что существует в действительности. А в окружающей нас действительности нет ничего, чтобы не подчинялось определённым, ПОСТИГАЕМЫМ законам… Читать далее
А в окружающей нас действительности нет ничего, чтобы не подчинялось определённым, ПОСТИГАЕМЫМ законам… Читать далее
Математик, в свободное время пишу и снимаю научную-фантастику · 23 янв 2020
Смотря, что именно в ней. Если реч о самой концепции, то есть три простых способа: 1) Комната: обратите внимание ребенка, что вещи в комнате оказываются разбросаны, хотя никто не ставил цели их разбросать, но они не когда не буду собаны, если никто не поставит себе цели их собрать (сила прилагаемая для создания хауса меньше, силы необходимой для его устранения) 2)Песок:… Читать далее
Миха@
3 июля 2022Теория Хауса заключается в том что одно случайное действие влияетна другое а финал не предсказуемый.
Комментировать ответ…Комментировать…Татьяна Ивановна387Пенсионерка, врач, неработающая. · 13 нояб 2020
Что такое хаос? Видишь в комнате разбросанные по полу игрушки?
А ведь для каждой есть свое место, своя полка. Когда каждая игрушка стоит на своей полке — это порядок. А когда все разбросано — хаос. 🙄
Когда каждая игрушка стоит на своей полке — это порядок. А когда все разбросано — хаос. 🙄
Объяснение теории хаоса: погружение в непредсказуемую вселенную
Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
Теория хаоса демонстрируется на этом изображении, которое было создано с длительной экспозицией света на конце двойного маятника. (Изображение предоставлено: Wikimedia Commons/Cristian V.)Теория Хаоса объясняет поведение динамических систем, таких как погода, которые чрезвычайно чувствительны к начальным условиям.
Было бы здорово узнать прогноз погоды не только на неделю вперед, но и на месяц или даже на год вперед. Но предсказание погоды сопряжено с рядом сложных проблем, которые мы никогда не сможем полностью решить.
Причина не только в сложности — ученые регулярно решают сложные проблемы с легкостью — это нечто гораздо более фундаментальное. Это то, что было открыто в середине 20-го века: истина о том, что мы живем в хаотической вселенной, которая во многом совершенно непредсказуема. Но глубоко внутри этого хаоса скрыты удивительные закономерности, закономерности, которые, если мы когда-нибудь сможем их полностью понять, могут привести к более глубоким откровениям.
Это то, что было открыто в середине 20-го века: истина о том, что мы живем в хаотической вселенной, которая во многом совершенно непредсказуема. Но глубоко внутри этого хаоса скрыты удивительные закономерности, закономерности, которые, если мы когда-нибудь сможем их полностью понять, могут привести к более глубоким откровениям.
Связанный: Что такое теория струн?
Понимание теории хаоса
Одно из прекрасных свойств физики заключается в том, что она детерминистична. Если вы знаете все свойства системы (где «система» может означать что угодно, от одной частицы в коробке до погодных условий на Земле или даже эволюции самой Вселенной) и вы знаете законы физики, то вы можете прекрасно предсказывать будущее. Вы знаете, как система будет развиваться от штата к штату с течением времени. Это детерминизм. Именно это позволяет физикам предсказывать, как будут развиваться частицы, погода и вся Вселенная.
Однако оказывается, что природа может быть как детерминированной, так и непредсказуемой. Мы впервые получили намеки на этот путь еще в 1800-х годах, когда король Швеции предложил приз тому, кто решит так называемую задачу трех тел. Эта задача связана с предсказанием движения в соответствии с законами Исаака Ньютона. Если два объекта в Солнечной системе взаимодействуют только посредством гравитации, то законы Ньютона точно говорят вам, как эти два объекта будут вести себя в будущем. Но если вы добавите третье тело и позволите ему играть в гравитационную игру, то решения не будет, и вы не сможете предсказать будущее этой системы.
Мы впервые получили намеки на этот путь еще в 1800-х годах, когда король Швеции предложил приз тому, кто решит так называемую задачу трех тел. Эта задача связана с предсказанием движения в соответствии с законами Исаака Ньютона. Если два объекта в Солнечной системе взаимодействуют только посредством гравитации, то законы Ньютона точно говорят вам, как эти два объекта будут вести себя в будущем. Но если вы добавите третье тело и позволите ему играть в гравитационную игру, то решения не будет, и вы не сможете предсказать будущее этой системы.
Французский математик Анри Пуанкаре (вероятно, супергений) получил приз, так и не решив задачу. Вместо того, чтобы решить ее, он написал о проблеме, описав все причины, по которым ее не удалось решить. Одной из наиболее важных причин, которую он выделил, было то, как небольшие различия в начале системы приведут к большим различиям в конце.
Эта идея была в значительной степени отброшена, и физики продолжили, предполагая, что Вселенная детерминистична.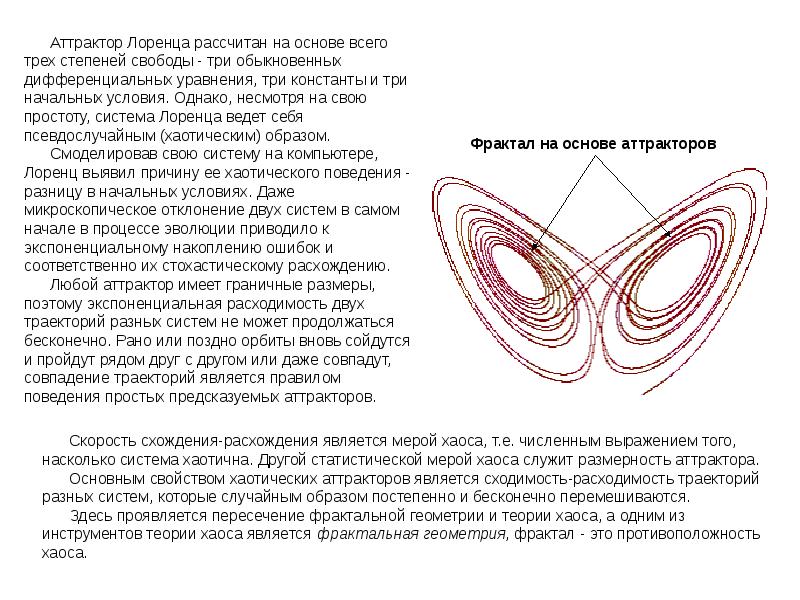 То есть они делали это до середины 20-го века, когда математик Эдвард Лоренц изучал простую модель земной погоды на одном из первых компьютеров. Когда он остановился и перезапустил симуляцию, он получил совершенно другие результаты, чего быть не должно. Он вводил одни и те же данные и решал задачу на компьютере, а компьютеры умеют делать одно и то же снова и снова.
То есть они делали это до середины 20-го века, когда математик Эдвард Лоренц изучал простую модель земной погоды на одном из первых компьютеров. Когда он остановился и перезапустил симуляцию, он получил совершенно другие результаты, чего быть не должно. Он вводил одни и те же данные и решал задачу на компьютере, а компьютеры умеют делать одно и то же снова и снова.
Он обнаружил удивительную чувствительность к начальным условиям. Одна крошечная ошибка округления, не более 1 миллионной, привела бы к совершенно другому поведению погоды в его модели.
По сути, Лоренц открыл хаос.
Хаотические системы повсюду
Термин «Эффект бабочки» был придуман Эдвардом Лоренцем, чтобы помочь описать сложную идею теории хаоса. Он описывает, как очень небольшое изменение в начальном состоянии может привести к большим различиям в более позднем состоянии. Лоренц описал этот эффект, проведя аналогию с бабочкой, взмахивающей крыльями и вызывающей образование урагана за много миль. (Изображение предоставлено: tovfla через Getty Images)
(Изображение предоставлено: tovfla через Getty Images)Это характерный признак хаотической системы, впервые идентифицированный Пуанкаре. Обычно, когда вы запускаете систему с очень небольшими изменениями в начальных условиях, вы получаете только очень небольшие изменения на выходе. Но это не относится к погоде. Одно крошечное изменение (например, взмах крыльев бабочки в Южной Америке) может привести к гигантской разнице в погоде (подобно формированию нового урагана в Атлантике).
Хаотические системы повсюду и доминируют во вселенной. Наденьте маятник на конец другого маятника, и вы получите очень простую, но очень хаотичную систему. Задача трех тел, над которой ломал голову Пуанкаре, представляет собой хаотическую систему. Популяция видов во времени представляет собой хаотичную систему. Хаос повсюду.
Эта чувствительность к начальным условиям означает, что для хаотических систем невозможно делать твердые предсказания, потому что вы никогда не можете знать точно, с точностью до бесконечности десятичной точки состояние системы. И если вы хоть немного ошибетесь, по прошествии достаточного количества времени вы не будете иметь ни малейшего представления о том, что делает система.
И если вы хоть немного ошибетесь, по прошествии достаточного количества времени вы не будете иметь ни малейшего представления о том, что делает система.
Вот почему невозможно точно предсказать погоду.
Связанный: 10 ошеломляющих вещей, которые вы должны знать о квантовой физике
Теория хаоса и секреты фракталов
В этой непредсказуемости и хаосе скрыто несколько удивительных особенностей. В основном они появляются в так называемом фазовом пространстве, карте, описывающей состояние системы в различные моменты времени. Если вы знаете свойства системы на конкретном «моментальном снимке», вы можете описать точку в фазовом пространстве.
По мере того, как система развивается и меняет свое состояние и свойства, вы можете сделать еще один снимок и описать новую точку в фазовом пространстве, со временем создавая набор точек. Имея достаточное количество таких точек, вы можете увидеть, как система вела себя с течением времени.
В некоторых системах присутствует паттерн, называемый аттракторами. Это означает, что независимо от того, где вы запускаете систему, в конечном итоге она переходит в определенное состояние, которое ей особенно нравится. Например, куда бы вы ни бросили мяч в долине, он окажется на дне долины. Это дно является аттрактором этой системы.
Это означает, что независимо от того, где вы запускаете систему, в конечном итоге она переходит в определенное состояние, которое ей особенно нравится. Например, куда бы вы ни бросили мяч в долине, он окажется на дне долины. Это дно является аттрактором этой системы.
Когда Лоренц посмотрел на фазовое пространство своей простой модели погоды, он обнаружил аттрактор. Но этот аттрактор не был похож ни на что, виденное прежде. Его погодная система имела регулярные закономерности, но одно и то же состояние никогда не повторялось дважды. Никакие две точки в фазовом пространстве никогда не пересекались. Всегда.
Противоречие и странные аттракторы
Регулярная погодная система без повторения одного и того же состояния казалась очевидным противоречием. Был аттрактор; т. е. система имела предпочтительный набор состояний. Но такое же состояние никогда не повторялось. Единственный способ описать эту структуру — как фрактал.
Если вы посмотрите на фазовое пространство простой погодной системы Лоренца и увеличите небольшой его фрагмент, вы увидите крошечную версию точно такого же фазового пространства. И если вы возьмете меньшую часть этого и снова увеличите масштаб, вы увидите уменьшенную версию точно такого же аттрактора. И так далее и так до бесконечности. Вещи, которые выглядят одинаково, когда вы смотрите на них ближе, являются фракталами.
И если вы возьмете меньшую часть этого и снова увеличите масштаб, вы увидите уменьшенную версию точно такого же аттрактора. И так далее и так до бесконечности. Вещи, которые выглядят одинаково, когда вы смотрите на них ближе, являются фракталами.
Истории по теме:
Итак, погодная система имеет аттрактор, но это странно. Вот почему их буквально называют странными аттракторами. И они проявляются не только в погоде, но и во всевозможных хаотических системах.
Мы не до конца понимаем природу странных аттракторов, их значение и то, как их использовать для работы с хаотическими и непредсказуемыми системами. Это относительно новая область математики и науки, и мы все еще пытаемся понять ее. Эти хаотические системы могут быть в некотором смысле детерминированными и предсказуемыми. Но это еще предстоит выяснить, так что пока нам придется довольствоваться нашим прогнозом погоды на выходные.
Дополнительные ресурсы
Узнайте больше о теории хаоса из этой пояснительной статьи от The Conversation. Прочтите об Эдварде Лоренце в этой короткой биографии из Университета Сент-Эндрюс. Изучите эффект бабочки более подробно в этой статье на научном коммуникационном веб-сайте «Интересная инженерия».
Прочтите об Эдварде Лоренце в этой короткой биографии из Университета Сент-Эндрюс. Изучите эффект бабочки более подробно в этой статье на научном коммуникационном веб-сайте «Интересная инженерия».
Узнайте больше, прослушав выпуск «Действительно ли Вселенная предсказуема?» в подкасте «Спросите космонавта», доступном в iTunes и в Интернете по адресу http://www.askaspaceman.com.
Пол М. Саттер — астрофизик в Университете штата Огайо , ведущий программ « Спросите космонавта «, и » Космическое радио ,» и автор» Ваше место во Вселенной .»
Спасибо Carlos T., Akanksha B., @TSFoundtainworks и Joyce S. за вопросы, которые привели к этой статье! Задайте свой вопрос в Твиттере, используя хэштег #AskASpaceman или подписавшись на Пола @PaulMattSutter и facebook.com/PaulMattSutter.
Библиография
Эскот Мангас, Лоренцо. «Краткая методологическая заметка по теории хаоса и ее недавним приложениям, основанным на новых компьютерных ресурсах». (2020).
(2020).
Острайхер, Кристиан. «История теории хаоса». Диалоги в клинической неврологии 9.3 (2007): 279.
Гис, Этьен. «Аттрактор Лоренца, парадигма хаоса». Хаос (2013): 1–54.
Уильямс, Гарнетт. Теория хаоса приручена. CRC Press, 1997.
Сивакумар, Белли. «Теория хаоса в геофизике: прошлое, настоящее и будущее». Хаос, солитоны и фракталы 19.2 (2004): 441-462.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: community@space.com.
Главные космические новости, последние новости о запусках ракет, наблюдениях за небом и многое другое!
Свяжитесь со мной, чтобы сообщить о новостях и предложениях от других брендов Future. Получайте электронные письма от нас от имени наших надежных партнеров или спонсоров. Пол М. Саттер — астрофизик из SUNY Stony Brook и Института Флэтайрон в Нью-Йорке. Пол получил докторскую степень по физике в Университете Иллинойса в Урбана-Шампейн в 2011 году и провел три года в Парижском институте астрофизики, после чего получил стажировку в Триесте, Италия. регионов Вселенной до самых ранних моментов Большого Взрыва до охоты за первыми звездами. В качестве «агента к звездам» Пол на протяжении нескольких лет страстно вовлекает общественность в популяризацию науки. Он ведущий популярной программы «Спроси космонавта!» подкаста, автор книг «Твое место во Вселенной» и «Как умереть в космосе», часто появляется на телевидении, в том числе на канале «Погода», где он является официальным специалистом по космосу.
Пол получил докторскую степень по физике в Университете Иллинойса в Урбана-Шампейн в 2011 году и провел три года в Парижском институте астрофизики, после чего получил стажировку в Триесте, Италия. регионов Вселенной до самых ранних моментов Большого Взрыва до охоты за первыми звездами. В качестве «агента к звездам» Пол на протяжении нескольких лет страстно вовлекает общественность в популяризацию науки. Он ведущий популярной программы «Спроси космонавта!» подкаста, автор книг «Твое место во Вселенной» и «Как умереть в космосе», часто появляется на телевидении, в том числе на канале «Погода», где он является официальным специалистом по космосу.
Объяснение теории хаоса: погружение в непредсказуемую вселенную
Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
Теория хаоса демонстрируется на этом изображении, которое было создано с длительной экспозицией света на конце двойного маятника. (Изображение предоставлено: Wikimedia Commons/Cristian V.)
(Изображение предоставлено: Wikimedia Commons/Cristian V.)Теория Хаоса объясняет поведение динамических систем, таких как погода, которые чрезвычайно чувствительны к начальным условиям.
Было бы здорово узнать прогноз погоды не только на неделю вперед, но и на месяц или даже на год вперед. Но предсказание погоды сопряжено с рядом сложных проблем, которые мы никогда не сможем полностью решить.
Причина не только в сложности — ученые регулярно решают сложные проблемы с легкостью — это нечто гораздо более фундаментальное. Это то, что было открыто в середине 20-го века: истина о том, что мы живем в хаотической вселенной, которая во многом совершенно непредсказуема. Но глубоко внутри этого хаоса скрыты удивительные закономерности, закономерности, которые, если мы когда-нибудь сможем их полностью понять, могут привести к более глубоким откровениям.
Связанный: Что такое теория струн?
Понимание теории хаоса
Одно из прекрасных свойств физики заключается в том, что она детерминистична. Если вы знаете все свойства системы (где «система» может означать что угодно, от одной частицы в коробке до погодных условий на Земле или даже эволюции самой Вселенной) и вы знаете законы физики, то вы можете прекрасно предсказывать будущее. Вы знаете, как система будет развиваться от штата к штату с течением времени. Это детерминизм. Именно это позволяет физикам предсказывать, как будут развиваться частицы, погода и вся Вселенная.
Если вы знаете все свойства системы (где «система» может означать что угодно, от одной частицы в коробке до погодных условий на Земле или даже эволюции самой Вселенной) и вы знаете законы физики, то вы можете прекрасно предсказывать будущее. Вы знаете, как система будет развиваться от штата к штату с течением времени. Это детерминизм. Именно это позволяет физикам предсказывать, как будут развиваться частицы, погода и вся Вселенная.
Однако оказывается, что природа может быть как детерминированной, так и непредсказуемой. Мы впервые получили намеки на этот путь еще в 1800-х годах, когда король Швеции предложил приз тому, кто решит так называемую задачу трех тел. Эта задача связана с предсказанием движения в соответствии с законами Исаака Ньютона. Если два объекта в Солнечной системе взаимодействуют только посредством гравитации, то законы Ньютона точно говорят вам, как эти два объекта будут вести себя в будущем. Но если вы добавите третье тело и позволите ему играть в гравитационную игру, то решения не будет, и вы не сможете предсказать будущее этой системы.
Французский математик Анри Пуанкаре (вероятно, супергений) получил приз, так и не решив задачу. Вместо того, чтобы решить ее, он написал о проблеме, описав все причины, по которым ее не удалось решить. Одной из наиболее важных причин, которую он выделил, было то, как небольшие различия в начале системы приведут к большим различиям в конце.
Эта идея была в значительной степени отброшена, и физики продолжили, предполагая, что Вселенная детерминистична. То есть они делали это до середины 20-го века, когда математик Эдвард Лоренц изучал простую модель земной погоды на одном из первых компьютеров. Когда он остановился и перезапустил симуляцию, он получил совершенно другие результаты, чего быть не должно. Он вводил одни и те же данные и решал задачу на компьютере, а компьютеры умеют делать одно и то же снова и снова.
Он обнаружил удивительную чувствительность к начальным условиям. Одна крошечная ошибка округления, не более 1 миллионной, привела бы к совершенно другому поведению погоды в его модели.
По сути, Лоренц открыл хаос.
Хаотические системы повсюду
Термин «Эффект бабочки» был придуман Эдвардом Лоренцем, чтобы помочь описать сложную идею теории хаоса. Он описывает, как очень небольшое изменение в начальном состоянии может привести к большим различиям в более позднем состоянии. Лоренц описал этот эффект, проведя аналогию с бабочкой, взмахивающей крыльями и вызывающей образование урагана за много миль. (Изображение предоставлено: tovfla через Getty Images)Это характерный признак хаотической системы, впервые идентифицированный Пуанкаре. Обычно, когда вы запускаете систему с очень небольшими изменениями в начальных условиях, вы получаете только очень небольшие изменения на выходе. Но это не относится к погоде. Одно крошечное изменение (например, взмах крыльев бабочки в Южной Америке) может привести к гигантской разнице в погоде (подобно формированию нового урагана в Атлантике).
Хаотические системы повсюду и доминируют во вселенной. Наденьте маятник на конец другого маятника, и вы получите очень простую, но очень хаотичную систему. Задача трех тел, над которой ломал голову Пуанкаре, представляет собой хаотическую систему. Популяция видов во времени представляет собой хаотичную систему. Хаос повсюду.
Наденьте маятник на конец другого маятника, и вы получите очень простую, но очень хаотичную систему. Задача трех тел, над которой ломал голову Пуанкаре, представляет собой хаотическую систему. Популяция видов во времени представляет собой хаотичную систему. Хаос повсюду.
Эта чувствительность к начальным условиям означает, что для хаотических систем невозможно делать твердые предсказания, потому что вы никогда не можете знать точно, с точностью до бесконечности десятичной точки состояние системы. И если вы хоть немного ошибетесь, по прошествии достаточного количества времени вы не будете иметь ни малейшего представления о том, что делает система.
Вот почему невозможно точно предсказать погоду.
Связанный: 10 ошеломляющих вещей, которые вы должны знать о квантовой физике
Теория хаоса и секреты фракталов
В этой непредсказуемости и хаосе скрыто несколько удивительных особенностей. В основном они появляются в так называемом фазовом пространстве, карте, описывающей состояние системы в различные моменты времени. Если вы знаете свойства системы на конкретном «моментальном снимке», вы можете описать точку в фазовом пространстве.
Если вы знаете свойства системы на конкретном «моментальном снимке», вы можете описать точку в фазовом пространстве.
По мере того, как система развивается и меняет свое состояние и свойства, вы можете сделать еще один снимок и описать новую точку в фазовом пространстве, со временем создавая набор точек. Имея достаточное количество таких точек, вы можете увидеть, как система вела себя с течением времени.
В некоторых системах присутствует паттерн, называемый аттракторами. Это означает, что независимо от того, где вы запускаете систему, в конечном итоге она переходит в определенное состояние, которое ей особенно нравится. Например, куда бы вы ни бросили мяч в долине, он окажется на дне долины. Это дно является аттрактором этой системы.
Когда Лоренц посмотрел на фазовое пространство своей простой модели погоды, он обнаружил аттрактор. Но этот аттрактор не был похож ни на что, виденное прежде. Его погодная система имела регулярные закономерности, но одно и то же состояние никогда не повторялось дважды. Никакие две точки в фазовом пространстве никогда не пересекались. Всегда.
Никакие две точки в фазовом пространстве никогда не пересекались. Всегда.
Противоречие и странные аттракторы
Регулярная погодная система без повторения одного и того же состояния казалась очевидным противоречием. Был аттрактор; т. е. система имела предпочтительный набор состояний. Но такое же состояние никогда не повторялось. Единственный способ описать эту структуру — как фрактал.
Если вы посмотрите на фазовое пространство простой погодной системы Лоренца и увеличите небольшой его фрагмент, вы увидите крошечную версию точно такого же фазового пространства. И если вы возьмете меньшую часть этого и снова увеличите масштаб, вы увидите уменьшенную версию точно такого же аттрактора. И так далее и так до бесконечности. Вещи, которые выглядят одинаково, когда вы смотрите на них ближе, являются фракталами.
Истории по теме:
Итак, погодная система имеет аттрактор, но это странно. Вот почему их буквально называют странными аттракторами. И они проявляются не только в погоде, но и во всевозможных хаотических системах.
Мы не до конца понимаем природу странных аттракторов, их значение и то, как их использовать для работы с хаотическими и непредсказуемыми системами. Это относительно новая область математики и науки, и мы все еще пытаемся понять ее. Эти хаотические системы могут быть в некотором смысле детерминированными и предсказуемыми. Но это еще предстоит выяснить, так что пока нам придется довольствоваться нашим прогнозом погоды на выходные.
Дополнительные ресурсы
Узнайте больше о теории хаоса из этой пояснительной статьи от The Conversation. Прочтите об Эдварде Лоренце в этой короткой биографии из Университета Сент-Эндрюс. Изучите эффект бабочки более подробно в этой статье на научном коммуникационном веб-сайте «Интересная инженерия».
Узнайте больше, прослушав выпуск «Действительно ли Вселенная предсказуема?» в подкасте «Спросите космонавта», доступном в iTunes и в Интернете по адресу http://www.askaspaceman.com.
Пол М. Саттер — астрофизик в Университете штата Огайо , ведущий программ « Спросите космонавта «, и » Космическое радио ,» и автор» Ваше место во Вселенной . »
»
Спасибо Carlos T., Akanksha B., @TSFoundtainworks и Joyce S. за вопросы, которые привели к этой статье! Задайте свой вопрос в Твиттере, используя хэштег #AskASpaceman или подписавшись на Пола @PaulMattSutter и facebook.com/PaulMattSutter.
Библиография
Эскот Мангас, Лоренцо. «Краткая методологическая заметка по теории хаоса и ее недавним приложениям, основанным на новых компьютерных ресурсах». (2020).
Острайхер, Кристиан. «История теории хаоса». Диалоги в клинической неврологии 9.3 (2007): 279.
Гис, Этьен. «Аттрактор Лоренца, парадигма хаоса». Хаос (2013): 1–54.
Уильямс, Гарнетт. Теория хаоса приручена. CRC Press, 1997.
Сивакумар, Белли. «Теория хаоса в геофизике: прошлое, настоящее и будущее». Хаос, солитоны и фракталы 19.2 (2004): 441-462.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: community@space. com.
com.
Главные космические новости, последние новости о запусках ракет, наблюдениях за небом и многое другое!
Свяжитесь со мной, чтобы сообщить о новостях и предложениях от других брендов Future. Получайте электронные письма от нас от имени наших надежных партнеров или спонсоров. Пол М. Саттер — астрофизик из SUNY Stony Brook и Института Флэтайрон в Нью-Йорке. Пол получил докторскую степень по физике в Университете Иллинойса в Урбана-Шампейн в 2011 году и провел три года в Парижском институте астрофизики, после чего получил стажировку в Триесте, Италия. регионов Вселенной до самых ранних моментов Большого Взрыва до охоты за первыми звездами. В качестве «агента к звездам» Пол на протяжении нескольких лет страстно вовлекает общественность в популяризацию науки. Он ведущий популярной программы «Спроси космонавта!» подкаста, автор книг «Твое место во Вселенной» и «Как умереть в космосе», часто появляется на телевидении, в том числе на канале «Погода», где он является официальным специалистом по космосу.

