Зависимые или независимые выборки
Следует отличать зависимые и независимые выборки, так как для них используются разные критерии при проверке гипотез. [15]
Независимые выборки, если мы из генеральной совокупности случайным образомвыбрали какое-либо количество человек и поделили выбранных нами людей на две группы либо также случайно, либо относительно некоего признака, например, пола.
Зависимые выборки, если мы случайным образом выбрали из генеральной совокупности некоторые пары, сформировав из них две группы, (близнецы, муж-жена и т.д.) или же <мерили> одного и того же респондента до и после эксперимента. Иными словами, выборка парная, — когда один респондент в первой группе по какому-либо содержательному признаку сопоставляется с соответствующим респондентом во второй группе, например, муж из первой группы сравнивается со своей женой, которая во второй группе. Все сказанное можно представить в виде картинки:
Теперь
определим, какие выборки у нас в трех
примерах, предложенных выше.
Таблица № 2.
Пример №1 | Пример №2 | Пример №3 |
Критерий для независимых выборок | Критерий для зависимых выборок | Критерий для независимых выборок |
При проверке статистической гипотезы обязательно должен учитываться объем выборки. Этой теме, а также проблеме репрезентативности выборки, посвящено большое количество работ. В нашем случае объем выборки говорит нам о том, какой критерий мы выберем для проверки гипотезы, и каким распределением будем пользоваться.
Когда
мы проверяем гипотезу о равенстве
средних, мы можем считать либо z-критерий,
либо t-критерий, который в свою очередь
делится на t-критерий для выборок с
равными дисперсиями и на t-критерий для
выборок с неравными дисперсиями.
Если
мы применяем z-критерий, то потом
пользуемся нормальным распределением,
если мы применяем t-критерий, то пользуемся
распределением Стьюдента (t-распределением).
Определить, какой критерий выбрать,
можно следующим образом:
1. Если известны дисперсиигенеральной совокупности, мы всегда используем z-критерий. (При этом, если объем выборки менее 30, значения переменной в генеральной совокупности должны быть распределены хотя бы примерно нормально.)
2. Если дисперсии неизвестны, но объем выборок достаточно большой[16] — более 30 — мы считаем, что выборочные дисперсии примерно равны дисперсиям генеральной совокупности и используем z-критерий.
3.
Если дисперсии
неизвестны и объем выборок небольшой —
менее 30 — используется t-критерий. При
этом если известно, что дисперсии двух
выборок равны, мы используем t-критерий
для равных дисперсий, иначе — t-критерий
для неравных дисперсий (Значения
переменной в генеральной совокупности
должны быть распределены хотя бы примерно
нормально).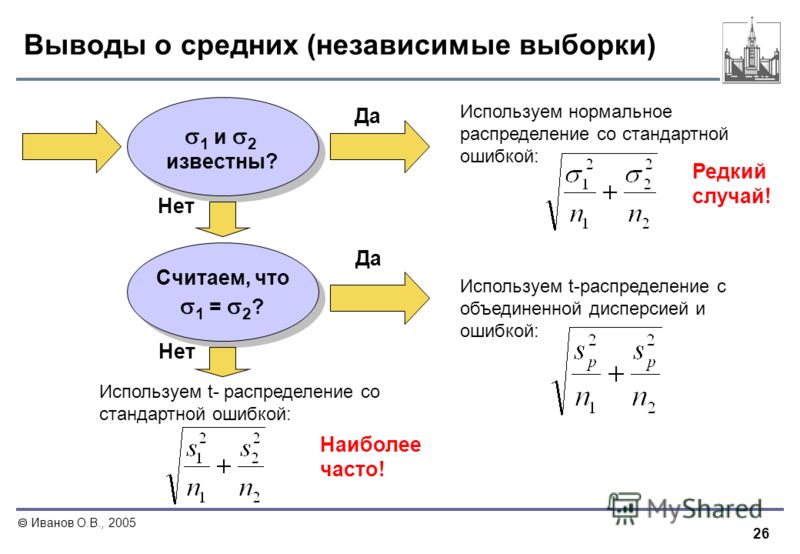
Сказанное можно представить
в виде схемы:
Несколько слов о сходстве и различии нормального распределения и распределения Стьюдента.
Сходства распределения Стьюдента со стандартизированным нормальным распределением N(0,1):
1. Оба распределения имеют форму колокола.
2. Оба распределения симметричны относительно среднего.
3. Среднее, мода и медиана равны нулю и находятся в центре распределения.
4. Кривая распределения не пересекает ось Х.
Отличия распределения Стьюдента от нормального распределения:
1. Дисперсия распределения Стьюдента больше единицы.
2. t-распределение относится к семейству распределений, каждое из которых определяется количеством степеней свободы, зависящим от объема выборки.
3. С увеличением объема выборки распределение Стьюдента стремиться к нормальному.
4.
t-распределение с меньшим числом степеней
свободы имеет более плоскую форму.
Чем
меньше количество степеней свободы,
тем более <размазанная> средняя часть
распределения и более длинные <хвосты>.
Зависимые и независимые выборки
- Главная страница 🏠
- 👉 Эконометрика 👈
- Шпоры по курсу Анализ данных
- Зависимые и независимые выборки
Нужна помощь в написании работы?
Узнать стоимость
При сравнении двух (и более) выборок важным параметром является их зависимость.
Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:
- пары близнецов,
- два измерения какого-либо признака до и после экспериментального воздействия,
- мужья и жёны
- и т. п.
В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:
- мужчины и женщины,
- психологи и математики.
Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.
Сравнение выборок производится с помощью различных статистических критериев:
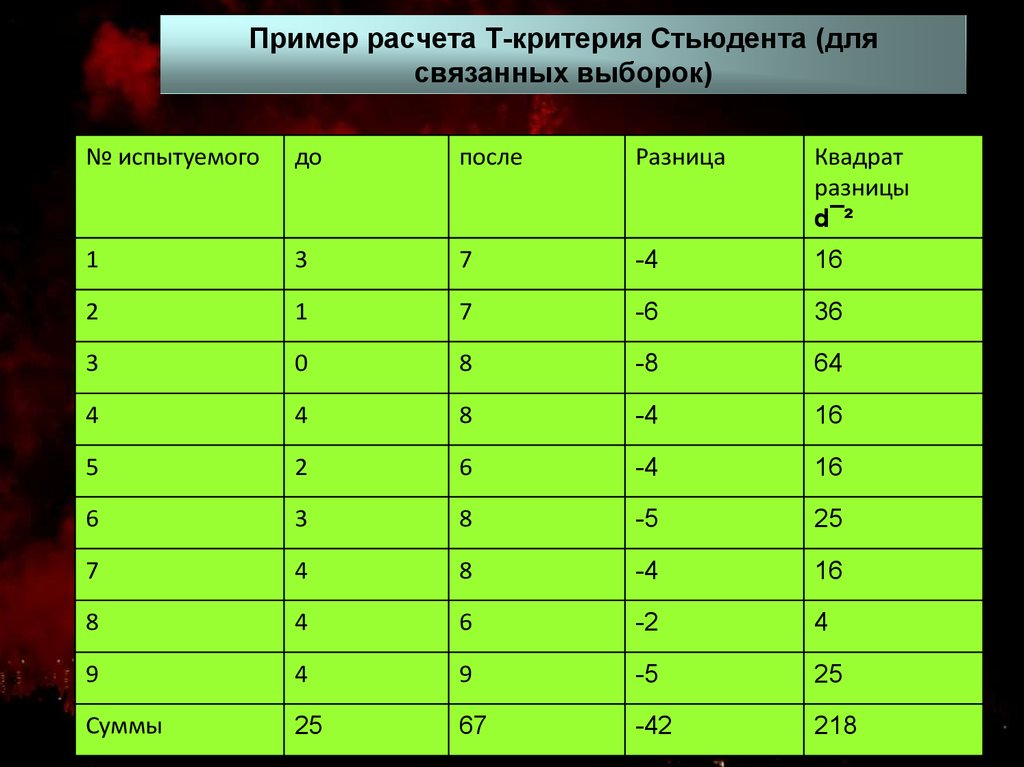
- t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента.
Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. - T-критерий Вилкоксона
- U-критерий Манна-Уитни — статистический критерий, используемый для оценки различий между двумя выборками по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками.
- Критерий знаков
- и др.
Поможем написать любую работу на аналогичную тему
Реферат
Зависимые и независимые выборки
От 250 руб
Контрольная работа
Зависимые и независимые выборки
От 250 руб
Курсовая работа
Зависимые и независимые выборки
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Меню
Предмет, методы, инструменты и сферы применения анализа данных (учебник).
Понятие статистика и статистический анализ. Статистические методы.
Статистический анализ конкретных данных
Классификация статистических методов
Прикладная статистика
Вероятностно-статистическое моделирование
Статистический анализ конкретных данных
Перспективы развития статистических методов
Основные понятия статистического анализа.
Добавить в избранное (необходима авторизация)
терминология — зависимые и независимые выборки
спросил
Изменено 10 лет, 7 месяцев назад
Просмотрено 21к раз
$\begingroup$
Я искал в сети термины зависимые и независимые выборки, но не смог найти ни правильного определения, ни сделать вывод, что это такое. Было бы неплохо, если бы кто-нибудь из вас мог объяснить это и дать нам знания.
- терминология
- образец
$\endgroup$
6
$\begingroup$
Читая все ответы и комментарии, становится ясно, что у нас есть небольшая Уловка-22.
Люди не могут ответить на вопрос без дополнительного контекста, но, похоже, вопрос требует для этого контекста.
Итак, я собираюсь попытаться угадать, что означает держатель стека безмятежности.
Две выборки (или более двух) являются зависимыми, если они каким-то образом связаны, не обязательно наличием сходных результатов, а тем, что один результат каким-то образом зависит от другого результата. Например, предположим, что меня интересует сравнение роста мужчин и женщин. Если я случайным образом выберу 50 женщин и 50 мужчин из некоторого населения, выборки будут независимыми, потому что рост одного человека не имеет отношения к росту другого человека. Одно не дает никакой информации о другом. Однако, если бы я выбрал 50 гетеросексуальных пар, две выборки были бы не быть независимыми, потому что люди склонны вступать в брак с людьми одинакового роста.
Надеюсь, это поможет!
$\endgroup$
$\begingroup$
@whuber прав, нам нужно немного больше контекста, чтобы расшифровать, что вы подразумеваете под «образцами».
Если вы имеете в виду «образцы» в смысле «результат выборки» и, таким образом, используете этот термин как синоним «реализации», тогда применяется следующее:
Образцы зависят от некоторых (или, возможно, отсутствующих) предварительных знаний тогда и только тогда, когда знание чего-то об одном образце может рассказать вам что-то новое о другом образце.
Наиболее распространен случай, когда выборки $x_1, x_2$ равны , предполагается, что распределены «независимо и одинаково» в соответствии с распределением $D$. В этом случае, учитывая, что вы знаете, что $D$ является, скажем, нормальным распределением со средним значением, равным нулю, и дисперсией, равной единице, зная, что значение $x_1$ равно $1,2$, вы по-прежнему верите в то, что $x_2$ соответствует $D$. Однако, не зная $D$, но зная, что выборки были идентифицированы из какого-то нормального распределения, выборки остаются явно зависимыми: знание чего-то об одном говорит вам что-то о $D$, что говорит вам что-то о другом.
Без предположения о зависимости или независимости между выборками невозможно узнать, зависимы они или независимы, но часто можно сделать хорошие предположения, пытаясь найти закономерности. Корреляция, приведенный выше пример, является лишь одним из таких паттернов.
$\endgroup$
9
$\begingroup$
терминология:
Я химик. У меня есть много выборок, которые вместе образуют одну выборку в статистическом смысле.
см. также: Как определить, что такое «образец»?
Может быть, для начала список с простыми случаями:
если ваши выборки коррелированы, то они не независимы (но вы не можете сделать вывод наоборот).
(очевидно): если одна выборка влияет на другую, они не являются независимыми
если вы знаете причину, влияющую на оба образца, они не являются независимыми
Если вы можете уточнить прогноз того, что вас интересует для одной выборки, когда вы знаете результат для другой выборки (то есть лучше, чем угадывать из общего распределения), то выборки не являются независимыми.
всегда трудно спорить о независимости: Представьте, что вы изучаете цвет волос и для этого каждые 30 минут собираете людей с улицы перед вашим офисом. Вы можете считать людей независимыми: нет лучшего способа предсказать цвет волос другого человека, чем угадать средний цвет волос. Но как узнать (доказать!), что вы не просто упустили нужную модель для предсказания цвета волос?
(Не)зависимость может обсуждаться в отношении объема исследования: теперь ваш коллега на другом конце земного шара присоединяется к вашему исследованию и посылает вам цвета волос людей перед его офисом. Теперь вы можете предсказать будущие волосы лучше, чем обычное предположение по последнему собранному цвету волос: цвет волос не зависит от географического региона.
Вы можете сказать, что изучаемая популяция должна быть четко определена, чтобы аргументировать (не)зависимость: это «цвет волос, появляющийся перед моим офисом» или это «цвет волос людей»?
$\endgroup$
5
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Зависимый T-тест — Введение в то, когда использовать этот тест и какие переменные необходимы
Зависимый T-тест — Введение в то, когда использовать этот тест и какие переменные необходимы | Статистика ЛаэрдЧто делает этот тест?
Зависимый t-критерий (также называемый парным t-критерием или t-тестом для парных выборок) сравнивает средние значения двух связанных групп, чтобы определить, существует ли статистически значимое различие между этими средними значениями.
Какие переменные нужны для зависимого t-критерия?
Вам нужна одна зависимая переменная, которая измеряется по шкале интервалов или отношений (см. наше руководство по типам переменных, если вам нужны разъяснения). Вам также нужна одна категориальная переменная, которая имеет только две связанные группы.
Присоединяйтесь к 10 000 студентов, ученых и профессионалов, которые полагаются на статистику Laerd.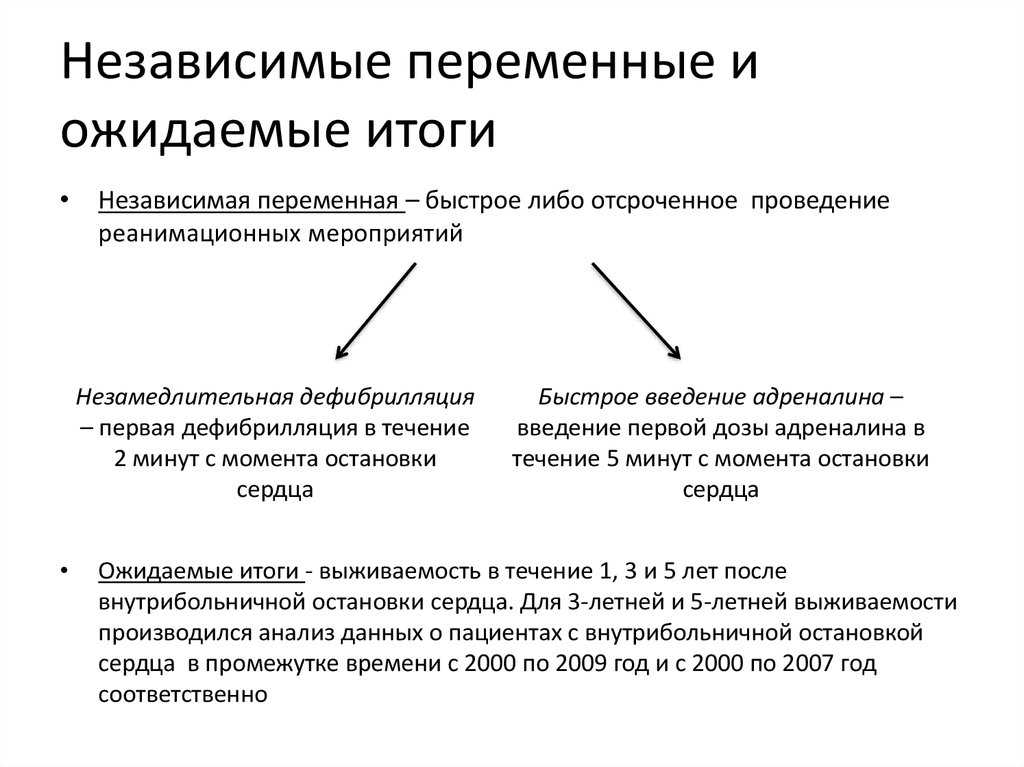
ПОСМОТРЕТЬ ПЛАНЫ ТУРОВ И ЦЕНЫ
Что подразумевается под «родственными группами»?
Зависимый t-критерий является примером статистического теста «внутри субъектов» или «повторных измерений». Это указывает на то, что одни и те же участники тестируются более одного раза. Таким образом, в зависимом t-критерии «связанные группы» указывают на то, что одни и те же участники присутствуют в обеих группах. Причина, по которой в каждой группе могут быть одни и те же участники, заключается в том, что каждый участник измерялся дважды по одной и той же зависимой переменной. Например, вы могли бы измерить результаты 10 участников теста на правописание (зависимая переменная) до и после того, как они прошли новую форму компьютеризированного метода обучения для улучшения правописания. Вы хотели бы знать, улучшилось ли компьютерное обучение их правописанию. Здесь мы можем использовать зависимый t-критерий, потому что у нас есть две связанные группы. Первая родственная группа состоит из участников в начале (до) компьютеризированного обучения заклинаниям, а вторая родственная группа состоит из тех же участников, но уже в конце компьютеризированного обучения.
Проверяет ли зависимый t-критерий «изменения» или «различия» между родственными группами?
Зависимый t-критерий можно использовать для проверки «изменения» или «различия» в средних значениях между двумя родственными группами, но не для того и другого одновременно. Измеряете ли вы «изменение» или «разницу» между средними значениями двух связанных групп, зависит от плана вашего исследования. Два типа дизайна исследования показаны на следующих диаграммах.
Как определить различия между экспериментальными условиями с помощью зависимого t-критерия?
Зависимый t-критерий позволяет искать «различия» между средними значениями, когда участники оцениваются по одной и той же зависимой переменной в двух разных условиях. Например, вы могли протестировать зрение участников (зависимая переменная) при ношении очков двух разных типов (независимая переменная). См. диаграмму ниже для общей схемы этого подхода к проектированию (щелкните изображение, чтобы увеличить его):
Узнайте больше о зависимом t-критерии на следующей странице.
