Выборки зависимые и независимые: Сравнение двух выборок

Сравнение двух выборок

Сравнение двух выборок Содержание > Процедуры > Анализ
С помощью этой процедуры вы можете сравнить две выборки (зависимую и независимую) по совокупности показателей используя t критерий Стьюдента или критерий W Вилкоксона. 
Как следует из проведенного эксперимента, результаты применения критериев W Вилкоксона и U Манна-Уитни практически идентичны.

Порядок выполнения процедуры:

1. Тип сравнения — в первую очередь вам надо определиться какие выборки вы хотите сравнить - зависимые или независимые.  Независимые выборки - сравниваются две разные группы, например мужчины и женщины, молодые и пожилые и т. д. Зависимые выборки как правило возникают, когда речь идет об одной группе испытуемых до и после эксперементального воздействия. Так же зависимыми выборками могут быть например мужья и жены, близнецы и т.п. При этом предполагается что в данных они (семья, пара близнецов, испытуемый до или после эксперимента)  занимают одну, а не две строчки.

2. Для Независимых выборок вам нужно указать 2 сравниваемые группы -перетащить из Структуры два сопоставляемых значения (например: Пол.Мужской и Пол.Женский). Затем нужно перетащить из Структуры список показателей, по которым будет производится сравнение в раздел Выбранные переменные.

3. Для Зависимых выборок вам нужно перетащить из Структуры два списка (список показателей в обоих списках должен быть идентичный):

• Выбранные переменные - список показателей, характеризующих первую выборку. 
• Сопоставляемые переменные — список показателей, характеризующих вторую выборку.

4. Критерий сравнения — определитесь какой критерий сравнения  является для вас основным — t-Стьюдента или W Вилкоксона.
С одной стороны, t-Стьюдента эффективен , если распределение по показателям близкое к нормальному, в противном случае более эффективен критерий W Вилкоксона. С другой стороны, при объеме (каждой)  выборки  более 50, результаты критерия W Вилкоксона, как правило,  начинают соответствовать результатам t-Стьюдента и на больших выборках более эффективным будет критерий Стьюдента.

5. Нажмите [Пересчитать] (при необходимости).

Программа рассчитает таблицу, содержащую следующие колонки:

• Среднее для 1 группы
• Среднее для 2 группы
• t — критерий Стьюдента
• Tp — вероятность ошибки для критерия Стьюдента.
• Wp — вероятность ошибки для критерия Вилкоксона.

Как правило, значимыми считаются различия, если вероятность ошибки менее 0,05 или 0,01.

Под таблицей вы можете посмотреть Подробности по каждой строке, содержащую пояснения и дополнительную информацию. Вы можете мышкой выделить фрагмент текста и правой кнопкой скопировать его в буфер обмена.

На странице Радиальная диаграммабудет представлено наглядное сопоставление  2х выборок. При этом значимые различия  (по t-Стьюдента или W Вилкоксона, в зависимости от выбора критерия сравнения) между группами будут отмечены особыми рамочками показателей. Если у вас много сопоставляемых показателей, то для их эффективного отображения на радиальной диаграмме их стоит либо разбить на несколько групп, либо назвать как можно кратко. См. дополнительно «Работа с радиальной диаграммой».

Дополнительные возможности:

• Если выбрана сегментирующая переменная, то справа внизу окна присутствует переключатель групп для анализа. Например, если таковой выбрана переменная Пол, то с его помощью вы можете быстро посмотреть таблицу для всего массива,  для мужчин, для женщин. Более сложную сегментацию вы можете настроить в меню программы с помощью кнопки [Подмассив].
• Вы можете копировать таблицу или радиальную диаграмму в буфер обмена с помощью кнопки [Копировать] в меню программы.

Зависимые или независимые выборки

Следует отличать зависимые и независимые выборки, так как для них используются разные критерии при проверке гипотез.

 [15]

Независимые выборки, если мы из генеральной совокупности случайным образомвыбрали какое-либо количество человек и поделили выбранных нами людей на две группы либо также случайно, либо относительно некоего признака, например, пола.

Зависимые выборки, если мы случайным образом выбрали из генеральной совокупности некоторые пары, сформировав из них две группы, (близнецы, муж-жена и т.д.) или же <мерили> одного и того же респондента до и после эксперимента. Иными словами, выборка парная, — когда один респондент в первой группе по какому-либо содержательному признаку сопоставляется с соответствующим респондентом во второй группе, например, муж из первой группы сравнивается со своей женой, которая во второй группе. Все сказанное можно представить в виде картинки:

Теперь определим, какие выборки у нас в трех примерах, предложенных выше. Нетрудно увидеть, что первый и третий примеры — независимые выборки, а второй пример — зависимые выборки.

Таблица № 2.

Пример №1	Пример №2	Пример №3
Критерий для независимых выборок	Критерий для зависимых выборок	Критерий для независимых выборок

При проверке статистической гипотезы обязательно должен учитываться объем выборки. Этой теме, а также проблеме репрезентативности выборки, посвящено большое количество работ. В нашем случае объем выборки говорит нам о том, какой критерий мы выберем для проверки гипотезы, и каким распределением будем пользоваться.

Когда мы проверяем гипотезу о равенстве средних, мы можем считать либо z-критерий, либо t-критерий, который в свою очередь делится на t-критерий для выборок с равными дисперсиями и на t-критерий для выборок с неравными дисперсиями. Если мы применяем z-критерий, то потом пользуемся нормальным распределением, если мы применяем t-критерий, то пользуемся распределением Стьюдента (t-распределением). Определить, какой критерий выбрать, можно следующим образом:

1.      Если известны дисперсиигенеральной совокупности, мы всегда используем z-критерий. (При этом, если объем выборки менее 30, значения переменной в генеральной совокупности должны быть распределены хотя бы примерно нормально.)

2.      Если 

дисперсии неизвестны, но объем выборок достаточно большой[16] — более 30 — мы считаем, что выборочные дисперсии примерно равны дисперсиям генеральной совокупности и используем z-критерий.

3.      Если дисперсии неизвестны и объем выборок небольшой — менее 30 — используется t-критерий. При этом если известно, что дисперсии двух выборок равны, мы используем t-критерий для равных дисперсий, иначе — t-критерий для неравных дисперсий (Значения переменной в генеральной совокупности должны быть распределены хотя бы примерно нормально). Сказанное можно представить в виде схемы:

Несколько слов о сходстве и различии нормального распределения и распределения Стьюдента.

 

Сходства распределения Стьюдента со стандартизированным нормальным распределением N(0,1):

1.      Оба распределения имеют форму колокола.

2.      Оба распределения симметричны относительно среднего.

3.      Среднее, мода и медиана равны нулю и находятся в центре распределения.

4.      Кривая распределения не пересекает ось Х.

Отличия распределения Стьюдента от нормального распределения:

1.      Дисперсия распределения Стьюдента больше единицы.

2.      t-распределение относится к семейству распределений, каждое из которых определяется количеством степеней свободы, зависящим от объема выборки.

3.      С увеличением объема выборки распределение Стьюдента стремиться к нормальному.

4.      t-распределение с меньшим числом степеней свободы имеет более плоскую форму. Чем меньше количество степеней свободы, тем более <размазанная> средняя часть распределения и более длинные <хвосты>.

 

Зависимые и независимые выборки • Простое объяснение

Чем отличается зависимая выборка от независимой выборки? И почему важно знать разницу? Независимо от того, получены ли данные от зависимого или независимая выборка определяет, какой используется проверка гипотез.

Если ваши данные независимы, например, независимые выборки t-критерий или ANOVA без повторных измерений вычислено. Если ваши данные зависят, t-критерий для зависимых выборок или ANOVA с повторными измерениями рассчитывается.

Пример независимой и зависимой переменной

Допустим, вы хотите узнать, влияют ли праздники на стресс людей. уровни. Чтобы узнать, вы создали небольшой онлайн-опрос на datatab.net, который позволяет вам для измерения уровня стресса людей. В опросе вы спрашиваете людей об их стрессе уровни до и после отпуска. Теперь у вас есть два варианта:

В левом случае у вас будет независимая выборка, потому что люди, которых вы интервью перед праздником не имеют ничего общего с людьми, которых вы интервьюировали после праздник.

В правильном случае у вас была бы зависимая выборка, вы бы опросили людей до того, как праздник и интервьюировать тех же людей после праздника, поэтому меры всегда доступны парами. В данном случае это предпочтительное решение для данного исследования. вопрос!

Зависимый образец

В зависимой выборке меры связаны между собой. Например, если взять образец людей, перенесших операцию на колене, и опросить их до и после операции, это зависимая выборка. Это потому, что один и тот же человек был опрошен в два разные времена.

Конечно, не обязательно должны быть отношения «до и после». изучал.

Например, если вы хотите выяснить, влияет ли новая бейсбольная бита на производительность ватина, и одни и те же люди играют один раз со старой битой и один раз с новый, то у вас зависимый образец. В этом случае измерения также доступны в парах, каждый игрок использовал обе биты, поэтому есть два измерения для каждый игрок.

И это не обязательно должен быть один и тот же человек. Например, если вы хотите узнать если в отношениях между мужчинами и женщинами женщины больше занимаются садоводством, чем мужчины, вы также будет иметь зависимую выборку. У вас будет две меры, которые всегда идут вместе парами, всегда одна женщина и один мужчина.

Независимый образец

В независимых выборках значения поступают из двух или более разных групп. Например, если мужскую группу и женскую группу спросить об их доходах, независимые образцы есть. В этом случае лицо из одной выборки не может быть отнесено к лицу из другого образца.

Более двух зависимых или независимых образцов

Конечно, в случае независимой и зависимой выборки их может быть более двух. образцы. Важно то, что в случае независимой выборки группы или выборки никак не связаны друг с другом, а в случае зависимых выборке респондент появляется во всех группах.

Проверка гипотез для зависимых и независимых выборок

В общем, всегда есть проверка гипотезы для независимых выборок и аналог для зависимых выборок. Вместо термина зависимый и независимый, парный и непарные часто используются в случае дисперсионного анализа с повторением и без него. меры, а также парные и непарные в случае t-критерия.

Зависимый образец	Независимый образец
t-критерий для зависимых выборок	t-критерий для независимых выборок
ANOVA с повторным измерением	ANOVA без повторного измерения
Тест Уилкоксона	U-тест Манна-Уитни
Тест Фридмана	Тест Крускала-Уоллиса

В DATAtab вы можете одним щелчком выбрать, хотите ли вы рассчитать соответствующий проверка гипотезы для зависимых или независимых выборок.

В зависимости от формата, в котором вы вставляете свои данные, предварительно выбирается вариант. Обычно серия — это респондент или, в более общем смысле, случай. Поэтому, метрические значения находящиеся в ряду, изначально считаются зависимыми.

Если метрика и категориальная переменная при нажатии автоматически выбирается соответствующий независимый тест.

Терминология

— зависимые и независимые выборки

спросил 11 лет, 2 месяца назад

Изменено 11 лет, 2 месяца назад

Просмотрено 21к раз

$\begingroup$

Я искал в сети термины зависимые и независимые выборки, но не смог найти ни правильного определения, ни сделать вывод, что это такое. Было бы неплохо, если бы кто-нибудь из вас мог объяснить это и дать нам знания.

• терминология
• образец

$\endgroup$

6

$\begingroup$

Читая все ответы и комментарии, становится ясно, что у нас есть небольшая Уловка-22. Люди не могут ответить на вопрос без дополнительного контекста, но вопрос, кажется, , задающий для этого контекста.

Итак, я собираюсь попытаться угадать, что означает держатель стека безмятежности.

Две выборки (или более двух) являются зависимыми, если они каким-то образом связаны, не обязательно наличием сходных результатов, а тем, что один результат каким-то образом зависит от другого результата. Например, предположим, что меня интересует сравнение роста мужчин и женщин. Если я случайным образом выберу 50 женщин и 50 мужчин из некоторого населения, выборки будут независимыми, потому что рост одного человека не имеет отношения к росту другого человека. Одно не дает никакой информации о другом. Однако, если бы я выбрал 50 гетеросексуальных пар, две выборки были бы а не быть независимыми, потому что люди склонны вступать в брак с людьми одинакового роста.

Надеюсь, это поможет!

$\endgroup$

$\begingroup$

@whuber прав, что нам нужно немного больше контекста, чтобы расшифровать, что вы подразумеваете под «образцами». Если вы имеете в виду «образцы» в смысле «результат выборки» и, таким образом, используете этот термин как синоним «реализации», тогда применяется следующее:

Образцы зависят от некоторых (или, возможно, отсутствующих) предварительных знаний тогда и только тогда, когда знание чего-то об одном образце может рассказать вам что-то новое о другом образце.

Наиболее распространен случай, когда выборки $x_1, x_2$ равны , предполагается, что распределены «независимо и одинаково» в соответствии с распределением $D$. В этом случае, учитывая, что вы знаете, что $D$ является, скажем, нормальным распределением со средним значением, равным нулю, и дисперсией, равной единице, зная, что значение $x_1$ равно $1,2$, вы по-прежнему верите в то, что $x_2$ соответствует $D$.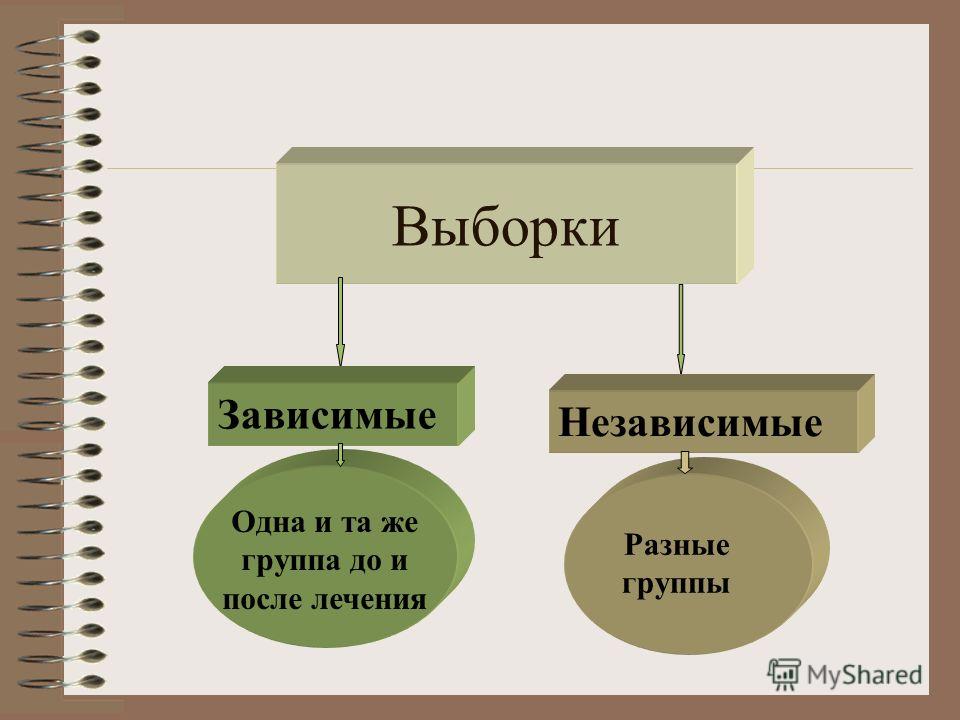 Однако, не зная $D$, но зная, что выборки были идентифицированы из какого-то нормального распределения, выборки остаются явно зависимыми: знание чего-то об одном говорит вам что-то о $D$, что говорит вам что-то о другом.

Без предположения о зависимости или независимости между образцами невозможно узнать, зависимы они или независимы, но часто можно сделать хорошие предположения, пытаясь найти закономерности. Корреляция, приведенный выше пример, является лишь одним из таких паттернов.

$\endgroup$

9

$\begingroup$

терминология:
Я химик. У меня есть много выборок, которые вместе образуют одну выборку в статистическом смысле.
см. также: Как определить, что такое «образец»?

Может быть для начала список с простыми случаями:

• если ваши выборки коррелированы, то они не независимы (но вы не можете сделать вывод наоборот).

• (очевидно): если одна выборка влияет на другую, они не являются независимыми

• если вы знаете причину, влияющую на оба образца, они не являются независимыми

• Если вы можете уточнить прогноз того, что вас интересует для одной выборки, когда вы знаете результат для другой выборки (то есть лучше, чем угадывать из общего распределения), то выборки не являются независимыми.