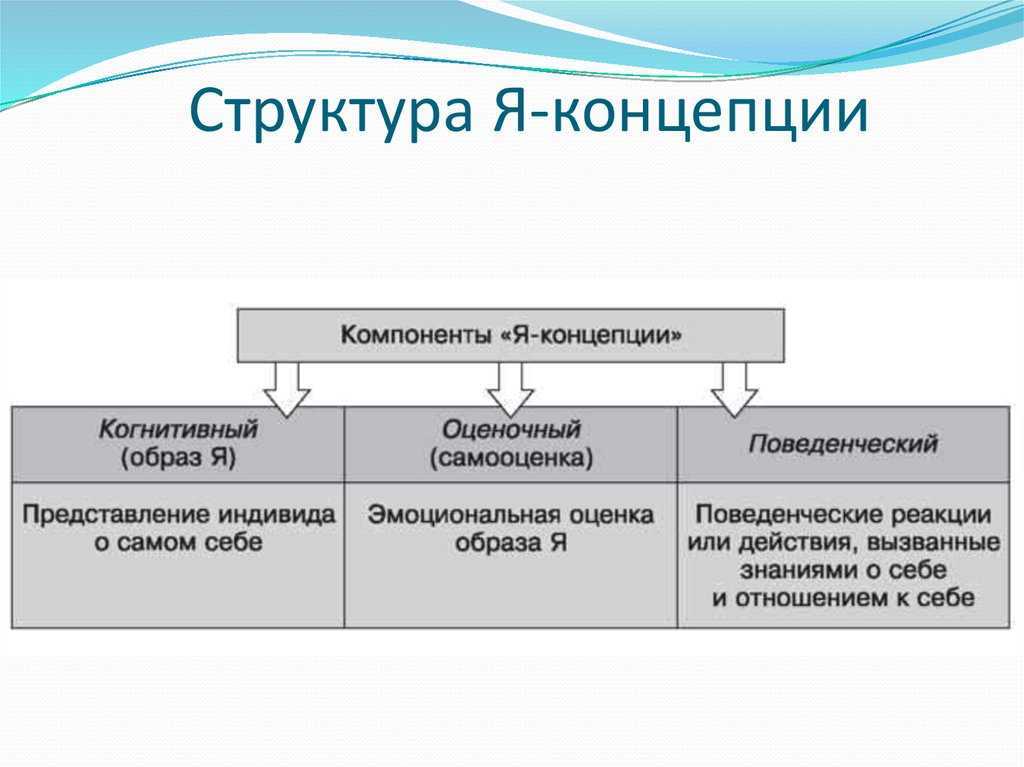
2. Функции я-концепции. Пять основных измерений я-концепции
Функциями Я-концепции являются:
1. Способствует достижению внутренней согласованности личности.
2. Является важным фактором интерпретации жизненного опыта.
3. Является источником ожиданий.
Достижение
внутренней согласованности личности.
Столкновение противоречащих друг другу
представлений, чувств, идей, относящихся
к представлениям человека о себе,
вызывает у него ощущение психологического
дискомфорта. И человек всячески пытается
этого избежать, предпринимая действия,
способствующие достижению утраченного
равновесия, стараясь избежать внутренней
дисгармонии. Поэтому, когда человек
сталкивается с новым опытом, знанием о
себе, он либо:
1) принимает,
ассимилирует этот опыт, когда он не
противоречит представлениям индивида
о себе, либо 2) отказывается видеть вещи
такими как они есть, верить людям,
сообщающим ему что-либо о себе, или 3)
стремится изменить каким-либо образом
себя или окружающих.
Если изменения образа себя, привносимые новой информацией, не сильно отличаются от прежних представлений о себе, то индивид иногда может их принять, если эти изменения не превышают его адаптационные возможности. Противоречивый опыт, вносящий рассогласование в структуру личности, может также усваиваться с помощью защитно-психологических механизмов, таких как рационализация, когда новый опыт объясняется на основании уже имеющегося, искажение или отрицание.
Таким образом, Я-концепция может выступать как некий защитный экран, охраняющий самосогласованный образ себя от влияний, которые могут его нарушить.
Сложившаяся Я-концепция обладает свойством самоподдержания. Благодаря этому у человека создается ощущение своей постоянной определенности, само- тождественности.
Самосогласованность
Я-концепции не является абсолютной.
Поведение индивида бывает разным в
зависимости от ситуации, в которой он
находится, от принятой им психологической
или социальной роли.
Даже при относительной
жесткости Я-концепции человек сохраняет
возможности для адаптации к меняющимся
внешним условиям, для самоизменения,
развития, необходимого для решения
стоящих перед ним задач. Неожиданное
осознание неадекватности существующего
Я-образа, вызванное этим замешательство
и последующее исследование, направленное
на поиск новой идентичности, более
соответствующей реальности, — это процесс
самопознания и самостроительства,
который идет всю жизнь.
Стабильность Я-концепции обеспечивает человеку чувство уверенности в направлении своего жизненного пути, в восприятии своих различных жизненных ситуаций как единого непрерывного в своей преемственности опыта (Э. Эриксон).
Еще одна функция Я-концепции — интерпретация жизненного опыта. Сталкиваясь с одним и тем же событием, разные люди по разному его понимают, как принято говорить, «смотрят каждый со своей колокольни». Проходя через фильтр Я-концепции, информация осмысливается, и ей присваивается значение, соответствующее уже сформировавшимся представлениям человека о себе и о мире.
Например, человек
с низкой самооценкой может интерпретировать
искреннюю похвалу в свой адрес как
замаскированную насмешку. Такой человек
обычно чувствует себя неуверенно,
тревожен, напряжен, что в свою очередь
нередко вызывает дискомфорт и напряженность
у партнеров по общению. Люди, не верящие
в свои возможности, выбирают соответствующие
жизненные цели, друзей, будущее.
Очень важно с раннего детства формировать у человека позитивное отношение к себе, уважение к себе, уверенность в себе и своих силах, способствующие более полной жизненной реализации.
Сформировавшиеся представления о себе также определяют ожидания человека в отношении своего будущего. Так, если ребенка убедили, что он глуп, он соответствующим образом будет вести себя в школе, и не будет прилагать никаких усилий к учебе, так как уже знает, что «глуп, не дано, у него не получится». Если человек уверен в собственной значимости, он ждет соответствующего отношения от окружающих.
Связь между
ожиданиями по отношению к себе,
обусловленными Я-концепцией, и поведением
человека лежит в основе механизма
«самореализующихся пророчеств». Поэтому
от визитов к гадалкам и предсказателям
будущего может быть определенный вред.
Поверив в предсказанное, то есть приняв
полученную информацию в образ «будущего
Я», человек начинает действовать в
соответствии с ожиданиями, и сам приводит
себя к предсказанному будущему.
Осознание этого механизма позволяет увидеть, что работа с Я-концепцией как с объектом вашего осознанного творчества может позволить человеку перестать быть рабом собственного прошлого, сформировавшихся в нем убеждений и стать творцом собственного настоящего и будущего. Использование этих закономерностей лежит в основе метода управляемой визуализации, широко используемого разными направлениями гуманистической психологии для избавления от ограничивающего опыта прошлого, формирования желательного для клиента будущего.
Выделяют 5 основных измерений Я-концепции:
1) степень интеграции;
2) уровень осознания;
3) стабильность;
4) самооценка;
5) степень согласия относительно данной персонификации.
Степень интеграции.
В современном мере фрагментарность
Я-концепции, видимо, является неизбежной,
но люди сильно различаются по тому,
насколько каждый может интегрировать
свои действия.
Обычно люди формируют несколько относительно обособленных Я-образов, соответствующих отличающимся, но повторяющимся ситуациям своей жизни.
Следующий критерий — уровень осознанности человеком своей Я-концепции. Разные люди в разной степени могут осознавать определенные части своей Я-концепции. Так, многие люди не замечают свои недостатки.
Подвижность и
гибкость Я-концепции проявляется в том,
меняется ли человек под давлением
ситуации. Некоторые люди охотно
изменяются, подчиняясь ситуации, легко
формируют требуемые образы Я и способы
поведения.
О самооценке и факторах, на нее влияющих, было сказано выше.
Я-концепции могут также в различной степени поддерживаться взглядами других людей, т.е. быть или не быть согласованными с ними. Крайности располагаются от высшей степени согласия, которая достигается в отношении тех, чья позиция в обществе хорошо определена и кто эффективно исполняет свои роли. Например, уважаемый в общине священник. Другая крайность — пациент у психиатра, утверждающий, что он Наполеон. Тут согласие отсутствует полностью. Обычно же существуют согласие в отношении одних элементов Я-концепции и разногласия в отношении других. Мы обычно не сомневаемся в определении собеседником своего пола, но можем не соглашаться с тем, как он оценивает свои моральные качества.
Я-концепция. Игры, в которые играет «Мы».
Основы психологии поведения: теория и типология Я-концепция. Игры, в которые играет «Мы». Основы психологии поведения: теория и типологияВикиЧтение
Игры, в которые играет «Мы». Основы психологии поведения: теория и типология
Калинаускас Игорь Николаевич
Содержание
Я-концепция
Поскольку в системе социальных отношений Я-концепция стоит между человеком как таковым и его отношениями, постольку она является важным структурным элементом всей системы социального ориентирования, значит, знакомясь со своей системой социального ориентирования, мы неминуемо должны познакомиться и со своей Я-концепцией.
Прежде всего возникает вопрос: является ли Я-концепция стабильным образованием и может ли она изменяться в течение жизни? Это важно знать, чтобы понять цель изучения собственной Я-концепции: то ли это будет простой констатацией факта, то ли этот процесс может дать исходную информацию для дальнейшего, осознанного ее изменения.
Автор убежден, что Я-концепция, являясь достаточно устойчивым психологическим образованием, все же поддается изменению, и нет причин передоверять эту работу кому-то, если вы всерьез решили заняться творчеством своей жизни. Многолетняя практика работы с людьми вполне подтверждает жизнеспособность такой установки. Работая со своей Я-концепцией, человек, может обратиться за помощью к специалисту, но советы последнего — это лишь подсказка. Без осознанной самостоятельной работы желаемых результатов добиться не удастся.
Сложившаяся Я-концепция — не приговор и она может быть осознанно изменена, хоть это и требует определенных усилий и времени.
? На свободу — с чистой совестью!
Кроме того, можно с уверенностью сказать, что спонтанная динамика Я-концепции также возможна и зависит от возраста и образа жизни человека, но редко бывает им замечена в силу упомянутого выше отождествления ее с «самим собой».
Концепция DIR
Концепция DIR В названии концепции DIR (развитие — индивидуальные различия — отношения) понятие «закономерности развития» относится к тем шести стадиям развития, которые описаны в третьей главе, под «индивидуальными различиями» понимаются присущие ребенку
Концепция личности
Концепция личности
Психодинамический подход к личности подчеркивает влияние бессознательных психических процессов на детерминацию мыслей, чувств и поведение человека.
Теория личности Фрейда начинается с допущения, что люди рождаются с базальными инстинктами или
Концепция невроза
Концепция невроза Невроз развивается в результате раннего (до шестилетнего возраста) вытеснения сексуальных и агрессивных влечений, хотя симптомы могут проявиться гораздо позднее – вследствие активизации фрустрированных либидинальных импульсов под воздействием
Концепция невроза
Концепция невроза Невроз – психогенное расстройствоВ. Н. Мясищев рассматривал невроз прежде всего как функциональное, психогенное нервно-психическое заболевание, вытекающее из тяжелых переживаний личности, неразрывно связанных с условиями ее жизни. Здесь возникают
Концепция психотерапии
Концепция психотерапии
Патогенетическая (также психогенетическая) психотерапия Н.
В. Мясищева является единственным динамически ориентированным подходом в России. Сам создатель этого подхода относил его к «рациональной» психотерапии, обосновывая это следующими
Концепция нарушений
Концепция нарушений В основе всех нарушений лежит ограничение способности индивида к поддержанию оптимального равновесия со средой, нарушение процесса саморегуляции организма. В гештальт-терапии описывается пять наиболее часто встречающихся форм нарушения
Концепция терапии
Концепция терапии По мнению Перлза, основной целью гештальт-терапии является рост потенциала человека, или повышение его силы и возможностей путем процесса интеграции и развития. Генез эмоциональных нарушений и ограничений возможностей он видит в связи между индивидом
Я-концепция
Я-концепция Поскольку в системе социальных отношений Я-концепция стоит между человеком как таковым и его отношениями, постольку она является важным структурным элементом всей системы социального ориентирования, значит, знакомясь со своей системой социального
Я-концепция
Я-концепция
Как и нравственность, Я-концепция — большая, многогранная тема.
Так же как и изложение темы нравственности, изложение темы Я-концепция будет избирательным, с соблюдением общепринятого разделения на подтемы. В данном случае производится деление на
Концепция бессилия
Концепция бессилия В основе подчинительно-противительной ориентации лежит представление о том, что человек сам по себе бессилен. Если можно пользоваться обстоятельствами или восставать против них, где же тогда сила? Явно не в человеке, а в обстоятельствах. Сила
«Я»-концепция
«Я»-концепция Особую роль в человеческом сознании имеет так называемая «Я»-концепция, или осознание человеком самого себя. «Я»-концепция – это управляющая функция интеллекта. Без нее интеллект работать не может.«Я»-концепция, как и любая другая концепция, состоит из
Концепция как изобретение
Концепция как изобретение Рассуждая о теории красоты и красоте теории Эдвард де Боно в девятой главе книги «Использование латерального мышления» отмечал:«В известном смысле наука является высшей формой искусства, поскольку здесь совершенство новой идеи не является
Функция | Определение, типы, примеры и факты
кубическое уравнение
Просмотреть все СМИ
- Ключевые люди:
- Поль Пенлеве Карл Вейерштрасс Эмиль Борель Эдвард Чарльз Титчмарш Питер Густав Лежен Дирихле
- Похожие темы:
- специальная функция корень преемственность Дзета-функция Римана рекурсивная функция
Просмотреть весь связанный контент →
функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной).
Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые дал в 1837 году немецкий математик Петер Дирихле:
Если переменная y так связано с переменной х , что всякий раз, когда числовое значение присваивается х , существует правило, согласно которому определяется уникальное значение y , тогда y называется функция независимой переменной x .
Это отношение обычно обозначается как y = f ( x ) — что называется « f из x » — и y x связаны между собой так, что для каждого 9 и связаны между собой.0026 x , есть уникальное значение y . То есть f ( x ) не может иметь более одного значения для одного и того же x . Говоря языком теории множеств, функция связывает элемент x с элементом f ( x ) в другом наборе.
Набор значений x называется доменом функции, а набор значений f ( x ), порожденных значениями в домене, называется диапазоном функции. В дополнение к f ( x ), другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда природа функция неизвестна или не определена.
Общие функции
Многие широко используемые математические формулы являются выражениями известных функций. Например, формула площади круга: A = π r 2 дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных (называемые многомерными или многомерными функциями), также распространены в математике, как это видно из формулы площади треугольника A = b h /2, которая определяет A в зависимости от b (основание) и h (высота).
В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.
Викторина «Британника»
Числа и математика
Формула площади круга является примером полиномиальной функции. The general form for such functions is P ( x ) = a 0 + a 1 x + a 2 x 2 +⋯+ a n x n , где коэффициенты ( A 0 , A 1 , A 2 ,…, A N ). x — это счетные числа (1, 2, 3,…). (Когда степени x могут быть любым действительным числом, результат известен как алгебраическая функция.
) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно.
Полиномиальные функции могут иметь геометрическое представление с помощью аналитической геометрии. Независимая переменная x откладывается по оси x (горизонтальная линия), а зависимая переменная y откладывается по оси y (вертикальная линия). Когда график отношения между x и y строится в плоскости x — y , отношение является функцией, если вертикальная линия всегда проходит только через одну точку графической кривой; то есть была бы только одна точка f ( x ) соответствует каждому x , что является определением функции.
Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Другим распространенным типом функций, которые изучались с древних времен, являются тригонометрические функции, такие как sin x и cos x , где x — мера угла ( см. рисунок ). Из-за своего периодического характера тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».
Экспоненциальная функция представляет собой отношение вида y = a x с независимой переменной x , ранжирующийся по всей строке действительных чисел как показатель степени положительного числа a .
Вероятно, наиболее важной из экспоненциальных функций является y = e x , иногда пишется как y = exp ( x ), в которой e (2,7182818) является основанием натурального числа. система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.
Сложные функции
Практические приложения функций, переменными которых являются комплексные числа, не так просто проиллюстрировать, но тем не менее они очень обширны. Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена в виде z = x + i y , где i — мнимая единица (корень квадратный из −1), а x и y — действительные переменные ( см.
цифру ). возможно разделить сложную функцию на реальные и воображаемые детали: F ( Z ) = P ( x , Y ) + I Q ( x , y ) ( x , y ) Q ( x , y ) Q ( x , y ). .
Основные концепции функций
ГБ Алгебра средней школы, Математика средней школы
Примечание. Это вторая часть серии функций. Чтобы просмотреть другие части, нажмите на ссылку ниже.
Часть I. Введение в функции
Часть II. Основные понятия функций
***
множества, во втором множестве есть ровно одно соответствующее значение. Мы раскрасили большие кубики, разрезали их на единичные кубики и нашли закономерность относительно количества кубиков с 3, 2, 1 и без окрашенных граней.
Рисунок 1. Кубы окрашены и нарезаны на единичные кубики.
Мы выяснили, что если куб имеет сторону n единиц, если мы закрасим все его грани и разрежем его на единичные кубы, то будут выполнены следующие соотношения: кубов (кубиков с 0 окрашенными гранями) куба со стороной n
g(n) = количество стеновых кубов (кубиков с 1 окрашенной гранью) куба со стороной n
h(n) = количество реберных кубов (кубов с 2 окрашенными гранями) куба с длиной стороны Длина N
Затем
F (N) = (N- 2) 3 = N 3 — 9N 2 + 27N- 27
g (n) = 6 (n- 2) 2 = 6n 2 – 24n + 24
h(n) = 12(n-1) = 12n- 12
k(n) = 8
Чтобы дать вам более четкое представление о функциях, рассмотрим еще несколько примеров: x существует ровно одно соответствующее значение y .
2.) Если человек работает, у которого заработная плата исчисляется в час, мы можем сказать, что его заработная плата является функцией времени (количество часов), обозначаемой f(t) он работал. Если мы допустим, что s будет зарплатой, а t будет временем, мы можем написать s = f(t) . Отношение является функцией, так как для любого количества часов работы существует точная соответствующая заработная плата.
3.) Отношение f(x) = (x – 2) 3 является функцией, поскольку для каждого x существует ровно одно f(x). Некоторые значения x и f(x) показаны на крайнем левом графике на рис. 1.
Рисунок 2. Отображение функций и отношений.
4.) Отношение h( x ) = 8 является функцией, поскольку для каждого x существует только одно значение для f ( x ) , которое равно 2 .
8 . Отображение показано на центральной диаграмме, показанной на рисунке 1.
5.) Отношение x = y 2 , показанное на рисунке 2, не является функцией, поскольку мы можем найти x с разными значениями f(x). Например, когда x = 4 , тогда y 2 = 2 и y 2 = -2 . Отображение элементов s = y 2 показано на самой правой диаграмме на рисунке 1.
Рисунок 3 – График x = y в квадрате.
6.) Единственными возможными значениями n в нашей задаче о кубе являются целые числа больше 1 . У нас не может быть куба с дробной длиной, такой как 5,6 метра, потому что наше условие говорит разрезать куб на единичные кубы (кубы со стороной 1 единица). Более того, n не может иметь отрицательных значений, так как отрицательное число единичных кубов не имеет смысла.
Возможные значения n, , которые делают значение f(n) осмысленным, называются областью функции.
7.) В соотношении h(n) = 12n – 12 число реберных кубов h(n) зависит от длины стороны n куб. Например, если n равно 100 , мы можем легко вычислить значение h(n) . Мы называем n нашей независимой переменной и h(n) нашей зависимой переменной . Обратите внимание, что не всем h(n) соответствует значение n . Например, значение h(n) = 21 не имеет соответствующего значения n .
8.) Любое значение n , k(n)=8 . Мы называем k постоянной функцией . На рисунке 3, если мы позволим нашему домену быть набором действительных чисел, тогда у нас будет горизонтальная линия.
Рисунок 4 – График k(n) = 8.
9.) Иногда функции называют по букве их имени, не включая независимую переменную. Например, вместо f(x) мы можем назвать это просто f .
10.) Степень функции – это высшая степень упрощенного многочлена. Глядя на упрощенную формулу выше, мы видим, что f имеет степень 3, g имеет степень 4, а h имеет степень 1. Функции степени три называются кубическими функциями , функции степени 2 называются квадратичными функциями , а функции степени 1 называются называется линейных функций .
11.) Для некоторых функций указан домен. Если спецификация недоступна, то предполагается, что домен представляет собой набор действительных чисел. Область определения функции h(n) = 12n – 12 — это набор целых чисел больше 1. Возможные значения f(n) называются диапазоном из h(n).
Следовательно, домен h(n) равен 2, 3, 4 и т. д., а его диапазон h(n) равен 12, 24, 36 и т. д., или множество положительных целых чисел, кратных 12 .
12.) Функция подобна машине, в которой каждый вход выдает один (и только один) выход. На рис. 5 (слева) значения x — это наши входные шары, а f ( x ) значения – это наши выходные шары. Как видите, каждый входной шар возвращает один выходной шар; то есть мяч одного цвета. То же самое и на рисунке справа (где h(x) — наши выходные шары), хотя значения всех выходных шаров одинаковы.
Рисунок 5. Функциональная машина
Напротив, на рисунке 6 каждый входной шар имеет два выходных шара. Это означает, что отношения не являются функцией.
Рисунок 6 – Отношение, не являющееся функцией.
В следующем посте мы обсудим тест горизонтальной и вертикальной линии и их связь с определением и свойствами функций.
