2. Функции я-концепции. Пять основных измерений я-концепции
Функциями Я-концепции являются:
1. Способствует достижению внутренней согласованности личности.
2. Является важным фактором интерпретации жизненного опыта.
3. Является источником ожиданий.
Достижение
внутренней согласованности личности.
Столкновение противоречащих друг другу
представлений, чувств, идей, относящихся
к представлениям человека о себе,
вызывает у него ощущение психологического
дискомфорта. И человек всячески пытается
этого избежать, предпринимая действия,
способствующие достижению утраченного
равновесия, стараясь избежать внутренней
дисгармонии. Поэтому, когда человек
сталкивается с новым опытом, знанием о
себе, он либо:
1) принимает,
ассимилирует этот опыт, когда он не
противоречит представлениям индивида
о себе, либо 2) отказывается видеть вещи
такими как они есть, верить людям,
сообщающим ему что-либо о себе, или 3)
стремится изменить каким-либо образом
себя или окружающих.
Если изменения образа себя, привносимые новой информацией, не сильно отличаются от прежних представлений о себе, то индивид иногда может их принять, если эти изменения не превышают его адаптационные возможности. Противоречивый опыт, вносящий рассогласование в структуру личности, может также усваиваться с помощью защитно-психологических механизмов, таких как рационализация, когда новый опыт объясняется на основании уже имеющегося, искажение или отрицание.
Таким образом, Я-концепция может выступать как некий защитный экран, охраняющий самосогласованный образ себя от влияний, которые могут его нарушить.
Сложившаяся Я-концепция обладает свойством самоподдержания. Благодаря этому у человека создается ощущение своей постоянной определенности, само- тождественности.
Самосогласованность
Я-концепции не является абсолютной.
Поведение индивида бывает разным в
зависимости от ситуации, в которой он
находится, от принятой им психологической
или социальной роли.
Даже при относительной
жесткости Я-концепции человек сохраняет
возможности для адаптации к меняющимся
внешним условиям, для самоизменения,
развития, необходимого для решения
стоящих перед ним задач. Неожиданное
осознание неадекватности существующего
Я-образа, вызванное этим замешательство
и последующее исследование, направленное
на поиск новой идентичности, более
соответствующей реальности, — это процесс
самопознания и самостроительства,
который идет всю жизнь.
Стабильность Я-концепции обеспечивает человеку чувство уверенности в направлении своего жизненного пути, в восприятии своих различных жизненных ситуаций как единого непрерывного в своей преемственности опыта (Э. Эриксон).
Еще одна функция Я-концепции — интерпретация жизненного опыта. Сталкиваясь с одним и тем же событием, разные люди по разному его понимают, как принято говорить, «смотрят каждый со своей колокольни». Проходя через фильтр Я-концепции, информация осмысливается, и ей присваивается значение, соответствующее уже сформировавшимся представлениям человека о себе и о мире.
Например, человек
с низкой самооценкой может интерпретировать
искреннюю похвалу в свой адрес как
замаскированную насмешку. Такой человек
обычно чувствует себя неуверенно,
тревожен, напряжен, что в свою очередь
нередко вызывает дискомфорт и напряженность
у партнеров по общению. Люди, не верящие
в свои возможности, выбирают соответствующие
жизненные цели, друзей, будущее.
Очень важно с раннего детства формировать у человека позитивное отношение к себе, уважение к себе, уверенность в себе и своих силах, способствующие более полной жизненной реализации.
Сформировавшиеся представления о себе также определяют ожидания человека в отношении своего будущего. Так, если ребенка убедили, что он глуп, он соответствующим образом будет вести себя в школе, и не будет прилагать никаких усилий к учебе, так как уже знает, что «глуп, не дано, у него не получится». Если человек уверен в собственной значимости, он ждет соответствующего отношения от окружающих.
Связь между
ожиданиями по отношению к себе,
обусловленными Я-концепцией, и поведением
человека лежит в основе механизма
«самореализующихся пророчеств». Поэтому
от визитов к гадалкам и предсказателям
будущего может быть определенный вред.
Поверив в предсказанное, то есть приняв
полученную информацию в образ «будущего
Я», человек начинает действовать в
соответствии с ожиданиями, и сам приводит
себя к предсказанному будущему.
Осознание этого механизма позволяет увидеть, что работа с Я-концепцией как с объектом вашего осознанного творчества может позволить человеку перестать быть рабом собственного прошлого, сформировавшихся в нем убеждений и стать творцом собственного настоящего и будущего. Использование этих закономерностей лежит в основе метода управляемой визуализации, широко используемого разными направлениями гуманистической психологии для избавления от ограничивающего опыта прошлого, формирования желательного для клиента будущего.
Выделяют 5 основных измерений Я-концепции:
1) степень интеграции;
2) уровень осознания;
3) стабильность;
4) самооценка;
5) степень согласия относительно данной персонификации.
Степень интеграции.
В современном мере фрагментарность
Я-концепции, видимо, является неизбежной,
но люди сильно различаются по тому,
насколько каждый может интегрировать
свои действия.
Обычно люди формируют несколько относительно обособленных Я-образов, соответствующих отличающимся, но повторяющимся ситуациям своей жизни.
Следующий критерий — уровень осознанности человеком своей Я-концепции. Разные люди в разной степени могут осознавать определенные части своей Я-концепции. Так, многие люди не замечают свои недостатки.
Подвижность и
гибкость Я-концепции проявляется в том,
меняется ли человек под давлением
ситуации. Некоторые люди охотно
изменяются, подчиняясь ситуации, легко
формируют требуемые образы Я и способы
поведения.
О самооценке и факторах, на нее влияющих, было сказано выше.
Я-концепции могут также в различной степени поддерживаться взглядами других людей, т.е. быть или не быть согласованными с ними. Крайности располагаются от высшей степени согласия, которая достигается в отношении тех, чья позиция в обществе хорошо определена и кто эффективно исполняет свои роли. Например, уважаемый в общине священник. Другая крайность — пациент у психиатра, утверждающий, что он Наполеон. Тут согласие отсутствует полностью. Обычно же существуют согласие в отношении одних элементов Я-концепции и разногласия в отношении других. Мы обычно не сомневаемся в определении собеседником своего пола, но можем не соглашаться с тем, как он оценивает свои моральные качества.
Я Концепция
11. 11.2011
11.2011
Понятие Я-концепции появилось в 1950-е гг. в русле гуманистической психологии, представители которой стремились к рассмотрению целостного, уникального человеческого Я.
Зародившись в зарубежной психологической литературе, в последние десятилетия XX в. понятие «Я-концепция» прочно вошло в обиход отечественной психологии. Однако в литературе нет единой трактовки этого понятия, ближе всего по смыслу к нему находится понятие «самосознание». Соотношение понятий «Я-концепция» и «самосознание» до сих пор точно не определено. Часто они выступают как синонимы. Вместе с тем существует тенденция рассматривать Я-концепцию в отличие от самосознания как результат, итоговый продукт процессов самосознания.
Что же означает термин «Я-концепция», какой реальный психологический смысл в него вкладывается? Психологические словари трактуют Я-концепцию как динамическую систему представлений человека о самом себе. Английский психолог Р. Берне в книге «Развитие Я-концепции и воспитание» определяет Я-концепцию как «совокупность всех представлений индивида о себе, сопряженную с их оценкой». Я-концепция возникает у человека в процессе социального взаимодействия как неизбежный и всегда уникальный результат психического развития, как относительно устойчивое и в то же время подверженное внутренним изменениям и колебаниям психическое приобретение. Первоначальная зависимость Я-концепции от внешних влияний бесспорна, но в дальнейшем она играет самостоятельную роль в жизни каждого человека. Окружающий мир, представления о других людях воспринимаются нами сквозь призму Я-концепции, формирующейся в процессе социализации, но имеющей и определенные соматические, индивидуально-биологические детерминанты.
Я-концепция возникает у человека в процессе социального взаимодействия как неизбежный и всегда уникальный результат психического развития, как относительно устойчивое и в то же время подверженное внутренним изменениям и колебаниям психическое приобретение. Первоначальная зависимость Я-концепции от внешних влияний бесспорна, но в дальнейшем она играет самостоятельную роль в жизни каждого человека. Окружающий мир, представления о других людях воспринимаются нами сквозь призму Я-концепции, формирующейся в процессе социализации, но имеющей и определенные соматические, индивидуально-биологические детерминанты.
Каким образом происходит формирование Я-концепции индивида? Взаимосвязи человека с миром богаты и разносторонни. В системе этих взаимосвязей ему приходится выступать в разных качествах, в разных ролях, быть субъектом самых разнообразных видов деятельности. И из каждого взаимодействия с миром вещей и миром людей человек «выносит» образ своего Я. В процессе самонализа, расчленения отдельных конкретных образов своего Я на составляющие их образования — внешние и внутренние психологические особенности — происходит как бы внутреннее обсуждение с самим собой своей личности. Каждый раз в результате самоанализа, по словам С.Л. Рубинштейна, образ своего Я «включается во все новые связи и в силу этого выступает во все новых качествах, которые фиксируются в новых понятиях… он как бы поворачивается каждый раз другой стороной, в нем выявляются все новые свойства».
Каждый раз в результате самоанализа, по словам С.Л. Рубинштейна, образ своего Я «включается во все новые связи и в силу этого выступает во все новых качествах, которые фиксируются в новых понятиях… он как бы поворачивается каждый раз другой стороной, в нем выявляются все новые свойства».
Так постепенно возникает обобщенный образ своего Я, который как бы сплавляется из многих единичных конкретных образов Я в ходе самовосприятия, самонаблюдения и самоанализа. Этот обобщенный образ своего Я, возникая из отдельных, ситуативных образов, содержит общие, характерные черты и представления о своей сущности и выражается в понятии о себе, или Я-концепции. В отличие от ситуативных образов Я Я-концепция создает у человека ощущение своей константности, самотождественности.
Сформировавшаяся в процессе самопознания Я-концепция в то же время не есть нечто раз и навсегда данное, застывшее, ей присуще постоянное внутреннее движение. Ее зрелость, адекватность проверяется и корректируется практикой.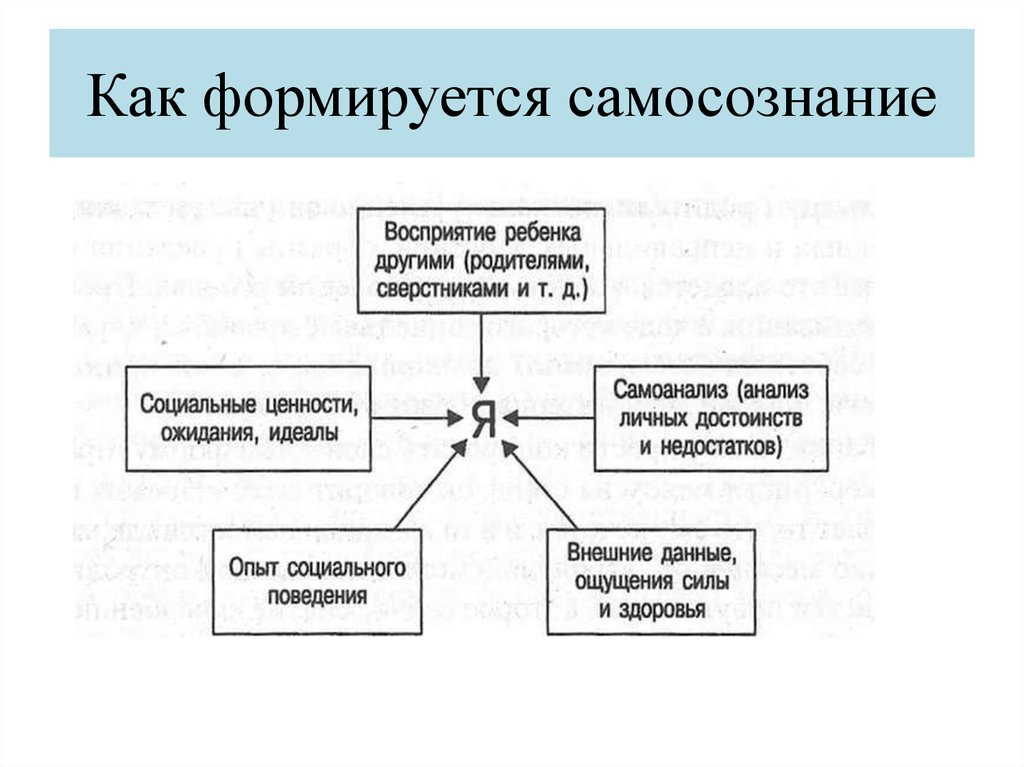 Я-концепция в значительной степени влияет на весь строй психики, мировосприятия в целом, обусловливает основную линию поведения человека.
Я-концепция в значительной степени влияет на весь строй психики, мировосприятия в целом, обусловливает основную линию поведения человека.
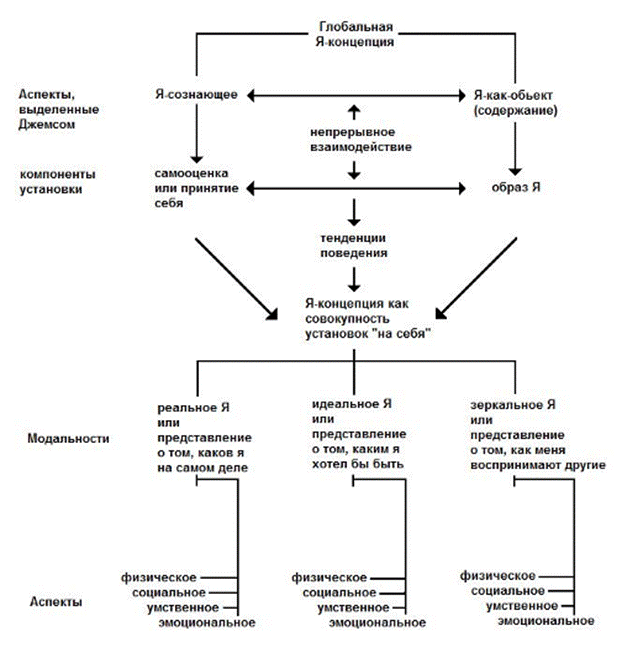
Какова структура Я-концепции? Р. Берне (как и многие отечественные психологи) выделяет три составляющих в структуре Я-концепции: когнитивную, оценочную и поведенческую. Когнитивная составляющая, или образ Я, включает представления индивида о самом себе. Оценочная составляющая, или самооценка, включает аффективную оценку этого представления о себе. Поведенческая составляющая включает в себя потенциальные поведенческие реакции либо конкретные действия, которые могут быть вызваны знаниями о себе и отношением к себе. Такое деление Я-концепции на компоненты условно, на самом деле Я-концепция — это целостное образование, все компоненты которого, хотя и обладают относительной самостоятельностью, тесно взаимосвязаны.
Какую роль играет Я-концепция в жизни личности?
Я-концепция играет, по существу, тройственную роль в жизни личности: она способствует достижению внутренней согласованности личности, определяет интерпретацию ее опыта и является источником ожиданий.
Первой, важнейшей функцией Я-концепции является обеспечение внутренней согласованности личности, относительной устойчивости ее поведения. Если новый опыт, полученный индивидом, согласуется с существующими представлениями о себе, он легко ассимилируется, входит в Я-концепцию. Если же новый опыт не вписывается в существующие представления о себе, противоречит уже имеющейся Я-концепции, то срабатывают механизмы психологической защиты, которые помогают личности тенденциозно интерпретировать травмирующий опыт либо отрицать его. Это позволяет удерживать Я-концепцию в уравновешенном состоянии, даже если реальные факты ставят ее под угрозу. Это стремление защитить Я-концепцию, оградить ее от разрушающих воздействий является, по мнению Бернса, одним из основополагающих мотивов всякого нормального поведения.
Вторая функция Я-концепции заключается в том, что она определяет характер интерпретации индивидом его опыта. Я-концепция действует как своего рода внутренний фильтр, который определяет характер восприятия человеком любой ситуации. Проходя сквозь этот фильтр, ситуация осмысливается, получает значение, соответствующее представлениям человека о себе.
Проходя сквозь этот фильтр, ситуация осмысливается, получает значение, соответствующее представлениям человека о себе.
Третья функция Я-концепции заключается в том, что она определяет также и ожидания индивида, т.е. представления о том, что должно произойти. Люди, уверенные в собственной значимости, ожидают, что и другие будут относиться к ним так же и, наоборот, люди, сомневающиеся в собственной ценности, считают, что они никому не могут нравиться, и начинают избегать всяких социальных контактов.
Таким образом, развитие личности, ее деятельность и поведение находятся под существенным влиянием Я-концепции.
Ключевые слова: Я
Источник: Карпов А.В., Общая психология
| Материалы по теме |
|---|
Особенности Я-концепции при девиантном поведении Реан А. А., Психология личности. |
Структура и строение «Я-концепции» Кравченко А. И., Общая психология : учебное пособие. — Москва : Проспект. 2011.-432с. |
Теоретические подходы к «Я-концепции» Кравченко А. И., Общая психология : учебное пособие. — Москва : Проспект. 2011.-432с. |
Формирование «Я-концепции» Кравченко А. И., Общая психология : учебное пособие. — Москва : Проспект. 2011.-432с. |
Теория множественности «Я» Кравченко А. И., Общая психология : учебное пособие. — Москва : Проспект. 2011.-432с. |
«Я»-концепция в психологии … |
Сколько «Я» у человека? Кравченко А. И., Общая психология : учебное пособие. |
Развитие Я-концепции Мельник С.Н., Психология личности |
Общие представления о «Я-концепции»
Р.Бернс (1986) определил Я-концепцию как совокупность установок, которые направлены на самого себя. В предыдущей статье уже было сказано, что в структурном плане Я-концепция представляет собой неразрывное единство когнитивной, оценочной и поведенческой составляющих. В этой статье коснемся этого вопроса несколько подробнее.
Когнитивная составляющая Я-концепции
Все самоописательные характеристики, такие как надежный, совестливый, общительный, добрый и др. человек включает в образ себя. Способы самовосприятия могут быть разными. Иерархия и значимость элементов самоописания в зависимости от контекста, жизненного опыта или влияния какого-то момента, способны меняться.
Самоописания носят, как правило, обобщенный характер и с реальными контекстами не очень соотносятся, потому что отражают общее самовосприятие.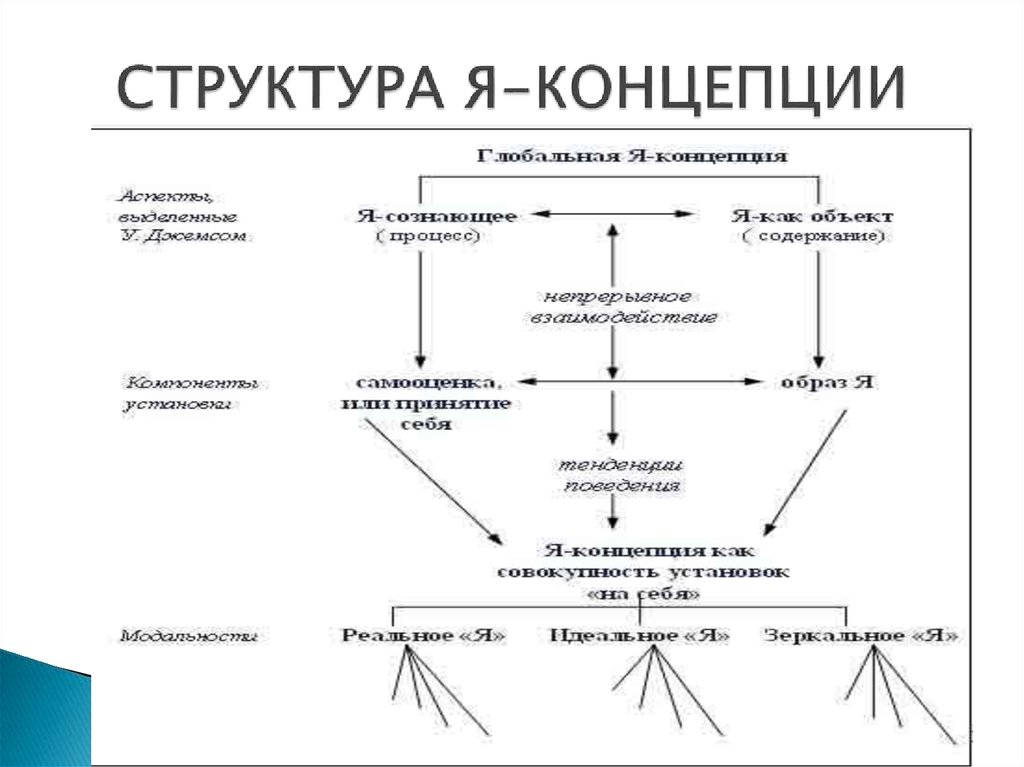 С одной стороны, как элементы обобщенного образа индивида, они отражают устойчивые тенденции его поведения, а с другой стороны отражают избирательность нашего восприятия.
С одной стороны, как элементы обобщенного образа индивида, они отражают устойчивые тенденции его поведения, а с другой стороны отражают избирательность нашего восприятия.
Описывая самого себя человек, пытается выразить основные характеристики своего привычного самовосприятия, например, описание имущества, жизненных целей и др. С различным удельным весом они все входят в образ Я, только одни представляются индивиду более значимыми, а другие – менее. Р. Бернс считал самоописание способом охарактеризовать неповторимость каждой личности через сочетаниея её отдельных черт.
Оценочная составляющая Я-концепции
Самооценка изменяется в зависимости от обстоятельств и не является постоянной. Социокультурное окружение индивида является источником оценочных знаний различных представлений о нем. Эти оценочные знания нормативно фиксируются в языковых значениях. Социальные реакции, самонаблюдение тоже могут быть источником оценочных представлений индивида. Самооценка отражает то, что входит в сферу Я индивида, а это степень развития у него чувства самоуважения, ощущения собственной ценности, позитивного отношения ко всему окружающему. Проявляется она и в сознательных суждениях индивида, в которых делается попытка сформулировать свою значимость. В скрытой или в явной форме она присутствует в любом самоописании.
Проявляется она и в сознательных суждениях индивида, в которых делается попытка сформулировать свою значимость. В скрытой или в явной форме она присутствует в любом самоописании.
Для понимания самооценки есть три момента.
- Представление о том, каким человек хотел бы быть. Кто в реальности достигает характеристик, определяющих для него идеальный образ Я, как правило, имеют высокую самооценку. Если же между характеристиками и реальностью достижений есть разрыв, то самооценка будет низкой, считает Р. Бернс;
- Интериоризация социальных реакций на данного индивида. В данном случае человек склонен оценивать себя так, как, по его мнению, его оценивают другие;
- Успешность действий оценивается через призму идентичности. Удовлетворение испытывается от того, что индивид избрал определенное дело и делает его хорошо.
Самооценка всегда носит субъективный характер, независимо от того, что лежит в её основе – собственные суждения индивида о себе или интерпретации суждений других людей.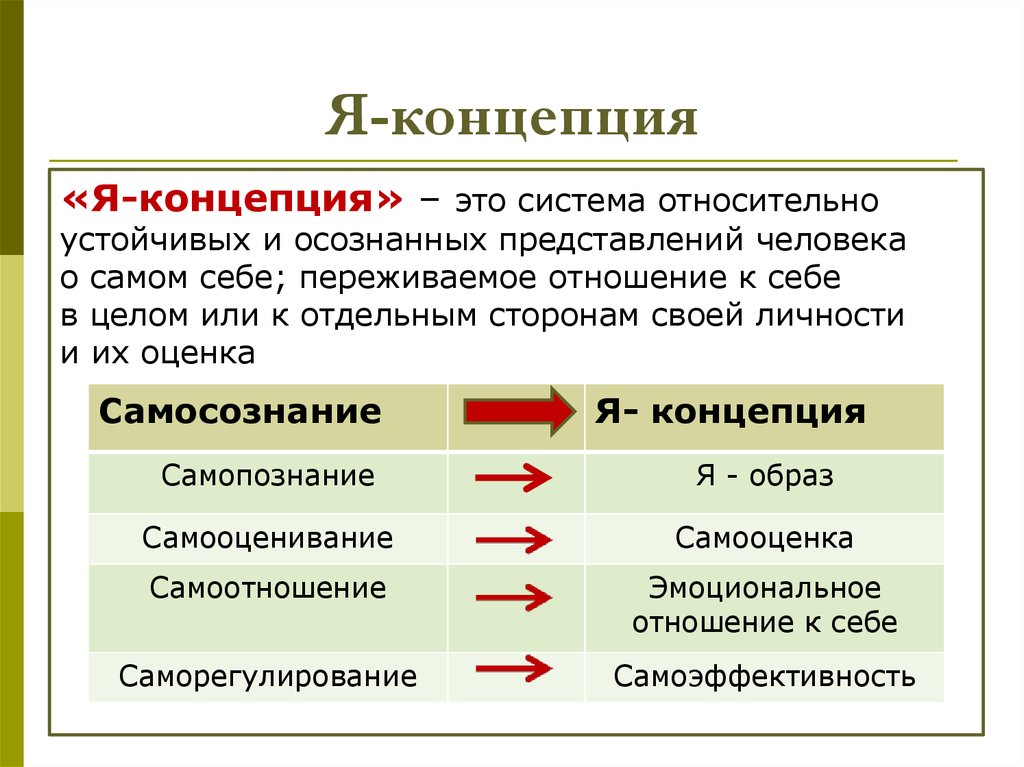 Источники самооценки:
Источники самооценки:
- Отраженная самооценка. Мнения значимых для индивида людей;
- Критериальная самооценка. По определенным критериям сравнение себя с другими людьми, а также с эталоном, который является общим для всех;
- Рефлексивная самооценка. Сравнение Я-реального и Я-идеального. Сопоставление своих собственных качеств с самим собой. Высокая степень совпадения этих сравнений говорит о психическом здоровье;
- Идентификационная самооценка. В целом это желание индивида с наибольшим успехом «вписаться» в структуру общества». Она играет важную роль в поддержании человеком своей идентичности.
Поведенческая составляющая Я-концепции
Хорошо известен тот факт, что люди не всегда поступают в соответствии со своими убеждениями. Непосредственное выражение установки в поведении может сдерживаться в силу его социальной неприемлемости, каких-то сомнений индивида или страха перед возможными последствиями. Любая установка – эмоционально окрашенное убеждение и связано оно с определенным объектом, которым в концепции является сам носитель установки.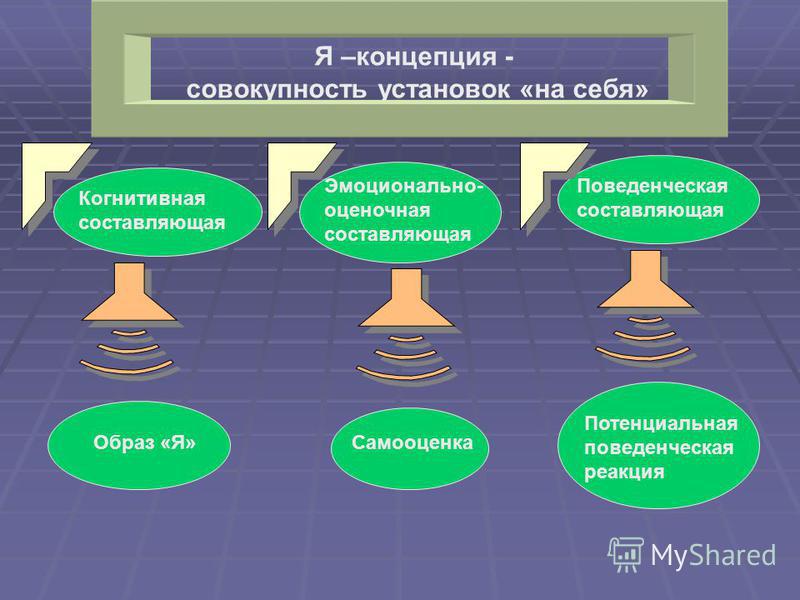 Все эмоции и оценки, связанные с образом Я, в результате этой самонаправленности, являются очень сильными и устойчивыми. Достаточно просто не придавать значения отношению к тебе другого человека – есть арсенал психологической защиты.
Все эмоции и оценки, связанные с образом Я, в результате этой самонаправленности, являются очень сильными и устойчивыми. Достаточно просто не придавать значения отношению к тебе другого человека – есть арсенал психологической защиты.
Другое дело, если речь идет об отношении к самому себе – вербальные манипуляции здесь могут оказаться бессильными. Просто так взять и изменить свое отношение к самому себе никто не может.
Данная составляющая имеет два вектора:
- Ожидания в отношении себя, т.е. готовность самому действовать;
- Ожидания к другим по отношению к себе. Эта составляющая может быть выражена такими высказываниями «я всегда готов…», «со мной всегда так происходит» и др.
Иногда может возникнуть впечатление, что поведенческая составляющая одновременно самая чувствительная к особенностям жизненной ситуации и самая ригидная, т.е. мало изменяющаяся по своей сути, использующая одни и те же сценарии решения жизненных задач.
Эта составляющая Я-концепции менее всего описана специалистами.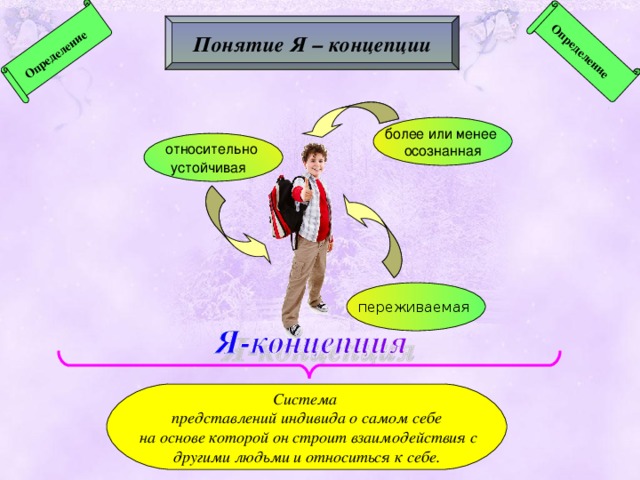
Функции Я-концепции
Я-концепция выполняет следующую «работу»:
- Предварительная настройка восприятия, оценки и поведения. Выступающая как совокупность ожиданий, она дает возможность спрогнозировать вероятное развитие событий, т.е. приготовиться к участию в них. Ожидания и прогнозы могут долгое время оставаться в имплицитной форме, они не обязательно осознаются даже в рамках Я-концепции;
- Интерпретация актуальных событий и полученного опыта. Концепция выступает как средство категориальной оценки событий настоящих или уже произошедших. Например, женщина, которой в автобусе уступил место мужчина, может увидеть в этом поступке черты хорошего воспитания, заподозрить намек на свой возраст или воспринять это как попытку знакомства. Любая из этих интерпретаций и её Я-концепция очень тесно связаны между собой. В подобных ситуациях Я-концепция действует как внутренний фильтр и определяет характер восприятия ситуации человеком, при этом она выступает как активное начало и изменить её достаточно трудно.

- Обеспечение внутренней согласованности Эго-идентичности. Р. Бернс считает, что существенным фактором внутренней согласованности является то, что индивид думает о самом себе, поэтому в своих действиях руководствуется самовосприятием.
Полученный индивидом новый опыт легко ассимилируется и входит внутрь Я-концепции, если он согласуется с существующими представлениями о себе. В противном случае новый опыт не допускается и отторгается как чужеродное тело, не нарушая сбалансированности организма.
Если отличие нового опыта от имеющихся представлений индивида о себе не принципиальны, то он может внедриться в структуру Я-концепции насколько позволят адаптационные возможности составляющих её самоустановок.
Для того, чтобы поддержать свой образ Я, улучшить самооценку, сохранить привычные стратегии решения жизненных задач человек использует порой грубые и инфантильные, а порой изощренные и тонкие средства психологической защиты.
функция | Определение, типы, примеры и факты
кубическое уравнение
Просмотреть все СМИ
- Ключевые люди:
- Поль Пенлеве Карл Вейерштрасс Эмиль Борель Эдвард Чарльз Титчмарш Питер Густав Лежен Дирихле
- Похожие темы:
- специальная функция корень преемственность Дзета-функция Римана рекурсивная функция
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
функция , в математике выражение, правило или закон, определяющие связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной). Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые было дано в 1837 году немецким математиком Петером Дирихле:
Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые было дано в 1837 году немецким математиком Петером Дирихле:
Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y Говорят, что является функцией независимой переменной x .
Это соотношение обычно изображается как y = f ( x ) — что называется « f из x » — и y и x связаны таким образом, что для каждых x существует уникальное значение y . То есть f ( x ) не может иметь более одного значения для одного и того же x . Говоря языком теории множеств, функция связывает элемент x с элементом f ( x ) в другом наборе. Набор значений х называется областью определения функции, а набор значений f ( х ), сгенерированный значениями в домене, называется диапазоном функции. В дополнение к f ( x ) другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функции неизвестен или не определен.
Набор значений х называется областью определения функции, а набор значений f ( х ), сгенерированный значениями в домене, называется диапазоном функции. В дополнение к f ( x ) другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функции неизвестен или не определен.
Общие функции
Многие широко используемые математические формулы являются выражениями известных функций. Например, формула площади круга A = π r 2 дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных (называемые многомерными или многомерными функциями), также распространены в математике, как это видно из формулы площади треугольника A = b h /2, которая определяет A в зависимости от b (базовый) и h (высота).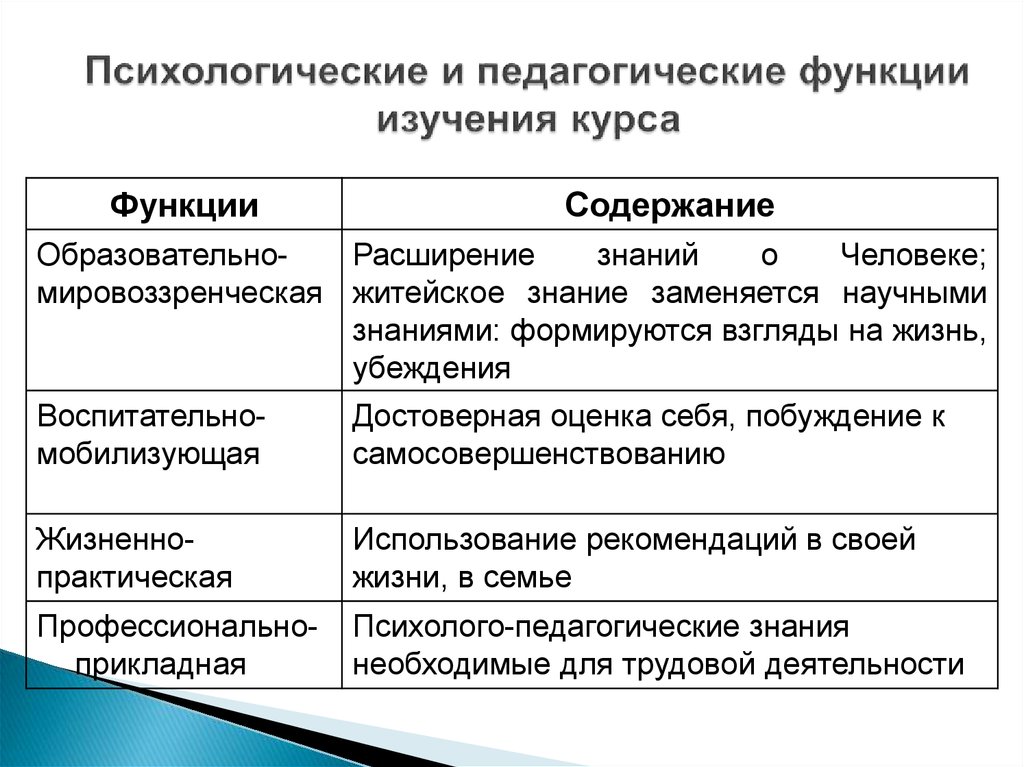 В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.
В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.
Britannica Quiz
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Формула площади круга является примером полиномиальной функции. Общая форма для таких функций составляет P ( x ) = A 0 + A 1 X + A 2 X 31 2 135 2 x 31 2 2 x 31 2 2 x 31 2 2 x 2 2 4 2 2 2 2 . n x n , where the coefficients ( a 0 , a 1 , a 2 ,…, a n ), x может быть любым действительным числом, а все степени x являются счетными числами (1, 2, 3,…). (Когда степени x могут быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно.
n x n , where the coefficients ( a 0 , a 1 , a 2 ,…, a n ), x может быть любым действительным числом, а все степени x являются счетными числами (1, 2, 3,…). (Когда степени x могут быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно.
Полиномиальные функции могут иметь геометрическое представление с помощью аналитической геометрии. Независимая переменная x откладывается по оси x (горизонтальная линия), а зависимая переменная y откладывается по оси y (вертикальная линия). Когда график отношения между х и y строится в плоскости х — y , отношение является функцией, если вертикальная линия всегда проходит только через одну точку на графике кривой; то есть была бы только одна точка f ( x ) соответствует каждому x , что является определением функции. Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2.
Независимая переменная x откладывается по оси x (горизонтальная линия), а зависимая переменная y откладывается по оси y (вертикальная линия). Когда график отношения между х и y строится в плоскости х — y , отношение является функцией, если вертикальная линия всегда проходит только через одну точку на графике кривой; то есть была бы только одна точка f ( x ) соответствует каждому x , что является определением функции. Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Другим распространенным типом функций, которые изучались с древних времен, являются тригонометрические функции, такие как sin x и cos x , где x — мера угла ( см.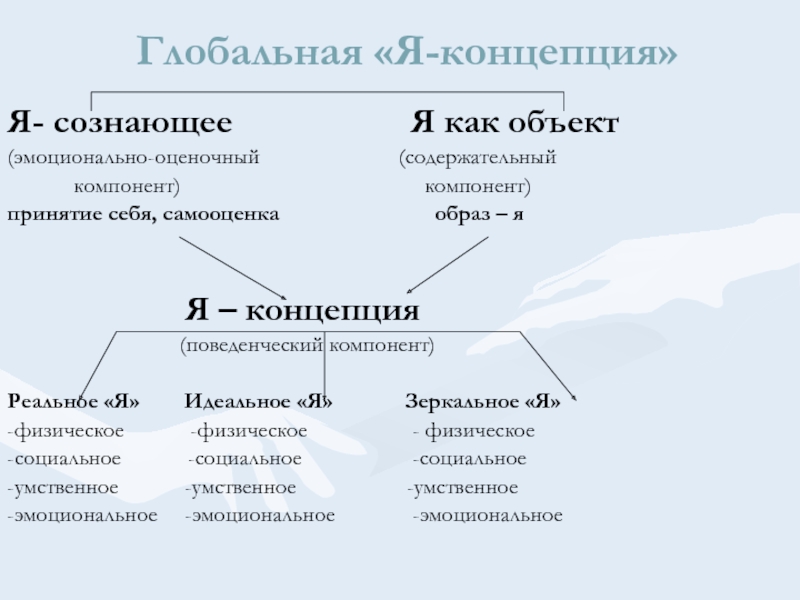 рисунок ). Из-за своего периодического характера тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».
рисунок ). Из-за своего периодического характера тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».
Экспоненциальная функция представляет собой отношение вида y = a x с независимой переменной x в диапазоне по всей строке действительных чисел как показатель степени положительного числа a . Вероятно, наиболее важной из экспоненциальных функций является y = e x , иногда пишется как y = exp ( x ), в которой e (2,7182818) является основанием натурального числа. система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.
Сложные функции
Практические приложения функций, переменными которых являются комплексные числа, не так просто проиллюстрировать, но тем не менее они очень обширны. Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена в виде z = x + i y , где i — мнимая единица (квадратный корень из −1), а x и y — действительные переменные ( см. цифру 9). возможно разделить сложную функцию на реальные и мнимые детали: F ( Z ) = P ( x , Y ) + I Q ( X , Y ). .
Функция «один к одному» — график, примеры, определение
Термин «отношение один к одному» на самом деле относится к отношениям между любыми двумя элементами, в которых один элемент может принадлежать только одному другому элементу. В математическом смысле эти отношения можно назвать функциями один к одному, в которых имеется равное количество элементов, или один элемент может быть соединен только с одним другим элементом. Имя человека и номер зарезервированного места этого человека в поезде — это простой повседневный пример функции «один к одному».
Имя человека и номер зарезервированного места этого человека в поезде — это простой повседневный пример функции «один к одному».
Если вам интересно, что делает функции one-to-one особенными, то эта статья поможет вам узнать об их свойствах и оценить эти функции. Используя решенные примеры, давайте рассмотрим, как идентифицировать эти функции на основе выражений и графиков.
| 1. | Что такое функция «один к одному»? |
| 2. | Проверка горизонтальной линии |
| 3. | Свойства функции «один к одному» |
| 4. | Как определить, является ли функция один к одному? |
| 5. | График функции один к одному |
| 6. | Обратная функция один к одному |
| 7. | шагов, чтобы найти функцию, обратную единице |
| 8. | Часто задаваемые вопросы о функции One to One |
Что такое функция «один к одному»?
Обычная функция может фактически иметь два разных входных значения, которые могут дать один и тот же ответ, тогда как функция «один к одному» этого не делает. Давайте продолжим и начнем с определения и свойств функций one-to-one.
Давайте продолжим и начнем с определения и свойств функций one-to-one.
Определение функции «один к одному»
Функция «один к одному» — это специальная функция, которая сопоставляет каждый элемент диапазона ровно с одним элементом своего домена, т. е. выходные данные никогда не повторяются. Например, функция g(x) = x — 4 является функцией один к одному, поскольку она дает разные ответы для каждого входа. Кроме того, функция g(x) = x 2 НЕ является функцией один к одному, поскольку она дает 4 в качестве ответа, когда входные данные равны 2 и -2. Функция, которая не является взаимно однозначной, называется функцией многие к одному.
Алгебраически мы можем определить функцию «один к одному» следующим образом:
функция g: D -> F называется взаимно однозначной, если ) ⇒ х 1 = х 2
для всех элементов x 1 и x 2 ∈ D. Функция один к одному также считается инъекцией, т. е. функция инъективна, только если она является взаимно однозначной. Противоположностью этому определению является функция g: D -> F взаимно однозначна, если x 1 ≠ х 2 ⇒ г (х 1 ) ≠ г (х 2 ). Давайте визуализируем это, сопоставив две пары значений для сравнения функций, которые являются и не являются один к одному.
е. функция инъективна, только если она является взаимно однозначной. Противоположностью этому определению является функция g: D -> F взаимно однозначна, если x 1 ≠ х 2 ⇒ г (х 1 ) ≠ г (х 2 ). Давайте визуализируем это, сопоставив две пары значений для сравнения функций, которые являются и не являются один к одному.
На рис. (а) (один к одному) x — это домен, а f (x) — кодовый домен, аналогично на рис. (b) (который не один к одному) x — домен и g(x) является доменом кода.
На рис. (a) для каждого значения x существует только одно уникальное значение f(x), и, таким образом, f(x) является функцией один к одному.
На рис. (b) разные значения x, 2 и -2 сопоставляются с общим значением g(x) 4 и (также разные значения x -4 и 4 сопоставляются с общим значением 16). Таким образом, g(x) — это функция, которая не является взаимно однозначной функцией.
Проверка горизонтальной линии
Тест горизонтальной линии используется для определения того, является ли функция однозначной, когда задан ее график. Мы уже видели условие (g(x 1 ) = g(x 2 ) ⇒ x 1 = x 2 ), чтобы определить, является ли функция g(x) однозначной алгебраически. С другой стороны, чтобы проверить, является ли функция один-один на ее графике,
Мы уже видели условие (g(x 1 ) = g(x 2 ) ⇒ x 1 = x 2 ), чтобы определить, является ли функция g(x) однозначной алгебраически. С другой стороны, чтобы проверить, является ли функция один-один на ее графике,
- просто возьмите горизонтальную линию (рассмотрите горизонтальную палочку) и проведите ее через график.
- Если горизонтальная линия НЕ проходит более чем через одну точку графика в любой момент времени, то функция однозначная.
- Если горизонтальная линия в какой-то момент проходит более чем через одну точку графика, то функция НЕ является однозначной.
Пример: Рассмотрим график ниже.
На приведенном выше графике
- f(x) = x 2 (квадратичная функция) НЕ является единицей, поскольку она не прошла тест горизонтальной линии (поскольку горизонтальная линия проходит через более чем одну точка графика)
- f(x) = x 3 (которое является кубической функцией) равно единице, так как оно прошло тест горизонтальной линии (поскольку горизонтальная линия каждый раз проходит только через одну точку графика)
Свойства функции «один к одному»
Взаимно-однозначная функция, т. е. инъективная функция, которая отображает отдельные элементы своей области определения в различные элементы своей сообласти. Вот некоторые свойства, которые помогают нам понять различные характеристики функций один к одному:
е. инъективная функция, которая отображает отдельные элементы своей области определения в различные элементы своей сообласти. Вот некоторые свойства, которые помогают нам понять различные характеристики функций один к одному:
- Если две функции f(x) и k(x) равны один к одному, то составная функция f ◦ тоже одна функция. (f ◦ k) (x 1 ) = (f ◦ k) (x 2 ) ⇒ f(k(x 1 )) = f(k(x 2 )) ⇒ k(x 1 ) = k(x 2 ) ⇒ x 1 = x 2
- Область определения функции g равна области значений g -1 , а область значений g равна области значений g -1
- Если рассматривать функцию как один к одному, то ее график будет либо всегда возрастать, либо всегда убывать.
- g -1 (g(x)) = x для каждого x в области g и g(g -1 (x)) = x для каждого x в домене g -1 .
- Если f ◦ k является взаимно однозначной функцией, то k(x) также гарантированно является взаимно однозначной функцией
- График функции и график обратной функции симметричны друг другу относительно прямой y = x.

Как определить, является ли функция один к одному?
Проверка вертикальной линии используется для определения того, является ли данное отношение функцией или нет. Кроме того, мы можем определить, является ли функция взаимно однозначной, используя два метода:
- Проверка функции один к одному графически: Если график g(x) каждый раз проходит через уникальное значение y, то говорят, что функция является функцией один к одному (проверка горизонтальной линией).
- Алгебраическая проверка функции один к одному: говорят, что функция g является взаимно однозначной, если a = b для каждого g(a) = g(b)
- Проверка функции один к одному с использованием производных: говорят, что функция g(x) является взаимно однозначной тогда и только тогда, когда либо g'(x) > 0, либо g'(x) < 0 во всей области. т. е. если функция везде либо возрастает, либо убывает, то она однозначна. Например, экспоненциальная функция f(x) = e x является полностью возрастающей функцией во всей своей области определения (-∞, ∞) и, следовательно, однозначно.
 Нарисуй один раз и проверь.
Нарисуй один раз и проверь.
График функции «один к одному»
Любую функцию можно представить в виде графика. Эта функция представлена путем рисования линии/кривой на плоскости в соответствии с декартовой системой. Домен отмечен горизонтально относительно оси x, а диапазон отмечен вертикально в направлении оси y. Если функция g взаимно однозначна, то никакие две точки (x 1 , y 1 ) и (x 2 , y 2 ) имеют одинаковое значение y. Следовательно, никакая горизонтальная линия не пересекает график уравнения y = g(x) более одного раза. На следующем рисунке (график прямой линии y = x + 1) показана функция один-один. Обратите внимание, что никакие две точки на нем не имеют одинаковую координату y (или) он проходит тест горизонтальной линии.
Обратная функция один к одному
Для того, чтобы понимать концепцию обратных функций и решать определенные типы уравнений, необходимо понимать концепцию взаимно однозначных функций. Во-первых, у функции g есть обратная функция, g -1 , тогда и только тогда, когда g один к одному. На приведенном ниже изображении функция, обратная однозначной функции g, обозначена как g -1 , где упорядоченные пары g -1 получаются путем замены координат в каждой упорядоченной паре g. Здесь домен g становится диапазоном g -1 , а диапазон g становится доменом g -1 .
Во-первых, у функции g есть обратная функция, g -1 , тогда и только тогда, когда g один к одному. На приведенном ниже изображении функция, обратная однозначной функции g, обозначена как g -1 , где упорядоченные пары g -1 получаются путем замены координат в каждой упорядоченной паре g. Здесь домен g становится диапазоном g -1 , а диапазон g становится доменом g -1 .
Свойства функции, обратной функции «один к одному»
Функция, обратная функции «один к одному», отменяет то, что исходная функция сделала со значением в своей области, чтобы вернуться к исходному значению y. Вот свойства обратной функции один к одному:
- Функция f имеет обратную функцию тогда и только тогда, когда f является взаимно однозначной функцией, т. е. только взаимно однозначные функции могут иметь обратную.
- Если функции g и f обратны друг другу, то обе эти функции можно рассматривать как взаимно однозначные.

- Если f и g обратны друг другу тогда и только тогда, когда (f ◦ g) (x) = x, x в области определения g и (g ◦ f) (x) = x, x в области определения f. Здесь f ◦ g — функция композиции, состоящая из ‘f’ из ‘g’.
- Если f и g обратны друг другу, то область определения f равна области значений g, а область значений g равна области определения f.
- Если f и g обратны друг другу, то их графики будут отражать друг друга на прямой y = x.
- Если точка (c, d) находится на графике f, то точка (d, c) находится на графике f -1 .
шагов, чтобы найти обратную функцию один к одному
Пошаговая процедура получения обратной функции g -1 (x) для взаимно однозначной функции g(x) выглядит следующим образом:
- Установить g(x) равным y
- Поменяйте местами x с y, поскольку у каждого (x, y) есть (y, x) партнер
- Найдите у
- В только что найденном уравнении переименуйте y как g -1 (x).

Пример: Найти обратную функцию g -1 (x) функции g(x) = 2 x + 5,
Теперь давайте выполним 4 шага:
| Установите g(x) = y | у = 2х + 5 |
|---|---|
| Переключатель x с y | х = 2у + 5 |
| Найдите у | у = (х — 5)/2 |
| Переименовать y как g -1 (x). Это обратное. | г -1 (х) = (х — 5)/2 |
Важные примечания по функции One to One:
Вот несколько моментов, которые следует помнить при изучении функции «один к одному»:
- В математическом смысле функции «один к одному» — это функции, в которых одинаковое количество элементов в домене и в диапазон, или один может быть соединен только с другим элементом.
- Для того, чтобы понимать концепцию обратных функций и решать определенные типы уравнений, важно понимать концепцию функций один к одному.

- Можно легко определить, является ли функция взаимно однозначной как геометрически, так и алгебраически.
☛ Связанные темы:
- Графические функции
- Линейные функции
- Калькулятор обратной функции
Часто задаваемые вопросы о функции One to One
Что такое определение функции «один к одному»?
Функции «один к одному» — это специальные функции, которые сопоставляют каждый элемент диапазона с единичным элементом домена. Это означает, что функция y = f(x) является однозначной только тогда, когда ни для каких двух значений x и y мы имеем f(x), равный f(y). Обычная функция может фактически иметь два разных входных значения, которые могут дать один и тот же ответ, тогда как функция «один к одному» этого не делает.
В чем разница между тестом вертикальной линии и тестом горизонтальной линии?
Вот различия между тестом вертикальной линии и тестом горизонтальной линии.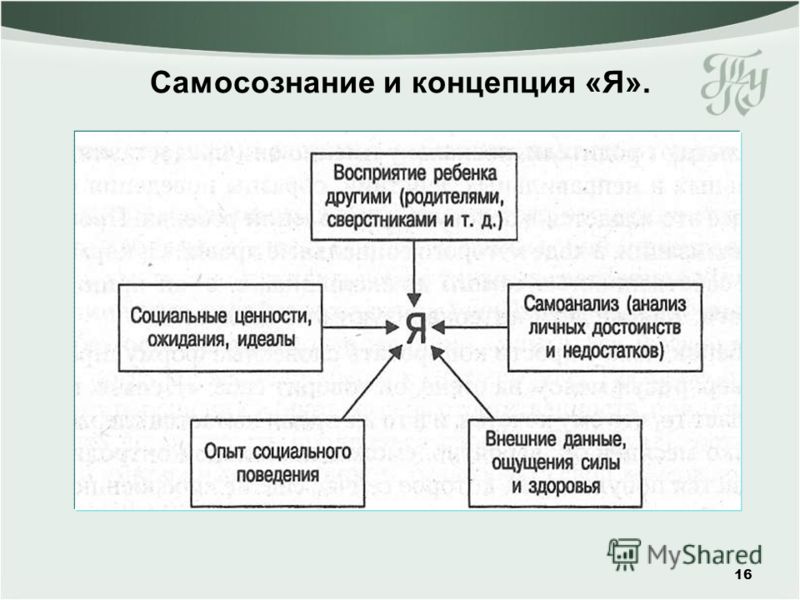
| Проверка вертикальной линии | Проверка горизонтальной линии |
|---|---|
| Проверка вертикальной линии используется для определения того, является ли отношение функцией. | Тест горизонтальной линии используется для определения того, является ли функция один-один. |
| Чтобы использовать этот тест, проведите вертикальную линию через график, и если вертикальная линия НЕ совпадает с графиком более чем в одной точке в любом случае, то график является функцией. | Чтобы использовать этот тест, проведите через график горизонтальную линию, и если горизонтальная линия НЕ пересекается с графиком более чем в одной точке в любом случае, то график представляет собой функцию один к одному. |
Как проверить, является ли функция взаимно однозначной?
Можно проверить, является ли функция один к одному, используя любой из этих двух методов:
- Геометрическое тестирование функции один к одному: если график функции проходит тест горизонтальной линии, то функцию можно считать единицей.
 к одной функции.
к одной функции. - Алгебраическая проверка функции один к одному: говорят, что функция g является взаимно однозначной, если для каждого g(x) = g(y), x = y.
Какие типы функций относятся к функциям One-to-One?
Функция «один к одному» либо строго убывающая, либо строго возрастающая.
- Если f(x) возрастает, то f'(x) > 0 для каждого x в его области определения
- Если f(x) убывает, то f ‘(x) < 0 для каждого x в его области определения
В функции «один к одному» одинаковые значения не назначаются двум разным элементам домена.
Что это значит, если функция не является функцией один к одному?
В функции, если горизонтальная линия проходит через график функции более одного раза, то функция не считается однозначной функцией. Функция, которая не является один к одному, считается как много к одному.
Каковы этапы решения обратной функции один к одному?
Вот шаги решения обратной однозначной функции g(x):
- Переименовать g(x) в y
- Поменять местами переменные x и y.

- Решите уравнение для y. Если есть только одно решение, то может существовать и обратное; иначе нельзя.
- В только что найденном уравнении переименуйте y как g -1 (x).
Что является примером функции «один к одному»?
Функция f(x) = x + 5 является функцией один к одному, поскольку она дает разные выходные данные для разных входных данных x. И чтобы функция была один к одному, она должна возвращать уникальный диапазон для каждого элемента в своей области. Здесь f(x) возвращает 6, если x равно 1, 7, если x равно 2, и так далее. Человек и его тень — реальный пример функции один к одному.
Что не является функцией один к одному?
Функция f(x) = x 2 не является функцией один к одному, поскольку она дает 9 в качестве ответа, когда входные данные равны 3 и -3. И чтобы функция была один к одному, она должна возвращать уникальный диапазон для каждого элемента в своей области. Здесь f(x) возвращает 9в качестве ответа для двух разных входных значений 3 и -3.
Функции парабол один к одному?
Нет, параболы не являются взаимно однозначными функциями. Функция g(y) = y 2 не является однозначной функцией, поскольку g(2) = g(-2). График функции g(y) = y 2 является параболической функцией, и горизонтальная линия дважды проходит через параболу.
Как мы можем применить концепцию функции «один к одному» в повседневной жизни?
Мы можем видеть эти отношения один к одному повсюду. Один из очень распространенных примеров отношений один на один, которые мы видим в нашей повседневной жизни, — это когда у одного человека есть один паспорт для себя, и этот паспорт должен использоваться только этим одним человеком.
Функция Определение и значение | Dictionary.com
- Верхние определения
- Викторина
- Связанный контент
- Примеры
- British
- Medical
- Scentre
- Cultular
- Учитель .
- Также называется соответствием, картой, отображением, преобразованием. отношение между двумя множествами, в котором каждому элементу первого множества ставится в соответствие один элемент второго множества, как выражение у = х2; оператор.
- Также называется многозначной функцией. отношение между двумя множествами, в котором каждому элементу первого множества присваиваются два или более элемента второго множества, как y2 = x2, которое присваивает каждому x два значения y = +x и y = -x.

- набор упорядоченных пар, в котором ни один из первых элементов пар не встречается дважды.
- формула, выражающая отношение между углами треугольника и его сторонами в виде синуса или косинуса.
- гиперболическая функция.
- грамматическая роль языковой формы или место, которое она занимает в определенной конструкции.
- грамматические роли или позиции лингвистической формы или класса формы в совокупности.
Не на каждом веб-сайте она есть, и даже на тех, которые имеют очень поверхностные функции.
Как внедрять цифровые инновации, необходимые во время пандемии|Ник Часинов|16 сентября 2020 г.|Search Engine Watch
Отчасти это было связано с оставшейся неопределенностью в отношении того, как вирус распространяется наиболее эффективно.
Анализ сбивающих с толку комментариев Трампа о ношении масок|Филип Бамп|16 сентября 2020 г.|Washington Post
Вспомогательные вещества являются важными материалами и выполняют широкий спектр функций.
«Неактивные» ингредиенты в ваших таблетках могут навредить вам|Елена Ионова/The Conversation|15 сентября 2020 г.
 |Popular-Science
|Popular-ScienceНапример, доставка и прослушивание социальных сетей звучат как разрозненные функции, но на самом деле они тесно связаны.
Глубокое погружение: как лето 2020 года заставило бренд-маркетинг измениться к лучшему|jim cooper|14 сентября 2020|Digiday
Это потому, что ежедневные упражнения не только помогают детям оставаться физически и эмоционально здоровыми, но и повышает когнитивную функцию.
15-недельный план упражнений для детей и семей|Криста Ланглуа|12 сентября 2020 г.|Outside Online
Но медь выполняет еще одну важную функцию: работает как катализатор в процессе дистилляции.
Когда дело доходит до отличного виски, размер вашего по-прежнему имеет значение||9 декабря 2014|DAILY BEAST
iPad стал еще большим хитом, тем более что он имел новую функцию, которая позволяла ему играть в рисунок назад.
Множество жизней художника Дэвида Хокни|Уильям О’Коннор|23 ноября 2014 г.
 |DAILY BEAST
|DAILY BEASTОткрытость также может быть функцией сексуальности и пола.
Извращенный выход к своему доктору в черном и синем|Хизер Бернер|25 октября 2014 г.|DAILY BEAST
Под названием «Пожалуйста, идите домой» пародия на Даниэля Францезе, известного как «слишком гей, чтобы функционировать». Дамиан из «Дрянных девчонок».
Голограммы аниме-поп-звезд, возвращение «свежего принца» Карлтона и другие вирусные видео|Алекс Чанси|12 октября 2014 г.|DAILY BEAST
Секс — это основная человеческая функция; физиологический драйв, который мы не можем игнорировать.
Христианские правые любят порно: новые исследования предполагают, что библейский пояс имеет извращенную сторону|Аврора Сноу|11 октября 2014|DAILY BEAST
Функция Внимания.
Ассимиляционная память|Маркус Дуайт Ларроу (также известный как профессор А. Луазетт)
Маленькие девочки, возможно, представляют привлекательную функцию украшения: им нравится, когда их считают красивыми.

Children’s Ways|Джеймс Салли
Вряд ли это функция — вечеринки даже в больших политических загородных домах более или менее неформальны.
Предки|Gertrude Atherton
Однако до сих пор не было представлено никаких определенных доказательств этой позиции, и функция соединения полностью неизвестна.
Элементы агрохимии|Томас Андерсон
После того, как было выпущено официальное объявление, мероприятие было завершено банкетом, устроенным для 200 известных повстанцев.
The Philippine Islands|John Foreman

[ fuhngk-shuhn ]
/ ˈfʌŋk ʃən /
Сохранить это слово!
См. синонимы для: функция / функционировал / функционировал / функции на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
сущ.
вид действия или деятельности, присущий лицу, предмету или учреждению; цель, для которой что-то разработано или существует; роль.
любое торжественное общественное или общественное собрание или событие.
фактор, связанный с другими факторами или зависящий от них: Цена является функцией спроса и предложения.
Математика.
Геометрия.
Грамматика.
Социология. вклад, вносимый социокультурным явлением в существующую социальную систему.
глагол (используется без объекта)
для выполнения определенного действия или деятельности; Работа; эксплуатация: компьютер сейчас не работает. Он редко работает до полудня.
иметь или выполнять какую-либо функцию; serve: в более раннем английском языке настоящее время часто функционировало как будущее. Этот оранжевый ящик может служить стулом.
Этот оранжевый ящик может служить стулом.
ВИКТОРИНА
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма обычно используется с другими глаголами для выражения намерения?
Происхождение функции
1525–35; <лат. functiōn- (основа functiō) исполнение, исполнение, эквивалентное funct(us) (причастие прошедшего времени от fungī) выполненное, исполненное + -iōn--ion
ДРУГИЕ СЛОВА ОТ функция
интерфункция, прилагательноемногофункциональность, прилагательноенефункционирование, прилагательноенадфункционирование, прилагательное
предфункция , существительное-функция, глагол (используется без дополнения)подфункция, существительное-су-функция, существительное-функция-инг, прилагательное-функция-инг, прилагательное
Слова рядом с функцией
Funafuti, funambulist, развлечения и игры, Funchal, functio laesa, функция, функциональный, функциональный, функциональный анализ, функциональная анатомия, функциональная слепота
Dictionary.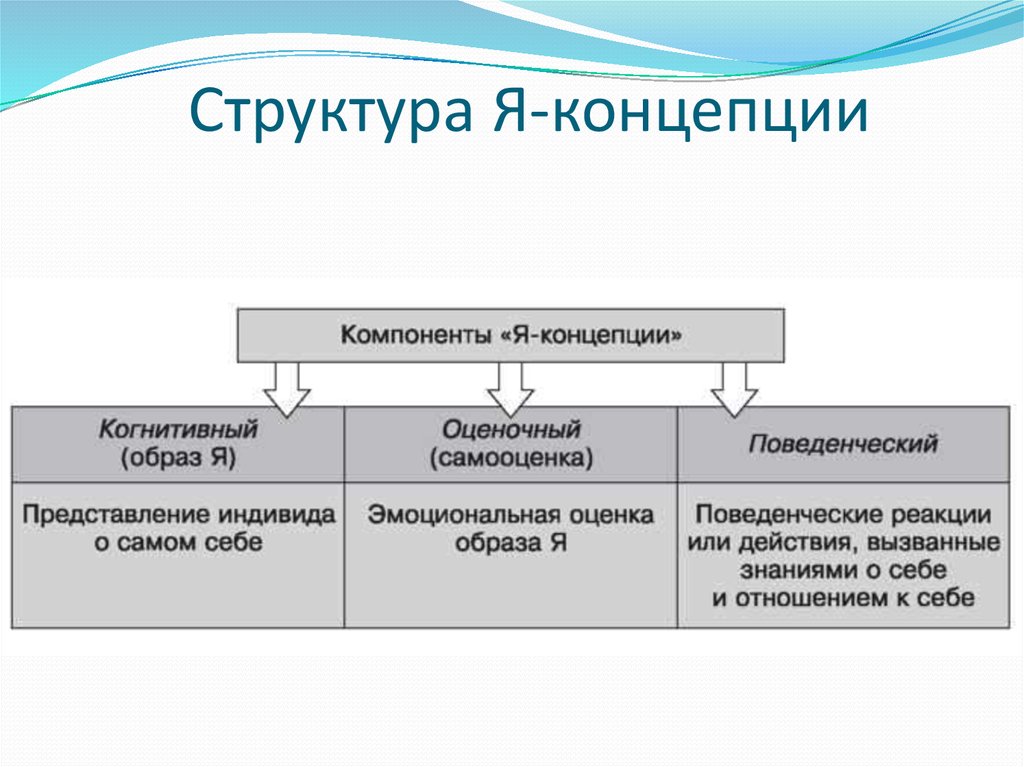 com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Слова, относящиеся к функции
действие, деятельность, дело, поведение, бизнес, долг, упражнение, цель, операция, часть, власть, цель, ответственность, роль , услуга, ситуация, задача, работа, сбор, встреча
Как использовать функцию в предложении
Британский словарь определений для функции
функция
/ (ˈfʌŋkʃən) /
существительное цель естественного действия или предназначенная вещь
молоток для забивания гвоздей в дерево
официальное или официальное общественное собрание или церемония
фактор, зависящий от другого или других факторовпродолжительность полета зависит от погоды
Также называется: карта, сопоставление, математическая логика, отношение между двумя множествами, которое связывает уникальный элемент (значение) второго (диапазона) с каждым элементом (аргументом) первого (домена): множество-один связь. Символ: f(x) Значение f(x) для x = 2 равно f(2)
Символ: f(x) Значение f(x) для x = 2 равно f(2)
глагол (intr)
действовать или выполнять, как указано; правильно работать
(следовать как) выполнять действие или роль (чего-то или кого-то) монета может работать как отвертка
Производные формы функции
functionless, прилагательноеПроисхождение слова для функции
C16: от латинского functiō, от fungī выполнять, разряжать
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Медицинские определения функции
функция
[ fŭngk′shən ]
n.
Физиологическое свойство или особое действие органа или части тела.
Нечто, тесно связанное с другим объектом и зависящее от него в своем существовании, ценности или значимости, например рост в результате питания.
Математическая переменная, так связанная с другой, что для каждого значения, принятого одной, есть значение, определенное для другой.
Правило соответствия между двумя наборами, при котором каждому элементу первого набора соответствует уникальный элемент второго набора.
Общие свойства вещества, зависящие от его химического характера и отношения к другим веществам, которые обеспечивают основу, на которой его можно отнести к кислотам или основаниям.
Особая реакционноспособная группа в молекуле.
Медицинский словарь Стедмана The American Heritage® Copyright © 2002, 2001, 1995, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin.
Научные определения функции
функция
[ fŭngk′shən ]
Связь между двумя наборами, которая сопоставляет каждому элементу первого набора уникальный элемент второго набора. Функции часто выражаются в виде уравнения, такого как y = x + 5, что означает, что y является функцией x, так что для любого значения x значение y будет на 5 больше, чем x.
Величина, значение которой зависит от значения, присвоенного одной или нескольким связанным величинам.

 — СПб.: Питер, 2013. — 288 с.: ил. — (Серия «Мастера…
— СПб.: Питер, 2013. — 288 с.: ил. — (Серия «Мастера… — Москва : Проспект. 2011.-432с.
— Москва : Проспект. 2011.-432с.

 Нарисуй один раз и проверь.
Нарисуй один раз и проверь.


 к одной функции.
к одной функции.

 |Popular-Science
|Popular-Science |DAILY BEAST
|DAILY BEAST