Что изучает логика формальная: Формальная логика — Алфавитный каталог — Электронная библиотека Руниверс

Что такое и как устроены логика и софистика? Как доказать невозможное? — Алексей Черныш на vc.ru

Для того чтобы понять как устроены процессы формирования мнений и что лежит в их основе нужно разобраться с устройством формальной логики.

2510 просмотров

Формальная логика

Формальная логика — наука о формах и законах суждения, показывающая как из исходных суждений, о которых мы договорились что они истинные, гарантированно получать истинные суждения.

Что значит о формах?
Возьмем формочку в детской песочнице, насыплем туда чего-нибудь и содержимое стало такой же формы, что и формочка. Чего туда не сыть или лей все примет ту же форму. Формула также придает форму и в зависимости от того, что считаем то и подставляем в неё.

Истинное знание невозможно, так как истина — это соответствие наших знаний – действительности. Проблема в том, что мы не имеем действительности, а имеем только знания о ней, для того, чтоб проверить. Поэтому истина всегда существует с ошибкой и её поиск сводится к уменьшению нами этой ошибки, а как мы знаем, чем точнее измерения, тем они дороже.

Как договорились определять истину?

Сначала определяются понятия. И есть 2 способа их определения:

1) Дедуктивное – это объяснение накопленных фактов используя общее понятие, добавляя к нему специфические признаки. Например, что такое зеркало? Это приспособление, имеющее высокую отражающую способность, и применяется для подачи заднего вида в глаза водителя.

2) Эмпирическое – накопление понимания при употреблении понятия в контексте, по которому можно понять зачем оно нужно. Например. Он пускал солнечные зайчики по комнате; пока он ехал, глаза поглядывали назад; он взглянул на себя с утра и увидел следы помады на щеке. То есть по контексту мы понимаем, что за слово.

Из понятий формируются суждения с помощью добавления к понятию утверждение или отрицание. На основе суждений строятся умозаключения, которые бывают 2х видов:

1) Дедуктивные – от общего к частному. (круги эйлера)

2) Индуктивные – из нескольких частных случаев выводится общее правило. (не достоверные, а вероятностные)

По каким законам получают в итоге истинные суждения?

1) закон тождества — любая мысль должна быть тождественна самой себе.

2) закон противоречия — если одно суждение что-то утверждает, а другое это одновременно отрицает, то такие суждения не могут быть истинными, если речь об одном и том же предмете в одном и том же отношении.

3) закон исключенного третьего – не может быть высокий/низкий/средний, а может быть высокий/не высокий

4) закон достаточного основания – утверждение должно быть обосновано

Софистика

Софистика – это учение древнегреческих преподавателей красноречия, суть которого в использовании софизмов. Софизм (хитрая выдумка, уловка) – ошибочное рассуждение, выглядящее логичным, целью которого является привести человека к заведомо неверному выводу, запутать, обмануть.

В софистике можно выделить несколько основных видов используемых логик.

Прагматическая логика

Прагматическая логика – это формальная логика, использующая софизмы. Целью прагматической логики является достижение психологического чувства правоты. Правота и истина не одно и то же. Это видно на примере стреляющих друг в друга солдат или столкновения полиции с протестующими. Каждый считает, что его сторона права, а другого неправа. С точки зрения формальной логики нельзя провести по 1 точки единственную прямую, по 2м точкам можно. С точки зрения прагматической логики можно. Провести туда куда нравится. Прагматическую логику часто называют «женской», так как чаще её применяют женщины, хотя, как мне кажется, чиновники применяют чаще.

Благодаря прагматической логике, к примеру, когда несколько человек спорят по какому-то вопросу все участники спора могут оказаться правы.

А такое возможно, когда спор между ними ведется в разных плоскостях. Например, 1 говорит про финансовую плоскость вопроса (снизим пенсионный возраст и будут в бюджете дополнительные деньги) другой про моральную (люди не доживают до этого возраста, как можно так обмануть всю жизнь работающих людей) третий про временную (давай сейчас поднимем возраст, а потом больше заплатим пенсию).

Разные плоскости спора с точки зрения формальной логики — нарушение закона тождества. Те, кто хочет доказать свою правоту чаще всего прибегают к нарушению именно этого закона используя аналогии.

Правда лежащая в одной плоскости спора по конкретному вопросу (конкретный вопрос значит, что нему не может быть мнения) может быть только одной, кроме того случая, когда борьба идет за уточнение выгоды. (мы делили апельсин, но одному нужна корка, а другому мякоть) Тогда выгода «разделяется» пополам и выигрывают обе стороны.

Другой пример двое заехали на узкую улицу и моргают друг другу фарами, но один уточнил выгоду, прижался к краю и второй смог проехать.

Третий пример. Муж и жена живут с тёщей, теща уехала, и они решили разводиться. Когда они жили вместе, они выигрывали за счет третьей стороны, а третья сторона проигрывала. Когда третьей стороны не стало они начали враждовать между собой. Часто объединяет дружба против кого-то.

4 вариант, когда оба отказываются от выгоды ради сохранения отношений.

5 вариант – перемаркировка. Заменить выгоду другой, которую могут получить обе стороны.

Т.е. 5 вариантов выигрыша обеих сторон: компромисс, уточнение выгоды, выигрыш за счет 3-ей стороны, отказ от выгоды и перемаркировка.

Эклектическая логика

Эклектическая логика – целью является получение имиджа истины. Формальная логика может не нарушаться, но за основу логических конструкций берутся догмы. Пример – книги по научному доказательству существования бога. Создать ощущение доказанности. Лоббисты табачных, алкогольных, нефтяных корпораций. Часто используют мошенники чтобы создать ощущение осведомленности в вопросе, рассказывая о фактах, которые находятся рядом с объектом обсуждения, но им не являются.

Интуитивная логика

Интуитивная логика – цель принятое управленческое решение на основе чувства (эмоций), продиктованного эмпирическим жизненным опытом. Все аргументы против, но внутри чувство, что надо по-другому сделать. Делаешь и получается то, что нужно.

Псевдологика – целью ее является уговорить самого себя принять решение, которое ты уже принял. И тут какие бы аргументы не приводились переубеждать бесполезно так как решение уже принято.

Аристотелевская силлогистика с точки зрения современной формальной логики

Аристотелевская силлогистика с точки зрения современной формальной логики

Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. Пер. с англ. — М.: Издательство иностранной литературы, 1959. – 313 с. Предлагаемая вниманию читателей книга польского логика Яна Лукасевича (1878—1956) является одним из выдающихся его трудов. Настоящая работа состоит из исторической части и систематической части. В исторической части я пытался излагать аристотелевское учение, как можно ближе следуя текстам Аристотеля, однако везде стремясь объяснить их с точки зрения современной формальной логики. В систематической части я пытался объяснить некоторые теории современной формальной логики, которые необходимы для понимания силлогистики Аристотеля, и пытался пополнить эту силлогистику в пределах, установленных самим Аристотелем. Я стремился быть ясным, насколько это возможно, так чтобы мое изложение могло быть понято учащимися, не тренированными в области символического или математического мышления. Поэтому я надеюсь, что эта часть моей работы сможет быть использована как введение в современную формальную логику. Оглавление ВСТУПИТЕЛЬНАЯ СТАТЬЯ ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ ГЛАВА I. ЭЛЕМЕНТЫ СИСТЕМЫ § 1. Истинная форма аристотелевского силлогизма § 2. Посылки и термины § 3. Почему единичные термины были опущены Аристотелем § 4. Переменные § 5. Силлогистическая необходимость § 6. Что такое формальная логика? § 7. Что такое формализм? ГЛАВА II. ПОЛОЖЕНИЯ СИСТЕМЫ § 8. Положения и правила вывода § 9. Фигуры силлогизма § 10. Больший, средний и меньший термины § 11. История одной ошибки § 12. Порядок посылок § 13. Ошибки некоторых комментаторов нового времени § 14. Четыре галеновские фигуры ГЛАВА III. СИСТЕМА § 15. Совершенные и несовершенные силлогизмы § 16. Логика терминов и логика предложений § 17. Доказательства посредством обращения § 18. Доказательства посредством reductio ad impossibile § 19. Доказательства посредством выделения § 20. Отбрасываемые формы § 21. Некоторые нерешенные проблемы ГЛАВА IV. АРИСТОТЕЛЕВСКАЯ СИСТЕМА В СИМВОЛИЧЕСКОЙ ФОРМЕ § 23. Теория дедукции § 24. Кванторы § 25. Основания силлогистики § 26. Выведение силлогистических положений § 27. Аксиомы и правила для отбрасываемых выражений § 28. Недостаточность наших аксиом и правил ГЛАВА V. ПРОБЛЕМА РАЗРЕШИМОСТИ § 29. Число неразрешимых выражений § 30. Правило отбрасывания Слупецкого § 31. Дедуктивная эквивалентность § 32. Сведение к элементарным выражениям § 33. Элементарные выражения силлогистики § 34. Арифметическая интерпретация силлогистики § 35. Заключение ГЛАВА VI. АРИСТОТЕЛЕВСКАЯ МОДАЛЬНАЯ ЛОГИКА ПРЕДЛОЖЕНИЙ § 37. Модальные функции и их соотношения § 38. Основная модальная логика § 39. Законы экстенсиональности § 40. Аристотелевское доказательство M-закона экстенсиональности § 41. Необходимые связи между предложениями § 42. «Материальная» или «строгая» импликация? § 43. Аналитические предложения § 44. Аристотелевский парадокс § 45. Случайность у Аристотеля ГЛАВА VII. СИСТЕМА МОДАЛЬНОЙ ЛОГИКИ § 47. C-N-b-p-система § 48. «дельта»-определения § 49. Четырехзначная система модальной логики § 50. Необходимость и четырехзначная система модальной логики § 51. Парные возможности § 52. Случайность и четырехзначная система модальной логики § 53. Некоторые дальнейшие проблемы ГЛАВА VIII. МОДАЛЬНАЯ СИЛЛОГИСТИКА АРИСТОТЕЛЯ § 54. Модусы с двумя аподиктическими посылками § 55. Модусы с одной аподиктической и одной ассерторической посылкой § 56. Отбрасываемые модусы с одной аподиктической и одной ассерторической посылкой § 57. Разрешение спора § 58. Модусы с возможными посылками § 59. Законы обращения случайных предложений § 60. Исправление ошибок Аристотеля § 61. Модусы со случайными посылками § 62. Философские выводы из модальной логики ДОПОЛНИТЕЛЬНЫЕ РЕДАКЦИОННЫЕ ПРИМЕЧАНИЯ

Формальная логика была разработана для понимания природы дедуктивного

Даже если мы согласимся со всем, что мы только что сделали в отношении логической структуры языка, скептически настроенный специалист по лингвистике все же может возразить, что большая часть того, чему его на самом деле учат во вводном символическом Логический класс не имеет прямого отношения к пониманию естественного языка.

Это разумное возражение. Многие студенты заканчивают полный курс символической логики и уходят, не зная, какое отношение этот курс имеет к пониманию языка.

У такого замешательства есть причина, это не просто признак плохого обучения.

Причина в том, что вопросы, для ответа на которые была разработана формальная логика, касаются не только логической структуры естественного языка.

Давайте подробнее об этом.

В типичном первом курсе символической логики вы познакомитесь с тремя различными системами логики: категорической (или аристотелевской) логикой, пропозициональной логикой и предикат логика.

В каждой системе вы научитесь переводить утверждения естественного языка на формальный символический язык и (среди прочего) узнаете, как представлять аргументы и проверять их правильность в рамках данного языка.

Например, высказывание на естественном языке, такое как «коровы — это млекопитающие», будет представлено как «Все C являются M» в категориальной логике.

В логике высказываний вы просто использовали бы одну заглавную букву для представления утверждения «коровы — это млекопитающие», потому что логика высказываний безразлична к субъектно-предикатной структуре языка — она имеет дело только с логическими отношениями между предложениями, взятыми как единое целое.

В логике предикатов выражение «коровы — это млекопитающие» будет представлено как «(x)(Cx ⊃ Mx)». Вы можете прочитать это как «для любого индивидуума x, если x — корова, то x — млекопитающее».

Большая часть вашего времени в символическом классе будет посвящена изучению методов ответов на следующие виды вопросов, работающих в рамках каждой из этих логических систем:

• Как бы вы записали следующее утверждение на естественном языке в символической форме?
• Является ли следующий набор утверждений последовательным или противоречивым?
• Выражает ли следующее утверждение тавтологию (необходимая истина), противоречие (необходимая ложь) или случайный факт (возможная истина, возможная ложь)?
• Является ли следующий аргумент допустимым или недопустимым?
• Можете ли вы построить действительное дедуктивное доказательство данного вывода, исходя из следующих предпосылок и стандартных правил вывода?

Большинство страниц учебника по символической логике посвящено методам обучения ответам на эти вопросы.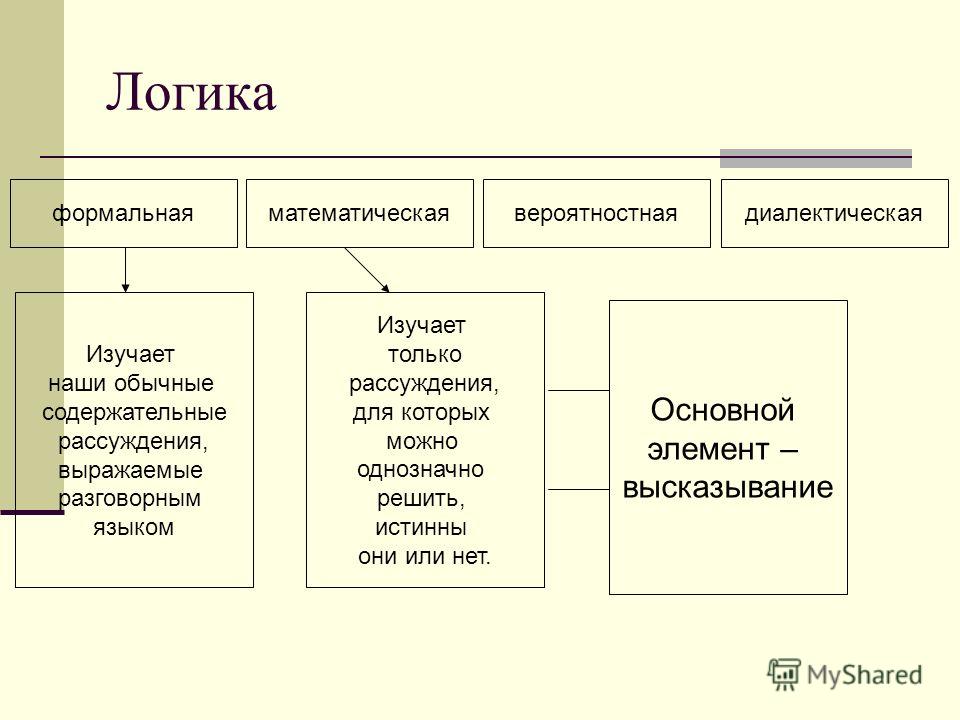

Но эти вопросы отражают исторические интересы философов и логиков, а не лингвистов.

Вот реальность: формальная логика была разработана как инструмент для понимания природы дедуктивных рассуждений и дедуктивных доказательств . Его предметом является природа логической истины и логический вывод , а не структура естественного языка.

Чтобы быть более конкретным, вот вопросы, которые стимулировали развитие формальной логики (особенно за последние пару сотен лет):

1. Как мы можем определить, является ли часть рассуждения действительным дедуктивным аргументом?
2. Как мы можем определить, является ли вывод необходимым набором предпосылок? Как мы можем найти действительный дедуктивный аргумент, демонстрирующий эту необходимую связь — т.е. е. это показывает почему вывод следует с необходимостью?
3. Что такого в структуре мира, структуре языка и отношениях между словами, мыслями и вещами, что делает возможным дедуктивное умозаключение ?

Мы видим связь с языком в этом последнем вопросе, но связь эта косвенная, движимая основной философской целью достижения глубокого понимания природы дедуктивных рассуждений.

Теперь оказывается, что формальная очень полезная логика для исследования логической структуры естественного языка. Но эту удачу лучше всего рассматривать как побочный продукт или приложение формальной логики.

Преднамеренное использование формальных методов для моделирования семантики естественного языка — формальная логика на службе лингвистики — на самом деле относится к середине и концу ^-го -го века. Большинство философов, которые преподают вводную символическую логику, не знакомы с формальной семантикой в ​​​​лингвистике, и во вводных учебниках эти разработки отсутствуют. В философии она рассматривается как специализированная область, пересекающаяся с философией языка и лингвистикой. Более продвинутые курсы по логике иногда охватывают темы в этой области, но формальная семантика обычно преподается только на уровне выпускников по более специализированным программам.

Теперь давайте обратимся к третьему и последнему пункту, который я хотел сделать об отношениях между логикой и языком.

Логика

Логика Логика :

Логика – это изучение предложений и их использования в аргументация. Это исследование может быть проведено на очень абстрактном уровне, т. как в формальной логике, или он может сосредоточиться на практическом искусстве правильного рассуждения, как в прикладной логике.

Действительные аргументы имеют две основные формы. Те, что рисуют новые предложение (вывод) из данного предложения или набора пропозиции (посылки), в которых можно подумать, что она скрыта называются дедуктивными. Эти аргументы позволяют убедительно утверждать, что вывод следует по строгой необходимости из посылок или в других словами, что утверждать посылки, но отрицать заключение было бы непоследовательно и самопротиворечиво. Аргументы, что венчурный генерал выводы из конкретных фактов, которые кажутся доказательствами для них называются индуктивными. Эти аргументы делают более слабое утверждение что посылки придают определенную степень вероятности или обоснованность выводов.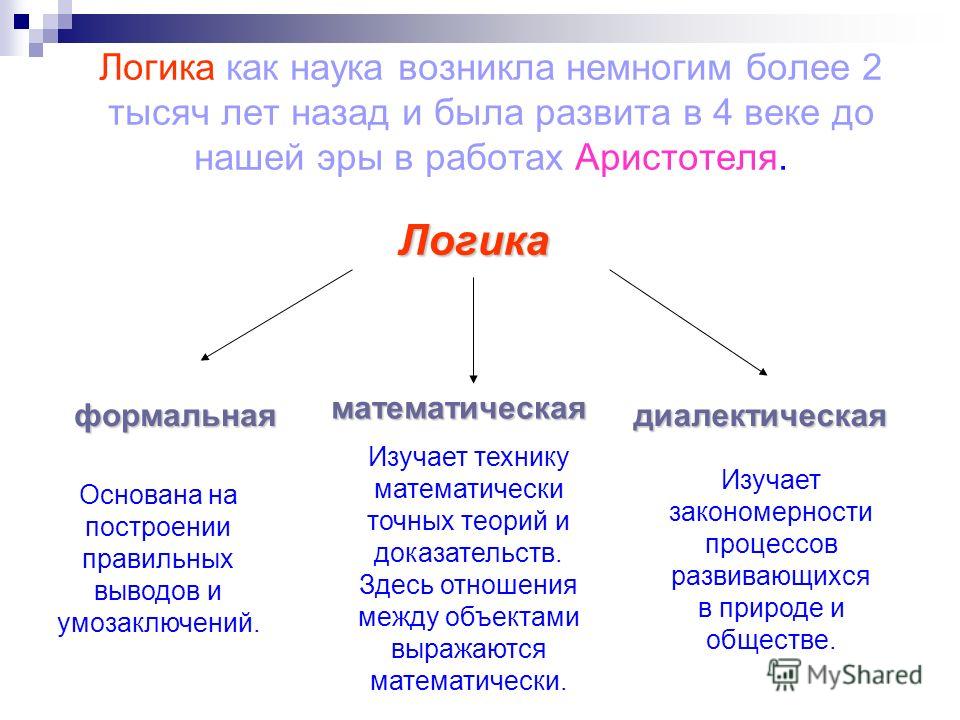 Логика индуктивности аргументация стала фактически синонимом методологии физические, социальные и исторические науки и больше не лечится по логике. Логика в том виде, в каком она понимается в настоящее время, касается самой себя. с дедуктивными процессами. Таким образом, он включает в себя принципы, какие предложения связаны друг с другом и методы мысль, с помощью которой эти отношения могут быть исследованы и обоснованы сделанные о них заявления.

В самом узком смысле дедуктивная логика делится на логику пропозиций (называемых также сентенциальной логикой) и логикой сказуемые (или именные выражения). В самом широком смысле он охватывает различные теории языка (такие как логический синтаксис и семантика), металогика (методология формальных систем), теории модальностей (анализ понятий необходимости, возможности, невозможность и случайность), а также изучение парадоксов и логические ошибки. Оба эти чувства можно назвать формальными или чистыми. логики в том, что они строят и анализируют абстрактную совокупность символы, правила соединения этих символов в формулы, и правила работы с этими формулами. Когда определенные значения привязаны к этим символам и формулам, и этот механизм адаптирован и развернуты по конкретным вопросам определенного круга специальных предметы, логика, как говорят, применяется. Анализ вопросов, которые выходят за рамки формальных вопросов чистой или прикладной логики, таких как как исследование значения и следствий понятий и предположения любой дисциплины, является областью философии логики.

Логика разрабатывалась самостоятельно и доводилась до некоторой степени систематизация в Китае (5-3 вв. до н.э.) и Индии (от с 5 века до н.э. по 16 и 17 века нашей эры). Логика как она есть известен на Западе родом из Греции. Основываясь на важном традиции математики и риторики и философии аргументации, Аристотель в 4 веке до н.э. разработал первую система логики именных выражений. Логика предложений возникла в трудах ученика Аристотеля Теофраста и в том Мегарской школы диалектиков и логиков IV в. школа стоиков. После упадка греческой культуры логика возродился первым среди арабских ученых в 10 веке.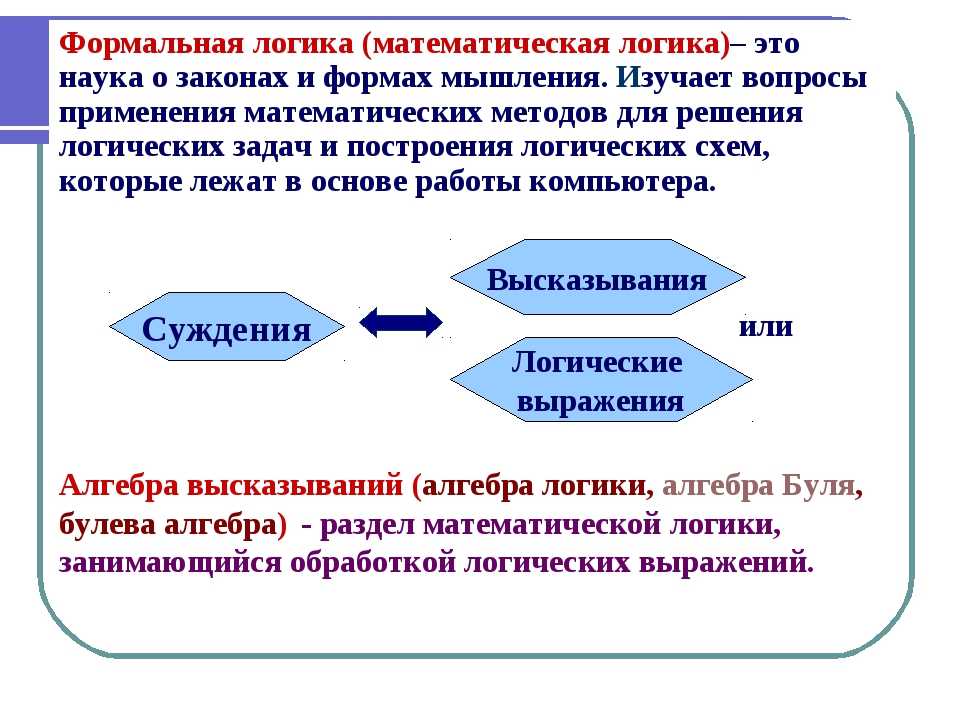 Средневековый интерес к логике восходит к работам св. Ансельма Кентерберийского и Питер Абеляр. Его апогеем был 14 век, когда Схоласты развивали логику, особенно анализ предложений, далеко за пределы того, что было известно древним. Риторика и естественность наука во многом затмила логику в эпоху Возрождения. Современная логика начал развиваться с работ математика Г.В. Лейбниц, который пытался создать универсальное исчисление разума. Большие успехи были сделаны в 19век в развитии символической логики, привело к весьма плодотворному слиянию логики и математики в формальный анализ.

Современная формальная логика — это изучение форм вывода и суждений. Его простейшая и самая основная ветвь — это пропозициональная исчисление (или ПК). В этой логике предложения или предложения образуют только семантическая категория. Они рассматриваются как простые и остаются не проанализированный; внимание сосредоточено на том, как они связаны с другими предложения с помощью пропозициональных связок (таких как «если. .. то», «и», «или», «это не так» и т. д.) и, таким образом, сформировались в аргументы. Представляя предложения с помощью символов, называемых переменные и связки с символическими операторами, и приняв решение о набор правил трансформации (аксиом, определяющих достоверность и предоставить отправные точки для вывода дальнейших правил, называемых теоремы), можно моделировать и изучать абстрактные характеристики и последствия этой формальной системы в некотором роде подобно исследованиям чистой математики. Когда переменные относятся не к целым предложениям, а к существительным выражениям (или предикаты) в предложениях, полученная формальная система известна как нижнее исчисление предикатов (или LPC).

Изменение операторов, переменных или правил таких формальных систем дает разную логику. Некоторые системы ПК, например, добавляют третье «среднее» значение к двум традиционным возможным значениям — true или ложные — предложений. Важным шагом в современной логике является открытие что можно исследовать и охарактеризовать другие формальные системы с точки зрения логики, вытекающей из их элементов, операций и правила формирования; таково изучение логических основ математика, теория множеств и сама логика.