Что такое иррациональное: Математика — 9

Прежде чем говорить про решение иррациональных уравнений, следует хорошо разобраться с вопросом, что такое иррациональные уравнения. Сейчас мы этим и займемся: познакомимся с определением иррационального уравнения и рассмотрим примеры уравнений этого вида.

Следует заметить, что определения немного отличаются от одной математической книги к другой.

Подробный разговор про иррациональные уравнения и их решение ведется на уроках алгебры и начал анализа в старших классах школы. Однако некоторые авторы вводят в рассмотрение уравнения этого вида раньше. Например, те, кто занимаются по учебникам Мордковича А. Г., узнают про иррациональные уравнения уже в 8 классе: в учебнике [1, с. 174] утверждается, что

Определение

Иррациональным уравнением называют уравнение, если в нем переменная содержится под знаком квадратного корня.

Там же приводятся примеры иррациональных уравнений , , , и т.п. Очевидно, в каждом из приведенных уравнений под знаком квадратного корня содержится переменная x, значит, по приведенному выше определению эти уравнения – иррациональные.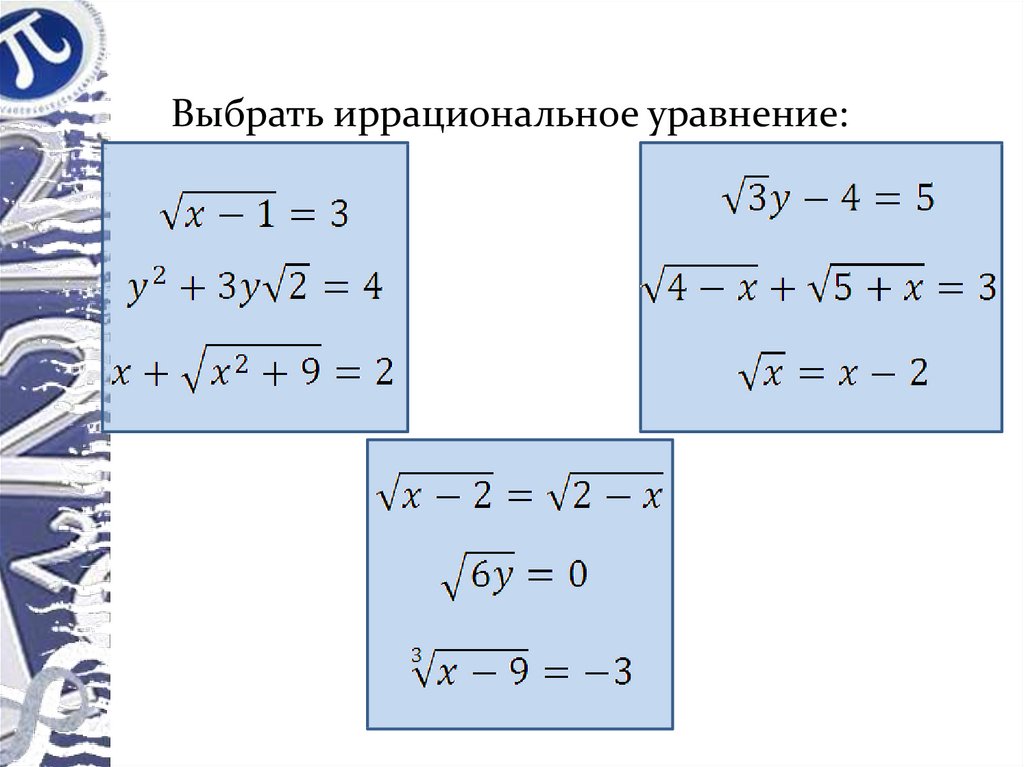

В учебниках Колмогорова А. Н. [3, с. 214] и Колягина Ю. М. [4, с. 193]

Определение

иррациональными называют уравнения, в которых под знаком корня содержится переменная.

Обратим внимание на принципиальное отличие данного определения от предыдущего: здесь говорится просто корень, а не квадратный корень, то есть, не уточняется степень корня, под которым находится переменная. Значит, корень может быть не только квадратным, но и третьей, четвертой и т.д. степени. Таким образом, последнее определение задает более обширную группу уравнений.

Возникает закономерный вопрос, почему в старших классах мы начинаем использовать это более широкое определение иррациональных уравнений? Все объяснимо и просто: когда в 8 классе происходит знакомство с иррациональными уравнениями, нам хорошо известен лишь квадратный корень, ни о каких кубических корнях, корнях четвертой и более высоких степеней мы еще не знаем. А в старших классах обобщается понятие корня, мы узнаем про корень степени n, и при разговоре об иррациональных уравнениях уже не ограничиваемся квадратным корнем, а имеем в виду корень произвольной степени.

Для наглядности продемонстрируем несколько примеров иррациональных уравнений. — здесь под знаком кубического корня расположена переменная x, поэтому это уравнение иррациональное. Другой пример: — здесь переменная x находится как под знаком квадратного корня, так и корня четвертой степени, то есть, это тоже иррациональное уравнение. Вот еще пара примеров иррациональных уравнений более сложного вида: и .

Приведенные определения позволяют для себя отметить, что в записи всякого иррационального уравнения имеются знаки корней. Также понятно, что если знаков корней нет, то уравнение не является иррациональным. Однако не все уравнения, содержащие знаки корней, являются иррациональными. Действительно, в иррациональном уравнении под знаком корня должна быть переменная, если переменной под знаком корня нет, то уравнение не является иррациональным. В качестве иллюстрации приведем примеры уравнений, которые содержат корни, но не являются иррациональными. Уравнения и не являются иррациональными, так как не содержат переменных под знаком корня – под корнями стоят числа, а переменных под знаками корней нет, поэтому эти уравнения не иррациональные.

Некоторые сборники задач для подготовки к ЕГЭ в разделе «иррациональные уравнения» содержат задания, в которых переменная находится не только под знаком корня, но еще и под знаком какой-либо другой функции, например, модуля, логарифма и т.п. Вот пример , взятый из книги [5], а вот — из сборника [6]. В первом примере переменная x находится под знаком логарифма, а логарифм еще под знаком корня, то есть, мы имеем, если так можно выразиться, иррациональное логарифмическое (или логарифмическое иррациональное) уравнение. Во втором примере переменная находится под знаком модуля, а модуль еще и под знаком корня, с Вашего позволения назовем его иррациональным уравнением с модулем.

Считать ли уравнения подобного вида иррациональными? Вопрос хороший. Вроде переменная под знаком корня есть, но смущает что она не в «чистом виде», а под знаком еще одной или большего числа функции. Другими словами, вроде нет противоречия тому, как мы определили выше иррациональные уравнения, но присутствует некоторая степень неуверенности из-за наличия других функций. С нашей точки зрения, не стоит фанатично подходить к «называнию вещей своими именами». На практике достаточно сказать просто «уравнение» без уточнения, какого именно оно вида. А все эти добавки «иррациональное», «логарифмическое» и т.п. служат по большей части для удобства изложения и группировки материала.

В свете информации последнего абзаца интерес представляет определение иррациональных уравнений, данное в учебнике под авторством Мордковича А. Г. за 11 класс [2, с. 237]

Определение

Иррациональными

Здесь, помимо уравнений с переменной под знаком корня, иррациональными считаются и уравнения с переменными под знаком возведения в дробную степень. Например, согласно этому определению уравнение считается иррациональным. С чего вдруг? Мы же уже привыкли к корням в иррациональных уравнениях, а здесь не корень, а степень, и это уравнение больше хочется назвать, к примеру, степенным, а не иррациональным? Все просто: степень с дробным показателем определяется через корни, и на ОДЗ переменной x для данного уравнения (при условии x²+2·x≥0) его можно переписать с использованием корня как , а последнее равенство представляет собой привычное нам иррациональное уравнение с переменной под знаком корня. Да и методы решения уравнений с переменными в основании дробных степеней абсолютно такие же, как и методы решения иррациональных уравнений. Так что удобно их назвать иррациональными и рассматривать в этом свете. Но будем честными с собой: изначально перед нами уравнение , а не , и язык не очень охотно поворачивается называть исходное уравнение иррациональным из-за отсутствия корня в записи.

Избежать подобных спорных моментов можно и через более строгое определение. Пример такого определения можно найти в справочнике советских времен [7, с. 64]:

Определение

Иррациональным называется уравнение, в котором некоторое рациональное или алгебраическое выражение от неизвестного находится под знаком радикала.

Согласно этому определению в иррациональном уравнении под знаком радикала может находиться только выражение, в котором над переменной не совершается иных действий, кроме сложения, вычитания, умножения, деления, возведения в степень (натуральную) и извлечения корня. Это определение исключает нахождения переменной в иррациональном уравнении под знаками логарифмов, тригонометрических функций, в показателе степени и др.

Какое из приведенных выше определений предпочесть? Наверное, стоит называть иррациональными только такие уравнения, которые не противоречат ни одному из записанных определений, а остальные называть просто уравнениями без уточнения, что это за уравнение.

Пара слов о количестве переменных в записи иррациональных уравнений. Все приведенные выше иррациональные уравнения содержат единственную переменную x, то есть, являются уравнениями с одной переменной. Однако ничто не мешает рассматривать и иррациональные уравнения с двумя, тремя и т.д. переменными. Приведем пример иррационального уравнения с двумя переменными и с тремя переменными .

Но при этом обязательно нужно заметить, что в школе обычно рассматривается решение иррациональных уравнений только с одной переменной. Иррациональные уравнения с несколькими переменными встречаются не для решения, а в составе систем уравнений или при алгебраическом описании геометрических объектов. Например, можно встретить задание «решите систему уравнений », или увидеть описание полуокружности с центром в начале координат, радиусом 3 единицы, лежащей в верхней полуплоскости, при помощи уравнения .

В школе также рассматриваются иррациональные уравнения с параметром. Приведем пример: , здесь x – переменная, a — параметр. Как понять, что это уравнение с параметром, а не уравнение с двумя переменными? Как правило, это указывается в задании.

В заключение скажем, что встречается термин «простейшие иррациональные уравнения». Так что рекомендуем ознакомиться, что понимают под простейшими иррациональными уравнениями.

Иррациональные числа

Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби:

  1,5 рационально, но π иррационально

Иррациональное означает Нерациональное (без соотношения)

Давайте посмотрим, что делает число рациональным или иррациональным. ..

Рациональные числа

A Rational Число можно записать как 0003 Отношение двух целых чисел (т.е. простой дроби).

Пример: 1,5 является рациональным, поскольку его можно записать как отношение 3/2

Пример: 7 рационально, потому что его можно записать как отношение 7/1

Пример 0,333… (3 повторения) также является рациональным, поскольку его можно записать как отношение 1/3

Иррациональные числа

Но некоторые цифры нельзя записать как отношение двух целых чисел…

…их называют Иррациональные Числа .

Пример:

π  = 3,1415926535897932384626433832795… (и больше)

Мы не можем s записать простую дробь, которая равна Пи.

Популярное приближение ²² / ₇ = 3,1428571428571. .. близко, но неточное .

Еще одна подсказка заключается в том, что десятичная дробь продолжается вечно, не повторяясь.

Не может быть записан как дробь

Это иррационально потому что его нельзя записать как отношение (или дробь),
не потому что это безумие!

Таким образом, мы можем определить, является ли число рациональным или иррациональным, попробовав записать число в виде простой дроби.

Пример:

9,5 = 19 2

Итак, это рациональное число (и поэтому не иррациональное )

Вот еще несколько примеров:

Номер		Как дробь		Рациональное или Иррациональное?
1,75		7 4		Рационал
. 001		1 1000		Рационал
√2 (квадратный корень из 2)		?		Неразумно !

Квадратный корень из 2

Давайте посмотрим на квадратный корень из 2 более внимательно.

Ответом является квадратный корень из 2 , который равен 1.4142135623730950…(и т.д.)

Но это не число вроде 3 или пяти третей или что-то в этом роде…

… на самом деле мы не может записать квадратный корень из 2, используя отношение двух чисел…

… (вы можете узнать , почему , на странице «Иррационально ли это?»). ..

… и так мы знаем это иррациональное число .

Известные иррациональные числа

Но √4 = 2 рационально, а √9 = 3 рационально…

… так что не все корни иррациональны.

Примечание по умножению иррациональных чисел

Взгляните на это:

• π × π = π ² известно, что иррационально
• Но √2 × √2 = 2 равно рациональному

Так что будьте осторожны. .. умножение иррациональных чисел может дать рациональное число!

Забавные факты….

Вероятно, Гиппас (один из учеников Пифагора) открыл иррациональные числа, когда пытался записать квадратный корень из 2 в виде дроби (считается, что с помощью геометрии). Вместо этого он доказал квадратный корень из 2·9.0093 нельзя было записать в виде дроби, поэтому иррационально .

Но последователи Пифагора не могли принять существование иррациональных чисел, и говорят, что Гиппас был утоплен в море в наказание богов!

434 435 1064 2022 3987 1065 3988 2023 2990 2991

Иррациональные числа — определение, свойства, примеры, значение

Иррациональные числа — это те действительные числа, которые не могут быть представлены в виде отношения. Другими словами, те действительные числа, которые не являются рациональными числами, известны как иррациональные числа. Гиппас, философ-пифагорейец, открыл иррациональные числа в V веке до нашей эры. К сожалению, его теория была высмеяна, и он был брошен в море. Но иррациональные числа существуют, давайте заглянем на эту страницу, чтобы лучше понять концепцию, и, поверьте нам, вас не выбросит в море. Скорее, зная эту концепцию, вы также будете знать список иррациональных чисел, разницу между иррациональными и рациональными числами и то, являются ли иррациональные числа действительными числами.

1.	Что такое иррациональные числа?
2.	Свойства иррациональных чисел
3.	Как определить иррациональное число?
4.	Символ иррациональных чисел
5.	Набор иррациональных чисел
6.	Рациональные и иррациональные числа
7.	Рабочие листы по рациональным и иррациональным числам
8.	Часто задаваемые вопросы об иррациональных числах

Что такое иррациональные числа?

Иррациональные числа — это множество действительных чисел, которые не могут быть выражены в виде дроби p/q, где p и q — целые числа. Знаменатель q не равен нулю (q ≠ 0). Кроме того, десятичное расширение иррационального числа не заканчивается и не повторяется.

Иррациональные числа Определение: Иррациональные числа — это действительные числа, которые не могут быть представлены в виде простой дроби. Они не могут быть выражены в виде отношения, такого как p/q, где p и q — целые числа, q≠0. Это противоречие рациональных чисел.

Распространенные примеры иррациональных чисел

Ниже приведены несколько конкретных иррациональных чисел, которые обычно используются.

• ㄫ (пи) — иррациональное число. π=3⋅14159265… Десятичное значение никогда не останавливается ни в какой точке. Поскольку значение ㄫ ближе к дроби 22/7, мы принимаем значение числа пи как 22/7 или 3,14 (Примечание: 22/7 — рациональное число.)
• √ 2 — иррациональное число. Рассмотрим прямоугольный равнобедренный треугольник, у которого две равные стороны АВ и ВС имеют длину 1 единицу. По теореме Пифагора гипотенуза AC будет равна √2. √2=1⋅414213⋅⋅⋅⋅
• Число Эйлера e — иррациональное число. е=2⋅718281⋅⋅⋅⋅
• Золотое сечение, φ 1,61803398874989….

Свойства иррациональных чисел

Свойства иррациональных чисел помогают нам выделить иррациональные числа из набора действительных чисел. Ниже приведены некоторые свойства иррациональных чисел:

• Иррациональные числа состоят из непрерывных и неповторяющихся десятичных знаков.
• Это только действительные числа.
• При сложении иррационального и рационального чисел результатом или их суммой является только иррациональное число. Для иррационального числа x и рационального числа y их результат x + y = иррациональное число.
• При умножении любых иррациональных чисел на любое ненулевое рациональное число их произведение будет иррациональным числом. Для иррационального числа x и рационального числа y их произведение xy = иррационально.
• Для любых двух иррациональных чисел их наименьшее общее кратное (НОК) может существовать, а может и не существовать.
• Сложение, вычитание, умножение и деление двух иррациональных чисел могут быть или не быть рациональными числами.

Как определить иррациональное число?

Мы знаем, что иррациональные числа — это только действительные числа, которые не могут быть выражены в виде p/q, где p и q — целые числа, а q ≠ 0. Например, √ 5 и √ 3 и т. д. — иррациональные числа. С другой стороны, числа, которые могут быть представлены в виде p/q, такие, что p и q являются целыми числами и q ≠ 0, являются рациональными числами.

Символ иррациональных чисел

Прежде чем знакомиться с символом иррациональных чисел, давайте обсудим символы, используемые для других типов чисел.

• N — Натуральные числа
• I — Воображаемые числа
• R — Реальные числа
• Q — Рациональные числа.

Действительные числа состоят как из рациональных, так и из иррациональных чисел. (R-Q) определяет, что иррациональные числа могут быть получены путем вычитания рациональных чисел (Q) из действительных чисел (R). Это также можно записать как (R\Q). Следовательно, символ иррациональных чисел = Q’.

Набор иррациональных чисел

Набор иррациональных чисел можно получить, записав несколько иррациональных чисел в скобках. Множество иррациональных чисел можно получить по некоторым свойствам.

• Все квадратные корни, не являющиеся полным квадратом, являются иррациональными числами. {√ 2 , √3 , √5 , √8}
Число Эйлера 90 313, золотое сечение и число Пи — одни из самых известных иррациональных чисел. {е, ∅, ㄫ}
• Квадратный корень из любого простого числа является иррациональным числом.

Таблица иллюстрирует список некоторых иррациональных чисел .

Иррациональное число	значение
№	3.14159265….
и	2.7182818…..
√2	1.414213562…
√3	1.73205080…
√5	2.23606797….
√7	2,64575131….
√11	3.31662479…
√13	3,605551275…
-√3/2	-0,866025. …
∛47	3.60882608

Рациональные и иррациональные числа

Любое число, которое определяется в виде дроби p/q или отношения , называется рациональным числом. Он может состоять из числителя (p) и знаменателя (q), где q не равно нулю. Рациональное число может быть целым числом или целым числом.

• 2/3 = 0,6666 = 0,67. Поскольку десятичное значение является повторяющимся (повторяющимся). Итак, мы приблизили его к 0,67
• √4 = 2 и -2, где 2 и -2 являются целыми числами.

В таблице показано различие между рациональными и иррациональными числами.

Рациональные числа	Иррациональные числа
Это может быть выражено в виде дроби или отношения, т.е. p/q, где q ≠ 0	Нельзя выразить в виде дроби или отношения.
Десятичное расширение завершается или не завершается повторяющимся (повторяющимся)	Десятичное расширение не является завершающим и неповторяющимся в любой точке.
Пример: 0,33333, 0,656565.., 1,75	Пример: π, √ 13, e

Интересные факты об иррациональных числах

Есть несколько крутых и интересных фактов об иррациональных числах, которые заставляют нас глубже понять почему за чем.

1. Случайное изобретение √2

Квадратный корень из 2 или √2 был первым изобретенным иррациональным числом при вычислении длины равнобедренного треугольника. He used the famous Pythagoras formula a ² = b ² + c ²

AC ² =AB ² +BC ² ⇒ AC ² =1 ² +1 ² ⇒ AC = √ 2

√2 лежит между числами 1 и 2, так как значение равно 1,41421… Таким образом, он обнаружил, что длина AC не может быть выражена в виде дробей или целые числа.

2. Значение числа π

Значение числа π вычисляется приблизительно как более 22 триллиона цифр без конца. Компьютеру потребовалось около 105 дней с 24 жесткими дисками, чтобы вычислить значение числа Пи.

3. Изобретение числа Эйлера e

Число Эйлера впервые было введено Леонардом Эйлером, , швейцарским математиком в 1731 году. Это «e» также называют Числом Нейпира , которое в основном используется в логарифмировании. и тригонометрия.

Доказательство иррационального числа:

Давайте разберемся, как доказать, что данный несовершенный квадрат иррационален. Вот пошаговое доказательство того же.

Чтобы доказать: √2 — иррациональное число. 92\end{align}\)

Отсюда следует, что 2 также является простым делителем q ² . Опять же из теоремы можно сказать, что 2 также является простым множителем числа q.

Согласно исходному предположению p и q взаимно просты, но полученный выше результат противоречит этому предположению, так как p и q имеют 2 в качестве общего простого делителя, отличного от 1. Это противоречие возникло из-за неверного предположения, что √2 рациональный.

Итак, √2 иррационально.

☛Также читайте

• Докажите, что корень 2 иррационален
• Докажите, что корень 3 иррационален
• Докажите, что корень 5 иррационален
• Докажите, что корень 6 иррационален
• Докажите, что корень 7 иррационален
• Докажите, что корень 11 иррационален

Рабочие листы по рациональным и иррациональным числам

Рабочие листы по рациональным и иррациональным числам помогут лучше понять, почему рациональные и иррациональные числа являются частью действительных чисел. Рабочие листы по рациональным и иррациональным числам включают множество задач и примеров, основанных на операциях и свойствах рациональных и иррациональных чисел. Он состоит из творческих и увлекательных забавных заданий, в которых ребенок может подробно изучить сквозные концепции рациональных и иррациональных чисел с помощью практических иллюстраций.

Важные моменты

• Произведение любых двух иррациональных чисел может быть как рациональным, так и иррациональным. Пример (а): Умножьте √2 и π ⇒ 4,4428829… — иррациональное число. Пример (б): Умножьте √2 и √2 ⇒ 2 — рациональное число.
• Множество иррациональных чисел не замкнуто относительно процесса умножения, в отличие от множества рациональных чисел.
• Сложение или умножение двух иррациональных чисел может быть рациональным; например, √2 × √2 = 2. Здесь √2 — иррациональное число. Если его умножить дважды, то конечный результат будет рациональным числом, т. е. 2.

☛Статьи по теме

Ознакомьтесь с еще несколькими интересными статьями, посвященными иррациональным числам.

• Десятичное представление иррациональных чисел
• Рациональные числа
• Рационализировать знаменатель
• Является ли пи рациональным или иррациональным числом

Примеры иррациональных чисел

1. Пример 1: Джон играет со своим другом в игру «Бросьте кости с числами». Джон делает ход и бросает кубик. Он получает 5. Если он получает 5, он должен собрать все иррациональные числа у своего друга. Помогите Джону собрать все иррациональные числа, не пропустив ни одного. {е, -5, √9 , √13 , π, -2/8}

   Решение:

   -5 — целое число. √9 — идеальный квадрат. -2/8 имеет повторяющееся конечное десятичное значение. Эти числа являются рациональными числами. Иррациональные числа — это e, √13, π. Поэтому Джон собрал все иррациональные числа, а именно e, √13 и π.

2. Пример 2: У Джейд есть коробка с четырьмя иррациональными числами. Джейд хочет только одно иррациональное число, которое ближе всего к 3 и не должно превышать 3. Помогите Джейд найти правильное число. Иррациональные числа в коробке √3 , √6 , √10 , √5.

   Решение:

   Сначала найдем значение этих иррациональных чисел. √3 = 1,732020.., √6 = 2,449489.., √10 = 3,162277.., √5 = 2,236067… Таким образом, √6 = 2,449489… ближе всего к 3. Следовательно, √6 является ближайшим числом до 3.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по иррациональным числам

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об иррациональных числах

Что такое иррациональные числа в математике?

Иррациональные числа — это набор действительных чисел, которые не могут быть выражены в виде дробей или отношений. Пример: π, √2, e, √5

Как определить иррациональное число?

Ибо любое число, не являющееся рациональным, считается иррациональным. Иррациональные числа можно записать в виде десятичных дробей, но точно не в виде дробей. Кроме того, эти числа, как правило, имеют бесконечные неповторяющиеся цифры справа от десятичной запятой.

Рациональные и иррациональные числа — одно и то же?

Нет, рациональные и иррациональные числа не совпадают. Все числа, представленные в виде p/q, где p и q — целые числа, а q не равно 0, — рациональное число. Примеры рациональных чисел: 1/2, -3/4, 0,3 или 3/10. Принимая во внимание, что мы не можем выразить иррациональные числа в виде p/q.

В чем разница между рациональными и иррациональными числами?

Рациональные числа — это те, которые заканчиваются или не заканчиваются повторяющимися числами, а иррациональные числа — это те, которые не заканчиваются и не повторяются после определенного количества знаков после запятой.

Является ли 2/3 иррациональным числом?

Нет, 2/3 не иррациональное число. 2/3 = 0,666666…. повторяющееся десятичное число. Следовательно, 2/3 — рациональное число.

Почему рациональные и иррациональные числа входят в набор действительных чисел?

Числа, которые могут быть представлены в виде десятичных дробей, считаются действительными числами. Если мы говорим о рациональных и иррациональных числах, обе формы чисел могут быть представлены в виде десятичных знаков, следовательно, и рациональные числа, и иррациональные числа находятся в множестве действительных чисел.

Почему Пи — иррациональное число?

Пи определяется как отношение длины окружности к ее диаметру. Значение Пи всегда постоянно. Пи (π) приблизительно равно 3,14159265359… и является непрерывающимся неповторяющимся десятичным числом. Следовательно, «пи» — иррациональное число.

Сколько иррациональных чисел лежит между корнем 2 и корнем 3?

У нас может быть бесконечно много иррациональных чисел между корнем 2 и корнем 3.