Площадь фигуры / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга.
Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок.
Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
Квадратный сантиметрКвадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 40.
Урок 16,
Петерсон, Учебник, часть 2
Страница 50. Урок 19, Петерсон, Учебник, часть 2
Страница 58. Урок 23, Петерсон, Учебник, часть 2
Страница 61. Урок 24, Петерсон, Учебник, часть 2
Страница 65. Урок 26, Петерсон, Учебник, часть 2
Страница 79. Урок 32, Петерсон, Учебник, часть 2
Страница 85. Урок 35, Петерсон, Учебник, часть 2
Страница 88. Урок 37, Петерсон, Учебник, часть 2
Страница 33. Урок 11, Петерсон, Учебник, часть 3
Страница 90.
Урок 35,
Петерсон, Учебник, часть 3
3 класс
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 10. Урок 3, Петерсон, Учебник, часть 1
Страница 87.
Урок 32,
Петерсон, Учебник, часть 1
Страница 11. Урок 5, Петерсон, Учебник, часть 2
Страница 20. Урок 9, Петерсон, Учебник, часть 3
4 класс
Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы
Страница 52. Тест 2. Вариант 1, Моро, Волкова, Проверочные работы
Страница 50, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 4, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 3.
Урок 1,
Петерсон, Учебник, часть 1
Площадь прямоугольника
Урок 15. Математика 3 класс ФГОС
На этом уроке Матюша наглядно объясняет, как найти площадь прямоугольника. Составляется формула, на основе которой решаются задачи не только на нахождение площади, но и на нахождение длины и ширины прямоугольника. Особое внимание уделяется тому, что обозначать площадь фигур надо не в линейных, а в квадратных сантиметрах.
Конспект урока «Площадь прямоугольника»
Здравствуйте-здравствуйте! Ну, вот мы и опять свиделись.
В прошлый раз я рассказал вам о том, что такое площадь. Помните, как в книге это говорится:
Площадь – это часть плоскости, ограниченная замкнутой кривой или ломаной линией.
А еще я рассказал вам, как можно сравнить
площади разных фигур – на «глазок» или наложив одну фигуру на другую.
Но
лучше всего, конечно, сначала узнать площадь фигур, а потом сравнить полученные
результаты.
На прошлом уроке мы находили площадь фигур,
укладывая по всей их площади квадратные сантиметры. Получалось, как будто пол
квадратной плиткой выложили. Сколько плиточек – квадратных сантиметров
– такова и площадь фигуры. Конечно, так можно находить площадь, но это довольно
долго и не совсем удобно. Но моя волшебная математическая книга предлагает
другой, более короткий способ нахождения площади, если надо найти
Итак, вот перед вами прямоугольник со сторонами 5 см
и 3 см. Проведём в нем горизонтальные и вертикальные линии, расстояние между
которыми – один сантиметр. Получилось, что вся площадь прямоугольника
как бы разделена на квадратные сантиметры. Посчитаем, сколько таких квадратных
сантиметров в первом ряду – один, два, три, четыре, пять. Во втором ряду тоже
пять и в третьем – так же пять.
По пять квадратных сантиметров три раза находим
действием умножения. Получается, что площадь этого прямоугольника
равна пятнадцати квадратным сантиметрам.
5 · 3 = 15 (см2)
Ответ: площадь прямоугольника 15 см2 .
Ну, а если посчитать по-другому? В первом столбике квадратных сантиметра, во втором тоже три, и в третьем, и в четвёртом, и в пятом. По три квадратных сантиметра пять раз. Всё равно получилось, что площадь прямоугольника равна пятнадцати квадратным сантиметрам.
3 · 5 = 15 (см2)
Ответ: площадь прямоугольника 15 см2.
А теперь давайте найдем площадь вот этого прямоугольника. Длина равна шести сантиметрам, ширина – четырем сантиметрам. Делим его на квадратные сантиметры.
Получается, по шесть квадратных сантиметров четыре
раза или по четыре квадратных сантиметра шесть раз. И так, и этак, площадь
этого прямоугольника равна двадцати четырем квадратным сантиметрам.
6 · 4 = 24 (см2) 4 · 6 = 24 (см2)
Ответ: площадь прямоугольника 24 см
А вы обратили внимание, когда находили площадь первого прямоугольника, мы перемножали числа пять и три. А эти числа являются длиной и шириной нашего прямоугольника. А когда находили площадь второго прямоугольника, перемножали числа шесть и четыре. Они тоже являются его длиной и шириной. Значит, можно сделать вывод:
Чтобы найти площадь прямоугольника, надо измерить длину и ширину этого прямоугольника и найти произведение полученных чисел.
Вот, к примеру, длина прямоугольника равна восьми сантиметрам, а ширина – четырём.
Площадь мы находим, умножив длину на ширину.
Произведение чисел восемь и четыре равно тридцати
двум. Значит, площадь этого прямоугольника равна
тридцати двум квадратным сантиметрам. Не забудьте, что площадь измеряется
именно в квадратных единицах.
А для того, чтобы легче было запомнить, как находить площадь прямоугольника, можно записать памятку-формулу: S = a · b, где S это площадь, а а и b стороны прямоугольника.
А вот теперь я хочу предложить вам вот такую задачу. Площадь прямоугольника равна восемнадцати квадратным сантиметрам, а ширина его – два сантиметра. Чему равна длина этого прямоугольника?
И вот тут-то на помощь нам придёт формула S = a · b. Площадь – это произведение, длина и ширина – множители. В задаче надо найти длину, то есть множитель. А ведь мы знаем правило: Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
Частное чисел восемнадцать и два равно девяти.
Значит, длина этого прямоугольника равна девяти сантиметрам.
18 : 2 = 9 (см)
Ответ: длина прямоугольника равна 9 см.
Ну, а если необходимо найти ширину прямоугольника, как например, вот в этой задаче?
Чему равна ширина прямоугольника, если его площадь – 12 см2, а длина – 4 см?
Конечно так же, как и длину – делением. Ведь ширина в нашей формуле тоже является неизвестным множителем. Двенадцать делим на четыре, получается три. В этом прямоугольнике ширина равна трем сантиметрам.
12 : 4 = 3 (см)
Ответ: длина прямоугольника равна 3 см.
Ну вот и пришла пора нам с вами сегодня расстаться. Но я надеюсь, что вы хорошо усвоили, что:
Чтобы найти площадь прямоугольника надо его длину умножить на ширину.
Чтобы найти неизвестную сторону прямоугольника, если известна его площадь и вторая сторона, надо площадь разделить на известную сторону.
Ну и, конечно, не забывайте, что площадь измеряется
в квадратных единицах измерения.
Пока я познакомил вас только с
квадратными сантиметрами (1 см2, 15 см2 , 24 см2).
Но очень скоро вы познакомитесь и с другими единицами измерения площади. А я прощаюсь
с вами, буду дальше читать эту интересную книгу. До свидания, ребята.
Предыдущий урок 14 Площадь фигур. Единица площади — квадратный сантиметр
Следующий урок 16 Таблица умножения и деления с числом 8
Получите полный комплект видеоуроков, тестов и презентаций Математика 3 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Купить Лабораторная работа по ООП на JAVA и скачать
Лаб 1
Грузовой поезд формируется следующим образом: первые «N» вагоны имеют объем 250 м3, следующие «2*N» — 200 м3, следующие «3*N» — 150 м3, а все остальные — 100 м3 .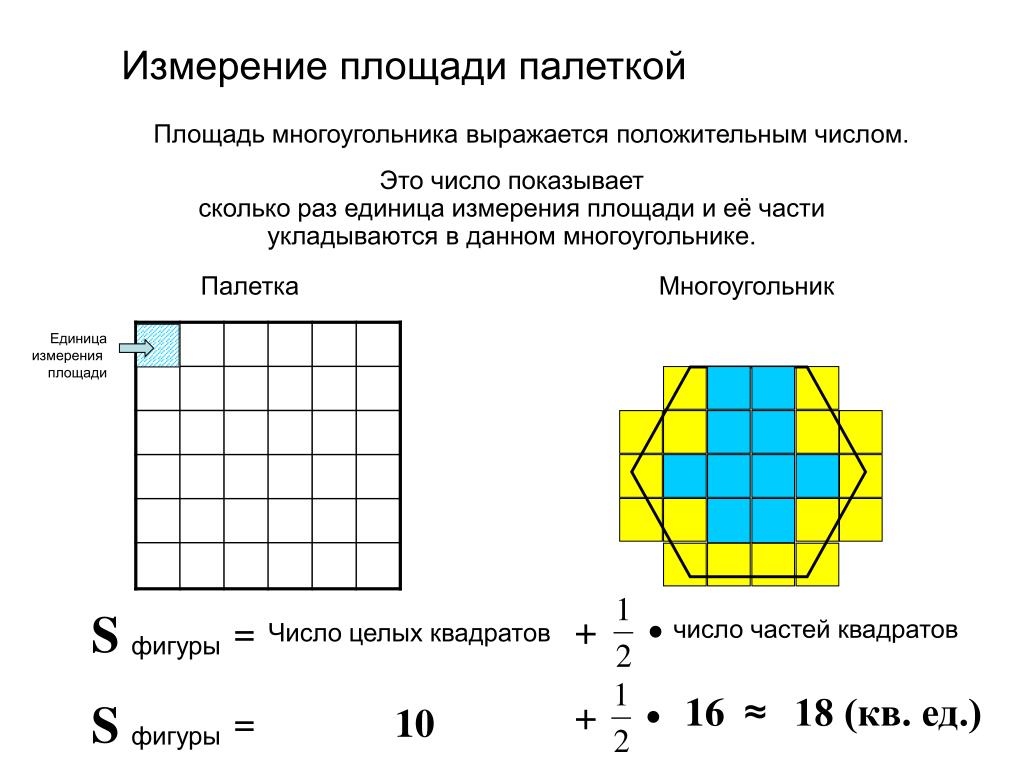
Было сформировано три соединения из 45 вагонов, каждый со следующими параметрами: N = 5 — для 1-го, N = 3 — для 2-го и N = 8 — для третьего. В 1-й части было затоплено дерево, во 2-й — уголь, а в 3-й — песок. Определять:
какая из композиций была загружена больше всего?
сколько вагонов объемом 100 м3 каждого состава?
как отличается погрузка вагонов объемом 250 м3 3-го состава от количества вагонов объемом 150 м3 1-го и 2-го составов?
Лаборатория 2
Опишите класс алгоритма моделирования машины, перемещающей грузы по некоторым маршрутам, представители которых хранят информацию о характере каждой операции, а также максимальное количество для заданного алгоритма и начальное значение позиции машины.
Лаборатория 3
Базовый класс и его методы: плоскость кольца. Расчет площади внешней и внутренней границы и площади самой фигуры.
Подкласс 1 и его методы: объемное кольцо — шайба; расчет объема, расчет массы.
Подкласс 2: Объемное кольцо случайным образом заданного размера.
Практическое применение:
Из листового металла необходимо выпилить шайбы размером 5х4 мм. Сколько голов получится на 1 м2 круглой заготовки, если коэффициентом герметичности принять размещение 0,85? Сколько голов получается 2,5 и 5 м2?
Каковы будут цели серийного производства и какая масса металла пойдет в отходы в каждом случае? Материал для каждого случая соответственно: сталь (7800 кг/м3), латунь (8500 кг/м3) и бумага (1000 кг/м3) и толщиной 1,5 мм.
В ящике находится смесь 300 латунных и 200 стальных шайб произвольного размера: наружный диаметр — 2…20 см, внутренний — 80 % от наружного. Какова общая масса содержимого ящика?
Лаборатория 4
В некоторых странах по результатам переписи было решено определить совокупный показатель благосостояния по демографической ситуации в трех районах и уверенно сделать следующие показатели: рождаемость %, смертность %, уровень безработицы, уровень социальная защита, наличие опасных и вредных производств, частота стихийных бедствий.
Характер данных различен для каждого региона. Промоделируйте ситуацию и определите наиболее и наименее благополучные. Оцените наиболее подходящий район по шкале «хуже некуда», «можно жить», «могло бы быть и лучше», «вполне нормально», «очень хорошо», «лучше некуда» (градация условно) тремя баллами. соседние, принимая в каждом случае уровень максимально возможного благосостояния.
Лаборатория 5
Функциональная схема такого вида состоит из блоков, реализующих работу протокола с типом данных string:
модуль: выход каждого канала соответствует входному значению по модулю;
sinus: на выходах 0, 1 и 2 будут величины вида sin(x), a*sin(x) и a*sin(x)+b, где a и b — дополнительный информационный блок;
возведение в степень: повышается значение на входе 0, которое берется из входа 1. Используйте функцию pow class Math.
Проверить работу схемы, установив 7-NIL разные значения на входах схемы.
Лаборатория 6
В примерах реального класса есть возможность вызвать исключение во время выполнения.
