Площадь фигуры | это… Что такое Площадь фигуры?
У этого термина существуют и другие значения, см. Площадь (значения).
Пло́щадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Содержание
|
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.

Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона. — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
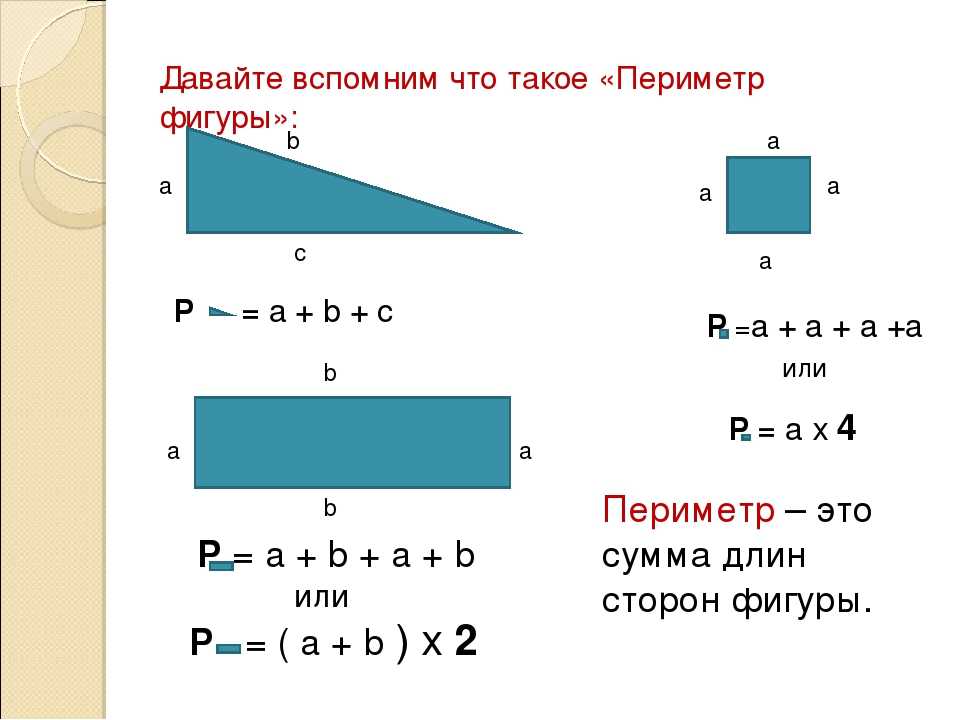
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См.
 также
также- Площадь
- Мера Бореля
- Мера Жордана
- Мера Лебега
- Ориентированная площадь
- Площадь поверхности
- Теорема Бойяи — Гервина о равносоставленности равновеликих многоугольников
- Исчезновение клетки
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
Площадь фигуры / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.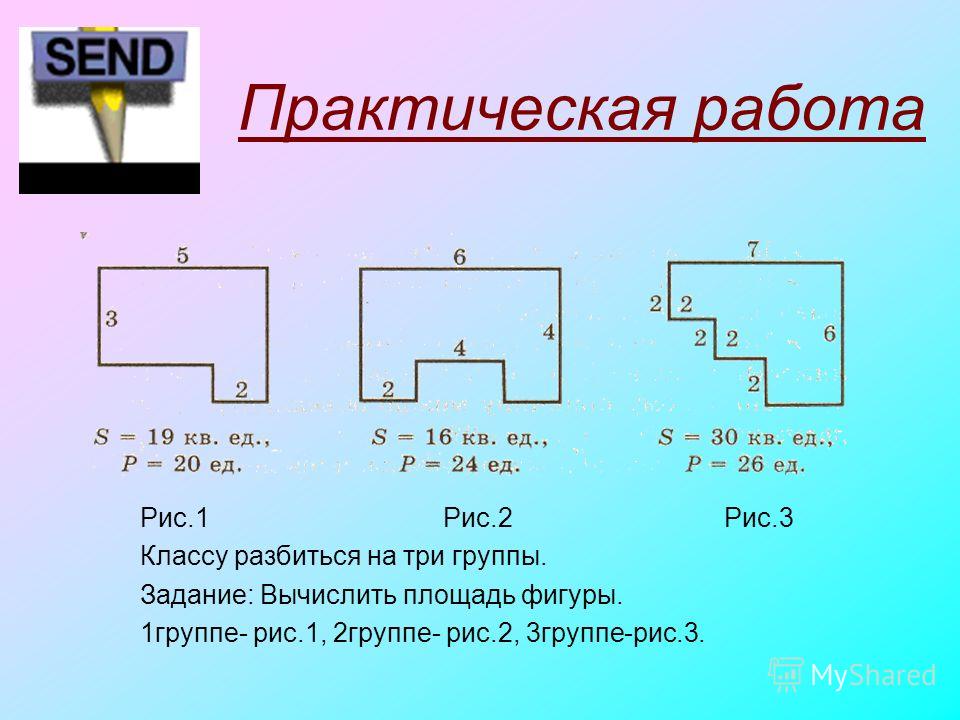
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
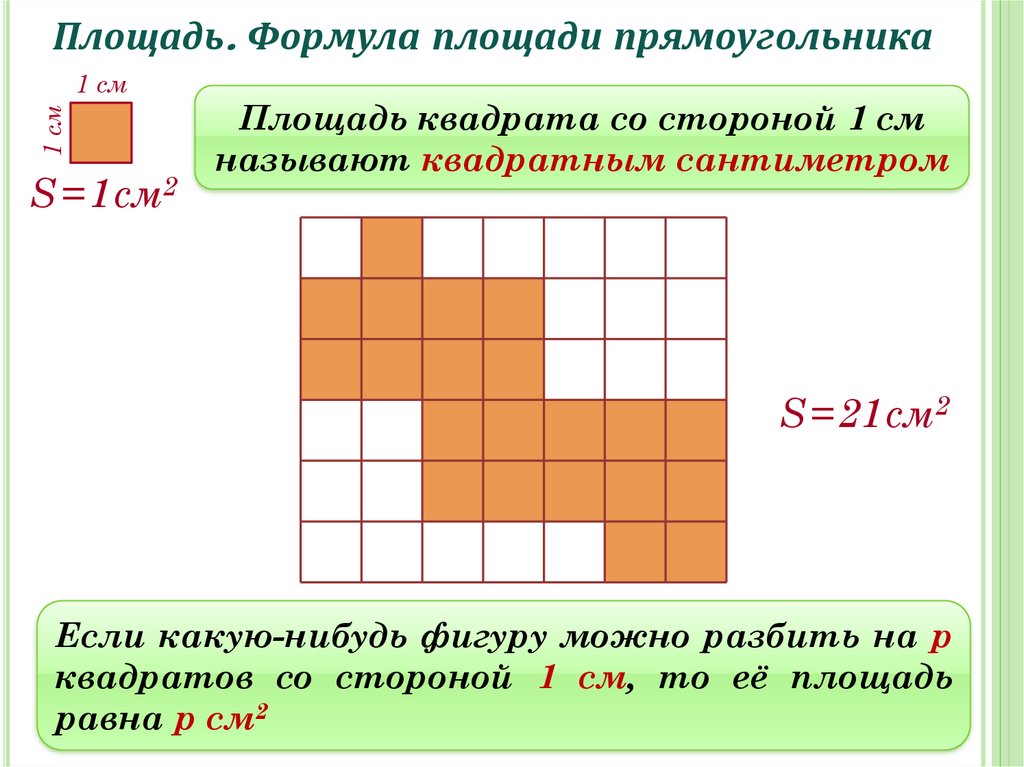
Квадратный сантиметрКвадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 40. Урок 16, Петерсон, Учебник, часть 2
Страница 44.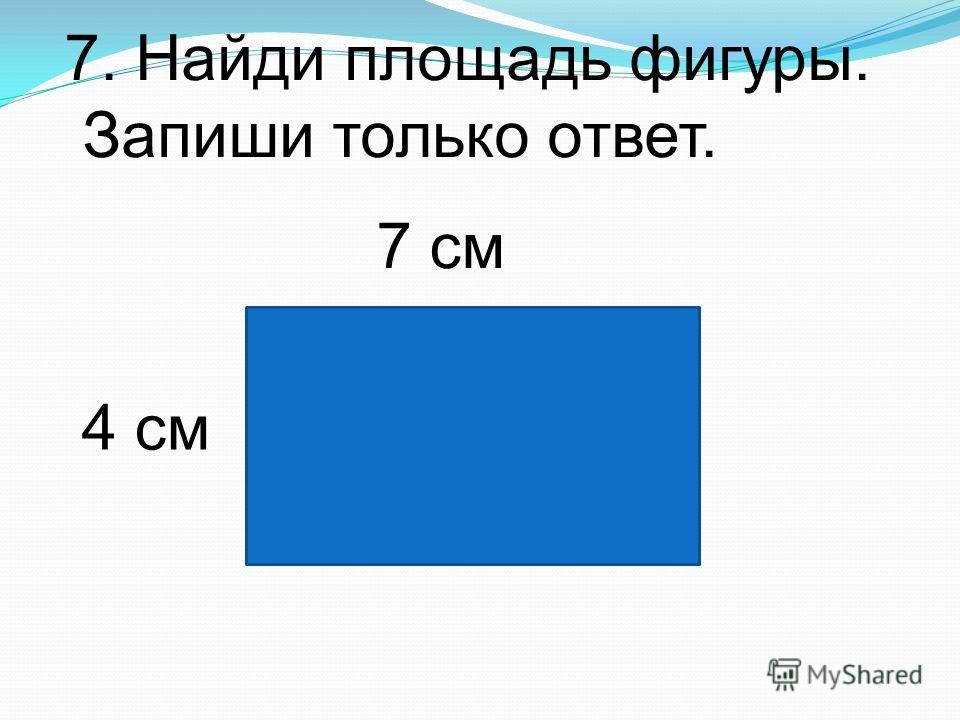 Урок 17,
Петерсон, Учебник, часть 2
Урок 17,
Петерсон, Учебник, часть 2
Страница 45. Урок 17, Петерсон, Учебник, часть 2
Страница 65. Урок 26, Петерсон, Учебник, часть 2
Страница 81. Урок 33, Петерсон, Учебник, часть 2
Страница 85. Урок 35, Петерсон, Учебник, часть 2
Страница 40. Урок 14, Петерсон, Учебник, часть 3
Страница 47. Урок 16, Петерсон, Учебник, часть 3
Страница 52. Урок 18, Петерсон, Учебник, часть 3
Страница 56. Урок 20, Петерсон, Учебник, часть 3
3 класс
Страница 57, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 71, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 105, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 92, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 1
Урок 4,
Петерсон, Учебник, часть 1
Страница 79. Урок 28, Петерсон, Учебник, часть 1
Страница 87. Урок 32, Петерсон, Учебник, часть 1
Страница 18. Урок 7, Петерсон, Учебник, часть 2
4 класс
Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 33. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы
Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 64, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 70, Моро, Волкова, Рабочая тетрадь, часть 2
Составьте площадь прямоугольника.
 Ввод данных в калькулятор для расчета площади прямоугольника
Ввод данных в калькулятор для расчета площади прямоугольникаС таким понятием, как площадь, нам приходится сталкиваться в нашей жизни каждый день. Так, например, при строительстве дома его необходимо знать, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Без этого определения не обойтись даже ремонт в квартире. Поэтому вопрос, как найти площадь прямоугольника, возникает у нас очень часто и важен не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура с равными противоположными сторонами и углами по 90 градусов. Для обозначения области в математике используется английская буква S. Измеряется в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попробуем дать развернутый ответ на вопрос, как найти площадь прямоугольника. Есть несколько способов определить это значение. Чаще всего мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник шириной b и длиной k. Чтобы вычислить площадь данного прямоугольника, умножьте ширину на длину. Все это можно представить в виде формулы, которая будет выглядеть так: S = b*k.
Чтобы вычислить площадь данного прямоугольника, умножьте ширину на длину. Все это можно представить в виде формулы, которая будет выглядеть так: S = b*k.
Теперь давайте рассмотрим этот метод на конкретном примере. Необходимо определить площадь садового участка шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в математике, приходится определять площадь другими способами, так как во многих случаях мы не знаем ни длины, ни ширины прямоугольника. В то же время известны и другие величины. Как найти площадь прямоугольника в этом случае?
- Если мы знаем длину диагонали и один из углов, составляющих диагональ с любой стороной прямоугольника, то в этом случае нам нужно запомнить площадь. Ведь если разобраться, прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определенному значению. Сначала нужно определить косинус угла. Умножьте полученное значение на длину диагонали. В результате получаем длину одной из сторон прямоугольника.
 Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.
Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d — длина диагонали
- Другой способ определения площади прямоугольника проходит через вписанную в него окружность. Это применимо, если прямоугольник является квадратом. Чтобы воспользоваться этим методом, нужно знать Как вычислить площадь прямоугольника таким способом? Конечно, по формуле. Мы не будем это доказывать. А выглядит это так: S = 4 * r2, где r — радиус.
Бывает, что вместо радиуса мы знаем диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2, где d — диаметр.
- Если известны одна из сторон и периметр, то как в этом случае узнать площадь прямоугольника? Для этого нужно произвести ряд простых расчетов. Как известно, противоположные стороны прямоугольника равны, поэтому из значения периметра необходимо вычесть известную длину, умноженную на два.
 Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника. В форме формулы это будет выглядеть так:
Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника. В форме формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видите, площадь прямоугольника можно определить разными способами. Все зависит от того, какие величины мы знаем до рассмотрения этого вопроса. Конечно, новейшие вычислительные методы в жизни практически не встречаются, но для решения многих задач в школе они могут пригодиться. Возможно, эта статья будет полезна для решения ваших проблем.
Периодически нам необходимо знать площадь и объем помещения. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке строительных материалов и во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но сначала придется поработать рулеткой – измерить все требуемые размеры. О том, как рассчитать площадь комнаты и стен, объем комнаты и пойдет речь дальше.
Площадь помещения в квадратных метрах
- Рулетка. Лучше — с защелкой, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или посчитайте в столбик или в уме).
Набор инструментов простой, есть в каждом хозяйстве. Измерять с помощником проще, но можно и самому.
Сначала нужно измерить длину стен. Желательно делать это вдоль стен, но если они все заставлены тяжелой мебелью, можно провести замеры и посередине. Только в этом случае следите, чтобы рулетка лежала вдоль стен, а не наискосок – погрешность измерения будет меньше.
Прямоугольное помещение
Если помещение правильной формы, без выступающих частей, то легко рассчитать площадь помещения. Измерьте длину и ширину, запишите их на листе бумаги. Цифры записывайте в метрах, после запятой ставьте сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Перемножаем найденные числа, получаем площадь комнаты в квадратных метрах. Если обратиться к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв.м. В этом значении обычно две цифры после запятой оставляются, значит, округляем. Всего расчетная квадратура комнаты составляет 14,14 кв.
Если обратиться к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв.м. В этом значении обычно две цифры после запятой оставляются, значит, округляем. Всего расчетная квадратура комнаты составляет 14,14 кв.
Комната неправильной формы
Если вам нужно вычислить площадь комнаты неправильной формы, то ее делят на простые формы — квадраты, прямоугольники, треугольники. Затем измеряют все необходимые размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Пример на фото. Поскольку оба являются прямоугольниками, площадь рассчитывается по одной и той же формуле: умножьте длину на ширину. Найденную цифру необходимо вычесть или прибавить к размеру помещения в зависимости от комплектации.
Площадь помещения комплекса
- Считаем квадратуру без уступа: 3,6 м * 8,5 м = 30,6 кв.м.
- Считаем размеры выступающей части: 3,25 м * 0,8 м = 2,6 кв.м.
- Складываем два значения: 30,6 кв. м. + 2,6 кв.
 м. = 33,2 кв.м.
м. = 33,2 кв.м.
Также есть комнаты со скошенными стенами. В данном случае разделяем его так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для этого случая требуется наличие пяти размеров. Его можно было бы разделить по-другому, поставив вертикальную, а не горизонтальную линию. Не имеет значения. Для этого просто требуется набор простых фигур, и способ их выбора произволен.
В данном случае порядок расчета такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, то получится 9,0 кв.м.
- Вычисляем небольшой прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляя в большую сторону, получаем 5,1 кв. м.
- Вычисляем площадь треугольника. Поскольку он с прямым углом, он равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9м) / 2 = 1,235 кв.м. После округления получаем 1,2 кв. м.
- Теперь складываем все, чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 квадратных метра.
 м.
м.
Планировка помещений может быть самой разнообразной, но общий принцип вы понимаете: делим на простые фигуры, измеряем все необходимые размеры, вычисляем квадратуру каждого фрагмента, потом все складываем.
Еще одно важное замечание: площадь комнаты, пола и потолка — все это одинаковые величины. Отличия могут быть, если есть какие-то полуколонны, не доходящие до потолка. Затем квадратура этих элементов вычитается из общей квадратуры. В результате получается площадь пола.
Как рассчитать площадь стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.д. Этот расчет требует дополнительных измерений. К уже имеющейся ширине и длине помещения вам потребуются:
- высота потолка;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все размеры указаны в метрах, так как площадь стен также обычно измеряется в квадратных метрах.
Так как стены прямоугольные, площадь рассчитывается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры оконных и дверных проемов, вычитаем их габариты. Для примера рассчитаем площадь стен, показанных на схеме выше.
Таким же образом вычисляем размеры оконных и дверных проемов, вычитаем их габариты. Для примера рассчитаем площадь стен, показанных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв.м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м * 0,9м = 1,89 кв.м.
- стена без дверного проема — 14 кв.м — 1,89 кв.м. м = 12,11 кв.м
- Стена с окном:
- площадь малых стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв.м, округляем в большую сторону, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв.м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не сложно. Складываем все четыре числа: 14 кв.м + 12,11 кв.м. + 8 кв.м. + 6,25 кв.м. = 40,36 кв.м.
Объем помещения
Для некоторых расчетов требуется объем помещения. В этом случае перемножаются три значения: ширина, длина и высота помещения. Эта величина измеряется в кубических метрах (кубических метрах), также называется кубатурой. Для примера используем данные из предыдущего пункта:
Для примера используем данные из предыдущего пункта:
- длина — 5,6 м; ширина
- — 3,2 м;
- высота — 2,5 м.
Если все перемножить, то получим: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3 . Итак, объем помещения 44,8 куб.
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, предложения. Все материалы проверяются антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И. Зубарева и А.Г. Мордкович
Тренажер по учебнику Г.В. Дорофеев и Л.Г. Петерсон
Определение и понятие площади фигуры
Чтобы лучше понять, что такое площадь фигуры, рассмотрим фигуру.
Эта произвольная фигура разделена на 12 маленьких квадратов. Сторона каждого квадрата равна 1 см. А площадь каждого квадрата равна 1 квадратному сантиметру, что записывается так: 1 см2.
Тогда площадь фигуры 12 квадратных сантиметров. В математике площадь обозначается латинской буквой S.
Значит площадь нашей фигуры равна: S цифры = 12 см 2 .
Площадь фигуры равна площади всех маленьких квадратов, из которых она состоит!
Ребята, помните!
Площадь измеряется в квадратных единицах длины. Единицы площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для измерения площади участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики при рисовании цифр в тетради).
4. Квадратный миллиметр — мм 2.
Площадь треугольника
Рассмотрим два вида треугольников: прямоугольный и произвольный.
Чтобы найти площадь прямоугольного треугольника, нужно знать длину основания и высоту. В прямоугольном треугольнике одна из сторон заменяет высоту. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны 7 см и 4 см. Формула вычисления площади треугольника записывается так:
S прямоугольного треугольника ABC = BC * SA: 2
S прямоугольного треугольника ABC = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота 6 см, а основание 8 см. Как и в предыдущем примере, вычисляем площадь по формуле:
S произвольного треугольника ABC = BC * h: 2.
Подставляем наши данные в формулу и получаем:
S произвольного треугольника ABC = 8 см * 6 см: 2 = 24 см 2 .
Площадь прямоугольника и квадрата
Возьмем прямоугольник ABCD со сторонами 5 см и 8 см.
Формула вычисления площади прямоугольника:
S прямоугольника ABCD = AB * BC.
S прямоугольника ABCD = 8 см * 5 см = 40 см 2.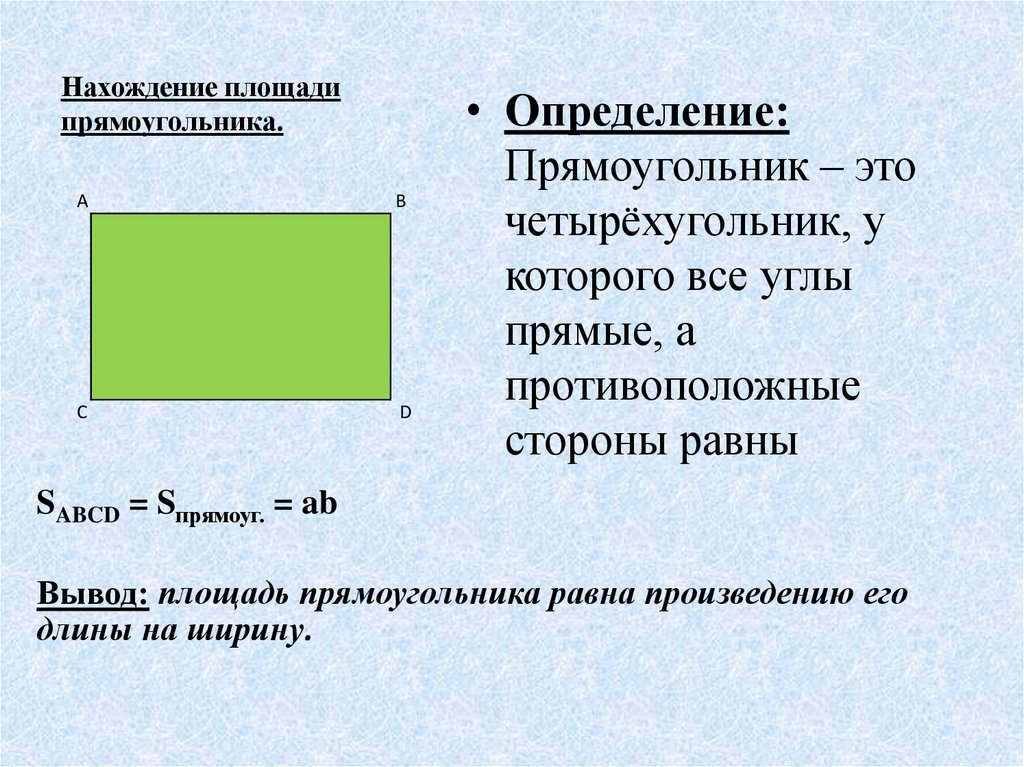
Теперь посчитаем площадь квадрата. В отличие от прямоугольника и треугольника, чтобы найти площадь квадрата, нужно знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрата ABCD = AB * BC = AB 2.
Подставляем наши данные в формулу и получаем:
S квадрат ABCD = 9 см * 9 см = 81 см 2.
С таким понятием, как площадь, нам приходится сталкиваться в нашей жизни каждый день . Так, например, при строительстве дома его необходимо знать, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Без этого определения не обойтись даже ремонт в квартире. Поэтому вопрос, как найти площадь прямоугольника, очень часто возникает на нашем жизненном пути и важен не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы равны 90°. Для обозначения области в математике используется английская буква S.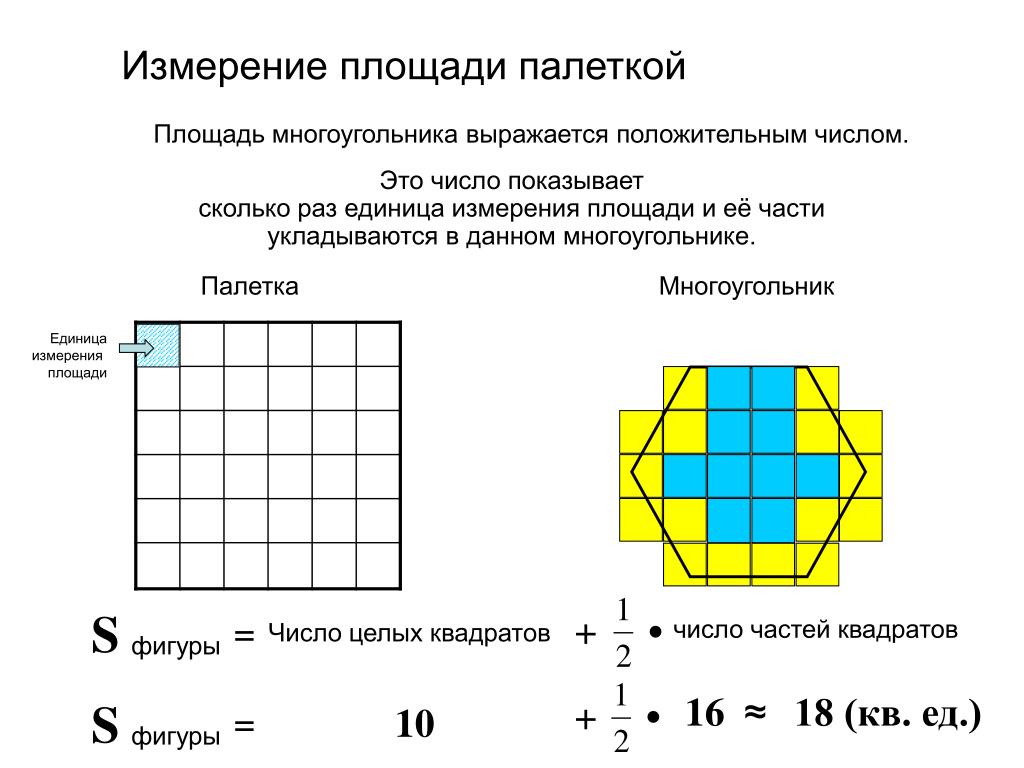 Измеряется в квадратных единицах: метрах, сантиметрах и так далее.
Измеряется в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попробуем дать развернутый ответ на вопрос, как найти площадь прямоугольника. Есть несколько способов определить это значение. Чаще всего мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник шириной b и длиной k. Чтобы вычислить площадь данного прямоугольника, умножьте ширину на длину. Все это можно представить в виде формулы, которая будет выглядеть так: S = b * k
Теперь давайте рассмотрим этот метод на конкретном примере. Необходимо определить площадь садового участка шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в старших классах, приходится определять площадь другими способами, так как во многих случаях мы не знаем ни длины, ни ширины прямоугольника. В то же время известны и другие величины. Как найти площадь прямоугольника в этом случае?
Если мы знаем длину диагонали и один из углов, составляющих диагональ с любой стороной прямоугольника, то в этом случае нам нужно запомнить площадь прямоугольного треугольника.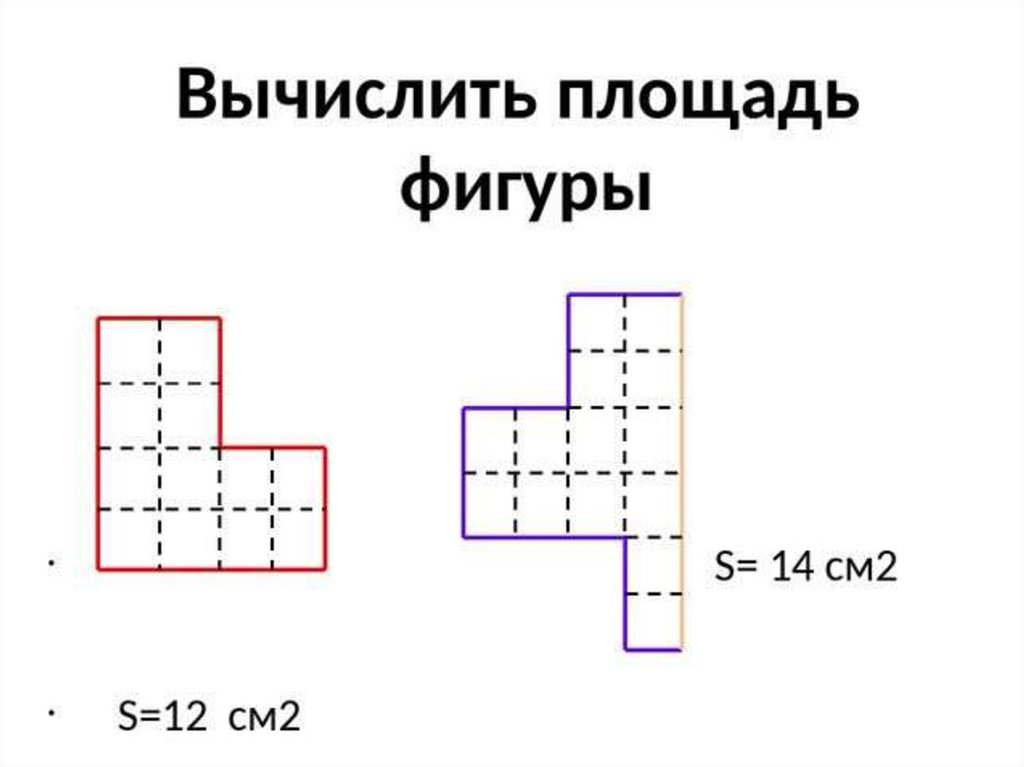 Ведь если посмотреть, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определенному значению. Сначала нужно определить косинус угла. Умножьте полученное значение на длину диагонали. В результате получаем длину одной из сторон прямоугольника. Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.
Ведь если посмотреть, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определенному значению. Сначала нужно определить косинус угла. Умножьте полученное значение на длину диагонали. В результате получаем длину одной из сторон прямоугольника. Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d — длина диагонали
Другой способ определения площади прямоугольника: через вписанную в него окружность. Это применимо, если прямоугольник является квадратом. Чтобы использовать этот метод, вам нужно знать радиус окружности. Как посчитать площадь прямоугольника таким способом? Конечно, по формуле. Мы не будем это доказывать. А выглядит это так: S = 4 * r2, где r — радиус.
Бывает, что вместо радиуса мы знаем диаметр вписанной окружности. Тогда формула будет выглядеть так:
Тогда формула будет выглядеть так:
S=d2, где d — диаметр.
Если известны одна из сторон и периметр, то как в этом случае узнать площадь прямоугольника? Для этого нужно произвести ряд простых расчетов. Как известно, противоположные стороны прямоугольника равны, поэтому из значения периметра необходимо вычесть известную длину, умноженную на два. Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника. В форме формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видите, площадь прямоугольника можно определить разными способами. Все зависит от того, какие величины мы знаем до рассмотрения этого вопроса. Конечно, новейшие вычислительные методы в жизни практически не встречаются, но для решения многих задач в школе они могут пригодиться. Возможно, эта статья будет полезна для решения ваших проблем.
Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Такой расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если вам нужно рассчитать площадь комнаты при ремонте квартиры, рассчитать необходимое количество материалов.
Такой расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если вам нужно рассчитать площадь комнаты при ремонте квартиры, рассчитать необходимое количество материалов.
Удобная навигация по артикулам:
Как вычислить площадь прямоугольникаПрямоугольником обычно называют геометрическую плоскую фигуру, у которой противоположные стороны параллельны под углами 90 градусов. Длина этой геометрической фигуры является величиной, имеющей большую сторону. В этом случае за ширину принимается значение меньшей стороны. Чтобы правильно рассчитать площадь прямоугольника, нужно знать определенные параметры, которыми обладает эта фигура. Среди них:
- диагональ;
- ширина;
- так называемый угол наклона к одной из сторон диагонали;
- длина.
Таким образом, вычислить площадь прямоугольника можно различными способами. Все зависит от количества информации о фигуре, а именно от того, какие величины мы точно знаем.
Как вычислить площадь прямоугольника по линейным параметрам его сторон?
Обозначим длину прямоугольника буквой «а», его ширину буквой «b», а буквой «S» обозначим площадь геометрической фигуры. В соответствии с этим наша формула будет выглядеть так: S = a x b.
Зная линейные параметры прямоугольника, можно легко определить его периметр по следующей формуле: P = 2(a + b), где в качестве обозначения периметра используется буква «P».
Как можно вычислить площадь прямоугольника, зная величину одной из его сторон и диагонали?
Как известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь вам необходимо выполнить следующую процедуру:
- Сначала нужно найти длину неизвестной стороны. Для этого воспользуемся формулой Пифагора: b = V c2 — a2.
- После этого мы должны определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Str = ½ (a x in).

- Согласно схеме расчета, описанной выше, площадь прямоугольника в этом случае будет равна: S = 2 x Str = a x b.
В том случае, если нам известен периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P — 2xa), по следующей формуле: S = a x b.
Если нам известна величина диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить с помощью следующих тригонометрических функций: Str = ½ x c2 x sinФ x cosФ.
При этом общая площадь в этом случае будет S = 2 x Str.
Площадь прямоугольника. Видео урок.
4.7 Наследование, иерархия классов и полиморфизм
Мы уже упоминали построение иерархии классов с помощью наследования и полиморфизма как двух основных принципов объектно-ориентированного программирования в дополнение к инкапсуляции. Чтобы познакомить вас с этими понятиями, давайте начнем с другого упражнения по объектно-ориентированному моделированию и написанию классов на Python. Представьте, что вам нужно написать очень простую ГИС или программу векторного рисования, которая имеет дело только с геометрическими элементами трех типов: кругами и прямоугольниками и квадратами, выровненными по осям. Вам нужна возможность хранить произвольное количество объектов этих трех видов и управлять ими, а также выполнять простые операции с этими объектами, такие как вычисление их площади и периметра и перемещение объектов в другое положение. Как бы вы написали классы для этих трех видов геометрических объектов?
Представьте, что вам нужно написать очень простую ГИС или программу векторного рисования, которая имеет дело только с геометрическими элементами трех типов: кругами и прямоугольниками и квадратами, выровненными по осям. Вам нужна возможность хранить произвольное количество объектов этих трех видов и управлять ими, а также выполнять простые операции с этими объектами, такие как вычисление их площади и периметра и перемещение объектов в другое положение. Как бы вы написали классы для этих трех видов геометрических объектов?
Начнем с класса Circle: круг в двумерной системе координат обычно определяется тремя значениями: координатами x и y центра круга и его радиусом. Таким образом, они должны стать свойствами (= переменными экземпляра) нашего класса Circle, и для вычисления площади и периметра мы предоставим два метода, которые возвращают соответствующие значения. Метод перемещения круга будет принимать в качестве параметров значения того, насколько круг должен быть перемещен по осям x и y, но ничего не возвращать.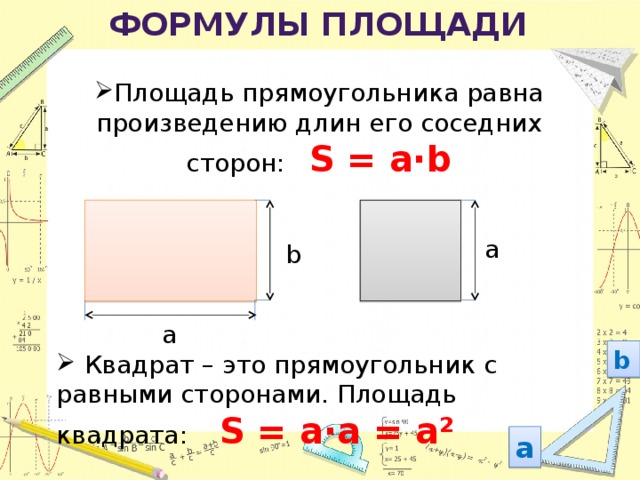
импорт математики
класс Круг():
def __init__(я, х = 0,0, у = 0,0, радиус = 1,0):
я.х = х
селф.у = у
self.radius = радиус
определение вычислительной области (я):
вернуть math.pi * self.radius ** 2
def вычислить периметр (сам):
вернуть 2 * math.pi * self.radius
def move(self, deltaX, deltaY):
self.x += deltaX
self.y += deltaY
защита __str__(я):
return 'Окружность с координатами {0}, {1} и радиусом {2}'.format(self.x, self.y, self.radius)
В конструкторе у нас есть аргументы ключевого слова со значениями по умолчанию для трех свойств круга, и мы присваиваем значения, предоставляемые этими тремя параметрами, соответствующим переменным экземпляра нашего класса. Мы импортируем математический модуль стандартной библиотеки Python, чтобы можно было использовать константу math.pi для вычисления площади и периметра круглого объекта на основе переменных экземпляра. Наконец, мы добавляем метод __str__() для создания строки, описывающей объект круга с его свойствами. Теперь должно быть понятно, как создавать объекты этого класса и, например, применять calculateArea () и move(…) методы.
Теперь должно быть понятно, как создавать объекты этого класса и, например, применять calculateArea () и move(…) методы.
круг1 = круг(10,4,3) печать (круг1) печать (круг1.computeArea()) круг1.переместить(3,-1) печать (круг1)
Выход: Окружность с координатами 10, 4 и радиусом 3 28.274333882308138 Окружность с координатами 13, 3 и радиусом 3
Как насчет аналогичного класса для прямоугольников, выровненных по оси? Такие прямоугольники могут быть описаны координатами x и y одного из их углов вместе со значениями ширины и высоты, поэтому всего четыре переменные экземпляра принимают числовые значения. Вот получившийся класс и краткий пример его использования:
класс Прямоугольник():
def __init__(self, x = 0.0, y = 0.0, ширина = 1.0, высота = 1.0):
я.х = х
селф.у = у
собственная ширина = ширина
self.height = высота
определение вычислительной области (я):
вернуть self.width * self.height
def вычислить периметр (сам):
вернуть 2 * (собственная ширина + собственная высота)
def move(self, deltaX, deltaY):
self. x += deltaX
self.y += deltaY
защита __str__(я):
return 'Прямоугольник с координатами {0}, {1}, шириной {2} и высотой {3}'.format(self.x, self.y, self.width, self.height )
прямоугольник1 = прямоугольник (10,10,3,2)
печать (прямоугольник1)
печать (прямоугольник1.computeArea())
прямоугольник1.переместить(2,2)
печать (прямоугольник1)
x += deltaX
self.y += deltaY
защита __str__(я):
return 'Прямоугольник с координатами {0}, {1}, шириной {2} и высотой {3}'.format(self.x, self.y, self.width, self.height )
прямоугольник1 = прямоугольник (10,10,3,2)
печать (прямоугольник1)
печать (прямоугольник1.computeArea())
прямоугольник1.переместить(2,2)
печать (прямоугольник1) Выход: Прямоугольник с координатами 10, 10, шириной 3 и высотой 2 6 Прямоугольник с координатами 12, 12, шириной 3 и высотой 2
Есть несколько вещей, которые можно заметить при сравнении двух только что созданных классов Circle и Rectangle: конструкторы, очевидно, различаются, потому что кругам и прямоугольникам нужны разные свойства для их описания и , в результате вызовы при создании новых объектов для двух классов тоже выглядят по-разному. Все остальные методы имеют точно такие же подпись , что означает те же параметры и тот же тип возвращаемого значения; просто способ их реализации отличается. То есть разные вызовы для выполнения определенных действий с объектами (вычисление площади, перемещение объекта, печать информации об объекте) также выглядят совершенно одинаково; не имеет значения, содержит ли переменная объект класса Circle или класса Rectangle. Если вы сравните две версии метода move(…) , то увидите, что они даже не отличаются по своей реализации, они совершенно одинаковы!
Если вы сравните две версии метода move(…) , то увидите, что они даже не отличаются по своей реализации, они совершенно одинаковы!
Все это ясно указывает на то, что мы имеем дело с двумя классами объектов, которые можно рассматривать как разные специализации более общего класса геометрических объектов. Разве не было бы здорово, если бы теперь мы могли написать остальную часть нашей игрушечной ГИС-программы, управляющей набором геометрических объектов, не заботясь о том, является ли объект кругом или прямоугольником в остальной части нашего кода? И, кроме того, иметь возможность легко добавлять классы для других геометрических примитивов, не внося никаких изменений во весь остальной код, а в своих определениях классов описывать только то, чем они отличаются от уже определенных классов геометрии? Это действительно возможно, если расположить наши классы геометрии в иерархии классов, начиная с абстрактного класса для геометрических объектов вверху и производя дочерние классы для Circle и Rectangle от этого класса, добавляя как свои специализированные свойства, так и поведение. Назовем класс верхнего уровня Geometry. Получившаяся очень простая иерархия классов показана на рисунке ниже.
Назовем класс верхнего уровня Geometry. Получившаяся очень простая иерархия классов показана на рисунке ниже.
Рисунок 4.17 Простая иерархия классов с тремя классами. Классы Circle и Rectangle являются производными от родительского класса Geometry.
Наследование позволяет программисту определить класс с общими свойствами и поведением и вывести из него один или несколько специализированных подклассов, которые наследуют эти свойства и поведение, а также могут изменять их, добавляя более специализированные свойства и реализуя более специализированное поведение. Мы используем термины производный класс и базовый класс 9.0342 для обозначения двух классов, задействованных, когда один класс является производным от другого.
Давайте изменим наш пример так, чтобы и Circle, и Rectangle были производными от такого общего класса, который называется Geometry. Этот класс будет абстрактным классом в том смысле, что он не предназначен для использования для создания объектов. Его цель — ввести свойства и шаблоны для методов, которые являются общими для всех геометрических классов в нашем проекте.
Его цель — ввести свойства и шаблоны для методов, которые являются общими для всех геометрических классов в нашем проекте.
класс Геометрия():
def __init__(я, х = 0,0, у = 0,0):
я.х = х
селф.у = у
определение вычислительной области (я):
проходить
деф вычислить периметр (я):
проходить
def move(self, deltaX, deltaY):
self.x += deltaX
self.y += deltaY
защита __str__(я):
return 'Абстрактный класс Geometry не должен создавать экземпляры, и производные классы должны переопределять этот метод!' Конструктор класса Geometry выглядит довольно обычно, он просто инициализирует переменные экземпляра, которые являются общими для всех наших объектов геометрии, а именно координаты x и y, чтобы описать их положение в нашей 2D системе координат. Затем следуют определения методов ComputeArea() , ComputePerimeter() , move(…) и __str__() , которые должны поддерживать все объекты геометрии. Для move(…) мы уже можем предоставить реализацию, потому что она полностью основана на переменных экземпляра x и y и работает одинаково для всех объектов геометрии.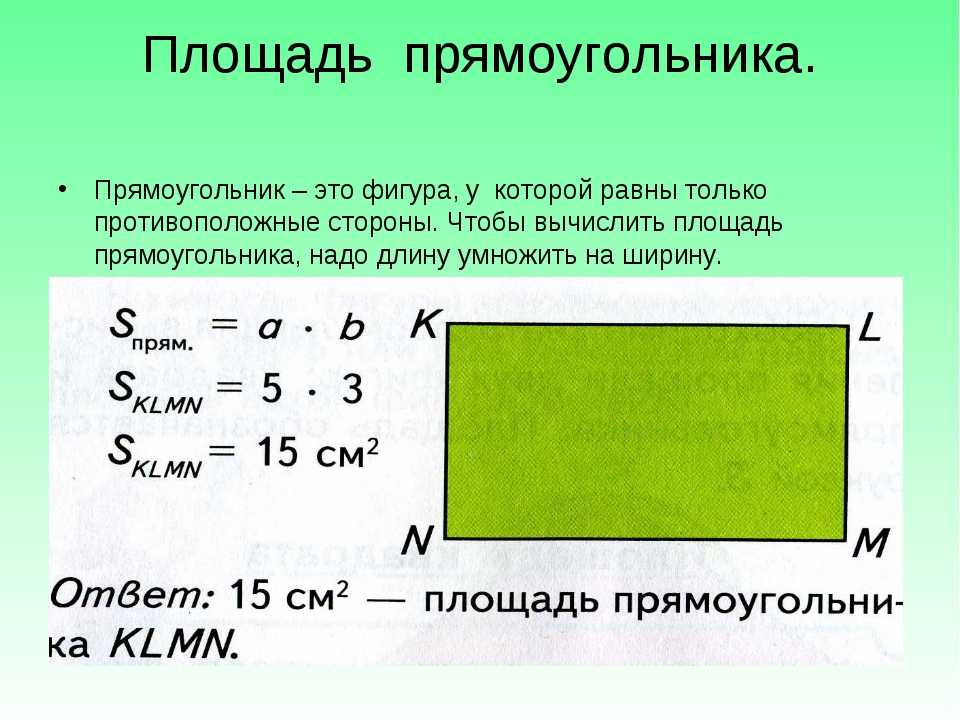 Это означает, что производные классы для Circle и Rectangle не должны будут предоставлять свою собственную реализацию. Напротив, вы не можете осмысленно вычислить площадь или периметр только по положению объекта. Поэтому мы использовали ключевое слово pass, чтобы указать, что мы покидаем тело calculateArea () и calculatePerimeter() методы намеренно пусты. Эти методы должны быть переопределены в определениях производных классов с реализацией их специализированного поведения. Мы могли бы сделать то же самое для __str__() , но вместо этого мы возвращаем предупреждающее сообщение о том, что этот класс не должен был быть создан.
Это означает, что производные классы для Circle и Rectangle не должны будут предоставлять свою собственную реализацию. Напротив, вы не можете осмысленно вычислить площадь или периметр только по положению объекта. Поэтому мы использовали ключевое слово pass, чтобы указать, что мы покидаем тело calculateArea () и calculatePerimeter() методы намеренно пусты. Эти методы должны быть переопределены в определениях производных классов с реализацией их специализированного поведения. Мы могли бы сделать то же самое для __str__() , но вместо этого мы возвращаем предупреждающее сообщение о том, что этот класс не должен был быть создан.
Стоит отметить, что во многих объектно-ориентированных языках программирования концепции абстрактного класса (= класс, который не может быть создан) и абстрактный метод (= метод, который должен быть переопределен в каждом подклассе, который может быть создан) ) встроены в язык. Это означает, что существуют специальные ключевые слова для объявления класса или метода абстрактным, и тогда невозможно создать объект этого класса или его подкласса, который не предоставляет реализацию для абстрактных методов. В Python это было добавлено поверх языка через модуль в стандартной библиотеке под названием abc (для a bstract b ase c девочки). Хотя мы не будем использовать его в этом курсе, рекомендуется проверить его и использовать, если вы участвуете в более крупных проектах Python. Эта страница абстрактных классов является хорошим источником для получения дополнительной информации.
В Python это было добавлено поверх языка через модуль в стандартной библиотеке под названием abc (для a bstract b ase c девочки). Хотя мы не будем использовать его в этом курсе, рекомендуется проверить его и использовать, если вы участвуете в более крупных проектах Python. Эта страница абстрактных классов является хорошим источником для получения дополнительной информации.
Вот наше новое определение класса Circle, которое теперь является производным от класса Geometry. Мы также используем несколько команд в конце, чтобы создать и использовать новый объект Circle этого класса, чтобы убедиться, что все действительно работает, как раньше:0003
импорт математики
класс Круг (геометрия):
def __init__(я, х = 0,0, у = 0,0, радиус = 1,0):
супер(Круг,я).__init__(x,y)
self.radius = радиус
определение вычислительной области (я):
вернуть math.pi * self.radius ** 2
def вычислить периметр (сам):
вернуть 2 * math.pi * self.radius
защита __str__(я):
return 'Окружность с координатами {0}, {1} и радиусом {2}'. format(self.x, self.y, self.radius)
круг1 = круг(10, 10, 10)
печать (круг1.computeArea())
печать (круг1.computePerimeter())
круг1.переместить(2,2)
печать (круг1)
format(self.x, self.y, self.radius)
круг1 = круг(10, 10, 10)
печать (круг1.computeArea())
печать (круг1.computePerimeter())
круг1.переместить(2,2)
печать (круг1) Вот что нам нужно было сделать в коде:
- В строке 3 нам пришлось изменить заголовок определения класса, чтобы включить в него имя базового класса, из которого мы получаем Circle («Geometry»). скобки.
- Конструктор Circle принимает те же три параметра, что и раньше. Однако он только инициализирует новую переменную экземпляра , радиус в строке 7. Для инициализации двух других переменных он вызывает конструктор своего базового класса, то есть класса Geometry, в строке 6 командой «super(Circle,self). __init__(x,y)». Это говорит о том, что «вызвать конструктор базового класса класса Circle и передать ему значения x и y в качестве параметров». Обычно рекомендуется вызывать конструктор базового класса в качестве первой команды в конструкторе производного класса, чтобы исключить все общие инициализации.

- Затем мы предоставляем определения calculateArea () и calculatePerimeter() , специфичные для кругов. Эти определения переопределяют «пустые» определения базового класса Geometry. Это означает, что всякий раз, когда мы вызываем calculateArea() или calculatePerimeter() для объекта класса Circle, будет выполняться код из этих специализированных определений.
- Обратите внимание, что мы не даем определения для метода move(…) в этом определении класса. Это означает, что когда move(…) будет вызываться для объекта Circle, будет выполняться код из соответствующего определения в его базовом классе Geometry.
- Мы переопределяем метод __str__() для создания строки того же типа с информацией обо всех переменных экземпляра, что и в предыдущем определении. Обратите внимание, что эта функция обращается как к переменным экземпляра, определенным в родительском классе Geometry, так и к дополнительной, добавленной в определение Circle.

Новое определение класса Rectangle, теперь производное от Geometry, выглядит очень похоже на определение Circle, если заменить «Circle» на «Rectangle». Только реализации переопределенных методов выглядят иначе, используя версии, специфичные для прямоугольников.
класс Прямоугольник (геометрия):
def __init__(self, x = 0.0, y = 0.0, ширина = 1.0, высота = 1.0):
супер(Прямоугольник, я).__init__(x,y)
собственная ширина = ширина
self.height = высота
определение вычислительной области (я):
вернуть self.width * self.height
def вычислить периметр (сам):
вернуть 2 * (собственная ширина + собственная высота)
защита __str__(я):
return 'Прямоугольник с координатами {0}, {1}, шириной {2} и высотой {3}'.format(self.x, self.y, self.width, self.height )
прямоугольник1 = прямоугольник (15,20,4,5)
печать (прямоугольник1.computeArea())
печать (прямоугольник1.computePerimeter())
прямоугольник1.переместить(2,2)
печать (прямоугольник1) В целом, новые определения Circle и Rectangle стали короче и содержат избыточный код, как и реализация move(…) появляется только один раз, а именно в самом общем классе Geometry.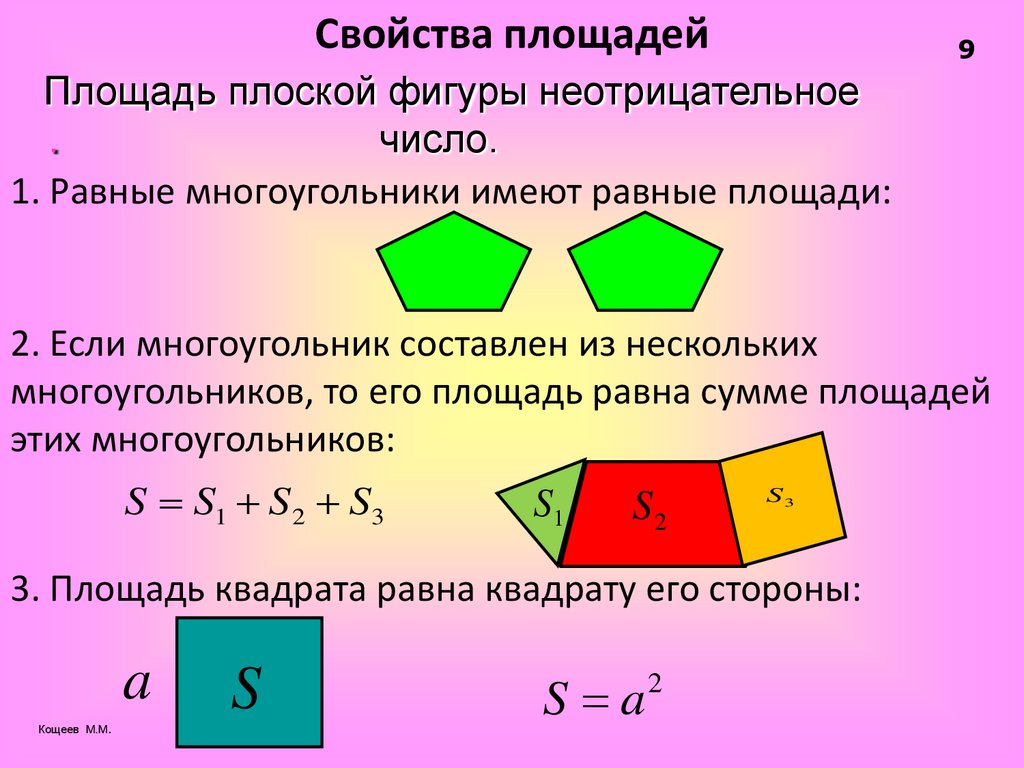 Давайте добавим в иерархию еще один класс, класс для выровненных по оси объектов Square. Конечно, вы можете возразить, что нашего класса Rectangle уже достаточно для представления таких квадратов. Это правильно, но мы хотим проиллюстрировать, как это будет выглядеть, если вы дополнительно специализируете класс, уже производный от геометрии, и можно было бы представить себе более сложную версию нашего игрушечного примера ГИС, в котором квадраты добавят какую-то другую форму специализации. Результирующая иерархия классов будет выглядеть так, как показано на изображении ниже. Новый класс Square — это является производным классом от класса Rectangle (поэтому Rectangle является его базовым классом ), но он также косвенно является производным от класса Geometry. Поэтому мы говорим, что и Geometry, и Rectangle являются 90 341 суперклассами 90 342 Square, а Square — 90 341 подклассом 90 342 обоих этих классов. Обратите внимание, что в данном случае термины базовый и производный класс описывают взаимосвязь между двумя узлами, напрямую соединенными одной стрелкой на иерархическом графике, а суперкласс и подкласс являются более общими и описывают отношения между двумя классами, которые связаны через любое количество направленных стрелок на графике.
Давайте добавим в иерархию еще один класс, класс для выровненных по оси объектов Square. Конечно, вы можете возразить, что нашего класса Rectangle уже достаточно для представления таких квадратов. Это правильно, но мы хотим проиллюстрировать, как это будет выглядеть, если вы дополнительно специализируете класс, уже производный от геометрии, и можно было бы представить себе более сложную версию нашего игрушечного примера ГИС, в котором квадраты добавят какую-то другую форму специализации. Результирующая иерархия классов будет выглядеть так, как показано на изображении ниже. Новый класс Square — это является производным классом от класса Rectangle (поэтому Rectangle является его базовым классом ), но он также косвенно является производным от класса Geometry. Поэтому мы говорим, что и Geometry, и Rectangle являются 90 341 суперклассами 90 342 Square, а Square — 90 341 подклассом 90 342 обоих этих классов. Обратите внимание, что в данном случае термины базовый и производный класс описывают взаимосвязь между двумя узлами, напрямую соединенными одной стрелкой на иерархическом графике, а суперкласс и подкласс являются более общими и описывают отношения между двумя классами, которые связаны через любое количество направленных стрелок на графике.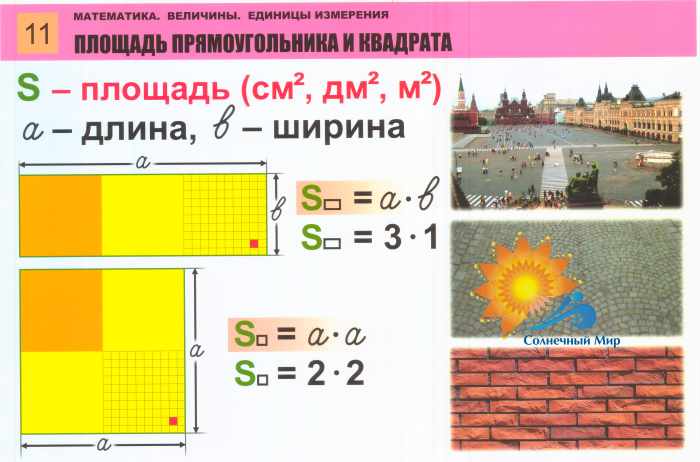
Рисунок 4.18 Иерархия классов после добавления класса Square. Square является подклассом Geometry и Rectangle. Оба этих класса являются суперклассами Square.
Вот код класса Square:
class Square(Rectangle):
def __init__(self, x = 0.0, y = 0.0, sideLength = 1.0):
super(Square,self).__init__(x, y, sideLength, sideLength)
защита __str__(я):
return 'Квадрат с координатами {0}, {1} и sideLength {2}'.format(self.x, self.y, self.width )
квадрат1 = квадрат (5, 5, 8)
печать (square1.computeArea())
печать (square1.computePerimeter())
квадрат1.переместить(2,2)
печать (квадрат1) Правильно, определение Square очень короткое; мы только определяем новый конструктор, который принимает только координаты x и y и одно значение sideLength, а не значения ширины и высоты. В конструкторе мы вызываем конструктор базового класса Rectangle и предоставляем sideLength для параметров ширины и высоты этого конструктора. Нет новых переменных экземпляра для инициализации, так что это все, что нужно сделать в конструкторе.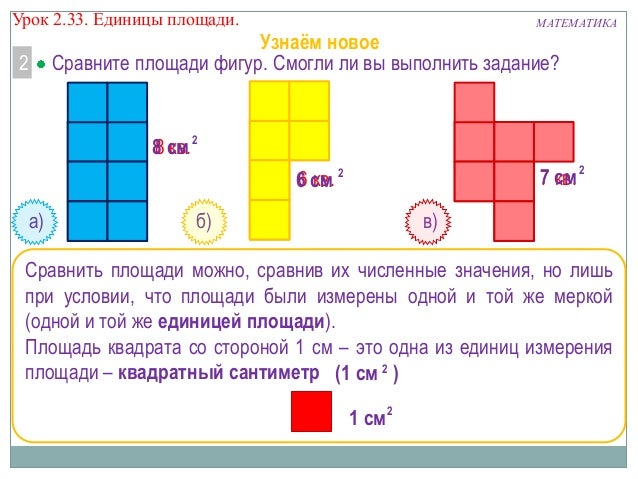 Тогда единственное, что нам нужно сделать, это переопределить __str__() метод для создания выходного сообщения, специфичного для квадрата, с использованием self.width для информации о длине стороны квадрата. (Конечно, мы могли бы с тем же успехом использовать здесь self.height.) Реализации методов calculateArea() и calculatePerimeter() унаследованы от класса Rectangle, а реализация move (…) косвенно из класса Геометрия.
Тогда единственное, что нам нужно сделать, это переопределить __str__() метод для создания выходного сообщения, специфичного для квадрата, с использованием self.width для информации о длине стороны квадрата. (Конечно, мы могли бы с тем же успехом использовать здесь self.height.) Реализации методов calculateArea() и calculatePerimeter() унаследованы от класса Rectangle, а реализация move (…) косвенно из класса Геометрия.
Теперь, когда у нас есть иерархия классов, состоящая из одного абстрактного и трех инстанцируемых классов, следующий пример кода иллюстрирует мощь полиморфизма. Представьте, что в нашей игрушечной ГИС мы создали слой, состоящий из объектов разных типов геометрии. Если мы теперь хотим реализовать функцию ComputeTotalArea(…) , который вычисляет объединенную площадь всех объектов в слое, это можно сделать следующим образом: 20, 5) ]
def вычислитьTotalArea (геометрический слой):
площадь = 0
для геометрии в геометрическом слое:
площадь += geom. computeArea()
зона возврата
print(computeTotalArea(слой))
computeArea()
зона возврата
print(computeTotalArea(слой))
Вывод: 677.6282702997526
В строке 1 вы видите, как мы можем создать список объектов различных классов из нашей иерархии для представления слоя. Мы включили объекты, которые мы уже создали ранее, в переменные Circle1, Rectangle1 и Square1, но также добавили еще один объект Circle и еще один объект Square, которые мы создаем непосредственно в квадратных скобках […]. Функция calculateTotalArea(…) затем просто берет список слоев, перебирает его элементы и вызывает calculateArea() для каждого объекта в списке. Возвращаемые значения площади суммируются и возвращаются как общая площадь.
Код для этого действительно компактен и элегантен, и нет необходимости в if-else для реализации некоторого различия регистра на основе типа геометрии данного объекта в переменной geom . Предположим далее, что мы хотели бы добавить в нашу иерархию еще один класс, класс Polygon, который, поскольку многоугольники не являются ни специализированными версиями кругов, ни прямоугольников, должен быть производным от корневого класса Geometry.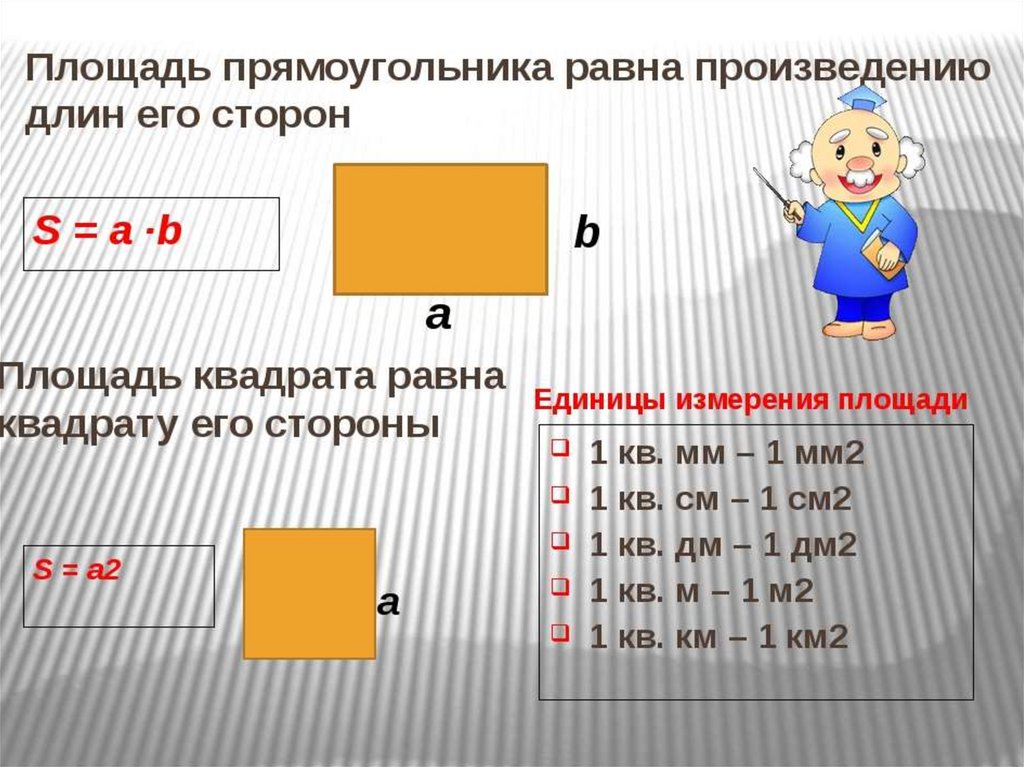


 Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения.
Аналогично, но уже используя определение синуса, можно определить длину второй стороны. Как теперь найти площадь прямоугольника? Да, очень просто перемножить полученные значения. Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника. В форме формулы это будет выглядеть так:
Разделите результат на два и получите длину второй стороны. Ну а дальше стандартный прием, умножаем обе стороны и получаем площадь прямоугольника. В форме формулы это будет выглядеть так: м. = 33,2 кв.м.
м. = 33,2 кв.м.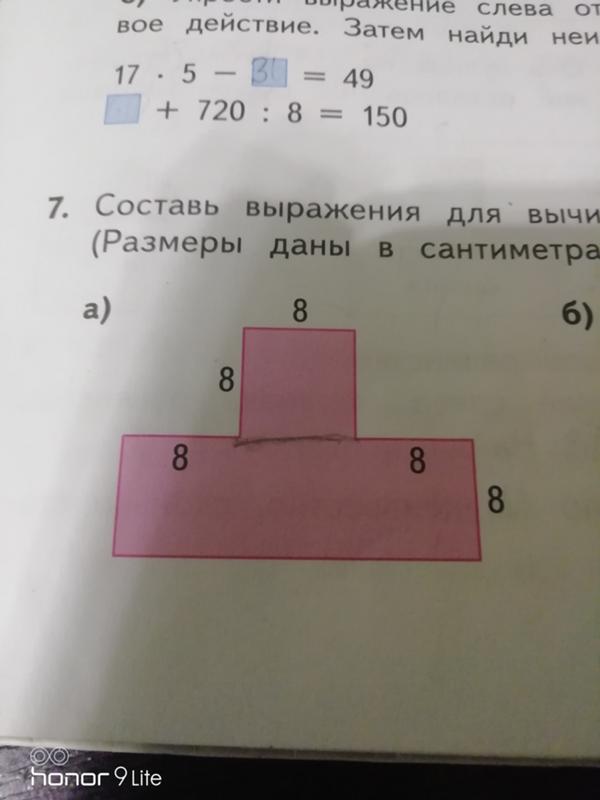 м.
м.
 x += deltaX
self.y += deltaY
защита __str__(я):
return 'Прямоугольник с координатами {0}, {1}, шириной {2} и высотой {3}'.format(self.x, self.y, self.width, self.height )
прямоугольник1 = прямоугольник (10,10,3,2)
печать (прямоугольник1)
печать (прямоугольник1.computeArea())
прямоугольник1.переместить(2,2)
печать (прямоугольник1)
x += deltaX
self.y += deltaY
защита __str__(я):
return 'Прямоугольник с координатами {0}, {1}, шириной {2} и высотой {3}'.format(self.x, self.y, self.width, self.height )
прямоугольник1 = прямоугольник (10,10,3,2)
печать (прямоугольник1)
печать (прямоугольник1.computeArea())
прямоугольник1.переместить(2,2)
печать (прямоугольник1)  format(self.x, self.y, self.radius)
круг1 = круг(10, 10, 10)
печать (круг1.computeArea())
печать (круг1.computePerimeter())
круг1.переместить(2,2)
печать (круг1)
format(self.x, self.y, self.radius)
круг1 = круг(10, 10, 10)
печать (круг1.computeArea())
печать (круг1.computePerimeter())
круг1.переместить(2,2)
печать (круг1)