Эффект поля: 4.4. Эффект поля в полупроводниках

4.4. Эффект поля в полупроводниках

Эффект поля заключается в изменении концентрации носителей заряда в приповерхностном слое полупроводника под воздействием внешнего электрического поля. При этом в полупроводнике в зависимости от знака и величины поля могут возникнуть два основных вида приповерхностных слоев. Обогащенный слой — это слой с повышенной концентрацией основных носителей заряда (в сравнении с концентрацией носителей в объеме полупроводника).Обедненный слойхарактеризуется пониженной концентрацией основных носителей заряда в приповерхностном слое.

Рассмотрим сущность эффекта поля, наблюдаемого в структуре металл-диэлектрик-полупро­вод­ник (МДП-структура). Если в качестве диэлектрика используется окисел, то соответствующая структура называется МОП-структурой. Для упрощения дальнейшего изложения при анализе происходящих явлений не будем учитывать влияние поверхностных состояний, неизбежно возникающих на границе диэлектрик-полупроводник.

МДП-структура представляет собой полупроводниковую пластину, на поверхности которой путем специального окисления или осаждения из газовой фазы выращен тонкий слой диэлектрика толщиной 0,1.

..1 мкм (например, окисел SiO₂на поверхности пластины кремния). Для создания электрических контактов на противоположные грани полупроводниковой пластины методом вакуумного напыления наносятся металлизированные площадки, как изображено на рис. 4.19,а. Следовательно, МДП-структура является плоским конденсатором, у которого прокладкой является слой диэлектрика, а одной из обкладок служит полупроводниковый кристалл.

Распределение потенциала в МДП-структуре при подключении источника напряжения Uминусом к поверхности диэлектрика и плюсом к поверхности полупроводника представлено на рис. 4.19,б. Из рисунка следует, что потенциал электрического поля снижается по абсолютной величине вдоль координатых, направленной внутрь полупроводника, от значения минус

Uна поверхности МДП-структуры до значения поверхностного потенциала минус_sна границе полупроводник-диэлектрик. На этой границе появляется отрицательный поверхностный заряд, который, в силу выполнения условия электронейтральности, компенсируется положительным зарядом дырок, притянутых к поверхности полупроводника. Поэтому поверхностный слой полупроводника оказывается обедненным носителями одного знака со знаком поверхностного заряда и обогащенным носителями противоположного знака.

Длина области, обогащенной носителями заряда (в нашем случае дырками) обозначается через L_Dи, как известно, называетсядебаевской длиной экранирования. Значение дебаевской длины экранирования зависит от типа проводимости полупроводника и знака поверхностного потенциала, достигая величин порядка 1…10 мкм.

Рассчитаем распределение объемного потенциала  и значение дебаевской длины экранирования

L_D по глубине полупроводника в области объемного заряда. С этой целью воспользуемся дифференциальным уравнением Пуассона, которое в одномерном случае имеет вид

, (4.30)

где _o— электрическая постоянная; — диэлектрическая проницаемость полупроводника;  плотность объемного заряда, Кл/м³.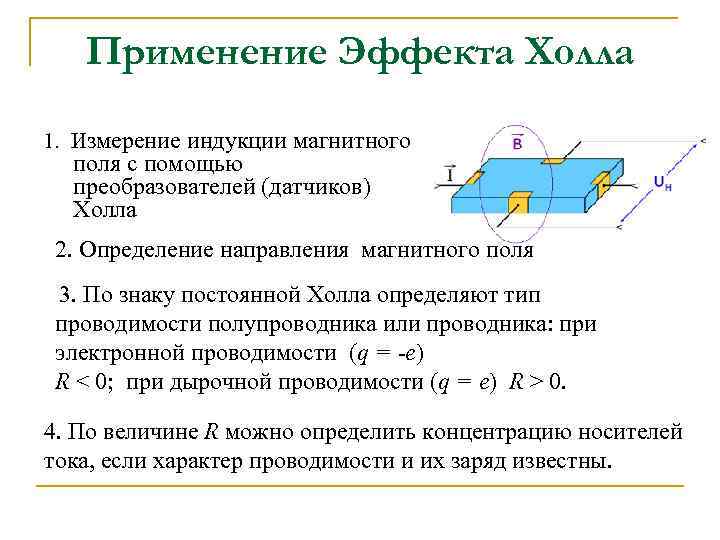

Для собственного полупроводника значение  определяется из соотношения вида

, (4.31)

где  значение объемного потенциала на глубине х; _т0,026 В — тепловой потенциал при температуре Т=300 К;q — заряд электрона, 2n_i=n

_i+p_i -концентрация электронов и дырок в собственном полупроводнике, м^-3.

Из соотношения (4.31) следует, что плотность объемного заряда снижается по экспоненциальному закону по мере удаления от поверхности вглубь полупроводника, а при 0 (вдали от поверхности) значение . Экспоненциальный член в формуле (4.31) можно разложить в ряд Маклорена по степеням /_т:

ехр(-/_т)=1- /_т+(1/2!)(/_т)²-…

С учетом первых двух членов этого разложения соотношение (4.29) можно представить в виде линейной функции объемного потенциала :

. (4.32)

Наконец, подставляя значение  из (4.31) в (4.29), запишем уравнение Пуассона в виде

, (4.33)

где L_D — дебаевская длина экранирования. Значение L_D рассчитывается из выражения

. (4.34)

Из (4.34) следует, что дебаевская длина экранирования уменьшается с ростом концентрации собственных носителей заряда в полупроводнике.

В чистом кремнии (=12) при комнатной температуре (n_i210¹⁶ м^-3) значение L_D является достаточно большой величиной, достигающей 14 мкм.

Общий вид решения дифференциального уравнения (4.33):

.

Коэффициенты С₁ и С₂ определим, рассматривая граничные условия: x=, С₁=0; x=0, С₂=_s. Подставляя значения

С₁ и С₂ в общее решение получаем окончательное выражение для распределения потенциала в области объемного заряда:

. (4.35)

Как и следовало ожидать, значение потенциала (x) в области объемного заряда убывает по экспоненциальному закону от значения, равного_sна поверхности полупроводника (приx=0) до нуля при. В результате, как показано на рис. 4.20, границы энергетических зон на зонной диаграмме приповерхностного участка полупроводника, построенной в координатах энергетических потенциалов, изгибаются вверх (при наличии отрицательного потенциала на поверхности, рис. 4.20,а), или вниз (при положительном потенциале на поверхности полупроводника, рис. 4.20,б).

Из рис. 4.20 следует, что при отрицательном потенциале на поверхности концентрация дырок p_s в приповерхностной области собственного полупроводника превышает концентрацию дырок

p_iв валентной зоне (p_s>p_i), а при положительном потенциале на поверхности концентрация электроновn_sв приповерхностной области превышает концентрацию электроновn_iв зоне проводимости (n_s>n_i).

Эффект поля | это… Что такое Эффект поля?

Эффект поля в МОП-структуре

Эффект поля (англ. Field-effect) в широком смысле состоит в управлении электрофизическими параметрами поверхности твердого тела с помощью электрического поля, приложенного по нормали к поверхности^[1].

В качестве способа регистрации изменений электрофизических параметров под действием электрического поля могут быть использованы измерение проводимости, дифференциальной ёмкости — метод вольт-фарадных характеристик, поверхностной фото-ЭДС. Чаще всего под эффектом поля понимают изменение проводимости твердого тела под действием на него поперечного электрического поля.

В полупроводниковой технике под эффектом поля понимается влияние внешнего электрического поля на электропроводность полупроводника. В общем случае рассматривается полубесконечный полупроводник, имеющий как минимум одну поверхность, свойства которой и рассматриваются. Основным «дефектом» такого полупроводника является наличие поверхности (обрыв периодичности кристаллической решетки), что по умолчанию детерминирует наличие поверхностных состояний. Кроме того, на поверхности присутствуют различные дефекты и примеси, также вносят свой ​​вклад в плотность поверхностных состояний. Основной теоретической проблемой эффекта поля является нахождение распределения поверхностного и внутреннего потенциала в полупроводнике, особенно при приложении внешнего электрического поля. Основной экспериментальной проблемой эффекта поля фиксация поверхностных состояний при изменении внешних факторов, долгое время не давало возможности для полноценного исследования поверхностной проводимости и практической реализации МДП-транзисторов. Эта проблема была решена с разработкой технологии пассивации поверхности кремния в начале 60-х годов 20-го века.

Содержание 1 История проблемы 2 Решение уравнения Пуассона на поверхности полупроводника 2.1 Основные допущения теории поверхности 2.2 Заряды и потенциалы на поверхности полупроводника 2.3 Заряд инверсного слоя и эффективная толщина обедненной области 3 Экспериментальные методы исследования поверхности полупроводника 3. 1 МДП-структура 3.2 Емкость МДП-структуры 3.3 Поверхностная проводимость МДП-структуры 4 Литература 5 См. также 6 Примечания

История проблемы

Безусловно и само название эффект поля и ее развитие на первом этапе благодаря Уильяму Шокли. Очевидно, что данная проблема относится к проблеме междисциплинарного класса, лежащий на пересечении фундаментальной физики и инженерных наук. Она зародилась в конце 20-х годов 20-го века, как прикладная реакция на стремительное развитие фундаментальной науки — квантовой механики. Тогда же вполне стихийным образом, фундаментальная наука начала свое стремительное внедрение в практику, что вылилось во второй половине 20-го века в т. н. лозунг «наука — производственная сила технического прогресса». На протяжении почти 80-ти лет своего существования данное направление развития науки переживало свои взлеты и падения, пока на одном из этапов фундаментальные исследования не указывали путь развития.

Следует отметить, что сама проблема возникла в области инженерии, поэтому приоритет был защищен патентами в США — Лилиенфельд^[2][3], а в Великобритании — Оскар Хайл (англ.)русск.^[4]. Это были довольно тривиальные идеи по практической реализации полупроводникового усилителя, управление которого осуществлялось электрическим полем. Осуществить эти идеи на практике попытался Шокли в конце 30-х годов 20-го века. В качестве полупроводника тогда использовали германий, в качестве диэлектрика — пластинки слюды, роль металлического электрода — металлическая пластинка или металлизированное покрытие пластинки слюды. Конечно Шокли получил модуляцию проводимости поверхности германия, однако эффект был незначительным. Более того, довольно нестабильным во времени, что не позволяло внедрить его в серийное производство. Только во второй половине 40-х годов 20-го века, стало ясно, что основным дестабилизирующим фактором были т. н. поверхностные состояния в полупроводнике. Да и сам выбор полупроводника (германий) был не самым лучшим (даже сегодня практически отсутствует технология изготовления МДП-структур на основе германия).

Первым заметил доминирующую роль поверхностных состояний в полупроводнике Бардин, который затем вместе с Браттейном открыл т. н. биполярный эффект. Здесь необходимо отметить, что в то время еще не существовало теории выпрямляющих переходов в полупроводнике и поэтому даже сам процесс выпрямления приписывался поверхностным состояниям. Размещая достаточно близко точечные контакты будущих эмиттера и коллектора Бардин, вместе с Браттейном и «открыли» биполярный эффект, а по сути впервые предложили практическую реализацию биполярного транзистора на точечных контактах. Очевидно, что в то время никакой теории не было, и поэтому мифическое взаимодействие контактов эмиттера и коллектора (чем ближе расположены, тем сильнее усиление) и воспринималась в то время, как физическое явление (эффект), теория которого как надеялись тогда будет разработана позднее. Само название эффект поля появилось впервые в работе Шокли и Пирсона, в которой экспериментально было доказано существование поверхностных состояний в полупроводнике. Роль Шокли на этом этапе была незначительна, поскольку он подвергся разочарованию, вызванной невозможностью того времени реализации эффекта поля. Однако «открытие» биполярного эффекта стимулировало Шокли на фундаментальные исследования сначала точечного перехода, затем сплавного перехода и, наконец всем известного p-n-перехода, что со временем и вылилось в теорию p-n-перехода Шокли, а затем и в теорию биполярного транзистора, базировавшаяся на понятии квазиуровня Ферми.

С появлением полупроводниковых переходов и биполярных транзисторов началась новая технологическая эра обработки полупроводников, с первым германия, а затем и кремния. Отрабатывались инженерные методы выращивания кристаллов и технологии разрезания пластин с последующим их шлифовкой. Более того, разрабатываемые методы диффузии и эпитаксии примесей путем фотолитографии и т.  д. И только в конце 50-х годов 20-го века уровень развития технологий достиг зрелости, и путем разработки технологии пассивации поверхности кремния Аталлою и Канго наконец была создана МДП-структура на кремнии с более или менее стабильными характеристиками.

Пассивация поверхности кремния стабилизовала поверхностные состояния и стала возможна практическая реализация МДП-транзисторов. Первые феноменологические модели МДП-транзисторов появились в пионерских работах Хофштейна, Хеймана, Ихантолы и Молла. Однако, основная фундаментальная работа по созданию теории МДП-транзистора, который базируется на фундаментальных принципах поверхностной проводимости была создана в 1964 году учеником Шокли — Са.

Решение уравнения Пуассона на поверхности полупроводника

Основные допущения теории поверхности

При теоретическом исследовании хода потенциала и распределения зарядов в полупроводнике вводятся следующие предположения:

1. Полупроводник легированный однородно и имеет бесконечную толщину. Вторая часть этого предположения выполняется для кристаллов, толщина которых превышает несколько десятых миллиметра. Условие однородного легирования не всегда выполняется на практике вследствие перераспределения примесей при окислении поверхности. Это необходимо учитывать при исследовании режима плоских зон. В режимах аккумуляции и инверсии этим эффектом можно пренебречь.
2. Полупроводник является невырожденным. В этом случае можно использовать статистику Максвелла-Больцмана. На практике в режимах аккумуляции и инверсии уровень Ферми может подходить близко к краям зон, что приводит к необходимости использования статистики Ферми-Дирака, что существенно затрудняет вычисления. Для упрощения рассматривают случай, когда уровень Ферми находится на несколько kT ниже/выше края соответствующих зоны.
3. Ток через окисел, находящегося на поверхности полупроводника, отсутствует. Это предположение означает, что система является равновесная и поэтому можно пользоваться понятие уровня Ферми. Позднее при рассмотрении будет введен квазиривень Ферми, что позволит учесть неравновесные процессы и использовать полученные результаты при моделировании МДП-транзисторов.
4. Плотность зарядов, локализованных на поверхности полупроводника и в объеме диэлектрика, не зависит от приложенного напряжения (электрического поля). На поверхности кремния, для которого приняты предосторожности по уменьшению и стабилизации поверхностных эффектов, эти условия выполняются.
5. Эффекты, обусловленные наличием сильного электрического поля в полупроводнике, не учитываются. В общем случае изменение потенциала с расстоянием от поверхности может быть очень быстрой (при сильной инверсии), поэтому использование обычных полуклассических методов решения (например, использование уравнения Пуассона) требуют обоснования.

Заряды и потенциалы на поверхности полупроводника

Рассмотрим полупроводник p — типа. Плотность зарядов в полупроводнике ρ(x) определяется суммой зарядов электронов n, дырок p и примесей N:

. (1)

В случае невырожденного полупроводника

(2a)

, (2b)

где β=q/kT — обратный температурный потенциал, n_i — концентрация носителей в собственном полупроводнике. Поскольку при и , а поэтому из (1) и (2) следует, что

. (3)

Подстановка (2) и (3) в (1) дает:

(4)

а одномерное уравнение Пуассона запишется в виде:

где  — диэлектрическая проницаемость полупроводника. В более компактной форме это уравнение будет:

(5)

где дебаевской длина экранирования в собственном полупроводнике ,  — безразмерные потенциалы. Интегрируя (5) от до и учитывая, , и , находим:

(6)

где знак «+» берется при . Таким образом, величина электрического поля на поверхности полупроводника будет:

(7)

Полный заряд на единицу поверхности полупроводника может быть найден из последнего уравнения путем использования теоремы Гаусса :

(8)

Для нахождения зависимости необходимо проинтегрировать (6) от до :

(9)

что в общем случае можно сделать численными методами. Подстановка (9) в (4) дает возможность определения зависимости для заданных значений и . В случае собственного полупроводника () решение (9) находится в аналитическом виде. Уравнение (9) при этом переходит в

откуда находим:

(10)

а из (4) и (8) находим:

(11)

(12)

Интегрируя (11) и используя (5), можно найти выражение для полного заряда на единицу поверхности:

(13)

Разделив (13) на (12), находим:

Это соотношение определяет относительную величину заряда, который сосредоточен в слое от до , где потенциал равен u. С помощью (10) величина выражается в явном виде через отношение . Другой случай, допускающий аналитическое решение уравнения (9) — случай сильной инверсии на поверхности полупроводника:

(14)

Здесь в подкоренное выражение уравнения (9) учитывается только средний член, так что интегрирование дает:

(15)

Аналогичным образом из (4) находим:

или исключая u с помощью (15),

(16)

Необходимо отметить, что область использования (16) достаточно узкая, поскольку величина u не должна быть слишком большой, чтобы выполнялось предположение об отсутствии вырождения, и в то же время она не должна быть малой для выполнения условия (14).

Заряд инверсного слоя и эффективная толщина обедненной области

Полный заряд в полупроводнике создается электронами, дырками и ионизированными примесями. Заряд электронов в инверсном слое можно получить интегрированием величины от до , где :

.

Изменив переменную интегрирования с помощью (2) находим:

. (17)

Необходимо отметить, что здесь необходимо использовать статистику Ферми-Дирака (статистика Максвелла-Больцмана дает завышенные результаты), когда уровень Ферми близок к зоне проводимости, или находится в ее середине. Эффективная толщина обедненной области x_d определяется из уравнения

Здесь предполагается, что при плотность объемного заряда равна нулю, а при имеем . Когда заряд инверсного слоя мал по сравнению с зарядом обедненной области, , а в случае сильной инверсии величина становится практически независимой от , и приближается к предельному значению :

(18)

Для кремния при комнатной температуре в диапазоне концентраций примесей можно пользоваться следующим приближенным соотношением:

(19)

Экспериментальные методы исследования поверхности полупроводника

МДП-структура

МДП-структура — это плоская трехслойная структура, состоящая из тонкого слоя металла, чуть более толстого слоя диэлектрика и толстого слоя полупроводника (металл-диэлектрик/окисел- полупроводник).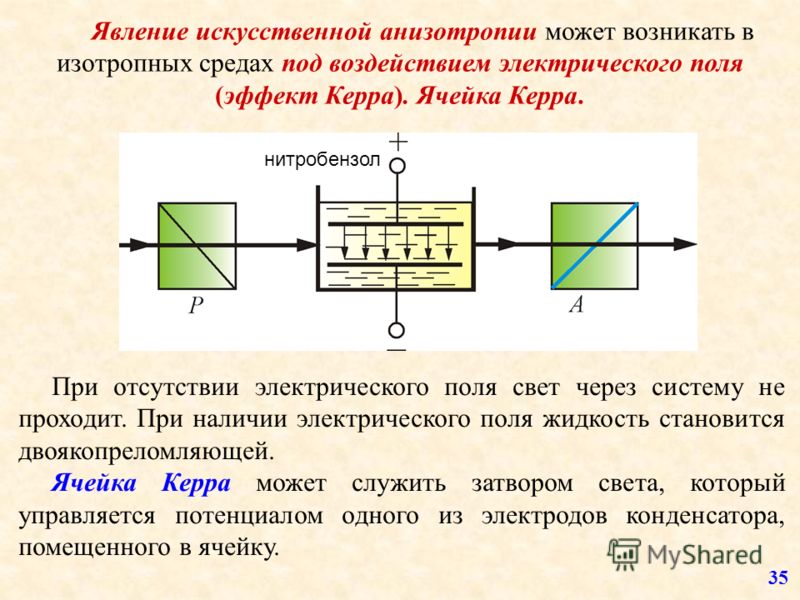 В свободной природе не встречается. Отсюда истоки некоторого пренебрежения, как к самой МДП структуре так и эффекту поля, связанные с искусственностью самой структуры и явлений, что в ней наблюдаются. На самом деле МДП-структура есть идеальный физический объект (хоть и искусственный), в котором легко реализуется однородность электрического поля (в атомах реализуется идеальная изотропность). Отсюда также вытекает её идеалистичность для исследования эффекта поля на поверхности полупроводника, и всех тех попутных явлений (классических и квантовых), которые связаны с этим эффектом.

Впервые МДП-структура была получена на практике в 1960 году после успешной реализации технологии пассивации кремния Канго и Аталлою. В рамках этой технологии МДП-структура создавалась в одном технологическом процессе: сначала поверхность кремния окислялась, а уже на окись напыливалась металлизация. Благодаря единому процессу, металлический электрод практически был эквидистантно поверхности раздела окисел — кремний, что обеспечивало однородность электрического поля на всей площади МДП-структуры. На основе этих МДП-структур были изготовлены первые МДП-транзисторы.

Следует отметить, что тривиальный учет статистики Ферми-Дирака вместо Максвелла-Больцмана не выводит теорию за пределы квазиклассического подхода. Более того, даже учета т. н. треугольной потенциальной ямы на поверхности полупроводника, что приводит к появлению дискретных уровней энергии в зоне проводимости (валентной зоне) также не выводит за указанные пределы.

Основной особенностью МДП-структуры является то, что на поверхности раздела диэлектрик-полупроводник индуцируется p-n — переход, в котором носители заряда имеют свойства двумерной (2D-) системы, поведение которой до сих пор практически не изучена. Отсюда и т. н. «Неожиданность» с открытием квантового эффекта Холла, плоского атома и т. д.

Емкость МДП-структуры

Поверхностная проводимость МДП-структуры

Если на поверхности полупроводника в МДП-структуре созданы омические контакты, то измеряя проводимость между ними в зависимости от напряжения смещения, можно получить ряд полезных сведений о свойствах поверхности. Этот метод исследования был использован в классических экспериментах Шокли и Пирсона.

Наиболее простой путь вычисления поверхностной проводимости состоит в нахождении избыточной поверхностной плотности электронов и дырок ΔN и ΔP в функции поверхностного потенциала. Обозначая через и плотности носителей заряда в случае плоских зон , можно записать:

где

или

Здесь выражение для был представлен формулой (6). Если предположить, что носители заряда не захвачуються поверхностными ловушками, тогда изменение поверхностной проводимости будет выражена как:

где и  — эффективные подвижности носителей заряда, которые зависят в общем випалдку от . Зависимость для Si и Ge была вычислена рядом авторов. Здесь только стоит внимания то, что величина для легированного полупроводника имеет минимум при

Графическое представление этой зависимости проводят для случая . Здесь рост проводимости при u<0 соответствует «режима аккумуляции», при u>0 с удалением уровня Ферми сверху валентной зоны, когда проводимость падает, а затем снова резко возрастает за счет образования инверсного слоя.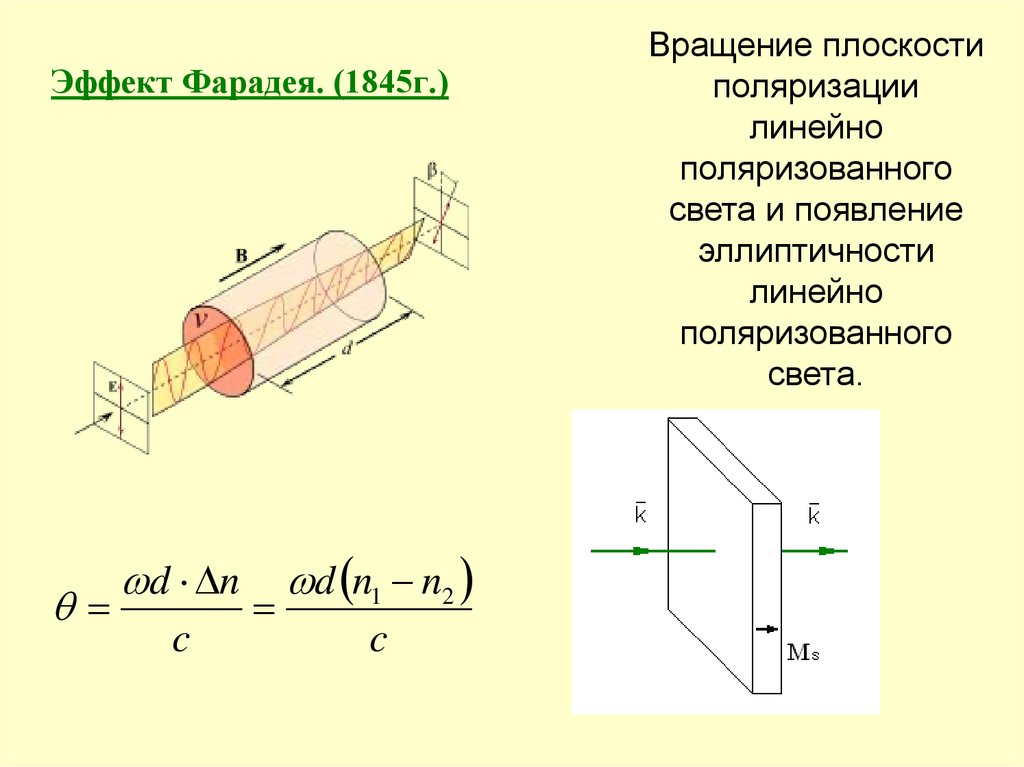

Если использовать выпрямительные контакты при измерении проводимости, тогда величина определяется носителями заряда одного типа. Поэтому в подынтегральная выражениях следует принимать только один из составляющих.

Исследованию эффективной подвижности носителей заряда в приповерхностных слоях полупроводника посвящено много теоретических и экспериментальных работ. Дж. Шриффером была развита классическая теория поверхностной подвижности, из которой следует, что за счет дополнительного рассеяния носителей на границе раздела диэлектрик-полупроводник и воздействия электрического поля величина падает с ростом поверхностного потенциала и всегда остается меньше подвижности в объеме полупроводника. Затем теория Шриффера была усовершенствована путем введения в рассмотрение анизотропии кристалла, зеркального отражения носителей от поверхности и ряда других эффектов, однако результаты расчетов плохо совпадают с экспериментальными данными. Основная причина этих различий состоит в том, что классический подход к проблеме поверхности не является справедливое, поскольку здесь мы имеем малую толщину слоя, в котором движутся носители заряда.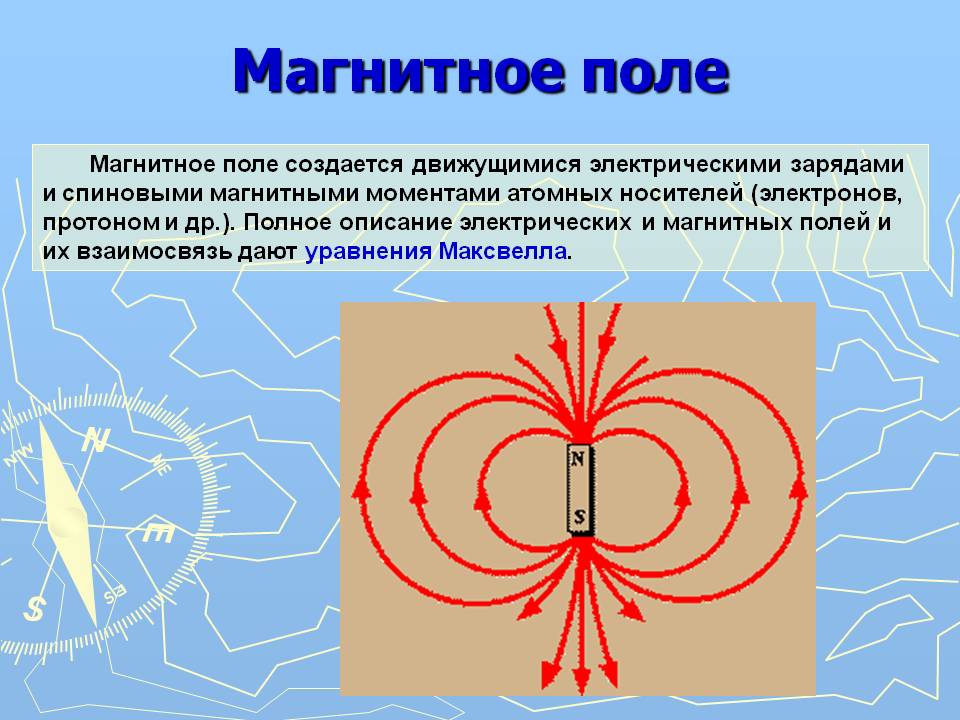 Эта толщина является величина одного порядка с длиной волны де Бройля и поэтому наличие сильного электрического поля приводит к появлению квантовых явлений.

Численные эксперименты по исследованию поверхностной подвижности, в которых особое внимание уделялось стабильности и воспроизводимости результатов, показали что в инверсных слоях значения и примерно вдвое меньше чем в объеме полупроводника и не зависят от электрического поля.

Поверхностная рухливисить основных носителей, которая изучалась на МДП-структурах в режиме аккумуляции, несколько превышает подвижность в инверсных слоях. При увеличении электрического поля значения падают медленнее, чем предсказывает теория.

Литература

• Lilienfeld JE Method and Apparatus for Controlling Electric Currents. US Patent # 1745175, 1930 <january.
• Heil O. Impruvements in or Relating to Electric Amplifiers and other Control Arrangements. UK Patent # 439457, 1935, December.
• Bardeen J., Phys. Rev., 71, 1947, p. 717.
• Shokley W., Pearson GL Modulation of Conductance of Thin Films of Semiconductors by Surface Charges. Phys. Rev., 1948, 74, July, p.232-233.
• Atalla MM, Tannenbaum E., Scheiber EJ Stabilization of Silicon Surfaces by Thermally Grown Oxides. Bell Syst. Tech. J., 1959, 38, May, p.749-783.
• Kahng D., Atalla MM Silicon-Silicon Dioxide Field Induced Devices. Solid-State Device Research Conference, Pittsburgh, Pa., 1960, June.
• Hofstein SR, Heiman FP The silicon Insulated-Gate Field-Effect Transistor. Proc. IEEE, 1963, 51, September, p.1190-1202.
• Ihantola HKJ, Moll JL Design Theory of a Surface Field-Effect Transistor. Solid-State Electronics, 1964, 7, June, p.423-430.
• Sah CT Characteristics of the Metal-Oxide-Semiconductoe Transistor. IEEE Trans. Electron Devices, 1964, ED-11, July, p.324-345.
• Бонч-Бруевич В. Л., Калашников С. Г. Физика полупроводников. М.: Наука, 1977.-672с.
• Кобболд Р. Теория и применение полевых транзисторов. Ленинград: Энергия, 1975.-304с.

См. также

Полевой транзистор

Примечания

1. ↑ Киселев В. Ф., Козлов С. Н., Зотеев А. В. Основы физики поверхности твёрдого тела. — М.: Изд-во Московского университета. Физический факультет МГУ, 1999.
2. ↑ Vardalas, John, Twists and Turns in the Development of the Transistor IEEE-USA Today’s Engineer, May 2003.
3. ↑ Lilienfeld, Julius Edgar, «Method and apparatus for controlling electric current» U.S. Patent 1 745 175 1930-01-28 (filed in Canada 1925-10-22, in US 1926-10-08).
4. ↑ Шаблон:Patent

Field Effect: Решения по кибербезопасности для малого и среднего бизнеса

Получите комплексную защиту, обеспечивающую максимальную безопасность, минимальную сложность и обеспечивающую подлинное спокойствие.

Откройте для себя продукты

Получите комплексную защиту, обеспечивающую максимальную безопасность, минимальную сложность и обеспечивающую подлинное спокойствие.

Откройте для себя продукты

Управляемое обнаружение и реагирование без помощи рук.

Спите спокойно, зная, что Covalence защищает ваши конечные точки, сеть и облачные сервисы — и все это на одной платформе.

Заказать демонстрацию

Узнать больше

Обучение безопасности на основе моделирования.

Повысьте квалификацию своей команды кибербезопасности с помощью аутентичных виртуальных сред для обучения, оценки, репетиций, соревнований и повышения квалификации.

Заказать демонстрацию

Узнать больше

Партнерская программа

Развивайте свой бизнес. Защитите своих клиентов.

Сотрудничайте с нами, чтобы предоставлять дифференцированные услуги по кибербезопасности, которые привлекают бизнес, повышают прибыль и ускоряют рост доходов.

Заказать демонстрацию

Узнать больше

Рекомендуемые услуги

Нужна специализированная помощь?

Если вы столкнулись с атакой, нуждаетесь в долгосрочном руководстве по кибербезопасности или что-то среднее, мы вас поддержим.

Экспертное реагирование на инцидент

Восстановите контроль после кибератаки с помощью точной поддержки реагирования на инциденты. Наша команда немедленно приступает к расследованию, чтобы выявить, изолировать и разрешить инциденты.

Узнать больше

Виртуальный CISO

(vCISO)

Получите доступ по запросу к проверенным лидерам в области кибербезопасности, которые могут предложить стратегическое консультирование, разработку политик, управление рисками и многое другое.

Узнать больше

Обучение симуляции фишинга

Измеряйте, тестируйте и повышайте осведомленность сотрудников с помощью безопасных, контролируемых имитаций фишинга, адаптированных к вашим потребностям.

Узнать больше

Планирование реагирования на инциденты

Сократите риски, затраты и время восстановления с помощью упреждающего планирования и рекомендаций по укреплению защиты вашей компании.

Узнать больше

Награды и признание

Признан отраслевыми властями.

Эксперты мирового класса по кибербезопасности

От людей, которые помогли сформировать национальные стратегии кибербезопасности.

Наша миссия — произвести революцию в индустрии кибербезопасности, предлагая передовые решения и услуги предприятиям любого размера. С нашими сложными, но простыми в использовании и управлении решениями каждый владелец бизнеса может получить ожидаемую кибербезопасность без помощи рук и полноценный сон по ночам, которого они заслуживают.

Познакомьтесь с командой

Новости и информация

Ознакомьтесь с последними статьями, новостями и информацией об угрозах.

Начать

Усильте свою кибербезопасность уже сегодня.

Давайте поговорим

Будущее технологии ферроэлектрических полевых транзисторов

«>

Ма, Т. и Хан, Дж.-П. Почему энергонезависимая ферроэлектрическая память полевого транзистора до сих пор неуловима? IEEE Электронное письмо об устройстве. 23 , 386–388 (2002).

Артикул Google Scholar

Миколайк Т., Шредер У. и Шлезазек С. Прошлое, настоящее и будущее ферроэлектрических воспоминаний. IEEE Trans. Электронные устройства 67 , 1434–1443 (2020).

Артикул Google Scholar

Sugibuchi, K., Kurogi, Y. & Endo, N. Сегнетоэлектрическое запоминающее устройство с полевым эффектом, использующее Bi ₄ Ti ₃ O ₁₂ пленка. J. Appl. физ. 46 , 2877–2881 (1975). В этой работе был продемонстрирован один из первых сегнетоэлектрических полевых транзисторов, в котором использовался сегнетоэлектрик на основе оксида перовскита.

Артикул Google Scholar

«>

Scott, J. F. Ferroelectric Memories Vol. 3 (Спрингер, 2000).

Бёске, Т. и др. Фазовые переходы в сегнетоэлектрическом оксиде гафния, легированном кремнием. Заяв. физ. лат. 99 , 112904 (2011).

Артикул Google Scholar

Бёске, Т., Мюллер, Дж., Бройхаус, Д., Шредер, У. и Беттгер, У. Сегнетоэлектричество в оксиде гафния: КМОП-совместимые ферроэлектрические полевые транзисторы. В 2011 Междунар. Встреча электронных устройств 24.5.1–24.5.4 (IEEE, 2011). В этой работе продемонстрирован сегнетоэлектрический полевой транзистор с сегнетоэлектриком на основе оксида гафния 9.0096 .

Салахуддин С., Ни К. и Датта С. Эпоха гипермасштабирования в электронике. Нац. Электрон. 1 , 442–450 (2018).

Артикул Google Scholar

«>

Али, М. М. С. и др. Энергоэффективные вычисления с большими объемами данных: N3XT 1000x. Компьютер 48 , 24–33 (2015).

Google Scholar

Кешаварци, А. и ван ден Хук, В. Интеллект Edge — на сложном пути к триллиону интеллектуальных подключенных IoT-устройств. IEEE Des. Тест 36 , 41–64 (2019).

Артикул Google Scholar

Вонг, Дж. К. и Салахуддин, С. Транзисторы с отрицательной емкостью. Проц. IEEE 107 , 49–62 (2018).

Артикул Google Scholar

Дистельхорст М. и Дрождин К. Стохастический резонанс и переключение доменов. Сегнетоэлектрики 291 , 217–224 (2003).

Артикул Google Scholar

Херон Дж. и др. Детерминированное переключение ферромагнетизма при комнатной температуре с помощью электрического поля. Природа 516 , 370–373 (2014).

Артикул Google Scholar

Si, M. et al. Сегнетоэлектрический полупроводниковый полевой транзистор. Нац. Электрон. 2 , 580–586 (2019).

Артикул Google Scholar

Иевлев А. и др. Перемежаемость, квазипериодичность и хаос в переключении сегнетоэлектрических доменов, индуцированном зондом. Нац. физ. 10 , 59–66 (2014).

Артикул Google Scholar

Müller, K. A. & Burkard, H. SrTiO ₃ : собственный квантовый параэлектрик при температуре ниже 4 K. Phys. B 19 , 3593 (1979).

Артикул Google Scholar

«>

Джерри, М. и др. Аналоговый синапс сегнетоэлектрических полевых транзисторов для ускорения обучения глубоких нейронных сетей. В 2017 IEEE Int. Встреча электронных устройств (IEDM) , 6.2.1–6.1.4 (IEEE, 2017). В этой работе продемонстрирована многоуровневая (5-разрядная) весовая ячейка/аналоговый синапс на основе сегнетоэлектрического полевого транзистора для приложений-ускорителей глубоких нейронных сетей с модуляцией проводимости ×4 и программными импульсами ~75 нс .

Сео, М. и др. Первая демонстрация совместимого с логическим процессом синапса сегнетоэлектрических плавников без контактов для нейроморфных приложений. IEEE Электронное письмо об устройстве. 39 , 1445–1448 (2018).

Артикул Google Scholar

Chung, W., Si, M. & Peide, D.Y. Первая демонстрация Ge ферроэлектрического полевого транзистора с нанопроводом в качестве синаптического устройства для онлайн-обучения в нейронной сети с большим числом состояний проводимости и г _макс. / г _мин. . В 2018 IEEE International Electron Devices Meeting (IEDM) , 15.2.1–15.2.4 (IEEE, 2018).

Ни, К. и др. Многоразрядный весовой датчик FeMFET, совместимый с логикой SoC, для нейроморфных приложений. В 2018 IEEE Int. Встреча электронных устройств (IEDM) 13.2.1–13.2.4 (IEEE, 2018).

Сун, X., Ван, П., Ни, К., Датта, С. и Ю, С. Использование гибридной точности для обучения и логического вывода: Аналоговая синаптическая ячейка веса на основе 2T-1FeFET. В 2018 IEEE Междунар. Встреча электронных устройств (IEDM) 3.1.1–3.1.4 (IEEE, 2018).

Li, X. et al. Включение энергосберегающих энергонезависимых вычислений с полевым транзистором с отрицательной емкостью. IEEE Trans. Электронные устройства 64 , 3452–3458 (2017).

Артикул Google Scholar

«>

Wang, Z. et al. Экспериментальная демонстрация сегнетоэлектрических импульсных нейронов для неконтролируемой кластеризации. В 2018 IEEE Междунар. Встреча электронных устройств (IEDM) 13.3.1–13.3.4 (IEEE, 2018). В этой работе экспериментально продемонстрирована концепция генераторов на основе ферроэлектрических полевых транзисторов и импульсных нейронов .

Fang, Y. et al. Нейромиметическая динамика спайкового нейрона на основе сегнетоэлектрического полевого транзистора. IEEE Электронное письмо об устройстве. 40 , 1213–1216 (2019).

Артикул Google Scholar

Ван, З., Хандельвал, С. и Хан, А. И. Сегнетоэлектрические генераторы и их связанные сети. IEEE Электронное письмо об устройстве. 38 , 1614–1617 (2017).

Артикул Google Scholar

«>

Fang, Y. et al. Решатель оптимизации роя, основанный на нейронных сетях с сегнетоэлектрическими шипами. Перед. Неврологи. 13 , 855 (2019).

Артикул Google Scholar

О, С., Хван, Х. и Ю, И. Сегнетоэлектрические материалы для нейроморфных вычислений. АПЛ Матер. 7 , 091109 (2019).

Артикул Google Scholar

Гокмен Т. и Власов Ю. Ускорение обучения глубокой нейронной сети с помощью резистивных кросс-точечных устройств: вопросы проектирования. Перед. Неврологи. 10 , 333 (2016).

Артикул Google Scholar

Ни, К. и др. Сегнетоэлектрическая троичная память с адресацией по содержанию для однократного обучения. Нац. Электрон. 2 , 521–529 (2019).

Артикул Google Scholar

«>

Tan, A.J. et al. Экспериментальная демонстрация сегнетоэлектрической ячейки памяти с адресацией содержимого на основе HfO ₂ . IEEE Electron Device Lett . (2019).

Wang, Y. et al. Энергонезависимый процессор с временем пробуждения 3 мкс на основе ферроэлектрических триггеров. В 2012 Проц. ESSCIRC 149–152 (IEEE, 2012).

Мулаосманович, Х., Миколайк, Т. и Шлезазек, С. Накопление инверсии поляризации в наноразмерных сегнетоэлектрических транзисторах. Приложение ACS Матер. Интерфейсы 10 , 23997–24002 (2018 г.). В этой работе продемонстрированы нетривиальные эффекты, связанные с переключением сегнетоэлектрической поляризации в масштабированных поперечных размерах, а именно накопление метапластичности/поляризации, однодоменное переключение и вероятностное переключение в короткоканальных сегнетоэлектрических полевых транзисторах .

Артикул Google Scholar

«>

Ни, К. и др. Вычислительный примитив в памяти для объединения данных датчиков в технологии 28 нм HKMG FeFET. В 2018 IEEE International Electronic Devices Meeting (IEDM) , 16.1.1–16.1.4 (IEEE, 2018).

Мулаосманович, Х., Миколайк, Т. и Шлезазек, С. Генерация случайных чисел на основе ферроэлектрического переключения. IEEE Электронное письмо об устройстве. 39 , 135–138 (2017).

Артикул Google Scholar

Луо, Дж. и др. Безконденсаторный стохастический нейрон FeFET с утечкой как возбуждающих, так и тормозных соединений для SNN с уменьшенной стоимостью оборудования. В 2019 IEEE Int. Встреча электронных устройств (IEDM) 6–4 (IEEE, 2019).

Флоран, К. и др. Вертикальный сегнетоэлектрический HfO ₂ FET на основе архитектуры 3-D NAND: к плотной маломощной памяти. В 2018 IEEE Междунар. Встреча электронных устройств (IEDM) 2.5.1–2.5.4 (IEEE, 2018).

Тирумала, С. К. и Гупта, С. К. Реконфигурируемый ферроэлектрический транзистор — часть I: конструкция устройства и работа. IEEE Trans. Электронные устройства 66 , 2771–2779 (2019).

Артикул Google Scholar

Тасним, Н. и Хан, А. И. О возможности динамической настройки и схлопывания окна сегнетоэлектрического гистерезиса/памяти в асимметричном устройстве DG MOS: путь к реконфигурируемому устройству с логической памятью. В 2018 г. 76-я конференция по исследованию устройств (DRC) 1–2 (IEEE, 2018 г.).

Wang, Z. et al. Криогенная характеристика сегнетоэлектрического полевого транзистора. Заяв. физ. лат. 116 , 042902 (2020).

Артикул Google Scholar

«>

Чен К.-Ю., Цай Ю.-С. и Ву, Ю.-Х. Влияние ионизирующего излучения на характеристики памяти сегнетоэлектрических полевых транзисторов на основе HfO ₂ . Электронное устройство IEEE Lett. 40 , 1370–1373 (2019).

Артикул Google Scholar

Шум, Д. и др. Демонстрация функциональности самовыравнивающейся ячейки NVM с раздельным затвором 1,1 В высокой плотности, встроенной в LP 40-нм CMOS для автомобильных приложений и приложений для смарт-карт. В 2015 IEEE Int. Семинар по памяти (IMW) https://doi.org/10.1109/IMW.2015.7150288 (IEEE, 2015).

Канда, А. и др. 24-мегабайтная встроенная флэш-система на основе 28-нм SG-MONOS с операциями чтения на частоте 240 МГц и надежным обновлением программного обеспечения по беспроводной сети для автомобильных приложений. IEEE Solid-State Circ. лат. 2 , 273–276 (2019).

Артикул Google Scholar

«>

Цуда, С. и др. Первая демонстрация MONOS с раздельным затвором FinFET для высокоскоростной и высоконадежной встроенной флэш-памяти в узлах 16/14 нм и выше. В 2016 IEEE Int. Встреча электронных устройств (IEDM) , 11.1.1–11.1.4 (IEEE, 2016).

Wei, L. et al. 7 МБ STT-MRAM по технологии 22FFL FinFET с временем считывания 4 нс при 0,9.V с использованием схемы записи-проверки-записи и метода обнаружения смещения-отмены. В 2019 IEEE Int. Конференция по твердотельным схемам (ISSCC) , 214–216 (IEEE, 2019).

Lee, K. et al. Встроенная STT-MRAM высокой плотности 1 Гбит по технологии 28 нм FDSOI. В 2019 IEEE Int. Встреча электронных устройств (IEDM) 2.2.1–2.2.4 (IEEE, 2019).

Джейн, П. и др. Встроенная энергонезависимая макрокоманда ReRAM объемом 3,6 Мб, 10,1 Мб/мм2, выполненная по технологии FinFET 22 нм, с адаптивными схемами формирования/установки/сброса, дающими выходное напряжение до 0,5 В со временем считывания 5 нс при 0,7 В. В 2019 IEEE Междунар. Конференция по твердотельным схемам (ISSCC) 212–214 (IEEE, 2019).

Ву, Дж. и др. 40-нанометровая технология памяти с низким энергопотреблением, совместимая с фазовым переходом. В 2018 IEEE Int. Встреча электронных устройств (IEDM) 27–6 (IEEE, 2018).

Дюнкель, С. и др. Сверхбыстрая встраиваемая технология NVM со сверхнизким энергопотреблением на основе FEFET для 22-нм FDSOI и более поздних версий. В 2017 IEEE Int. Встреча электронных устройств (IEDM) 19–7 (IEEE, 2017). В этой работе продемонстрированы масштабированные сегнетоэлектрические полевые транзисторы на полностью обедненной платформе кремний-на-изоляторе (КНИ) на узле 22 нм .

Trentzsch, M. et al. Встроенная технология NVM со сверхнизким энергопотреблением 28 нм HKMG на основе ферроэлектрических полевых транзисторов. В 2016 IEEE Int. Встреча электронных устройств (IEDM) , 11–5 (IEEE, 2016).

Лю, Х., Си, М., Шреста, П., Чунг, К. и Е, П. Первое прямое измерение субнаносекундного переключения поляризации в сегнетоэлектрическом оксиде гафния-циркония. В 2019 IEEE Междунар. Встреча электронных устройств (IEDM) 15–2 (IEEE, 2019).

Wei, Y. et al. Магнитоионный контроль спиновой поляризации в мультиферроидных туннельных переходах. npj Кол-во Матер. 4 , 1–6 (2019).

Артикул Google Scholar

Cheema, S.S. et al. Повышенное сегнетоэлектричество в ультратонких пленках, выращенных непосредственно на кремнии. Природа 580 , 478–482 (2020). Эта работа продемонстрировала масштабируемость толщины сегнетоэлектриков на основе оксида гафния .

Артикул Google Scholar

Ледерер, М. и др. Локальное кристаллографическое обнаружение фазы и картирование текстуры в сегнетоэлектрических пленках HfO ₂ , легированных Zr, методом пропускания EBSD. Заяв. физ. лат. 115 , 222902 (2019).

Артикул Google Scholar

Гримли, Э. Д., Шенк, Т., Миколайк, Т., Шредер, У. и ЛеБо, Дж. М. Атомная структура доменных и межфазных границ в сегнетоэлектрике HfO ₂ . Доп. Матер. интерф. 5 , 1701258 (2018).

Артикул Google Scholar

Ни, К., Чакраборти, В., Смит, Дж., Грисафе, Б. и Датта, С. Фундаментальное понимание и контроль вариаций от устройства к устройству в крупномасштабных ферроэлектрических полевых транзисторах. В Симпозиум 2019 г. по технологии СБИС , T40–T41 (IEEE, 2019 г.).

Maekawa, K. et al. Воздействие однородно диспергированных нанокластеров al при внедрении монослоя Si в пленку Hf _0,5 Zr _0,5 O ₂ на массив памяти FeFET с жестким пороговым распределением напряжения. В 2019 IEEE Int. Встреча электронных устройств (IEDM) 15–4 (IEEE, 2019).

Мигита С., Морита Ю., Мидзубаяси В. и Ота Х. Получение эпитаксиального HfO 9Пленка 0113 2 (EOT=0,5 нм) на подложке Si методом атомно-слойного осаждения аморфной пленки и быстрой термической кристаллизации (RTC) в резком градиенте температуры. В 2010 Int. Встреча электронных устройств , 11.5.1–11.5.4 (IEEE, 2010).

Чаттерджи, К. и др. Самовыравнивающийся, последний затвор, FDSOI, запоминающее устройство с ферроэлектрическим затвором с 5,5-нм Hf _0,8 Zr _0,2 O ₂ , высокая износостойкость и восстановление после пробоя. IEEE Электронное письмо об устройстве. 38 , 1379–1382 (2017).

Артикул Google Scholar

Чау, Р. Инновации в процессах и упаковке для продолжения действия закона Мура и за его пределами. В 2019 Int. Встреча электронных устройств 1.1 (IEEE, 2019).

Козодаев М.Г. и др. Уменьшение эффекта пробуждения и повышение износостойкости тонких пленок сегнетоэлектриков HfO ₂ -ZrO ₂ за счет осторожного легирования La. J. Appl. физ. 125 , 034101 (2019).

Артикул Google Scholar

Muller, J. et al. Стратегии высокой износостойкости для сегнетоэлектрического полевого транзистора на основе оксида гафния. 16-й симпозиум по технологиям энергонезависимой памяти (NVMTS) https://doi.org/10.1109/NVMTS.2016.7781517 (IEEE, 2016).

Ни, К. и др. Критическая роль прослойки в Hf _0,5 Zr _0,5 O ₂ производительность энергонезависимой памяти на ферроэлектрических полевых транзисторах. IEEE Trans. Электронные устройства 65 , 2461–2469 (2018). В этой работе содержится информация об оптимизации конструкции затворного стека современного ферроэлектрического полевого транзистора для повышения надежности .

Артикул Google Scholar

Юрчук Э. и др. Происхождение ухудшения долговечности новых ферроэлектрических энергонезависимых запоминающих устройств на основе HfO ₂ 1T. В 2014 IEEE Междунар. Симпозиум по физике надежности 2E.5.1–2E.5.5 (IEEE, 2014).

Топрасертпонг, К., Такенака, М. и Такаги, С. Прямое наблюдение за поведением заряда на границе раздела в FeFET с помощью квазистатического разделения CV и методов Холла: выявление работы FeFET. В 2019 IEEE Int. Встреча электронных устройств (IEDM) 23.7.1–23.7.4 (IEEE, 2019). В этой работе продемонстрирован метод расчета количества захваченных носителей на интерфейсах, экранирующих сегнетоэлектрическую поляризацию в сегнетоэлектрическом полевом транзисторе .

Тан, А. и др. Горячие электроны как основной источник деградации полевых транзисторов HZO FeFET размером менее 5 нм. В 2020 Симпозиум по технологии СБИС (IEEE, в печати).

Андо, Т. Предельное масштабирование диэлектриков под затвором с высоким содержанием κ : Высшее κ или очистка межфазного слоя? Материалы 5 , 478–500 (2012).

Артикул Google Scholar

Ченг, К.-Х. & Chin, A. Память типа DRAM с малым током утечки, использующая однотранзисторный ферроэлектрический MOSFET с диэлектриком затвора на основе Hf. IEEE Электронное письмо об устройстве. 35 , 138–140 (2013).

Артикул Google Scholar

Ханна, С. и др. Энергонезависимая логика MCU SoC на основе FRAM, демонстрирующая 100% сохранение цифрового состояния при VDD = 0 В, обеспечивающая нулевую утечку со временем пробуждения < 400 нс для приложений ULP. IEEE J. Solid-State Circ. 49 , 95–106 (2013).

Артикул Google Scholar

Moise, T. et al. Демонстрация 4 Мб сегнетоэлектрической памяти высокой плотности, встроенной в логический процесс 130 нм, 5 лм Cu/FSG. В Digest Int. Встреча электронных устройств 535–538 (IEEE, 2002).

Век сегнетоэлектричества. Нац. Мать . 19 , 129 (2020).

Метереллиоз М. и др. Встроенная память DRAM 2-го поколения с в 4 раза меньшей мощностью самообновления в 22-нм технологии Tri-Gate CMOS. Симпозиум 2014 года по схемам СБИС. Дайджест технических документов https://doi.org/10.1109/VLSIC.2014.6858415 (IEEE, 2014).

Ломбардо, С. и др. Изображение переключения поляризации в атомном масштабе в (анти) сегнетоэлектрическом запоминающем материале: цирконии (ZrO ₂ ).