Экспрессии это: ЭКСПРЕССИЯ | это… Что такое ЭКСПРЕССИЯ?

Страница не найдена

Размер:

AAA

Цвет: C C C

Изображения Вкл. Выкл.

Обычная версия сайта

RUENBY

Гомельский государственный
медицинский университет

• Университет
  • Университет
  • История
  • Руководство
  • Устав и Символика
  • Воспитательная деятельность
  • Организация образовательного процесса
  • Международное сотрудничество
  • Система менеджмента качества
  • Советы
  • Факультеты
  • Кафедры
  • Подразделения
  • Первичная профсоюзная организация работников
  • Издания университета
  • Гордость университета
  • Выпускник-2021
  • Первичная организация «Белорусский союз женщин»
  • Одно окно
  • ГомГМУ в международных рейтингах
  • Структура университета
• Абитуриентам
  • Приёмная комиссия
  • Университетская олимпиада по биологии
  • Целевая подготовка
  • Заключение, расторжение «целевого» договора
  • Льготы для молодых специалистов
  • Архив проходных баллов
  • Карта и маршрут проезда
  • Порядок приёма на 2023 год
  • Специальности
  • Контрольные цифры приёма в 2022 году
  • Стоимость обучения
  • Информация о ходе приёма документов
  • Приём документов и время работы приёмной комиссии
  • Порядок приёма граждан РФ, Кыргызстана, Таджикистана, Казахстана
  • Горячая линия по вопросам вступительной кампании
• Студентам
  • Первокурснику
  • Расписание занятий
  • Расписание экзаменов
  • Информация для студентов
  • Студенческий клуб
  • Спортивный клуб
  • Общежитие
  • Нормативные документы
  • Практика
  • Стоимость обучения
  • Безопасность жизнедеятельности
  • БРСМ
  • Профком студентов
  • Учебный центр практической подготовки и симуляционного обучения
  • Многофункциональная карточка студента
  • Анкетирование студентов
• Выпускникам
  • Интернатура и клиническая ординатура
  • Докторантура
  • Аспирантура
  • Магистратура
  • Распределение
• Врачам и специалистам
  • Профессорский консультативный центр
  • Факультет повышения квалификации и переподготовки
• Иностранным гражданам
  • Факультет иностранных студентов
  • Стоимость обучения
  • Регистрация и визы
  • Полезная информация
  • Правила приёма
  • Информация о возможностях и условиях приема в 2022 году
  • Официальные представители ГомГМУ по набору студентов
  • Страхование иностранных граждан
  • Приём на Подготовительное отделение иностранных граждан
  • Прием иностранных граждан для обучения на английском языке / Training of foreign students in English
  • Повышение квалификации и переподготовка для иностранных граждан
• Научная деятельность
  • Направления научной деятельности
  • Научно-педагогические школы
  • Инновационные технологии в ГомГМУ
  • Научно-исследовательская часть
  • Научно-исследовательская лаборатория
  • Конкурсы, гранты, стипендии
  • Научные мероприятия
  • Работа комитета по этике
  • В помощь исследователю
  • Совет молодых ученых
  • Студенчеcкое научное общество
  • Диссертационный совет
  • Патенты
  • Инструкции на метод
  • «Горизонт Европа»
  • Госпрограмма (ЧАЭС)

• Главная

Анализ экспрессии генных ансамблей поможет в диагностике патологий

Сайт Наука в Сибири 4 августа 2021 г.
Сайт Новости Сибирской Науки 4 августа 2021 г.
Электронное периодическое издание Научная Россия 4 августа 2021 г.
Мультимедийный портал Поиск 4 августа 2021 г.
Сайт Академгородок 5 августа 2021 г.
Газета Наука в Сибири №42 (3303) от 28 октября 2021 г.

Поиск новых биомаркеров патологий человека и прогнозирование клинических исходов для пациентов является сложной задачей, стоящей сегодня перед мировым научным и медицинским сообществом. Международный коллектив, куда вошел сибирский ученый, занялся изучением генного шума у людей, больных свиным гриппом, COVID-19 и сепсисом. Сравнивая данные экспрессии генов у пациентов, исследователи выявили общие нарушения для всех этих заболеваний. На основе полученных данных был разработан альтернативный подход, который можно применить для анализа молекулярных изменений, связанных с инфекционными заболеваниями и сепсисом, как наиболее острой формой их проявления. Новый многообещающий метод — шум ансамбля генов — не только помогает выявить критические пути и предсказать тяжесть заболевания при свином гриппе, COVID-19 и смертность у пациентов с сепсисом, но и поможет в борьбе с будущими пандемиями. Результаты работы опубликованы в журнале Scientific Reports.

“Экспрессия генов описывается двумя параметрами: среднее число копий РНК и шум (отклонение) в числе копий РНК. Практически все исследования по регуляции экспрессии генов фокусируются на определении изменений в среднем числе копий РНК при заболеваниях либо при других условиях эксперимента. Нас же заинтересовали изменения в генном шуме: как независимая величина, отражающая стабильность функционирования биологической системы и как фактор риска развития патологий, — рассказывает ведущий научный сотрудник лаборатории генетики лабораторных животных ФИЦ “Институт цитологии и генетики СО РАН”, научный сотрудник лаборатории молекулярной цитогенетики Института молекулярной и клеточной биологии СО РАН кандидат биологических наук Юрий Михайлович Мошкин. — Действительно, увеличение генного шума неизбежно повлечет за собой рост отклонений в числе копий белка на клетку, а дальше, поскольку многие белки являются ферментами, этот процесс приведет к нежелательным флуктуациям (случайным отклонениям) в концентрации метаболитов и, как результат, к разбалансировке всех функций организма. Подобное состояние возникает при старении организма (ранее в одной из наших работ мы показали, что с возрастом генный шум возрастает для большинства генов), также у людей в годах увеличиваются общие риски развития патологий: рак, деменция, метаболические нарушения и так далее). Поэтому шум генов хорошо отражает старение организма и неизбежно связанные с ним патологические процессы на уровне разбалансировки экспрессии генов, а не на уровне изменений в средней экспрессии отдельных генов”.

На практике генный шум можно определить, только исследуя популяцию людей или животных и, например, после проведения статистического сравнения по каждому гену для выборки пациентов, больных каким-либо заболеванием (COVID-19, рак и так далее), по отношению к здоровым. Но как определить генный шум для конкретного человека? Теоретически это возможно сделать путем многократных измерений экспрессии генов в течение некоторого времени, чтобы понять, насколько устойчива экспрессия генов у индивидуума в конкретный промежуток времени. Однако для медицинской диагностики это неприемлемо, поскольку в таком случае человек должен будет сдавать анализы в течение месяца практически каждый день. Однако так как шум является статистическим признаком, необходима какая-то выборка. 

“Здесь возник первый Eureka moment (момент прозрения) — мы можем определить генный шум не для отдельных генов, а для их наборов, объединенных общими свойствами по какому-либо признаку, что мы и назвали шумом генных ансамблей. Примечательно, что любые изменения в шуме генных ансамблей будут отражать изменения как в самом генном шуме, так и нарушения в стехиометрии (пропорциях) в экспрессии генов ансамбля. И первое, и второе будет свидетельствовать о разбалансировке экспрессии ансамбля, а значит, и о нарушениях в биологических функциях, за которые он отвечает. Таким образом, концепция шума генных ансамблей позволяет выявлять и исследовать нарушения не на уровне индивидуальных генов, как это обычно делается, а целиком для биологических функций, кодируемых ансамблями генов”, — отмечает Юрий Мошкин.

Мировая пандемия COVID-19 предоставила ученым возможность проверить разрабатываемый подход на практике, хотя изначально у исследователей не было доступных данных по экспрессии генов в крови у пациентов, инфицированных коронавирусом. “Тут возник второй Eureka moment. Я задался вопросом: а почему вообще вирус приводит к смерти? На самом деле на репликацию вирусных частиц уходит всего лишь 2 % клеточной энергии (АТФ), то есть для клетки, в наиболее общем смысле и отбросив специфические варианты взаимодействий вируса с клеткой, наличие вируса не представляет какой-то серьезной проблемы. Так что же приводит к гибели? В большинстве случаев риск смерти обуславливается острой иммунной реакцией организма хозяина на патоген, то есть сепсисом. Он возникает как при вирусных, так и при бактериальных инфекциях, и ключевым моментом при его развитии является резкое увеличение энергозатрат, обусловленное ростом воспалительного процесса.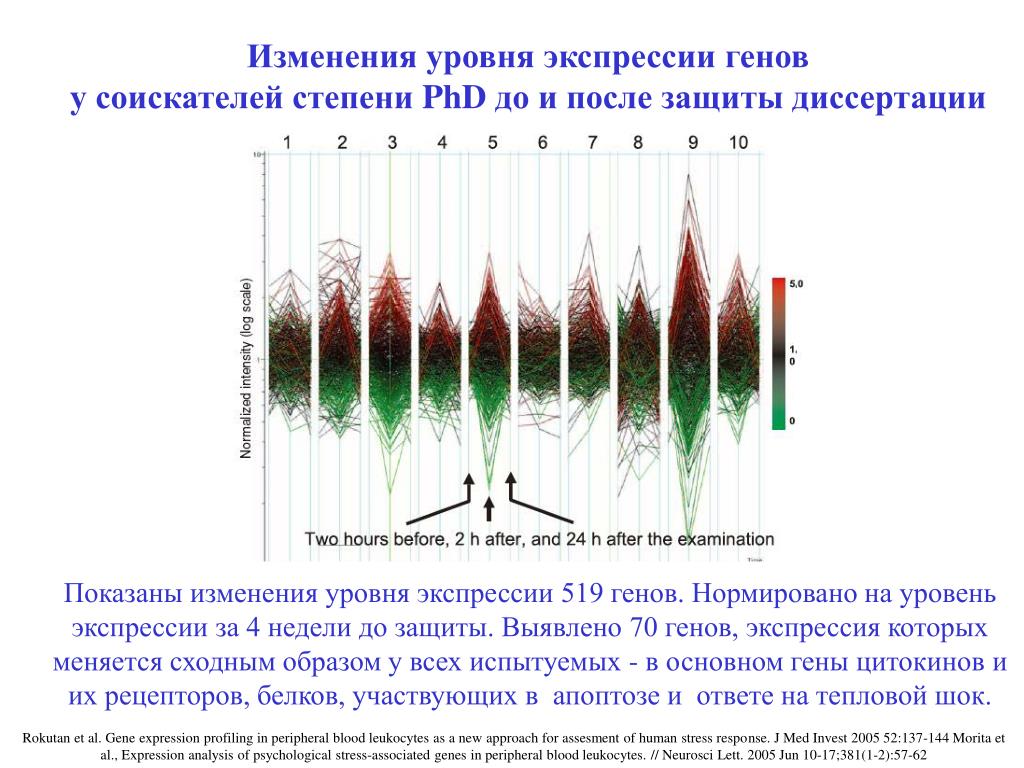 При сепсисе затраты клеточной энергии увеличиваются на 20-50%, а при септическом шоке еще больше, в итоге организм убивает сам себя”, — добавляет ученый.

К сожалению, современная медицина не умеет эффективно лечить сепсис. Например, в Нидерландах и Великобритании ежегодный процент смертности от сепсиса у пациентов реанимационных отделений составляет около 20-30%, без влияния коронавируса. Большая часть смертей от COVID-19 вызвана пневмонией, которая развивается из-за воздействия сепсиса. Поскольку создание вакцин и поиск специфических противовирусных препаратов требуют времени и определенного везения, авторы исследования предположили, что первой линией обороны от новых пандемий (в том числе и коронавируса) может стать эффективное лечение сепсиса. Тем самым человечество может быть подготовлено как к пандемии COVID-19, так и к любой другой, новой.

Держа эти рассуждения в уме, ученые занялись исследованием шума генных ансамблей у пациентов реанимационных отделений Нидерландов и Великобритании с пневмонией и сепсисом, вызванными бактериальной инфекцией. Для сравнения в работе использовались данные по РНК-секвенированию крови больных свиным гриппом h2N1 на ранней и поздней стадиях заражения. В итоге ученые обнаружили, что генный шум существенно возрастает у больных сепсисом и у больных свиным гриппом, тем самым подтвердили тезис об общей дестабилизации экспрессии генов. Кроме того, изменения в шуме генных ансамблей оказались достаточно схожими как у больных сепсисом, так и у больных свиным гриппом, поэтому поиск путей лечения сепсиса действительно будет являться первичным инструментом для борьбы с любыми пандемиями на ранней стадии, до создания вакцин и антивирусных препаратов.

“Обнаруженные нами изменения в шуме генных ансамблей дают основания предположить, что при сепсисе дестабилизируются функции митохондрий, пероксисом и других биологических путей. Следовательно, в данном случае анализ шума генных ансамблей позволяет обнаруживать новые фармакологические мишени (которые обычно ускользают при простом анализе изменений в средней экспрессии генов). Исходя из этого, мы предложили, что можно использовать ряд известных и относительно безопасных фармакологических препаратов для стабилизации данных функций и, возможно, для лечения сепсиса. Кроме того, на этапе публикации статьи стали доступны данные по экспрессии генов в крови и для пациентов с COVID-19. И, к нашему счастью, оказалось, что в данном случае происходят достаточно схожие изменения в шуме генных ансамблей по сравнению с больными сепсисом и свиным гриппом. А значит, ключом к раннему реагированию на пандемии должен стать поиск эффективных подходов лечения сепсиса как саморазрушающей и неспецифической иммунной реакции организма на практически любой патоген”, — говорит Юрий Мошкин.

Примечательно, что недавние исследования независимо подтверждают выводы ученых о том, что при развитии воспалительного процесса (сепсиса), как часть неспецифической иммунной реакции, нарушается функция митохондрий, что приводит к эффекту Варбурга. Он связан в основном с раковыми клетками, в которых нарушена функция митохондрий и клеточный метаболизм перестраивается на активный гликолиз. В современной онкологии уже отрабатывается ряд подходов к лечению рака путем восстановления функции митохондрий и подавления гликолиза, то есть эффекта Варбурга. Подобные явления наблюдаются и в иммунных клетках при развитии острой воспалительной реакции. Таким образом, для лечения сепсиса, гриппа, коронавируса и так далее можно заимствовать подходы из онкологии. Кроме того, другим немаловажным маркером сепсиса является окислительный стресс — это процесс, при котором происходит накопление реактивных форм кислорода (пероксид водорода, супероксид и другие), которые и повреждают клетки организма. Здесь на сцену выходит пероксисома — клеточная органелла, участвующая в удалении активных форм кислорода. Иными словами, увеличение шума в генном ансамбле, кодирующем компоненты пероксисом, дает молекулярное объяснение окислительному стрессу при сепсисе и указывает на то, что препараты, способствующие биогенезу (формированию) пероксисом, также могут использоваться для лечения сепсиса, гриппа, коронавируса.

Благодаря исследованию ученых шум генных ансамблей может использоваться для диагностики различных заболеваний, включая прогнозирование вероятности смерти при сепсисе, предсказания, насколько остро будет проходить коронавирусная инфекция, эффективности лечения рака, посттравматического стрессового расстройства. В случае сепсиса авторы работы сделали также ряд интересных открытий: “Мы установили, что вероятность смерти слабо зависит от возраста, шум генных ансамблей оказался достаточно эффективным для подобной диагностики. Точность наших диагностических моделей для предсказания смертности при сепсисе превзошла диагностическую модель, разработанную крупным голландским консорциумом MARS (Molecular Diagnosis and Risk Stratification of Sepsis), которая основывалась на более традиционном подходе. Таким образом, шум генных ансамблей может широко использоваться для диагностики различных заболеваний и, что не менее важно, для поиска альтернативных мишеней и разработки новых способов лечения, в частности путем перепозиционирования известных фармакологических препаратов”, — рассказывает Юрий Мошкин.

Андрей Фурцев

PDF-файл статьи

Источник: 

https://www.sbras.info/articles/nauka-dlya-obschestva/analiz-ekspressii-…

Источник: 

http://www.sib-science.info/ru/news/analiz-ekspressii-gennykh-04082021

Источник: 

https://scientificrussia.ru/articles/analiz-ekspressii-gennyh-ansamblej-…

Источник: 

https://poisknews.ru/themes/genetics/analiz-ekspressii-gennyh-ansamblej-…

Источник: 

https://academcity.org/content/gennyy-shum

Что такое выражение в математике? Значение, определение, типы, примеры

Определение выражения в математике?

Выражение в математике — это предложение, содержащее не менее двух чисел или переменных и не менее одной математической операции. Эта математическая операция может быть сложением, вычитанием, умножением или делением. Структура выражения:

Выражение (число/переменная, математический оператор, число/переменная)

Примеры выражений:

94 + 9$ $–$ $4 ÷ 15$

Во всех приведенных выражениях между двумя числами используется математический оператор.

Не примеры выражений:

Пример 1: A

Пример 2: 4 $

Пример 3: $ 7,89 $

Части выражения в математике

из следующих:

a) Константа: it — фиксированное числовое значение.

Пример: $7, 45, 4\frac{1}{3}, −18, \sqrt{5}, 7 + \sqrt{11}$ 

b) Переменные: они не принимают никаких фиксированных значений . Значения назначаются в соответствии с требованием.

Пример: a, p, z

c) Термины: могут быть константами, переменными или константами, умноженными на переменную/(и). Каждый термин в выражении отделяется знаком ‘+’ или ‘-‘

Пример. В $5\text{a} + 2\text{b}$ $-$ $7$ термины: $5\text{a }, 2\text{b}$ и $7$.

d) Операторы: Четыре операции сложения (+), вычитания (−), умножения (×), деления (÷) используются для объединения членов выражения и называются операторами.

Типы выражений в математике

Числовое выражение

Числовое выражение в математике состоит из чисел и арифметических операторов. Он не содержит неизвестных переменных, символов равенства или неравенства.

Примеры: 92$ $\text{q}$

Типы алгебраических выражений

Алгебраические выражения классифицируются на основе количества членов в выражении. Различные типы алгебраических выражений:

1. Мономиальные выражения содержат только один термин. Например. $4\текст{х}$
2. Биномиальные выражения содержат два непохожих члена. Например. $2\текст{ху} +х$
3. Трехчленные выражения содержат только три непохожих члена. Например. $3\текст{т}2$ $-$ $4\текст{т} + 9$
4. Полиномиальные выражения содержат два или более члена. Сюда входят также двучлены и трехчлены, а также все другие выражения с четырьмя или более терминами. Например. $2\текст{х} + 3\текст{у} + 5\текст{г}; 4\text{t} + 5$ $−$ $4\text{u} + \text{z}$

Выражение против уравнения

Математическое выражение отличается от математического уравнения.

Разница между выражениями и уравнениями заключается в том, что выражение означает комбинацию чисел, переменных и символов операций, тогда как уравнение всегда будет использовать оператор равенства (=) между двумя математическими выражениями. Также обе стороны знака «равно» имеют одинаковое значение.

For example,

Expression	Equation
$22 + 5$	$22 + 5 = 29$ $–$ $2$
$9 \times 5$	$9 \times 5 = 45$
$50 \дел 10$	$45 \дел 9 = 50 \дел 10$
$15 + 7$ $–$ $6$	$15 + 7$ $–$ $6 = 16$
$25 + 7$	$25 + 7 = 64 \дел 2$
$20 \times 5 $ 15

Где используются выражения?

Выражения помогают нам в решении текстовых задач. Математические выражения формируются с использованием слов задачи.

В качестве примера рассмотрим следующую задачу:

Давайте рассмотрим задачу со словами и научимся писать выражения по математике

1. Том должен заполнить коробку апельсинами и яблоками. Количество яблок должно быть на 5 больше, чем апельсинов. Том срывает каждый раз по 3 апельсина и повторяет это 5 раз. Подсчитайте общее количество апельсинов и яблок.

Чтобы решить эту задачу, сформулируйте математические выражения следующим образом:

Количество апельсинов = 3 доллара США умножить на 5 долларов

Количество апельсинов = 15 долларов США

Количество яблок = количество апельсинов $ + 5$

Количество яблок = $15 + 5$

Количество яблок = $20$

Общее количество фруктов = количество апельсинов + количество яблок

Третье математическое выражение будет таким:

Общее количество фруктов = 15 долларов США + 20 долларов 

2. Класс школьников собирается в путешествие. Каждый студент должен заплатить индивидуальную плату в размере $\$$8 и групповую плату в размере $\$$30. Напишите алгебраическое выражение для полной стоимости поездки. Найдите общую стоимость поездки, если в поездке едет 56 студентов.

Пусть n представляет количество студентов.

Алгебраическое выражение будет:

$\$$8 n + $\$$30

Чтобы найти полную стоимость поездки, когда n = 56.

$\$$8 n 90 \ $$ 30

$ \ $$ 8 (56) + $ \ $$ 30 (замена N с 56)

$ \ $$ 448 + $ \ $$ 30

$ \ $ 478

Pedmas

Pedmas является аббревиатурой, где P означает круглые скобки, E для степени, D для деления, M для умножения, A для сложения и S для вычитания. 92)$

$= (5 × 4 − 7) + × (19 − 16)$

$= (20 − 7) + 3$

$= 13 + 3$

$= 16$

Применение:

Знание применения математических операций над числами является первым шагом к формированию у детей базовых арифметических рассуждений и логики. Формулирование математических выражений с использованием соответствующего навыка закладывает прочную основу для изучения алгебры и преобразования реальных задач в подходящие математические модели.

Решенные примеры выражения:

Пример 1 : Укажите, является ли каждый из них выражением или уравнением.

(а) $4 + 8$	(б) $4 + 12 = 16$	(в) $5 х 35$
$ – 4 + $2$	(e) $8 \times 4 \div 2 = 16$	(f) $72+94$

Solution:

$

Expression	Equation
$4 + 8$	4$ + 12 = 16
$5 \times 35$	$8 \times 4 \div 2 = 16$
$16 \div 4 + 9$ $–$ $2$
$72+94$

Пример 2 : Напишите каждое слово фразы как выражение.

1. Сумма 10$ и 14$
2. 3 больше числа $7$
3. Дважды по 11$, умножить на 1$
4. 19 меньше, чем произведение 15$ и 4$
5. Частное $33$ и $3$

Решение:

1. 10$ + 14$
2. 7$ + 3$
3. $2 \умножить на 11 + 1$
4. $15 \× 4$ $–$ $19$
5. $33\дел 3$

Пример 3 : Классифицируйте следующее выражение как арифметическое или алгебраическое.

1. $4\text{a}$ $–$ $7\text{b}$
2. 23$ + 42$ $–$ 6$
3. $715$ $-$ $911$ 
4. $2$ $-$ $5\text{x}9\text{y}$
5. $22$ $–$ $5 + 8$
6. $7\текст{у} + 19\text{x}$ $–$ $4\text{z}$

Solution:

Arithmetic	Algebraic
$23 + 42$ $–$ $6$	$4\text{a}$ $–$ $7\text{b}$
$22$ $–$ $5 + 8$	$7\text{y} + 19\text{x}$ $–$ $4\text{z}$
$715$ $-$ $911$	$2 $ $-$ $5x9y$

Пример 4. Запишите члены данного выражения $4uv + 7u − 9z + 6z$ .

Решение:

$4\text{uv}, 7\text{u}$, $−$ $9\text{z}$ и $6\text{z}$ являются членами данного выражения.

Пример 5: В книге 250$ страниц. Рону осталось прочитать 62$ страниц. Напишите выражение, чтобы найти количество прочитанных страниц.

Решение:

$250$ $–$ $62$

Пример 6: $X$, $Y$ и $Z$ имеют несколько резинок для волос. У $Y$ больше резинок для волос на $20$, чем у $X$. $Z$ говорит, что у нее на пять ободков больше, чем у $X$ и $Y$ вместе взятых. Выразить это в виде выражения?

Решение : Пусть количество резинок для волос с $X$ равно $ = \text{x}$.

 Тогда у $Y$ есть $(\text{x}+20)$ ободков.

$Z$ имеет $\text{x} + (\text{x}+20) + 5=2\text{x}+25$ повязки на голову.

Следовательно, у $Z$ есть $(2\text{x}+25)$ ободков.

Практическая задача

1

Какое из этих выражений?

$6 + 8 = 14$

$0$ $–$ $16 =$ $–$ $16$

$\frac{4}{7}+ \frac{4}{7}$ $-$ $\frac {1}{7}$

5

$5\text{x}$ $-$ $7\text{y}=15$

Правильный ответ: $\frac{4}{7}+ \frac{4}{7}$ $-$ $\ frac{1}{7}$
Так как в нем есть числа (дробь) и математические операторы, другими вариантами являются уравнения, так как он имеет оператор равенства $(=)$ между двумя математическими выражениями.

2

Какое из этих выражений является алгебраическим?

$3\text{a}+7\text{b}$ $-$ $6\text{c}=5\text{x}$

$9$ $-$ $5\text{w}$

$ \frac{1}{2}+\frac{3}{4}$

$44 + 55$

Правильный ответ: $9$ $-$ $5\text{w}$
Содержит переменные, числа и математический оператор. Вариант (a) представляет собой уравнение, вариант (c) и вариант (d) представляют собой арифметические выражения, а не алгебраические, поскольку в них не участвуют переменные.

3

Будет ли называться любое алгебраическое выражение, содержащее только три члена?

Одночлен

Бином

Трехчлен

Ни один из этих

Правильный ответ: Трехчлен
Если в выражении три члена, мы называем это трехчленным выражением.

4

Если значение термина в выражении не меняется, как оно называется?

Переменная

Константа

Член

Коэффициент

Правильный ответ: Константа
Член, который не меняет своего значения, называется константой.

5

Напишите выражение для этой словесной фразы: ‘Трижды число 14, уменьшенное на 10

$3\times14$

$10$ $−$ $3 \times 14$

$3 \times 10$ $ −$ $14$

$3 \times 14$ $−$ $10$

Правильный ответ: $3 \times 14$ $−$ $10$
Трижды число 14 равно $3 \times 14$.
Уменьшение на 10 равно $3 \times 14$ $−$ $10$

6

Томас зарабатывает $\$9,75 в час как библиотекарь. Какое из этих выражений показывает, сколько он зарабатывает за 40 часов?

$\$$$(9,75 + 40)$

$\$$$(40 $–$ 9,75)$

$\$$$(9,75 х 40)$

$\$$$( 9.75 $–$ 40)$

Правильный ответ: $\$$$(9.75 х 40)$
Сумма, заработанная за час $=$ $\$$9,75
Сумма, заработанная за 40 часов $=$ $\$$$(9,75 х 40)$

Часто задаваемые вопросы

Что такое выражение в математике?

Выражение – это набор чисел или переменных, объединенных с помощью операций $+$,  $–$, $\times$ или $\div$.

Что такое типы выражений?

Арифметическое выражение, содержащее только числа и математические операторы, и алгебраическое выражение, содержащее переменные, числа и математические операторы.

 Можем ли мы решить математическое выражение?

Нет, мы не можем решить математическое выражение, так как оно не имеет знака «равно» $(=)$, но мы можем упростить выражения.

В чем разница между арифметическим выражением и алгебраическим выражением?

Математические выражения содержат только числа и операторы, в то время как алгебраические выражения содержат как числа, так и переменные в терминах, разделенных промежуточными операторами.

Выражение – определение, значение и синонимы

Выражение вашего лица — грустное, счастливое, скучающее, веселое — это выражение . Ваше выражение позволяет людям понять, что вы чувствуете, если только вы не умеете скрывать свои эмоции.

Выражение происходит от латинского слова, означающего «выдавливать», и его до сих пор можно использовать таким образом. Если вы готовите свежевыжатый апельсиновый сок, соковыжималка помогает отжимать сок из фруктов. Если кто-то использует искусство, чтобы выразить свои чувства к миру, это художественное самовыражение: что-то, что чувствуется внутри, выявляется и делится. Мы также используем выражение для способов что-то сказать, например выражение «что случилось?»

Определения выражения

1. существительное

   сообщение (в устной или письменной форме) ваших убеждений или мнений

   « выражений доброй воли»

   «он помог мне найти устные выражение для моих идей»

   синонимы: словесное выражение, словесность

2. существительное

   выражение без слов

   «слезы выражение горя»

   синонимы: проявление, отражение, отражение

3. существительное

   стиль самовыражения

   «его манера выражение показало, как сильно он заботится»

   синонимы: формулировка

4. существительное

   слово или фраза, которые определенные люди используют в определенных ситуациях

   «простите выражение ”

   синонимы: словосочетание, высказывание

5. существительное

   чувства, выраженные на лице человека

   «грустный выражение ”

   синонимы: вид, лицо, выражение лица, взгляд

6. существительное

   группа символов, составляющих математическое утверждение

   синонимы: формула

7. существительное

   группа слов, входящих в состав предложения и рассматриваемых как единое целое

   синонимы: конструкция, грамматическая конструкция

8. существительное

   (генетика) процесс экспрессии гена

9. существительное

   акт вытеснения чего-либо путем сжатия или нажатия

Независимо от того, являетесь ли вы учителем или учеником, Vocabulary.