Формальная логика как теория правильного мышления
Закон непротиворечия действует в отношении всех несовместимое суждений.
Для правильного его понимания необходимо иметь в виду следующее. Утверждая что-либо о каком-либо предмете, нельзя, не противореча себе, отрицать (1) то же самое (2) о том же самом предмете, (3) взятом в то же самое время и (4) в том же самом отношении.
Понятно, что не будет противоречия между суждениями, если в одном из них утверждается принадлежность предмету одного признака, а в другом — отрицается принадлежность этому же предмету другого признака; (1) и если речь идет о разных предметах.
(3) Противоречия
не будет и в том случае,
если, мы что-либо утверждаем и
то же самое отрицаем относительно
одного лица, но рассматриваемого в
разное время. Допустим, что обвиняемый
Н. в начале следствия дал ложные показания,
однако в конце следствия он был вынужден
под тяжестью изобличающих его улик признаться
и дать истинные показания.
(4) Наконец один и тот же предмет нашей мысли может рассматриваться в разных отношениях. Так, о студенте Щукине можно сказать, что он хорошо знает немецкий язык, так как его знания удовлетворяют требованиям» предъявленным к поступающим в институт, однако этих знаний недостаточно для работы в качестве переводчика. В этом случае мы вправе сказать: «Щукин плохо знает немецкий язык». В двух суждениях знание Щукиным немецкого языка рассматривается с точки зрения разных требований, следовательно, эти суждения также не противоречат друг другу.
Закон непротиворечия
выражает одно из коренных свойств логического
мышления –непротиворечивость, последовательность
мышления. Его сознательное использование
помогает обнаруживать и устранять противоречия
в своих и чужих рассуждениях, вырабатывает
критическое отношение ко всякого рода
неточности, непоследовательности в мыслях
и действиях.
Н.Г. Чернышевский подчеркивал, что непоследовательность в мыслях ведет к непоследовательности в поступках. У кого не уяснены принципы во всей логической полноте и последовательности, писал он, у того не только в голове сумбур, но и в делах чепуха.
Умение вскрывать и устранять логические противоречия, нередко встречающиеся в показаниях свидетелей, обвиняемого, потерпевшего, играет важную роль в судебной и следственной практике.
Одно из основных
требований, предъявляемых к версии
в судебном исследовании, состоит в
том, чтобы при анализе совокупности фактических
данных, на основе которых она построена,
эти данные не противоречили друг другу
и выдвинутой версии в целом. Наличие таких
противоречий должно привлечь самое серьезное
внимание следователя. Однако бывают случаи,
когда следователь, выдвинув версию, которую
он считает правдоподобной, не принимает
во внимание факты, противоречащие этой
версии, игнорирует их, продолжает развивать
свою версию вопреки противоречащим фактам.
В процессе судебного разбирательства обвинитель и защитник, истец и ответчик выдвигают противоречащие друг другу положения, отстаивая свои доводы и оспаривая доводы противной стороны.
Поэтому необходимо
тщательно проанализировать все обстоятельства
по Делу, чтобы окончательное решение
суда основывалось на достоверных и непротиворечивых
фактах.
Недопустимы противоречия в судебных актах. К числу обстоятельств, по который приговор Признается несоответствующим фактическим обстоятельствам дела, уголовно-процессуальное право относит существенные противоречия, содержащиеся в выводах суда, изложенных в приговоре.
Закон исключенного третьего. Закон непротиворечия действует по отношению ко всем несовместимым друг с другом суждениям. Он устанавливает, что одно из них необходимо ложно. Вопрос о втором суждении остается открытым: оно может быть истинным, но может быть и ложным.
Закон исключенного
третьего действует только в отношении
противоречащих (контрадикторных) суждений. Он формулируется следующим образом: два противоречащих
суждения не могут быть
одновременно ложными,
одно из них необходимо
истинно: а есть либо b, либо не-b. Истинно либо утверждение
некоторого факта, либо его отрицание.
Он формулируется следующим образом: два противоречащих
суждения не могут быть
одновременно ложными,
одно из них необходимо
истинно: а есть либо b, либо не-b. Истинно либо утверждение
некоторого факта, либо его отрицание.
Противоречащим (контрадикторным) называются суждения, в одном из которых что-либо утверждается (или отрицается) о
 Например: «П. привлечен к административной
ответственности» и «П. не привлечен к
административной ответственности». Одно
из этих суждений необходимо истинно,
другое— необходимо ложно.
Например: «П. привлечен к административной
ответственности» и «П. не привлечен к
административной ответственности». Одно
из этих суждений необходимо истинно,
другое— необходимо ложно. Этот закон
можно записать с помощью
Подобно закону непротиворечия закон исключенного третьего выражает последовательность, непротиворечивость мышления, не допускает противоречий в мыслях, вместе с тем, действуя только в отношении противоречащих суждений, он устанавливает, что два противоречащих суждения не могут быть не только одновременно истинными (на что указывает закон непротиворечия), но также и одновременно ложными: если ложно одно из них, то другое необходимо истинно, третьего не дано.
Конечно, закон
исключенного третьего не может указать, какое именно из данных
суждений истинно. Этот вопрос решается
другими средствами. Значение закона состоит
в том, что он указывает направление в
отыскании истины: возможно только два
решения вопроса, причем одно из них (и
только одно) необходимо истинно.
Значение закона состоит
в том, что он указывает направление в
отыскании истины: возможно только два
решения вопроса, причем одно из них (и
только одно) необходимо истинно.
Закон исключенного третьего требует ясных, определенных ответов, указывая на невозможность отвечать на один и тот же вопрос в одном и том же смысле и «да» и «нет», на невозможность искать нечто среднее между утверждением чего-либо и отрицанием того же
самого.
Важное значение имеет этот закон в юридической практике, где требуется категорическое решение вопроса. Юрист должен решать дело по форме «или — или». Данный факт либо установлен, либо не установлен. Обвиняемый либо виновен, либо не виновен. Jus (право) знает только: «или — или».
Закон
достаточного основания. Наши мысли
о каком-либо факте, явлении, событии могут
быть истинными или ложными. Высказывая
истинную мысль, мы должны обосновать
ее истинность, т.е. доказать ее соответствие
действительности. Так, выдвигая обвинение
против подсудимого, обвинитель должен
привести необходимые доказательства,
обосновать истинность своего утверждения.
В противном случае обвинение будет необоснованным.
Так, выдвигая обвинение
против подсудимого, обвинитель должен
привести необходимые доказательства,
обосновать истинность своего утверждения.
В противном случае обвинение будет необоснованным.
Требование доказанности, обоснованности мысли выражает закон достаточного основания: всякая мысль признается истинной, если они имеет достаточное основание. Если есть b, то есть и его основание а.
Достаточным
основанием мыслей может быть личный
опыт человека. Истинность некоторых суждений
подтверждается путем их непосредственного
сопоставления с фактами действительности.
Так, для человека» явившегося свидетелем
преступления, обоснованием истинности
суждения «Н. совершил преступление» будет
сам факт преступления, очевидцем которого,
он был. Но личный опыт ограничен. Поэтому
человеку в своей деятельности приходится
опираться на опыт других людей, например
на показания Очевидцев того или иного
события. К таким основаниям прибегают
обычно в следственной и судебной практике
при расследовании преступлений.
Благодаря развитию научных знаний человек все шире использует в качестве основания своих мыслей опыт всего человечества, закрепленный в законах и аксиомах науки, в принципах и положениях, существующих в любой области человеческой деятельности.
Истинность законов, аксиом подтверждена практикой человечества и не нуждается поэтому в новом подтверждении. Для подтверждения какого-либо частного случая нет необходимости обосновывать его при помощи личного опыта. Если, например, нам известен закон Архимеда (каждое тело погруженное в жидкость, теряет в своем весе столько сколько весит вытесненная им жидкость), то нет никакого смысла погружать в жидкость какой-либо предмет, чтобы выяснить сколько он теряет в весе. Закон Архимеда будет достаточным основанием для подтверждения любого частного случая.
Благодаря науке,
которая в своих законах и принципах
закрепляет общественно-историческую
практику человечества, мы для обоснования
наших мыслей не прибегаем всякий раз
к их проверке, а обосновываем их логически,
путем выведения из уже установленных
положений.
Таким Образом, достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной мысли.
Если из истинности суждения а следует истинность суждения b, то а будет основанием для b, а b — следствием это основания.
Связь основания
и следствия является отражением
в мышлении объективных, в том
числе причинно-следственных связей,
которые выражаются в том, что одно явление
(причина) порождает другое явление (следствие).
Однако это отражение не является непосредственным.
В некоторых случаях логическое основание
может совпадать с причиной явления (если,
например; мысль о том, что число дорожно-транспортных
происшествий увеличилось, обосновывается
указанием на причину этого явления —
гололед на дорогах). Но чаще всего такого
совпадения нет. Суждение «Недавно был
дождь» можно обосновать суждением «Крыши
домов мокрые»; след протекторов автомобильных
шил — достаточное основание суждения
«В данном месте прошла автомашина».
Обоснованность — важнейшее свойство логического мышления. Во всех случаях, когда мы утверждаем что-либо, убеждаем в чем-либо других, мы должны доказывать наши суждения, приводить достаточные основания, подтверждающие истинность наших мыслей. В этом состоит коренное отличие научного мышления от мышления ненаучного, которое характеризуется бездоказательностью, способностью принимать на веру различные положения и догмы. Это особенно характерно для религиозного мышления, опирающегося не на доказательство, а на веру.
Закон достаточного
основания не совместим с различными
предрассудками и суевериями. Например,
существуют нелепые приметы: разбить зеркало—к
несчастью, рассыпать соль—к ссоре и т.д.,
хотя между разбитым зеркалом и несчастьем,
рассыпанной солью и ссорой нет причинной
связи. Логика —враг суеверий и предрассудков,
она требует обоснованности суждений
и не совместима поэтому с утверждениями,
которые строятся по схеме «после этого
– значит, по причине этого». Эта логическая
ошибка возникает в случаях, когда причинная
связь смешивается с простой последовательностью
во времени, когда предшествующее явление
принимается за причину последующего.
Логика —враг суеверий и предрассудков,
она требует обоснованности суждений
и не совместима поэтому с утверждениями,
которые строятся по схеме «после этого
– значит, по причине этого». Эта логическая
ошибка возникает в случаях, когда причинная
связь смешивается с простой последовательностью
во времени, когда предшествующее явление
принимается за причину последующего.
Закон достаточного основания имеет важное теоретическое и практическое значение. Фиксируя внимание на суждениях, обосновывающих истинность выдвинутых положений, этот закон помогает отделить истинное от ложного и прийти к верному выводу.
Значение
закона достаточного основания в
юридической практике состоит, в частности,
в следующем, Всякий вывод суда или следствия
должен быть обоснован. В материалах по
поводу какого-либо дела, содержащих, например,
утверждение о виновности обвиняемого,
должны быть данные, являющиеся достаточным
основанием обвинения. В противном случае
обвинение не может быть признано правильным. Вынесение мотивированного приговора
или решения суда во всех, без исключения,
случаях является важнейшим принципом
процессуального права.[4]
Вынесение мотивированного приговора
или решения суда во всех, без исключения,
случаях является важнейшим принципом
процессуального права.[4]
Истинность мысли формальная правильность рассуждений
Понятие истинности (ложности) относится лишь к конкретному содержанию того или иного суждения. Если в суждении верно отражено то, что имеет место в действительности, то оно истинно, в противном случае оно ложно. Например, суждение «Все волки – хищные животные» истинно, а суждение «Все грибы — ядовиты» ложно.
Понятие формальной правильности рассуждения относится лишь к логическим действиям и операциям мышления. Если в числе посылок умозаключения встречается ложная посылка, то при соблюдении правил логики мы в заключении можем получить и истину, и ложь. Чтобы это показать, возьмем два умозаключения:
- Все металлы — твердые тела.
Ртуть не является твердым телом.
Ртуть не является металлом.
- Все небесные тела — планеты.
Юпитер — небесное тело.
Юпитер — планета.
В первом умозаключении заключение получилось ложным именно потому, что в качестве первой посылки взято ложное суждение. Во втором же умозаключении, несмотря на первую ложную посыпку, заключение является истинным суждением. Чтобы заключение было истинным, обе посылки должны быть истинными суждениями и соблюдаться правила логики. При несоблюдении правил логики (если посылки при этом истинны) мы также можем получить как истинное, так и ложное заключение. Чтобы это показать, возьмем такие умозаключения:
3. Все тигры полосатые.
Это животное полосатое.
Это животное — тигр.
Логика как наука
Лекция 1. Логика как наука Что изучает логика?
Итак, логика изучает мышление, но не всякое, а лишь те мыслительные процессы, которые направлены на обнаружение и обоснование истины, на решение некоторых задач.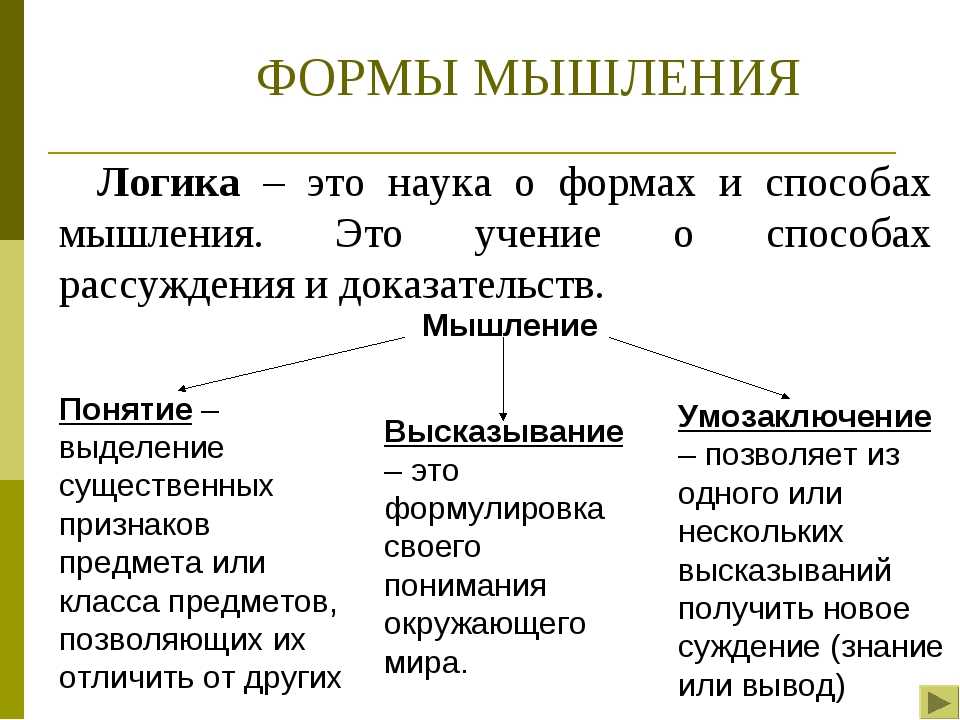
Логику интересуют прежде всего познавательные процессы.
Логика как раз и изучает те формы, в которых протекает познающее мышление, и те общие принципы, которым оно должно подчиняться, чтобы достигнуть поставленной цели. Различие между: «что мыслим?» – философия и «как мыслим?» – логика. Логика изучает формы мысли, а не языка, поэтому ее законы и принципы справедливы для всякого мышления, независимо от того, в какой языковой оболочке оно представлено. Открытие Аристотеля: правильность рассуждения зависит только от формы этого рассуждения. Логика – это теория рассуждений и их элементов, которая отличает правильные рассуждения от неправильных на основании одной только их формы. Главный вопрос ло-гики – не «почему?», а «как?». Чтобы выявить логическую форму рассуждения, следует отвлечься от его содержания. В логике принято с этой целью заменять содержательные элементы рассуждения (имена и высказывания) переменными, т. е. знаками, не имеющими никакого содержания и указывающими только на вид заменяемого выражения.
Здесь очень важно определиться с понятием истинности суждения.
Что же такое правильное рассуждение? Это рассуждение, которое при истинных посылках, т.е. исходных данных, необходимо приводит к истинному выводу. Логическая правильность рассуждения есть его соответствие правилам, законам логики. Если вы опираетесь на истинные данные и рассуждаете правильно, то
вы всегда получите истинное заключение. Это логика гарантирует. К сожалению, можно правильно рассуждать, но исходить при этом из ложных посылок. В таком случае вы можете прийти к любому заключению – как к истинному, так и к ложному. Как говорится, из лжи следует все что угодно. Например, если вы приняли посылку «Все тигры питаются травой», то из нее вы можете сделать как истинный вывод: «Некоторые травоядные полосаты», так и ложный – «Некоторые травоядные есть тигры». Важно иметь в виду следующее: логика не может сказать, истинны ли те или иные посылки – это задача конкретных наук и повседневной практики, – но она помогает нам сделать наши рассуждения правильными.
Причем важно подчеркнуть: полуистина – это еще не истина, а полуложь – это уже ложь. Логика не может сказать, истинны те или иные посылки – это задача кон-кретных наук и повседневной практики,– но она помогает нам сделать наши рассуждения правильными.
Таким образом, можно сделать вывод, что логика изучает законы и формы
познающего мышления, т.е. такого мышления, которое направлено на поиск истины.
Рассмотрим основные особенности мышления.
1. Мышление отражает действительность в обобщенных обраюх.
В отличие от чувственного познания мышление абстрагируется от единичного, выделяет в предметах общее, повторяющееся, существенное. Так, выделяя общие всем людям свойства — способность трудиться, мыслить, обмениваться мыслями при помощи языка, — мышление обобщает эти свойства и создает абстрактный образ человека Подобным же образом создаются понятия юридического лица, государственного суверенитета, правоспособности и т. п. Благодаря обобщению абстрактное мышление глубже проникает в действительность, открывает присущие ей законы.
2.Мышление — процесс опосредствованного отражения действительности. При помощи органов чувств можно познать лишь то, что непосредственно воздействует или воздействовало на органы чувств. Мы видим березовую рошу, слышим пение птиц, вдыхаем аромат цветов. Благодаря мышлению мы получаем новые знания не непосредственно, а на основе уже имеющихся знаний, т. е. опосредствованно. По указанию термометра можно сулить о погоде, не выходя на улицу. Не наблюдая самого факта преступления, можно на основании прямых и косвенных улик установить преступника.
Знание, полученное из уже имеющихся знаний, без обращения в каждом конкретном случае к опыту, к практике, называется выводным. Получение новых знаний путем выведения находит широкое применение в познавательной деятельности человека.
3.Мышление неразрывно связано с языком. Какая бы мысль ни возникла в голове человека, она может возникнуть и существовать лишь
ствительности, выражая их не только средствами естественного языка, но и в символах языка формализованного, играющего важную роль в современной науке.
Итш, обобщенный иопосредствованный характер отражения действи-тельности, неразрывная связь с языком, активный характер отражения — таковы основные особенности мышления.
Зачем же изучать логику?
Помимо того, что это просто интересно, в чем, я надеюсь, вы убедитесь на наших занятиях, логику стоит изучать еще по нескольким причинам:
Занятия логикой приучают точно мыслить и ясно их излагать.
Логика учит анализировать свои и чужие рассуждения. Логика вооружает нас и средствами, позволяющими обнаружить, точно обозначить и устранить ошибку рассуждения. Она помогает нам справиться с демагогией и софистикой, избавляет нас от того земляного простодушия, которое легко толкает нас в объятия сладкоречивых жуликов. Обращаются, например, к вам с таким рассуждением: «Я – человек, а вы – не я, следовательно, вы – не человек». И даже если вы чувствуете, что здесь что-то не так, сможете ли вы достойно возразить? Вряд ли. В лучшем случае буркнете что-то вроде «Сам дурак!» и отойдете с чувством интеллектуального унижения. Знакомство с логикой даст вам возможность определить, что это за рассуждение, каким требованиям оно должно удовлетворять и какое из этих требований здесь нарушено. Указав на все это, вы пристыдите демагога или невежду, и уже он отойдет от вас, посыпав голову пеплом.
Знакомство с логикой даст вам возможность определить, что это за рассуждение, каким требованиям оно должно удовлетворять и какое из этих требований здесь нарушено. Указав на все это, вы пристыдите демагога или невежду, и уже он отойдет от вас, посыпав голову пеплом.
Логика воспитывает умение убеждать и обосновывать свои идеи. Если вы способны обосновать свою мысль, решение того или иного вопроса, то ваша речь будет не только ясной, но и убедительной. Каким бы родом деятельности вы ни занимались, часто это – необходимое условие ее успеха.
Наконец, логика учит спорить. И в повседневной жизни, и в профессиональной деятельности нам часто приходится вступать в полемику по разным поводам. Спорить мы, как правило, не умеем, и наши столкновения чаще всего заканчиваются перебранкой, криком, а то и дракой. Познакомившись с логикой, вы научитесь корректно отстаивать свое мнение, опровергать ошибочное убеждение своего оппонента, находить компромиссы, разоблачать недобросовестные приемы и уловки.
И все-таки самое важное – логика вырабатывает привычку думать. Современная жизнь вынуждает человека много знать, поэтому системы школьного и высшего образования построены таким образом, чтобы вложить в голову учащегося как можно больше информации. Но они, как правило, не учат думать, не стремятся развить эту драгоценную способность человека. Поэтому многие не любят и не умеют думать. Вместо того чтобы задуматься и найти свое решение тех или иных проблем, мы охотно полагаемся на мнение какого-нибудь телевизионного вещателя, друзей или знакомых.
Этапы развития логики
Логика является одной из древнейших наук, оформившихся в самостоятельную дисциплину. Ее создателем считается древнегреческий философ и ученый Аристотель (384-322 гг. до н.э.).
Аристотель систематизировал логические знания, сформулировал главные логические законы и написал несколько сочинений, в которых представил логику как средство доказательства и защиты истины и разоблачения софистики и лжи. Вообще изначально учителей в Греции называли софистами (от греческого слова «софия» – мудрость), что означало первоначально «мудрец» или «учитель мудрости». Они учили детей грамоте, основам наук, воспитывали умение ясно и убедительно говорить, отстаивать в спорах свое мнение. Со временем, однако, софисты стали изобретать приемы, направленные на то, чтобы одурачить собеседника, представить противника в смешном или глупом виде, внушить недоверие к истине, а ложь, напротив, представить в белоснежных ризах истины. Такие недобросовестные приемы и уловки получили наименование «софизмы», а слово «софист» приобрело тот негативный оттенок, который сохранился у него до сих пор. Вот примеры некоторых софизмов, сохранившихся в трудах древних авторов:
Они учили детей грамоте, основам наук, воспитывали умение ясно и убедительно говорить, отстаивать в спорах свое мнение. Со временем, однако, софисты стали изобретать приемы, направленные на то, чтобы одурачить собеседника, представить противника в смешном или глупом виде, внушить недоверие к истине, а ложь, напротив, представить в белоснежных ризах истины. Такие недобросовестные приемы и уловки получили наименование «софизмы», а слово «софист» приобрело тот негативный оттенок, который сохранился у него до сих пор. Вот примеры некоторых софизмов, сохранившихся в трудах древних авторов:
«То, чего ты не терял, у тебя есть. Ты не терял рогов. Следовательно, ты рогат». «Сидящий встал. Кто встал, тот стоит. Следовательно, сидящий стоит».
Всере-дине XIX в. логика пережила свою научную революцию: возникла и стала развиваться математическая (символическая) логика, применяющая для анализа рассуждений математические средства и методы. Именно она заложила теоретические основы последующей разработки языков программирования.
Аристотелевская логика с тех пор стала называться традиционной.
ВРоссии до 1917 г. логику преподавали в старших классах гимназий, затем только в конце 40-х гг. XX в. она вновь возвращается сначала в юридические институты и университеты, а в последние годы логику преподают и в некоторых школах.
Слово «логика» употребляется нами довольно часто, но в разных значениях. Нередко говорят о логике событий, логике характера и т.д. В этих случаях имеется
ввиду определенная последовательность и взаимозависимость событий или поступков. Слово «логика» употребляется и для характеристики процессов мышления. Так мы говорим о логичном и нелогичном мышлении, имея в виду его определенность, последовательность, доказательность и т.п. Процесс познания сложен и противоречив. Логике в этом процессе отводится немаловажная роль. Логические операции — такие, как определение, классификация, доказательство, опровержение и т.п. — применяются каждым человеком в его мыслительной деятельности, однако, зачастую неосознанно и нередко с ошибками, без отчетливого представления обо всей глубине и сложности тех мыслительных действий, с которыми связан каждый, даже самый элементарный акт мышления. Основываясь на наиболее общих законах развития природы, общества и человеческого мышления, логика формирует свой научный метод познания действительности. Мышление представляет интерес для логики, во-первых, в качестве важного инструмента познания объективной реальности, во-вторых, с точки зрения верности
Основываясь на наиболее общих законах развития природы, общества и человеческого мышления, логика формирует свой научный метод познания действительности. Мышление представляет интерес для логики, во-первых, в качестве важного инструмента познания объективной реальности, во-вторых, с точки зрения верности
выводов, и, в-третьих, в качестве процесса, подчиняющегося определенным законам. Законы мышления представлены в логике как общечеловеческие, поскольку мыслительный процесс имеет универсальный характер. Логика, абстрагируясь от частного, анализирует общее. Логическое мышление не является врожденным. Его необходимо развивать.
Логическая теория своеобразна. Она высказывает об обычном (человеческом мышлении) то, что может показаться на первый взгляд сложным. К тому же основное ее содержание формулируется на особом, созданном специально для своих целей искусственном языке. Отсюда сложность первого знакомства с логикой: на привычное и устоявшееся надо взглянуть новыми глазами и увидеть глубину за тем, что представлялось само собой разумеющимся. Некоторые считают собственное мышление таким же естественным процессом, как, например, ходьба или дыхание. Но они ошибаются. Знакомство уже с первыми разделами данного курса покажет необоснованность такого убеждения. Глубокое и последовательное изучение логики является одним из наиболее эффективных способов развития абстрактного мышления. А это, в свою очередь, помогает избегать неясностей, ошибок, правильно организовывать собственную мысль.
Некоторые считают собственное мышление таким же естественным процессом, как, например, ходьба или дыхание. Но они ошибаются. Знакомство уже с первыми разделами данного курса покажет необоснованность такого убеждения. Глубокое и последовательное изучение логики является одним из наиболее эффективных способов развития абстрактного мышления. А это, в свою очередь, помогает избегать неясностей, ошибок, правильно организовывать собственную мысль.
Изучение логики способствует повышению культуры мышления, что ведет к взаимопониманию, точному выражению мыслей, умению находить ошибки в рассуждениях. Студентам логика поможет оптимально овладеть информацией: распознавать главное и второстепенное, критически воспринимать определения и различного рода классификации, находить доказательства для своих высказываний и учиться опровергать ложные.
Предмет и задачи логики. Мышление как объект изучения формальной логики
Человек, обладая сознанием, отражает действительность и получает знания о природе, обществе, о самом себе. Знание только тогда ценно, когда оно позволяет человеку правильно ориентироваться в мире, осуществляя свою жизнедеятельность. Поэтому цель познания заключается в получении истинных знаний, использование которых приводит к верным и полезным результатам.
Знание только тогда ценно, когда оно позволяет человеку правильно ориентироваться в мире, осуществляя свою жизнедеятельность. Поэтому цель познания заключается в получении истинных знаний, использование которых приводит к верным и полезным результатам.
Есть знания, истинность которых очевидна. Такие суждения, как: «Я чувствую, что на улице холодно», или «Я слышу звук скрипки», отражают факты, которые человек познает в процессе непосредственного физического взаимодействия с объектом познания при помощи органов чувств. Такие факты очевидны, так как они не нуждаются в доказательстве. К числу очевидных знаний относятся, прежде всего, те, которые являются результатом чувственного познания, а также внутреннего опыта (например, воспоминания).
Кроме непосредственных знаний, есть знания, истинность которых видна опосредованно, то есть через призму других знаний. Все те факты, которые совершаются в наше отсутствие (прошедшие или будущие) могут быть познаны только опосредованно. Например, по многочисленным памятникам и остаткам военных сооружений и укреплений на Бородинском поле можно представить, какое сражение здесь происходило 5-7 сентября 1812 года.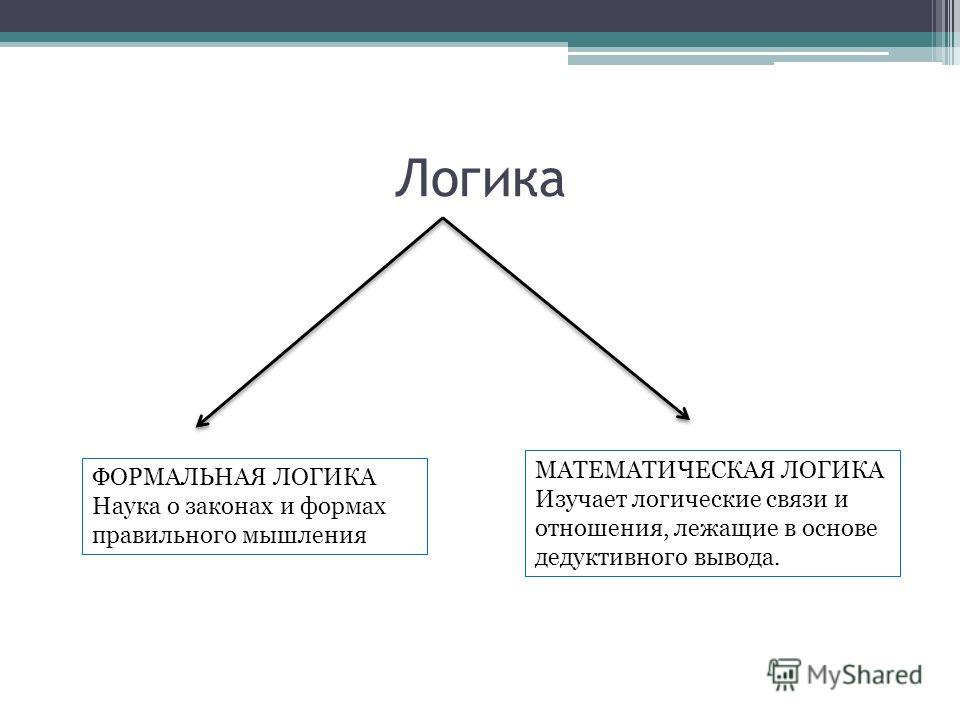 Опосредованное знание доказывается при помощи непосредственных положений и фактов. Происходит это на уровне абстрактного мышления.
Опосредованное знание доказывается при помощи непосредственных положений и фактов. Происходит это на уровне абстрактного мышления.
Все содержание нашего познания об окружающей действительности зафиксировано в научных теориях, понятиях, категориях. Отражение действительности осуществляется чувственными формами и фиксируется мышлением. Абстрактное мышление отражает мир и его процессы глубже и полнее, чем чувственное познание. Таким образом, объектом логики как науки выступает абстрактное мышление.
Мысль человека всегда выражена в языке, который представляет собой материализацию мысли. Однако связь языка и мышления достаточно сложна. Они образуют единство, но это не означает, что язык и мышление тождественны друг другу. Между ними существуют и качественные различия.
. . отношение между языком и мышлением в процессе отражения человеком действительности не может быть представлено в виде простого соответствия мыслительных и языковых структур. Специфика языкового отражения заключается в том, что работа мышления не прямо и непосредственно воспроизводится в формах языка, а закрепляется в нем особым символическим образом;
. • различие существует и в строении. Основными формами мышления являются понятия, суждения и умозаключения. Составными частями языка являются: звук (аллофон), фонема, морфема, лексема, предложение;
• различие существует и в строении. Основными формами мышления являются понятия, суждения и умозаключения. Составными частями языка являются: звук (аллофон), фонема, морфема, лексема, предложение;
. . мышление в своем развитии фиксирует противоречивые моменты любого движения, воспроизводя их в идеальных образах разной степени глубины и детализации, постепенно приближаясь к их определенности. А там, где начинается закрепление, вступает в силу язык. Он фиксирует в своих формах содержание мыслительных образов; . . на язык оказывают влияние предметная деятельность и традиции культуры общества, а мышление связано с личностью субъекта, его познавательными способностями.
Язык и мышление оказывают друг на друга взаимное влияние. С одной стороны, мышление представляет содержательную основу для языка, оно контролирует использование языковых средств, саму речевую деятельность, обеспечивает опыт употребления языка, определяет уровень языковой культуры. С другой стороны язык является средством формирования, формулирования и «свершения» мысли, делает мысль доступной для других людей, придает мышлению форму, в которой мысль легче обрабатывать, перестраивать, развивать, выступает как средство тренировки, оттачивания, совершенствования мысли.
Определение и структура формальной логики.
Формальная логика изучает объективно сложившуюся структуру мыслительного процесса, установившиеся отношения понятий и суждений при выведении нового знания. Устойчивые связи элементов правильного мышления приобрели характер законов. Анализ таких связей, наряду с описанием структурных форм мышления, составляет предмет изучения формальной логики.
Формальная логика — наука об основных законах и формах правильного мышления.
Задача формальной логики — установить правила обеспечения стройности и последовательности правильного мышления. Следует подчеркнуть, что логика использует уже сложившуюся форму, рассматривая ее как нечто готовое и данное.
Логические формы и законы мышления являются общими для всех людей. Внутренняя структура мысли непосредственно связана с человеческой деятельностью и определяется свойствами и отношениями объективного мира. Очевидно, что содержание мыслей юриста отличается от содержания мыслей биолога или музыканта; ученый использует в своих исследованиях такие понятия и термины, которые не используются в повседневной жизни.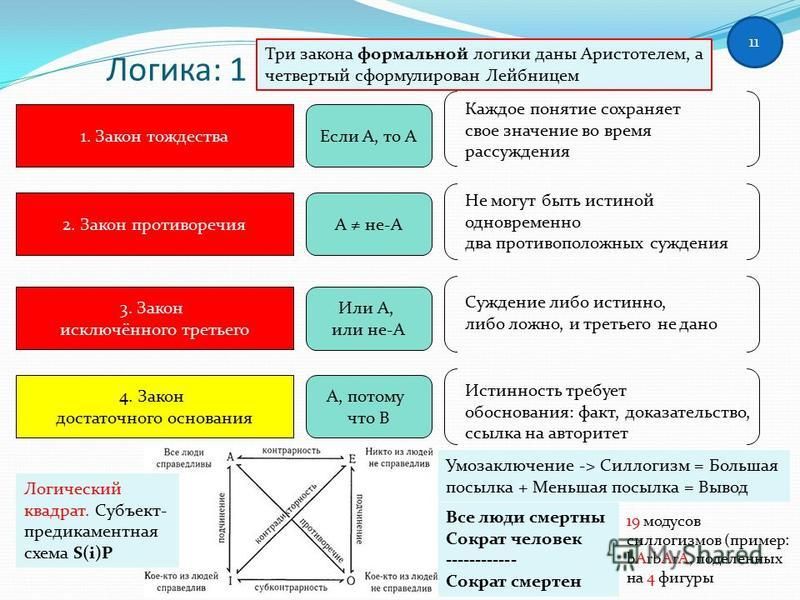 Однако во многих различных по содержанию мыслях можно обнаружить нечто общее. Это общее характеризуется не конкретным содержанием мыслей, а схемой, способом построения. Какую бы словесную оболочку не принимали наши мысли, на каком бы языке они не излагались, они обязательно должны принять общепринятую форму. Без этого не возможно взаимопонимание.
Однако во многих различных по содержанию мыслях можно обнаружить нечто общее. Это общее характеризуется не конкретным содержанием мыслей, а схемой, способом построения. Какую бы словесную оболочку не принимали наши мысли, на каком бы языке они не излагались, они обязательно должны принять общепринятую форму. Без этого не возможно взаимопонимание.
Таким образом, логика – это наука об общезначимых формах и средствах мысли, необходимых для рационального познания в любой области. Следовательно, предмет логики составляют:
законы, которым подчиняется мышление в процессе познания объективного мира; формы мыслительного процесса; методы получения нового знания;
способы доказательства истинности знаний.
1.3. Понятие логической формы и логических законов
Логика использует уже сложившуюся структуру мыслительного процесса. Сложный процесс формирования и совершенствования внутренней структуры мысли лежит за пределами предмета формальной логики; она раскрывает форму мышления, не рассматривая проблему исторического развития познания.
Основными формами абстрактного мышления являются понятия, суждения и умозаключения.
Логическая форма представляет собой исторически установившийся способ связи между составными элементами человеческой мысли. И отражает общие и простые связи и отношения бытия и человеческой деятельности. При этом в каждом мыслительном акте можно выделить как предмет мысли, так и то, что мыслится о предмете: его свойства, состояния, действия, а также отношения с другими предметами. Мысль о предмете логически связана с другими мыслями в умозаключении.
Законы логики — это законы правильного мышления, способ выражения в мысли норм и принципов человеческой деятельности. Они отражают существенные, необходимые, устойчивые и повторяющиеся связи и отношения человеческого бытия и реализуются в процессе рассуждения, направленного на получение истинного выводного знания. Соблюдение законов логики — необходимое условие достижения истины в процессе рассуждения. Основными формальнологическими законами являются:
. | . | закон тождества; |
. | • | закон непротиворечия; |
. | . | закон исключенного третьего; |
. | • | закон достаточного основания. |
Формальная логика | Определение, примеры, символы и факты
Альфред Норт Уайтхед
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См. весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдений. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивное. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь.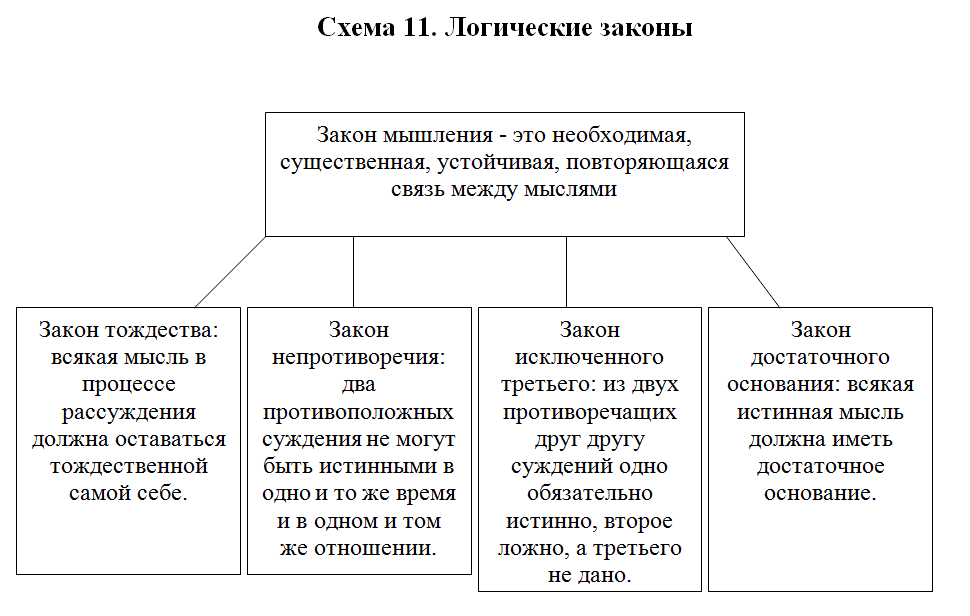 различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами.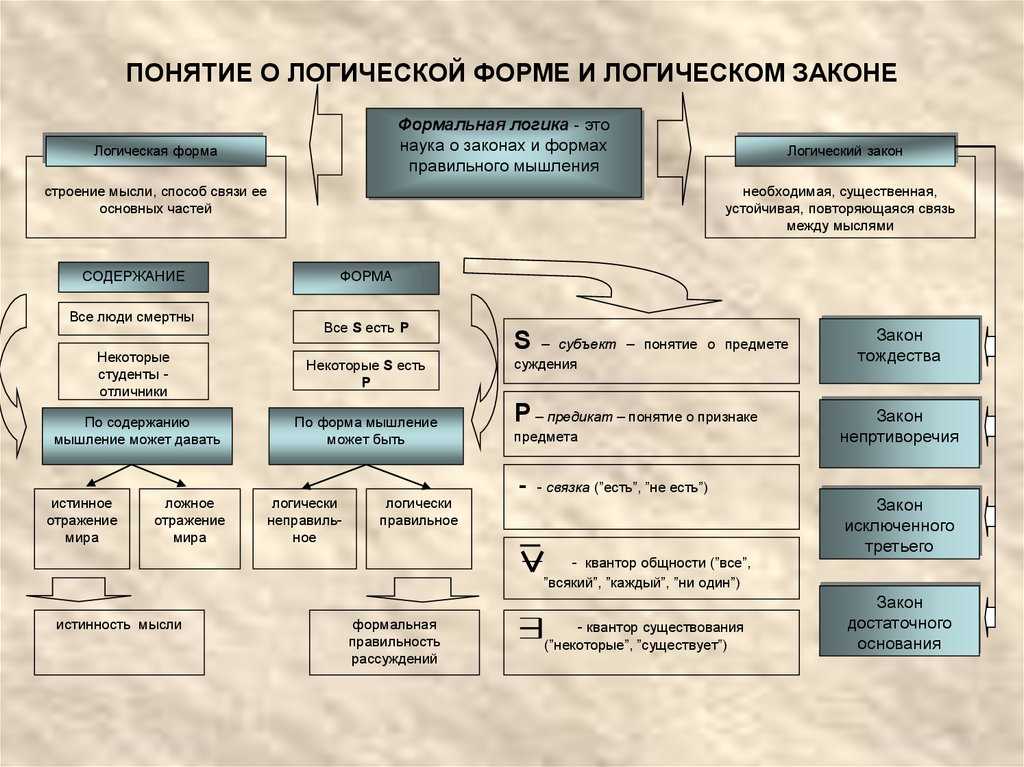 Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы.
В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.
Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или умственными построениями?
Формальная логика | Определение, примеры, символы и факты
Альфред Норт Уайтхед
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См. весь связанный контент →
весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдений. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивное. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее.
Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода.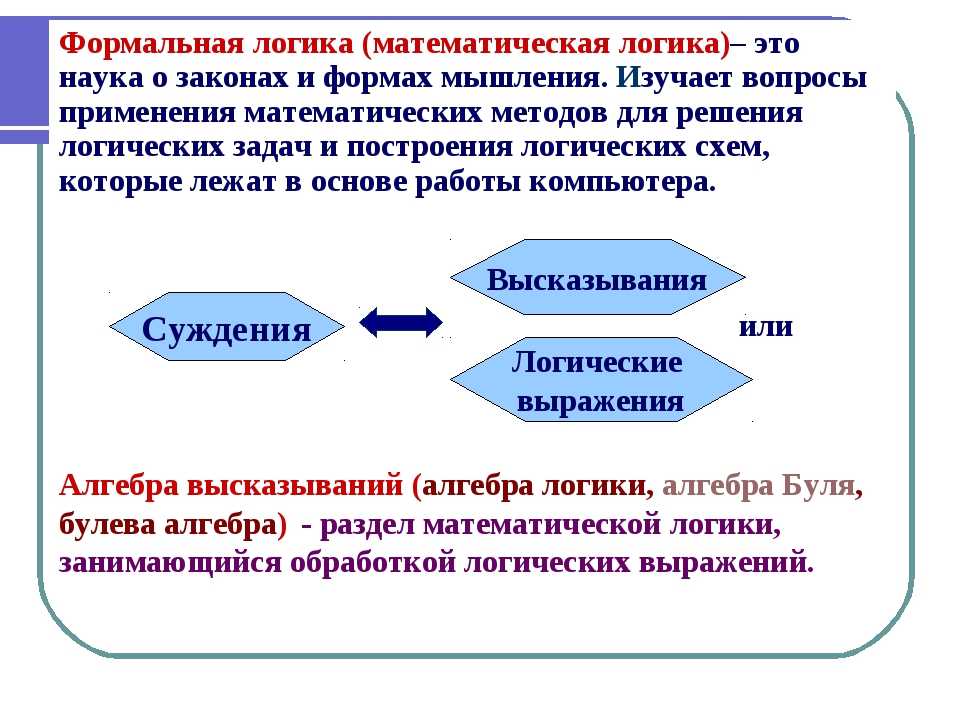 На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны.
Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.
В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.

