Основы формальной логики: как не дать собой манипулировать
Мы начинаем серию материалов о манипулятивных техниках, автором которой выступил известный журналист, редактор (и преподаватель философии) Дмитрий Шишкин. В первой части разберёмся, как связаны казахстанские медийные скандалы последнего времени с древними греками Протагором и Аристотелем.
А связаны они очень даже явно — через приёмы словесного мошенничества, названного 2500 лет назад «софизмом». Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам.
Искусство манипуляции людьми появилось вместе с речью. Правильно подобранными словами можно отправлять в атаку на врага или обращать в бегство, ввергать в депрессию или мотивировать к свершениям. Но в целом смысл манипуляции всегда один — заставлять делать или думать что-то, что мы делать и думать не собирались — то есть, использовать нас.
Что не так в противостоянии людей, желающих сохранить урочище Кок-Жайляу диким местом, и теми, кто хочет его застроить? На первый взгляд обычный гражданский конфликт — урбанистов и экологов.
Или, например, когда вся страна была взбудоражена новостями о распространении менингита, на одном из ресурсов вышла статья «Кто заказал министра здравоохранения Елжана Биртанова?». Это – классическая уловка Ignoratio elenchi («невежественное опровержение» или подмена тезиса). (Подробно об этом во второй части материала).Со
Такие примеры встречаются ежедневно. И мы предлагаем вам учиться разбираться в них не по наитию, а научно.
Немного истории
Софистика
Более 2500 лет назад в Древней Греции активно распространились школы софистики. Там давали уроки начинающим политикам: как при помощи ораторского искусства добиваться своих целей.
От философов, также процветавших в древних полисах, софисты отличались в основном тем, что не считали важными какие-то универсальные задачи и теоретические размышления, а главным признавали достижение практической цели.
Интересно, что софистика появилась раньше логики как оформленной науки, и, скорее всего, именно софисты подтолкнули философов к её созданию (в качестве инструмента противодействия демагогам, вводившим народ в заблуждение ради собственных целей).
«Он (Протагор, живший примерно в период 485 – 410 годов до нашей эры, за сто лет до Аристотеля – прим. авт.) первый заявил, что о всяком предмете можно сказать двояко и противоположным образом… о мысли он не заботился, спорил о словах, и повсеместное нынешнее племя спорщиков берёт своё начало от него», – писал о самом ярком представителе софистов Диоген Лаэртский в своей книге «О жизни, учениях и изречениях знаменитых философов».
Аристотель побеждает всех
Софистов ругал ещё Платон, а его ученик Аристотель решил положить конец одурачиванию народа (по крайней мере, попытался — мы и сейчас попадаемся на те же самые уловки, что были известны ещё 2500 лет назад). Он создал научную базу формальной логики (которую сам он называл «Аналитикой») и классифицировал логические ошибки, используемые софистами.
В принципе, логическая ошибка и логическая уловка — это одно и то же, просто ошибка допускается несознательно, а уловка специально вводится в речь.
Аристотель в своём труде «О софистических опровержениях» наглядно показал, что если разложить любой софизм, будет видна специально внедрённая в него ошибка, благодаря которой выводы софиста кажутся логичными.
После Аристотеля немало в развитие формальной логики внесли римляне Цицерон и Квинтилиан, а затем и средневековые схоласты – мы будем в дальнейшем пользоваться их типологией логических ошибок, так что пусть вас не удивляют латинские термины.
Немного теории
Теория — это самая скучная часть формальной логики, и передо мной стоит трудная задача: уложить в рамки современного «лонгрида» курс, который в институте преподаётся в течение года. Поэтому отсечём всё ненужное современному человеку, имеющему интернет и способному самостоятельно найти недостающие фрагменты.
Главное, что есть в формальной логике — это её четыре основных закона
Три из них сформулировал ещё Аристотель:
— закон тождества,
— закон противоречия,
— закон исключённого третьего.
А четвертый закон – достаточного основания — был добавлен немецким математиком и философом Лейбницем в начале XVIII века.
Закон тождества
«…иметь не одно значение — значит не иметь ни одного значения», писал по этому поводу Аристотель в своей «Метафизике».
То есть каждая мысль и каждый термин в процессе рассуждения должны иметь одно и то же значение. Подмена понятия в ходе рассуждения — это классическая логическая ошибка (или уловка).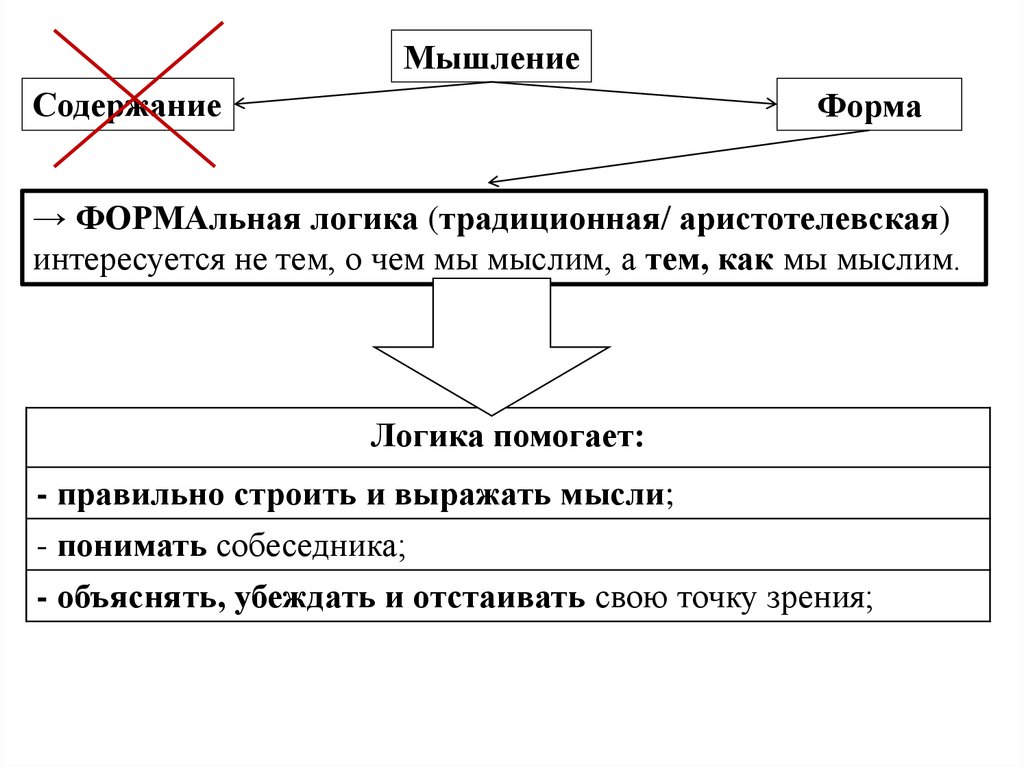
Например:
– Гражданин N хороший человек, скромный и любит ездить на велосипеде.
– Из него получится хороший аким города!
Здесь мы видим, как в первой части утверждения говорится о личных качествах человека, а вывод делается о его профессиональных качествах — что далеко не тождественно.
Закон противоречия
Два противоречащих друг другу суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно.
… невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель, «Метафизика»)
Например:
Мы часто встречаем заявления от официальных лиц и даже целых институтов о том, что:
– Народ Казахстана неоднократно демонстрировал свою политическую зрелость, отдавая голоса на выборах президента и депутатов парламента за стабильность!
– Вместе с тем, наш народ не готов пока к выборности акимов и прочим демократическим преобразованиям.
Налицо явное противоречие: получается, народ Казахстана с одной стороны политически подкован, а с другой — настолько дремуч, что не готов к такому элементарному процессу, как выборы акима.
Закон исключённого третьего
Два противоречащих друг другу суждения не могут быть одновременно оба истинными или оба ложными.
…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать (Аристотель, «Метафизика»)
Противоречащими называют такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается.
Например:
– Цензура запрещена!
– Если в интересах общества, то цензура разрешена.
Оба эти утверждения об одном и том же явлении не могут быть одновременно правдивыми или ложными. Если делается исключение, то первое утверждение ложное – «третьего не дано».
Закон достаточного основания
Всякая правильная мысль должна быть обусловлена другими мыслями, истинность которых доказана.
…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны (Готфрид Вильгельм Лейбниц, «Монадология»)
Это, в общем — именно то, чем занимается «Фактчек в Казахстане» — поиском достаточных оснований для публикаций. В отличие от первых трёх законов, которые можно применять формальными методами, просто соотнося какие-то утверждения с правилами, для установки достаточности основания необходимо включать критическое мышление и затем прилагать усилия для проверки суждений, в которых вы засомневались.
Например, самые яркие примеры мы встречаем довольно часто в виде панических слухов, распространяемых через мессенджеры и социальные сети.
В случае со скандалом вокруг заболеваемости менингитом: неверными оказались как утверждения об эпидемии, так и «рецепт», в котором утверждалось, что для профилактики менингита всем необходимо пропить курс антибиотиков (что, как пояснили затем врачи, назначается только людям, контактировавшим с больными).
На законе достаточного основания также базируется важный юридический принцип: «презумпция невиновности», гласящий, что никто не виновен, пока его вина не была доказана.
В соцсетях и даже СМИ он нарушается настолько часто, практически ежедневно, что примеры вы легко найдёте сами. Людей называют ворами и убийцами до судов, друг друга лжецами безо всяких доказательств и опровержений и т.д.
В следующей части читайте о логических уловках, построенных на нарушении этих законов логики:
- Ignoratio elenchi или «подмена тезиса»
- Argumentum Ad Hominem или «переход на личности»
Внесите свой вклад в борьбу с дезинформацией!
8.Основные понятия и операции формальной логики. Законы логики. Логические переменные. Логические выражения и их преобразования. Построение таблиц истинности.
Логика — совокупность правил, которым подчиняется
процесс мышления. Формальная
логика —
наука о формах и законах мышления.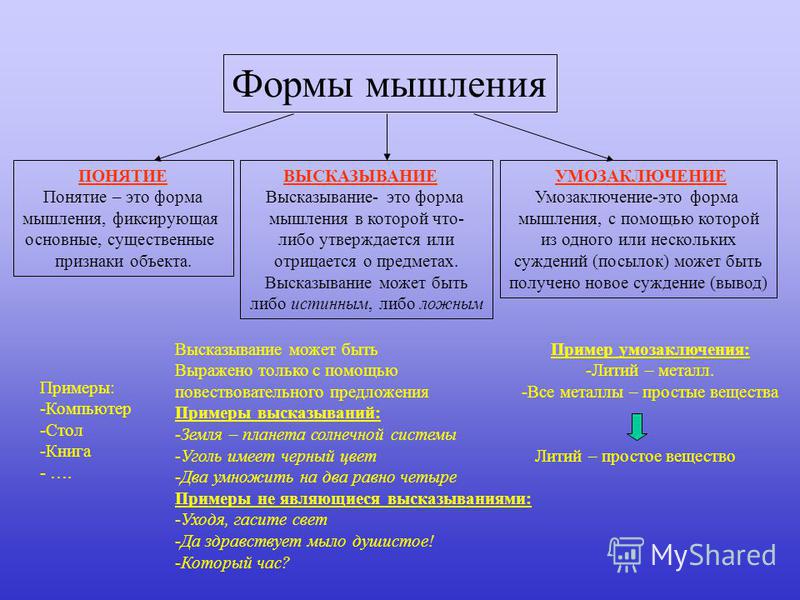
Законы
логики отражают в сознании человека
свойства, связи и отношения объектов
окружающего мира. Логика как наука
позволяет строить формальные модели
окружающего мира, отвлекаясь от
содержательной стороны. Основными
формами мышления являются понятия,
суждения и умозаключения.
Понятие — это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других. Например, компьютер, человек, ученики.
Суждения — это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета и которая может быть либо истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение. Вопросительные и побудительные предложения суждениями не являются.
Суждения рассматриваются не с точки зрения их
смысла и содержания, а только с точки
зрения их истинности или ложности.
Истинным будет суждение, в котором связь
понятий правильно отражает свойства и
отношения реальных объектов. «Дважды
два равно четырем» — истинное суждение,
а вот «Процессор предназначен для
печати» — ложное.
Умозаключение — прием мышления, позволяющий на основе одного или нескольких суждений-посылок получить новое суждение (знание или вывод). Примерами умозаключений являются доказательства теорем в геометрии. Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда и умозаключение будет истинным. Иначе можно прийти к ложному умозаключению.
Логическое выражение — это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Логическое отрицание (инверсия).
В обыденной речи
мы часто пользуемся словом «НЕ»,
или словами «НЕВЕРНО, ЧТО», когда
хотим что-то отрицать. Пусть, например,
кто-то сказал: «Тоска зеленая.
» (А).
Если Вы не согласны, Вы скажете:» Тоска
НЕ зеленая.» Или:» Неверно, что тоска
зеленая.» (В). Нетрудно заметить, что
значения истинности высказываний А и
В находятся в определенной связи: если
А истинно, то В ложно, и наоборот. Операция,
с помощью которой из высказывания А
получается высказывание В, называется
логическим отрицанием и само высказывание
В называется отрицанием высказывания
А и обозначается ¬ А.
Таким образом, отрицанием ¬ А некоторого высказывания А называется такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно. Отрицание высказывания А обозначим ¬А. Определение отрицания может быть записано с помощью так называемой таблицы истинности:
А | ¬ А (В) |
И | Л |
Л | И |
В ней указано,
какие значения истинности (Истина, Ложь)
принимает отрицание ¬ А в зависимости
от значений истинности исходного
высказывания А.
Логическое умножение (конъюнкция) от латинского conjunctio — союз, связь.
А | ¬ А (В) | А&B |
И | И | И |
И | Л | Л |
Л | И | Л |
Л | Л | Л |
Если два высказывания
соединены союзом «И», то полученное
сложное высказывание обычно считается
истинным тогда и только тогда, когда
истинны оба составляющие его высказывания.
Если хотя бы одно из составляющих
высказываний ложно, то и полученное из
них с помощью союза «И» сложное
высказывание также считается ложным.
Например, возьмем два высказывания: «У
кота есть хвост» (А), «У зайца есть
хвост» (В). Сложное высказывание «У
кота есть хвост и у зайца есть хвост»
истинно, т.к. истинны оба высказывания
А и В. Но если взять другие высказывания:
«У кота длинный хвост» (С), «У
зайца длинный хвост» (D), то сложное
высказывание «У кота длинный хвост
и у зайца длинный хвост» будет ложным,
т.к. ложно высказывание (D). Таким образом,
исходя из обычного смысла союза «И»,
приходим к определению соответствующей
логической операции — конъюнкции.
Таким образом, конъюнкцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
Логическое сложение (дизъюнкция) от латинского disjunctio — разобщение, различие.
А | В | АVB |
И | И | И |
И | Л | И |
Л | И | И |
Л | Л | Л |
Если два высказывания
соединены союзом «ИЛИ», то полученное
сложное высказывание обычно считается
истинным, когда истинно хотя бы одно из
составляющих высказываний.
Например,
возьмем два высказывания: «Мел черный.»
(А), «Доска черная.» (В). Высказывание
«Мел черный или доска черная» будет
истинным, т.к. одно из исходных высказываний
(В) истинно.
Таким образом, дизъюнкцией двух высказываний называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.
Логическое следование (импликация) от латинского implico — тесно связываю.
А | В | А=>В |
И | И | И |
И | Л | Л |
Л | И | И |
Л | Л | И |
В наших рассуждениях,
особенно в математических доказательствах,
мы часто пользуемся сложными высказываниями,
образованными с помощью слов «если.
..,
то…». Рассмотрим пример: из арифметики.
Вам должно быть известно, что утверждение
«если каждое слагаемое делится на 3,
то и сумма делится на 3» истинно, т.е.
из высказывания «каждое слагаемое
делится на 3» следует высказывание
«сумма делится на 3». Если же взять
числа 4 и 5, то посылка будет ложной, а
заключение истинным. Для чисел 4 и 7 и
посылка и заключение ложны. Очевидно,
что только один случай невозможен: мы
не найдем таких двух слагаемых, чтобы
каждое из них делилось на 3, а их сумма
не делилась на 3, т.е. чтобы посылка была
истинной, а заключение ложным. Из истины
не может следовать ложь, иначе логика
теряет смысл. Высказывание «Если А,
то В» с логической точки зрения имеет
тот же смысл, что и высказывание «неверно,
что А истинно и В ложно».
Логическое тождество (эквиваленция).
А | В | А<=>В |
И | И | И |
И | Л | Л |
Л | И | Л |
Л | Л | И |
Интуитивно можно догадаться,
что высказывания эквивалентны
(равносильными), когда их значения
истинности одинаковы.
Например,
эквивалентны высказывания: «железо
тяжелое» и «пух легкий», так же
как и высказывания: «железо легкое»
и «пух тяжелый». Обозначим эквиваленцию
символом <=> и запись «А <=> В»
будем читать «А эквивалентно В»,
или «А равносильно В», или «А,
если и только если В».
Таким образом, эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.
Приведем примеры записи сложных высказываний с помощью обозначения логических связок:
«Быть иль не быть — вот в чем вопрос.» (В. Шекспир) А V ¬ A <=> В
«Если хочешь быть красивым, поступи в гусары.» (К. Прутков) А => В
Логическая
функция —
это функция, в которой переменные
принимают только два значения: логическая
единица или логический ноль. Истинность
или ложность сложных суждений представляет
собой функцию истинности или ложности
простых.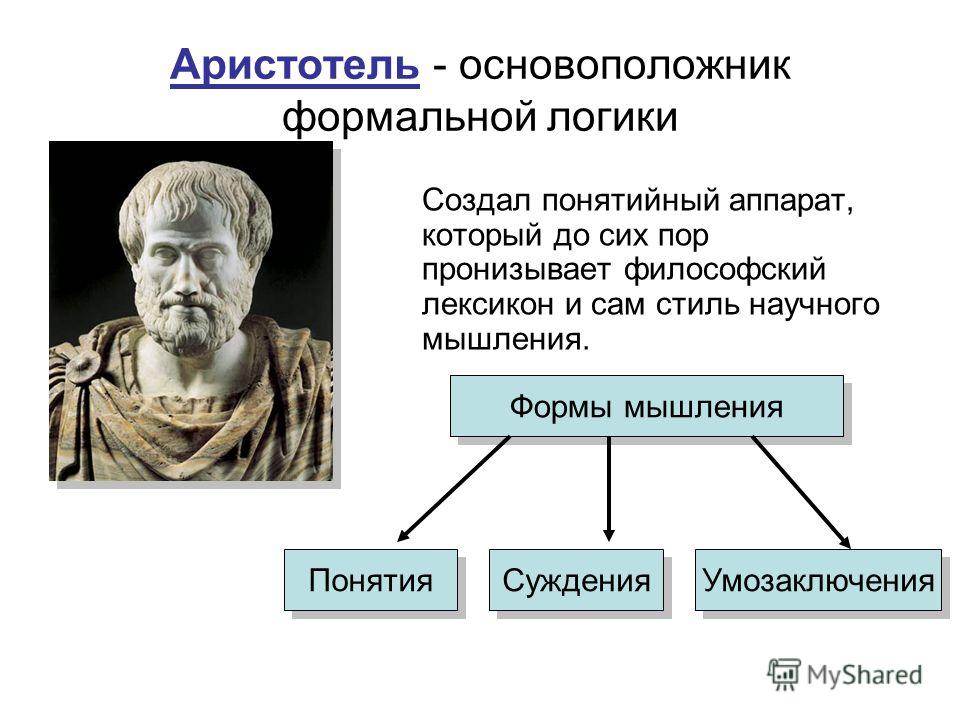
Эту функцию называют булевой
функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части — соответствующие значения логической функции.
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность.
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Предлагается следующий алгоритм построения таблицы истинности.
1. Определить
количество наборов входных переменных
— всевозможных сочетаний значений
переменных, входящих в выражения, по
формуле: Q=2n , где n — количество входных
переменных.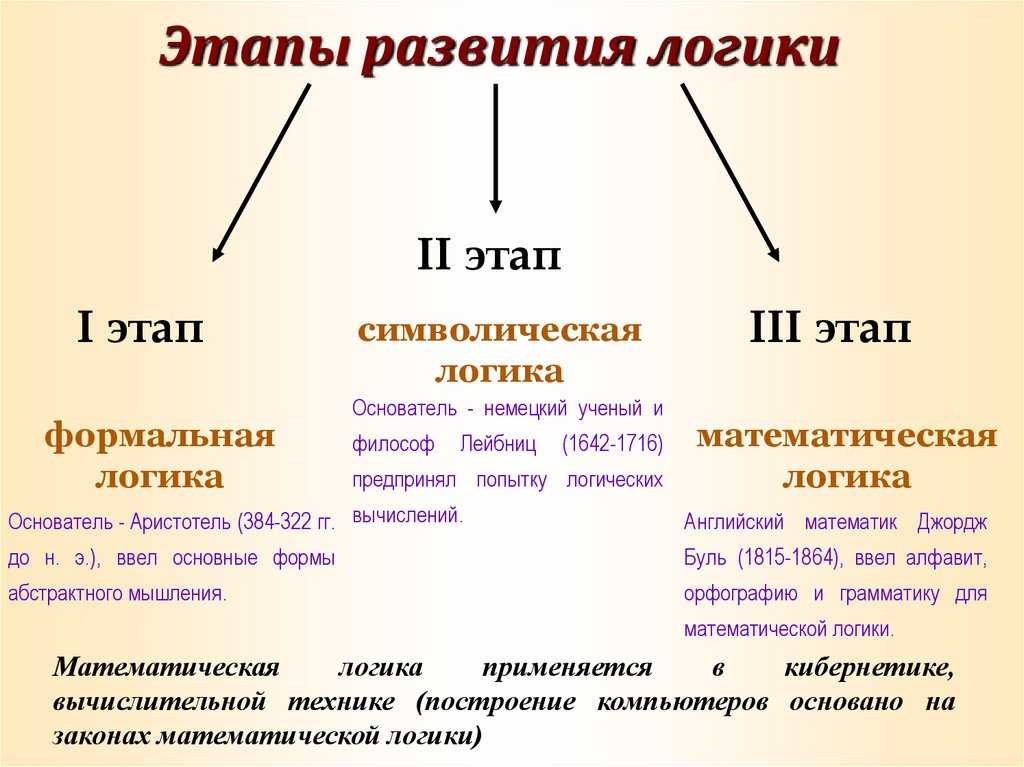
Оно определяет количество
строк таблицы.
2. Внести в таблицу все наборы входных переменных.
3. Определить количество логических операций и последовательность их выполнения.
4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
Неполнота формальной логики: Часть I
Неполнота формальной логики: Часть IФилософская критика символического исчисления
Дэниел Дж. Кастеллано
(2012)
Часть I: Введение В англоязычном мире в философии преобладает парадигма, предполагающая, что философская логика идентична символической или математической логике. Многие преподаватели философии имеют опыт работы с логикой, которую преподают в математике или информатике, и именно эта обедненная логика считается философской или истинной логикой. На самом деле математическая логика — это исчисление, независимое от содержания объектов, с которыми оно связано.
Поскольку он основан исключительно на форме аргумента или доказательства, независимо от содержания его посылок или переменных, она правильно называется формальной логикой. Формальная логика обязательно неполна и неспособна создать систему эпистемологии или метафизики. При всех наших успехах в развитии формальной логики она остается бедной и неадекватной философской логикой, так как не учитывает категориального содержания своих посылок. Этим объясняется хаотическое состояние современной философии, которая не смогла продемонстрировать каких-либо общепринятых положений метафизики, поскольку формальная логика может доказывать только бесплодные тавтологии.
Следует помнить, что стремление свести философскую логику к формальной логике предполагало, что последняя имплицитно будет содержать все богатство первой. Готтлоб Фреге надеялся доказать, что, поскольку все логические операции следуют набору правил, которые должны применяться к предложениям независимо от их специфического содержания, эту логику можно было бы описать как исчисление.
К сожалению, попытки формализовать философскую логику не учитывали должным образом тот факт, что логика действительно зависит от категориального содержания ее переменных, оставляя много пробелов и целые классы метафизических тезисов, которые, хотя и являются безусловно верными, не могут быть доказаны формальной, символической логикой. Только из этих соображений задолго до Гделя должно было быть очевидно, что формальная логика0023 неполный.
Критики формальной логики, прежде всего Бертран Рассел, часто предполагали такое же безразличие к категориальному или семантическому содержанию. Знаменитый парадокс самореферентности Рассела, например, использует неспособность формальной логики адекватно трактовать заместители по отношению к их антецеденту. С философской точки зрения парадокс Рассела не является истинным парадоксом, поскольку любой, кто имеет элементарное представление о том, как анализировать смысл в английском языке, может исправить ошибку. Парадокс не является истинным парадоксом, потому что логика Фреге не является истинной логикой, а представляет собой неполноценное подмножество последней.
Это подмножество традиционной логики в смысле типа информации, которую она может доказать. В другом смысле традиционную логику можно рассматривать как подмножество формальной логики, причем последняя слишком широка и не имеет отношения к онтологической реальности. Классическая логика основана на реальности и, как следует из ее названия, основана на logos , слово
, которое, как предполагается, связано с описываемой им реальностью. Без этой связи с реальностью (актуальной или виртуальной) нет причин рассматривать слова как нечто иное, как произвольные ярлыки, и точно так же произвольно определять правила относительно отношений между этими ярлыками (словами или предложениями).
Этот факт не был упущен из виду современными логиками, которые чувствовали себя свободными конструировать небулевы логики,
с математически или практически (например, информатика) полезными результатами. Эти успехи лишь доказывают, что эти другие формальные логики полезны 9 .0017 исчисления , но некоторые из их сторонников опрометчиво пришли к выводу, что выбор логики произволен, и даже принципы непротиворечия и исключенного среднего
могут быть предметом переговоров.
Эта неспособность отличить символическую логику от реальной логики , являющейся (в которой самоочевидно, что бытие и небытие исключают друг друга, когда высказываются однозначно) приводит к полной неспособности достичь даже самых элементарных философских истин, поскольку все принципы подлежат обсуждению или произвольны. На самом деле неаристотелевские логики (включая булеву логику) — это просто исчисления, неявно основанные на аристотелевской логике бытия. Если бы это было не так, вряд ли можно было бы проводить математические доказательства о этих логиках (метадоказательствах), показывая, что они внутренне непротиворечивы. При таком сценарии каждый изучающий логику мог бы утверждать, что он заслуживает отличной оценки, поскольку правила математического доказательства произвольны. По сей день все математические доказательства, в том числе доказательства неаристотелевской логики
(исчисления), предполагают аристотелевские принципы непротиворечия и исключенного третьего.
Современное предприятие по формализации логики не ставило своей целью выйти за пределы аристотелевской логики, а скорее ограничить ее масштабы, очистив ее от метафизики. Эта цель была четко сформулирована Бертраном Расселом (среди прочих), который стремился свести всю философию к философии естествознания. Это желание вычеркнуть метафизику из философии само было основано на метафизическом допущении: философском натурализме. С этой точки зрения нет ничего, что можно было бы узнать за пределами естествознания, поэтому не может быть никакой метанауки (метафизики или метафизической логики), которая могла бы быть эталоном истины. Следовательно, единственной логикой является логика науки, предикатами которой являются объекты естествознания. Рассуждения здесь явно цикличны. Мы предполагаем, что нет ничего познаваемого за пределами естествознания, и определяем нашу логику только для рассмотрения объектов естествознания. В нашу логику встраивается чахлая эпистемология, в которой физический эмпиризм является единственным действительным способом познания, который затем используется для показывают
, что для метафизики нет логической основы.
Это общая черта философского натурализма: от метафизики уклоняются, отказываясь от любых логических или эпистемологических средств достижения ее. Это все равно, что выколоть себе глаза, чтобы отрицать существование цвета. Точно так же философы-аналитики и другие натуралисты практикуют то, что Николас Капальди справедливо назвал усеченным аристотелизмом,
отрицая метафизику, просто игнорируя ее. На самом деле все, что они сделали, — это встроили свои эпистемические и метафизические предположения в свою логику, а не позволили логике выносить суждения об этих предположениях, которые не выдерживают такой тщательной проверки.
Если бы действительно было правдой, что ничто не может быть познано за пределами естествознания, а философия была бы лишь логикой науки, не было бы реальной необходимости в философии как отдельной дисциплине. Если философия не является судьей других наук, а является совершенно производной от естественных наук, то зачем ученым философы? Наверняка практикующие каждую науку понимают логику своих дисциплин, включая используемые ими понятия и предписания, которые якобы дают истину обо всем.
Если к натурализму относиться серьезно, логика не должна добавлять к естественным наукам никаких знаний, кроме того, что может быть определено в рамках наук. Действительно, в своем рвении прославить наука
(как если бы существовала единая эпистемология для всех областей исследования), главным образом для того, чтобы бросить тень на системы метафизики и теологии, аналитические философы и другие натуралисты делают себя неуместными. Гораздо лучше спросить физика, чем философа, о логике физики, если это не что иное, как физика. Нам лучше обратиться к настоящим ученым, а не к их прихлебателям, которые не являются ни философами, ни учеными.
Если бы логицизм преуспел, он мог бы установить интеллектуальную автономию тех наук, которые основаны на математике. Однако символическая логика имеет несколько серьезных недостатков. Поскольку формальная логика абстрагируется от понятийного содержания, имея дело только с формой утверждений, она ограничена в том, что она может доказать, и часто не в состоянии отличить связные утверждения от несвязных, потому что она не основана на здравых априорных понятиях.
Даже как формальная логика, символическая логика терпит неудачу, приводя к парадоксам, таким как антиномия Рассела, которые являются результатом пренебрежения априорных онтологических понятий, таких как субстанция. Кроме того, он предполагает онтологию объекта-свойства, поэтому он не способен работать с универсалиями.
Наконец, даже в области математики символическая логика неполна и не может привести ко всем возможным выводам. Искусство математического доказательства не может быть сведено к алгоритму, как доказал Курт Гдель своими неполнотами
теорем, которые показали недостаточность символической логики даже для чисто математических доказательств. Даже в ее собственной области математики нам нужно нечто более сильное, чем символическая логика.
Формальная логика предполагает, что содержание утверждений не имеет значения, а касается только их формы в целях достоверного вывода. Таким образом, он охватывает только те выводы, которые следуют из формы.
Тем не менее, даже эти выводы содержат неявные предположения об универсалиях и частностях, а также о том, что значит быть экземпляром универсального, как в для каждых
(∀) и существует
(∃). Таким образом, даже формальная логика имеет концептуальное содержание. В математической логике мы интерпретируем для каждых
(∀) и существует
(∃) в теоретико-множественном смысле, а не в терминах универсалий и частностей. В аристотелизме, когда всеобщее находится в частном, его сущность находится в частном, так что вы можете сказать, что особенное в известном смысле есть всеобщее. Это отношение инстанцирования отличается от атрибуции, когда вы приписываете субъекту некоторую случайность. Истинная логика должна быть способна трактовать такие отношения, а не отбрасывать их с ходу. Только тогда логика может быть действительно a priori , а не post hoc рационализация существующих наук.
Без здравых онтологических концепций логика — это всего лишь произвольный набор правил, и мы могли бы легко определить другой формализм.
Проект логицизма потерпел неудачу, потому что он пытался отбросить онтологию и метафизику, все время контрабандой внося свои собственные специфические онтологические и метафизические предположения, многие из которых не были здравыми. Мы должны сделать нашу онтологию явной и позволить логике охватить все, что может представить разум, не ограничиваясь постоянно меняющимися парадигмами современной науки. Логика должна выйти за пределы теории, а не ограничиваться теорией. Логицизм был сильно нагружен теорией и слеп к ошибочности викторианской идеи о том, что наука
может быть целью.
Когда логика освобождается от эмпирической смирительной рубашки, она может подвергнуть эпистемологии и теории физики и метафизики тщательному анализу в соответствии с законами мысли.
Любая попытка восстановить истинную логику из трясины современного формализма должна начинаться с понимания значения символов, стараясь отличать семантику от синтаксиса, подчеркивая при этом важность обоих.
Мы сделали это в некоторой степени уже в Логика и язык , но мы подытожим наши результаты чуть позже. Далее мы рассмотрим исторический переход от классической логики терминов к современной логике предикатов и его интеллектуальные мотивы. Затем мы подробно проанализируем логику предикатов первого порядка, постаравшись выявить ее скрытые онтологические предположения. В частности, мы будем иметь дело с проблематичным понятием материальной импликации, а также с упомянутыми выше кванторами ∀ и ∃, показывая, как они смешивают универсалии и партикулярии. Далее мы перейдем к логике более высокого порядка и правилам вывода или доказательства. Это, естественно, приведет к обсуждению утверждений о том, что может доказать символическая логика, и окончательному опровержению этих утверждений Гделем.
Мы подробно рассмотрим теоремы Гделя о неразрешимости и неполноте, прежде чем перейти к обсуждению формальной теории множеств и, в частности, аксиомизации Цермело-Френкеля. Ограничения логики Рассела сделали необходимым несколько экзистенциальных аксиом, особенно неуклюжую аксиому подстановки, призванную обойти парадокс Рассела.
Если бы логика строилась на более прочном семантическом фундаменте, в таких импровизированных средствах не было бы необходимости. Теория множеств не имеет адекватного отношения к универсалиям, как и логика предикатов. Предстоит крупная коррекция.
Эта дискуссия завершится разработкой формальной логики, которая сохраняет большую часть семантического богатства классической логики, сохраняя при этом точность символической логики. Мы начнем с предложенного Джоном Троттером исчисления предикатов, в котором используется обычная языковая обработка заместителей, а затем проверим онтологическую устойчивость. Наконец, мы воспользуемся предложением Троттера построить новую аксиомизацию теории множеств без экзистенциальных аксиом. Мы также проясним загадочные понятия элементности и множественности.
Провалу логицизма уже восемьдесят лет, но лишь немногие сделали очевидный вывод о том, что необходима более надежная логика, восстанавливающая некоторые возможности классической логики.
Многие до сих пор считают, что символическая логика была единственной логикой, и видят в Гделе обвинение самой логике. Вместо этого большинство аналитических философов спустились еще глубже в бункер сциентизма, обратившись к лингвистике или нейропсихологии в поисках основы логики. Мы кратко рассмотрим эту школу мысли и укажем на ее эпистемическую непоследовательность. Парадоксально, что аналитические философы, которые были реалистами, противостоявшими кантианскому повороту в философии, теперь прибегают к открытому психологизму, хотя и якобы к психологии.0023 научный материалистический психологизм. Более тщательное опровержение их обожествления эмпиризма ждет работы по эпистемологии, но мы можем, по крайней мере, показать, используя нашу надежную логическую систему, что нет никаких рациональных препятствий для реальности за пределами естественных наук. Что касается предполагаемой интеллектуальной автономии наук, то со временем мы увидим, что каждая из них имеет свои характерные онтологические допущения, подлежащие логическому анализу.
Такая философская критика направлена не столько на опровержение наук, сколько на прояснение онтологического и метафизического содержания их притязаний, в исправление грандиозных философских притязаний популяризаторов науки. Те, кто отрицает метафизику, не могут избежать ее, но в конечном итоге делают это плохо, слепо к своим предположениям, которые мы будем разъяснять на протяжении всей этой работы.
Перейти к части II
© 2009-2012 Даниэль Дж. Кастеллано. Все права защищены. http://www.arcaneknowledge.org
| Дом | Топ |
Самый быстрый словарь в мире | Vocabulary.com
ПЕРЕЙТИ К СОДЕРЖАНИЮ
формальная логика любая логическая система, которая отделяет форму утверждений от их содержания, чтобы установить абстрактные критерии непротиворечивости и достоверности
крабы-пауки семейства Majidae
грозный чрезвычайно впечатляющий по силе или совершенству
виртуальное изображение отраженное оптическое изображение (видимое в плоском зеркале)
формалистический, связанный или характеризующийся строгим соблюдением признанных форм (особенно в религии или искусстве)
приготовление рецептуры в соответствии с инструкциями
формулировать экспресс в виде формулы
большое затылочное отверстие большое отверстие в основании черепа, через которое проходит спинной мозг
формулировка Действие по изобретению или придумыванию идеи или объяснения
молочная жидкость, выделяемая в первые или два дня после родов
червеобразный, полностью покорный
обнародовать или объявить
формула группа символов, составляющих математическое утверждение
факсимильный копировальный аппарат, передающий копию по проводам или по радио
08″>шаблонный в соответствии с некоторым установленным правилом, стилем или образцом
75″>формулировать экспресс как формулу
