логика тест 2
Вопрос | Ответ | Верно |
1.1. Логика – это: | наука о формах и законах правильного мышления | да |
1.10. Укажите вид модальности высказывания «Запрещено переходить перекресток на красный сигнал светофора»: | деонтическая модальность | да |
1.12. Формальная логика появилась: | в Античности | да |
1. | аристотелевской | да |
1.14. Интуитивная логика – это: | стихийно сформированное в процессе жизненного опыта знание форм и принципов правильного мышления | да |
1.16. Создателем логики считается древнегреческий философ: | Аристотель | да |
1.17. Математическая или символическая логика появилась: | в XIX в. | да |
1.19. Английский ученый конца XVI — начала XVII века, разработавший в произведении «Новый Органон» основы индуктивной логики: | Ф. | да |
1.2. С точки зрения формальной логики высказывание: «Все Снегурочки – это геометрические фигуры»: | построено по форме: «Все A есть B» | да |
1.20. Английский ученый XIX века, развивший теорию научной индукции: | Д.С. Милль | да |
1.3. Понятие – это | форма мышления | да |
1.4. Истинность в логике означает: | соответствие мысли объекту | да |
1. | математики | да |
1.7.Что означает слово «logos»? | закон, мысль, слово, смысл. | да |
1.8. Модальная логика относится к: | неклассической логике | да |
Бэкон
6.
Символическая логика является разделом:Соседние файлы в предмете Логика
- #
20.01.201912.88 Кб222логика тест 2.docx
- #
20.01.201915.16 Кб147логика тест.docx
Формальная логика Аристотеля — Libtime
- Главная
- Экспертные системы
- Формальная логика Аристотеля
libre 7484
В экспертных системах для представления знаний кроме правил могут использоваться символы формальной логики.
Напомним, что логика — это наука, изучающая правила формирования обоснованных соображений.
Термин «формальный» означает, что логика, к которой он относится, распространяется только на форму логических утверждений, но не учитывает их значение. Иными словами, в формальной логике рассматривается только синтаксис утверждений и не рассматривается их семантика.
В результате отделения формы от семантики появляется возможность объективно оценивать правильность доказательства, не подвергаясь действию предубеждений, вызванных семантикой. В качестве аналогии, по отношению к формальной логике, может рассматриваться алгебра, в которой правильность таких выражений, как X + X = 2X остается неоспоримым, независимо от того, что обозначает X: количество яблок или аэропланов.
Такое свойство формальной логики является полезной при создании экспертных систем, поскольку позволяет отделить знания от соображений. То есть, высказывания, которые, на первый взгляд, выглядят, как рассуждения, могут, в действительности, выполнять роль знаний.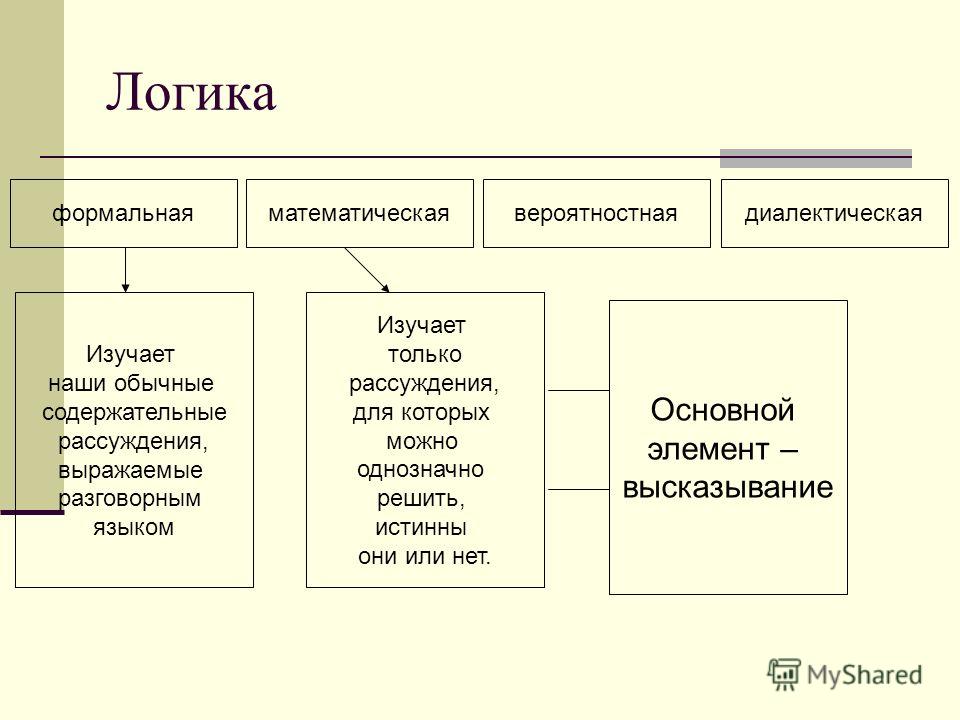
Формальная логика философа Аристотеля
Важной частью процесса проведения рассуждений является логический вывод выводов из посылок.
На этом основывается наиболее ранняя система формальной логики, которая была разработана древнегреческим философом Аристотелем в IV веке до н.э..
Ключевым понятием Аристотелевой логики является силлогизм. В силлогизме посылки выполняют роль свидетельств, из которых должен обязательно быть сформирован вывод.
Силлогизмы имеют две посылки и один вывод, который из них вытекает. Классический пример силлогизма может иметь следующий вид: Посылка 1: Все люди смертны Посылка 2: Преподаватель — человек Вывод: Преподаватель смертный.
Для графического способа представления силлогизмов хорошо подходят диаграммы Венна. С точки зрения математики, каждый эллипс на диаграмме Венна представляет некоторое множество, то есть коллекцию объектов. Таким образом, механизм теории множеств может быть успешно применен для формального представления знаний в логической модели.
Джордж Буль и символическая логика
Аристотеля силлогизмы оставались фундаментом логики до 1847 года, в котором английский математик Джордж Буль (George Boole) опубликовал первую книгу с описанием символической логики
. Одним из новых понятий, предложенных Булем, появилась модификация аристотелевского представление под названием «экзистенциальное значение», согласно которому субъект рассуждений должен существовать.Например, согласно классическим Аристотелевским взглядам, такое выражение, как «Дед Мороз приносит подарки 31 декабря», не может использоваться, как посылка или следствие, поскольку Деда Мороза в действительности не существует.
Булевы представления, имеющие пока статус современных представлений, позволяют рассуждать о пустых классы объектов. То есть, позволяют создавать логические конструкции для прогнозирования последствий использования результатов последовательности действий, которые планируется получить впервые.
Еще один вклад в развитие символической логики, сделанный Булем, заключался в том, что ученый дал определение понятия формулировкой аксиом.
Формулировка аксиом, согласно Булем, состоит из символов, которые используется для представления объектов и классов, а также операций алгебры — для манипулирования этими символами.
Рейтинг: 5/5 — 2 голосов
Является ли формальная логика разделом философии?
Хорошо, я думаю, что нужно кое-что разобрать, чтобы ответить на этот вопрос. На мой взгляд, ответ на этот вопрос должен сначала ответить на следующие вопросы:
- Что такое философия?
- Что такое логика?
Я обращусь к ним по очереди (хотя мой ответ на первый, я подозреваю, не очень удовлетворит большинство).
Что такое философия?
Это действительно мой наименее любимый «философский» вопрос. Я думаю, что этот вопрос следует, по большому счету, списать на пустую трату времени. Здесь нет жестких и быстрых границ, по крайней мере, как это практикуется сейчас. Во-первых, в философии существует аналитическое/континентальное разделение (различие несовершенное, но единственное, о котором я знаю).
В современной аналитической философии многие области практически неотличимы от нефилософских аналогов. Есть логики-философы, работа которых неотличима от работы математических логиков. Есть философы сознания, которые работают в тандеме с учеными-когнитивистами и, в буквальном смысле, делают то же самое. Означает ли это, что когнитивная наука — это философия? Нет, но это не означает, что философия сознания также является когнитивной наукой.
Вопреки точке зрения, изложенной в ответе Криса Сунами, я отмечу, что многие следуют за W.V.O. Куайн утверждает, что «философия неразрывно связана с наукой». Иногда это называют «натурализмом». Вот Куайн по этому поводу (из этой статьи IEP):
Что отличает заботы онтологического философа от …[зоология, ботаника и физика] — это только широта категорий. Данный физических объектов вообще, естествоиспытатель — это человек, решить о вомбатах и единорогах.
Учитывая классы … это математик, чтобы сказать, существуют ли, в частности, какие-либо четные простые числа… С другой стороны, это пристальное внимание к этому некритическому принятие царства самих физических объектов или классов, и т. д., что зависит от онтологии. (Куайн 1960, 275)
Из той же статьи:
Основная концепция философии и философской практики, сообщает, что дискуссия [Куайна] о науке широко известна как натурализм, точку зрения, которая рекомендует «отказ от цели первого философии до естествознания» (1981, 67), что еще больше включает в себя «готовность рассматривать философию как естественнонаучную подготовку». на себя и разрешил свободное использование научных открытий» (1981, 85). и, наконец, признает, что «…это внутри самой науки, а не в какая-то предварительная философия, что реальность должна быть идентифицирована и описана». (1981, 21).
Я думаю, лучшее, что вы могли бы сказать, это то, что философию отличает от других дисциплин методология, но даже это зыбко и трудно определить.
Мне нравится думать об этом примерно так, как судья Стюарт охарактеризовал порнографию: «Я не могу сказать вам, что это такое, но я узнаю это, когда увижу» (перефразируя).
Что такое логика?
Во-первых, как я отметил в своем комментарии к ответу Криса Сунами, существует различие между философской логикой и математической логикой. (См. также ответ Питера Смита, на который я ссылался в своем комментарии выше.) Опять же, границы здесь нечеткие, но я думаю, что различие в чем-то проявляется.
(Кроме того, то, что вы называете «неформальной логикой», обычно преподается в классах критического мышления . Однако она редко изучается на исследовательском уровне и обычно преподается только на уровне бакалавриата. Это не сказать, что нет некоторых философов, которые занимаются исследованиями в этой области, просто это не то, что большинство подумает, когда они думают о «логике».)
Итак, что отличает философскую логику от математической логики? Что ж, философская логика, как правило, сосредоточена на определенных приложениях формальной логики к традиционным философским вопросам.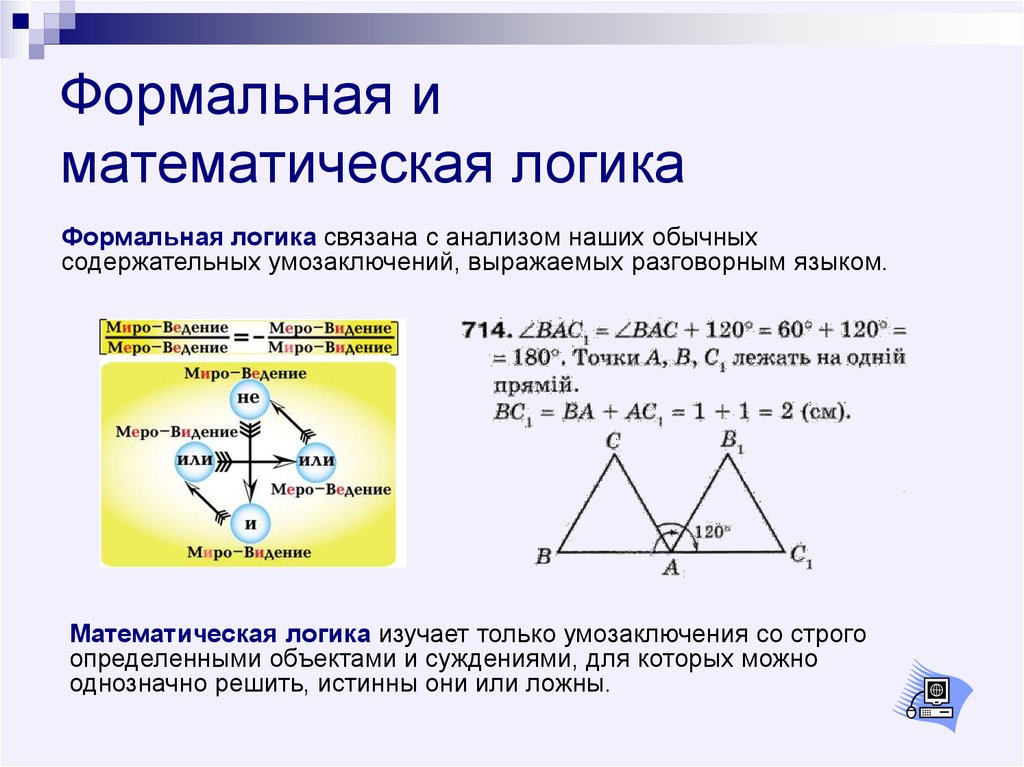
Например, W.V.O. Куайн в своей знаменательной статье по онтологии «О том, что есть» использовал формализм логики первого порядка для решения вопросов существования. В этой статье Куайн дал нам свое знаменитое изречение «быть — значит быть значением переменной», эффективно сводя вопросы существования к вопросам диапазона наших кванторов первого порядка. (Другие расширили этот критерий, включив в него значения переменных более высокого порядка, в частности интерпретируя переменные второго порядка как имеющие в качестве значений сущности, подобные свойствам.)
Другой пример — изучение модальной логики. В рамках философских традиций модальная логика обычно изучается как логика метафизической необходимости/возможности (обычно модальная логика S5). При выполнении модальной логики с ее традиционной семантикой Крипке между фреймами существует отношение доступности. В модальной логике S5 это игнорируется, поскольку доступность S5 является отношением эквивалентности, и поэтому, при условии, что только один возможный мир является действительным, каждый мир имеет доступ ко всем другим мирам.
Иногда это называют абсолютная модальность . Более слабая модальная логика обычно понимается как улавливающая некоторое понятие относительной возможности. Другие приложения (обсуждаемые в статье SEP по ссылке выше) следующие:
Модальная логика
□ Необходимо, чтобы ..
◊ Возможно, что …
Деонтическая логика
3 O Обязательно что …
P Разрешается …
F Запрещается …
Темпоральная логика
G Всегда будет так, что …
F Будет так, что …
H Всегда было так, что …
P Так было, что …
Доксатическая логика
Bx x считает, что …
Напротив, модальная логика в рамках математической логики имеет совершенно разные интерпретации. Например, существуют алгебраические подходы, где, например, модальная логика S4 интерпретируется как внутренняя алгебра.
И философы, и математики заинтересованы в применении модальной логики к изучению доказуемости под заголовком так называемой «логики доказуемости».
Кроме того, работа Джоэла Дэвида Хэмкинса (основателя Mathoverflow) представляет значительный интерес как для математиков, так и для философов. Его обсуждение теоретико-множественной Мультивселенной оказало влияние на тех, кто выступает за плюралистическую концепцию математической истины.
Кроме того, теорию групповых множеств и теорию моделей часто называют «математической логикой». Обе ветви представляют огромный интерес для философов и математиков (а также лингвистов, специалистов по информатике и т. д.). Если бы мне пришлось охарактеризовать различие между этими двумя областями, я бы сказал, что философы, как правило, больше заинтересованы в выводе «общих» выводов о природе, например, математической истины, тогда как математики, как правило, больше озабочены тем, что может быть доказано. от чего — но это, по меньшей мере, сильное упрощение.
Является ли логика частью философии?
Теперь, когда я потратил много времени , а не , отвечая на ваш вопрос, что бы я ответил? С моей точки зрения, формальная логика настолько вплетена в современную аналитическую философию, что любое определение философии, исключающее ее, было бы до неузнаваемости ущербным.
Итак, да, формальная логика является частью философии. Но и математики. И лингвистика. И информатика. (И, возможно, некоторые другие области, о которых я не знаю.) Все эти разделы вносят существенный вклад в существующую литературу по формальной логике, но ни один из них не может претендовать на исключительное господство над ним.
Введение в символическую логику
Введение в символическую логику
| ||||||||||
Домашняя страница > Логика > Символика Логика > Язык символической логики | ||||||||||
|
| Философия
103: Введение в логику Реферат: Соглашения для
перевод операторов обычного языка в символическую запись
изложил.
| ||||||||
«Чарльз усердно работает». (Предполагается
контекстуально, что значение исходного утверждения не
что Джон и Чарльз усердно работают вместе, но, возможно, не так
отдельно)
