Конспект урока по математике для 3 класса на тему: «Площадь геометрических фигур. Сравнение площадей фигур»
Государственное бюджетное образовательное учреждение города Москвы
средняя общеобразовательная школа № 654 имени А.Д.Фридмана
Конспект урока по математике
в 3 классе
Тема: «Площадь геометрических фигур. Сравнение площадей фигур»
подготовила
учитель математики в начальных классах
Панина Елена Михайловна
г. Москва
2013
Тема: «Площадь геометрических фигур. Сравнение площадей фигур».
Тип урока: ознакомление с новым материалом.
Цель: познакомить с новой величиной – площадью фигуры.
Универсальные учебные действия учащихся:
познавательные УУД – найти и использовать разные способы сравнения и вычисления площади фигуры, познакомить с квадратным сантиметром как единицей измерения площади;
регулятивные УУД – уметь организовывать свое рабочее место, использовать линейку как простейший чертежный прибор;
личностные УУД – формировать интерес к предмету, развивать психические процессы (воображение, внимание, память, мышление, речь), уважать мнение одноклассников;
коммуникативные УУД – участвовать в диалоге на уроке, отвечать на вопросы учителя, слушать и понимать речь других.
Ход урока
Организация работы учащихся
Сообщение темы и цели урока
— Ребята, тема нашего урока «Площадь геометрических фигур». Сегодня первый урок по данной теме. На нем вы узнаете, что такое площадь фигуры. Научитесь сравнивать площади разных фигур.
3. Объяснение нового материала
1) Введение понятия.
Сначала можно предложить ребятам самим дать определение площади, опираясь на их жизненный опыт. Обобщение делает учитель.
— Каждый предмет на плоскости занимает определенное место. Например, ковер лежит на полу, тетрадка лежит на парте, доска в классе висит на стене. Так вот, место, которое предмет занимает на плоскости, называют площадью этого предмета.
— Что вы можете сказать о площадях стены и двери, учебника и крышки парты?
— То же касается геометрических фигур. Место, которое занимает фигура на плоскости, называют площадью этой фигуры. Обозначается площадь латинской буквой S.
Обозначается площадь латинской буквой S.
Например, посмотрите на доску. Желтым цветом закрашена площадь каждой
фигуры.
2) Сравнение площадей фигур.
— Что можете сказать о площади треугольника по сравнению с площадью других фигур?
(В таких случаях говорят, что площадь треугольника меньше, чем площадь других фигур).
— Каким способом вы это определили? (Это видно на глаз).
— Назовите предметы в классе, которые имеют площадь (парта, стол, окно). Площадь какого предмета больше?
— Какой способ нашли? (вывод)
— А можно на глаз сравнить площадь квадрата и площадь круга?
( Нет, дети ищут другой способ).
Дети накладывают фигуры друг на друга, сравнивают.
— Сравните площади тетради, учебника, альбомного листа.
— Что можете сказать об их площадях? (ответы)
— Какой способ сравнения площадей фигур мы еще нашли? (Наложение одной фигуры на другую).
На доске фигуры: прямоугольник и квадрат, имеющие одинаковую площадь, но разные длины сторон (у учителя эти фигуры с обратной стороны разделены на квадраты).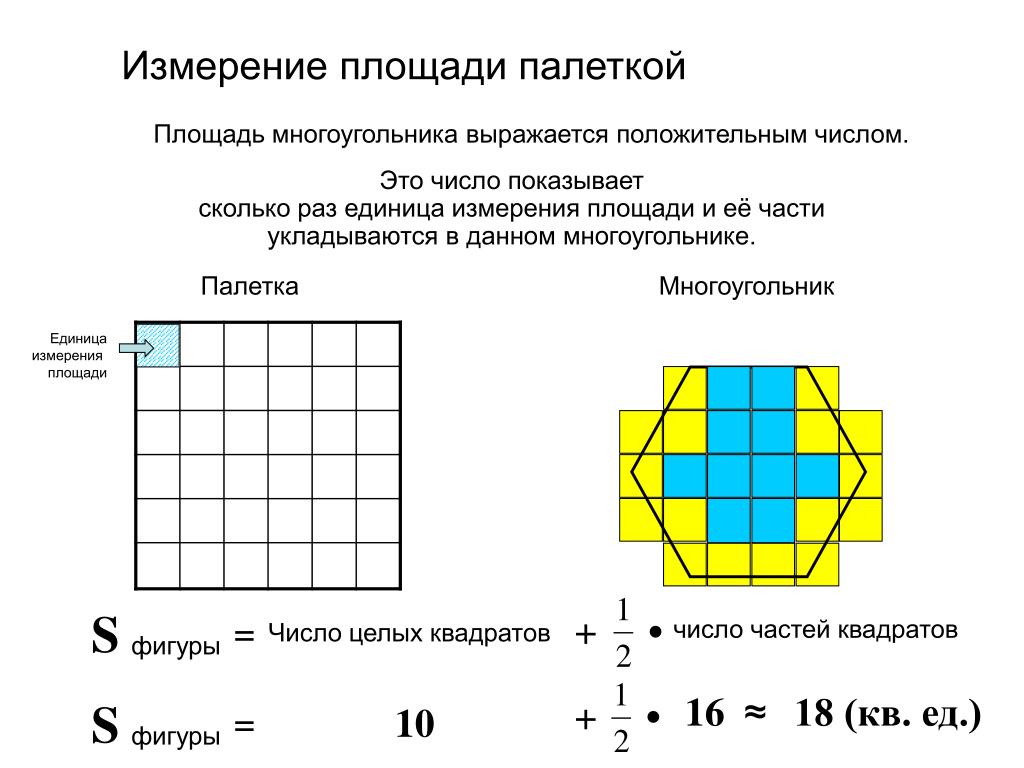
2см
2 см 4 см
1 см
— Какие фигуры на доске? Сравните площади этих фигур.
— Можно площади фигур сравнить на глаз? наложением одной на другую? (нет)
Докажите! (рассуждения детей)
Проблема: Как сравнить площади фигур, если наложение одной на другую не помогает?
Если верного ответа нет, учитель переворачивает фигуры обратной стороной.
— Я разбила фигуру на квадратики – «площадки». Что дальше?
(Кто- то предложит квадраты посчитать.)
— Давайте попробуем. (Определяется количество квадратов в каждой фигуре. Сравниваются площади данных фигур.)
— Что можно сказать о площадях этих фигур? (Площади квадрата и прямоугольника равны.)
— Сделайте вывод: как еще можно сравнить площади фигур? (Путем деления фигур на одинаковые квадраты – «площадки»).
4. Физкультминутка.
Потрудилась детвора —
Отдыхать пришла пора!
Хороша физкультминутка:
В ней улыбка, солнце, шутка!
Будем весело шагать,
От друзей не отставать.
Мы руками хлоп-хлоп,
Мы ногами топ-топ.
Раз — сюда, два — туда,
Посмотрите, господа!
Не робей, не зевай,
Выше плечи поднимай!
Вправо- влево наклонись
И соседу улыбнись.
А теперь мы Ваньки-Встаньки,
Не нужны нам даже няньки,
Раз — наклон, два — наклон,
Тётю лень прогоним вон!
Побежим теперь вприпрыжку,
Не догонят нас мальчишки,
Не обгонят нас девчонки,
Мы поскачем им вдогонку.
5. Первичное закрепление.
Учебник с.5 №1
6. Разрешение проблемной ситуации.
(Мультимедийный учебник «Уроки Кирилла и Мефодия».Часть 1. Урок 12.
8 задание)
1 ситуация
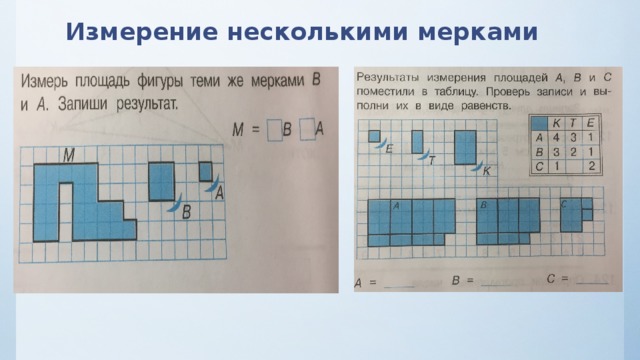
— Перед вами 2 поля. Сравните площади этих полей, сосчитав количество участков, которые помещаются на каждом поле. Засадите поле меньшей площади, пользуясь мерками.
Засадите поле меньшей площади, пользуясь мерками.
( Мнения учащихся расходятся. Одни считают, что первое поле имеет меньшую площадь, т.к.1 поле содержит 8 участков, а 2 поле содержит 16 участков. Другие считают, что первое поле имеет большую площадь, несмотря на числовые значения, т.к. зрительно видно, что первое поле намного больше второго.)
— Как же нам разрешить спор? В чем проблема?
(Учащиеся сами приходят к выводу о том, что проблема в разных размерах участков, на которые поделены поля. Чтобы сравнить площади разных фигур или объектов, необходимо использовать общую мерку.)
2 ситуация
— Перед вами 4 поля. Измерьте площади полей, используя предложенные мерки. Площади каких полей вы можете сравнить?
(Можно сравнить площади 1 и 3 полей, 2 и 4 полей, т.к. для измерения площади используются одинаковые мерки. Площадь 1 поля (4 мерки) больше площади 3 поля (2 мерки), площадь 2 поля (16 мерок) больше площади 4 поля (8 мерок).)
7. Введение единицы измерения площади – квадратного сантиметра.
Введение единицы измерения площади – квадратного сантиметра.
— Для того, чтобы не было путаницы при измерении площадей, люди договорились при измерении площади использовать общие для всех мерки. сегодня мы познакомимся с одной из стандартных мерок измерения площади квадратным сантиметром. Это квадрат со стороной 1 см. Чтобы отличать его от просто см, ставят после сокращения см цифру 2.
Учитель на доске, а дети в тетради чертят квадратный сантиметр и записывают его обозначение.
— квадратный сантиметр
— Потренируемся! Предлагаю вам определить площадь данных фигур в кв.см (каждый ребенок получает набор одинаковых многоугольников на клетчатой основе, содержащих равное количество квадратных сантиметров)
— Что для этого нужно? Как мы будем это делать? (Необходимо поделить каждую фигуру на квадратные сантиметры и сосчитать их количество.)
— Чему равна площадь каждой фигуры? (проверка)
Подведение итогов урока.
 Рефлексия.
Рефлексия.
— С какой величиной познакомились?
— Как мы научились сравнивать площадь фигур, вычислять площадь?
— С какой единицей измерения площади мы сегодня познакомились?
— Оцените себя, как вы поняли новый материал. Если вам все было понятно выберите из данного вам набора фигур фигуру с большей площадью, чем у квадрата. Если не все понятно, выберите фигуру с меньшей площадью, чем у квадрата. Покажите фигуры, которые вы выбрали.
— Спасибо!
Использованные материалы
— набор геометрических фигур;
— Моро М.И. Математика 3 класс. В 4 ч. Ч. 2. – М.: Просвещение, 2010.
— Мокрушина О.А. Поурочные разработки по математике. – М., ВАКО, 2005.
— мультимедийная установка;
— Уроки Кирилла и Мефодия. Математика. 3 класс. – М.: КМ, Нью Медиа
Дженерейшн, 2009.
Площади фигур 3 класс | План-конспект урока по математике (3 класс) на тему:
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЕРШОВСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №14
«ПЛОЩАДЬ ФИГУР»
РАЗРАБОТАЛА И ПРОВЕЛА
УЧИТЕЛЬ НАЧАЛЬНЫХ КЛАССОВ
СТОЛИЦЫНА НАТАЛЬЯ ВЛАДИМИРОВНА
Технологическая карта урока
Предмет: Математика
Класс: 3
УМК: Гармония
Тема: Площадь фигур
Тип урока: открытие новых знаний
Цель урока: учиться сравнивать площади фигур с помощью мерок
Планируемые предметные результаты:
— разбивать фигуры на группы по величине их площадей;
— сравнивать площади фигур наложением и с помощью мерки;
Ход урока:
Этап урока | Деятельность учителя | Деятельность обучающихся | Формируемые УУД |
1. | |||
Мы продолжаем путешествие по великой стране Математике. | Слушают. | Положительное отношение к уроку. (Л) | |
2.Актуализация знаний и фиксация затруднений | |||
— Назовите фигуры, которые лежат перед вами на парте. — Сравните фигуры. — Разбей фигуры на 2 группы так, чтобы любая фигура одной группы помещалась в любой фигуре другой группы. — Как будете действовать? — Возьмите большой синий прямоугольник и большой красный квадрат. — Сравните площади этих фигур. | Называют фигуры. Сравнивают фигуры. Находят основание для классификации. Классифицируют фигуры. Используют известные способы сравнения площадей фигур. | Осуществлять действия сравнения, анализа, классификации. (П) Высказывать своё мнение. Планировать свою деятельность | |
3.Выявление места и причины затруднения | |||
— Можно ли сравнить площади данных фигур, наложив одну на другую? — Как сравнить площади этих фигур? — Чем мы займёмся сегодня на уроке? — Сформулируйте цель нашего урока. | Нет, так как никакая фигура не помещается внутри другой полностью. Будем искать новый способ сравнения фигур. | Осуществлять действия сравнения, анализа (П). Строить рассуждения (П) Участвовать в коллективной беседе (К) | |
4. | |||
Поворачивает фигуры другой стороной, которая разделена на маленькие квадратики. | Выдвигают свои гипотезы. Пересчитывают число квадратов в каждой фигуре. Делают вывод о способах нахождения площади фигур | Выполнять действие обобщения (П) Выдвигать гипотезы (П) | |
5.Реализация построенного проекта. Открытие нового знания. | |||
— Прочтите диалог Маши и Миши с. 30 | Читают материал учебника с. 30 Делают вывод. | Отличать новое от уже известного (П) Выделять необходимую информацию. (П) | |
6. | Физминутка | Выполняют действия | Снять мышечное напряжение |
7. | |||
Используя различные мерки, посчитай площадь прямоугольника и квадрата № 104, с. 32 | Считают площадь фигур разными мерками Делают вывод. | Организовывать сотрудничество. Слушать собеседника (К) Допускать возможность существования различных мнений | |
8.Самостоятельная работа с самопроверкой по эталону. | |||
Предъявляет фигуры разные по форме. — Верно ли, что площади данных фигур одинаковы? — Правильный ответ найдёте на обратной стороне фигур. | Выполняют самостоятельную работу. Выбирают мерку, подсчитывают количество мерок в каждой фигуре. Выполняют проверку по эталону. | Выполнять действия самоконтроля и коррекции после завершения работы (Р) Строить рассуждения (П) | |
9. | |||
Прочитайте задание 105, с. 32. — Что значит «в 2 раза больше»? — Как вы ответите на вопрос задачи? | Читают задание. Обсуждают в парах задание. | Выполнять действие анализа (П) Слушать собеседника, излагать своё мнение и аргументировать его. Сотрудничать с соседом по парте.(К) | |
10.Домашнее задание | |||
Даёт задания трёх уровней трудности. | Выбирают задание по своим силам | Выбирать задание по способностям | |
11.Рефлексия учебной деятельности | |||
— Какую цель вы поставили перед собой в начале урока? — Удалось вам достичь цели? — Что вызвало у вас трудности? — С чем легко справились? — Над чем ещё нужно поработать? Оцените свою работу на уроке. | Оценивают свою работу по «лесенке успеха». | Оценивать свою деятельность на уроке (Р) | |
Измерьте площадь прямоугольника с разными сторонами. Формулы Square Trapezia
Прямоугольник является частным случаем четырехугольника. Это означает, что прямоугольник имеет четыре стороны. Его противоположные стороны равны: Например, если одна из его сторон равна 10 см, то и противоположная ей сторона тоже будет равна 10 см. Особым случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно использовать тот же алгоритм, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, нужно умножить его длину на ширину: площадь = длина × ширина. В указанном ниже случае: Площадь = АВ × ВС.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника по длине диагонали и одной из сторон . Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, вы можете определить вторую сторону прямоугольника, используя теорему Пифагора. После этого задача сводится к предыдущему пункту. 92 × sin (острый угол между диагоналями) / 2.
Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, вы можете определить вторую сторону прямоугольника, используя теорему Пифагора. После этого задача сводится к предыдущему пункту. 92 × sin (острый угол между диагоналями) / 2.
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, по которой можно определить размер любой поверхности геометрической фигуры.
На протяжении многих веков было так необходимо, что расчет площади называли квадратурой. То есть, чтобы узнать площадь простых геометрических фигур, достаточно подсчитать количество одиночных квадратов, которые были условно покрыты фигурами. А фигура, имевшая площадь, называлась квадратичной.
Таким образом, можно подытожить, что площадь – это такая величина, которая показывает нам размер плоскости, соединенной между собой отрезками.
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть четырехугольник, у которого четыре прямых угла и противоположные стороны, называется прямоугольником.
То есть четырехугольник, у которого четыре прямых угла и противоположные стороны, называется прямоугольником.
Как найти площадь прямоуголь к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в квадратных сантиметрах. Например, на рисунке видно, что прямоугольник приходится на 12 квадратов, значит, его площадь равна 12 квадратным метрам. см.
Но для нахождения площади больших объектов, например квартиры, нужен более универсальный метод, поэтому доказана формула нахождения площади прямоугольника, чтобы умножить его длину на ширина.
А теперь попробуем ответить на правило нахождения площади прямоугольника в формуле. Обозначим площадь нашей фигуры буквой S, буквой А будет обозначена ее длина, а буквой В ширина.
В итоге получаем такую формулу:
S = а*б.
Если наложить эту формулу на рисунок прямоугольника выше, то получим те же 12 кв.см, потому что а=4 см, b=3 см, а S=4*3=12 кв. .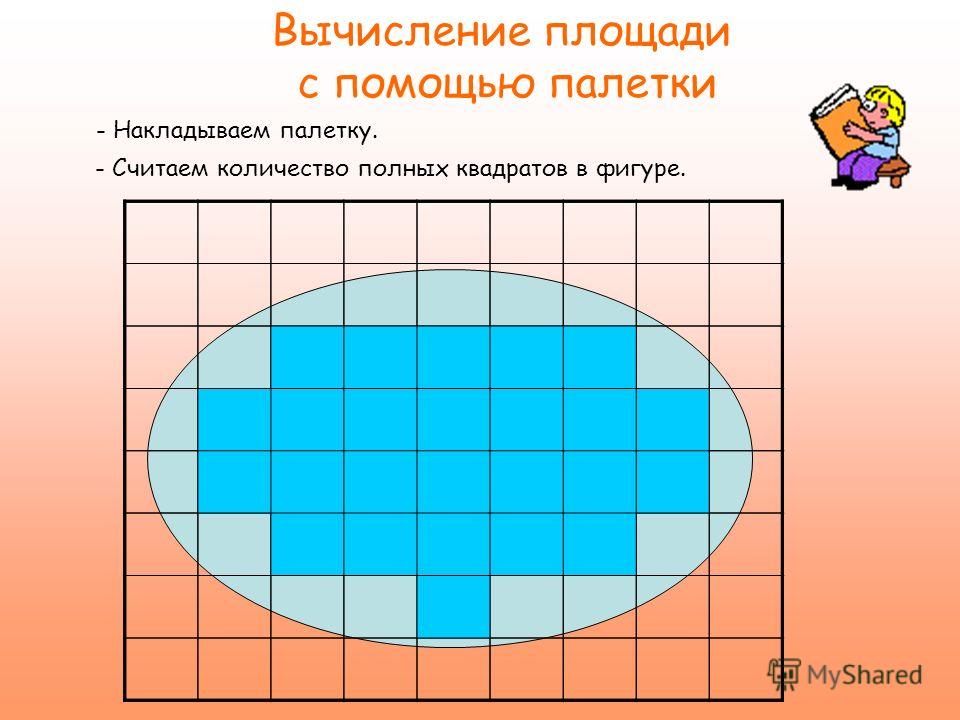 м.
м.
Если взять две одинаковые фигуры и наложить их одну на другую, то они совпадут, но будут называться равными. Такие равные фигуры также будут равны своей площади и периметру.
Зачем уметь находить площадь
Во-первых, если вы знаете, как найти площадь какой-то фигуры, то с помощью ее формулы вы сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачи, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписанный в прямоугольник или около него.
В-третьих, зная такую простую формулу, как s=a*b, вы получаете возможность без особых проблем решать любые несложные бытовые задачи (например, найти s квартиры или дома), а со временем и применить их к решать сложные архитектурные проекты.
То есть, если совсем упростить формулу Квадрата, то она будет выглядеть так:
N = d x sh
Что обозначает n — искомая площадь, D — ее длина, w — обозначает ее ширину, а x — знак умножения.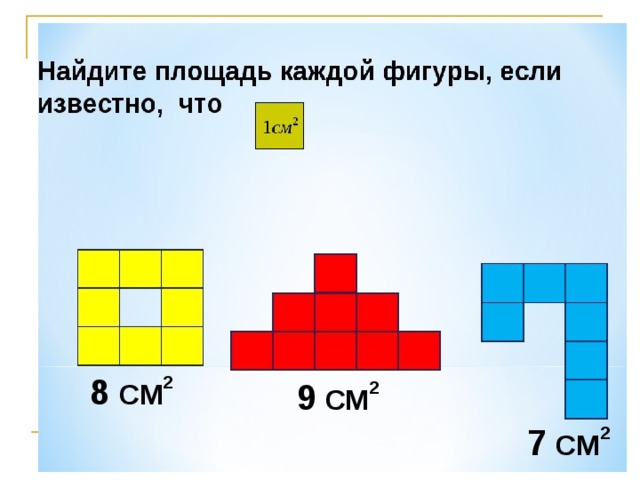
Известно ли вам, что площадь любого полигона можно освятить на определенное количество квадратных блоков, находящихся внутри этого полигона? Чем отличается площадь от периметра
Попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огорожен забором — общая длина этого забора будет периметром, а пространство, которое находится внутри забора, — площадью.
Единицы измерения Квадрат
Если периметр измеряется в линейных единицах, такими как дюймы, футы и метры, то s относится к двумерному исчислению и имеет длину и ширину.
И измеряется в квадратных единицах, например:
Один квадратный миллиметр, где s квадрат имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет такой квадрат, у которого сторона равна одному сантиметру;
Квадратный дециметр — это площадь этого квадрата со стороной в один дециметр;
Квадратный метр имеет площадь S, сторона которой равна одному метру;
Наконец, у квадратного километра есть квадрат, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли применяют такие единицы, как:
Один АР или плетение — если s квадрат имеет сторону десять метров;
Один гектар равен квадрату, сторона которого равна ста метрам.
Задания и упражнения
А теперь рассмотрим несколько примеров.
На рисунке 62 нарисована фигура, которая состоит из восьми квадратов и каждая сторона этих квадратов равна одному сантиметру. Следовательно, S такого квадрата будет квадратным сантиметром.
Если записать, то это будет выглядеть так:
1 см2. А s всей этой фигуры, состоящей из восьми квадратов, будет 8 кв.м.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Р см2.
Посмотрим на прямоугольник, изображения на рисунке 63. Этот прямоугольник состоит из трех полос, и каждая такая полоса разделена на пять равных квадратов со стороной 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.м.:
Рассмотрим следующий пример. На рис. 64 показан прямоугольник ABCD, ломаная линия KLMN разбита на две части. Его первая часть равна площади 12 см2, а вторая имеет площадь 9 см2. Теперь найдем площадь всего прямоугольника:
Итак, берем три и умножаем семь и получаем 21 кв.см:
3 7 = 21 кв.м. При этом 21 = 12 + 9.
И делаем вывод, что площадь всей нашей фигуры равна сумме площадей отдельных ее частей.
Рассмотрим другой пример. И так на рисунке 65 показан прямоугольник, который разбит на два равных треугольника ABC и ADC с отрезком АС
А так как мы уже знаем, что квадрат это такой же прямоугольник, только имеющий равные стороны, то площадь \ каждый треугольник будет равен половине площади всего прямоугольника.
Представим, что сторона квадрата равна, тогда:
S = A A = A2.
Делаем вывод, что формула квадрата квадрата будет иметь такой вид:
А запись A2 называется квадратом числа a.
Итак, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 4, то есть 4*2=16 кв.м.
Вопросы и задания
Найдите фигуру фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Запомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли быть одинаковые фигуры разных площадей? А периметры?
Если известны площади отдельных частей фигуры, как узнать ее общую площадь?
Слово и запиши чему равен квадрат.
Историческая справка
А знаете ли вы, что древние люди в Вавилоне умели вычислять площадь прямоугольника. Также древние египтяне производили расчеты различных цифр, но так как точных формул они не знали, то в расчетах были небольшие погрешности.
В своей книге «Начало» известный древнегреческий математик Евклид описывает различные способы вычисления площадей различных геометрических фигур.
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверяются антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И. Зубарева и А.Г. Мордкович
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона
Определение и понятие Квадрата Рисунок
Чтобы лучше понять, что такое площадь фигуры, рассмотрим чертеж.
Эта произвольная фигура разбита на 12 маленьких квадратов. Сторона каждого квадрата равна 1 см. А площадь каждого квадрата равна 1 квадратному сантиметру, что записывается так:
Тогда площадь фигуры равна 12 квадратных сантиметров. В математике площадь обозначается латинской буквой S.
Итак, площадь нашей фигуры равна: S Цифры = 12 см 2 .
Площадь фигуры равна площади всех маленьких квадратов, из которых она состоит!
Ребята, помните!
Площадь измеряется в квадратных единицах длины. Единицы измерения площади:
1. Квадратный километр — км 2 (когда площадь очень большая, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерить площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда фигуры рисуются в тетради).
4. Квадратный миллиметр — мм 2 .
Площадь треугольника
Чтобы найти площадь прямоугольного треугольника нужно знать длину основания и высоту. В прямоугольном треугольнике высота заменяет одну из сторон. Поэтому в формуле площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны 7 см и 4 см. Формула вычисления площади треугольника записывается так:
S прямоугольного треугольника ABC = Солнце * SA: 2
S прямоугольный треугольник ABC = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту до основания.
В нашем примере высота 6 см, а основание 8 см. Как и в предыдущем примере, вычисляем площадь по формуле:
S произвольный треугольник АВС = Солнце*Н:2.
Подставляем наши данные в формулу и получаем:
S произвольный треугольник ABC = 8 см * 6 см: 2 = 24 см 2 .
Прямоугольник и квадрат Квадрат
Возьмите прямоугольник AVD со сторонами 5 см и 8 см.
Формула вычисления площади прямоугольника записывается так:
S Прямоугольник AVD = AV*Sun.
S Прямоугольник AVD = 8 см * 5 см = 40 см 2.
Теперь посчитаем площадь квадрата. В отличие от прямоугольника и треугольника, чтобы найти площадь квадрата, нужно знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрат AVD = AB * Sun = AB 2.
Подставляем наши данные в формулу и получаем:
S Квадрат ABSD = 9 см * 9 см = 81 см 2.
Мы уже познакомились с понятием квадрат Цифра , узнали одну из единиц измерения Площадь —
Мы уже умеем находить площади фигур, которые делятся на квадратные сантиметры.
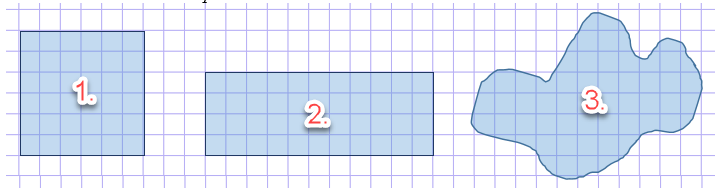
Например:
Определим, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длина стороны которого равна 3 см и 4 см?
Для решения задачи ломаем прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет 3*4 = 12 см 2 .
Тот же прямоугольник можно разделить на 3 полосы по 4 см 2 . прямоугольник будет 4 * 3 = 12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Находим площадь каждого прямоугольника.
Рассмотрим прямоугольник Акмо.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2.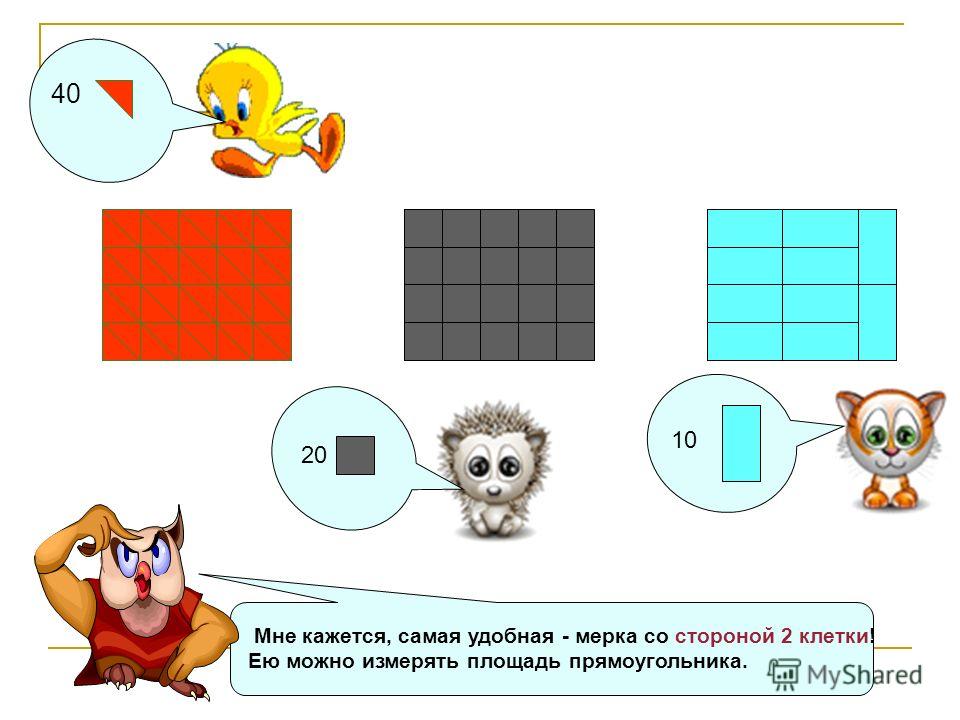
Цифра 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы изменили сторону прямоугольника, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике КДКО в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Цифра 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы изменили их и узнали площадь прямоугольника.
Делаем вывод: чтобы найти площадь прямоугольника, не нужно каждый раз разбивать цифру на квадратные сантиметры.
Для вычисления площади прямоугольника необходимо найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одинаковых единицах измерения), а затем вычислить произведение полученные числа (площадь будет выражена в соответствующих единицах площади)
Обобщая: площадь прямоугольника равна произведению его длины на ширину.
Решить задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина 2см.
Мы так спорим. В этой задаче известны длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины на ширину.
Записываем решение.
Ответ: Площадь прямоугольника 18 см 2
Как вы думаете, какой еще может быть длина стороны прямоугольника с такой площадью?
Ты можешь так говорить. Так как площадь есть произведение длин прямоугольника, значит нужно вспомнить таблицу умножения. При умножении каких чисел получится 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, прямоугольник может быть частью 6см и 3см и его площадь тоже будет равна 18см2.
Решить задачу.
Длина прямоугольника 8см, ширина 2см. Найдите его площадь и периметр.
Мы знаем длину и ширину прямоугольника. Необходимо помнить, что для нахождения площади необходимо найти произведение ее длины на ширину, а для нахождения периметра нужна сумма длины и ширины умноженная на два.
Записываем решение.
Ответ: Площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решить задачу.
Длина прямоугольника 4см, ширина 3см. Что такое треугольный квадрат? (см. рисунок)
Чтобы ответить на вопрос задачи, сначала нужно найти площадь прямоугольника. Мы знаем, что для этого нужно длину умножить на ширину.
Посмотрите на рисунок. Вы заметили, что диагональ делит прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо уменьшить 12 в 2 раза.
Ответ: Площадь треугольника равна 6 см 2.
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и научились применять это правило при решение задач на нахождение площади прямоугольника.
1. М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2-х частях, часть 1. М., «Просвещение», 2012.
2. М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2 ч., ч. 2. М., «Просвещение», 2012.
М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2 ч., ч. 2. М., «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативный документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011.
5. Школа России: Программы начальной школы. — М.: «Просвещение», 2011.
6. Волков С.И. Математика: контрольная работа. 3 класс. — М.: Просвещение, 2012.7. В.Н. Лодницкая. Тесты. М., «Экзамен», 2012 (127С.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Наклоните возможные варианты прямоугольников, площадь которых 18 см. 2.
4. Составьте задание по теме урока для своих товарищей.
Квадрат геометрической формы — Числовая характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром этой фигуры).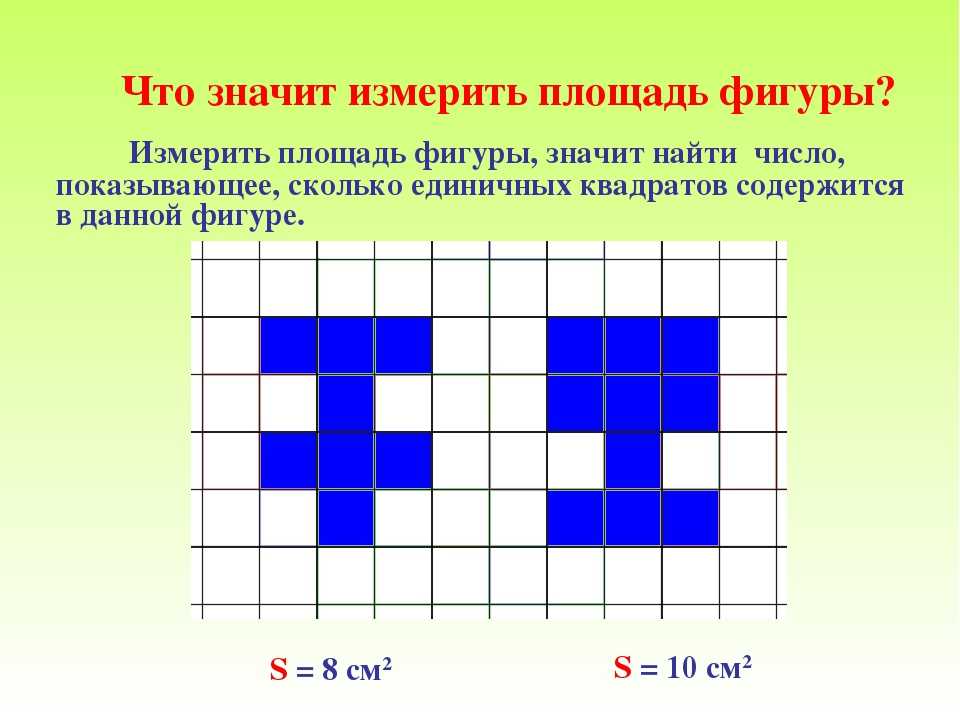 Величина площади выражается количеством квадратных единиц, входящих в нее.
Величина площади выражается количеством квадратных единиц, входящих в нее.
Формулы квадрата треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника Равен произведению полуверсионера треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длина стороны треугольника,
— высота треугольника,
— угол между сторонами и
— радиус вписанной окружности,
R — радиус описанной окружности ,
Формулы квадрат квадрат
- Формула квадрат квадрат сторона
Площадь квадрата равна квадрату длины его стороны.
- Формула Квадратная диагональ квадрата
Площадь квадрата Равна половине длины его диагонали.S =. 1 2 2 где S — площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула квадрата прямоугольника
- Квадратный прямоугольник равен произведению длины двух его смежных сторон
где S — площадь прямоугольника,
— Длина сторон прямоугольника.
Формулы площади паралилограммы
- Формула Квадрат Поллограмма сторона и высота
Квадрат Поллограмма - Формула параллелограмма по двум сторонам и углу между ними
Поллограмма квадрата Равен произведению его длин на угол между ними.
a·b·sin α
где S — площадь параллелограмма,
— длина сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы ромба
- Формула квадрата Сторона ромба и высота
Квадрат ромба Равен произведению длины его стороны на длину высоты на высоту. - Формула Квадрата Сторона и угол Рома
Квадрат Рома Равен произведению квадрата его стороны на его сторону и углового синуса между сторонами ромба. - Формула Квадрата Рома на длинах его диагоналей
Ромба Квадрата Равен половине длины его длин диагоналей. где s — площадь рома,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1, 2 — длины диагоналей.
Формула Квадрата Трапеции
- Формула ГЕОНОН для трапеции
Где S — площадь трапеции
— длина основания,
— длина стороны трапеции, 3
Урок 1 | Площадь | 3 класс Математика
Цель
Понять, что площадь является атрибутом плоских фигур, который измеряется в квадратных единицах. Найдите площадь фигуры с помощью шаблонных блоков, которые можно использовать как конкретные нестандартные единицы.
Найдите площадь фигуры с помощью шаблонных блоков, которые можно использовать как конкретные нестандартные единицы.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89503.MD.C.5 — Распознавать площадь как свойство плоских фигур и понимать принципы измерения площади.
3.MD.C.6 — Измеряйте площади, считая квадратные единицы (квадратные сантиметры, квадратные метры, квадратные дюймы, квадратные футы и импровизированные единицы).
Основополагающие стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89501.Г.А.2
Критерии успеха
Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Поймите, что площадь — это мера того, сколько плоского пространства занимает объект.

- Сравните площади различных фигур, имеющих общие размеры или свойства.
- Найдите площадь различных фигур, заполнив пространство бетонными нестандартными элементами без зазоров и перекрытий (МН.5, МН.6).
- Найдите площадь фигуры несколько раз, используя единицы измерения разных размеров для разных измерений.
- Объясните, как множественные измерения одной и той же фигуры связаны с размером выбранной единицы измерения (MP.3).
Советы учителям
Рекомендации учителям по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Учебные материалы
- блоков узоров (минимум 6 квадратов, 12 кубиков) трапеции, 2 шестиугольника на учащегося или малую группу) — они также понадобятся учащимся для выполнения домашнего задания
- Шаблон: Области шаблонных блоков (по 1 на учащегося или малую группу)
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Якорные задачи
Задания, предназначенные для обучения критериям успеха урока, и рекомендации, помогающие привлечь внимание учащихся Проблема 1
Какая фигура занимает больше места: трапециевидный блок или синий ромб? Обосновать ответ.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 2
Площадь — это мера того, сколько плоского пространства занимает объект.
Используйте блоки шаблонов, чтобы решить, какая фигура в шаблоне: Области блоков шаблонов имеет наибольшую площадь. Будьте готовы объяснить свои рассуждения.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Каталожные номера
Иллюстративная математика, 3 класс, блок 2, урок 1, задание 2
, 3 класс, блок 2, урок 1, занятие 2, доступ к которому был осуществлен 12 октября 2022 г.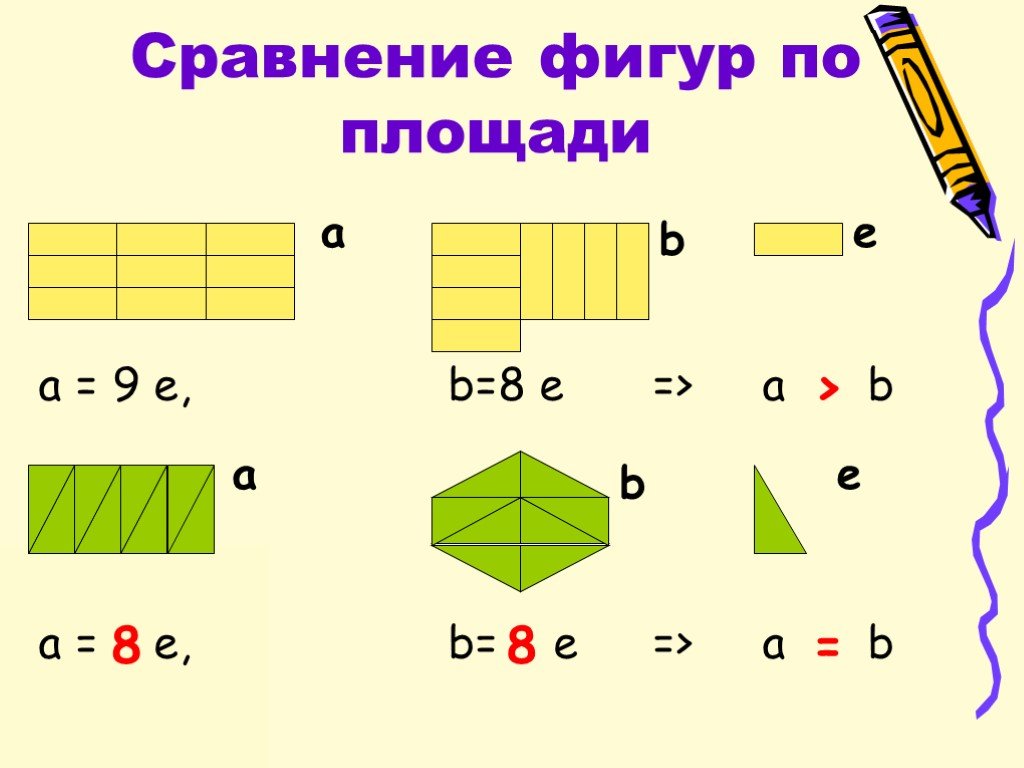 , 11:01, лицензирован Illustrative Mathematics в соответствии с CC BY 4.0 или CC BY-NC. -СА 4.0. Для получения дополнительной информации обращайтесь в Illustrative Mathematics.
, 11:01, лицензирован Illustrative Mathematics в соответствии с CC BY 4.0 или CC BY-NC. -СА 4.0. Для получения дополнительной информации обращайтесь в Illustrative Mathematics.
Изменено Fishtank Learning, Inc.
Ответ студента
Пример ответа на Целевое задание с ожидаемым от учащихся уровнем детализации.
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Создайте бесплатную учетную запись или войдите, чтобы просмотреть ответ учащегося
Набор задач и домашнее задание
Набор проблем
Домашнее задание
Ключи ответов
Ключи ответов для наборов задач и домашних заданий доступны при наличии подписки Fishtank Plus.
Обсуждение набора задач
- Сколько блоков треугольного узора нужно, чтобы покрыть блок ромбического узора? Используйте эту информацию, чтобы сказать о факте деления, который связывает количество треугольников, необходимых для покрытия фигуры А, с количеством ромбов, необходимых для покрытия той же фигуры.


 Рефлексия.
Рефлексия.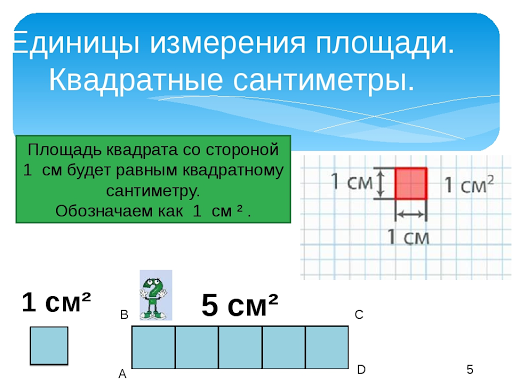 Мотивация к учебной деятельности
Мотивация к учебной деятельности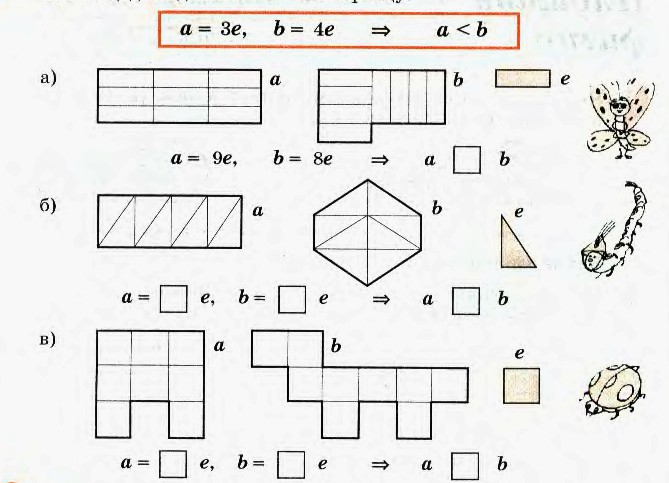
 Построение проекта выхода из затруднения
Построение проекта выхода из затруднения Первичное закрепление нового знания с проговариванием во внешней речи.
Первичное закрепление нового знания с проговариванием во внешней речи. Включение в систему знаний и повторение.
Включение в систему знаний и повторение.