Как посчитать площадь комнаты в квадратных метрах? – пошаговая инструкция и рекомендации
Подготовка к расчетам
Совсем несложно произвести расчеты обычной небольшой комнаты в 15 или 35 м квадратных при условии, что она обладает правильной, прямоугольной или квадратной формой. Обычно в типовой хрущевке самая большая комната имеет длину стен 4 м и 5 м, и соответственно общую площадь тут вычислить не составвит труда. Более маленькие правильные комнаты обладают стенами от 2 до 4 метров.
Ничего примечательного и сложного в подсчете площади таких комнат нет — банальная школьная арифметика просто находим произведение длины одной стены на ширину другой. Но не всегда все так просто, иногда бывают ситуации, когда для расчета придется поломать голову. Поговорим об этом ниже, а сейчас обсудим подготовительные моменты.
Для разных целей применяют разные единицы измерения. Обычно стены изначально измеряют в сантиметрах. И лишь затем готовую площадь пересчитывают в квадратные метры.
Важно! Первоначальные подсчеты делаются именно в сантиметрах для их большей точности. После полученная величина переводится в квадратные метры. Это сделано, чтобы избежать погрешностей в математических расчетах. Чтобы вычислить площадь комнаты в квадратных метрах, величину в квадратных сантиметрах необходимо разделить на 10000.
Произведение длины двух стен будет называться квадратной площадью комнаты или квадратурой помещения.
Для измерений потребуются немного инструментов, обычно хватает базового набора:
- ручная рулетка или электронная, лазерная рулетка;
- ручка/маркер/карандаш;
- лист бумаги;
- линейка;
- калькулятор.
Важно! Для помещений с нестандартной планировкой обязательно понадобится лист бумаги и карандаш, чтобы все измерения перенести на чертеж. Если комната имеет вид абсолютно правильной фигуры, то чертеж составлять нет необходимости. Но если есть сомнения в правильности углов комнаты, то необходимо проверить данные с помощью чертежа.
С таким минимальным набором инструментов легко получить необходимые данные и полностью рассчитать площадь комнаты.
Способы измерения
Измерять площадь комнаты можно несколькими способами. Самый простой метод подойдет для комнат в виде правильного, точного квадрата или прямоугольника. Для этого измеряются две смежные стены. Оба показателя нужно перемножить между собой.
По этой же формуле можно посчитать площадь стен, что зачастую нужно для закупки обоев:
- сначала измеряется высота и длина в сантиметра каждой из смежных стен;
- рассчитываются размеры смежных стен;
- показатели по каждой стене умножается на 2, так как вычисляется полная площадь стен по периметру;
- рассчитывается площадь окон и дверного проема;
- из общего размера вычитается площадь дверного и оконного проема.
Если есть сомнения в правильности фигуры помещения, то это проверить можно следующими способами:
- Вычисляем длину стен напротив и сравниваем между собой.
 Если она будет отличаться – значит помещение имеет неправильную форму. У комнаты правильной геометрической формы параллельные стены должны быть одинаковыми.
Если она будет отличаться – значит помещение имеет неправильную форму. У комнаты правильной геометрической формы параллельные стены должны быть одинаковыми. - Проверить по плану БТИ или по другим чертежам.
- Измерить длину всех стен и создать свой чертеж на бумаге. Этот кропотливый способ подойдет, если есть существенные сомнения в правильной форме комнаты, которые показали предварительные замеры.
В стандартном помещении общая площадь потолка равна площади пола. Но если есть уклон стен, то эти величины могут различаться. Если рассчитать размеры комнаты требуется для проверки других схем, например, показаний застройщика, то достаточно сделать измерения около пола. В квартире, где нет мебели, это сделать довольно удобно.
Если необходимо рассчитать количество строительных материалов для потолка и для пола обычно делают замеры в двух местах: ближе к полу и ближе к потолку.
Важно! Сравнение точных размеров пола и потолка покажет, есть ли существенная кривизна стен в этом помещении.
Пошаговая инструкция измерения
Сделать необходимые замеры для расчета размера комнаты несложно. Но здесь есть некоторые нюансы. Особенности измерений:
- перед измерением по возможности нужно освободить комнату от мебели;
- замеры необходимо делать вдоль стены в 5-10 см от пола и на таком же расстоянии от потолка;
- если освободить комнату от мебели не представляется возможным, то нужно замерять максимально ближе к потолку;
- при замерах держать инструмент: рулетку или лазерный луч – необходимо строго параллельно полу, для чего можно воспользоваться уровнем.
Важно! Располагайте инструмент либо близко к полу либо к потолку. Такое положение позволит избежать наклона и погрешностей в вычислении. Если вы измеряете где-то посередине стены, то очень сложно контролировать смещение измерительной ленты к полу или потолку.
Все измерения нужно записать на лист бумаги. Для точности расчета все измерения желательно проверить два раза.
После этого выполняется чертеж на бумаге с помощью карандаша и линейки. Если ваша комната правильной геометрической формы, то для расчета достаточно лишь перемножить длину двух смежных стен и перевести величину в квадратные метры. Пошаговый план действий будет во всех случаях одинаковый, единственное для комнат со сложной формой их будет значительно больше и важно будет сделать чертеж.
Если ваша комната правильной геометрической формы, то для расчета достаточно лишь перемножить длину двух смежных стен и перевести величину в квадратные метры. Пошаговый план действий будет во всех случаях одинаковый, единственное для комнат со сложной формой их будет значительно больше и важно будет сделать чертеж.
- Определяем две смежные стены и убираем все лишнее вдоль каждой.
- Фиксируем один край рулетки у основания первой.
- Тянем другой конец рулетки до упора в противоположную стену. Внимательно смотрим, чтобы не было провисаний и уклонов в стороны. Также важно, чтобы полотно было натянуто.
- Записываем размеры первой стороны в сантиметрах.
- Проделываем аналогичные манипуляции со смежной стеной.
- Для вычисления площади перемножаем и конвертируем в квадратные метры ( т.е. делим на 10000).
Ниже можете посмотреть видео-инструкцию для измерений площади с помощью дальномера:
Если выяснилось, что фигура помещения имеет малейшие отхождения от правильной формы, то определить площадь будет немного сложнее.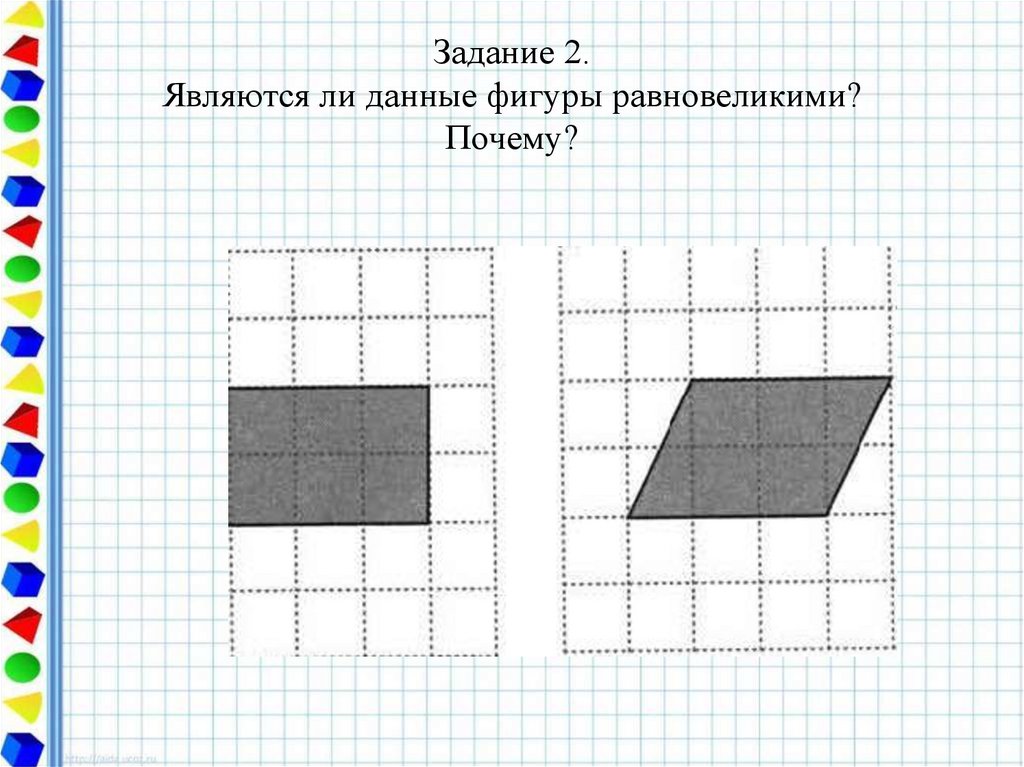
Особенности измерений нестандартных комнат
Для расчета размеров нестандартных помещений обычной формулы будет недостаточно. Комната будет иметь неправильную форму, если в ней есть такие элементы:
- эркеры;
- ниши;
- углы между смежными стенами больше или меньше прямого угла;
- срезанные углы;
- выступающие углы или другие элементы;
- скошенные стены.
То есть если одна стена будет длиннее противоположной на несколько сантиметров, то форма помещения будет неправильной, что повлечет изменения в расчетах. Для таких расчетов применяется простой метод:
- все помещение делится на несколько правильных фигур: трапецию, круг, треугольник;
- рассчитывается размер каждой фигуры в отдельности;
- полученные величины складываются между собой;
- величина переводится из квадратных сантиметров в квадратные метры.
Для расчета площади круга используют известную формулу:
S (площадь круга) = число Пи Х D(диаметр круга)2/4.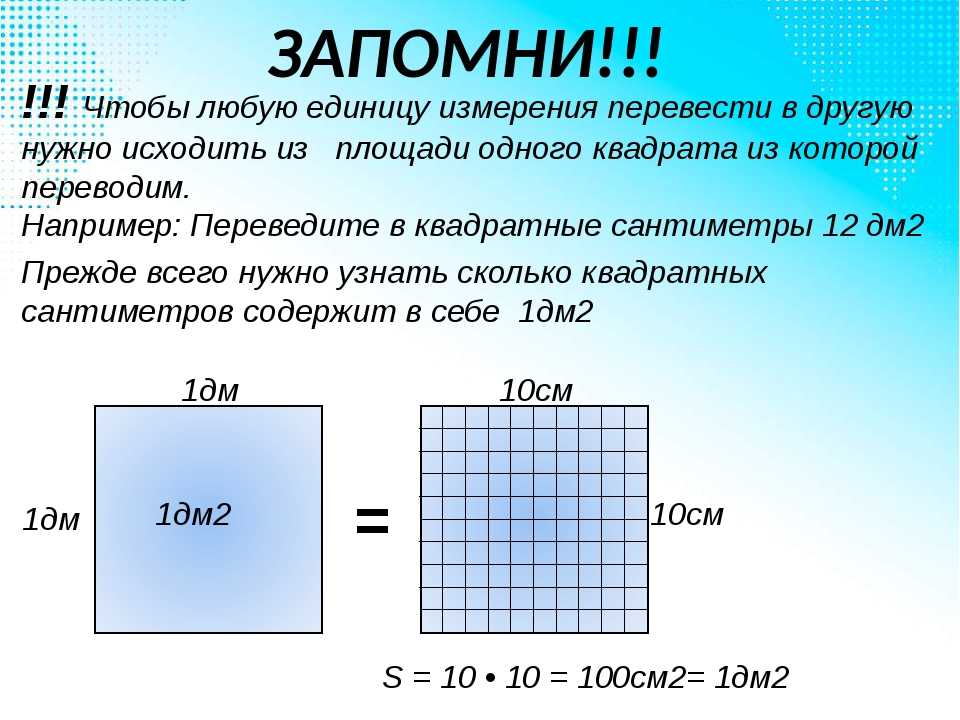
Если нужно рассчитать площадь полукруга – то полученную цифру достаточно просто разделить на 2.
Вычисления площади треугольника производятся по формуле:
S (площадь треугольника) = 1/2 b (высота треугольника) * h (основание треугольника).
Формула расчета площади трапеции также довольно проста:
S (площадь трапеции) = 1/2 h (высота трапеции) * (a (верхнее основание трапеции) + b (нижнее основание трапеции)
Важно! Все расчеты разных фигур, а затем сумму их площадей необходимо производить в сантиметрах. И лишь в финале их нужно округлить до метров. Иначе будут довольно большие погрешности.
Такие простые принципы расчета площади комнаты помогут вычислить размеры любого помещения, проанализировать его с точки зрения метража и закупить необходимые строительные материалы.
Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.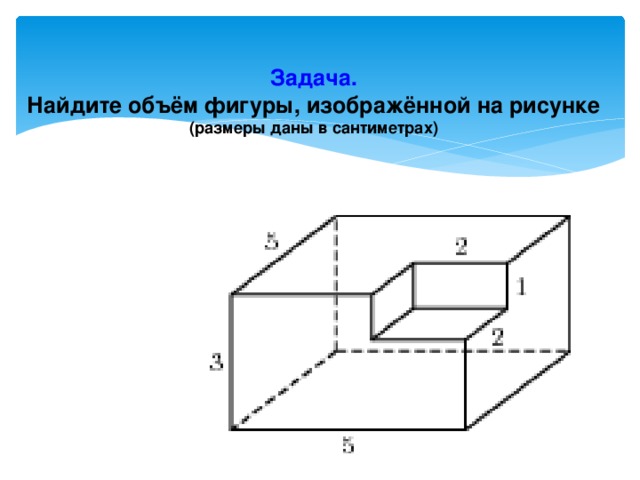
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3.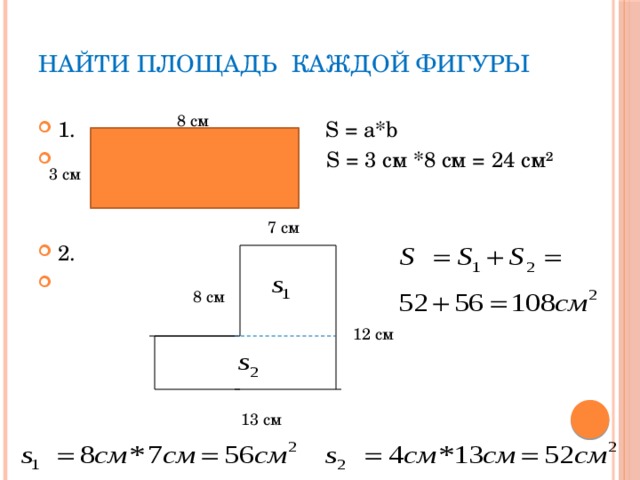 Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.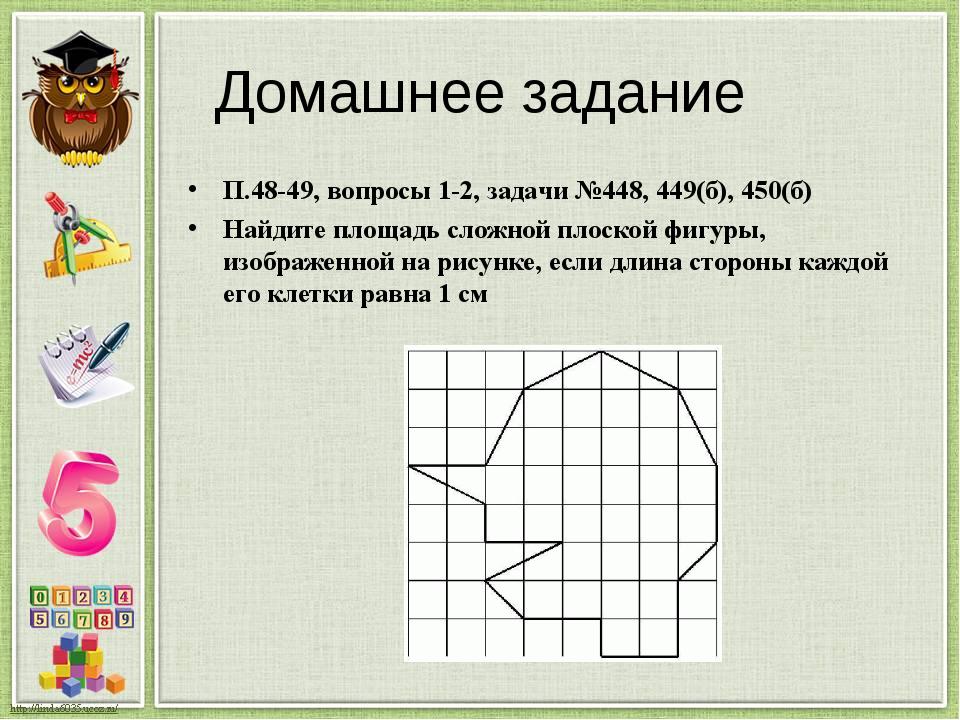
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. п. = 2 (ac + bc) |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Площадь земельного участка по документам не соответствует площади по замерам
Содержание статьи
У нас участок земли по документам 220 кв. м. Сосед с задней стороны участка сделал межевание, наш участок по одной стороне уменьшился на 0,6 м. В марте этого года мы занялись вопросом межевания. Пришел геодезист, замерил участок, площадь участка получилась 208 кв. м. Мы отказываемся подписывать документы, так как площадь по нашим документам не соответствует площади по замерам. Соседи предложили нам поставить забор по нашим документам, еще раз оплатить вызов геодезиста и провести новые замеры.
Какой путь является правильным?
Ольга Диулина
Консультаций: 58
Повторный вызов геодезиста с целью приведения границы в соответствиt с документами, по которым площадь участка равна 220 кв. м, и подписание документов об этом является менее затратным способом и более верным. В данном случае вы самостоятельно регулируете земельный спор. В противном случае — судебное разбирательство с проведением судебной землеустроительной экспертизы.
Добрый день. Хочу продать участок ИЖС в сельском поселении. Есть оформленное право собственности, кадастровый паспорт с указанием площади и планом участка.
Недавно соседи приглашали инженера и по замерам изменились контуры участка и площадь у него получилась меньше, чем в правоустанавливающих документах. Никаких договоров купли-продажи, дарения и т.д. с соседями не было. Скажите, нужно ли что-либо еще оформлять в связи с этим? (для продажи)
30 января 2017, 08:43 , Дмитрий, г. Казань Ответы юристов Макар Иванов Юрист, г.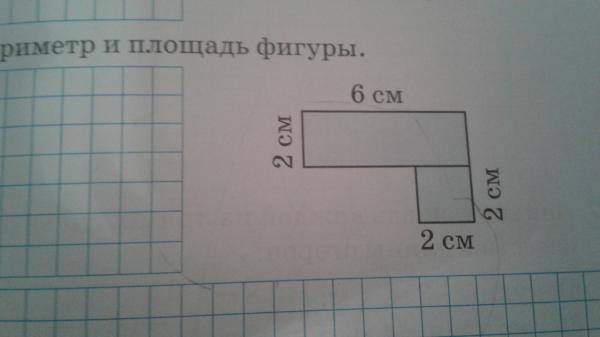 Самара Общаться в чате
Самара Общаться в чате
Здравствуйте. Для продажи нужен только договор, согласие супруги )если имущество куплено в браке). То, что Вы описываете это проблемы определения границ в связи с переходом от УСК к единой системе координат.
На отчуждение участка это не влияет.
30 января 2017, 08:53 Консультация юриста бесплатно Услуги юристов в Москве Мы договариваемся с юристами в каждом городе о лучшей цене. Похожие вопросы Недвижимость
Квартира не приватизировать, как её можно продать квартиросьемщику, если с ним прописан человек который отбывает срок,?
07 октября 2020, 07:46 , вопрос №2879711, татьяна, г. Москва Недвижимость
можно ли восстановить границы указанные в техпаспорте на жилой дом от 1979 года, на котором есть план земельного участка и в плане указаны только лишь длина и ширина участка. межевание было в 2009г.теперь сосед хочет оспорить свое же межевание и установить границы от 1979 года. и является ли план земельного участка в техпаспорте правоустанавливающим документом?
Показать полностью 04 декабря 2018, 05:26 , вопрос №2187257, Надежда, г. Куса Земельное право
Куса Земельное право
Обнаружено,что место положения земельного участка не соответствует его положению на кадастровой карте. Как это исправить? Участок в собственности 13 лет.
Ему присвоен адрес.В кадастровом отделе отказали в восстановлении настоящего месторасположения.
Показать полностью 11 июля 2017, 19:14 , вопрос №1693386, Людмила, г. Ростов-на-Дону Земельное право
Здравствуйте. Подскажите пожалуйта, что значит зонирование участка не соответствует цели. Хотела взять в аренду участок земли под установку не стационарного киоска для торговли, подала заявление на получение схемы в департамент , от них получила ответ что зонирование не соответствует цели.
В схеме отказали. Можно ли как то решить этот вопрос?
Показать полностью 09 октября 2016, 02:12 , вопрос №1401615, Светлана, г. Владивосток Земельное право
Справа смещена граница садового участка, вследствие чего уменьшена площадь садового участка (не соответствует кадастровому плану). У соседей имеются заборы, в том числе с бетонным основанием, тоже с наличием этого смещения (увеличена площадь крайнего правого участка в СНТ) . Для сохранения кадастровой площади участка и его благоустройства возможно смещение влево, здесь имеется огромная яма (мой участок крайний слева). В плане СНТ яма присутствует и моя граница должна идти по краю ямы. Раньше эта яма являлась частью системы водоотведения в целях осушения, сейчас этой системы не существует.
Для сохранения кадастровой площади участка и его благоустройства возможно смещение влево, здесь имеется огромная яма (мой участок крайний слева). В плане СНТ яма присутствует и моя граница должна идти по краю ямы. Раньше эта яма являлась частью системы водоотведения в целях осушения, сейчас этой системы не существует.
Я согласна вложить свои деньги и засыпать яму, чтобы привести участок в порядок и не тревожить соседей по вопросу переноса забора. Председатель кооператива категорически возражает и предлагает мне подать в суд или пользоваться участком меньшей площади, с чем я не согласна, так как участок мной был куплен очень дорого. Прошу Вашего совета, что мне делать.
Итак, вы планируете продать свой участок. А может купить новый или присоединить соседний? В любом случае вам необходимо знать точный размер владений.
Это поможет лучше сориентироваться в ценовом диапазоне и, что ещё важнее, правильно оформить документы на право собственности.
Итак, сколько квадратных метров в участке? Узнать это можно самостоятельно, не заказывая проект межевания у специалиста.
Есть несколько способов произвести расчет площади земли, но самым точным является аналитический. Он выполняется с помощью формул площади по измеренным линиям границ. На этом способе и остановимся.
Ведь линии границ у приусадебных или сельскохозяйственных угодий обычно чётко определены, а форма их зачастую представляет собой знакомую нам со школы фигуру – четырехугольник.
🔥 Вычисление площади по диагоналям и острому углу
Этот способ будет удобен в том случае, если участок слишком велик или непроходим для непосредственных измерений на местности, но имеется его вид сверху. Изображение на карте, на плане или даже фото с квадрокоптера.
Разумеется, для наиболее точных вычислений нужно как можно чётче выяснить масштаб. После этого нам понадобится измерить обе диагонали четырёхугольника (d1 и d2) и острый угол между ними (α).
Далее пользуемся формулой:
На калькуляторах манипуляции будут выглядеть так: сначала вводим величину острого угла, затем клавиша sin, перемножаем полученное число с данными о диагоналях и делим на два.
Вам необходимо сделать межевание своего участка в СНТ? В нашей статье есть перечень необходимых документов, а также правильный порядок действий.
В российском законодательстве есть несколько форм права владения землей. Подробно о каждом из них написано здесь.
🔥 Вычисление площади по сторонам
Если же границы участка можно измерить вручную, тогда нам пригодится второй способ. Здесь нам нужны будут лишь длины всех четырех сторон (a,b,c,d). Сложив их вместе и поделив полученное число пополам, мы получим полупериметр нашего четырехугольника (p):
Далее используем эту величину, вычислив корень из перемножения её с её же разностями со всеми четырьмя сторонами:
Для верности конечно лучше сочетать оба эти способа. Результаты вычислений должны совпасть или быть очень близкими. Однако каждый из них достаточно надёжен, если пользоваться точно рассчитанными величинами.
Наибольшая трудность здесь очевидно в выяснении исходных данных. Впрочем, их можно перепроверить, запросив официальные земельные документы у властей или поискав на официальных административных ресурсах. Стоит учитывать, что там площадь участков будет отмечена в гектарах.
Стоит учитывать, что там площадь участков будет отмечена в гектарах.
Или задайте вопрос юристу на сайте. Это быстро и бесплатно!
Онлайн калькулятор расчета площади земельного участка. Калькулятор расчета площади земельного участка по длине его четырех сторон. Введите длину сторон земельного участка и рассчитайте его площадь онлайн.
🔻 Калькулятор площади земельного участка
Простой способ рассчитать площадь земельного участка онлайн
🔻 Связанные Калькуляторы
Всем привет помогите рассчитать площадь участка земли по километражу это надо умножать на 1000 м чтобы получить в километрах
спасибо, очень помог при расчете на кривых участков
неправильно высчитывается площадь этим калькулятором. Меньше процента на 2.
зная только 4 стороны невозможно правильно определить площадьэто работает, только если участок примерно вписывается углами в окружностьчтобы правильно посчитать, нужно ещё два противолежащих угла знать. для этого нужны дирекционные углы из кадастрового плана
Как измерить сотку земли
Еще не так давно у большинства дачных участков размеры были одинаковыми, и за расчет принималась известная всем сотка. На сегодняшний день у многих владельцев в собственности нестандартные земельные наделы, в результате чего люди задаются вопросом как измерить сотку своего участка?
На сегодняшний день у многих владельцев в собственности нестандартные земельные наделы, в результате чего люди задаются вопросом как измерить сотку своего участка?
Интересный факт. Одной из старорусских мер длины считался ар, так вот в нем согласно современной системе исчисления ровно 100 квадратных метров или одна сотка. Чтобы стало окончательно понятно — это 10 метров в длину и столько же в ширину.
Существует множество способов узнать площадь земельного участка, это могут быть колышки, измерение сотки земли шагами, а также применение специальных средств таких как рулетка, дальномер, техномер и тому подобные современные технологии.
Автор статьи Харлов Андрей Юрьевич — директор ООО «Азия Стриж» — производство самозатачиваещегося садового инструмента Стриж с 1992 года. Перейти в каталог садового инструмента
🔥 Измерение сотки земли палкой
Для этого метода вычисления площади участка понадобится палка длина которой соответствует метру, двум или трем. Здесь каждый выбирает свои параметры для удобства. Замеры производятся очень просто: 10 раз проходят с палкой по ширине площади, а потом по длине, в сумме получается одна сотка.
Здесь каждый выбирает свои параметры для удобства. Замеры производятся очень просто: 10 раз проходят с палкой по ширине площади, а потом по длине, в сумме получается одна сотка.
Подобны промеры проводятся по всему участку, затем суммируются и подводится итог.
Маленькая хитрость. Некоторые землевладельцы к палке прикрепляют еще 2 ветки чтобы получился «шагающий» треугольник. В результате увеличивается точность всех замеров.
Измеряем сотку земли палкой
🔥 Как применить рулетку для замера земельного участка
Наиболее точный и простой метод при измерении участка получается с помощью рулетки. Площадь узнается в метрах, а затем переводится в сотки. В том случае, если владение относительно большое, для удобства нужно обзавестись колышками. Первый вбивается в начале участка, следующий как закончится длина рулетки и т.д.
Аналогичные действия проводятся по ширине. Если надел имеет форму правильного прямоугольника, то в измерениях противоположных сторон нет необходимости, они будут такими же.
Измеряем сотку земли в метрах рулеткой
🔥 Неправильная форма участка, как провести необходимые измерения
Вышеописанные методы удобны для проведения замеров на участке, имеющем правильную форму. Как измерить земельный участок в сотках если он имеет изгибы, или неравные стороны? В этом случае проводятся вычисления каждой стороны, а также измеряется градус углов, можно померить по диагоналям.
Полученные данные рекомендуется записать, чтобы не забыть и не запутаться.
Как измерить сотку земли неправильной формы
Для простоты работы можно разбить территорию на различные геометрические фигуры, а затем вычислить площадь каждой из них, просуммировать результат. Итог делится на сто, и конечная цифра равняется количеству соток.
При наличии преград, которые могут мешать производить замер, рекомендуется обратиться за помощью в геодезическую компанию.
Самозатачивающийся культиватор Стриж
🔥 Как замерить сотку земли, если она расположена на склоне
Далеко не все участки — это ровная поверхность, что же делать если есть склон? Для этого случая существует специальный прибор под названием нивелир.
Измеряем участок на склоне в сотках
Чтобы провести замеры при помощи механического устройства, по центру земли устанавливается рейка, а прибор для измерения устанавливается в горизонтальной плоскости. На межевом камне вертикально ставится рейка и проводятся замеры, полученный итог записывается. Затем рейка для измерений переносится к другому межевому камню, и снова определяются значения.
Таким образом, узнается наклон местности и при использовании правила треугольника получается нужное значение.
🔥 Как измерить сотку земли шагами
Если под рукой нет необходимых предметов для замеров, то узнать площадь участка можно простыми шагами. Данный метод весьма простой, главное учитывать, что у каждого человека индивидуальная длина шага. Изначально определяется метровое расстояние, а затем проводится несколько тренировок чтобы шаг был равен именно метру, для этого достаточно просто широко шагнуть.
Измеряем сотку земли шагами
Измерить сотку земли шагами можно проведя вычисление свободного шага в сантиметрах и последующем его переводе в метры, к примеру, шаг равняется 0,6 м. Но это создаст дополнительные трудности при выбранном способе измерения, лучше потренироваться шагать.
Но это создаст дополнительные трудности при выбранном способе измерения, лучше потренироваться шагать.
Для получения результата при измерении сотки земли шагами высчитывается количество шагов по длине и ширине участка. Затем обе цифры перемножаются и получается площади владений. Чтобы окончательно разобраться достаточно взглянуть на простой пример, когда были произведены измерения сотки земли шагами.
Берется длина шагов 50 соответственно она в метрах, и ширина 40. Цифры перемножаются и получается 2000 квадратных метров. Полученная площадь сотки делится на 100 и получается 20 соток.
Измерить сотку земли шагами очень просто.
🔥 Как измерить сотку земли в метрах
В статье уже упоминалось чему равна сотка земли, стоит остановиться на этом вопросе более подробно. Измерение сотки в метрах подходит для расчета небольшого надела земли каковым могут является дача или огород.
Интересный факт. Понятие сотки принято на официальном уровне, и нередко в документации встречается текст, где приводится расчет стоимости земельного надела именно в сотках.
Чтобы не запутаться, как измерить сотку земли в метрах нужно помнить:
Площадь одной сотки равняется ста метрам квадратным, достаточно представить земельный надел имеющий 10 метров в длину и столько же в ширину.
Измеряем сотку земли в метрах
🔥 Как измерить сотку земли, если площадь дана в других единицах измерения
Очень часто на документации предлагаемых для продажи земельных наделов стоят цифры площади в гектарах, акрах метрах или иных обозначениях, возникает вопрос, как измерить площадь участка в сотках?
В Российской Федерации площади участков земли измеряются следующим образом:
- в одной сотке – 10 х 10 = 100 метрам квадратным;
- 1 гектар равняется 100 х 100 метров = 10000 метрам квадратным = 100 соткам;
- 1 гектар равняется ста арам = 100 х 100 = 10 000 метров в квадрате
Принятое в настоящее время обозначение гектара образуется при добавлении частички «гекто» в единицы измерения площади ар.
Под понятием ара понимается площадь фигуры квадрат имеющая сторону в 10 метров, возникает вопрос, как измерить площадь участка в сотках если она приводится в арах? Нет ничего проще, вот простой пример.
Земельный надел 4 ара, а значит 1 ар равняется 10 х 10 метров. В этом случае 40 х 40 = 400 квадратных метров или 4 сотки.
На территории некоторых стран основной мерой измерения площади служит акр. Задумав приобрести участок за границей, нелишним будет ознакомиться, как измерить сотку земли в более привычных метрических системах.
В одном акре 4840 квадратных ярдов, что равняется 4046, 86 квадратных метров. Зная этот расчет, не составит труда совершить измерение участка в сотках.
Средние земельные участки для семей, имеющих нормальный доход располагаются на площади в 10 соток, что в итоге равняется сотне метров в квадрате. На таком земельном наделе, можно проживать вполне комфортно. Исходя из этого принципа, земельные наделы такой площади являются одними из самых востребованных.
Здесь можно возвести дом, разбить садовый участок и всячески наслаждаться единением с природой.
В статье было рассказано о наиболее популярных способах измерения участков, как перевести одну единицу измерения в другую, какие подручные средства можно использовать, и как обойтись без них в случае крайней необходимости.
Что делать , если площадь земельного садового участка , не соответствует площади заявленной в документах на собственность земельного участка?
🔻 Ответы:
Вы серьезно хотите получить компетентный ответ от незнакомых людей в интернете?
Смотрите, заходите сюда, оформляете бесплатный доступ на 2 дня ко всей базе знаний Консультант + и за это время находите и ответ на свой вопрос, и судебную практику, и все формы документов с примерами заполнения, какие вам только понадобятся.
Источники информации
http://pravo.rg.ru/rubrics/question/3308/
http://pravoved.ru/question/1518298/
http://chistayrabota.ru/kak-izmerit-uchastok-nepravilnoj-formy/
http://ppt.ru/question/?id=66663
как найти периметр? Общая для всех фигур теория
Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.
Общая для всех фигур теория
Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.
Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.
Формулы периметров разных фигур
Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.
Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).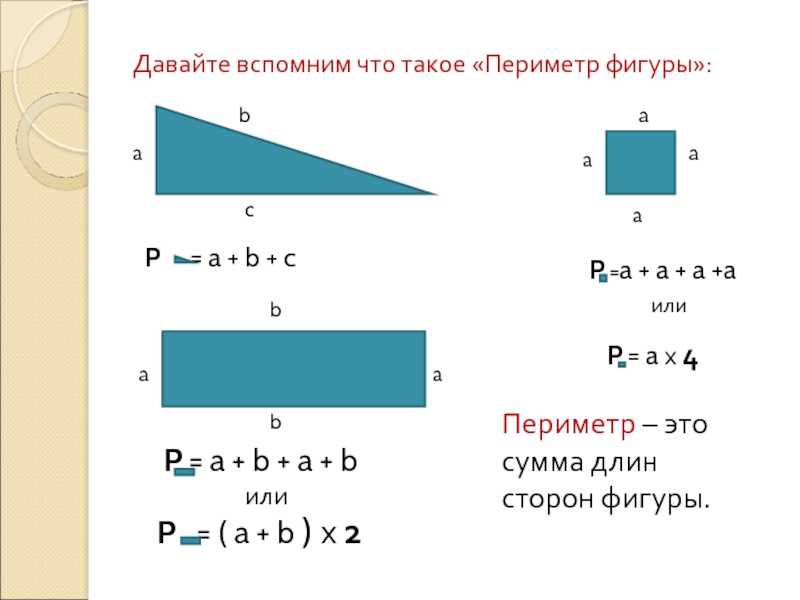
Как быть, если неизвестна длина одной или нескольких сторон треугольника?
Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).
Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.
Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.
В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.
Его нужно вывести из данной формулы и умножить на два.
Примеры задач
Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.
Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.
Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.
Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.
Как найти периметр обычного прямоугольника
Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:
Складываем все стороны.
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.
Решение (последовательность действий и рассуждения):
- Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда.
 Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины. - Складываем все стороны (3 + 3 + 6 + 6) = 18 см.
Ответ: P = 18 см.
Второй способ заключается в следующем:
Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.
В рамках данной задачи получим такое решение:
2×(3 + 6) = 2×9 = 18.
Ответ: P = 18.
Как найти периметр прямоугольника – квадрат
Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:
- Сложить все его стороны.
- Умножить его сторону на 4.
Пример: Найти периметр квадрата, если его сторона = 5 см.
Так как нам известна сторона квадрата, мы сможем найти его периметр.
Складываем все стороны: 5 + 5 + 5 + 5 = 20.
Ответ: P = 20 см.
Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.
Ответ: P = 20 см.
Как найти периметр прямоугольника – онлайн-ресурсы
Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.
Построение урока:
- Организация и мотивация учащихся к деятельности на уроке.
- Организация восприятия нового материала на основе наглядного материала
- Организация осмысления.
- Первичная проверка понимания нового материала.
- Организация первичного закрепления и самостоятельный анализ учебной информации.
- Применение полученных знаний на практикуме.
Цели урока:
- Обучающая. Обеспечить усвоение учащимися нахождения площади и периметра геометрических фигур;
визуального восприятия материала на уроке; осмыслено понимать, что такое площадь и периметр.
2. Развивающая. Использовать на уроке развивающие упражнения, активизировать
мыслительную деятельность школьников.
3. Воспитательная. Обеспечить развитие ценностно-смысловой культуры учащихся;
мотивации на умение правильно достигать поставленной цели —
совпадение ожидания и результата.
Оборудование:
- М.И.Моро и др. “Математика” — учебник для 3 класса начальной школы, 1 часть.
- Рабочая тетрадь по математике.
- Ручка, линейка, простой карандаш, треугольник, ножницы.
- Модели геометрических фигур для нахождения площади.
- Над доской плакаты с формулами нахождения площади и периметра.
Средства обучения:
- Дидактический материал.
- Наглядные пособия.
Приемы обучения:
- Сравнение предметов.
- Сопоставления способов нахождения площади
одной и той же фигуры.

Ход урока.
1. Организационный момент и сообщение темы урока.
Учитель: Здравствуйте, ребята. Сегодня мы продолжим изучение большой темы под названием “Площадь и периметр”. Тема нашего урока сегодня:“Умение применять знания в нахождении периметра и площади сложной фигуры”. Сложная фигура – это геометрическая фигура, состоящая из нескольких простейших фигур. Сначала, повторим то, что мы с вами изучили на прошлых уроках.
II. Устный счет.
Задачи на развитие.
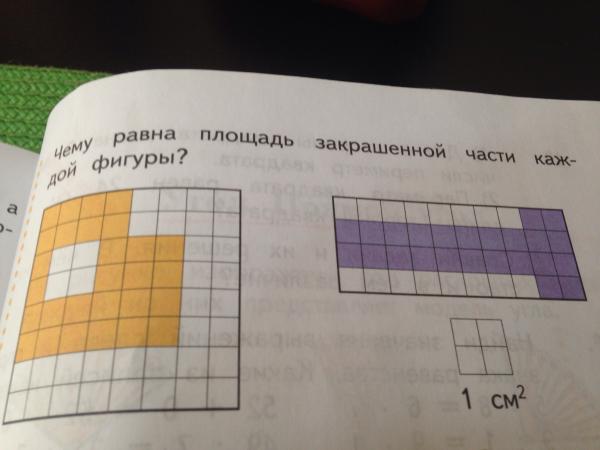
Учитель: Найдите площадь данной фигуры, если сторона квадрата 1 см.
Фигура изображена на доске.
Ученик: Если 1 квадрат имеет площадь 1 см 2 , а квадратов изображено 5, то площадь этой фигуры равна 5 см 2 .
Учитель: Правильно. Следующее задание. Уберите 3 палочки, чтобы осталось 3 таких квадрата.
Ученик выходит к доске и убирает 3 палочки.
Учитель: Уберите 4 палочки, чтобы осталось 3
таких же квадрата.
Ученик выходит к доске и убирает 4 палочки. Решение.
III. Работа по теме урока
Учитель: Какие геометрические фигуры вы уже знаете?
Ученик: Прямоугольник.
Ученик: Квадрат.
Учитель: Правильно. Что мы знаем о квадрате?
Ученик: У квадрата 4 стороны и 4 угла.
Учитель: Правильно. Каким свойством обладают стороны квадрата?
Ученик: Они равны.
Учитель: Правильно. А какие углы у квадрата?
Ученик: Они прямые.
Учитель: С помощью чего мы можем построить прямой угол?
Ученик: С помощью треугольника.
Учитель: Давайте построим квадрат со стороной 4 см в вашей тетради. С помощью каких инструментов мы будем чертить квадрат?
Ученик: С помощью линейки, карандаша и треугольника.
Ученики в тетрадях строят квадрат и раскрашивают его.
Учитель: Эта геометрическая фигура. Как найти периметр и площадь этого квадрата?
Ученик: Периметр – это сумма всех его сторон.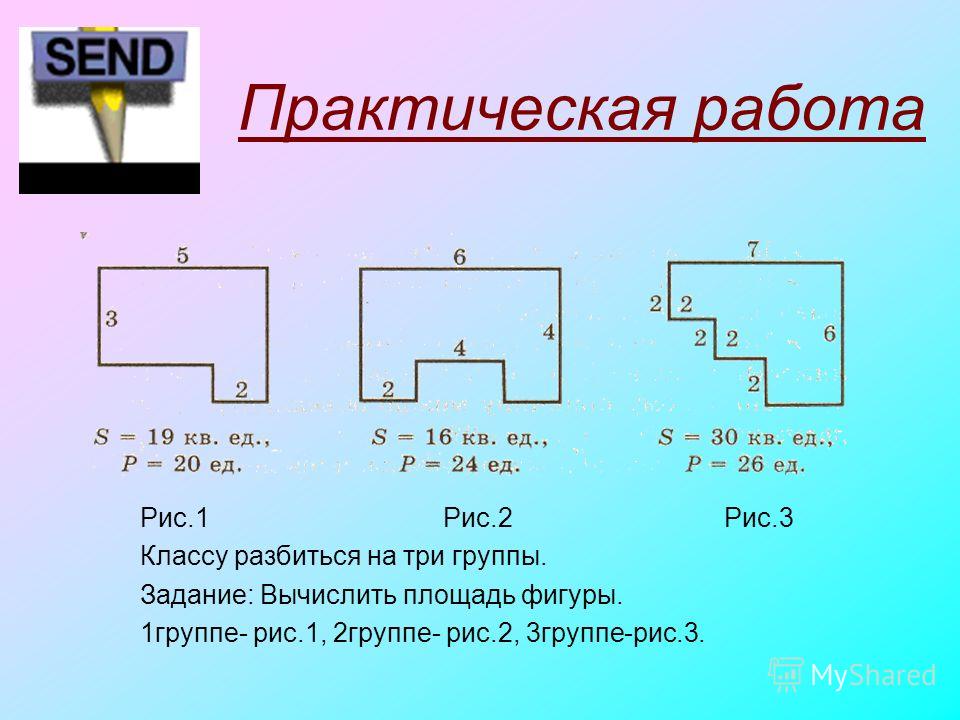 Сторон у квадрата 4. Значит, 4 сложим 4 раза.
Сторон у квадрата 4. Значит, 4 сложим 4 раза.
Учитель: Как это записать?
Ученики делают запись в тетради: “Найти площадь фигуры F1”.
Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 + 4 = 16 (см)
Ученики делают запись в тетради.
Учитель: В каких единицах еще измеряется периметр?
Ученик: В сантиметрах, в миллиметрах, в метрах, в дециметрах, в километрах.
Учитель: Молодец! Как еще можно записать периметр?
Ученик: С помощью умножения.
Ученик записывает на доске: Р = 4 · 4 = 16 (см)
Ученики записывают в тетради.
Учитель: А чему равна площадь квадрата?
Ученик: Длину квадрата умножаем на его ширину. Так как стороны у квадрата равны, то
S = 4 · 4 = 16 (см 2)
Ученики делают запись в тетрадке и записывают — “Ответ: S = 16 см 2 ”.
Учитель: Какие еще единицы измерения площади вы знаете?
Ученик: квадратный сантиметр, квадратный
дециметр, квадратный метр, квадратный миллиметр.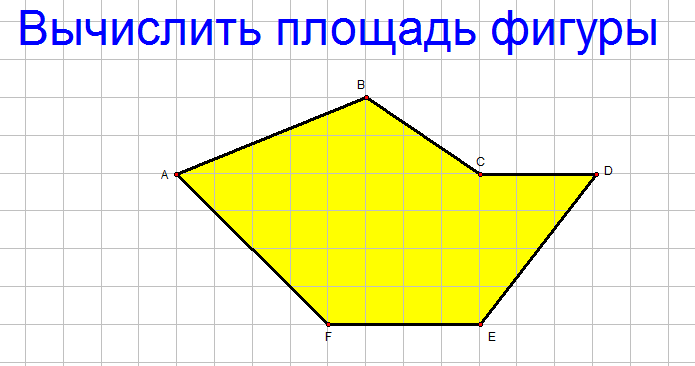
Учитель: А теперь усложним задачу. Перед вами лежит карточка.
На этой карточке изображен квадрат такой же, что и у вас в тетрадке. В середине этого квадрата — еще один квадрат со стороной 2 см. Сейчас вы возьмете ножницы и вырежете аккуратно этот маленький квадрат.
Ученики выполняют эту работу и делают запись в тетрадке: “Найти площадь фигуры F2”.
Учитель: У нас получилась фигура “с окошком” — F2. Как можно найти площадь этой интересной фигуры? Площадь квадрата уже известна и равна 16 см 2 .
Ученик: Нужно найти площадь маленького квадратика со стороной 2 см.
Ученик выходит к доске и записывает – S2 = 2 · 2 = 4 (см 2)
Ученики делают запись в тетрадке
Ученик: Из площади большого квадратика вычесть площадь маленького.
Учитель: Правильно.
Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12 (см 2)
Ученики делают запись в тетрадке.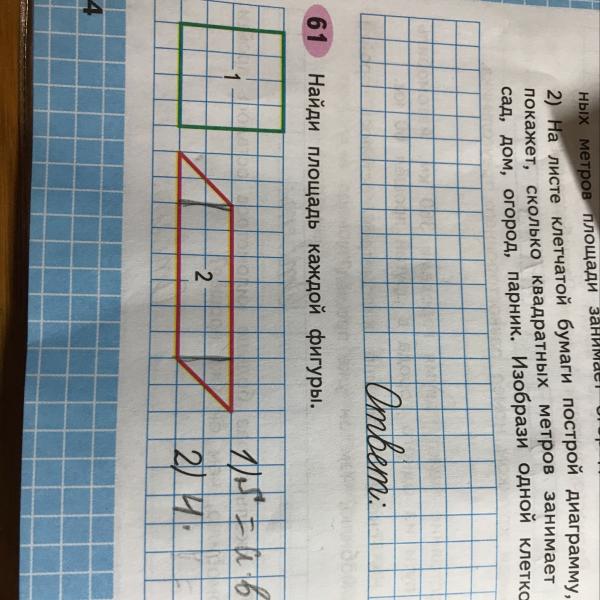
Учитель: Внимательно посмотрите на эту фигурку и скажите, как еще можно измерить площадь? Можно ли эту фигуру как-то разрезать, чтобы получить фигуры, уже знакомые вам?
Ученики думают и говорят разные варианты.
Один из вариантов оказался очень интересным.
Ученик: Можно так разрезать, чтобы
получились прямоугольники и показывает на доске, как это можно сделать.
Ученики разрезают фигуру, как показано на доске.
Учитель: А как находится площадь прямоугольника?
Ученик: Нужно длину умножить на ширину.
Учитель: У вас получилось четыре фигуры. Что можно сказать про них?
Ученик: Две фигурки, как близнецы – одинаковые, и вторые две – тоже одинаковые.
Можно найти площадь одной фигуры и умножить на 2.
Ученик решает на доске: S1 = 1 · 4 = 4 (см 2)
S2 = 1 · 2 = 2 (см 2)
S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см 2)
Учитель: Молодец! У нас получилась то же
значение площади, что и раньше.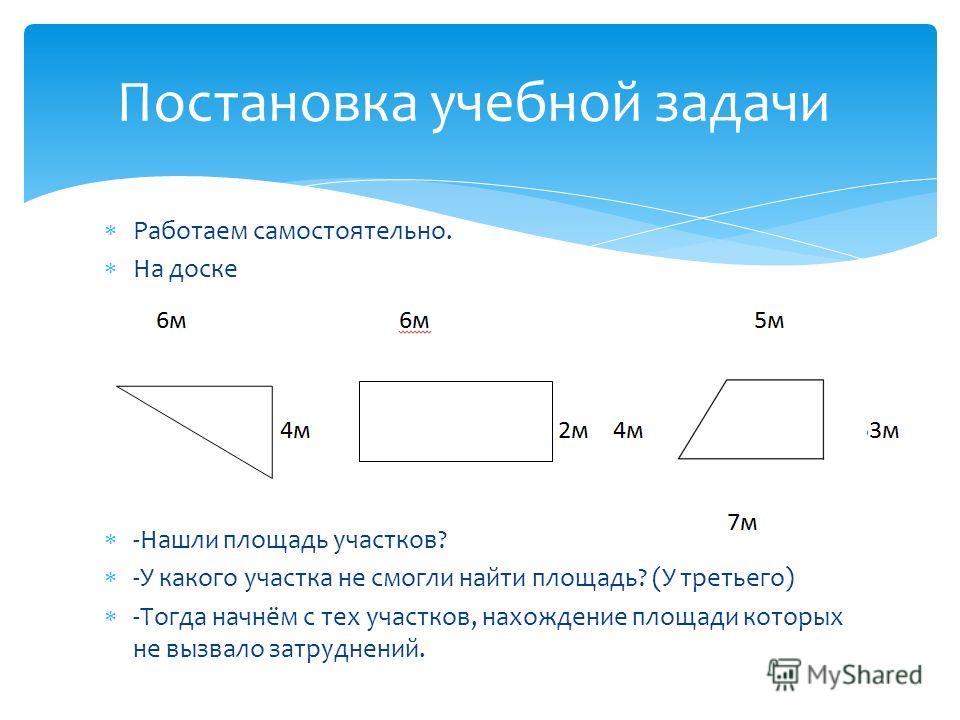
Ученики пишут в тетрадке – “Ответ: S = 12 см 2 .”
Учитель: Вы, наверное, устали?
Настало время отдыхать.
Предлагаю усталость
Физкультминуткой снять.
IV. Физкультминутка.
Каждый день по утрам
Делаем зарядку (ходьба на месте).
Очень нравится нам делать по порядку:
Весело шагать (ходьба),
Руки поднимать (руки вверх),
Приседать и вставать (приседание 4-6 раз),
Прыгать и скакать (10 прыжков).
Учитель: А теперь сели за парты и
посмотрите на следующую модель. Фигура F3
Как найти площадь этой интересной фигуры?
Ученик: Треугольник, который выступает
можно отрезать и подставить в ту часть, где
треугольник “уходит” внутрь.
Учитель: Давайте возьмем ножницы, отрежем треугольник и подставим в верхнюю часть.
Что за фигура у нас получилась?
Ученик: Прямоугольник!
Учитель: Как найти площадь этого прямоугольника,
Если стороны нам неизвестны.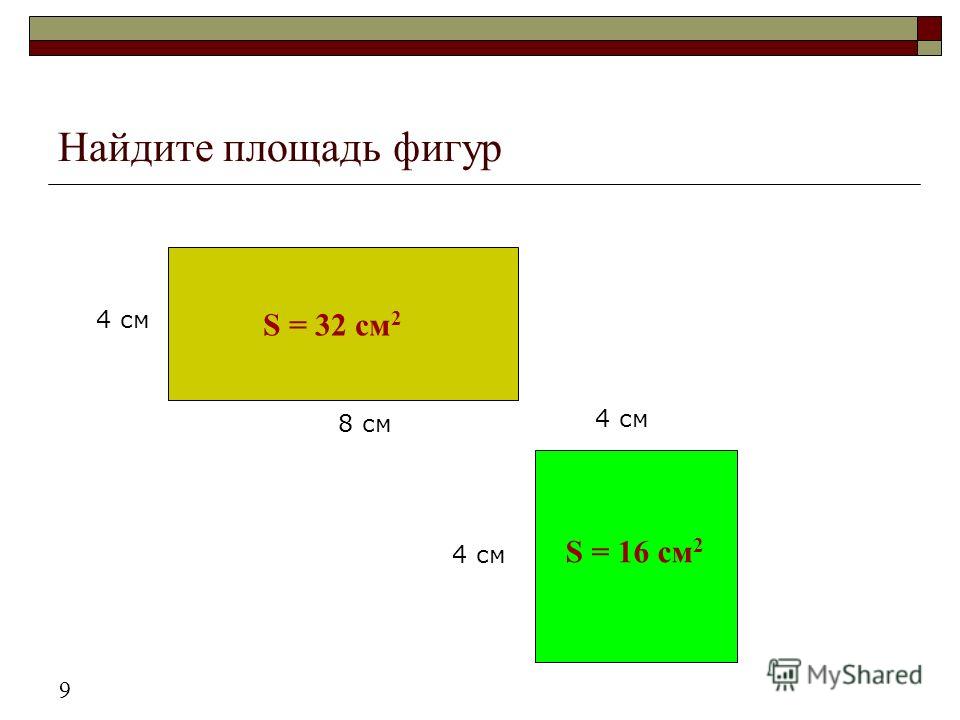
Ученик: Мы можем взять линейку и измерить
длину и ширину прямоугольника.
Ученики делают запись – “Найти площадь фигуры F3”.
Ученики линейкой измеряют длину и ширину. Получается длина, а = 6 см, ширина в = 2 см.
Ученик: Площадь данной фигуры равна S = 6 · 2 = 12 (см 2).
Ученики делают запись в тетрадке и записывают – “Ответ: S = 12 см 2 .
Учитель: Но это еще не все. Перед вами следующая фигура. Необходимо найти ее площадь.
Что за фигура перед вами?
Ученик: Треугольник. Но площадь треугольника
мы не умеем находить!
Учитель: Это правда. Из этого треугольника
сделаем прямоугольник. Я вам подскажу. Фигура F4
Сначала мы этот треугольник сложим пополам
Ученики: Мы поняли! Правую
сторону переворачиваем.
Получится прямоугольник.
Ученик: С помощью линейки измеряем
длину а и ширину в, и по S = а· в,
находим площадь.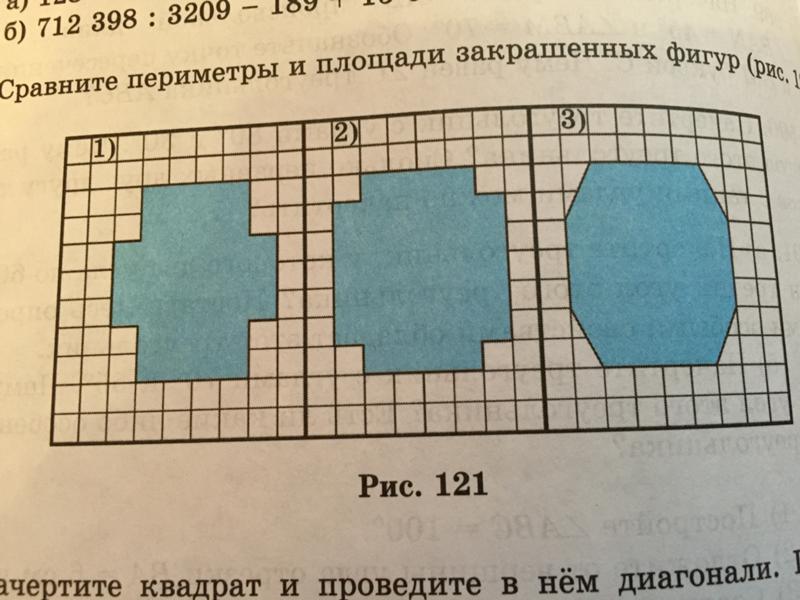
Учитель: Если мы при измерении, мы
получим, что длина
будет выражена в мм, а ширина в см,
что нам делать?
Ученик: Обязательно длину и ширину перевести в одну единицу измерения.
Ученики записывают в тетрадке: “Найти площадь фигуры F4”.
V. Работа в парах.
Учитель: А теперь я предлагаю поработать в паре. Вас за партой двое. Один ученик (I вариант) находит периметр данной фигуры, а второй (II вариант)- площадь.
Для этого начертим в тетради эту фигуру. После того, как вы выполните задание, поменяетесь тетрадями и проверите результаты друг у друга.
Ученики выполняют задание и результаты
записывают в тетрадь.
Учитель: Что у вас получилось?
Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)
S = 3 · 3 = 9 (см 2) 3 см
Ученики записывают: “Ответ: P = 12 см, S = 9 см 2 .
Учитель: Молодцы! А теперь я вам предлагаю
поработать самостоятельно.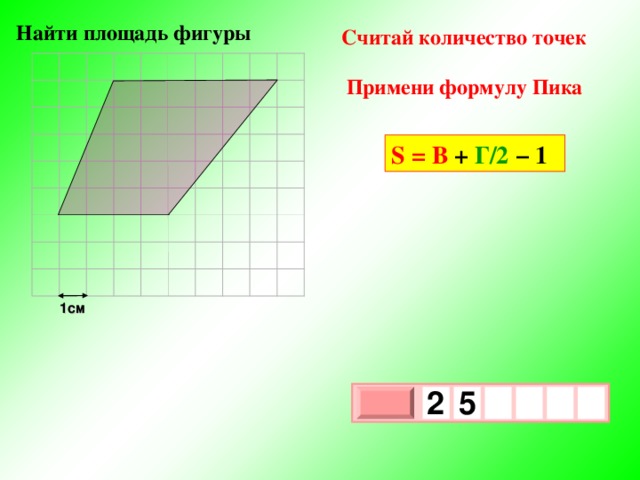
Найти площадь следующей фигуры. Она лежит перед вами.
VI. Самостоятельная работа по закреплению изученного материала.
Учитель раздает заранее заготовленные фигуры.
Ученики самостоятельно, без помощи учителя, разрезают эту фигуры, получают три прямоугольника.
Ученики делают запись: “ Найти площадь фигуры F5”.
Ученики находят S1 = 4 · 3 = 12(см 2), S2 = 2 · 1 = 2(см 2), потом находят площадь данной фигуры: S = S1 + S2 + S2 = 12 + 2 + 2 = 16 (см 2) и делают запись в тетради, затем
записывают: “Ответ: S = 16 см 2 ”.
Учитель: Понравился урок?
Ученики: Да.
Учитель: Что вы нового узнали на этом уроке?
Ученик: Мы научились находить площадь и периметр сложных фигур. Это оказалось очень просто. Нужно немного подумать и эту фигуру перестроить или переделать в ту, периметр и площадь, которой, мы уже умеем находить.
Учитель: Я очень рада, что вам понравилось.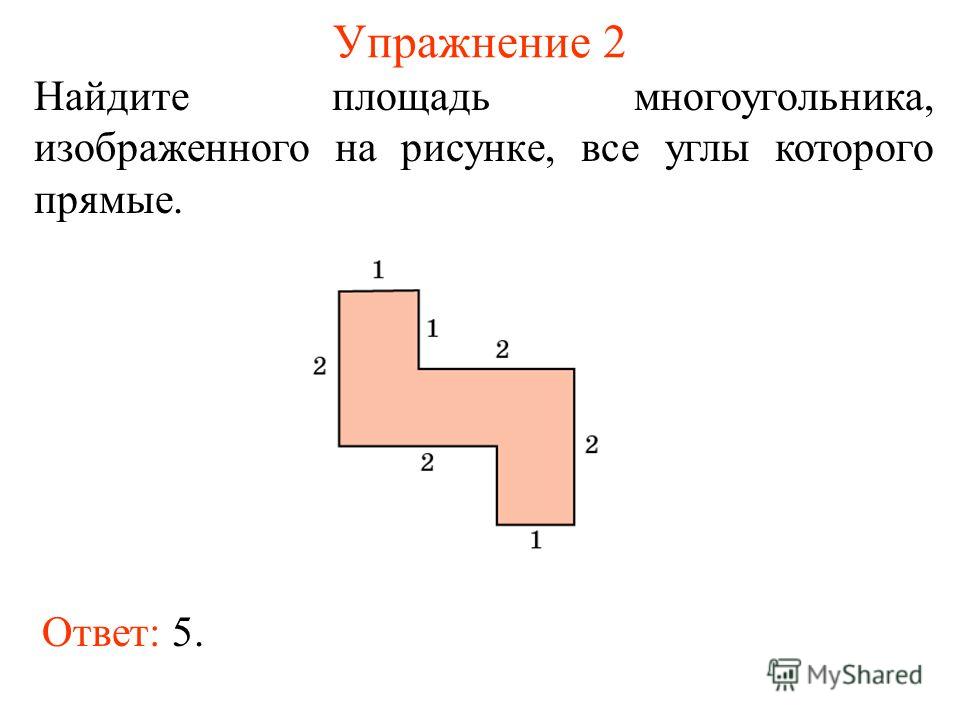 Дома еще раз повторить формулы нахождения
периметра и площади квадрата и прямоугольника;
вспомнить, как переводить одну единицу
Дома еще раз повторить формулы нахождения
периметра и площади квадрата и прямоугольника;
вспомнить, как переводить одну единицу
в другую. Сегодня хорошо отвечали следующие ученики. . .
Учитель выставляет оценки.
VII. Домашнее задание: учебник стр. 77 № 8.
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
Как найти периметр квадрата
Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.
Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Как найти периметр треугольника
Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Как найти периметр параллелограмма
Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Как найти длину окружности
Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.
Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).
Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.
Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.
C) .
Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника
В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника
В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .
C) .
После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.
Итого, P=32x+2∙2x+2∙x=38x .
?) .
Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .
D) .
Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.
Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.
Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .
E) .
Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .
B) .
Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .
D) .
Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.
В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.
Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .
B) .
Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:
P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .
«Как вычислить площадь фигуры неправильной формы?» — Яндекс Кью
ПопулярноеСообщества
Стать экспертом Кью
МатематикаГеометрияПлощадь
Анонимный вопрос
·
94,6 K
Ответить1УточнитьИнженер конструктор
169
Разработка чертежей и 3D моделей на заказ в Компас 3D и AutoCad. Опыт в инжиниринге… · 26 окт 2021 · pavelsamuta.business.site
Опыт в инжиниринге… · 26 окт 2021 · pavelsamuta.business.site
Отвечает
Павел Самута
Можно ее начертить в программе Компас 3 D и воспользоваться функцией расчет площади плоской фигуры. Либо разбить на фигуры правильной формы вашу деталь и посчитать методом суммирования и вычитания площадей.
Разработка чертежей и 3D моделей на заказ в Компас 3D и AutoCad. Опыт ≧ 12 лет
Перейти на pavel-samuta.livejournal.comКомментировать ответ…Комментировать…
Первый
Александр Бражник
Математика
48
Люблю математику, люблю решать задачи и учиться. · 22 янв 2021
Помещаем исходную фигуру F внутри фигуры K1, площадь которой легко посчитать ( например состоящей из квадратов). Далее размещаем внутри F фигуру L1, площадь которой аналогично легко посчитать. Положим
S1=( K1+L1)/2. Если точность оценки — например K1-L1< a — нас устраивает, то S1-искомая площадь. Если не устраивает, на втором шаге помещаем F внутри K2, так чтобы K2… Читать далее
Положим
S1=( K1+L1)/2. Если точность оценки — например K1-L1< a — нас устраивает, то S1-искомая площадь. Если не устраивает, на втором шаге помещаем F внутри K2, так чтобы K2… Читать далее
13,4 K
Комментировать ответ…Комментировать…
Первый
ВЛАДИМИР ДЕМИДОВ
1
20 сент 2020
Могу лишь намекнуть принцип. Из физики 8-го класса известно,что ЭДС фотоэлемента зависит от светового потока ,падающего на него Тогда идея измерения пощади будет заключаться в измерении напряжения ,вырабатываемого фотоэлементом при помощи откалиброванного в еденицах площади измерительного прибора,на который падает поток света. Если подложка из фотоэлемента ,например… Читать далее
11,2 K
Комментировать ответ…Комментировать…
Влад Самарин
59
Ученик 4 класса, отличник. Если смогу, обязательно отвечу! · 15 авг 2020
Если смогу, обязательно отвечу! · 15 авг 2020
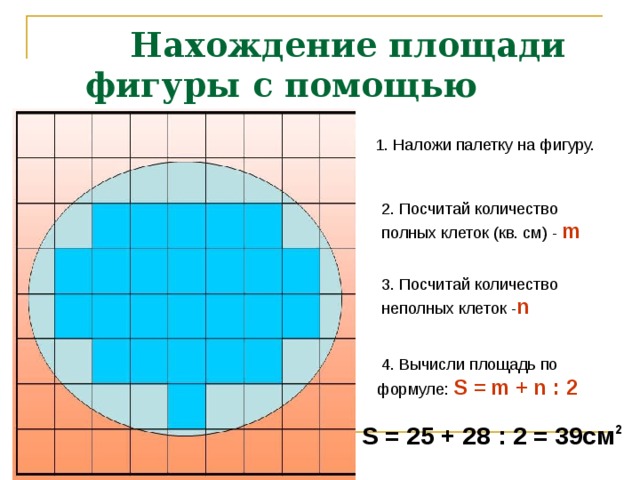
Площадь фигуры неправильной формы можно вычислить так: сначала делим фигуру на квадраты одинаковой формы, потом считаем количество полных квадратов(d) , потом не полных(f) , делим неполные пополам и складывает полные и неполные (разделённые пополам) . Формула: S = d + f : 2
15,2 K
Комментировать ответ…Комментировать…
Владимир с.
Уроженец г. Архангельска · 4 июл
Проложить по краяю измеряемой фигуры верёвочку, затем измерить длину этой верёвки и сделать из неё правильную геометрическую фигуру (квадрат) и тогда измерять площадь квадрата. Зная высоту неправильной фигуры можно вычислить объём этой фигуры
1 эксперт не согласен
Александр
возражает
4 июля
Если следовать предложенному алгоритму, то конечно будет допущена ошибка. В качестве примера возьмите круг и. .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Линар Загидуллин
Инженер Финансист Бухгалтер Начинающий предприниматель IT · 1 апр
Надо загуглить макросы для Corel Draw. Среди них есть готовые решения. Одна из таких Curve info, там же есть описание как устанавливать. Заодно посмотреть какие версии поддерживаются
Комментировать ответ…Комментировать…
По жизни с оптимизмом
1,2 K
23 янв 2019
Площадь неправильной фигуры высчитывается таким образом: фигура делится на квадраты, треугольники и прямоугольники так, чтобы они все максимально помещались в эту неправильную фигуру. Вычисляется площадь каждой составляющей фигуры и суммируется. Так, приблизительно подсчитывается площадь неправильной геометрической фигуры.
1 эксперт согласен
50,9 K
Владимир Тимошенко
23 июня 2020
если не сложно, можно формулой?
(не я вопрос писал)
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
1 ответ скрыто(Почему?)
Вычисление площадей фигур, изображенных на клетчатой бумаге
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник, параллелограмм, трапецию:
1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;
2) подставить найденные величины в формулу площади.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.
Рис. 1. Треугольник
Решение. Подсчитываем клеточки и находим: . По формуле получаем: .
2 Фигура представляет собой многоугольник
Если фигура представляет собой многоугольник то возможно использовать следующие методы.
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
2) вычислить площади полученных фигур;
3) найти сумму всех площадей полученных фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.
Рис. 2. Многоугольник
Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.
Рис. 3. Многоугольник. Метод разбиения
Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:
Метод дополнительного построения
1) достроить фигуру до прямоугольника
2) найти площади полученных дополнительных фигур и площадь самого прямоугольника
3) из площади прямоугольника вычесть площади всех «лишних» фигур.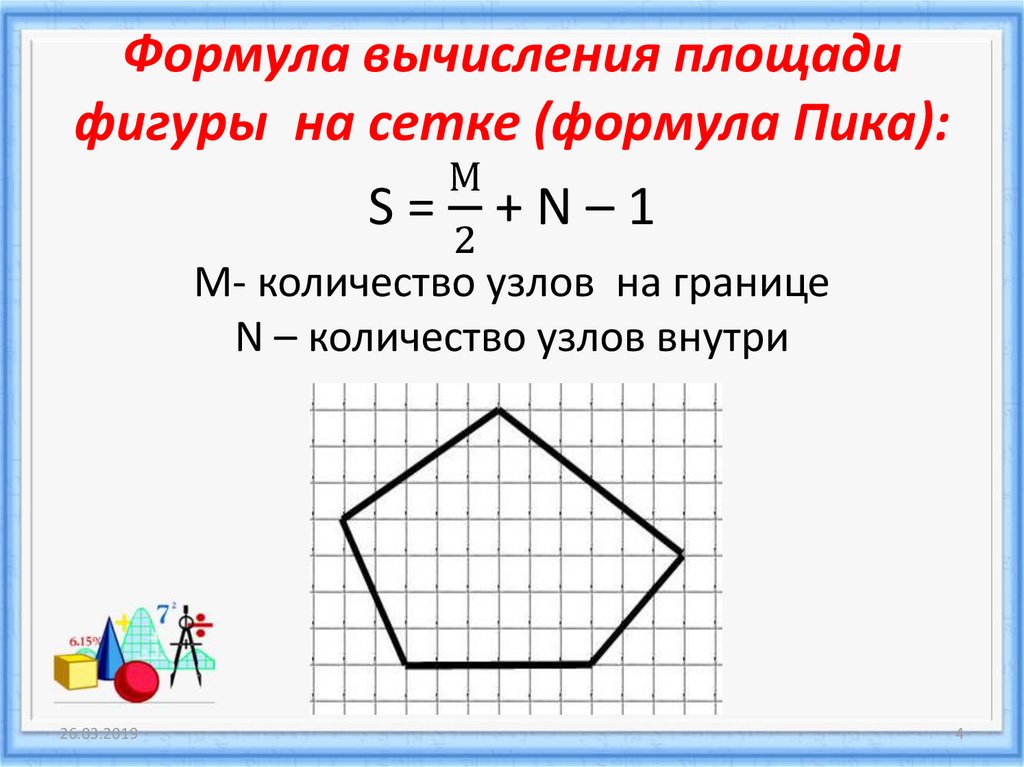
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.
Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.
Рис. 4. Многоугольник. Метод дополнения
Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.
Формула Пика
Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.
Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.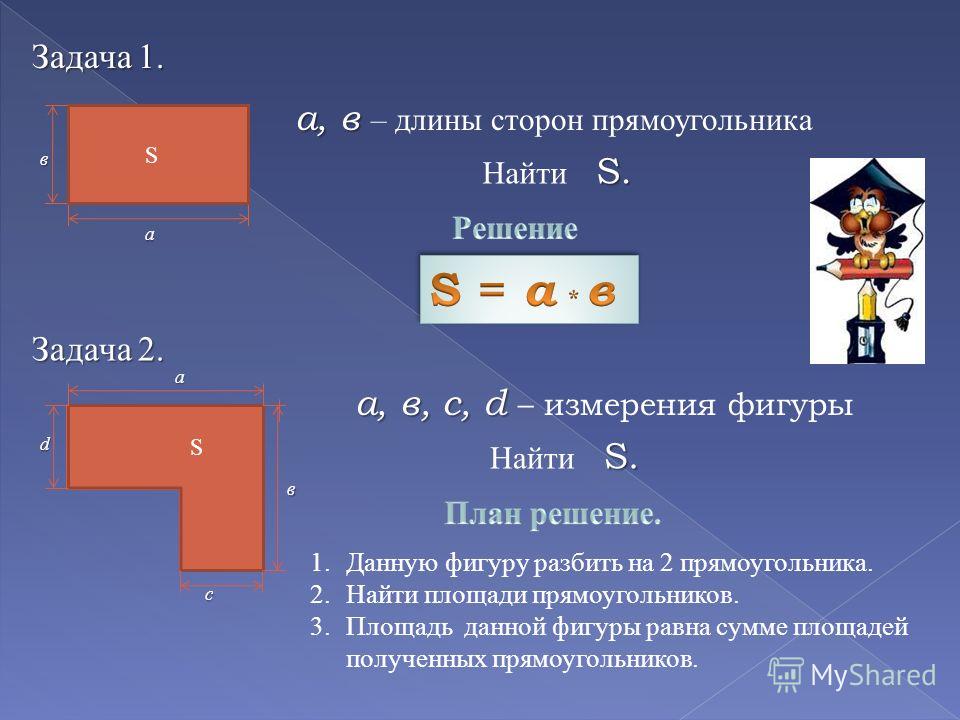
Например, для многоугольника, изображенного на рисунке 5.
Рис. 5. Узлы в формуле Пика
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.
Рис. 6. Многоугольник. Формула Пика
Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:
Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.
1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.
Рис. 7. Условие задачи 1
2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Рис. 8. Условие задачи 2
3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
Рис. 9. Условие задачи 3
4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.
Рис. 10. Условие задачи 4
5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии.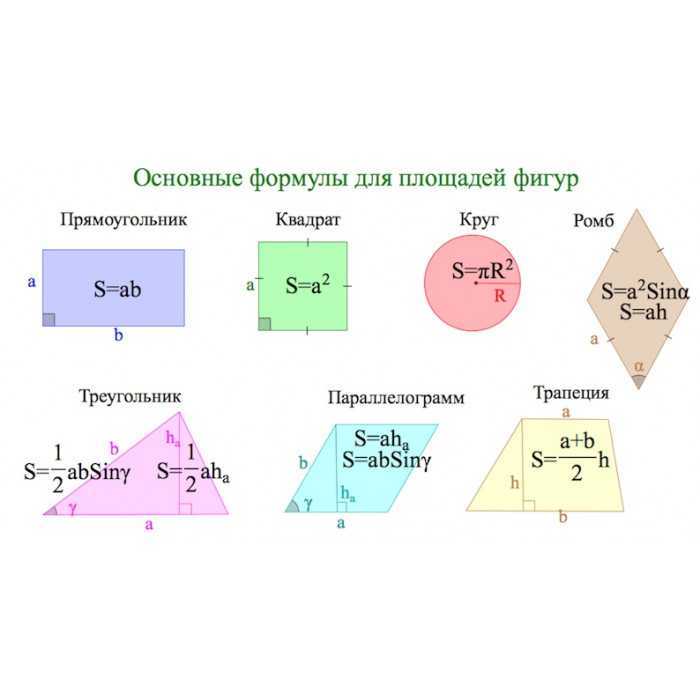 Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.
Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Литература:
- Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
- Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
- Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.
Основные термины (генерируются автоматически): формула Пика, клетчатая бумага, площадь фигуры, фигура, вычисление площадей, многоугольник, площадь, размер клетки, условие задачи, универсальная формула.
Обнаружение формул для площади – Элементарная математика
Формулы площади
Учащиеся, у которых есть неформальное представление о том, что площадь – это «количество двумерных «вещей»», содержащихся внутри области, могут изобрести для себя большинство формул, которые они часто используют попросил просто запомнить. Каждая формула, которую они заново изобретают, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, длина которого в 7 раз больше, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь вдвое большую площадь, поэтому площадь равна 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же имеет 3 строки по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадрата, поэтому его площадь составляет 21 квадратную единицу.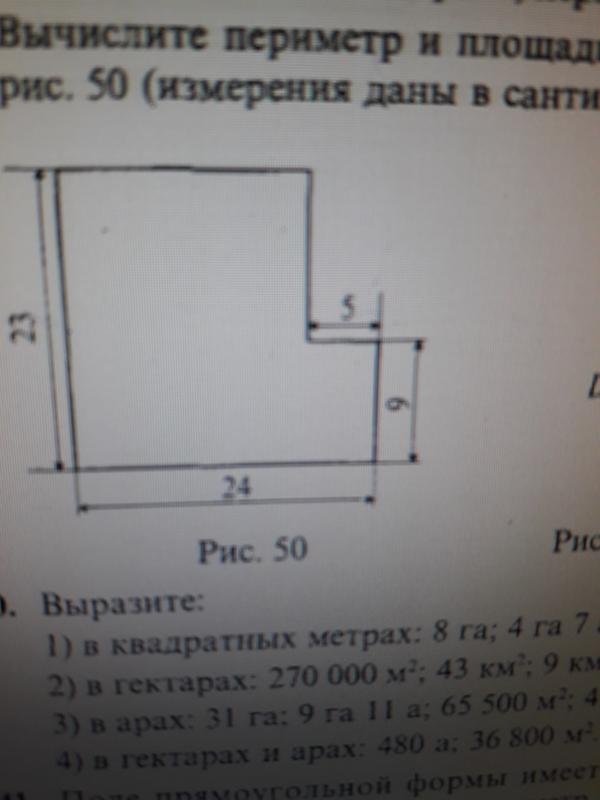
Количество квадратов в одном ряду равно длине прямоугольника. Количество строк равно высоте прямоугольника. Итак, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как любая сторона, которую вы выберете.
Подходит для подсчета чисел. Это работает даже для дробей. Синий прямоугольник, показанный здесь, имеет высоту в половину единицы длины и ширину в пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве нашей единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить все чисел, мы определить площадь прямоугольника как основание × высоту (где «основание» и «высота» означают длины этих сторон, измеренные в тех же единицах ).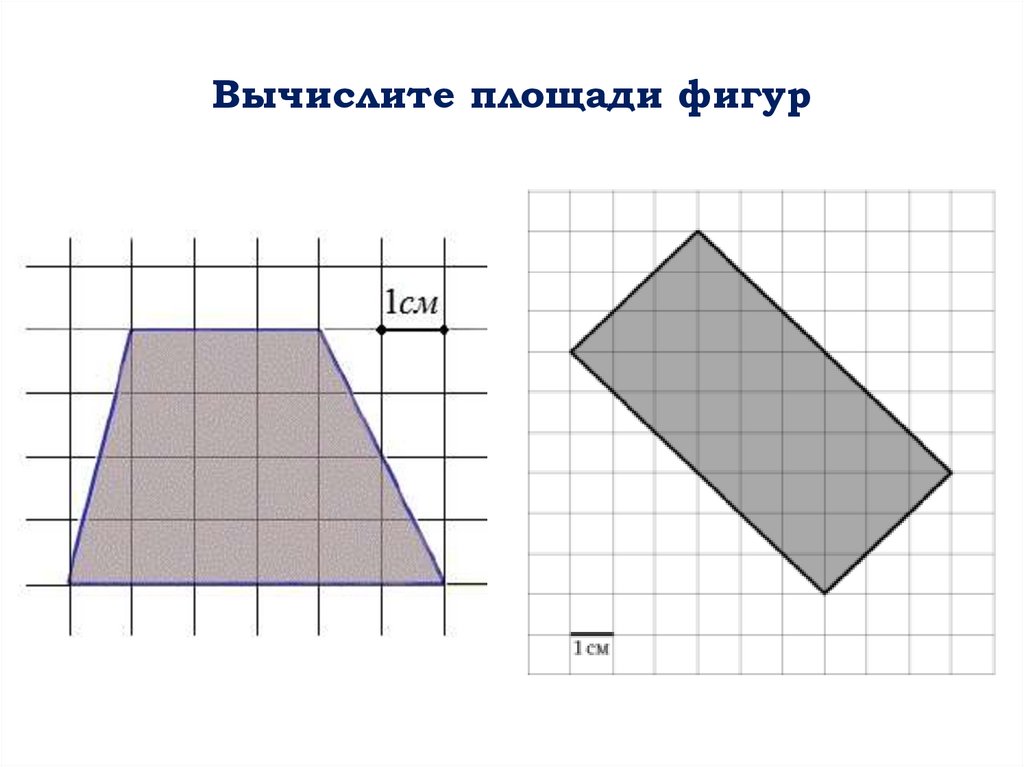
Площадь параллелограмма
Появление идеи
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части так, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одних и тех же частей, они обязательно имеют одинаковую площадь. (См. определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый). Поскольку Основание × Высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме для вычисления ее площади: База × HEIGHT 288 44444444444444444444444444444444444444444444444444444444444444444444444444444444. . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это сторона, которую вы выбрали первой. См. параллелограмм.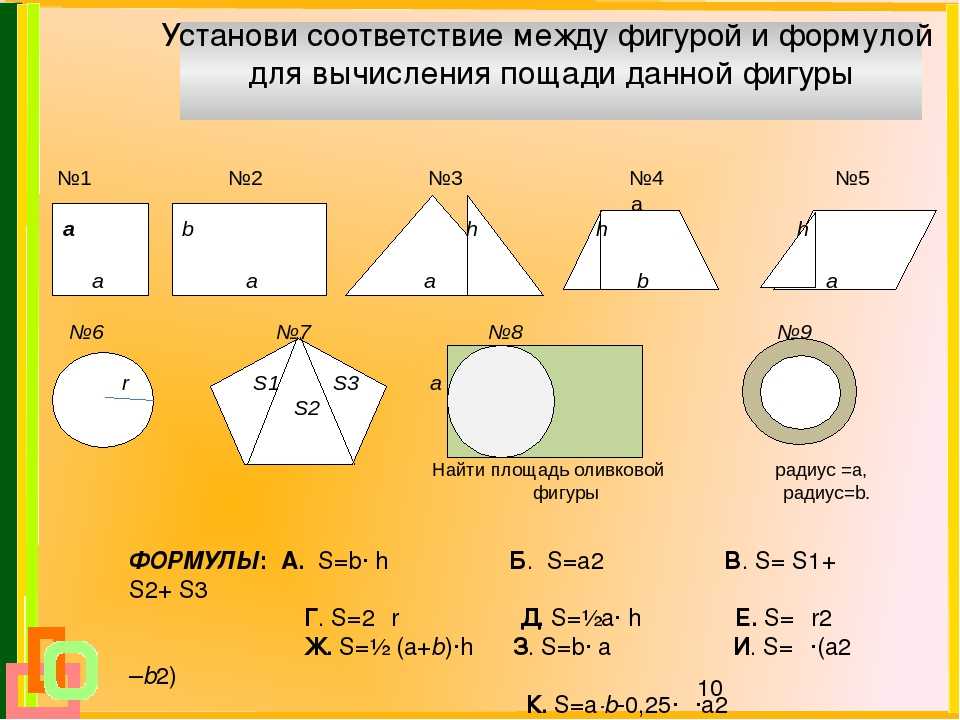 )
)
На разрезе, показанном выше, легко увидеть, что длина основания не изменилась. На самом деле перпендикулярный разрез можно сделать в любом месте вдоль основания.
Укрепление дыр
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причины того, что он должен быть таким, какой он есть. Но мы не задавались вопросом, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидать получить и результат, безусловно, выглядит так. Но внешность может быть обманчива. Что гарантирует нам, что при перемещении этого треугольника в результате получится прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результатом не всегда является идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника для разработки формулы параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если их правильно собрать, образуют прямоугольник.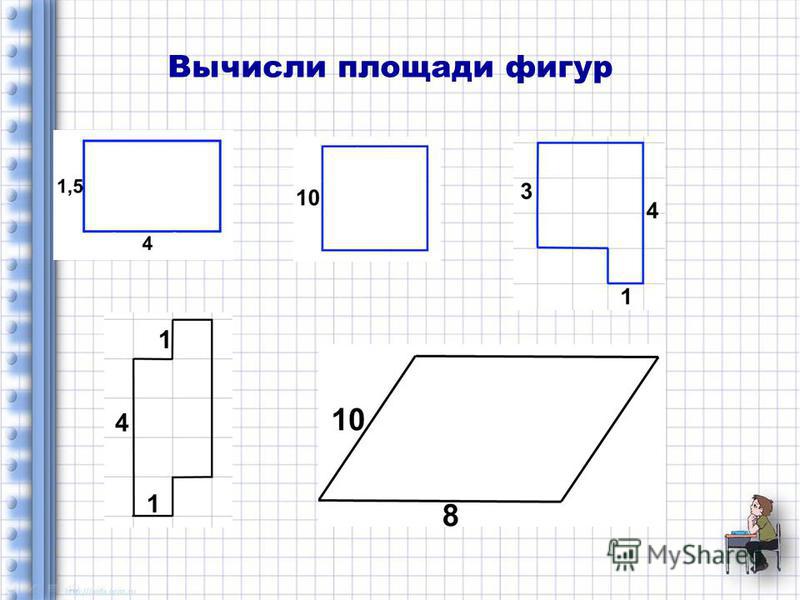 В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.
В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы вольны выбрать любую сторону в качестве базы; «высота» измеряется перпендикулярно стороне, которую мы выбрали в качестве основания. Если мы возьмем короткую сторону (синюю) за основу, показанное выше рассечение будет не таким убедительным. Разрезание по этой высоте и перестановка частей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Получается, что любой параллелограмм, каким бы длинным и тонким он ни был, можно разрезать таким образом, чтобы части — возможно, многие из них — можно было переставить в прямоугольник. Но требуется больше работы, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Несколько иная идея вскрытия значительно облегчает жизнь в этом случае. (Сами можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, равные , а не внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников к другому, пока они не сойдутся в прямоугольник. Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше усилий, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как если бы они совмещались, образуя прямоугольник, на самом деле подходят точно, а не только почти .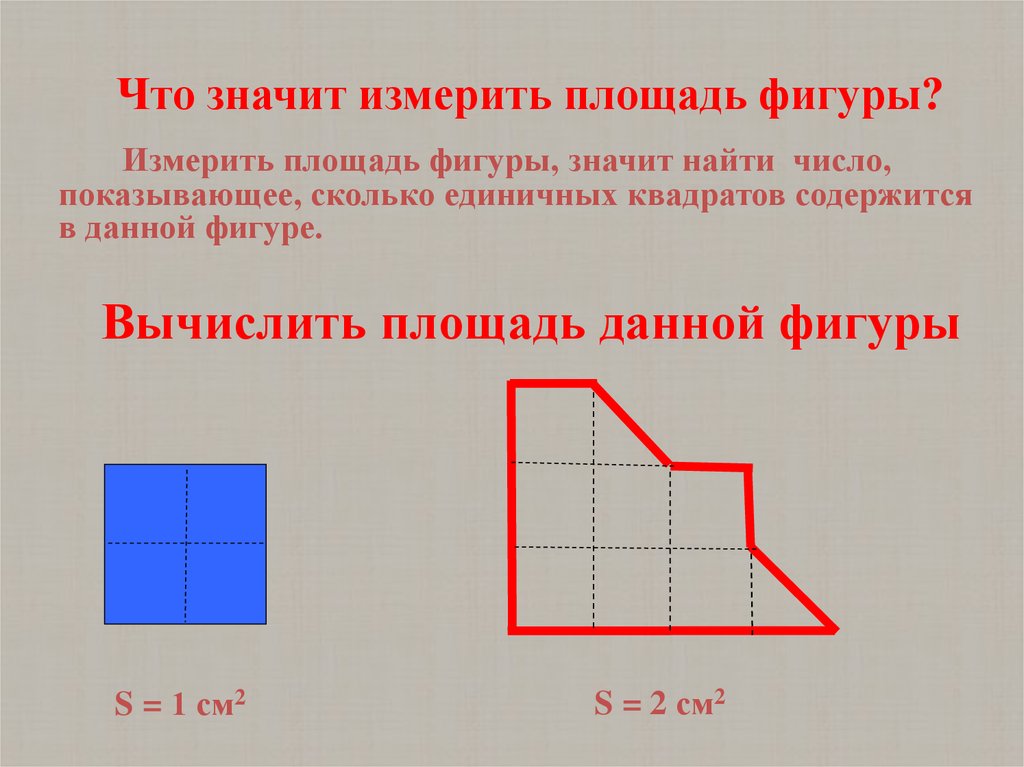
Почему так важно быть осторожным?
Когда мы будем строить другие формулы площади (см. ниже), мы захотим использовать наш способ нахождения площади параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы может быть уверенным, что перестановка частей не изменит площадь: в конце концов, именно так мы определяем площадь. Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем о , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило основания × высоты не зависит от удачного выбора основания.
В большинстве учебных программ учащиеся не имеют достаточно систематической базы геометрических знаний до 8 класса, чтобы убедительно доказать, что эти рассечения работают. Но интуитивного понимания достаточно для объяснения и обоснования формул, а также хорошей основы для последующего изучения геометрии.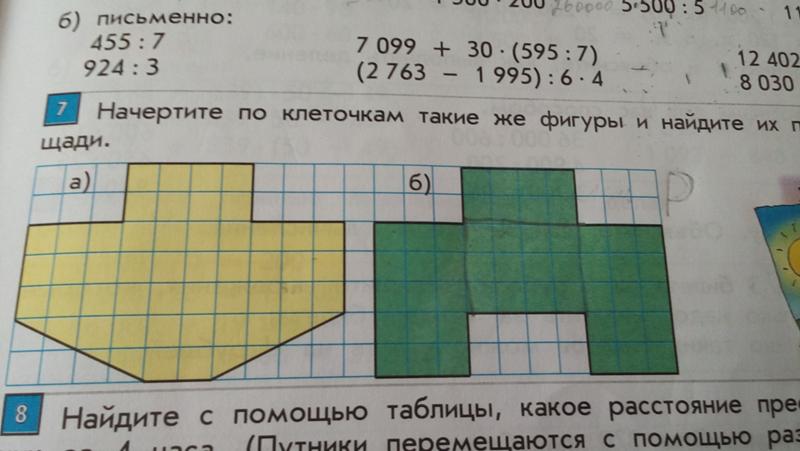
Площадь треугольника
Знание того, как найти площадь параллелограмма, поможет нам найти площадь треугольника.
Разрез треугольника
Мы можем разрезать треугольник на две части — одну на треугольник и одну на трапецию — разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с помощью этого среза, две части соединятся вместе, чтобы получить параллелограмм с тем же основанием , но наполовину меньше высоты .
Итак, основание × половина высоты дает площадь треугольника. Аналогичный разрез показывает полубаза × высота . Любой из них сводится к bh .
Удвоение треугольника с последующим делением полученной площади пополам
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.
Площадь параллелограмма равна основание × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника равна основания × высоты , как мы видели с методом рассечения.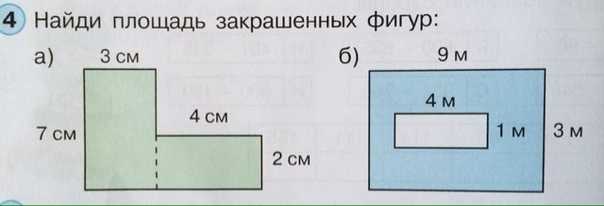
(Как всегда, выберите «основание» и измерьте высоту, перпендикулярную этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции, а затем уменьшение полученной площади пополам
Как и было с помощью треугольника две копии трапеции можно сложить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции. Таким образом, площадь параллелограмма равна высоты × ( основание1 + основание2 ). Но эта площадь равна двум трапециям, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Разрез трапеции
Мы также можем разрезать трапецию так же, как разрезали треугольник, с одним срезом, сокращающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого равно сумме двух оснований трапеции, а высота равна половине высоты трапеции.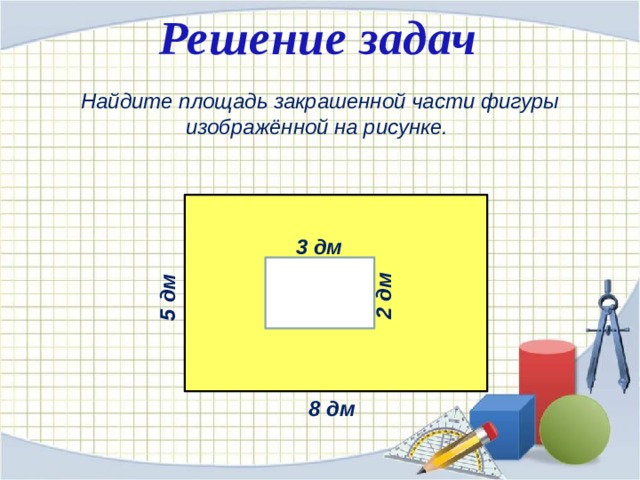
В случае трапеции основания нельзя выбирать произвольно. Две параллельных сторон являются основаниями, а высота, как всегда, является перпендикулярным расстоянием от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (половина высоты трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоты × ( основание1 + основание2 ). Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции равна × высота × ( основание1 + основание2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы получился параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (а), чтобы сформировать два конгруэнтных треугольника.
 Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы сформировать параллелограмм. Более короткая диагональ (a) становится основанием параллелограмма, а половина большей диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы сформировать параллелограмм. Более короткая диагональ (a) становится основанием параллелограмма, а половина большей диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба. - Другой подобный способ состоит в том, чтобы разрезать ромб на четыре конгруэнтных треугольника и перестроить их в прямоугольник с более короткой диагональю в качестве основания и половиной большей диагонали в качестве высоты.
- Разрезав ромб на два конгруэнтных треугольника, мы можем вычислить площадь одного из треугольников, которая равна * основание (а) * высота (b) = ab. Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь воздушного змея
Площадь воздушного змея можно найти аналогично площади ромба. Если пересечь более длинную диагональ, получится два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с большей диагональю (b) в качестве основания и половиной меньшей диагонали (a) в качестве высоты. Таким образом, площадь становится b * a = ab. Более сложный подход включает в себя немного алгебры. Разрежьте воздушного змея по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (а) в качестве основания. Таким образом, площадь первого треугольника равна * волнистой линии, где волнистая линия — высота. Площадь второго треугольника равна a * (b — волнистая линия), где (b — волнистая линия) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.
Таким образом, площадь становится b * a = ab. Более сложный подход включает в себя немного алгебры. Разрежьте воздушного змея по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (а) в качестве основания. Таким образом, площадь первого треугольника равна * волнистой линии, где волнистая линия — высота. Площадь второго треугольника равна a * (b — волнистая линия), где (b — волнистая линия) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.
Ну, что ты знаешь. По сути, вам нужно знать только формулу площади параллелограмма, а затем вывести формулы для остальных.
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 6А
- PDF (CC-BY-ND)
6Б класс
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
20011 — Геометрические фигуры и решение для области
Введение: Соединение вашего обучения
Большинство студентов, изучающих математику в старших классах и колледжах, задают вопрос: «Когда я буду использовать эту концепцию в реальной жизни?» На самом деле геометрия имеет множество практических применений как в повседневном, так и в компьютерном мире.
Геометрия может быть интересна, когда вы думаете о том, как она связана с дизайном компьютерных приложений, включая реальные и виртуальные объекты, или если вы пытаетесь определить информацию и свойства геопространственного местоположения или области. В этом модуле вы обсудите области геометрических фигур и объектов. К концу модуля вы должны знать значение и обозначения площади и формулы площади для некоторых распространенных геометрических фигур, а также уметь вычислять площади некоторых распространенных геометрических фигур.
Сосредоточение вашего обучения
Цели урока
К концу этого урока вы должны уметь:
- Вычислять площади обычных геометрических фигур.
Представление
Площадь
Площадь поверхности – это количество квадратных единиц длины, содержащихся на поверхности.
Вы начнете с изучения формул вычисления площади различных геометрических фигур. У каждой фигуры есть определенная формула, по которой нужно вычислить площадь, то есть количество квадратных единиц длины, содержащихся на поверхности.
Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)
Выберите следующую ссылку, чтобы увидеть представление площади на листе бумаги. Вы сможете увидеть, как измеряется площадь, разделив бумагу на маленькие квадратные единицы.
Площадь
Теперь, когда вы лучше понимаете, что такое площадь, посмотрите на квадрат. У него четыре равные стороны и четыре равных угла: Каждый угол равен 90°. Чтобы определить площадь квадрата, используйте следующую формулу.
У него четыре равные стороны и четыре равных угла: Каждый угол равен 90°. Чтобы определить площадь квадрата, используйте следующую формулу.
Площадь квадрата
Площадь = сторона ⋅ сторона = сторона 2
Пример
Вычислите площадь квадрата со стороной 6 дюймов.
Площадь = сторона ⋅ сторона = сторона 2
Площадь = 6 дюймов ⋅ 6 дюймов = 36 кв. 2 .
6 ⋅ 6 или 6 2 = 36 кв. дюймов
Пример
Вычислите площадь квадрата со стороной 9 см.
Площадь = сторона ⋅ сторона = сторона 2
Площадь = 9 см ⋅ 9 см = 81 кв. см
Поскольку сторона равна 9 см, вам нужно умножить 9 на 9, что также означает 9 2 .
9 ⋅ 9 или 9 2 = 81 кв. см
Теперь вы изучите формулы площади, чтобы ознакомиться с тем, как найти площадь следующих геометрических фигур.
Формулы площади
Площадь этих геометрических фигур можно определить с помощью следующих формул.
| Рисунок | Формула площади | Заявление||
| Треугольник | А = б ⋅ ч | Площадь треугольника равна половине произведения основания на высота. | |
Прямоугольник | А = л ⋅ ш | Площадь прямоугольника равна произведению длины на ширина. | |
Параллелограмм | А = б ⋅ ч | Площадь параллелограмма равна произведению основания на высоту. | |
Трапеция | А = ⋅( б 1 + б 2 )⋅ ч | Площадь трапеции равна половине суммы два основания умножить на высоту. | |
Круг | А = π r 2 | Площадь круга в π раз больше квадрата радиус. | |
На основе диаграмме выше, геометрические фигуры имеют разные формулы для площади в зависимости от их формы. Взгляните на некоторые примеры. | |||
Примеры: нахождение площадей обычных геометрических фигур
Найдите площадь треугольника.
A = ⋅ b ⋅ h = ⋅ 20 ⋅ 6 кв. футов = 10 ⋅ 6 кв. футов = 60 кв. футов = 60 футов 2
футов = 10 ⋅ 6 кв. футов = 60 кв. футов = 60 футов 2
Площадь этого треугольника составляет 60 квадратных футов, что часто записывается как 60 футов 2 .
Найдите площадь прямоугольника.
Прежде чем вы сможете вычислить площадь, вам нужно, чтобы длины сторон были в одних и тех же единицах.
1) Сначала переведите 4 фута 2 дюйма в дюймы.
Преобразуйте 4 дюйма в футы, умножив 4 на 12; в 1 футе 12 дюймов. В 4 футах 48 дюймов. Таким образом, 4 фута 2 дюйма составляют 48 дюймов + 2 дюйма, что составляет 50 дюймов
2) Формула площади (прямоугольник): A = L ∙ W
A = L ⋅ W
A = 50 дюймов. 8.
9
943 A = 50 дюймов. A = 400 кв. дюймов
Ответ: Площадь этого прямоугольника равна 400 кв. дюймов
Найдите площадь параллелограмма.
A = b ⋅ h = 10,3 см ⋅ 6,2 см = 63,86 кв. см
см
Площадь этого параллелограмма равна 63,86 кв.см.
Найдите площадь трапеции.
A = ⋅ ( B 1 + B 2 ) ⋅ H
A = ⋅ (14,5 мм + 20,4 мм) вно (4. 44. (14,5 м + 20,4 мм) вно (4. 44. (14.5 мм + 20,4 мм) (4. 444) (444). ) ⋅ (4,1 мм) = ⋅ (143,09 кв. мм)
A = 71,545 кв. мм
Площадь этой трапеции равна 71,545 кв. мм.
Найдите приблизительную площадь круга.
A = πt R 2 ≈ (3,14) ⋅ (16,8 фута) 2 ≈ (3.14) ⋅ (282,24 кв. Площадь этого круга составляет приблизительно 886,23 кв. фута.
Посетите следующий веб-сайт для получения дополнительной информации о том, как найти площадь обычных геометрических фигур.
Область геометрических фигур: плоские формы
Теперь, когда вы ознакомились с формулами и примерами, пришло время посмотреть несколько видеороликов Академии Хана. Эти видеоролики предоставят вам дополнительные пояснения и демонстрации вычисления площади, чтобы помочь вам глубже понять концепции.
Эти видеоролики предоставят вам дополнительные пояснения и демонстрации вычисления площади, чтобы помочь вам глубже понять концепции.
Математический видео-инструментарий: Основы области Площадь прямоугольников и треугольников Площадь круга |
Упражнение: нахождение площади
Теперь у вас есть шанс решить некоторые проблемы. Вам нужно будет взять лист бумаги и карандаш, чтобы выполнить практическое задание. Вы можете использовать калькулятор, если хотите. Внимательно изучите каждую из этих проблем; вы увидите похожие проблемы на проверке знаний урока. Выберите следующую ссылку, чтобы завершить практическое задание. Решение практических задач После завершения практического задания проверьте, насколько хорошо вы справились, выбрав следующую ссылку: Решения: Решение задач для местной практики |
Подведение итогов
На этом уроке вы познакомились с различными геометрическими фигурами и формулами для вычисления их площадей. Эта информация может быть использована для расчета площадей экранов телевизоров, мониторов компьютеров, объективов фотоаппаратов и многого другого.
Эта информация может быть использована для расчета площадей экранов телевизоров, мониторов компьютеров, объективов фотоаппаратов и многого другого.
Большинство курсов, которые вы будете изучать в колледже или техникуме, не всегда могут включать конкретные примеры, применимые к вашей программе обучения. Вместо этого они, как правило, дают широкий обзор ключевых понятий, оставляя вас желать большего. Как и в предыдущих уроках, вам предлагается исследовать, как каждая концепция связана с выбранной вами областью обучения. Этот процесс исследования является бесценной частью вашего образования; не упустите эту возможность продвинуть свои знания.
Оценка вашего обучения
Теперь, когда вы внимательно прочитали урок и попытались решить практические задачи, пришло время для проверки знаний. Обратите внимание, что этот является оцениваемой частью этого урока, поэтому убедитесь, что вы подготовились перед началом. |
- Заполните геометрические фигуры: нахождение площади.
Ресурс:
«Измерение и геометрия: площадь и объем геометрических фигур и объектов», Ellis, W. & Burzynski, D. © 2010, получено с http://cnx.org/content/m35023/1.2/. под лицензией Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. Это адаптация урока под названием «Геометрические фигуры и решение для площади», подготовленного Национальным консорциумом по информационной безопасности и геопространственным технологиям (NISGTC) под лицензией Creative Commons Attribution 3.0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0
Дополнительные атрибуты
Площадь квадрата — формула, как найти площадь квадрата?
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой фигуры. Другими словами, когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Другими словами, когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата также можно вычислить с помощью других измерений, таких как диагональ и периметр квадрата. Давайте попробуем понять больше о площади квадрата на этой странице.
| 1. | Какова площадь квадрата? |
| 2. | Площадь квадрата Формула |
| 3. | Как найти площадь квадрата? |
| 4. | Часто задаваемые вопросы о площади квадрата |
Какова площадь квадрата?
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общее пространство, занимаемое фигурой, — это площадь квадрата. Это четырехугольник со следующими свойствами.
Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общее пространство, занимаемое фигурой, — это площадь квадрата. Это четырехугольник со следующими свойствами.
- Противоположные стороны параллельны.
- Все четыре стороны равны.
- Все углы равны 90º.
Квадраты можно найти повсюду. Вот некоторые часто встречающиеся объекты, имеющие форму квадрата. Шахматная доска, часы, школьная доска, плитка — все это примеры квадрата.
Площадь квадрата Определение
Площадь квадрата – это мера занимаемой им площади или поверхности. Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.
Обратите внимание на квадрат, показанный ниже. Он занял 25 кв. Следовательно, площадь квадрата равна 25 квадратных единиц. Из рисунка видно, что длина каждой стороны равна 5 единицам. Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.
Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.
Квадрат Определение
Квадрат представляет собой двумерный четырехугольник с четырьмя сторонами, равными и параллельными друг другу. Углы этой фигуры равны 90 градусов.
Площадь квадрата Формула
Формула площади квадрата, если даны стороны:
Площадь квадрата = сторона × сторона = S 2
Алгебраически площадь квадрата можно найти, возведя число в квадрат представляет собой меру стороны квадрата. Теперь воспользуемся этой формулой, чтобы найти площадь квадрата со стороной 7 см. Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны как 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см 2 .
Площадь квадрата также можно найти с помощью диагонали квадрата. Формула, используемая для нахождения площади квадрата по диагонали:
Площадь квадрата по диагоналям = Диагональ 2 /2.
Давайте разберемся в выводе этой формулы с помощью следующего рисунка, где «d» — диагональ, а «s» — стороны квадрата.
Здесь сторона квадрата «s», а диагональ квадрата «d». Применяя теорему Пифагора, мы имеем d 2 = s 2 + s 2 ; д 2 = 2s 2 ; д = √2с; с = d/√2. Теперь эта формула поможет нам найти площадь квадрата, используя диагональ. Площадь = s 2 = (d/√2) 2 = d 2 /2. Следовательно, площадь квадрата равна d 2 /2.
Как найти площадь квадрата?
В предыдущем разделе мы рассмотрели определение площади квадрата, а также формулу площади квадрата. В этом разделе давайте разберемся, как использовать формулу площади квадрата, чтобы найти ее площадь с помощью нескольких приложений или реальных примеров.
Площадь квадрата по периметру квадрата
Пример: Найдите площадь квадратного парка, периметр которого равен 360 футов.
Решение:
Дано: периметр квадратного парка = 360 футов
Мы это знаем,
Периметр квадрата = 4 × сторона
⇒ 4 × сторона = 360
⇒ сторона = 360/4
⇒ сторона = 90 футов
Площадь квадрата = сторона 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка с периметром 360 футов составляет 8100 футов 2 .
Площадь квадрата, если известна сторона квадрата
Пример: Найдите площадь квадратного парка, сторона которого равна 90 футов
Решение:
Дано: сторона квадратного парка = 90 футов
Мы это знаем,
Площадь квадрата = футы 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка со стороной 90 футов составляет 8100 футов. .
.
Решение:
Дано: диагональ квадратного парка = 14 футов
Мы это знаем,
Формула площади квадрата при заданной диагонали = d 2 / 2
Следовательно, площадь квадратного парка = (14 × 14)/2 = 98 футов 2
Таким образом, площадь квадратного парка с диагональю 14 м составляет 98 футов 2 .
Площадь квадрата Советы:
Обратите внимание на следующие моменты, которые следует помнить при вычислении площади квадрата.
☛ Статьи по теме
- Диагональ квадрата
- Площадь квадратов и прямоугольников Рабочие листы
- Периметр квадрата
- Площадь поверхности квадратной призмы
Площадь квадрата Примеры
Пример 1: Какова площадь квадратного бассейна, одна сторона которого равна 8 м?
Решение:
Мы знаем, что одна сторона бассейна равна 8 м, поэтому воспользуемся формулой: Площадь квадрата = сторона × сторона = 8 × 8 = 64 м 2 .
 Следовательно, площадь бассейна составляет 64 квадратных метра.
Следовательно, площадь бассейна составляет 64 квадратных метра.Пример 2: Площадь квадратной доски составляет 3600 см 2 . Какова длина его стороны?
Решение:
Площадь квадратной доски = 3600 см 2 . Мы знаем, что Площадь = сторона × сторона = сторона 2 . Значит, сторона = √Площадь = √3600 = 60 см. Следовательно, сторона доски для каррома равна 60 см.
Пример 3: Найдите площадь квадратной комнаты на полу, состоящей из 100 квадратных плиток со стороной 15 дюймов.
Решение:
Площадь одной плитки = 15 дюймов × 15 дюймов = 225 квадратных дюймов. Мы знаем, что на полу комнаты 100 плиток. Таким образом, площадь, занимаемая 100 плитками, равна площади пола = 100 × 225 квадратных дюймов = 22500 квадратных дюймов. Следовательно, площадь пола составляет 22500 квадратных дюймов.
Пример 4: Найдите площадь квадратного ковра, диагональ которого равна 4 футам.

Решение:
Площадь квадрата, если дана его диагональ, равна D 2 /2. Дана диагональ d = 4 фута. Площадь ковра = (4 × 4)/2 = 16/2 = 8 квадратных футов. Следовательно, площадь ковра составляет 8 квадратных футов.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Куэмата.
Записаться на бесплатный пробный урок
Практические вопросы по площади квадрата
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади квадрата
Что такое площадь квадрата в геометрии?
В геометрии квадрат — это фигура с четырьмя равными сторонами. Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s 2 в квадратных единицах.
Какова площадь формулы квадрата?
Когда сторона квадрата известна, используется формула для нахождения площади квадрата со стороной s: Площадь = s × s = s 2 . Если дана диагональ d квадрата, то формула, используемая для нахождения площади, такова: Площадь = d 2 /2.
Как вычислить площадь квадрата?
Площадь квадрата рассчитывается по формуле: Площадь = s × s, где s — одна сторона квадрата. Поскольку площадь квадрата является двумерной величиной, она всегда выражается в квадратных единицах. Например, если мы хотим вычислить площадь квадрата со стороной 4 единицы, это будет: A = 4 × 4 = 16 единиц 2 . Проверьте сейчас калькулятор площади квадрата для быстрых расчетов.
Что такое периметр и площадь квадратных формул?
Периметр квадрата представляет собой сумму четырех сторон квадрата, то есть P = 4 × стороны. Она выражается в м, см, футах, дюймах.
Площадь квадрата = Площадь = s × s, где s — одна сторона квадрата. Дается в единицах м 2 , см 2 , футов 2 , в 2 .
Дается в единицах м 2 , см 2 , футов 2 , в 2 .
Чек:
- Формулы периметра
- Формулы объема
- Формулы площади поверхности
- Формулы измерения
Как найти площадь квадрата по диагонали квадрата?
Площадь квадрата также можно найти, если известна его диагональ. В этом случае используется следующая формула: Площадь квадрата по диагоналям = Диагональ²/2. Например, диагональ квадрата равна 6 единицам, Площадь = 6²/2 = 36/2 = 18 квадратных единиц.
Как найти площадь квадрата по периметру квадрата?
Площадь квадрата можно вычислить, если известен его периметр. Поскольку периметр квадрата: P = 4 × сторона, мы можем найти сторону квадрата ‘s’ = периметр/4. После получения стороны площадь квадрата можно вычислить по формуле: A = s × s. Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона. 32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
Каковы единицы измерения площади квадрата?
Поскольку площадь квадрата является двумерной фигурой, она всегда выражается в квадратных единицах. Общепринятыми единицами площади квадрата являются м 2 , дюймы 2 , см 2 , фут 2 .
Какова площадь квадрата, вписанного в окружность?
Если квадрат вписан в круг, то диагональ квадрата равна диаметру круга. Итак, если диаметр круга дан, это значение можно использовать как диагональ квадрата, а площадь квадрата можно рассчитать по формуле: Площадь квадрата с использованием диагоналей = Диагональ²/2.
Как найти площадь прямоугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти площадь прямоугольника
Периметр прямоугольника равен . Длина на десять метров больше ширины. Чему равна площадь прямоугольника?
Длина на десять метров больше ширины. Чему равна площадь прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Для прямоугольника общее уравнение для периметра и площади: где длина, а ширина.
Пусть = ширина и = длина
Итак, уравнение, которое нужно решить, становится таким образом, что ширина равна а длина равна .
Таким образом, область
Сообщить об ошибке
Какая из следующих сведений будет , а не , чтобы найти площадь прямоугольника?
Возможные ответы:
Длины одной стороны и диагонали.
Все остальные варианты перечисляют информацию, которой будет достаточно.
Периметр и длина одной стороны.
Длины одной пары противоположных сторон.
Длины одной пары смежных сторон.
Правильный ответ:
Длины одной пары противоположных сторон.
Объяснение:
Площадь прямоугольника можно вычислить, умножив длины двух соседних сторон. Все приведенные варианты содержат достаточную информацию, за одним исключением. Мы изучаем каждый из вариантов.
Длины одной пары смежных сторон: Этот выбор неверен, как прямо указано выше.
Периметр и длина одной стороны: Используя формулу периметра, вы можете найти длину соседней стороны, что делает этот выбор неверным.
Длины одной стороны и диагонали: используя теорему Пифагора, вы можете найти длину соседней стороны, что делает этот выбор неверным.
Длины одной пары противоположных сторон: это не дает вам возможности узнать длины смежных сторон. Это правильный выбор.
Сообщить об ошибке
Найти площадь многоугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Проведение вертикальной линии в конце стороны длины делит фигуру на прямоугольник и прямоугольный треугольник.
Сумма площадей двух фигур составляет площадь многоугольника. Умножьте длину прямоугольника на его ширину, чтобы найти площадь прямоугольника, и используйте формулу, где – основание, а – высота треугольника, чтобы найти площадь треугольника. Сложение их вместе дает ответ.
Сообщить об ошибке
Одна сторона прямоугольника 7 дюймов, а другая 9 дюймов. Чему равна площадь прямоугольника в дюймах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти площадь прямоугольника, умножьте его ширину на высоту. Если мы знаем две стороны прямоугольника разной длины, то у нас есть и высота, и ширина.
Сообщить об ошибке
Какова площадь прямоугольника на диаграмме?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь прямоугольника находится путем умножения длины на ширину.
Длина 12 см, ширина 7 см.
Следовательно, площадь 84 см 2 .
Сообщить об ошибке
Какова площадь прямоугольника, длина и ширина которого равны дюймам и дюймам соответственно?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь любого прямоугольника с длиной и шириной:
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 8 910 11 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Как найти площадь шестиугольника
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по математике для старших классов » Геометрия » Плоская геометрия » Шестиугольники » Как найти площадь шестиугольника
Рассчитайте приблизительную область. Регулярная шестиугольника со следующей длина стороны:
Возможные ответы:
нельзя определить
Правильно. :
:
Пояснение:
Есть несколько способов найти площадь шестиугольника.
- В правильном шестиугольнике разбейте фигуру на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.
Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
Теперь мы можем провести анализ, используя переменную-заменитель длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где – длина стороны.
Решение:
В данной задаче мы знаем, что длина стороны правильного шестиугольника равна:
Подставим это значение в формулу площади правильного шестиугольника и решим.
Упрощение.
Округлите ответ до ближайшего целого числа.
Сообщить об ошибке
Одна шестиугольная ячейка сот имеет диаметр два сантиметра.
Какова площадь клетки с точностью до десятых долей сантиметра?
Возможные ответы:
Невозможно определить
Правильный ответ:
Есть несколько способов найти площадь шестиугольника.
- В правильном шестиугольнике разбейте фигуру на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.
Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
Теперь мы можем провести анализ, используя переменную-заменитель длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где – длина стороны.
Решение:
В задаче сказано, что соты имеют диаметр два сантиметра. Чтобы решить задачу, нам нужно разделить диаметр на два. Это связано с тем, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в сотах. Найдем длину стороны правильного шестиугольника/соты.
Подставить и решить.
Нам известна следующая информация.
В итоге можем написать следующее:
Подставим это значение в формулу площади правильного шестиугольника и решим.
Упрощение.
Решить.
Округлить до десятых долей сантиметра.
Сообщить об ошибке
Какова площадь правильного шестиугольника с апофемой и длиной стороны ?
Возможные ответы:
Правильный ответ:
Пояснение:
Есть несколько способов найти площадь шестиугольника.
- В правильном шестиугольнике разбейте фигуру на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.
Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
Теперь мы можем провести анализ, используя переменную-заменитель длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где – длина стороны.
Решение:
В шестиугольнике количество сторон , а в этом примере длина стороны .
Периметр .
Затем мы подставляем числа для апофемы и периметра в исходное уравнение.
Район .
Сообщить об ошибке
Эта фигура представляет собой правильный шестиугольник со стороной со следующими размерами:
Вычислите площадь правильного шестиугольника.
Возможные ответы:
Правильный ответ:
Пояснение:
Есть несколько способов найти площадь шестиугольника.
- В правильном шестиугольнике разбейте фигуру на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.
Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Мы знаем, что у треугольника есть , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
Теперь мы можем провести анализ, используя переменную-заменитель длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где – длина стороны.

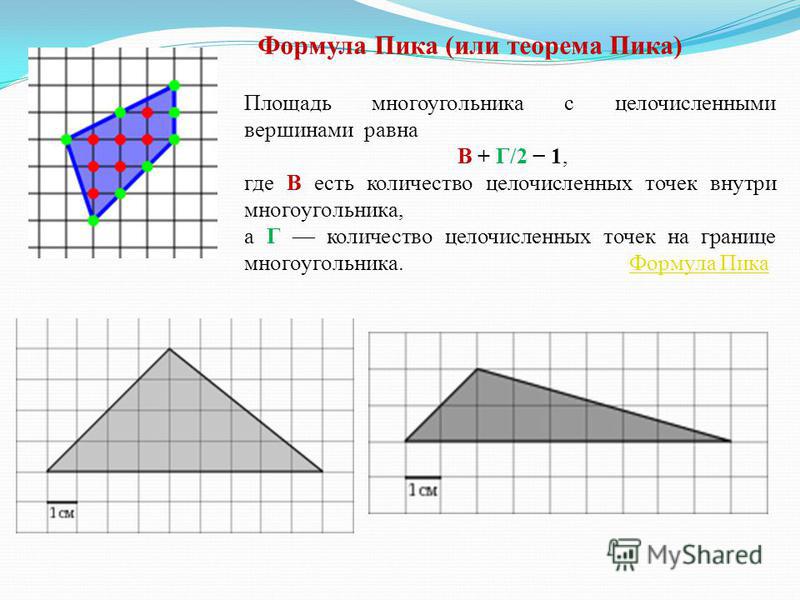 Если она будет отличаться – значит помещение имеет неправильную форму. У комнаты правильной геометрической формы параллельные стены должны быть одинаковыми.
Если она будет отличаться – значит помещение имеет неправильную форму. У комнаты правильной геометрической формы параллельные стены должны быть одинаковыми. п.)
п.)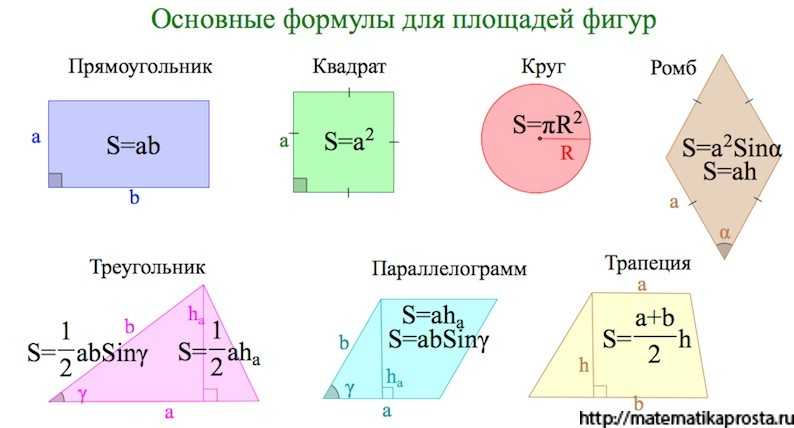
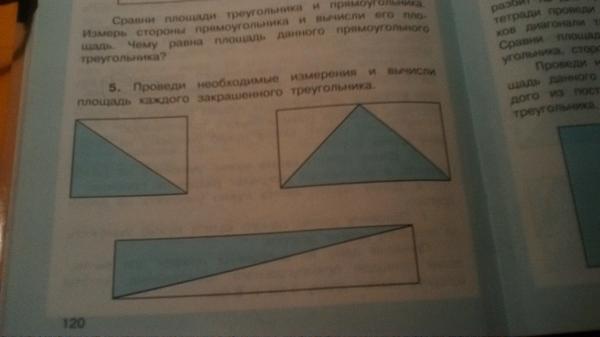 Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.