Как найти площадь ладони: воспользовавшись клетчатой бумагой, определите площадь своей ладони

Как правильно измерить ширину ладони?

Магазины › Что купить девушке › Как купить девушке перчатки?

Измеряют ширину ладони в самой широкой части кисти руки. Оберните измерительную ленту на руке по костяшкам пальцев и сожмите руку в полу-кулак (не сжимая сильно). Полученный результат проверяют по таблице и определяют размер.

1. Как меряют обхват ладони?
2. Как измерить длину и ширину ладони?
3. Какой нормальный размер ладони?
4. Как измерить толщину руки?
5. Что значит размер ладони?
6. Что значит размер перчаток 7?
7. Сколько сантиметров в ладошке?
8. Как измерить обхват ладони ребенка?
9. Какой размер перчаток у мужчин?
10. Как понять что у меня длинные руки?
11. Сколько ладоней в росте?
12. Что значит размер перчаток 10?
13. Сколько см должно быть запястье?
14. Как правильно измерить ширину запястья?
15. Как измерять толщину?
16. Как измерить обхват ладони для варежек?
17. Как измерить Дтс?
18. Как правильно измерить обхват запястья?

Как меряют обхват ладони?

Измерить окружность ладони — самой широкой части кисти, у основания четырех пальцев, без большого пальца. Измерить длину — расстояние от запястья и до кончика среднего пальца. Полученные размеры и определяют ваш размер рабочих перчаток (см.

Как измерить длину и ширину ладони?

Для того чтобы узнать ваш размер перчатки нужно сделать всего два измерения. При помощи сантиметровой ленты измерьте свою ладонь по обхвату, в самом широком месте, а затем измерьте длину вашей ладони от кончика среднего пальца до сгиба под ладонью. Важно! Следует измерять вашу доминантную руку.

Какой нормальный размер ладони?

Ладонь (palm) — единица измерения расстояния, равная четырём дюймам или 10,16 сантиметрам.

Как измерить толщину руки?

Оберните полоску из бумаги вокруг запястья и сделайте пометку. Лента не должна туго сжимать руку. Теперь распрямите ленту и приложите ее к линейке. Вы узнаете точный размер вашего запястья.

Что значит размер ладони?

Как определить размер перчаток

Первая мерка — обхват кисти. Вторая — обхват запястья. Третья — длина большого пальца. Четвертая — длина от кисти до кончика среднего пальца (этот параметр особенно важно измерить тем, у кого длинные пальцы.

Что значит размер перчаток 7?

Маркировка 6,5 указывает на то, что ладонь должна быть не менее 18 см в обхвате, цифра 7 соответствует 19 см, 7,5 указывает на обхват ладони в 20 см, а 8 — подойдет тем, у кого обхват ладони составляет не менее 22 см.

Сколько сантиметров в ладошке?

Согласно проведенным расчетам общая площадь поверхности тела взрослого человека в среднем составляет 17000 — 20000 см2, а площадь ладони человека — 170 — 200 см2, т. е. 1% поверхности тела.

Как измерить обхват ладони ребенка?

Российский размер перчаток и варежек для детей определяется по обхвату ладони без учета большого пальца в сантиметрах. Произведите измерительной лентой замеры обхвата ладоней в самой широкой части, без большого пальца. Важно выбрать обхват ладони доминирующей руки ребенка (правой или левой).

Какой размер перчаток у мужчин?

Самый популярный размер мужских перчаток — в числовом обозначении это 8; 8,5; 9; 9,5 и 10 размеры.

Как понять что у меня длинные руки?

Определить, насколько пропорциональна длина рук относительно тела можно так. В общем, когда линии А и B сливаются в одну, то длина рук пропорциональна телу. В ситуации, как на картинке, руки коротковаты. Ну, а если линия B ниже линии А, то руки слишком длинные.

Сколько ладоней в росте?

Природа распорядилась в строении человеческого тела следующими пропорциями: длина четырех пальцев равна длине ладони, четыре ладони равны стопе, шесть ладоней составляют один локоть, четыре локтя — рост человека.

Что значит размер перчаток 10?

Работники могут считать, что перчатки, которые на размер больше или меньше, чем измеренный, сидят на руке более удобно.Размеры перчаток

Размеры	Окружность (мм)	Длина (мм)
7 (S)	178	171
8 (M)	203	182
9 (L)	229	192
10 (XL)	254	204

Сколько см должно быть запястье?

Средний обхват запястья у женщин при нормальном телосложении считается около 16 см, а у мужчин — 18-20 см.

Как правильно измерить ширину запястья?

1) Возьмите рулетку или веревку и оберните ее вокруг запястья, пока два конца не коснуться без провисания. Размер запястья должен быть без слабины и не настолько плотным, чтобы он останавливал кровообращение. 2) Отметьте точную длину на веревке и используйте линейку, чтобы определить ваш истинный размер.

Как измерять толщину?

Толщина измеряется на расстоянии не менее 25 мм от кромок листа и посередине каждой стороны листа толщинометром (по ГОСТ 11358) либо микрометром (по ГОСТ 6507) с ценой деления не более 0,1 мм. Фактическая толщина — это среднее арифметическое значение результатов четырёх измерений.

Как измерить обхват ладони для варежек?

Чтобы правильно выбрать размер перчаток и варежек, необходимо измерить обхват ладони в районе «косточек», исключив большой палец. Измеряют ширину ладони в самой широкой части кисти руки. Оберните измерительную ленту на руке по костяшкам пальцев и сожмите руку в полу-кулак (не сжимая сильно).

Как измерить Дтс?

Дтс — измеряют расстояние от точки основания шеи до линии талии сзади параллельно позвоночнику. Дтп — измеряют расстояние от точки основания шеи через сосковую точку до линии талии спереди. Впк — измеряют кратчайшее расстояние от пересечения линии талии с позвоночником до плечевой точки.

Как правильно измерить обхват запястья?

Самый простой метод. Обхватите запястье одной руки большим и среднем пальцем другой. Померьте расстояние лентой, прибавьте к полученному значению 1-2 см.

Персональный сайт Баиновой Ольги — Площадь фигур.

Цель урока: познакомить с понятием «площадь фигуры» и различными способами сравнения площадей предметов и фигур.

Задачи урока:

1. Создать проблемную ситуацию, в ходе решения которой, сформировать представление о площади предметов и фигур.
2. Организовать познавательную деятельность для развития широкого спектра логических действий и операций, включающих вычислительные навыки и общие приемы решения задач.
3. Использовать возможности урока для воспитания адекватной мотивации учебной деятельности, включая учебные и познавательные мотивы, а так же умение работать в коллективе, в заданном темпе.

Формы, методы и приемы используемые на уроке:

• форма организации активной познавательной деятельности – проблемный урок;
• форма обучения на уроке – сотрудничества и совместной деятельности, фронтальная, индивидуальная, с учетом индивидуализации и дифференциации;
• проблемно-исследовательские методы;
• наглядно-словесные методы;
• практическо-поисковые методы;
• методы формирования умений и навыков;
• методы развития познавательной активности и творческой деятельности;
• ситуационный метод;
• методы устного контроля, самоконтроля;
• прием построения заданий для выявления закономерностей;
• прием свободы выбора для выполнения заданий;
• прием самостоятельного выбора или принятие сравнительного;
• прием постановки в равные условия;
• прием отстранения от помощи учащихся;
• прием разнообразия заданий, ритма, роли детей на уроке.

– Сегодня на уроке мы получим новые знания, продолжим работу над задачами, проведем математическую разминку. С чего хотите начать урок? (Дети самостоятельно определяют и обосновывают необходимость этапа начала урока.) Трудность такого варианта вхождения в урок заключается в том, что возникает опасение за возможность потерять время на одном из этапов урока. И это же дает большое преимущество для реализации воспитания умений планировать свои действия, научить планировать такие действия и уметь выбирать лучший вариант.

Этап урока – «Математическая разминка (минутка)»

Так как согласно занковской системе, устный счет проводится не на каждом уроке, то данная математическая минутка вполне может заменить устный счет. Такие математические минутки, составленные по своей завершенности, могут проводиться периодически, но не на каждом уроке (2–3 раза в неделю). Они позволяют неоднократно возвращаться к одному и тому же материалу, но с каждым разом выводят детей на новый уровень знаний и открытий, при работе с отрезком ряда чисел. К тому же математические минутки вполне соответствуют основным функциям учебного процесса:

• развивают такое свойство мыслительной деятельности как гибкость ума, быстроту переключения с одной проблемы на другую, математическую речь;
• совершенствуют (до автоматизма) вычислительные навыки;
• формируют умения работать в коллективе в заданном режиме.

Используемые в данном случае задания носят специфический характер.

7	6	8	5	1	9	4
7	9	11	13	15	17	19
42	30	56	82	78	24	66

Задание для первого урока.

А) – Рассмотрите внимательно ряды чисел.

– Что интересного заметили? Какие характерные признаки заметили в первом ряду? Докажите.

– Подумайте и назовите особенности построения второго ряда. Запомните их, пожалуйста.

– Докажите, что построение третьего ряда отличается от первого и второго.

– Как можно сгруппировать все числа? Найдите несколько вариантов и объясните свое решение. Правильно молодцы!

– Сегодня мы с вами будем работать над числами первого ряда.

– Как можно назвать числа первого ряда? (однозначные, числа первого десятка)

– Расположите данные числа в порядке возрастания, убывания.

– Назовите недостающие числа, самое большое однозначное число, самое маленькое.

– Найдите сумму, последовательно прибавляя по одному числу.

– Вы испытывали затруднение и потерю во времени? Предложите способ быстрого нахождения суммы.

– Какой можно сделать вывод? Сформулируйте правило.

– Перемножьте последовательно по одному числу.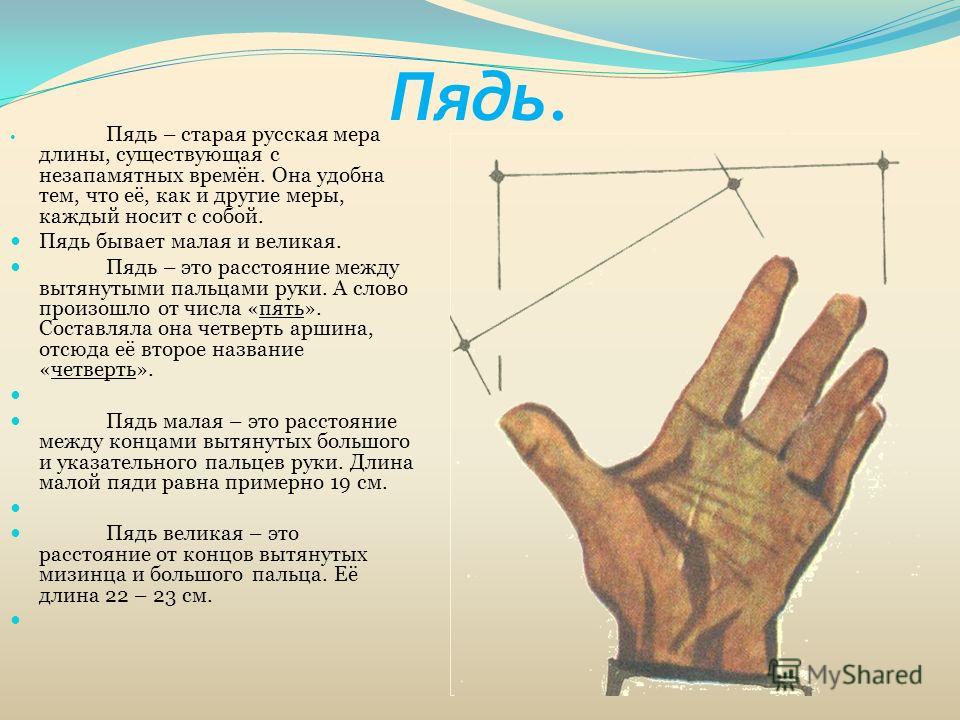 В чем ощутили трудность?

– Предложите свой способ нахождения произведения чисел данного ряда.

– Какой вывод напрашивается сам собой? Объясни свое решение.

– Посмотри внимательно на значение суммы и произведения.

– Постарайся дома составить еще несколько заданий для всего класса с вопросами по этому ряду чисел. Лучшему исследователю будет дана возможность самому подготовить и провести математическую разминку.

Задание на следующий урок.

«Математическая разминка» начинается с проверки заданий, которые приготовили ребята по ряду чисел с предыдущего урока. (ряды чисел вновь экспозируются перед детьми)

Б) – Кто приготовил дома задания по первому ряду чисел и готов представить их для товарищей?

– Как вы считаете, ребята, интересные вопросы приготовили……..? Что необычного для вас в задании? Что заинтересовало вас больше всего? Почему? Объясните. Может у кого-нибудь возникли непонятные сомнения, вопросы? Поделитесь.

– Запишите названный ряд (ряды) чисел.

– Вспомните и назовите особенность расположения второго ряда чисел.

– В чем эта особенность? Как можно назвать числа этого ряда? Докажите.

– Назовите недостающие числа, продолжите, назовите ещё 5 чисел.

– Что ещё необычного обнаружили? Догадайтесь и объясните закономерность построения этого ряда (+2). Объясните, что вы для этого сделали?

– Постойте, согласно данной закономерности, отрезок ряда начиная с 20 (7 чисел). 20 22 24 26 28 30 32

– Сравните два ряда чисел 7 9 11 13 15 17 19 и свой. Чем этот ряд чисел отличается от предыдущего? У вас возникли трудности? Почему? Объясните.

– Как называются числа получившегося ряда? Почему? Объясните.

– Какой можно сделать вывод?

– Подготовить дома самостоятельно задания для третьего ряда чисел. Что необходимо сделать, чтобы вы смогли справиться с заданием? Объясните свое решение, свой выбор. Докажите. Приготовьтесь к проведению следующего этапа математической минутки.

Задание на следующий урок.

«Математическая минутка» начинается с проверки домашнего задания, которое дети получили на предыдущем уроке для ряда (рядов) чисел.

В) – Давайте разберем задания предложенные ребятами, выберем самое интересное и постараемся аргументировать свои ответы. Кто из исследователей сегодня проведет математическую разминку?

– Что общего между третьим рядом чисел рядом составленным вами?

– Какое число на ваш взгляд можно исключить из третьего ряда? Почему? Объясни? Что вы предполагали сначала? А что оказалось на самом деле? Дайте характеристику этому числу.

– Замените числа третьего ряда разрядными слагаемыми. Сколько вариантов получилось? Почему у всех одинаково? Объясните.

– Замените число 24 на множители. Что вас удивило? Сколько в нашем классе мнений? Почему получилось несколько вариантов? Докажите.

– Запишите все получившиеся выражения. Подберите самостоятельно несколько чисел, которые можно заменить не одной группой множителей и подготовьтесь к объяснению и доказательству своего выбора для одноклассников.

Последнее задание является важнейшим моментом работы. Оно требует от учеников скрупулезного и всестороннего анализа заложенных в задании закономерностей. В зависимости от числа этих закономерностей дети либо отвергают, либо принимают предложенные решения.

Приведенные выше фрагменты урока «математической разминки» демонстрирует не только то, как идет процесс познания, но и атмосферу, в которой это происходит, что является немаловажной, а может быть и важнейшей особенностью занковской системы.

Этап урока – новые знания

А) Актуализация новых знаний.

– Рассмотрите внимательно картинку и дайте ответ: где елок больше справа или слева?

– Подумайте, можно ли сразу ответить на вопрос? Что для этого надо? Докажите.

– Назовите свойство, по которому идет сравнение.

– Молодцы, правильно. Настоящие елки можно сравнить по количеству, размеру, по массе (хотя эта информация не имеет практического применения) и другим свойствам.

– А теперь объясните свои наблюдения. Правильно: по размеру больше слева, по количеству больше справа.

– Как быть? Какая возникла проблема? Может ли из двух предметов (групп) один быть одновременно и большим и меньшим другого?

– Как доказать, решить проблему?

– Правильно. Необходимо знать точно, по каким свойствам идет сравнение длине, ширине, высоте, массе, количеству, цвету или другим свойствам.

Б) Введение нового.

– Можно ли сравнить по площади две поверхности или геометрические фигуры?

– Как сравнить площади двух поверхностей или геометрических фигур? Найдите несколько способов и продемонстрируйте их на раздаточном материале.

– Что интересного заметили? Достаточно ли тех знаний и умений, которые у вас есть?

– В чем затруднения? Как решить эту проблему? Что для этого необходимо?

– Кто попытается сформулировать тему урока? (можно спросить в конце урока какова была тема урока).

– Рассмотрите внимательно рисунки и подумайте, у каких предметов на рисунке есть площадь, выпишите номера этих фигур, предметов.

– Постройте в тетради 3 предмета или фигуры, у которых есть площадь и 3 предмета или фигуры, у которых площади нет.

– Объясни, как ты понимаешь слово площадь.

В) Работа по учебнику

– В математике слово площадь тоже встречается, например, говорят площадь фигур. Посмотрите внимательно вокруг, назовите те предметы, у которых есть площадь. Какой можно сделать вывод? (Площадь имеют все предметы).

– Имеет ли площадь ваша ладонь? Покажите площадь ладони. Почему у вас возникли трудности? Почему же вы не показали площадь ладони? Сформулируйте вывод, подведите итог.

– Итак, площадь ладони это не материальный объект, это абстрактное понятие. Площадь нельзя потрогать, нельзя выполнить с ней физические действия, такие действия можно выполнять только с предметами, фигурами имеющими площадь.

– Работа по учебнику на закрепление понятия площадь фигуры.

Работа с геометрическими объектами в данном случае позволяет активно использовать наглядно-действенные, наглядно-образные, наглядно-логические уровни мышления, которые наиболее близки младшим школьникам и, опираясь на которые, дети выводят на высшую ступень в своем развитии словесно-логический уровень, а так же способ развития плоскостного и пространственного воображения.

Этап урока – решение задачи

Одной из важнейших проблем обучения математике является формирование умений решать текстовые задачи. Решение задач вообще и математических в частности по своей сути – процесс творческий, требующий продуктивной деятельности. Главным в умении решать задачи является полноценная аналитическая деятельность, выявляющая все необходимые для решения связи. Задания, которые концентрируют внимание учеников на исследовании предлагаемых текстов, а не требующие сразу выполнения решения задачи, помогают осмыслить эти связи как таковые. Коллективное обсуждение предложений и ответов самих учеников, найденных в результате самостоятельной деятельности, есть самый продуктивный путь построения такой работы над задачей.

Важным направлением работы над задачами в 3 классе является знакомство с краткой записью задачи и разнообразием её оформления (схема, таблица, чертеж и т.д). Краткая запись – эффективное средство облегчения поиска путей решения задачи, в которой находят отражение глубина и полнота анализа математических связей, заложенных в задаче. Однако, это только тогда будет иметь наибольшую эффективность, когда дети самостоятельно и сознательно проходят весь путь сокращения текста задачи до полного исключения всех второстепенных деталей, лишних данных, фраз, слов. На данном уроке предлагается работа над задачей содержащей, лишние данные.

– Расстояние между двумя поселками, находящимися на разных берегах реки Быстрянки 32 километра. В 10 часов утра из поселка Рассвет в другой поселок Сосновка выехал велосипедист и проехал 15 километров. В это же время другой велосипедист выехал ему навстречу и проехал на 2 километра больше первого. Какое расстояние будет между велосипедистами через два часа?

– Прочитайте текст и докажите что это задача. Что необычного заметили в этой задаче? – Попытайтесь убрать «лишнее» количество слов, не имеющих значения для решения задачи и даже мешающих ей. Прочитайте, что у вас получилось. Объясните свой выбор.

– Сократите самостоятельно текст задачи до словесной записи настолько, насколько это возможно. Вспомните общеупотребительные условные обозначения задач данного вида и определите вид краткой записи данной задачи.

– Выберите тот вид краткой записи, который вам больше нравится и более понятен. (знаковая, схема, чертеж, таблица, рисунок и т.д.) Докажите свой выбор.

– Кто желает и успеет, может записать не одну краткую запись. (схему, чертеж, таблицу) – Подумайте и объясните как на ваш взгляд более рациональнее можно записать решение этой задачи: по действиям, с вопросами, с пояснением, выражением и т.д.

– Запишите решение задачи и оформите ответ.

– Что вас удивило в решении задачи? Какие трудности возникли при записи ответа. Сформулируйте правильный ответ. Объясните свое решение.

Одним из важнейших аспектов работы над задачами, особенно с «лишними» данными, на завершающем этапе является установление связей между компонентами задачи, которые можно проследить в ходе проверки решения задачи. Поэтому этап проверки будет являться важным. Он заключается в том, что дети могут пронаблюдать и оценить возможность нескольких вариантов записи и способов решения задачи. Преобразовать задачу в полноценную. Легко решаемую задачу для каждого ребенка, на его уровне трудности.

Наибольший эффект такая работа над задачей даст, если коллективное обсуждение исходного текста приводит к заключению, что в задаче имеются лишние данные, сменяется самостоятельной работой по её преобразованию, а затем возвратом к коллективному обсуждению и сравнению полученных записей решения и ответов задачи. Такая работа позволит ребенку выбрать для себя и лучше оценить тот способ, который облегчит ему решение задачи. Предоставить детям возможность выбрать самый оригинальный, самый рациональный, преимущественный способ решения, не навязывая насильно – вот задача учителя.

Этап урока – подведение итога

В конце урока необходимо обсудить, насколько удачен был предложенный порядок работы на уроке, сам выбор заданий. Что было интересного на уроке, что ещё хотелось бы рекомендовать. Что вызвало затруднение? Выяснить причины затруднений работы над заданиями на уроке. Напомнить о домашнем задании с рядами чисел, предложить ребятам попытаться самостоятельно найти способ измерения площади какой-нибудь фигуры у себя дома.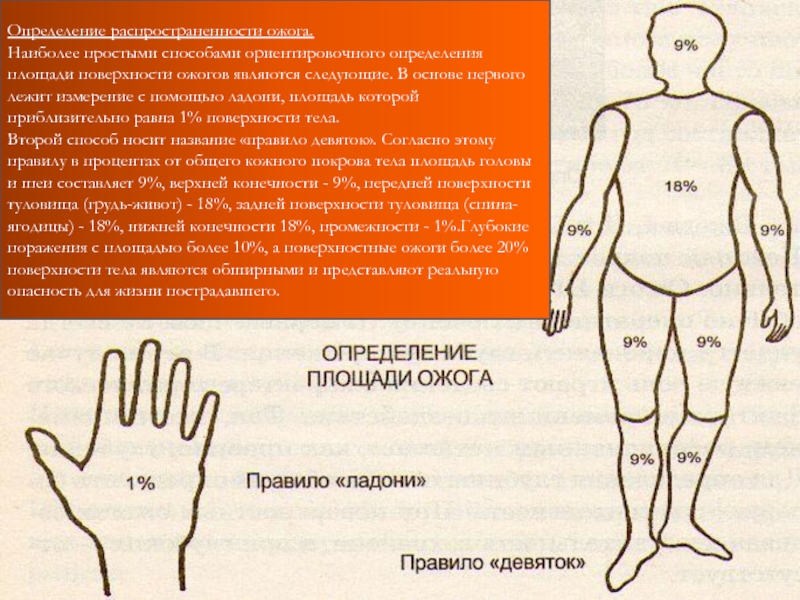 Прокомментировать и выставить оценки. Некоторые оценки выставлять во время выполнения заданий на уроке. В конце урока похвалить за работу весь класс и высказать надежду на дальнейшее благополучное изучение темы «Площадь» на уроках математики.

Площадь прямоугольного треугольника — Формула

Площадь прямоугольного треугольника

— это область, которая находится внутри границы прямоугольного треугольника. Прямоугольный треугольник – это треугольник, в котором один из углов прямой (90 градусов). Давайте узнаем больше о площади прямоугольного треугольника, как найти площадь прямоугольного треугольника с гипотенузой, а также некоторые примеры.

1.	Что такое площадь прямоугольного треугольника?
2.	Формула площади прямоугольного треугольника
3.	Вычисление площади прямоугольного треугольника по формуле
4.	Площадь прямоугольного треугольника с гипотенузой
5.	Часто задаваемые вопросы о площади прямоугольного треугольника

Что такое площадь прямоугольного треугольника?

Площадь прямоугольного треугольника — это пространство внутри него. Прежде чем узнать о площади прямоугольного треугольника, давайте посмотрим на прямоугольный треугольник.

В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой, а две другие стороны называются катетами. Две ножки взаимозаменяемо называются основанием и высотой. Обратите внимание на следующий рисунок, на котором показан прямоугольный треугольник вместе с его формулой.

Площадь прямоугольного треугольника Формула

Формула площади прямоугольного треугольника выражается так:

Площадь прямоугольного треугольника = 1/2 × основание × высота

Итак, воспользуемся этой формулой в следующих примерах.

Пример: Найдите площадь прямоугольного треугольника с основанием 4 см и высотой 6 см.

Решение: Основание = 4 см, высота = 6 см

Итак, найдем площадь треугольника по формуле

Площадь прямоугольного треугольника = 1/2 × основание × высота

После подстановки значений в формулу получаем,

Площадь прямоугольного треугольника = 1/2 × 4 × 6 = 12 квадратных см

Следовательно, площадь прямоугольного треугольника с основанием 4 см и высотой 6 см 12 см ²

Пример: Найдите площадь прямоугольного треугольника с основанием 3 см и высотой 1,42 см.

Решение: Основание = 3 см, высота = 1,42 см

Итак, найдем площадь треугольника по формуле

Площадь прямоугольного треугольника = 1/2 × основание × высота

После подстановки значений в формулу получаем,

Площадь прямоугольного треугольника = 1/2 × 3 × 1,42 = 2,13 квадратных см.

Следовательно, площадь прямоугольного треугольника с основанием 3 см и высотой 1,42 см равна 2,13 см

2

Вывод формулы площади прямоугольного треугольника

Формулу площади прямоугольного треугольника можно легко вывести, выполнив следующие действия.

• Шаг 1: Рассмотрим прямоугольник длины l и ширины w и проведите диагональ, как показано выше. Мы видим, что диагональ делит прямоугольник на два прямоугольных треугольника.
• Шаг 2: Следует отметить, что эти два прямоугольных треугольника конгруэнтны. Мы также знаем, что формула площади прямоугольника = длина × ширина.
• Шаг 3: Итак, площадь одного прямоугольного треугольника будет равна половине площади прямоугольника. Это можно выразить так: площадь одного прямоугольного треугольника = 1/2 × длина × ширина. Поскольку мы обычно представляем стороны прямоугольного треугольника как основание и высоту, формула площади прямоугольного треугольника может быть выражена как Площадь прямоугольного треугольника = 1/2 × основание × высота.

Площадь прямоугольного треугольника с гипотенузой

Площадь прямоугольного треугольника также можно вычислить с помощью гипотенузы. Вспомним теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон, т. е. (гипотенуза) ² = (основание) ² + ( высота) ²

Мы можем найти площадь прямоугольного треугольника, если мы знаем длину одного из катетов вместе с гипотенузой. Давайте разберемся в этом с помощью примера.

Пример: Найдите площадь прямоугольного треугольника с основанием 6 см и гипотенузой 10 см.

Решение: Основание = 6 см, гипотенуза = 10 см. Итак, мы можем найти значение недостающей ноги (высоты) по теореме Пифагора.

Давайте заменим заданные значения в теореме Pythagoras,

(гипотенуза) ² = (основание) ² + (высота) ²

10 ² = 6 ² + (высота). ²

100 = 36 + (Высота) ²

(Высота) ² = 64

Высота = √(64) = 8 см

Теперь мы можем найти площадь данного прямоугольного треугольника. в котором основание = 6 см, высота = 8 см

После подстановки значений в формулу получаем,

Площадь прямоугольного треугольника = 1/2 × основание × высота = 1/2 × 6 × 8 = 24 см ² .

 

Примеры площади прямоугольного треугольника

1. Пример 1: Самая длинная сторона прямоугольного треугольника равна 13 единицам. Если его высота равна 12 единицам, найдите его площадь по формуле площади прямоугольного треугольника.

   Решение:

   Мы знаем, что самая длинная сторона прямоугольного треугольника называется гипотенузой.

   Итак, дано, что гипотенуза = 13 единиц, а высота = 12 единиц. Длину основания можно найти по теореме Пифагора.

   После подстановки данных значений в теорему Пифагора,

   (гипотенуза) ² = (базовая) ² + (высота) ²

   13 ² = (основание) ² + (12) ²

   169 = (база) ²

   169 = (база) ² + 144

   (основание)

   2 = 25

   основание = √(25) = 5 единиц.

   Теперь мы можем вычислить площадь прямоугольного треугольника с основанием = 5 единиц, высотой = 12 единиц

   Площадь прямоугольного треугольника = 1/2 × основание × высота = 1/2 × 5 × 12 = 30 квадратных единиц.

   Следовательно, площадь прямоугольного треугольника = 30 квадратных единиц.

2. Пример 2: Бассейн имеет форму прямоугольного треугольника. Его стороны находятся в соотношении 3:4:5. Его периметр составляет 720 единиц. Найдите его площадь.

   Решение:

   Предположим, что стороны бассейна равны 3x, 4x и 5x.

   Дано, что его периметр = 720 единиц.

   3х + 4х + 5х = 720

   12х = 720

   x = 60

   Таким образом, стороны треугольника равны:

   3x = 3(60) = 180 единиц

   4x = 4(60) = 240 единиц

   5x = 5(60) = 300 единиц

   5

   Поскольку 300 единиц — это самая длинная сторона бассейна (который имеет форму прямоугольного треугольника), это и есть гипотенуза.

   Итак, 180 единиц и 240 единиц должны быть основанием и высотой бассейна взаимозаменяемы.

   Используя формулу площади прямоугольного треугольника,

   Площадь бассейна = 1/2 × основание × высота = 1/2 × 180 × 240 = 21 600 единиц ² .

   Следовательно, площадь данного бассейна = 21 600 единиц ² .

3. Пример 3: Найдите площадь прямоугольного треугольника, основание которого равно 1,2 м, а гипотенуза 3,7 м.

   Решение:

   Основание = 1,2 м, гипотенуза = 3,7 м. Итак, мы можем найти значение недостающей ноги (высоты) по теореме Пифагора.

   Подставим данные значения в теорему Пифагора,

   (гипотенуза) ² = (базовая) ² + (высота) ²

   (3,7) ² = (1,2) ² + (высота) ²

   13.69 = 1.4444444 +444 +444 +444 +444 +444 + 4. (Высота) ²

   (Высота) ² = 12,25

   Высота = √(12,25) = 3,5 м

   Теперь мы можем найти площадь данного прямоугольного треугольника, в котором основание = 1,2 м, высота = 3,5 м

   После подстановки значений в формулу получаем,

   Площадь прямоугольного треугольника = 1/2 × основание × высота = 1/2 × 1,2 × 3,5 = 2,1 м ² .

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по площади прямоугольного треугольника

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади прямоугольного треугольника

Какова площадь прямоугольного треугольника?

Площадь прямоугольного треугольника определяется как общее пространство или область, покрытая прямоугольным треугольником. Выражается в квадратных единицах. Некоторые распространенные единицы измерения площади: м ² , см ² , дюймы ² , ярды ² и т. д.

Какова формула площади прямоугольного треугольника?

Формула, используемая для нахождения площади прямоугольного треугольника, выражается следующим образом: Площадь прямоугольного треугольника = 1/2 × основание × высота. Здесь основание и высота — это два катета прямоугольного треугольника, а третья сторона — гипотенуза.

Как найти периметр и площадь прямоугольного треугольника?

Площадь прямоугольного треугольника находится по формуле Площадь прямоугольного треугольника = 1/2 × основание × высота, где основание и высота — две стороны прямоугольного треугольника. Обратите внимание на фигуру прямоугольного треугольника, приведенную выше на этой странице, чтобы определить стороны. Периметр прямоугольного треугольника получается сложением всех трех сторон треугольника. Если даны только две его стороны, то по теореме Пифагора находим третью сторону.

Как найти площадь прямоугольного треугольника без основания?

Если даны только высота и гипотенуза прямоугольного треугольника, то прежде чем найти площадь треугольника, надо сначала найти основание по теореме Пифагора. После вычисления основания мы можем использовать следующую формулу, чтобы найти его площадь: Площадь прямоугольного треугольника = 1/2 × основание × высота. Например, чтобы найти площадь прямоугольного треугольника с высотой 4 см и гипотенузой 5 см, нам сначала нужно найти его основание, используя теорему Пифагора. Это означает, что основание = √[(гипотенуза) ² — (высота) ² ] = √(5 ² — 4 ² ) = √9 = 3 см. После этого мы можем найти площадь следующим образом. Площадь прямоугольного треугольника = 1/2 × основание × высота = 1/2 × 3 × 4 = 6 см ² .

Как найти площадь прямоугольного треугольника без высоты?

Если даны только основание и гипотенуза прямоугольного треугольника, то прежде чем найти площадь треугольника, надо сначала найти высоту по теореме Пифагора. Затем мы можем использовать формулу Площадь прямоугольного треугольника = 1/2 × основание × высота, чтобы найти его площадь. Например, чтобы найти площадь прямоугольного треугольника с основанием 4 см и гипотенузой 5 см, сначала найдем его высоту по теореме Пифагора. Итак, получаем, высота = √[(гипотенуза) ² — (основание) ² ] = √(5 ² — 4 ² ) = √9 = 3 см. После этого шага мы можем найти площадь следующим образом. Площадь прямоугольного треугольника = 1/2 × основание × высота = 1/2 × 3 × 4 = 6 см ² .

Как найти площадь прямоугольного треугольника с гипотенузой?

Площадь прямоугольного треугольника можно вычислить, если мы знаем значение гипотенузы и одного из его катетов.

• Зная основание прямоугольного треугольника и гипотенузу, можно найти высоту по теореме Пифагора.
• Зная высоту прямоугольного треугольника и гипотенузу, можно найти основание по теореме Пифагора.
• Затем мы можем найти площадь прямоугольного треугольника, используя формулу 1/2 × основание × высота.

Как найти угол стрелок часов

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Учитесь по концепции

Справка по математике SAT » Геометрия » Плоская геометрия » Круги » Математика часов » Как найти угол стрелок часов

Сейчас 4 часа. Какова мера угла, образованного между часовой и минутной стрелками?

Возможные ответы:

Правильный ответ:

Объяснение:

В четыре часа минутная стрелка находится на 12, а часовая на 4. Образовавшийся угол составляет 4/12 от общего числа градусов в окружности, 360.

12/4 * 360 = 120 градусов

Сообщить об ошибке

Если часы показывают 20:15, какой угол составляют стрелки?

Возможные ответы:

Правильный ответ:

Пояснение:

Часы — это круг, а круг всегда содержит 360 градусов. Поскольку на часах 60 минут, каждая минутная отметка равна 6 градусам.

Минутная стрелка на часах будет указывать на 15 минут, что позволит нам рассчитать ее положение на круге.

Поскольку на часах 12 часов, каждый час равен 30 градусам.

Мы можем вычислить, где будет часовая стрелка в 8:00.

Однако на самом деле часовая стрелка будет между 8 и 9, поскольку мы смотрим на 8:15, а не на абсолютную часовую отметку. 15 минут равны одной четверти часа. Используйте то же уравнение, чтобы найти дополнительное положение часовой стрелки.

Ищем угол между двумя стрелками часов. будет равна разнице между двумя мерами угла.

Сообщить об ошибке

Чему равен меньший угол, образованный стрелками аналоговых часов, если часовая стрелка находится на 10, а минутная на 2?

Возможные ответы:

30°

90°

120°

56°

45°

9003 Правильный ответ:0004

120°

Объяснение:

Аналоговые часы разделены на 12 секторов в соответствии с числами от 1 до 12. Один сектор соответствует 30 градусам (360/12 = 30). Если часовая стрелка находится прямо на 10, а минутная на 2, это означает, что между ними есть 4 сектора по 30 градусов, то есть они находятся на расстоянии 120 градусов друг от друга (30 * 4 = 120).

Сообщить об ошибке

При какой угол находится между часовой и минутной стрелками на часах?

Возможные ответы:

Правильный ответ:

Объяснение:

В час часовая стрелка находится на  , а минутная – на . На часах есть пробелы, и эти стрелки разделены пробелами.

Таким образом, угол между ними – это градусы всего угла, который равен .

Поэтому мы умножаем их, чтобы получить ответ.

 

Мы можем сократить при умножении, чтобы получить: 

 

Сообщить об ошибке

Какова мера в градусах острого угла, образованного стрелками 12-часовых часов, показывающих ровно 3:10?

Возможные ответы:

65 °

72 °

35 °

55 °

60 °

Правильный ответ:

35 °

:

35 °

. Пояснение:

Все часы измеряют 360°. Поскольку часы разделены на 12 секций, расстояние между каждым числом равно 30° (360/12). Расстояние между цифрами 2 и 3 на часах равно 30°. Однако приходится считаться с прошедшими 10 минутами. 10 минут составляют 1/6 часа, поэтому часовая стрелка также переместилась на 1/6 расстояния между 3 и 4, что добавляет 5° (1/6 от 30°). Таким образом, общая мера угла равна 35°.

 

 

Сообщить об ошибке

Если сейчас 4:00, какова мера угла между минутной и часовой стрелками часов?

Возможные ответы:

120 градусов

90 градусов

125 градусов

45 градусов

100 градусов

Правильный ответ:

120 градусов

. Пояснение:

Часы имеют форму круга, состоящего из 360 градусов. На часах 12 цифр, обозначающих часы. Имея это в виду, мы можем сказать, что каждое число представляет собой угол. Мера угла между каждым числом определяется как .

Если сейчас 4:00, то минутная стрелка указывает на 12, а часовая указывает на 4.

Таким образом, мы можем сказать, что угол между двумя стрелками равен  градусам.

Еще один способ представить это — представить часы в ближайшем времени. В 3:00 стрелки часов образуют прямой угол 90 градусов. Поскольку мы знаем, что каждое число на часах отделено друг от друга 30 градусами, мы можем просто добавить 30 к 90 градусам и получить 120 градусов для угла в 4:00.

Сообщить об ошибке

Если сейчас 14:00, какова величина угла между минутной и часовой стрелками часов?

Возможные ответы:

90 градусов

30 градусов

45 градусов

60 градусов

120 градусов

Правильный ответ:

60 градусов

.