Как сделать объемную цифру 5 из картона: Большая объёмная цифра из картона (каркас с размерами)| Цифра 5 | DIY: number 5 — YouTube

Делаем объемную цифру из картона и бумаги тишью

All4party

Как из картона и бумаги сделать объемную цифру или букву для декора детского праздника.

Нам потребуются следующие материалы:

1. Картон (можно взять старую коробку из-под техники, или купить новую в строительном магазине).
2. Бумага (нам больше нравится тишью, она более легкая, летящая, но подойдет и гофробумага).
3. Клей-пистолет.
4. Клей ПВА.
5. Ножницы.
6. Линейка.

Рисуем на картоне цифру или букву нужного нам размера.

Вырезаем ее и делаем еще одну для задней стенки, а также вырезаем все остальные ребра, в итоге должна получиться единичка в развертке.

Из остатков картона, вырезаем тонкие полосочки и загибаем их, с помощью клея-пистолета закрепляем все стенки друг к другу.

Вот уже получилась объемная единичка, которая самостоятельно стоит, осталось ее только украсить 🙂

Берем бумагу тишью нужных цветов.

Разрезаем на полоски, примерно 4 см (в пакете 10 л бумаги 50х60 см, для единицы такого размера мы взяли по 5 листов каждого цвета).

Затем из каждой полоски нарезаем бахрому.

С помощью ПВА наклеиваем готовые полоски на цифру, начинаем снизу (бумага тишью очень тонкая, поэтому лучше брать два слоя бахромы).

Таким образом обклеиваем поэтапно всё изделие.

Такая цифра или буква станет настоящим украшением вашего праздника.

Придумывайте новые цвета и формы, на что у вас хватит фантазии 🙂

Рейтинг

☆

☆

☆

☆

☆

   0.0 (0 голосов)

All4party

Россия, Санкт-Петербург

Магазин

Блог (1)

Следите за творчеством мастера

Мастер-классы по теме

Ключевые слова

• Ключевые слова
• объемная буква
• буква из бумаги
• буква
• цифра
• декор
• детский праздник
• детский мастер-класс
• тишью

Рубрики мастер-классов

Do It Yourself / Сделай сам
Recycle / Вторая жизнь вещей
Tворим с детьми
Бижутерия своими руками
Валяние
Вышивка
Вязание
Декорирование
Декупаж
Дизайн и декор интерьера
Живопись и рисование
Керамика
Ковроделие
Косметика ручной работы
Кружевоплетение
Кулинария
Куклы и игрушки
Лепка
Материалы для творчества
Мебель своими руками
Миниатюра
Обувь своими руками
Одежда своими руками

Организация пространства
Пирография
Плетение
Прядение
Работа с бисером
Работа с бумагой
Работа с кожей
Работа с металлом
Работа с мехом
Работа со стеклом
Реставрация
Роспись
Свечи своими руками
Скрапбукинг
Столярное дело
Сумки своими руками
Ткачество
Упаковка своими руками
Флористика
Фотография и видео
Художественная резьба
Шитье

Трехмерные фигуры (трехмерные фигуры)

Что такое трехмерные фигуры?

В геометрии трехмерная форма может быть определена как твердая фигура или объект или форма, которая имеет три измерения: длину, ширину и высоту . В отличие от двухмерных фигур, трехмерные фигуры имеют высоту, которая совпадает с толщиной или глубиной. Трехмерность также записывается как 3D, и, следовательно, эти фигуры также обычно называют 3D-формами. Все трехмерные фигуры занимают пространство, которое измеряется объемом .

В трехмерных фигурах трехмерность означает трехмерность. Размеры обычно можно рассматривать как измерения в направлении. Длину, ширину и глубину можно считать размерами.

Связанные игры

История трехмерных фигур

Все трехмерные фигуры имеют три измерения: длину, ширину и высоту . Формы выглядят по-разному с разных сторон. Все 2D-формы измеряются только по длине и ширине. Аристотель говорил, что двумерные формы — это линии, а не фигуры или тела. Они всегда описываются как продолжение линий или областей, ограниченных линиями. И наоборот, трехмерные фигуры имеют объем.

По соглашению первые три измерения представлены в виде пространственных измерений x-y-z. Ширина, высота и глубина — это их имена.

Связанные рабочие листы

Примеры трехмерных фигур

Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные фигуры, которые мы видим вокруг себя.

Реальные примеры трехмерных фигур

Трехмерные фигуры можно увидеть повсюду вокруг нас. Мы можем видеть кубик в кубике Рубика и кубике, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в морковке и рожке мороженого, цилиндр в ведерке и бочка вокруг нас.

Ниже перечислены некоторые примеры трехмерных фигур из реальной жизни:

1. Конус: Дорожные конусы и кепки на день рождения имеют конусообразную форму.

2. Треугольная призма: Палатка имеет форму треугольной призмы.

3. Квадратная пирамида: Пирамида Гизы в Египте имеет форму квадратной пирамиды.

4. Прямоугольная призма: Коробки, такие как коробки для обуви и коробки для хлопьев, имеют форму прямоугольных призм.

Атрибуты трехмерных фигур

У трехмерной фигуры есть три атрибута: грань, ребро и вершина. Давайте подробно разберемся с трехмерными формами и их свойствами.

Лицо: Каждая отдельная поверхность, плоская или изогнутая, трехмерной фигуры называется ее гранью.

Край: Линия, где встречаются две грани трехмерных фигур, называется его краем.

Вершина : Каждый угол, где встречаются три грани трехмерных фигур, называется его вершиной. Вершины — это множественное число от вершины.

Список трехмерных фигур

Вот список названий трехмерных фигур с их изображениями и атрибутами.

Сфера

Все точки сферы находятся на одинаковом расстоянии от ее центра. Земля чем-то похожа на нее, за исключением одного: когда вы смотрите на нее издалека, она выглядит как сфера, но если вы смотрите на нее вблизи, она не совсем круглая. Сфера имеет несколько характеристик:

• Она идеально симметрична и имеет форму шара.
• Помимо радиуса, диаметра, длины окружности, объема и площади, у него также есть длина.
• Расстояние от центра до каждой точки на поверхности сферы одинаково.
• На одной грани не найдены ни ребра, ни вершины.
• Поскольку у него нет плоской грани, это не многогранник.

Куб и прямоугольный параллелепипед

Куб и прямоугольный параллелепипед — это большие блоки. Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные.

Цилиндр

Цилиндр имеет две круглые поверхности на обоих концах и одну изогнутую поверхность по всей длине. Он имеет высоту и радиус. Высота цилиндра перпендикулярна его поверхности сверху вниз. Ниже приведены некоторые основные характеристики цилиндров:

• Поверхность цилиндра изогнута.
• Форма снизу вверх остается неизменной.
• Два одинаковых конца формируют трехмерную форму объекта. Концы могут быть круглыми или овальными.
• У прямого цилиндра центры круглых оснований расположены на одной линии, а у наклонного цилиндра центры оснований расположены на разных линиях.

Формула трехмерных фигур

Сеть трехмерных форм

Сеть — это узор, полученный путем плоской разбивки поверхности трехмерной фигуры, показывающей каждую грань фигуры .

3D-фигуры могут иметь более одного шаблона цепей. Ниже показаны названия нескольких 3D-форм и их сетей:

Интересные факты :
Все трехмерные фигуры состоят из двумерных фигур.

Разница между 2D- и 3D-фигурами

Давайте различать 2D- и 3D-формы, разбираясь в двухмерных и трехмерных формах и их свойствах.

Решенные примеры трехмерных фигур

Пример 1: Что из следующего является трехмерной фигурой?

Конус Квадрат Сфера Кубоид Цилиндр Параллелограмм

Решение:

Cone Sphere Cuboid цилиндр

Пример 2: Укажите, представлены ли следующие True или False .

1. Трехмерная форма имеет 3 измерения.
2. Трехмерные фигуры также называются плоскими.
3. Трехмерные фигуры занимают пространство.
4. Все трехмерные фигуры имеют плоские грани.

Решение:

1. Правда
2. Ложь. Трехмерные формы также называют объемными формами.
3. Правда
4. Ложь. Сфера представляет собой трехмерную форму без плоской грани.

Пример 3: Заполните таблицу атрибутами перечисленных трехмерных фигур.

Решение:

Пример 4: Сопоставьте объект с его формой.

Решение:

1. (a) – (iii)
2. (б) – (и)
3. (в) – (iv)
4. (г) – (ii)

Пример 5: Вычислите площадь поверхности прямоугольного параллелепипеда шириной 4 единицы, длиной 3 единицы и высотой 5 единиц.

Решение:

Дан кубоид, имеющий три единицы длины, четыре единицы ширины и пять единиц высоты.

Площадь поверхности прямоугольного параллелепипеда $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ квадратных единиц

$= 2 \times (\text{lw} + \text {белая} + \text{левая})$

$= 2[(3 х 4) + (4 х 5) + (3 х 5)]$

$= 2(12 + 20 + 15)$

$= 2(47)$

$= 94$ квадратных единиц

Следовательно, площадь поверхности данного прямоугольного параллелепипеда равна 94 квадратных единиц.

Пример 6: Джейн любит пить молоко из цилиндрического стакана. Ее стакан имеет 15 единиц высоты и 3 единицы радиуса основания. Сколько молока она может налить в стакан?

Решение:

Учитывая, что высота стакана 15 единиц, а радиус основания 3 единицы. 92$

Таким образом, Джейн может налить в свой стакан приблизительно 424 кубических единицы молока.

Практические задачи трехмерных фигур

1

Какая фигура имеет две плоские грани и одну изогнутую?

Цилиндр

Сфера

Конус

Куб

Правильный ответ: Цилиндр
Цилиндр имеет две плоские поверхности, имеющие форму круга, и одну изогнутую поверхность.

2

Сколько квадратных фигур имеет сетка куба?

4

6

8

10

Правильный ответ: 6
Куб имеет 6 граней, которые являются квадратами. Итак, в сетке куба будет 6 квадратных фигур.

3

Что из следующего не имеет ребра?

Конус

Цилиндр

Куб

Сфера

Правильный ответ: Сфера
Сфера имеет одну сторону. Так что у него нет края.

4

Какая из данных фигур НЕ является трехмерной?

Трапеция

Призма

Пирамида

Куб

Правильный ответ: Трапеция
Трапеция — это двумерная фигура с четырьмя сторонами, одна пара противоположных сторон которых параллельна друг другу, а две другие стороны не параллельны.

5

Как называется пересечение двух граней объемной фигуры?

Вершина

Сторона

Грань

Ребро

Правильный ответ: Ребро
Ребра — это отрезки, соединяющие две грани. Грани куба пересекаются по линиям, называемым ребрами. Фигуры с несколькими ребрами называются сплошными фигурами. Пересечение нескольких плоскостей называется вершиной.

6

Трехмерные геометрические фигуры называются ________.

фигуры

тела

грани

многоугольники

Правильный ответ: тела
Трехмерные геометрические фигуры называются телами.

7

Что такое в математике сплошная заостренная фигура, соединенная с вершиной изогнутой поверхностью с плоским круглым основанием?

Конус

Сфера

Цилиндр

Пирамида

Правильный ответ: Конус
Конусы представляют собой трехмерные тела, состоящие из круглого основания, соединенного с одной точкой (называемой вершиной) изогнутыми сторонами. В качестве альтернативы вы можете думать о конусе как о круглой пирамиде.

Часто задаваемые вопросы о трехмерных фигурах

Какие существуют типы трехмерных фигур?

Куб, прямоугольный параллелепипед, цилиндр, сфера, конус, призма и пирамиды.

Каковы атрибуты трехмерных фигур?

Трехмерные фигуры имеют 3 измерения — длину, ширину и глубину. В результате этих размеров эти формы имеют атрибуты граней, ребер и вершин.

Что такое ребро?

Ребро — это линия, на которой сходятся две грани трехмерной формы.

Например, у куба 12 ребер.

Что такое вершины?

Вершины — это углы, в которых сходятся три грани. Например, прямоугольный параллелепипед имеет 8 вершин.

Какая польза от объема трехмерной формы?

Объем помогает найти пространство, занимаемое данной фигурой.

Из скольких квадратов состоит кубическая сеть?

Кубическая сеть состоит из шести квадратов.

3D-формы и сети | SkillsYouNeed

На нашей странице, посвященной трехмерным фигурам, мы представили трехмерные фигуры, называемые многогранниками , которые имеют несколько плоских поверхностей ( граней ), состоящих из 2D полигонов , соединенных прямыми ребрами и острыми углами ( вершин ).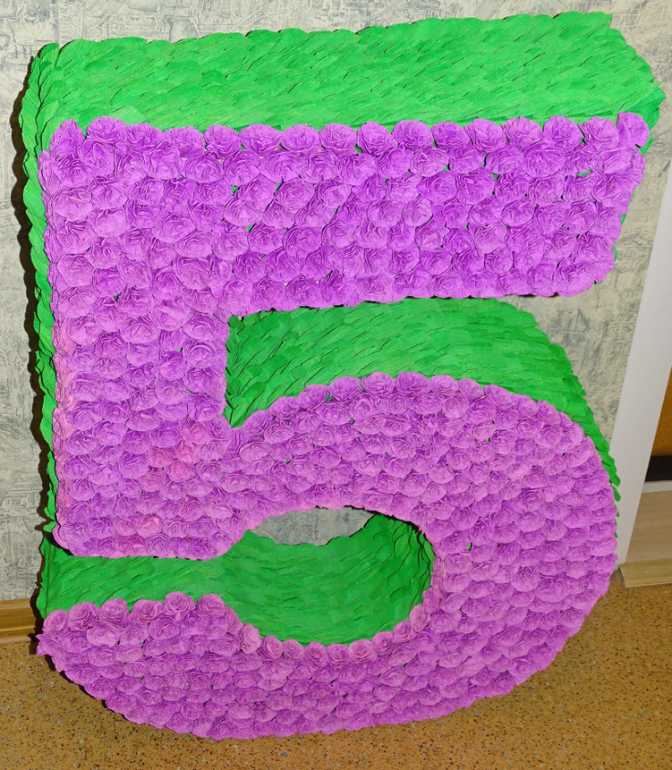

Полезным свойством этих объемных форм является то, что они могут быть описаны визуально в двух измерениях с помощью формы сетки .

Сеть в данном контексте совсем не похожа на рыболовную сеть или баскетбольную сетку! Это просто двумерное изображение того, как выглядела бы трехмерная фигура, если бы все ее стороны были расправлены. Представьте, например, открытую картонную коробку.

2D-сеть можно сложить, чтобы получилась 3D-форма.

Сетки кубов и прямоугольных параллелепипедов

На приведенной ниже диаграмме вы можете увидеть знакомую маркировку игральных костей, но это не 3D-куб, как можно было бы ожидать, а плоское 2D-представление игральных костей. Вы можете вырезать это и склеить вместе, чтобы сделать куб:

Шесть отдельных квадратов с знакомыми точками кубика на

форме сетки куба . Маленькие выступы по краям предназначены для склеивания кубиков.

Сети форм для кубов — нет единственного ответа

---

Сети кубов — одни из самых простых для визуализации, и это забавная проверка ваших пространственных навыков, чтобы увидеть, сколько вы можете создать. На самом деле существует сетей 11 форм, которые составляют куб .

На приведенной ниже диаграмме показано 16 различных расположений 6 квадратов, которые все выглядят так, как будто они могут быть кубическими сетями, но 6 из них таковыми не являются. Можете ли вы решить, какие сети куба являются действительными?

Ответ: 1, 4, 6, 7, 8, 9, 12, 13, 14 и 15 — допустимые сети куба.

2, 3, 5, 10, 11 и 16 не могут составить куб, и они не являются сетями . Отсутствует одна действующая сеть…. Вы можете это решить?

Это довольно сложно…

Теперь, когда вы начали тренировать свои пространственные навыки с обычными кубами, сети фигур кубоида должны быть более понятными.

Кубоид подобен кубу, но некоторые или все его стороны могут быть прямоугольными. Таким образом, сети имеют такие же характеристики, как и у куба, но выглядят совсем по-другому.

Вот сетка прямоугольного параллелепипеда со сторонами 10см, 20см и 40см.

В приведенной выше прямоугольной сети найдите вершину (угол), отмеченную красной точкой. Снова используя свои пространственные навыки, сможете ли вы определить, какие другие вершины, обозначенные цифрами от 1 до 6, соединятся с красной точкой, когда параллелепипед находится в трехмерной форме?

Сети могут рассказать нам больше….

---

Теперь, когда мы знаем размеры сети, мы можем узнать другие свойства этого тела, такие как его

объем и площадь поверхности .

Объем прямоугольного параллелепипеда вычисляется как произведение его длины, ширины и высоты:
Длина × Ширина × Высота = 40 × 20 × 10 = 192

Таким образом, объем этого параллелепипеда равен 8000 см ³ или 8 литров.

---

Площадь поверхности — это общая площадь всех шести сторон, сложенная вместе.

У нас есть две стороны 20 × 40см, 10 × 20см и 10 × 40см.
2 × 20 × 40 = 1600
2 × 10 × 20 = 200
и 2 × 10 × 40 = 800
16 + 200 + 800 = 2800

Таким образом, кубоид имеет площадь поверхности 2800 см ² или 0,28 м ²

99

---

54454544.

---

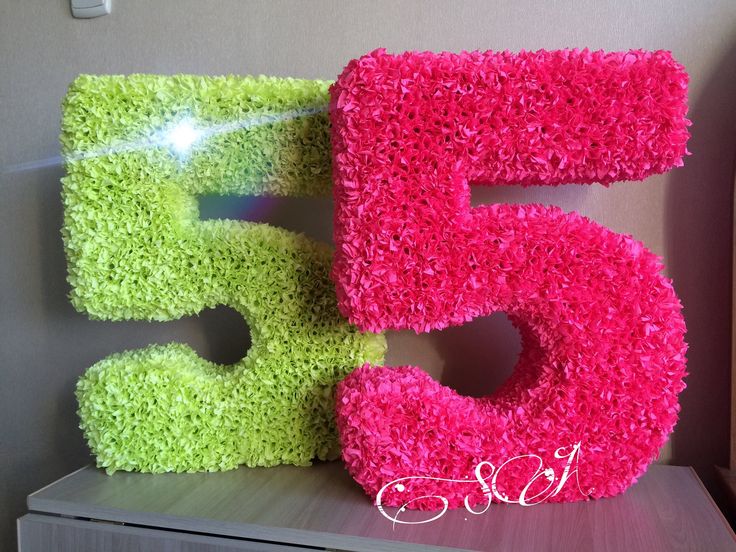
Сети призм, пирамид и других многоугольников

Как и в примере с кубом выше, любая трехмерная фигура может иметь несколько цепей, а не только одну, но вот некоторые трехмерные фигуры с примерами только одной из их цепей. Посмотрим, сможешь ли ты поработать еще.

Сетки криволинейных тел

Все приведенные выше примеры сосредоточены на многоугольниках с плоскими сторонами. Изогнутые формы тоже могут иметь сети. Их проще визуализировать и построить, если твердое тело имеет хотя бы одну плоскую поверхность. Вот некоторые примеры.

Сфера или шар

Сфера не имеет плоских поверхностей, это непрерывная кривая.

Создание плоской 2D-сети земного шара веками было проблемой для картографов (создателей карт). Когда мы смотрим на сетку сферы, мы можем понять, почему картографам было трудно ее использовать. Тем не менее, карты мира были созданы таким образом:

Представьте, что у вас есть апельсин, и вы разрезаете его на дольки. Когда вы съели мясо, у вас остались кусочки кожи. Если бы вы выстроили их в линию, то они были бы похожи на сетку сферы.

Однако у этого подхода есть недостаток. Независимо от того, сколько сегментов, каждый из них будет иметь плоскую поверхность.

Еще раз взглянув на ваши кусочки апельсиновой кожуры, вы увидите, что они не только изгибаются сверху вниз, но и изгибаются из стороны в сторону, в отличие от страницы, которая может изгибаться только в одном направлении. это называется двойная кривизна . Поэтому невозможно создать полностью точную 2D-сеть 3D-формы с двойной кривизной. Даже если бы в приведенной выше сети было 100 сегментов, это все равно было бы приближением.

Картографы в конце концов преодолели эту проблему, создав карты на основе цилиндра, называемого проекцией . Это тоже приближение, но оно включает искаженное изображение поверхности земного шара, что позволяет точно измерять расстояния на плоской карте. Подробнее об этом читайте на нашей странице полярная, цилиндрическая и сферическая системы координат .

---

Вывод: зачем вообще нужны сети?

Способность понимать, как трехмерная фигура состоит из двухмерных компонентов, является не только полезным навыком, если вам нужно построить коробку, но и жизненно важным навыком в любом аспекте трехмерного проектирования.

Инженеры и дизайнеры используют сложные и мощные пакеты автоматизированного проектирования (САПР) для проектирования всего, от мебели в разобранном виде до крупнейших в мире круизных лайнеров.

Важные пространственные навыки, которые вы приобретете на основе базового понимания форм-сетей, могут, таким образом, развиваться в других, более сложных приложениях проектирования.

---

Дальнейшее чтение из книги «Навыки, которые вам нужны»

---

Понимание геометрии
Часть руководства «Навыки, которые вам нужны» для счета

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и твердых тел.