Разные способы вычисления площадей фигур
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Боташева С.М. 1
1Дворец творчества детей и молодежи, г. Нальчик
Суншева З.Н. 1
1Дворец творчества детей и молодежи, г.Нальчик
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Математика – один из моих любимых школьных предметов. А самое сложное и одновременно самое интересное в математике — решение задач. Задачи в учебнике и сборниках попадаются самые разные и способов решения каждой задачи можно придумать несколько. Но один вид задач, как мне кажется, не похож на другие. Это задачи на клетчатой бумаге. Они кажутся необычными, более занимательными.
Это задачи на клетчатой бумаге. Они кажутся необычными, более занимательными.
А встречаются ли такие задачи старшеклассникам? Я решила посмотреть открытый банк заданий ОГЭ и ЕГЭ по математике, посетить сайты по подготовке выпускников 9 и 11 классов к экзаменам. Оказалось, что задачи на нахождение площадей многоугольников на клетчатой бумаге достаются на экзаменах почти каждому выпускнику.
Вывод прост: уметь решать задачи на сетке (в т.ч. на нахождение площадей) разными способами нужно уметь каждому школьнику. В этом я вижу актуальность моей работы, а ее новизну в том, что один из рассматриваемых способов решения не разбирается в школьных учебниках математики.
Цель исследования – изучить способы вычисления площадей фигур на клетчатой бумаге, и выбрать самый эффективный.
Для достижения данной цели необходимо выполнить следующие задачи:
- Подобрать литературу по данной теме.
- Изучить способы нахождения площадей фигур на клетчатой бумаге.

- Провести эксперимент.
- Сделать выводы.
Предмет исследования: площади фигур на клетчатой бумаге.
Объект исследования: фигуры на клетчатой бумаге.
Гипотеза: самым эффективным способом вычисления площадей фигур на клетчатой бумаге является – формула Пика.
Глава 1. Способы нахождения площадей фигур на клетчатой бумаге. 1.1Площадь фигуры как сумма площадей ее частей
Задача №1. Найти площадь фигуры на рисунке 1 (клетки размером 1х1 см).
Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.
S=S1+ S2+ S3+S4
S1=2*3= 6 см2; S2= *2*1=1 см2;
S3= *2*1= 1 см2; S4= *3*1= 1,5 см2
S= 6+1+1+1,5= 9,5 см2.
Рис. 1. Ответ: 9,5 см2
Задача №2. Найти площадь фигуры на рисунке 2 (клетки размером 1х1 см).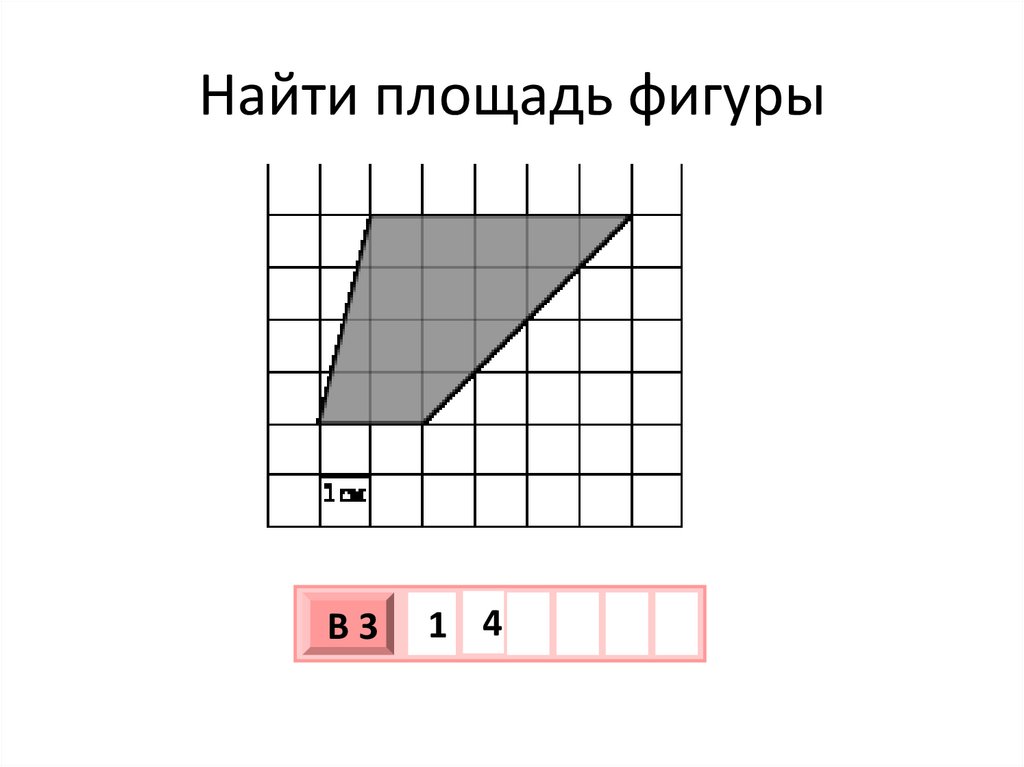
Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.
S=S1+ S2+ S3+S4
S1= *1*5= 2,5 см2; S2=4*2=8 см2;
S3= *1*2= 1 см2; S4= *2*4= 4 см2;
S= 2,5+8+1+4= 15,5 см2.
Ответ: 15,5 см2.
Рис. 2.
Задача №3. Найти площадь фигуры на рисунке 3 (клетки размером 1х1 см).
Разбиваем данную фигуру на три части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.
S=S1+ S2+ S3
S1= *2*5= 5 см2;
S2=5*5=25 см2;
S3= *2*5= 5 см2;
S= 5+25+5= 35 см2
Рис. 3. Ответ: 35 см2.
1.2. Площадь фигуры как часть площади прямоугольника
Задача № 4. Найти площадь фигуры на рисунке 4 (клетки размером 1х1 см).
Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:
S=Sпр – S1 – S2 – S3
Sпр=5*5=25 см2; S1= *5*4=10 см2;
S2= *5*2=5 см2; S3= *1*3=1,5 см2;
S=25-10-5-1,5=8,5 см2
Ответ: 8,5 см2.
Рис.4.
Задача №.5. Найти площадь фигуры на рисунке 5 (клетки размером 1х1см).
Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:
S=Sпр – S1 – S2 – S3 – S4
Sпр=7*7= 49 см2; S1= *2*5=5 см2;
S2= *2*5=5 см2; S3= *2*5=5 см2;
S4= *2*5=5 см2;
S= 49-5-5-5-5= 29 см2
Ответ: 29 см2.
Рис.5.
Задача №.6. Найти площадь фигуры на рисунке 6 (клетки размером 1х1см).
Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:
Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:
S=Sпр – S1 – S2
Sпр=5*5=25 см2;
S1= *3*1=1,5 см2; S2= *4*5=10 см2;
S= 25-1,5-10=13,5 см2.
Ответ: 13,5 см2.
Рис. 6.
1.3. Формула Пика
Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье. Его отец Адольф Йозеф Пик возглавлял частный институт. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).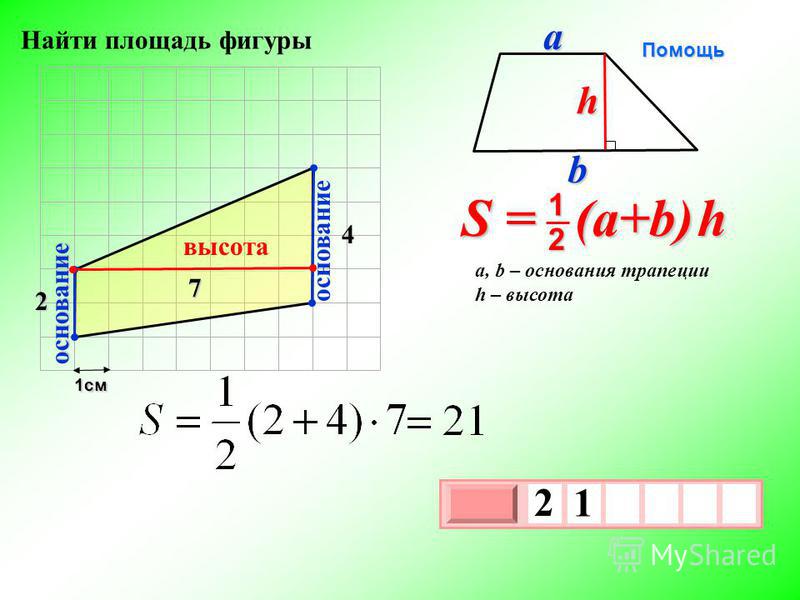
В 1900 – 1901 годах занимал пост декана философского факультета.
После того как Пик вышел в отставку в 1927 году, он получил звание почётного профессора и вернулся в Вену – город, в котором он родился. Однако в 1938 году после аншлюса Австрии 12 марта он вернулся в Прагу. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.
Круг математических интересов Георга Пика был чрезвычайно широк: 67 его работ посвящены многим темам, таким как линейная алгебра, интегральное исчисление, функциональный анализ, геометрия и др. Но больше всего он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года.
Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 году польский математик Гуго Штейнгауз включил теорему (или как её ещё называют – формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.
С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.
Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, S – его площадь. Тогда справедлива следующая формула:
S = В+ – 1 ,
Это и есть формула Пика.
Задача №7. Вычислить площадь многоугольника на рисунке 7. Воспользуемся формулой Пика.
Отметим узлы:
Г=9 (синие)
В=48 (красные)
Подставив в формулы наши данные, получаем:
Рис.7. S=48 + – 1 = 51,5 см2 .
Задача №8. Вычислить площадь многоугольника на рисунке 8. Воспользуемся формулой Пика.
Отметим узлы:
Г=9 (синие)
В=16 (красные)
Подставив в формулы наши данные, получаем:
S=16 + – 1 = 19,5 см2 .
Рис. 8.
Задача № 9. Вычислить площадь многоугольника на рисунке 9. Воспользуемся формулой Пика.
Отметим узлы:
Г=8 (синие)
В=24 (красные)
Подставив в формулы наши данные, получаем
S=24 + – 1 = 19 см2 .
Рис. 9.
Глава 2. Проведение эксперимента
2.1. Результаты эксперимента
Изучив все способы нахождения площадей фигуры на клетчатой бумаге, мы решили провести эксперимент. Исследование проводилось в объединении «Знаю и считаю» Дворца творчества детей и молодежи, в котором я обучаюсь. Вместе с нашим педагогом, который также является моим научным руководителем, мы объяснили ребятам все способы вычисления площадей фигур. Затем, мы им раздали задания: по три задачи по каждому способу, и предложили решить их на время. Мы с моим научным руководителем засекали время, а ребята решали задачи.
В Таблице 1 представлены результаты каждого обучающегося по трем способам:
|
№ |
Ф. |
Время, затраченное на решение задач 1-м методом (мин) |
Время, затраченное на решение задач 2-м методом (мин) |
Время, затраченное на решение задач 3-м методом (Формула Пика) (мин) |
|
1 |
Алина |
3,23 |
4,33 |
1,04 |
|
2 |
Дана |
4,12 |
4,54 |
1,43 |
|
3 |
Дарина |
5,07 |
4,46 |
2,15 |
|
4 |
Алина |
2,32 |
2,45 |
1,12 |
|
5 |
Инал |
2,17 |
2,34 |
0,52 |
|
6 |
Лалина |
5,43 |
6,31 |
3,23 |
|
7 |
Залина |
4,43 |
4,23 |
2,38 |
|
8 |
Руслан |
2,34 |
3,43 |
1,15 |
|
9 |
Алина |
3,56 |
4,52 |
2,43 |
|
10 |
Даяна |
3,15 |
3,49 |
1,34 |
|
11 |
Алихан |
2,24 |
2,15 |
0,54 |
|
12 |
Милена |
3,12 |
4,37 |
1,32 |
|
13 |
Артур |
5,34 |
5,12 |
2,33 |
|
14 |
Александр |
4,47 |
5,42 |
2,46 |
|
15 |
Ислам |
5,36 |
6,13 |
3,52 |
|
Всего: |
3,43 |
4,22 |
1,07 |
Как видно из таблицы, меньше всего времени ребята затратили, решая задачи формулой Пика.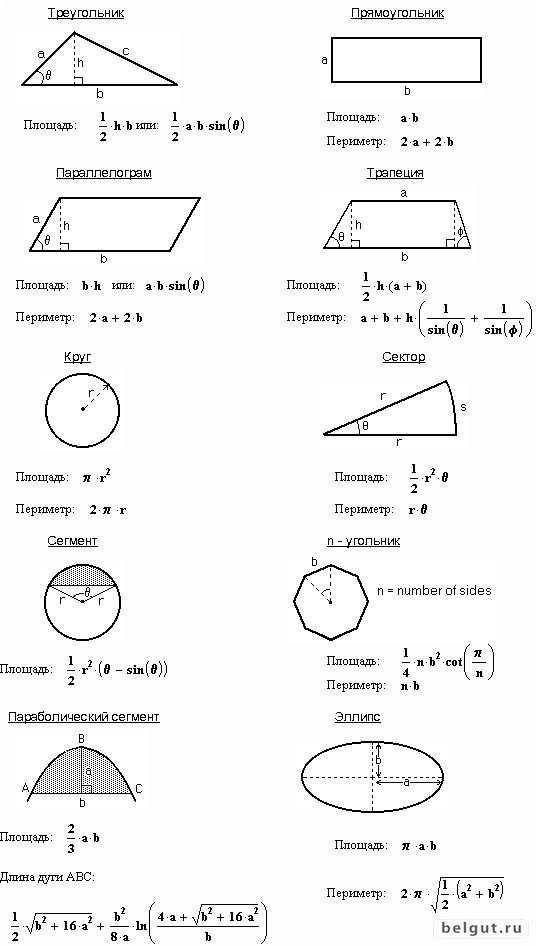 В среднем на три задачи ребята потратили 1 минуту, 7 секунд – формулой Пика, а на задача другими способами – 3 минуты 43 секунды и 4 минуты 22 секунды. Но быстро не всегда означает правильно, поэтому мы посчитали количество допущенных ошибок каждого обучающегося по всем способам. Результаты представлены в Таблице 2:
В среднем на три задачи ребята потратили 1 минуту, 7 секунд – формулой Пика, а на задача другими способами – 3 минуты 43 секунды и 4 минуты 22 секунды. Но быстро не всегда означает правильно, поэтому мы посчитали количество допущенных ошибок каждого обучающегося по всем способам. Результаты представлены в Таблице 2:
|
№ |
Ф.И. учащихся |
Количество допущенных ошибок в задачах, решенных 1 методом |
Количество допущенных ошибок в задачах, решенных 2 методом |
Количество допущенных ошибок в задачах, решенных 3 методом |
|
1 |
Алина |
1 |
2 |
0 |
|
2 |
Дана |
2 |
1 |
1 |
|
3 |
Дарина |
2 |
3 |
2 |
|
4 |
Алина |
0 |
0 |
0 |
|
5 |
Инал |
0 |
0 |
0 |
|
6 |
Лалина |
3 |
3 |
2 |
|
7 |
Залина |
1 |
2 |
1 |
|
8 |
Руслан |
1 |
1 |
0 |
|
9 |
Алина |
2 |
2 |
1 |
|
10 |
Даяна |
1 |
2 |
0 |
|
11 |
Алихан |
0 |
0 |
0 |
|
12 |
Милена |
1 |
1 |
0 |
|
13 |
Артур |
2 |
3 |
2 |
|
14 |
Александр |
2 |
2 |
1 |
|
15 |
Ислам |
3 |
3 |
1 |
|
Всего ошибок из 45 задач: |
21 |
25 |
11 |
Из таблицы видно, что меньше всего ошибок ребята сделали, решая задачи формулой Пика. По первому методу 21неправильных задач из 45, по второму методу 25 неправильных, а по третьему методу всего 11 неправильных задач из 45, причем 7 учеников из 15 сделали все три задачи правильно, пользуясь этим методом. Это означает, что формула Пика не только сокращает время, но и помогает избежать ошибок.
По первому методу 21неправильных задач из 45, по второму методу 25 неправильных, а по третьему методу всего 11 неправильных задач из 45, причем 7 учеников из 15 сделали все три задачи правильно, пользуясь этим методом. Это означает, что формула Пика не только сокращает время, но и помогает избежать ошибок.
Заключение
В данной работе мы рассмотрели все способы вычисления площадей фигур на клетчатой бумаге. В ходе исследования, наша гипотеза подтвердилась. В результате эксперимента, мы выяснили, что формула Пика является самым эффективным способом решения таких задач. Она проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника. Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.
Я уверена, что при сдаче выпускных экзаменов, задачи на вычисление площади фигур не будут вызывать затруднения, если ребята будут использовать формулу Пика.
Список использованной литературы
- Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009
- Математика? Легко!!! Площади фигур. – [Электронный ресурс].
- Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс].
Приложения
Приложение 1
Площадь фигуры равна сумме площадей ее частей.
Площадь фигуры как части площади прямоугольника.
Формулу Пика.
Просмотров работы: 698
Как посчитать площадь комнаты: калькулятор, формула, инструменты
- Главная >
- org/ListItem»> Все статьи >
Как посчитать площадь комнаты
Первый этап любых ремонтных работ – измерение размеров комнаты. Расчеты площади помещения требуются при покупке строительных материалов, проектировании отопительной и вентиляционной систем, а также при выборе мебели. Необходимо знать, как правильно снять мерки, особенно если речь идет о помещении неправильной формы. Рассказываем, как рассчитать площадь комнаты вручную или с помощью онлайн-калькулятора.
Содержание:
- Что необходимо для расчёта площади комнаты?
- Как рассчитать площадь комнаты?
- Как посчитать площадь стен?
Что необходимо для расчёта площади комнаты?
Для того, чтобы посчитать площадь комнаты в квадратных метрах, не нужно мастерски владеть особыми математическими навыками – имея нужные инструменты и зная простые формулы расчёта, с этим справится даже пятиклассник.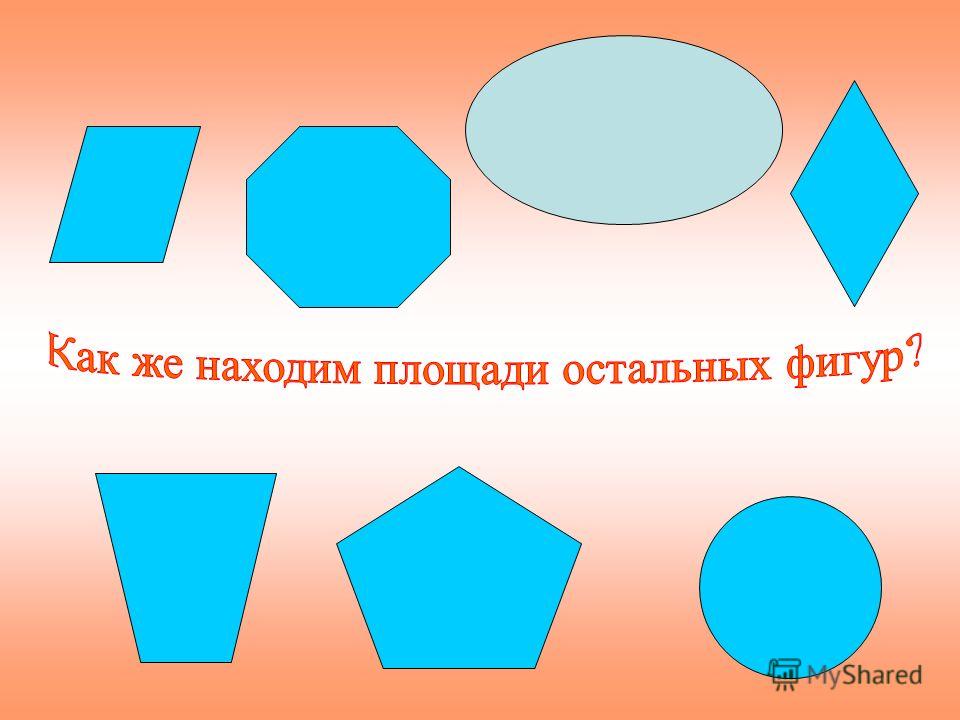
Инструменты
Вне зависимости от того, решили ли Вы посчитать площадь комнаты в онлайн-калькуляторе или вручную, Вам нужно произвести первоначальные измерения. Для этого потребуется простой набор инструментов, а именно:
-
рулетка или, в крайнем случае, мерная лента;
-
бумага и карандаш или заметки в телефоне;
-
калькулятор или бумажка для письменных подсчетов.
ПОМНИТЕ! Получить правильные значения гораздо проще, если проводить измерения в паре.
Исходные данные
Отвечая на вопрос о том, как найти площадь комнаты, отметим, что сначала Вам потребуется получить такие значения, как длина и ширина. Именно они будут использоваться при дальнейших расчётах.
Как рассчитать площадь комнаты?
Перед тем, как посчитать площадь ванной комнаты или любого другого помещения, нужно правильно измерить длину и ширину. Для этого необходимо выполнить несколько простых шагов, а затем воспользоваться формулой.
Для этого необходимо выполнить несколько простых шагов, а затем воспользоваться формулой.
Как измерить комнату?
Процесс измерения размеров комнаты прост и содержит два шага:
-
Снять замеры длины и ширины помещения вдоль стен. Чтобы результат получился наиболее правильным, рекомендуется делать это у нижнего основания каждой стены. Если же в комнате стоит массивная мебель, которую вряд ли удастся сдвинуть, можно снимать мерки посередине стены, однако не допускать отклонений рулетки в одну из сторон, чтобы не получить погрешность.
-
Внести получившиеся значения в план квартиры, схематично начерченный на листе бумаги. Если Вы указываете параметры в метрах, не забывайте округлять значения в большую сторону, а лучше указывать каждый замер вплоть до сантиметра.
Формула для расчётов
После получения всех необходимых значений, можно приступать к вопросу о том, как посчитать площадь комнаты в м2. Формула расчётов крайне проста: длина и ширина перемножаются друг с другом.
Формула расчётов крайне проста: длина и ширина перемножаются друг с другом.
Обратите внимание, что значения на рулетке указываются в сантиметрах, поэтому действовать можно одним из следующих способов:
-
Производить расчёты площади в сантиметрах, а затем полученное значение переводить в квадратные метры. Рассмотрим перевод значений на примере: комната длиной 500 см и шириной 700 см. В результате расчётов получим площадь 350 000 см2. Для перевода в метры это значение необходимо разделить на 10 000, то есть 350 000/10 000 = 35м2. То есть площадь комнаты составила 35 квадратных метров.
-
Если же Вас интересует, как посчитать площадь комнаты в квадратных метрах, необходимо сразу переводить сантиметры в метры из расчёта 100 сантиметров = 1 метр и затем приступать к вычислениям. Рассмотрим описанную ранее комнату размерами 500*700 см. Сначала каждое значение переводится в метры: 500 см = 5 м.
 , 700 см = 7 м. Затем они перемножаются: 5 м * 7 м = 35 м2.
, 700 см = 7 м. Затем они перемножаются: 5 м * 7 м = 35 м2.
ВАЖНО! С помощью этой формулы можно понять, как посчитать площадь комнаты, которая имеет форму прямоугольника. Если же помещение неправильной формы, алгоритм действий становится несколько сложнее.
Если Вы измеряете площадь для покупки стройматериалов, не забывайте вносить в подсчеты небольшой запас. В таком случае материалы не будут закуплены впритык, то есть их не потребуется экономить при подгонке и подрезке.
Калькулятор расчёта площади комнаты
Самый простой ответ на вопрос о том, как посчитать площадь комнаты – калькулятор, которым можно воспользоваться на нашем сайте в режиме онлайн. От Вас требуется лишь одно – правильно измерить длину и ширину помещения, чтобы итоговый результат оказался корректным, и подставить эти значения в формулу.
Длина комнаты м
Ширина комнаты м
Площадь комнаты м²
Расчёт площади помещения неправильной формы
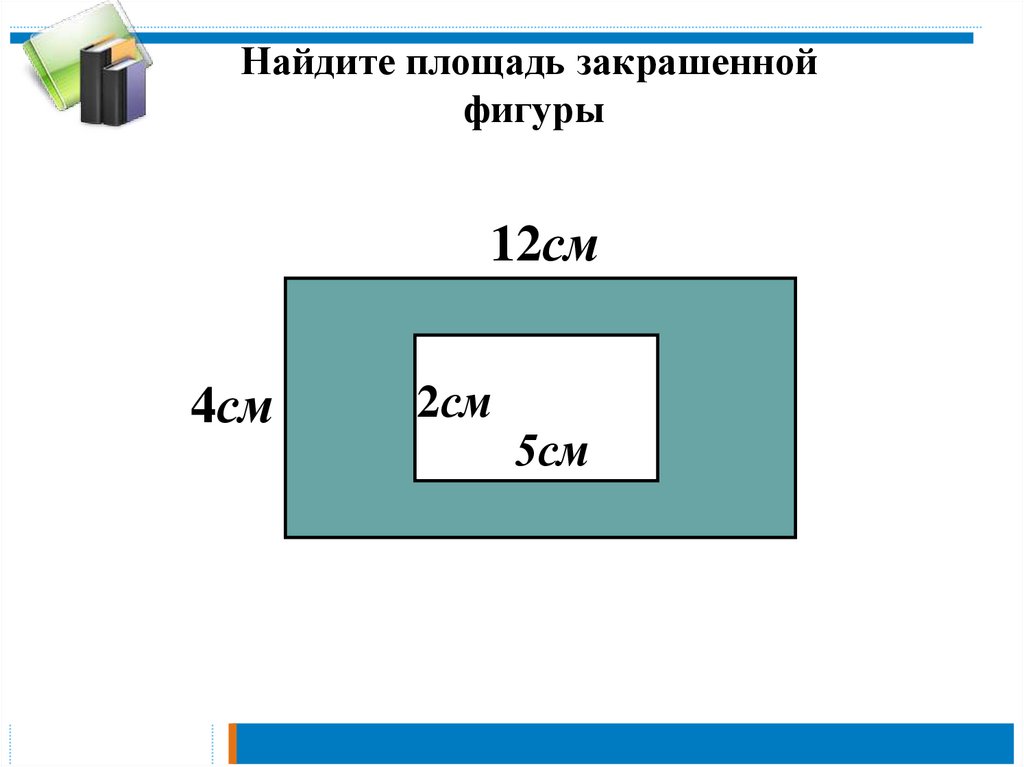
В том случае, если требуется посчитать площадь комнаты онлайн, то необходимо ввести значения длины и ширины. Но что делать, если помещение имеет форму буквы Г или срезанный угол? Тогда требуется разбить комнату на правильные фигуры (прямоугольник, квадрат или треугольник).
Но что делать, если помещение имеет форму буквы Г или срезанный угол? Тогда требуется разбить комнату на правильные фигуры (прямоугольник, квадрат или треугольник).
Рассмотрим помещение, форма которого в виде буквы Г. Измерить ее можно следующим образом:
-
Разбиваем комнату на две части, чтобы получить два прямоугольника.
-
Измеряем отдельно длину и ширину каждого из прямоугольников. Исходя из значений на рисунке, получаем прямоугольники со сторонами 3.5*4 метра и 5*6 м.
-
Отдельно считаем площади каждой фигуры. Тогда площадь первого – 3.5 * 4 = 14 м2, второго – 5 * 6 = 30 м2.
-
Суммируем значения, чтобы получить площадь комнаты: 14 + 30 = 44 м2.
Если же в комнате между стенами есть срезанный угловой участок, нужно выполнить следующие шаги:
-
Поделить комнату на три части: сначала отделяем треугольник, создавая комнату в форме буквы Г, а затем делим Г на два прямоугольника, как указано на рисунке.

-
Производим замеры: треугольник – 0.57*0.57 м., прямоугольники – 2.5*1.18 м. и 1.93*0.57 м.
-
Рассчитываем площадь прямоугольников по указанному ранее методу. В результате получаем два значения – 2.95 м2 и 1.1001 м2 (округлим в большую сторону – до 1.2 кв.м.).
-
Для того, чтобы посчитать площадь треугольника, визуально дорисуем его до прямоугольника, который разделен косой линией на две части. Остается перемножить стороны, чтобы получить площадь прямоугольника – 0.57 * 0.57 = 0.3249 м2. Далее делим это значение на два, поскольку нам прямоугольник состоит из двух одинаковых треугольников, площадь которого и требуется найти: 0.3249/2 = 0.16245 м2. Округляем в большую сторону и получаем 0.17 м2.
-
Суммируем получившиеся значения: 0.17 + 2.95 + 1.2 = 4.32 м2.
Как посчитать площадь стен?
Перед тем, как отправляться в магазин за отделочными материалами для стен (обои, краска, штукатурка и прочие), необходимо узнать, как посчитать площадь стен в комнате. Сделав расчёты заранее, Вам удастся купить точное количество материалов – не больше и не меньше. В таком случае добавляется еще несколько параметров:
Сделав расчёты заранее, Вам удастся купить точное количество материалов – не больше и не меньше. В таком случае добавляется еще несколько параметров:
-
высота потолка,
-
размер дверных проемов, то есть ширина и высота,
-
размер окон.
ОБРАТИТЕ ВНИМАНИЕ! Измерять стены принято исключительно в метрах, поэтому необходимо сразу переводить каждое значение из сантиметров в метры.
Процесс расчёта стены с дверью выглядит следующим образом:
-
Замеряем высоту и длину стены. Предположим, что они составляют 3 и 5 метров соответственно.
-
Замеряем размеры дверного проема: 2 и 0.8 м.
-
Считаем площадь стены и проема: 3 * 5 = 15 м2., 2 * 0.8 = 1.6 м2.
-
Из площади стены вычитаем размеры двери: 15 – 1.
 6 = 13.4 м2.
6 = 13.4 м2.
Стена с окном высчитывается аналогичным образом, но вычесть из размера стены нужно площадь оконного проема. Затем площадь каждой из четырех стен суммируется, чтобы получить итоговую площадь стен в помещении.
Теперь Вы понимаете, как узнать площадь комнаты и стен, поэтому без труда проведете измерение даже самого непростого помещения.
Филипп Глоба
Эксперт по недвижимости портала ВсеНовостройкиМосквы.рф
Поделиться:
Статья опубликована: 02 июня 2022
Обсуждение
Другие статьи
Города России, которые стоит посетить
Города России, которые стоит посетить каждому туристу. Топ-10 городов, их достопримечательности, цены на еду и проживание, а также на какие сувениры стоит обратить внимание.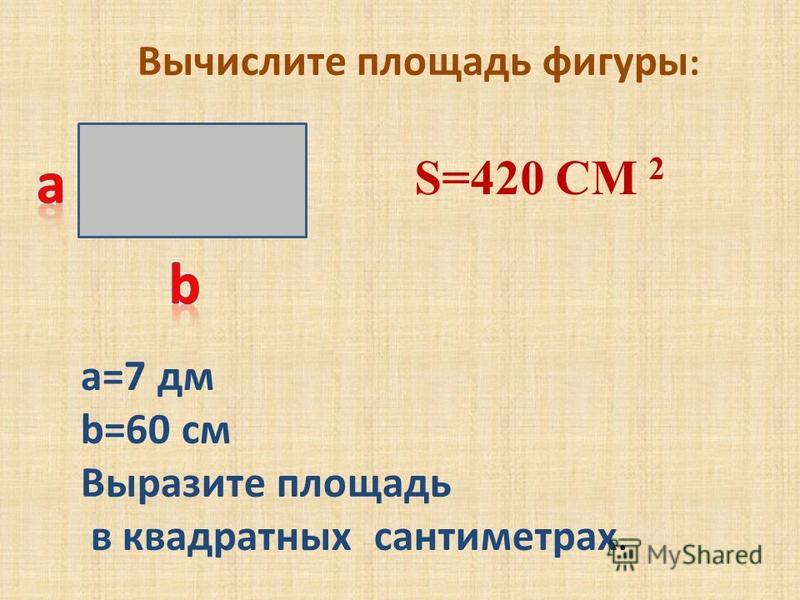
06 июня 2022
Где лучше жить в Геленджике на отдыхе в 2022 году
Обзор всех микрорайонов, где лучше жить в Геленджике на отдыхе в 2022 году. Плюсы и минусы каждого района, стоимость проживания, пляжи, развлечения и экскурсии, цены на еду.
03 июня 2022
Как избавиться от запаха гари в квартире
Как избавиться от запаха гари: перечисляем все эффективные способы — от народных до применения специальных препаратов и оборудования. А также рассказываем, что нельзя делать и почему.
03 июня 2022
Лучшие города Подмосковья в 2022 году
Рейтинг лучших городов Подмосковья в 2022 году: экология, расстояние от Москвы, безопасность, инфраструктура, транспортная доступность и стоимость жилья. Данные Минстроя и мнение россиян.
01 июня 2022
ТОП-10 самых дорогих домов в мире: фото
Рейтинг самых дорогих домов в мире, России и США. Фотографии, владельцы, описание домов и их стоимость. Самые дорогой дом на Рублевке, дом на колесах.
Самые дорогой дом на Рублевке, дом на колесах.
30 мая 2022
Беленый дуб в интерьере
Цвет мебели беленый дуб: сочетание в интерьере, применение в разных стилях. Преимущества цвета, оттенки и сочетание с другими цветами. Как подобрать оттенок беленого дуба.
30 мая 2022
Все статьи (469)Квартиры в Новостройках
- Студии
- Однокомнатные квартиры
- Двухкомнатные квартиры
- Трехкомнатные квартиры
- Четырехкомнатные квартиры
- Лофт и апартаменты
- Квартиры эконом класса
- Квартиры комфорт класса
- Квартиры элит класса
Квартиры по цене
- Квартиры до 1.5 миллионов
- Квартиры за 2 миллиона
- Квартиры за 3 миллиона
- Квартиры за 4 миллиона
Срок сдачи дома
- Квартиры в сданных домах
- Сдача в 2018 году
- Сдача в 2019 году
- Сдача в 2020 году
- Сдача в 2021 году
- Сдача в 2022 году
- Сдача в 2023 году
- Сдача в 2024 году
- Долгострой
Рейтинг Новостроек
- Самые дешевые
- Самые обсуждаемые
- Самые дорогие
- Старт продаж
Рейтинг Застройщиков
- Рейтинг строительных компаний
- Самые обсуждаемые застройщики
- Проблемные застройщики
- Рекомендуемые застройщики
- Новые застройщики
Льготная ипотека
- Новостройки по льготной ипотеке
- Банки с льготной ипотекой
Новости
- Скидки и льготы: почему россияне не покупают жильё даже по сниженным ценам
- Рынок недвижимости в Москве меняется: количество объектов бизнес-класса увеличилось в несколько раз
- ГК «А101» открывает продажи квартир в центральной части ЖК «Прокшино»
- Отечественные издатели сообщили о резком взлёте цен на печать книг
- Эксперт рассказал о причинах падения курса рубля в конце года
Все новости
Полезная информация
- Сталинки
- Расписка о получении денежных средств за квартиру
- Договор аренды квартиры
- Коптево в Москве
- Ипотека для самозанятых
Все статьи
Новостройки по районам
- Восточный АО
- Западный АО
- Зеленоградский АО
- Новомосковский АО
- Северный АО
- Северо-Восточный АО
- Северо-Западный АО
- Центральный АО
- Юго-Западный АО
- Южный АО
- Юго-Восточный АО
- Московская область
Новостройки у метро
- Сокольническая линия
- Кольцевая линия
- Замоскворецкая линия
- Каховская линия
- Арбатско-Покровская линия
- Филевская линия
- Калужско-Рижская линия
- Таганско-Краснопресненская линия
- Калининская линия
- Серпуховско-Тимирязевская линия
- Люблинско-Дмитровская линия
- Бутовская линия
Загородная недвижимость
- Дома и Коттеджи
- Таунхаусы
- Земельные участки
Главная страница Контакты Новостройки
Квартиры в Новостройках- Студии
- Однокомнатные квартиры
- Двухкомнатные квартиры
- Трехкомнатные квартиры
- Четырехкомнатные квартиры
- Лофт и апартаменты
- Квартиры эконом класса
- Квартиры комфорт класса
- Квартиры элит класса
- Квартиры до 1.
 5 миллионов
5 миллионов - Квартиры за 2 миллиона
- Квартиры за 3 миллиона
- Квартиры за 4 миллиона
- Квартиры в сданных домах
- Сдача в 2018 году
- Сдача в 2019 году
- Сдача в 2020 году
- Сдача в 2021 году
- Сдача в 2022 году
- Сдача в 2023 году
- Сдача в 2024 году
- Долгострой
- Самые дешевые
- Самые обсуждаемые
- Самые дорогие
- Старт продаж
- Рейтинг строительных компаний
- Самые обсуждаемые застройщики
- Проблемные застройщики
- Рекомендуемые застройщики
- Новые застройщики
- Новостройки по льготной ипотеке
- Банки с льготной ипотекой
НовостиСтатьи
Новостройки по районам- Восточный АО
- Западный АО
- Зеленоградский АО
- Новомосковский АО
- Северный АО
- Северо-Восточный АО
- Северо-Западный АО
- Центральный АО
- Юго-Западный АО
- Южный АО
- Юго-Восточный АО
- Московская область
- Сокольническая линия
- Кольцевая линия
- Замоскворецкая линия
- Каховская линия
- Арбатско-Покровская линия
- Филевская линия
- Калужско-Рижская линия
- Таганско-Краснопресненская линия
- Калининская линия
- Серпуховско-Тимирязевская линия
- Люблинско-Дмитровская линия
- Бутовская линия
- Дома и Коттеджи
- Таунхаусы
- Земельные участки
апартаменты владимир жидкин департамент градостроительной политики детский сад долгострой долевое строительство дороги жилая недвижимость застройщик ЗИЛ инфраструктура ипотека марат хуснуллин метро МКАД мосгосстройнадзор Москва-Сити москомстройинвест МФЦ налоги новая москва новостройки промзона процентные ставки реконструкция сергей левкин строительство СУ-155 субсидии суд ТиНАО Турция ФЗ-214 цены
Все формулы вычисления площади.
 Как вычислить площадь фигуры
Как вычислить площадь фигурыПлощади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.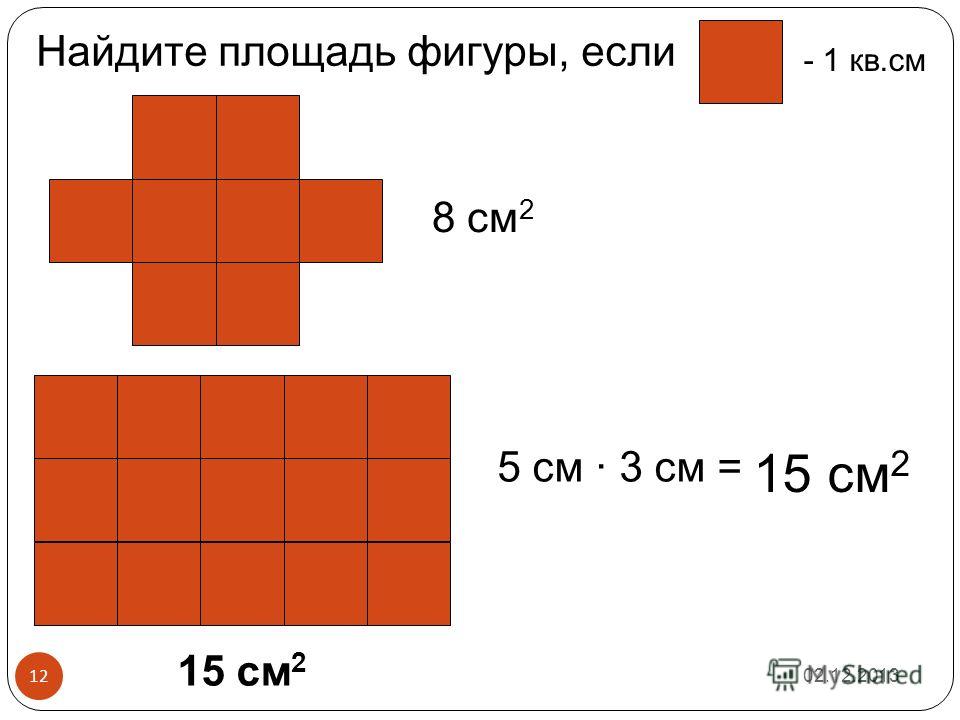
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.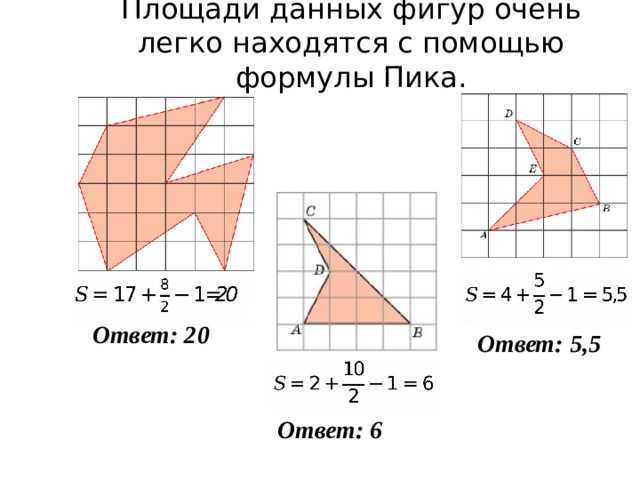
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т.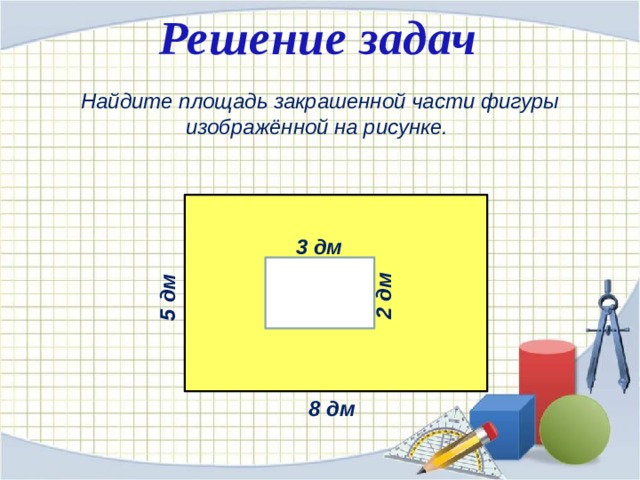 е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
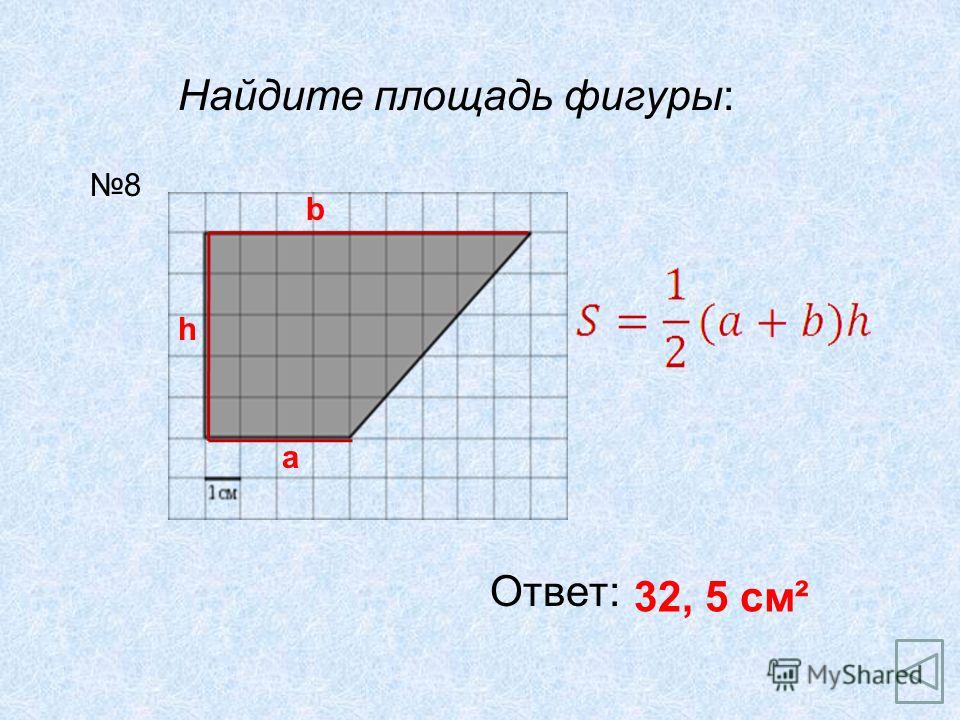
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра.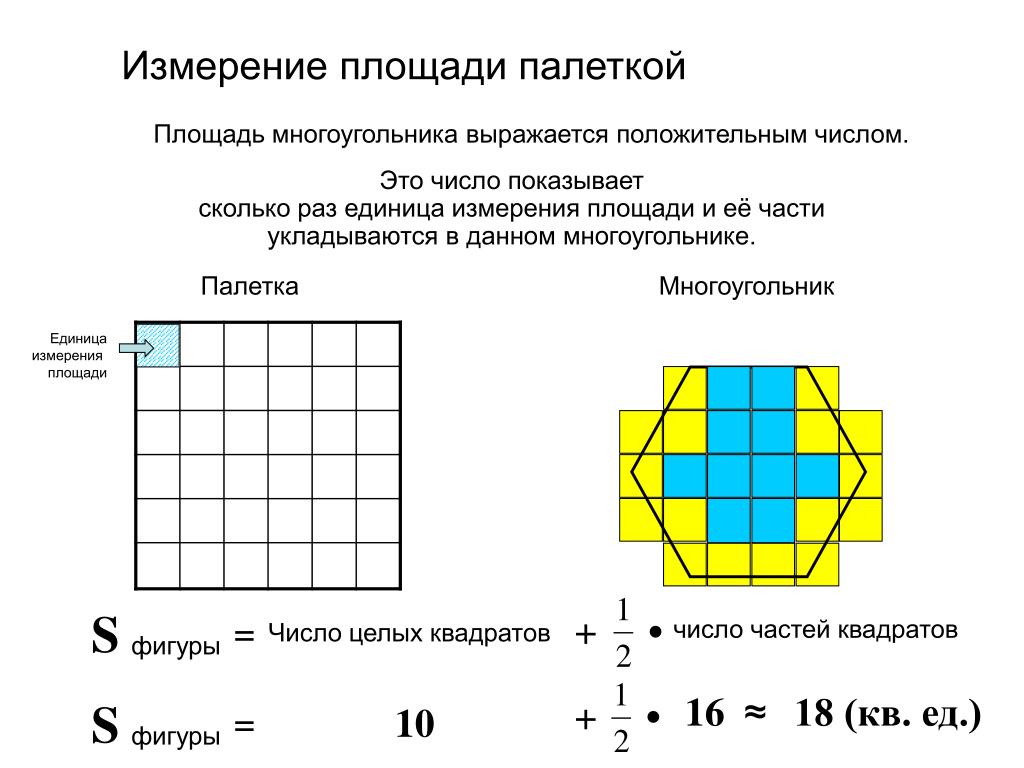 Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃ а b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃ а b f(x)dx.
Таким образом, S(G) = ʃ а b f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ а b f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х 3 ; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃ а b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х 3 ,
{у = 1.
Таким образом, имеем х 1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = S DACE – S DABE = ʃ 1 2 x 3 dx – 1 = x 4 /4| 1 2 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃ а b (√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√х| 4 9 – 2х| 4 9 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х 3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х 3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x 2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у min = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х 3 – 4х = 0 или х(х 2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х 1 = 0, х 2 = 2, х 3 = -2 (не подходит, т.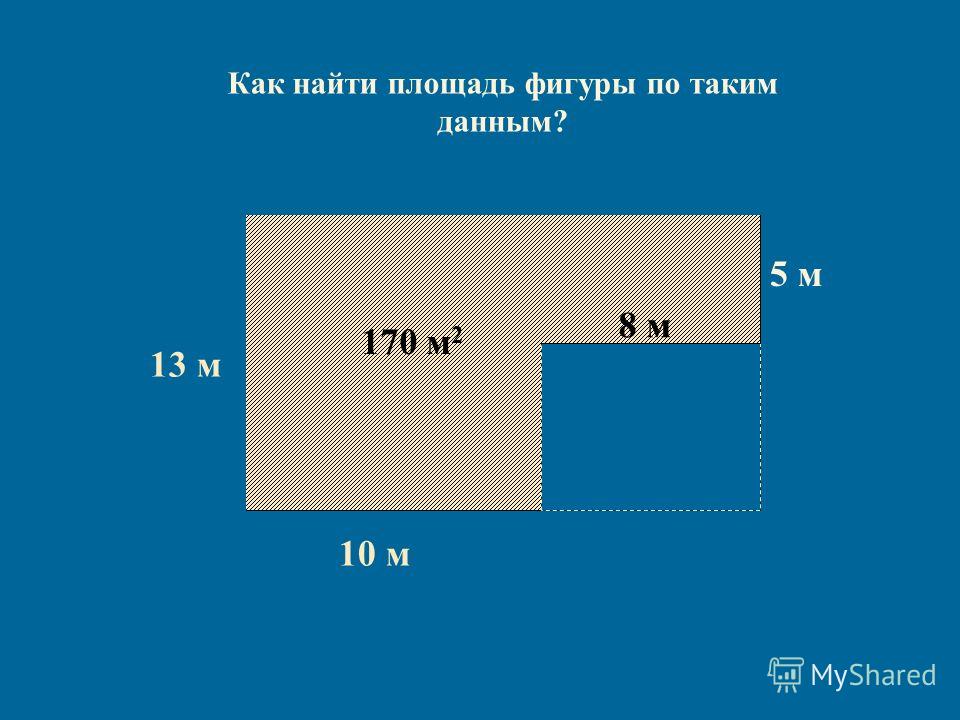 к. х ≥ 0).
к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х 3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ 0 2 (x 3 – 4x)dx|.
Имеем: ʃ 0 2 (x 3 – 4х)dx =(x 4 /4 – 4х 2 /2)| 0 2 = -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х 2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х 0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х 2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х 0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у 0 = 2 · 2 2 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х 2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Г у = 2х 2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х 2 – 2х + 1 = 0 не имеет решений (D
x b = 2/4 = 1/2;
y b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: S О A В D = S OABC – S ADBC .
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле S ADBC = 1/2 · DC · BC. Таким образом,
S ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
S OABC = ʃ 0 2 (2x 2 – 2х + 1)dx = (2x 3 /3 – 2х 2 /2 + х)| 0 2 = 10/3 (кв. ед.).
Окончательно получим: S О A В D = S OABC – S ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями . Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.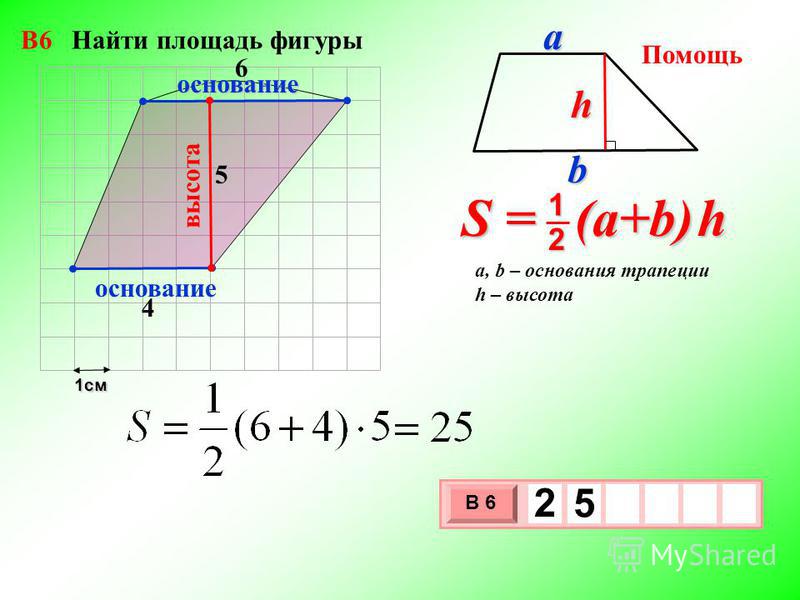
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Если вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.
Геометрическая форма комнаты
Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:
- Прямоугольные.
- Квадратные.
- Сложной конфигурации (например, круглые).
- С нишами и выступами.

Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Помещение прямоугольной или квадратной формы
Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:
S комнаты=A*B, где
А — длина помещения.
В — ширина помещения.
Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.
Помещение со сложной конфигурацией
Если ваша комната не попадает под определение «типичной», т.е. имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем. Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:
имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем. Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:
- Формула нахождения площади круга:
S комн.=π*R 2 , где
R — радиус помещения.
- Формула нахождения площади треугольника:
S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где
Р — полупериметр треугольника.
А, В, С — длины его сторон.
Отсюда Р=А+В+С/2
Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.
Площадь помещения с выступами и нишами
Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты.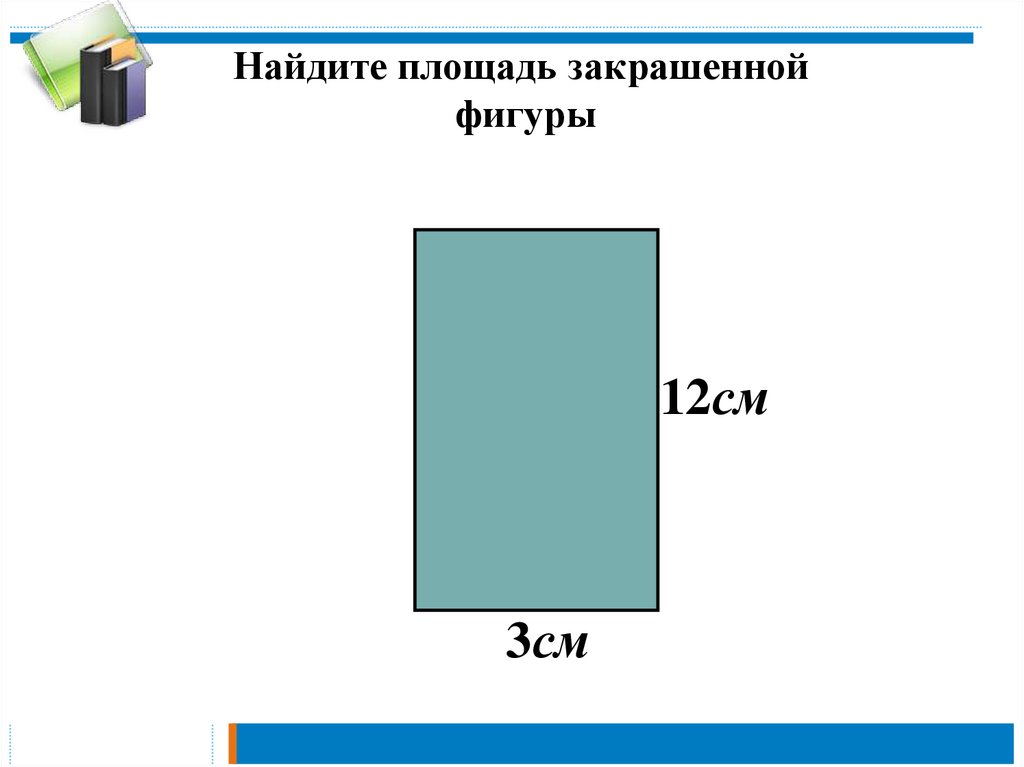 Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.
Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.
Площадь стены находится по формуле:
S стен = Р х С, где
Р — периметр
С — высота
Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.
Комната с многоуровневым потолком
Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.
Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:
- Найти размеры всех прямых участков стен.
- Найти площадь пола.
- Перемножить длину и высоту вертикальных участков.
- Суммировать получившееся значение с площадью пола.

Пошаговая инструкция по определению общей
площади помещения
- Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
- Визуально разделите комнату на участки правильной и неправильной формы. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
- Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
- Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете убедитесь, что луч лежит ровно на поверхности стены.
- Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.
 = S стен+S пола+S потолка
= S стен+S пола+S потолка
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным .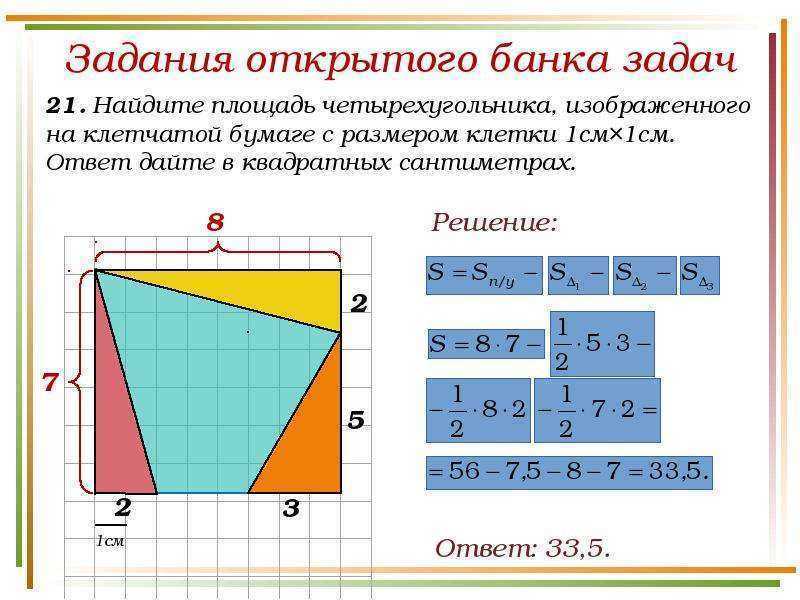 Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
 Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Онлайн калькуляторы для вычисления площадей плоских фигур
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 1 a · h 2 Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 a · b · sin γ 2 S = 1 a · c · sin β 2 S = 1 b · c · sin α 2 Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · с 4R Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,S = p · r
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 
2
Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника.
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,S = 1 d2 2
a — длина стороны квадрата,
d — длина диагонали квадрата.
Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата.
Формулы площади параллелограмма
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
где S — Площадь параллелограмма,S = 1 d1d2 sin γ 2
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма.
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,S = 1 d1 · d2 2
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Вы можете воспользоваться онлайн калькулятором для расчета площади ромба.
Формулы площади трапеции
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — площадь трапеции,S = 1 (a + b) · h 2
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции.
Формулы площади выпуклого четырехугольника
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,S = 1 d1 d2 sin α 2
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.

-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — Площадь круга,S = 1 π d2 4
r — длина радиуса круга,
d — длина диаметра круга.
Вы можете воспользоваться онлайн калькулятором для расчета площади круга.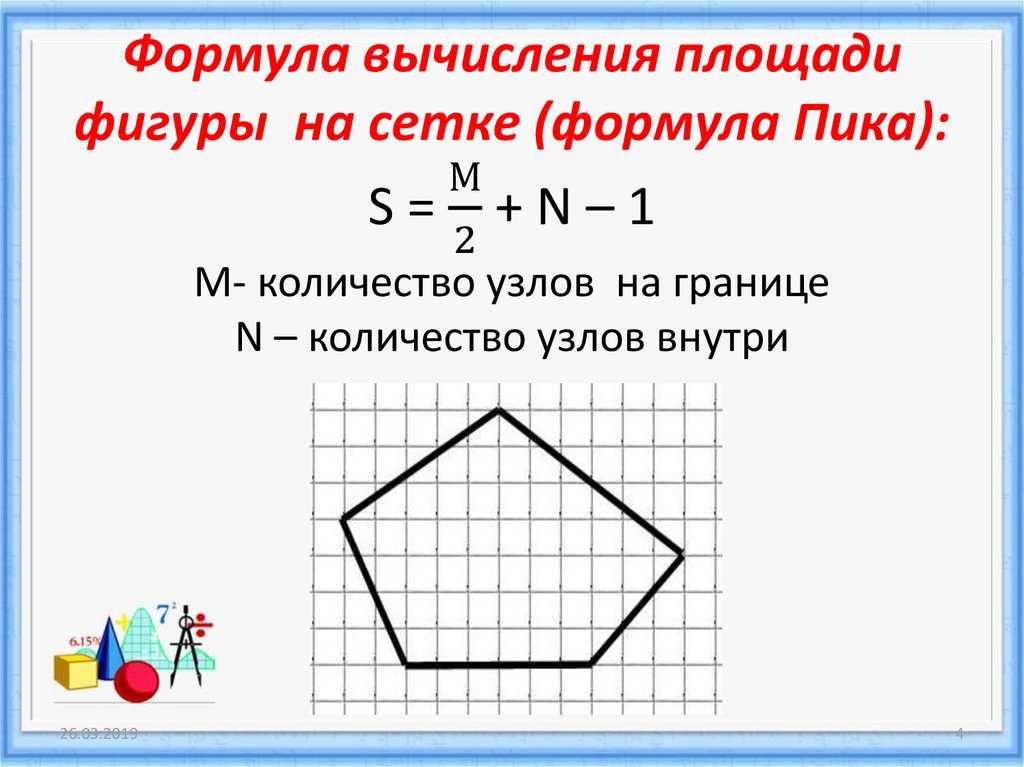
Все таблицы и формулы
Площадь фигуры. Все формулы
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму.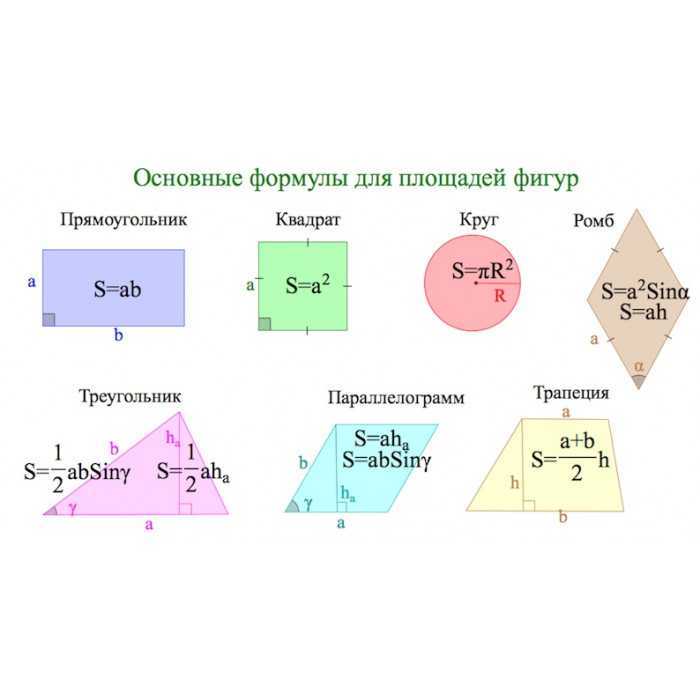 Для этого рассмотрим основные площади фигур в геометрии.
Для этого рассмотрим основные площади фигур в геометрии.
Содержание
- 1 Треугольник
- 2 Прямоугольник
- 3 Квадрат
- 4 Ромб
- 5 Трапеция
- 6 Цилиндр и параллелепипед
- 7 Кольцо
- 8 Многоугольник
Треугольник
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
- Через радиус окружности r. Для площади круга вычисление можно сделать следующим образом:
- Через диаметр окружности d. Найти площадь круга можно так:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы.
 Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Поделиться с друзьями:
Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.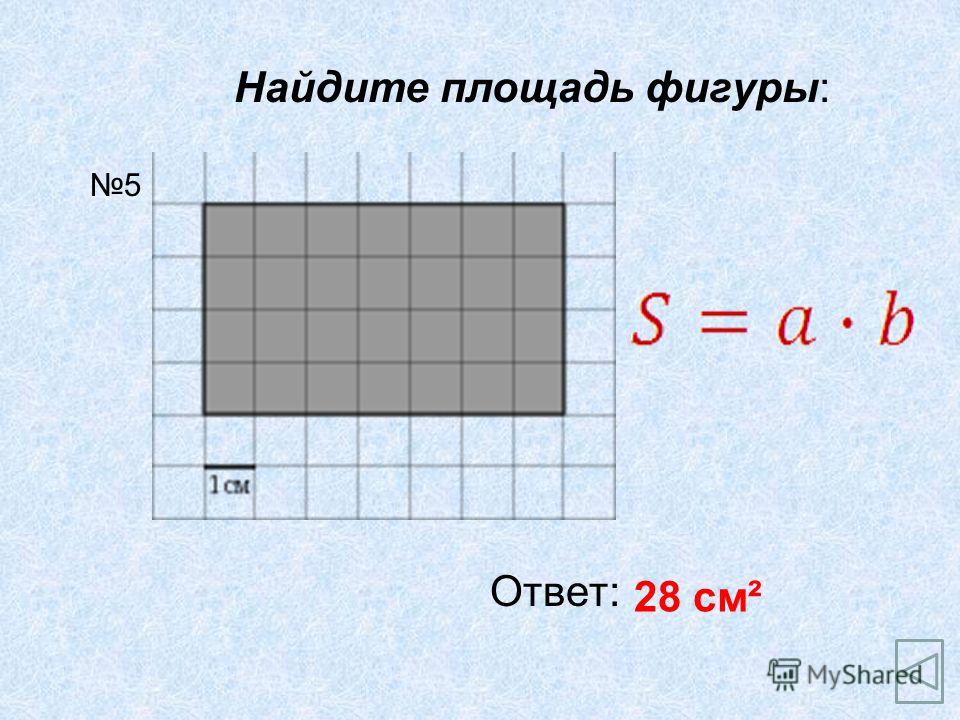
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими. - Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в раз больше, чем площадь треугольника АВС.
Тогда площадь треугольника в раз больше, чем площадь треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Поэтому
Ответ: 24.
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, .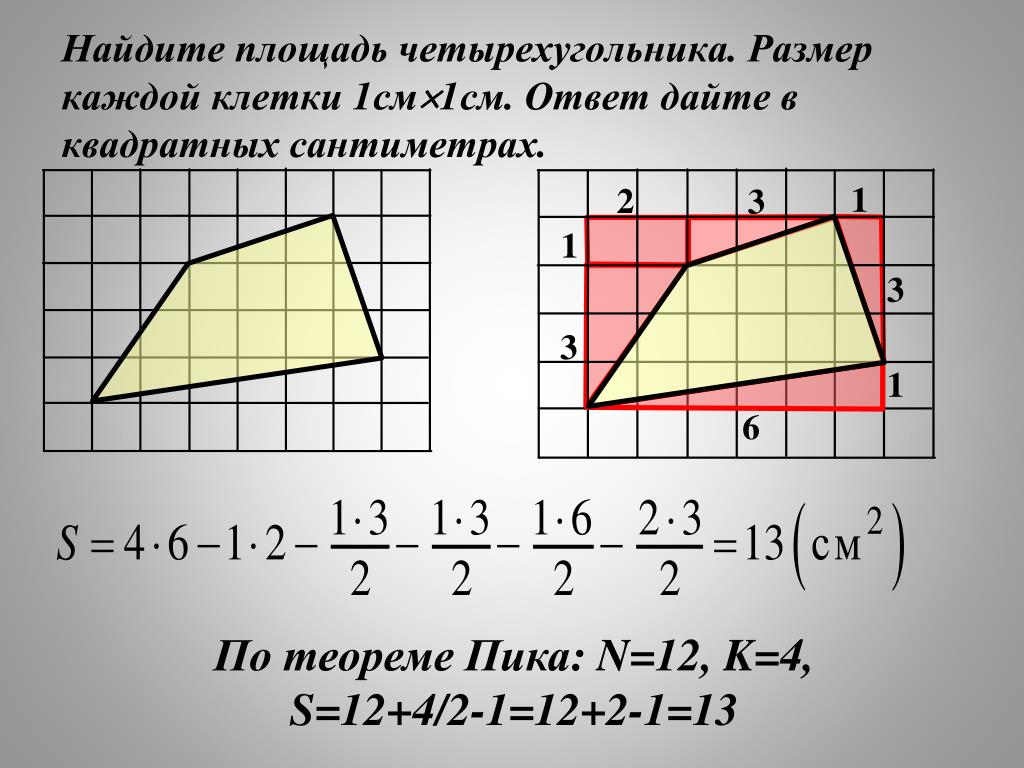
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен Тогда площадь параллелограмма равна а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ — применить формулу Пика.
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа.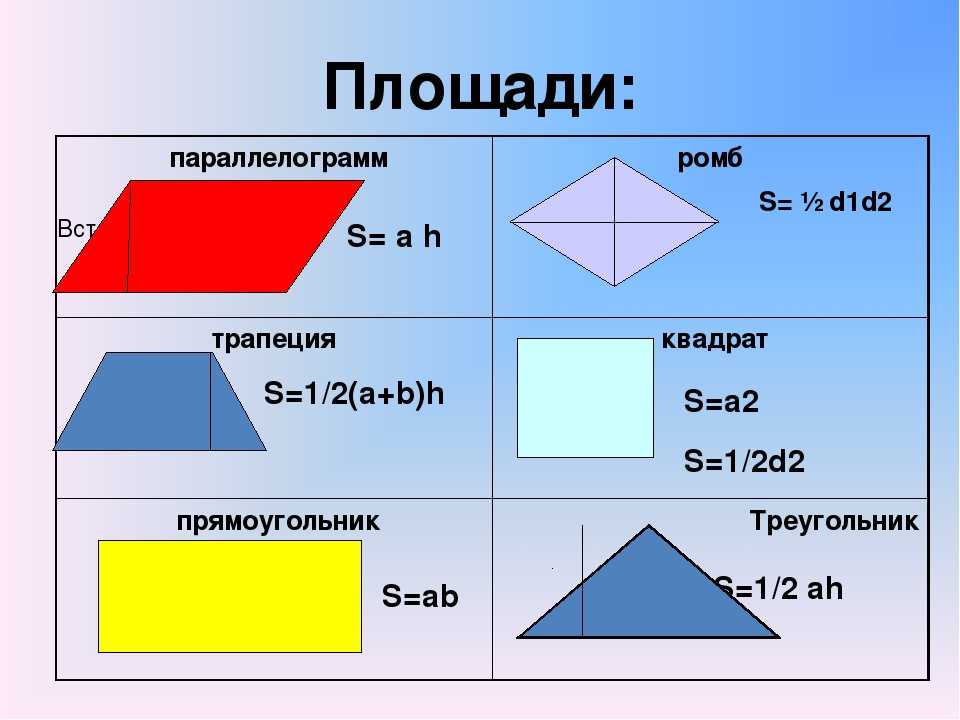 На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна
.
Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Что такое площадь? Определение, площадь фигур Формула
Площадь – это площадь, занимаемая двухмерной фигурой. Другими словами, это величина, измеряющая количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартной единицей площади являются квадратные единицы, которые обычно представляются как квадратные дюймы, квадратные футы и т. д. Давайте научимся вычислять площадь различных геометрических фигур с помощью примеров и практических вопросов.
1.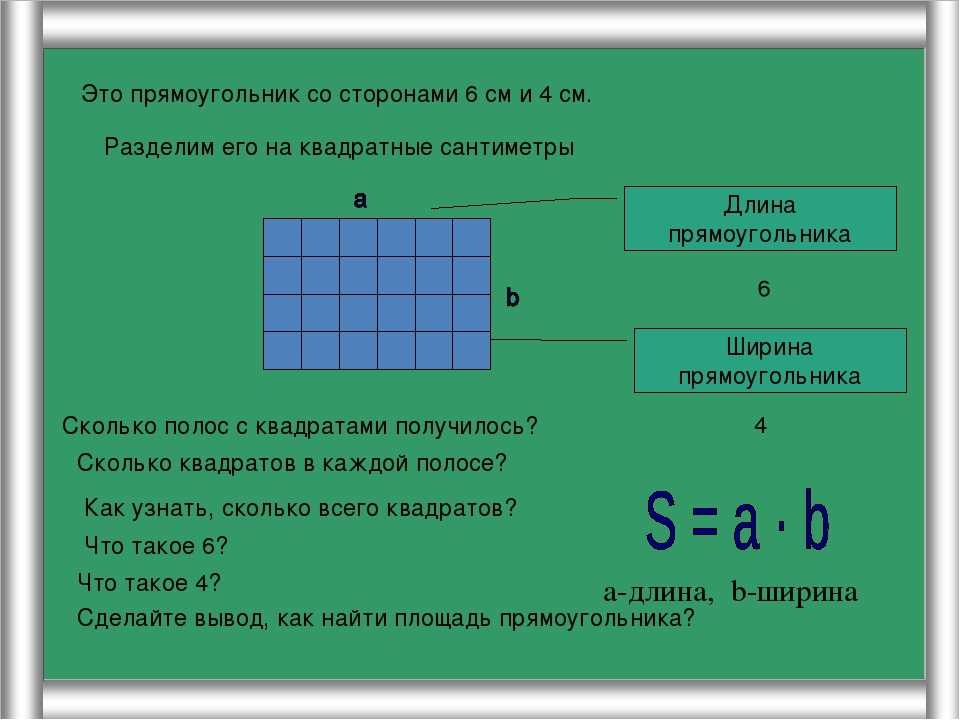 | Что такое площадь? |
| 2. | Как рассчитать площадь? |
| 3. | Площадь геометрических фигур — Формула |
| 4. | Часто задаваемые вопросы по Зоне |
Что такое площадь?
Слово «площадь» означает свободную поверхность. Площадь фигуры вычисляется с помощью ее длины и ширины. Длина одномерна и измеряется в таких единицах, как футы (футы), ярды (ярды), дюймы (дюймы) и т. д. Однако площадь формы является двумерной величиной. Следовательно, он измеряется в квадратных единицах, таких как квадратные дюймы или (в 2 ), квадратных футов или (ft 2 ), квадратных ярдов или (yd 2 ) и т. д. Большинство объектов или форм имеют края и углы. Длина и ширина этих ребер учитываются при расчете площади конкретной формы.
Как рассчитать площадь?
Давайте посмотрим, как вычислить площадь фигуры с помощью сетки. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 на 1 единицу. Площадь каждого из этих квадратов равна 1 квадратной единице. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь фигуры, начерченной на сетке.
Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 на 1 единицу. Площадь каждого из этих квадратов равна 1 квадратной единице. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь фигуры, начерченной на сетке.
Площадь этой фигуры равна количеству заштрихованных единичных квадратов.
Таким образом, площадь фигуры = 9 квадратных единиц. Теперь давайте посмотрим на другой пример. Когда фигура не занимает полного единичного квадрата, мы можем аппроксимировать и найти ее значение. Если он занимает примерно 1/2 единичного квадрата, мы можем объединить две такие половины, чтобы образовать площадь в 1 квадратную единицу. Обратите внимание на приведенный ниже рисунок.
Здесь площадь, занимаемая фигурой, равна 4 полным квадратам и 8 полуквадратам. Вместе это образует площадь 8 квадратных единиц.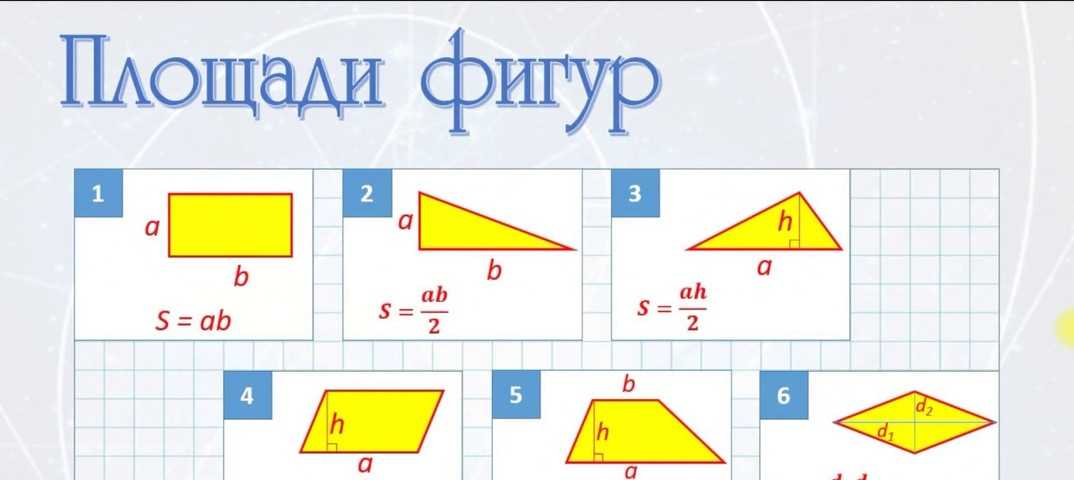 Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных фигур у нас есть определенные формулы для вычисления их площади. Обратите внимание, что это только приблизительное значение.
Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных фигур у нас есть определенные формулы для вычисления их площади. Обратите внимание, что это только приблизительное значение.
Площадь прямоугольника
Площадь прямоугольника — это площадь, занимаемая им. Рассмотрим желтый прямоугольник в сетке. Он занял 6 единиц.
В приведенном выше примере длина прямоугольника составляет 3 единицы, а ширина — 2 единицы. Площадь прямоугольника получается путем умножения его длины и ширины, что равносильно подсчету единиц квадратов. Таким образом, формула площади прямоугольника: : Площадь прямоугольника = длина × ширина. В данном случае это будет 2 × 3 = 6 квадратных единиц.
Площадь квадрата
Площадь квадрата – это занимаемая им площадь. Посмотрите на цветной квадрат, показанный в сетке ниже. Он занимает 25 квадратов.
Из рисунка видно, что длина каждой стороны цветного квадрата равна 5 единицам. Следовательно, площадь квадрата – это произведение его сторон, которое можно представить по формуле: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.
Следовательно, площадь квадрата – это произведение его сторон, которое можно представить по формуле: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.
Площадь круга
Круг представляет собой изогнутую форму. Площадь круга – это количество пространства, заключенного в границах круга. Узнайте больше о π и радиусе, прежде чем мы перейдем к формуле площади круга.
Площадь круга рассчитывается по формуле: π r 2 , где π – математическая константа, значение которой округляется до 3,14 или 22/7 и r — это радиус окружности.
Площадь геометрических фигур — Формула
Каждая форма имеет разные размеры и формулы. В следующей таблице показан список формул для площади различных фигур.
| Форма | Площадь фигур — Формула |
|---|---|
Квадрат | Площадь квадрата = x 2 квадратных единиц |
Прямоугольник | Площадь прямоугольника = длина × ширина = l × w квадратных единиц |
Круг | Площадь круга = π r 2 квадратных единиц |
Треугольник | Площадь треугольника = \(\dfrac{1}{2}\times b \times h\) квадратных единиц |
Параллелограмм | Площадь параллелограмма = основание × высота = b × h квадратных единиц |
Равнобедренная трапеция | Площадь равнобедренной трапеции = \(\dfrac{1}{2}(a+b) h\) квадратных единиц |
Ромб | Площадь ромба = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
Воздушный змей | Площадь воздушного змея = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц |
☛ Связанные темы по площади
Ознакомьтесь со следующими темами, касающимися областей различной формы, и узнайте больше о формулах площади.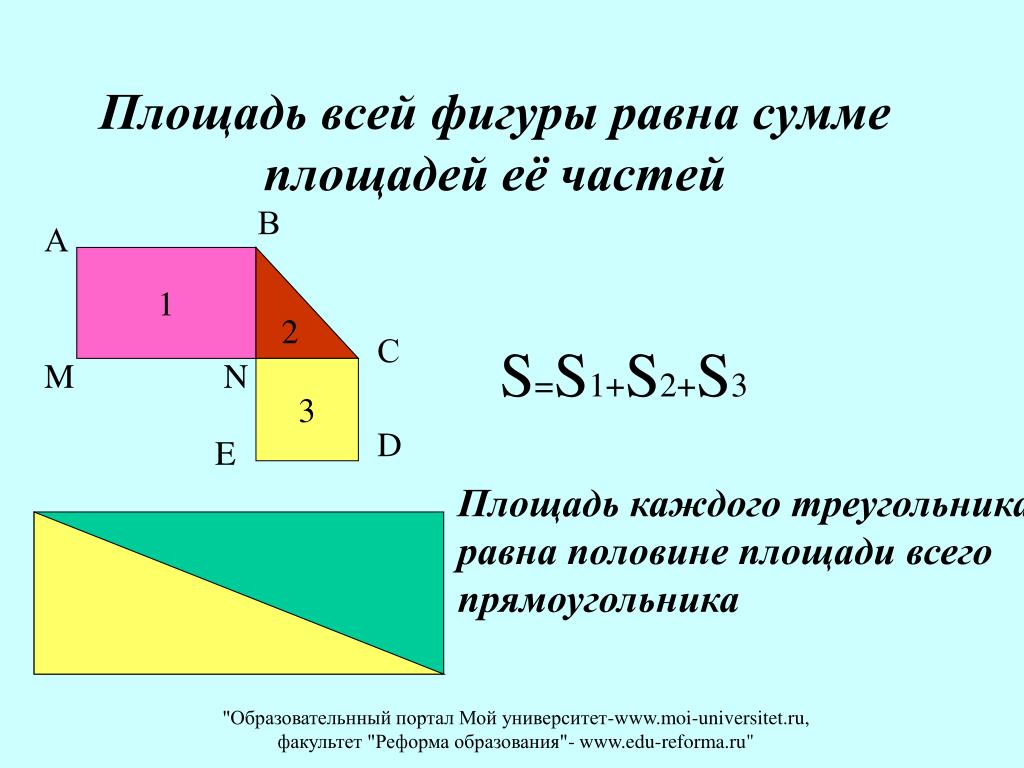
- Формула геометрической площади
- Площадь треугольника
Советы и подсказки
- Мы часто запоминаем формулы для вычисления площади фигур. Более простым методом было бы использование линий сетки, чтобы понять, как была получена формула.
- Мы часто путаем площадь и периметр фигуры. Полное понимание может быть построено путем отслеживания поверхности любой формы и наблюдения за тем, что область — это, по сути, пространство или область, покрытая формой.
Примеры на участке
Пример 1: Найдите площадь квадрата со стороной 7 см.
Решение :
Площадь квадрата = сторона × сторона. Здесь сторона = 7 см
Подставляя значения, 7 × 7 = 49.
Следовательно, площадь квадрата = 49 квадратных см.
Пример 2: Размеры прямоугольника 15 см и 8 см.
 Найдите его площадь.
Найдите его площадь. Решение :
Площадь прямоугольника равна произведению его длины на ширину, что можно представить по формуле: Площадь = l × w.
Подставляя данные значения, получаем площадь прямоугольника = 15 × 8 = 120 см 2Пример 3: Можете ли вы найти площадь круга с радиусом 14 см?
Раствор :
Радиус круга = 14 см
Площадь круга рассчитывается по формуле π r 2
Подставляя значения в формулу, площадь = \(\dfrac{22}{7}\) × 14 × 14 = 616 квадратных см.
Пример 4. Вычислите площадь заданной формы путем подсчета квадратов.
Решение: Давайте посчитаем полные квадраты и половинки квадратов.
Есть 24 единичных квадрата и 5 полуквадратов.
Следовательно, площадь фигуры = 24 + (5 × ½) = 24 + 2,5 26,5 квадратных единиц
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по области
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Зоне
Что такое площадь?
Площадь фигуры представляет собой двумерную величину, которая измеряется в квадратных единицах, таких как квадратные дюймы или (в 2 ), квадратные футы или (футы 2 ), квадратные ярды или (ярды 2 ), и т.д.
Как найти площадь неправильной формы?
Площадь неправильной формы можно найти, разделив фигуру на единичные квадраты. Когда фигура не занимает весь единичный квадрат, мы можем аппроксимировать и найти ее значение.
Как доказать площадь круга?
Если окружность сложить в треугольник, радиус станет высотой треугольника, а периметр станет его основанием, равным 2 × π × r. Мы знаем, что площадь треугольника находится путем умножения его основания и высоты, а затем деления на 2, что составляет: ½ × 2 × π × r × r. Следовательно, площадь круга равна π r 2 .
Следовательно, площадь круга равна π r 2 .
Что такое периметр и площадь треугольника?
Общая длина границы замкнутой формы называется ее периметром. Другими словами, периметр — это сумма сторон двумерной фигуры. Периметр треугольника равен сумме трех сторон треугольника, а площадь треугольника равна
Какие формулы площади и периметра квадрата и прямоугольника?
Формулы площади и периметра квадрата и прямоугольника следующие. Площадь квадрата = сторона × сторона. Периметр квадрата = 4 × сторона. Площадь прямоугольника = длина × ширина. Периметр прямоугольника = 2 × (длина + ширина)
Почему площадь выражается в квадратных единицах?
Площадь фигуры — это количество единичных квадратов, необходимое для ее полного покрытия. Поэтому он измеряется и выражается в квадратных единицах.
Периметр, площадь и объем
Горячая математика 1. периметр из
многоугольник (или любая другая замкнутая кривая, например круг) — это расстояние вокруг внешней стороны.
2. область из простая, замкнутая, плоская кривая — это объем пространства внутри.
3. объем из твердый 3 Д форма — это количество пространства, вытесненного ею.
Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже. Ответов один, два, или три измерения; периметр измеряется в линейные единицы , область измеряется в квадратные единицы , а также объем измеряется в кубические единицы .
Форма | Формула | Переменные |
Квадрат | п знак равно 4 с | с
это длина стороны квадрата.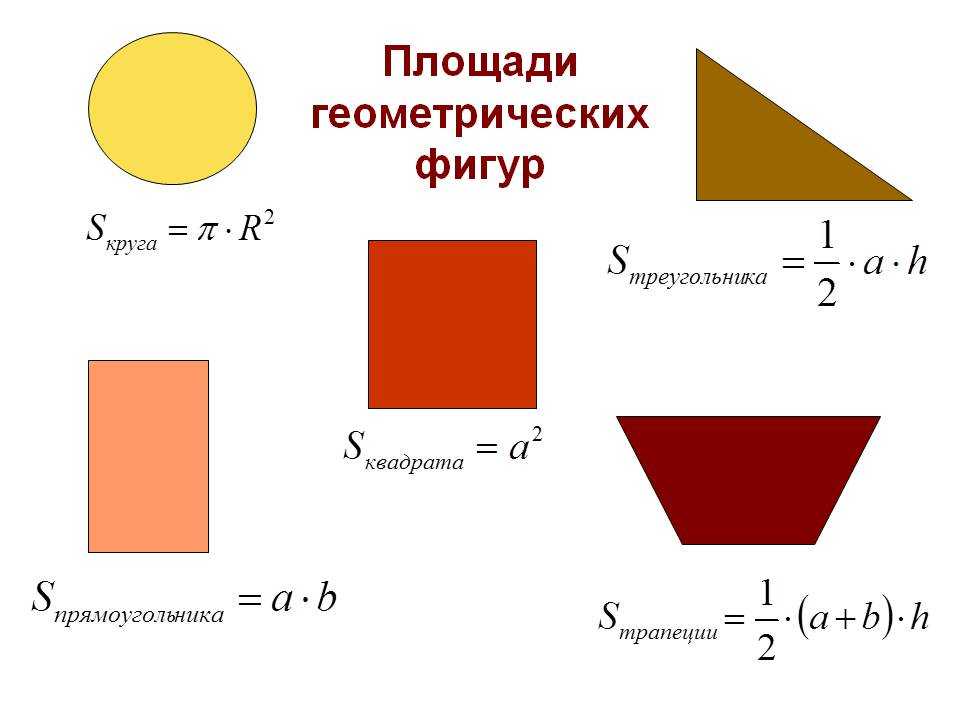 |
Прямоугольник | п знак равно 2 л + 2 Вт | л а также Вт длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + с | а , б , а также с являются длинами сторон. |
Прямоугольный треугольник с ножками а а также б (видеть Теорема Пифагора ) | п знак равно а + б + а 2 + б 2 | а а также б это длины двух катетов треугольника |
Круг |
| р
это радиус и
г
это диаметр.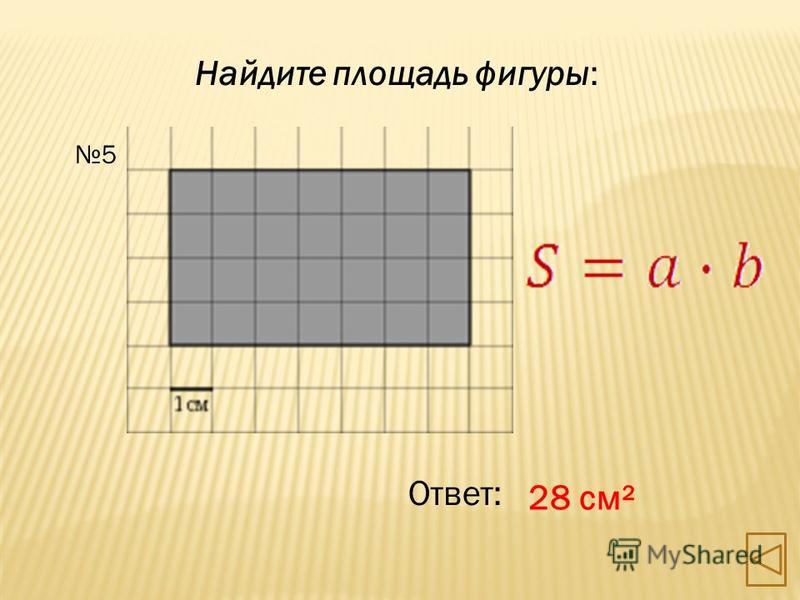 |
Форма | Формула | Переменные |
Квадрат |
| с это длина стороны квадрата. |
Прямоугольник |
| л
а также
Вт
длины сторон прямоугольника (длина и ширина). |
Треугольник | А знак равно 1 2 б час | б а также час это основание и высота |
Треугольник | А знак равно с ( с − а ) ( с − б ) ( с − с ) куда с знак равно а + б + с 2 | а , б , а также с это длины сторон и с это полупериметр |
Параллелограмм |
| б
это длина основания и
час
это высота. |
Трапеция | А знак равно б 1 + б 2 2 час | б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
Форма | Формула | Переменные |
Куб |
| с
это длина стороны. |
Правая прямоугольная призма |
| л это длина, Вт это ширина и ЧАС это высота. |
Призма или цилиндр | В знак равно А час | А площадь основания, час это высота. |
Пирамида или конус | В знак равно 1 3 А час | А
площадь основания,
час
это высота. |
Сфера |
| р это радиус. |
Калькулятор площади 📐 — Вычислите площадь квадрата, прямоугольника, треугольника, круга, паралеллограмма, трапеции…
Быстрая навигация:
- Как вычислить площадь любой формы?
- Площадь квадрата
- Площадь прямоугольника
- Площадь треугольника
- Площадь круга
- Площадь параллелограмма
- Площадь трапеции
- Площадь эллипса 90 сектор
- Площадь восьмиугольника
- Где использовать калькулятор площади?
Каждая геометрическая фигура имеет свою формулу для вычисления площади и различные требуемые размеры, которые необходимо знать. См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например. квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили…
См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например. квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили…
Расчет площади применяется в строительстве и отделке помещений (например, требуется покраска), в управлении земельными ресурсами, сельском хозяйстве, биологии, экологии и многих других дисциплинах.
Площадь квадратаФормула площади квадрата: сторона 2 , как показано на рисунке ниже:
единичное измерение. Однако, поскольку в большинстве практических ситуаций вам нужно измерить обе стороны, прежде чем вы узнаете, что это квадрат, разница может быть невелика, но, по крайней мере, ее легче вычислить.
Площадь прямоугольника
Формула площади прямоугольника: ширина x высота , как показано на рисунке ниже:
и просто умножить их вместе. Это одна из самых простых фигур для вычисления площади. Неправильные формы часто разбивают на ряд прямоугольников, чтобы можно было приблизительно рассчитать их площадь.
Площадь треугольникаФормула площади треугольника: высота x π x (радиус / 2) 2 , где (радиус / 2) — радиус основания (d = 2 x r), так что другой способ записи это высота x π x радиус 2 . Визуально на рисунке ниже:
Несмотря на простоту приведенного выше уравнения, в определенных ситуациях вы можете не знать эти два точных измерения. Существует несколько правил вычисления площади треугольника: SSS (сторона-сторона-сторона), SAS (две стороны и прилежащий угол), SSA (две стороны и не заключенный между ними угол), ASA (два угла и прилежащая сторона). . Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.
. Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.
Площадь круга
Формула площади круга: 2 x π x радиус , но диаметр круга равен d = 2 x r, поэтому его можно записать по-другому: 2 x π x (диаметр / 2) . Визуально на рисунке ниже:
Для площади круга вам нужен только его радиус. В большинстве практических ситуаций было бы проще рассчитать диаметр, поэтому наш калькулятор использует диаметр в качестве входных данных.
Площадь параллелограммаФормула площади параллелограмма равна ширина x высота , как показано на рисунке ниже: прямоугольник для вычисления площади, таким образом, формула в основном такая же, но мы используем высоту параллелограмма вместо его стороны.
Площадь трапеции
Формула площади трапеции равна (основание 1 + основание 2) / 2 x высота , как показано на рисунке ниже:
с помощью калькулятора площади.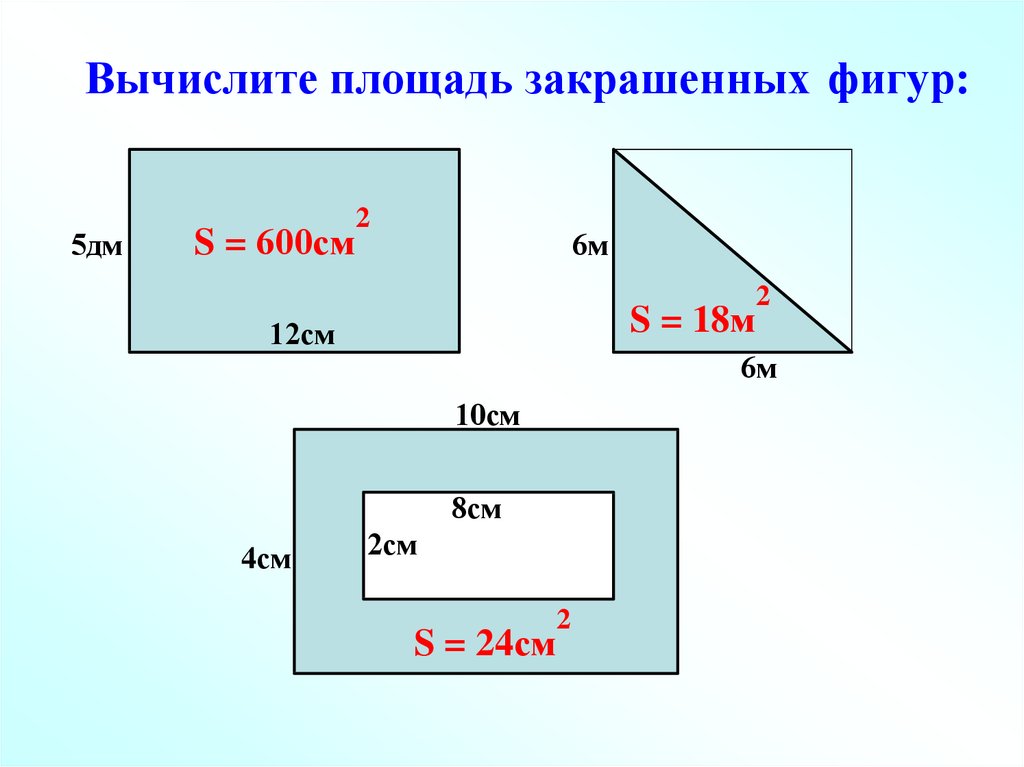 Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.
Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.
Формула площади эллипса: π x большой радиус x малый радиус , как показано на рисунке ниже:
Площадь овала аналогична площади круга, но поскольку у него два радиуса, немного отличается. Здесь вы можете измерить два диаметра и разделить на два, чтобы получить два радиуса.
Площадь сектора
Формула площади сектора: (угол / 360) x π x радиус , но диаметр круга равен d = 2 x r, так что другой способ записи (угол / 360) 2 x π x (диаметр / 2) . Визуально на рисунке ниже:
Поскольку сектор — это просто срез круга, формула очень похожа на формулу для площади круга, с той разницей, которая необходима для расчета того, какую часть круга покрывает сектор. В то время как радиус легко измерить, угол — нет, если только у вас нет под рукой надлежащего инструмента, который может быть необходимым условием для использования нашего калькулятора площади.
Формула площади восьмиугольника правильной формы: 2 · (1 + √2) · сторона 2 , где сторона показана ниже:
Требуется только одно измерение, допустимо что уже известно, что фигура действительно является правильным восьмиугольником. В противном случае нужно сначала измерить все стороны, чтобы убедиться, что все они равны, прежде чем приступить к вычислению его площади.
Где использовать калькулятор площади?
Специализированный калькулятор, безусловно, пригодится, если у вас есть домашняя работа по геометрии или если вам разрешено использовать онлайн-инструменты в классе. Помимо этого, специальный калькулятор может понадобиться людям, занимающимся определенными ремеслами, инженерным делом и даже многими искусствами. Многие домашние проекты DIY, садовые проекты и т. д. также требуют, чтобы вы рассчитали одну или несколько областей, чтобы вы знали, сколько материала нужно купить, например.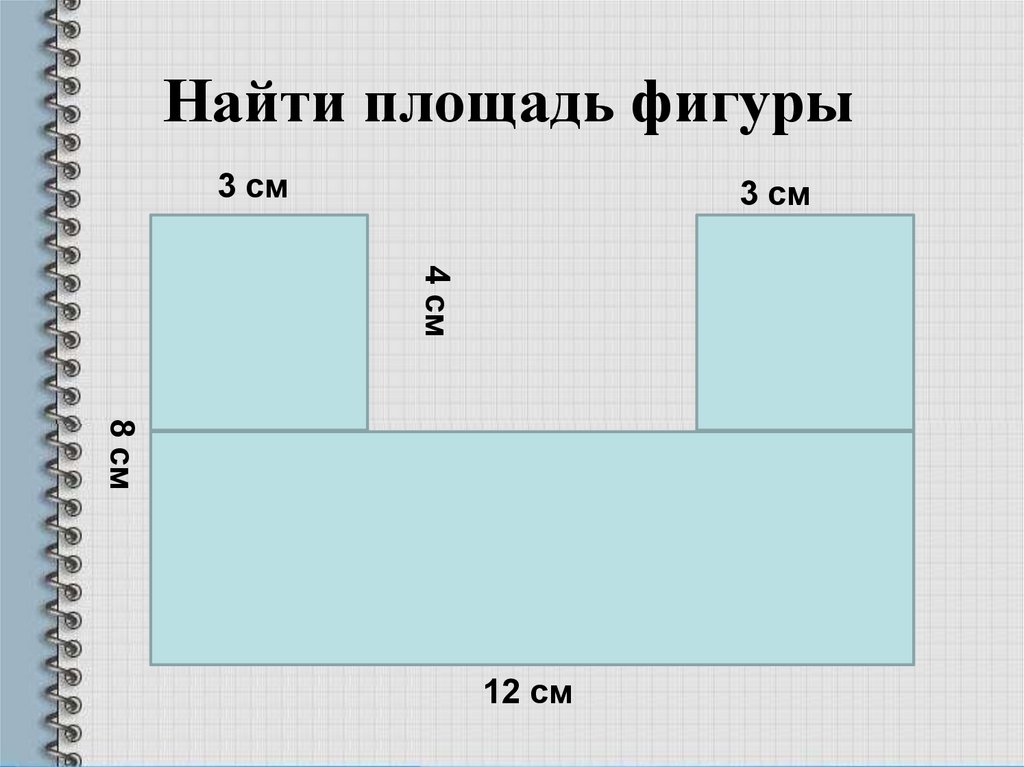 как в калькуляторе краски.
как в калькуляторе краски.
Площадь неправильных форм — расчет, примеры и часто задаваемые вопросы
Неправильные фигуры — это многоугольники с пятью или более сторонами разной длины. Эти формы или фигуры могут быть далее разложены на известные формы, такие как треугольники, квадраты и четырехугольники, для оценки площади.
Вот несколько примеров неправильной формы:
Предметы повседневной жизни неправильной формы
Как рассчитать площадь неправильной формы?
Определение площади неправильных форм
Различные методы оценки площади неправильных форм:
Оценка площади с использованием единицы измерения Квадраты.
Разделение неправильной формы на две или более правильных фигур.
Разделение неправильной формы с помощью кривых на две или более правильных фигур.

Как найти площадь неровной фигуры?
Оценка площади с использованием единичных квадратов
Мы можем использовать этот метод для фигур с кривыми, кроме идеального круга или полукруга и неправильных четырехугольников. В этом методе мы сначала делим фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, используется для определения общей площади.
Например: Рассчитайте площадь, подсчитав единицы квадратов на приведенном ниже рисунке
Ответ: Если мы обозначим каждую единицу площади в сантиметрах, площадь будет равна 6 см2.
Вычисление площади неправильной формы с изогнутыми краями
Разделение неправильной формы на две или более правильных фигур
Используйте этот метод для расчета площади неправильных фигур, которые представляют собой комбинацию треугольников и многоугольников. Используя предопределенные формулы, вычислите площадь таких фигур и сложите их вместе, чтобы получить общую площадь.
Например, в приведенной ниже неправильной форме мы разделим несколько ребер на треугольник и три многоугольника.
Общая площадь фигуры может быть рассчитана путем сложения отдельных площадей:
Общая площадь = площадь (ABIM) + площадь (BCGH) + площадь (CDEF) + площадь (JKL)
⇒ Общая площадь = (AB × BI ) + (BC × CG) + (CD × DE) + (12 × LJ × KO)
⇒Общая площадь = (10 × 5) + (3 × 3) + (2 × 2) + (1⁄2× 4 × 4)
⇒ Общая площадь = 50 + 9 + 4 + 8
⇒ Общая площадь = 71 см2
Вычисление площади неправильной формы
Чтобы вычислить площадь неправильной формы, разделите фигуру с кривыми на две или более правильных фигур.
В этом методе разделите неправильную форму на несколько квадратов, треугольников или других четырехугольников. В зависимости от формы или кривых часть фигуры может быть также кругом, полукругом или квадрантом.
Найдите площадь заданной неправильной формы с 8 сторонами, включая одну кривую.
Решение: Определим неизвестные величины по заданным размерам сторон. Сначала нам нужно разделить фигуру на два прямоугольника и полукруг.
Площадь фигуры ABCDEF равна:
Общая площадь (ABCDEF) = площадь (ABCG) + площадь (GDEF) + площадь (aob)
Общая площадь = (AB × AG) + (GD × DE) + ( 1⁄2 × π × ob2)
Общая площадь = (3 × 4) + (10 × 4) + (1/2 × 3,14 × 12)
Общая площадь = 12 + 40 + 1,57
Следовательно, общая площадь = 53,57 см2
Как найти площадь неправильной формы с помощью миллиметровой бумаги?
Какова площадь неровной поверхности?
Найдите площадь данного листа.
Решение: Чтобы найти площадь неправильной поверхности в приведенном выше случае листа, мы должны положить лист на миллиметровую бумагу и провести его границу.
Форма листа неправильная. Таким образом, мы предположим, что более половины площади, покрытой листом, будет считаться 1, а менее половины будет считаться 0.
Теперь подсчитайте количество полностью закрытых фигур. Полностью покрыты 64 квадрата.
Кроме того, посчитайте частично более чем наполовину закрытые квадраты, и каждый будет считать qs 1 квадрат. Есть 17 площади больше, чем половина площади.
Кроме того, подсчитайте частично менее половины закрытых Квадратов, и каждый из них будет считаться равным 0. Есть 16 Квадратов меньше половины Квадрата.
Теперь сложите все квадраты, чтобы найти площадь листа = 64 + 17 x 1 + 16 x 0 = 64 + 17 = 81 кв. единиц.
Отсюда Площадь листа будет 81 кв.ед.
Формула площади неправильных фигур
Чтобы найти площадь неправильных фигур, сначала нам нужно разделить неправильную форму на правильные фигуры, которые вы можете распознать, такие как треугольники, прямоугольники, круги, квадраты и так далее.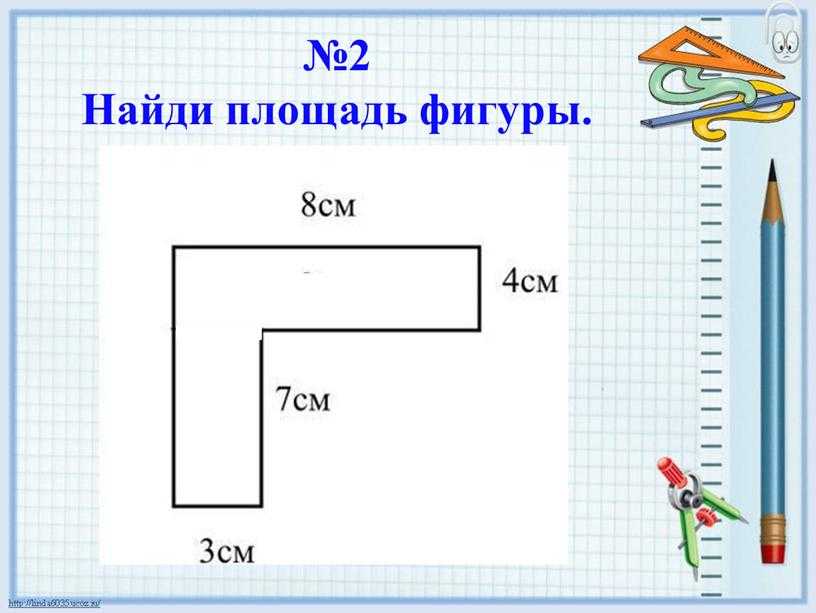
Затем найдите площадь этих отдельных фигур и сложите их, чтобы получить площадь неправильных форм.
Решенный пример
В. Найдите площадь заданной фигуры?
Решение: На рисунке выше есть три правильные фигуры. Начинайте делить сверху, у него есть треугольник, прямоугольник и трапеция.
Мы найдем площадь каждой из этих трех фигур и суммируем результаты, чтобы получить окончательную площадь фигуры.
Треугольник
Площадь треугольника = (основание × высота)/2
= (3 × 4)/2
= 12/2
= 6
Rectangle
Area of rectangle = length × width
= 3 × 10
= 30
Trapezoid
Area of trapezoid = ((b1 + b2) × h)/2
= ((3 + 5) × 2)/2
= (8) × 2/2
= 16/2
= 8
Следовательно, площадь данной Формы = 6 + 30 + 8 = 44.
Неправильные Формы
Пространство, занятое Фигурой, известно как Площадь Неправильной Формы; измеряется в квадратных единицах. Размер и длина фигур неправильной формы могут быть любыми. Существуют различные Неправильные Формы, которые мы можем видеть вокруг себя, такие как воздушные змеи, листья, алмазы и т. д. Следовательно, Неправильные Формы — это любые Формы, углы и длины которых не равны. Учащиеся могут изучать «Области неправильных форм» с предметными экспертами Vedantu, которые помогают учащимся понять каждую тему, чтобы было легче учиться и получать хорошие оценки.
Подробнее о неправильных формах
Область, покрываемая этой формой, называется площадью неправильных форм. Стороны и углы неправильных фигур различны. чтобы найти площадь неправильной формы, мы должны разложить ее или разделить на несколько известных фигур, а затем будет добавлена площадь этих фигур, чтобы получить общую площадь неправильной формы.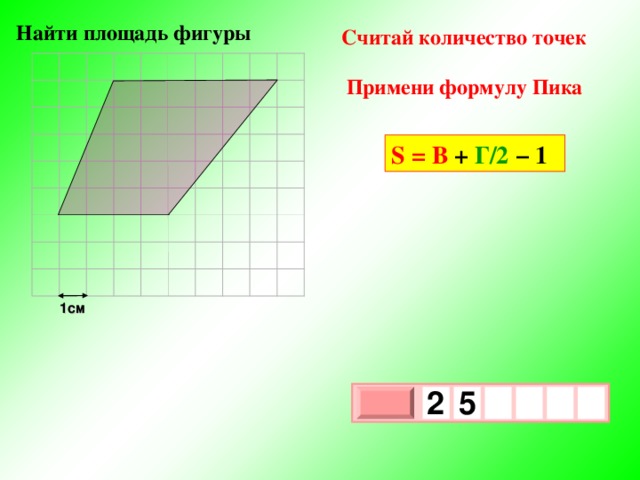 Неправильные формы можно увидеть повсюду вокруг нас в нашей повседневной жизни, например:
Неправильные формы можно увидеть повсюду вокруг нас в нашей повседневной жизни, например:
Лестница здания состоит из многоугольников, таких как прямоугольники и квадраты, площадь поверхности лестницы имеет неправильную форму.
Школьная игровая площадка с беговой дорожкой имеет неправильную форму, которая представляет собой комбинацию правильных форм.
Лист дерева или растения неправильной формы. И т. д.
Единица площади неправильной формы может быть выражена в м2, см2, дюйм2 или фут2.
Шаги по нахождению площади неправильных фигур
Шаг 1. Площадь неправильной формы нужно найти путем разложения неправильных фигур на знакомые формы.
Шаг 2. Учащиеся должны знать, как разложить неправильные фигуры.
Шаг 3. Разделение неправильной формы на разные знакомые фигуры и определение площади знакомых фигур
Шаг 4. Теперь сложите все площади знакомых фигур, чтобы узнать площадь неправильной формы.
Портал онлайн-обучения №1 Vedantu предоставляет учащимся полное руководство по изучению таких тем, как «Площадь неправильных форм — расчеты, примеры и т. д.». Студенты могут легко загрузить бесплатный PDF-файл и подготовиться к экзаменам. 100% точны и соответствуют последним рекомендациям и программе.
Площадь параллелограмма ИЛИ площадь неправильных форм – площадь в квадратных футах
Площадь параллелограмма ИЛИ площадь неправильных форм (squarefootagearea.com) Квадратные футы = Квадратные футы = Кв. футы = Кв. футы = кв. футы = футы 2
База ( б ):
Высота ( ч ):
Сторона а*:
Сторона б*:
Сторона с*:
Сторона d*:
Сумма 2 углов*:
Помните, что вводить можно только футы (футы), дюймы (дюймы), ярды (ярды), сантиметры (см), миллиметры (мм) и метры (м), но никогда не используйте комбинацию двух разных единиц измерения!. . Если у вас есть входы в разных единицах измерения. Пожалуйста, обратитесь к нашей таблице преобразования ниже.
. Если у вас есть входы в разных единицах измерения. Пожалуйста, обратитесь к нашей таблице преобразования ниже.
Формула
Площадь = b × h
Какая разница между правильной и неправильной формой?
Правильная форма: Все стороны и углы правильных фигур равны.
Неправильная форма: Стороны и углы неправильной формы могут быть любой длины и размера.
Правильная форма
Неправильная форма
Как вычислить площадь неправильной формы?
Теперь, когда мы знаем разницу между правильными и неправильными формами. Давайте упростим наш процесс расчета, разделив неправильную форму на правильные формы. Посмотрите пример ниже, здесь мы разделили фигуры на треугольники, которые имеют правильную форму.
Затем вы можете легко вычислить площадь каждого треугольника с помощью формулы Герона.
После вычисления площади каждого треугольника просто сложите их все, чтобы найти площадь неправильной формы.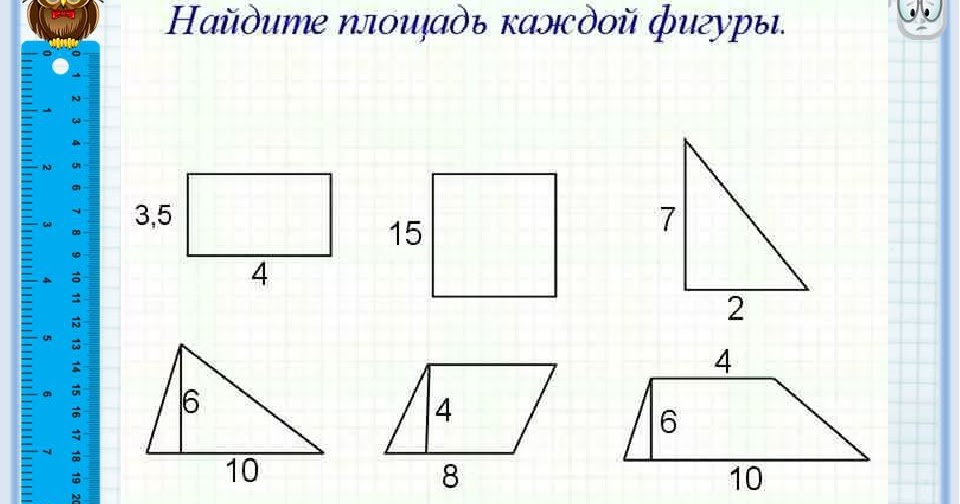
Как использовать калькулятор неправильной площади?
Шаг 1: Измерьте все стороны площади в одной единице (футы, метры, дюймы или любые другие).
Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2». И ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2». (См. изображение выше).
Шаг 3: Нажмите кнопку расчета. Вывод, который дает наш калькулятор, не зависит от единицы измерения. Например, если вы ввели значения в футах. Вывод всегда будет в футах.
Наша формула: Область = B × H
Сокращения. См 2 = 9 квадратных сантиметров0003
мм 2 = квадратные миллиметры
M 2 = квадратные метры
Шаг 1: Определите все стороны неправильной формы. Убедитесь, что все стороны имеют одинаковые единицы измерения.
Шаг 2: Нарисуйте площадь на листе бумаги, используя полученные измерения. Помните, что ваш рисунок должен быть в масштабе.
Шаг 3: Разделите рисунок на разные формы. Простые — это квадрат и прямоугольник, круги и треугольник могут быть немного сложными.
Шаг 4: Рассчитайте площадь каждой формы с помощью нашего калькулятора площади в квадратных футах. Для прямоугольников и квадратов умножьте ширину на высоту. Для треугольников умножьте основание на высоту, а затем разделите на 2. Для кругов умножьте квадрат радиуса на 3,14 (пи). Радиус круга — это расстояние от его центра до любой другой точки на краю круга.
Шаг 5: Сложите площади всех отдельных фигур, чтобы найти общую площадь в квадратных футах.
Наша формула: Площадь = b × h
Коэффициенты пересчета:
Для преобразования квадратных футов, квадратных дюймов, квадратных ярдов, квадратных сантиметров, квадратных миллиметров и квадратных метров вы можете использовать следующую таблицу преобразования.
ярдов| Квадратные футы в ярды | умножьте ft 2 на 0,11111, чтобы получить ярды 2 |
| Квадратные футы в метры | умножить фут 2 на 0,092903 чтобы получить м 2 |
| Квадратные ярды в квадратные футы | умножьте ярды 2 на 9, чтобы получить футы 2 |
| Квадратные ярды в квадратные метры | умножьте ярды 2 на 0,836127, чтобы получить м 2 |
| Квадратные метры в Квадратные футы | умножьте м 2 на 10,7639, чтобы получить футы 2 |
| Квадратные метры в квадратные ярды | умножить м 2 на 1.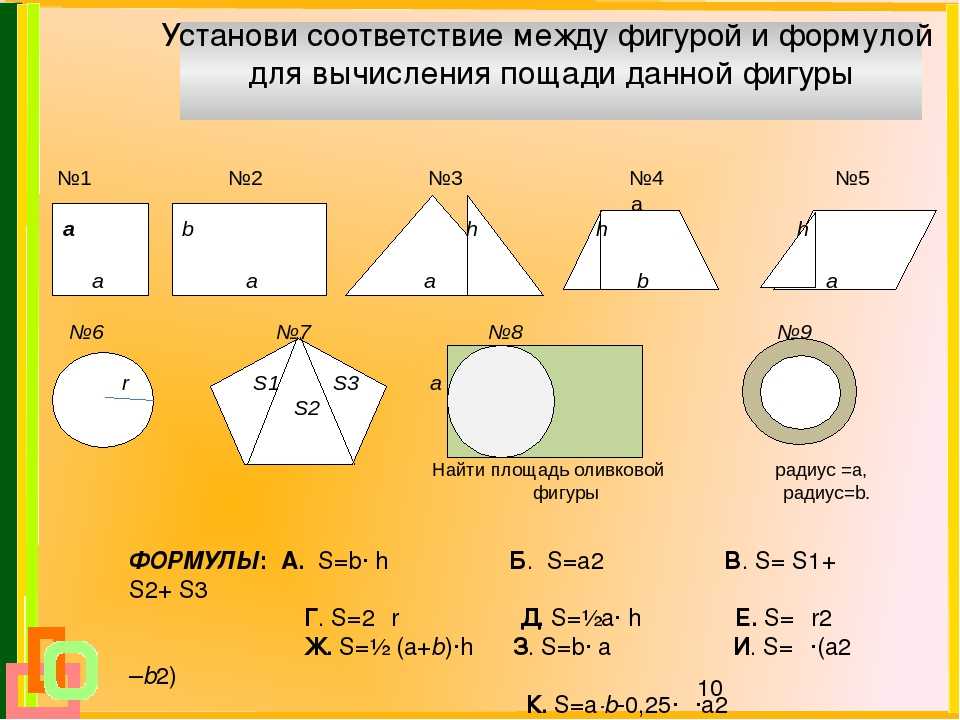 19599, чтобы получить 2 19599, чтобы получить 2 |
| Квадратные метры в квадратные миллиметры | умножьте значение m 2 на 1000000, чтобы получить мм 2 |
| Квадратные метры в квадратные сантиметры | умножьте значение m 2 на 10 000, чтобы получить см 2 |
| Квадратные сантиметры в Квадратные метры | умножьте значение см 2 на 0,0001, чтобы получить мм 2 |
| Квадратные сантиметры в квадратные миллиметры | умножьте значение см 2 на 100, чтобы получить мм 2 |
| Квадратные миллиметры в квадратные сантиметры | умножьте значение мм 2 на 0,000001, чтобы получить см 2 |
| Квадратные миллиметры в квадратные метры | умножьте значение мм 2 на 1000000, чтобы получить m 2 |
сообщите об этом объявлении
Формулы площади поверхности
| Формулы площади поверхности |
| (Математика | Геометрия | Формулы площади поверхности) |
( пи = = 3. 141592…)
141592…)
Поверхность
Формулы площади
Обычно площадь поверхности представляет собой сумму
все площади всех фигур, которые покрывают поверхность объекта.
Куб | Прямоугольный
призма | призма | Сфера
| Цилиндр | Единицы
Примечание: «ab» означает «а» умножить на «б». «а
2 » означает «а в квадрате», что равно «а», умноженному на «а».Будьте осторожны!! Считаются единицы. Используйте одни и те же единицы измерения для всех измерений. Примеры
| Площадь поверхности куба = 6 а 2 |
(а — длина стороны каждое ребро куба)
Другими словами, площадь поверхности куба — это площадь шести квадратов, которые
накрой это. Площадь одного из них равна a*a, или a 2 . Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше одной из сторон в квадрате.
Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше одной из сторон в квадрате.
| Площадь поверхности прямоугольного Призма = 2ab + 2bc + 2ac |
(a, b, c — длины трех сторон)
Другими словами, площадь поверхности прямоугольной призмы равна площади шести прямоугольники, которые его закрывают. Но нам не нужно вычислять все шесть, потому что мы знаем, что верх и низ одинаковы, перед и зад равны одинаковые, а левая и правая стороны одинаковые.
Площадь верха и низа (длины сторон а и
в) = а*с. Так как их два, то получается 2ac. Спереди и сзади
имеют длины сторон b и c. Площадь одного из них равна b*c, и там
их два, поэтому площадь поверхности этих двух равна 2bc. Левый и
правая сторона имеет длины сторон a и b, поэтому площадь поверхности одной из
они а*б. Опять же, их два, поэтому их общая площадь поверхности
это 2аб.
Левый и
правая сторона имеет длины сторон a и b, поэтому площадь поверхности одной из
они а*б. Опять же, их два, поэтому их общая площадь поверхности
это 2аб.
| Площадь поверхности любой призмы |
(b — форма из концов)
Площадь поверхности = боковая площадь + площадь двух концов
(Боковая площадь) = (периметр формы b ) * L
Площадь поверхности = (периметр формы b ) * L+ 2 * (Площадь формы b )
| Площадь поверхности сферы = 4 пи г 2 |
(r — радиус окружности)
| Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h |
(h высота цилиндр, r — радиус вершины)
Площадь поверхности = площади сверху и снизу + площадь сбоку
Площадь поверхности = 2 (площадь верха) + (периметр верха) * высота
Площадь поверхности = 2( pi r 2 ) + (2 pi r)*h
На словах проще всего представить банку. Площадь поверхности – это
площади всех частей, необходимых для покрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается вокруг середины.
Площадь поверхности – это
площади всех частей, необходимых для покрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается вокруг середины.
Можно найти площадь верха (или низа). Это формула площадь круга ( pi r 2 ). Так как есть и вершина, и дно, которое умножается на два.
Сторона похожа на этикетку банки. Если вы очистите его и положите плоский это будет прямоугольник. Площадь прямоугольника есть произведение две стороны. С одной стороны высота банки, с другой периметру круга, так как этикетка один раз оборачивается вокруг банки. Так площадь прямоугольника равна (2 pi r)*h.
Сложите эти две части вместе, и вы получите формулу поверхности. площадь цилиндра.
Площадь поверхности = 2( pi r 2 ) + (2 pi r)*h
Совет! Не забывайте про единицы. Related Posts |


 И. учащихся
И. учащихся , 700 см = 7 м. Затем они перемножаются: 5 м * 7 м = 35 м2.
, 700 см = 7 м. Затем они перемножаются: 5 м * 7 м = 35 м2.
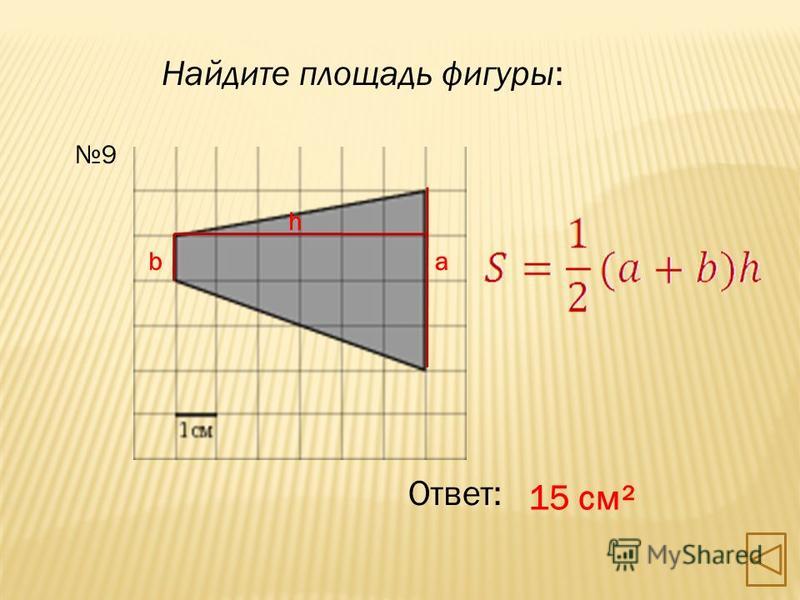
 6 = 13.4 м2.
6 = 13.4 м2.
 5 миллионов
5 миллионов

 = S стен+S пола+S потолка
= S стен+S пола+S потолка д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

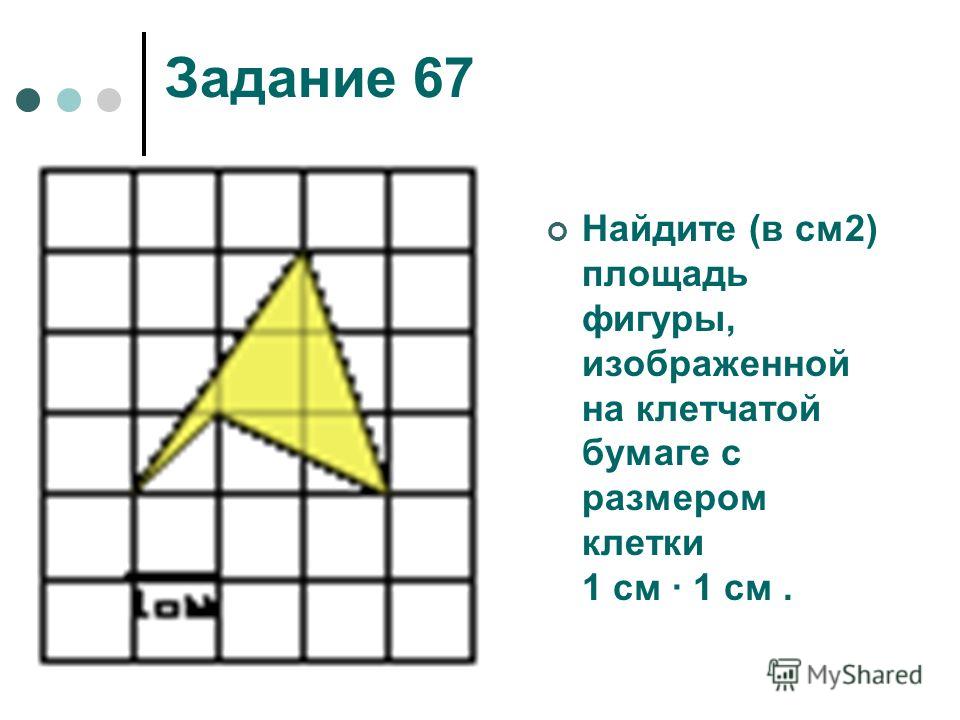

 Найдите его площадь.
Найдите его площадь. 