§ Площадь фигур. Площадь квадрата. Площадь прямоугольника. Площадь сложной фигуры
Определение площади Формулы площадей фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + S
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S ABC = SABCD : 2
S ABC = 20 : 2 = 10 см2
S ABC =
S ACD = 10 см2
Определение площади Формулы площадей фигур
Как обозначается площадь: какой буквой или знаком пишется параметр площади в математике
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки.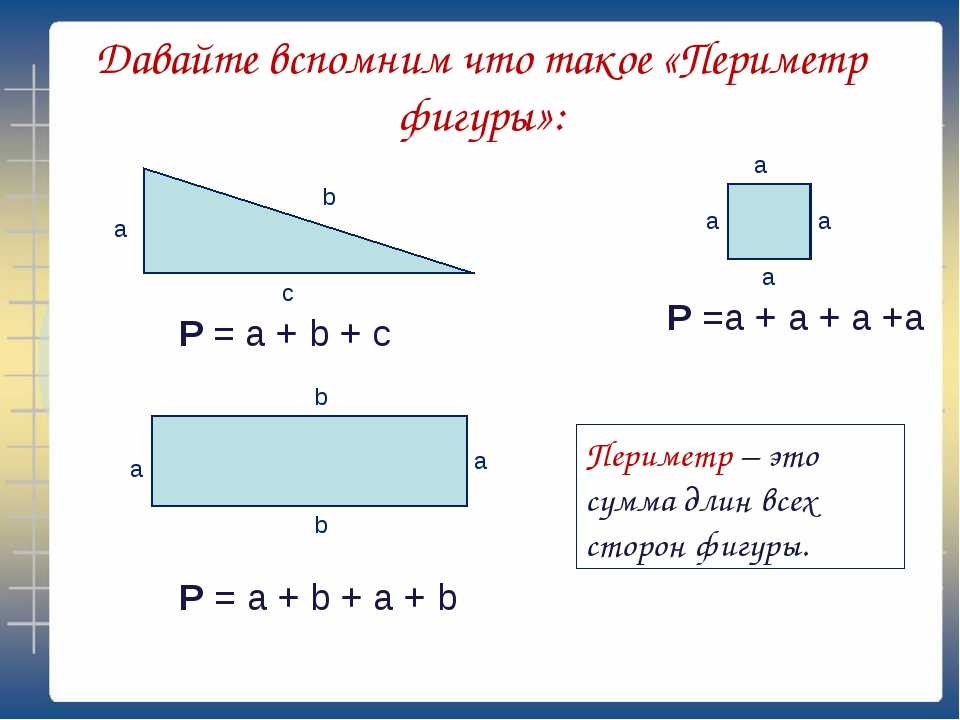 В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Содержание
Общие сведения
Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.
Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.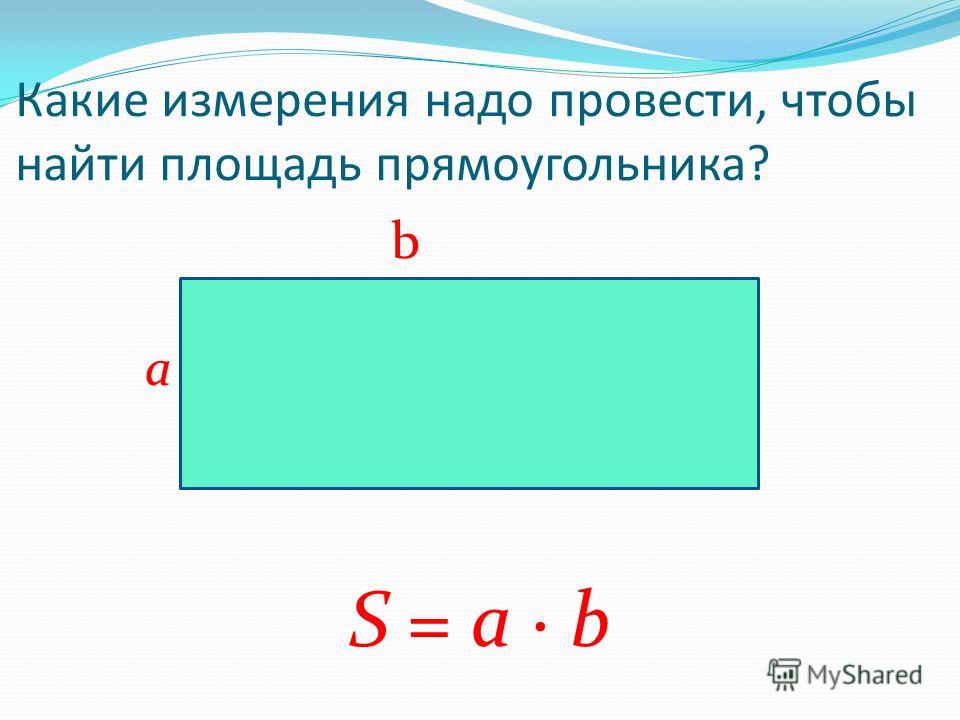
Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:
- Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.
- Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.

- Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
- Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
- Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.
Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.
Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики.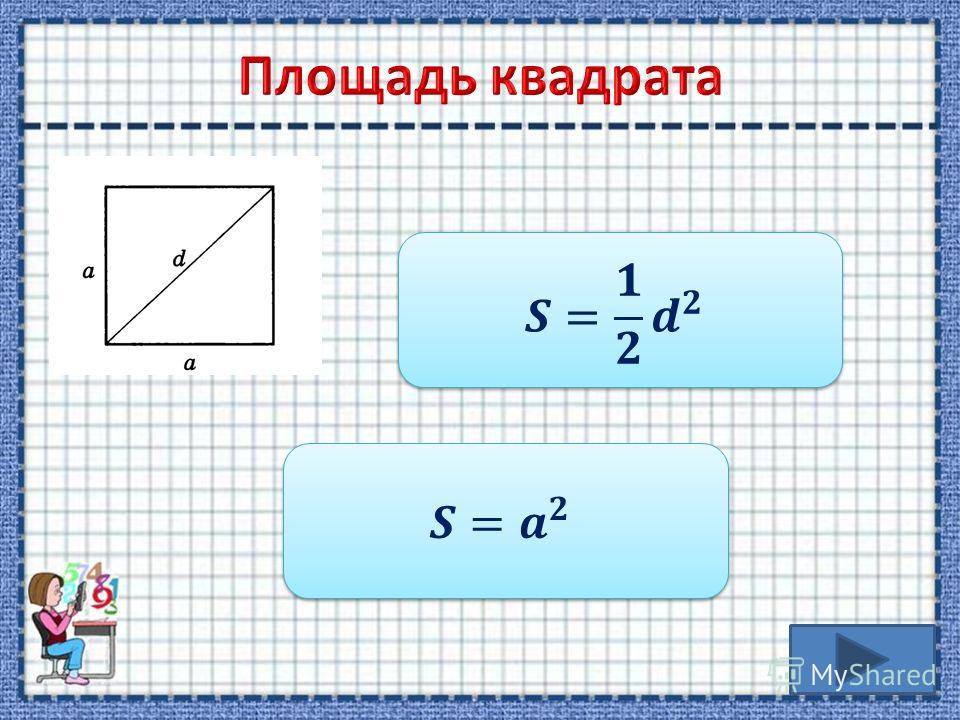 При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения
Понятие используется не только в математике. Оно актуально и для физики.
В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину. Проститутки в Екатеринбурге intim66.ru
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.
Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.
Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами.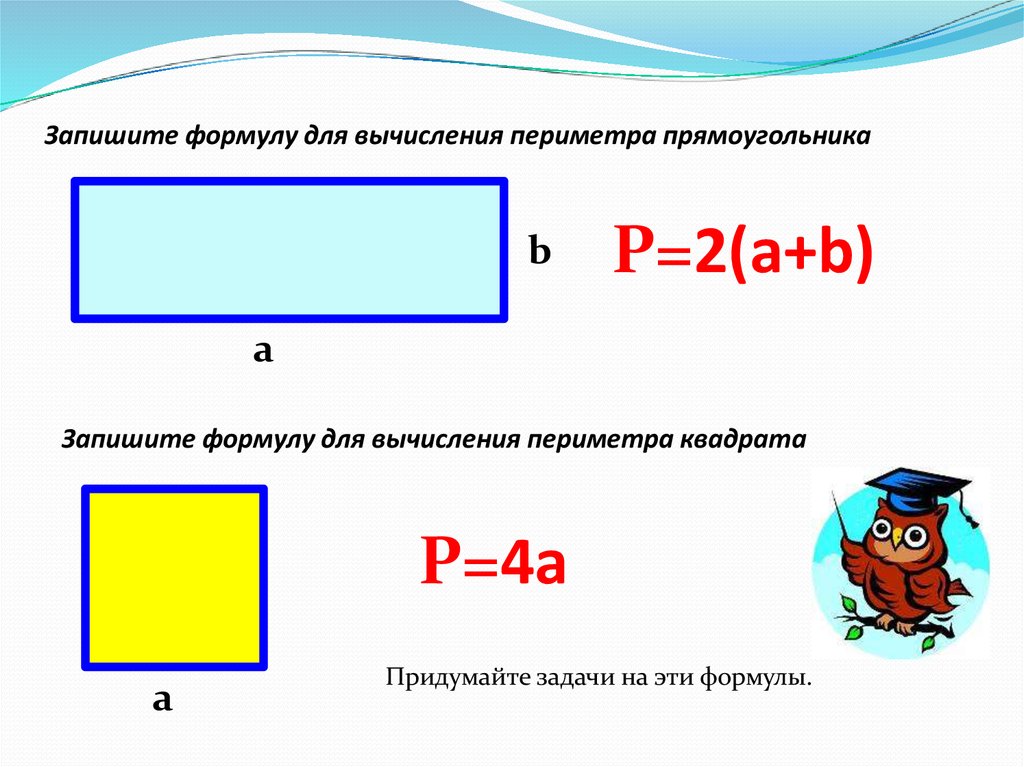 В качестве примера могут быть SAOB, SCLE, SOME.
В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Формулы площадиФормулы площади
| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
( пи = = 3. Район ФормулыПримечание: «ab» означает «a» умножить на «б». «а2 » означает «а в квадрате», что то же самое, что «а» умножить на «а».Будьте осторожны!! Считаются единицы. Используйте тот же единицы для всех измерений. Примерыsquare = a 2 rectangle = ab parallelogram = bh trapezoid = h/2 (b 1 + b 2 ) circle = пи r 2 эллипс = пи r 1 r 2
треугольник задан SAS (две стороны и противолежащий угол) треугольник, заданный a,b,c = [s(s-a)(s-b)(s-c)] когда s = (a+b+c)/2 (формула Герона) правильный многоугольник = (1/2) n sin(360°/n) S 2 Единиц Площадь измеряется в квадратных единицах. Площадь квадрата = сторона умноженная на сторону. Так как каждая сторона квадрата равна то же самое, это может быть просто длина одной стороны в квадрате. Если у квадрата одна сторона равна 4 дюймам, площадь будет равна 4 дюймам, умноженным на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также могут быть записаны в 2 .) Обязательно используйте одни и те же единицы измерения для всех измерений. Нельзя умножать футы на дюймы, это не дает квадрат измерение. Площадь прямоугольника равна длине стороны раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, то что это площадь? НЕПРАВИЛЬНО …. 4 раза по 6 = 24 ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута. Площадь 1/3 фута
умножить на 6 футов = 2 квадратных фута. | |||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Area — Math Open Reference
Area — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Что такое площадь?
Площадь — это мера того, сколько места есть на плоской поверхности. Например, площадь двух листов бумаги в два раза больше площади одного листа, потому что на них вдвое больше места для записи.
Различные фигуры имеют разные способы нахождения площади.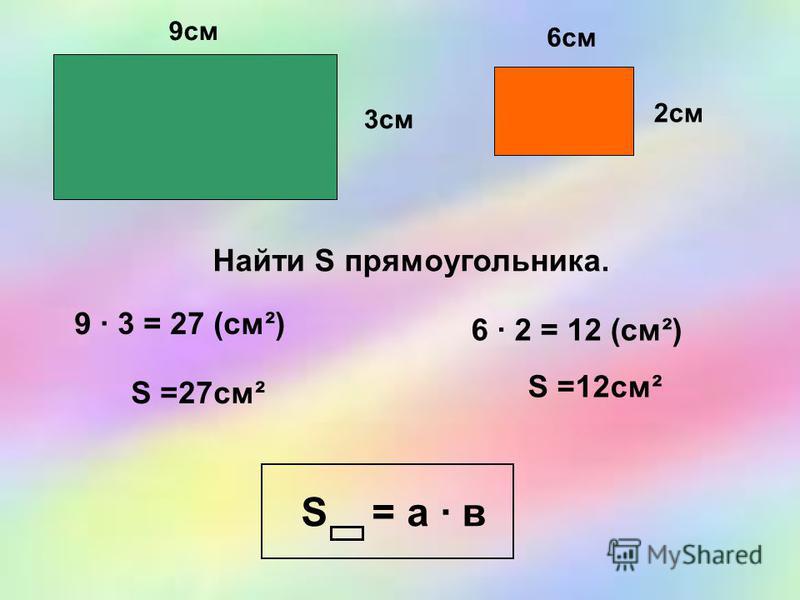 Например, в прямоугольнике мы находим площадь, умножая длину на ширину.
В прямоугольнике выше площадь равна 2 × 4 или 8. Если вы посчитаете маленькие квадраты, вы обнаружите, что их 8.
Например, в прямоугольнике мы находим площадь, умножая длину на ширину.
В прямоугольнике выше площадь равна 2 × 4 или 8. Если вы посчитаете маленькие квадраты, вы обнаружите, что их 8.
Единицы
Площадь измеряется в квадратных единицах. Например, в прямоугольнике выше, если стороны 2 и 4 метра, то площадь равна 8 квадратных метров. Если бы стороны были 2 фута и 4 фута в длину, площадь была бы 8 квадратных футов. Самое главное, что нужно помнить при расчете площади, это то, что
Обозначение
Мы говорим о прямоугольнике выше, имеющем площадь, скажем, 8 квадратных метров, но есть сокращенный способ записи. Мы пишем букву единицы с надстрочным индексом 2 после нее, вот так:
«8 квадратных метров» записывается как 8 м 2
«8 квадратных футов» записывается как 8 футов 2
Преобразование единиц
Есть много единиц площади. Например, площадь земли измеряется в таких единицах, как акры и гектары.
Самый простой способ конвертировать из одних единиц в другие — использовать поисковую систему Google.
Его малоизвестная особенность заключается в том, что если вы вводите проблему конверсии в поле поиска, она конвертирует ее для вас.
если он может понять, что вы имеете в виду.
Например, площадь земли измеряется в таких единицах, как акры и гектары.
Самый простой способ конвертировать из одних единиц в другие — использовать поисковую систему Google.
Его малоизвестная особенность заключается в том, что если вы вводите проблему конверсии в поле поиска, она конвертирует ее для вас.
если он может понять, что вы имеете в виду.Например, если вы введете «300 квадратных футов в квадратных метрах», вам будет сказано, что 300 квадратных футов равны 27,87 квадратных метров.
Площади плоских фигур
Для многих фигур существуют способы вычисления площади, например площадь круга. Они перечислены ниже со ссылками на страницы, которые объясняют каждую из них более подробно.
См. также
- Площадь поверхности твердых тел
См. Площадь квадрата | ||
| Прямоугольник | См. | |
| Треугольник | См. Площадь треугольника | |
| Треугольник (SAS) | См. Площадь треугольника (sas) | |
| Треугольник Даны 3 стороны | См. формулу Герона | См. формулу Герона |
| Равносторонний треугольник | См. Равносторонний участок | |
| Параллелограмм | См. область параллелограмма | |
| Трапеция | См. трапециевидную форму | |
| Ромб | 3 метода См. Площадь ромба | См. площадь ромба |
| Воздушный змей | , где D 1 , D 2 — диагонали.  | См. Площадь воздушного змея |
| Правильный многоугольник | 4 метода См. Площадь правильного многоугольника | См. Площадь правильного многоугольника |
| Круг | См. Площадь круга | |
| Эллипс | См. Площадь эллипса | |
| Сегмент окружности | См. Площадь круглого сегмента. | См. Площадь круглого сегмента |
| Кольцо | См. Площадь кольца |
Площади на координатной плоскости
Если вы знаете координаты x,y вершин фигуры, есть способы вычислить площадь по этим координатам. См. Многоугольники на координатной плоскости.
(C) Открытый справочник по математике, авторское право, 2011 г.


 141592…)
141592…) 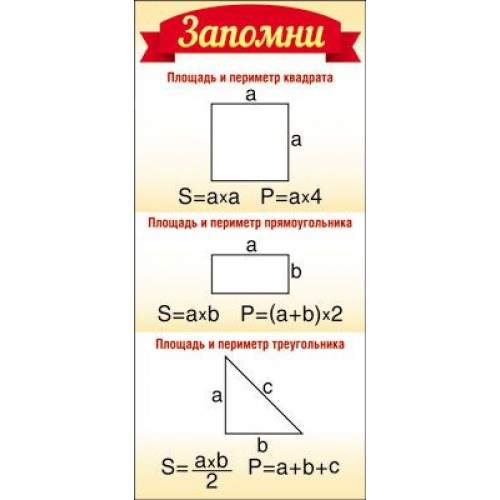 Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол. (или 2 кв. фута, или 2 фута 2 ).
(или 2 кв. фута, или 2 фута 2 ).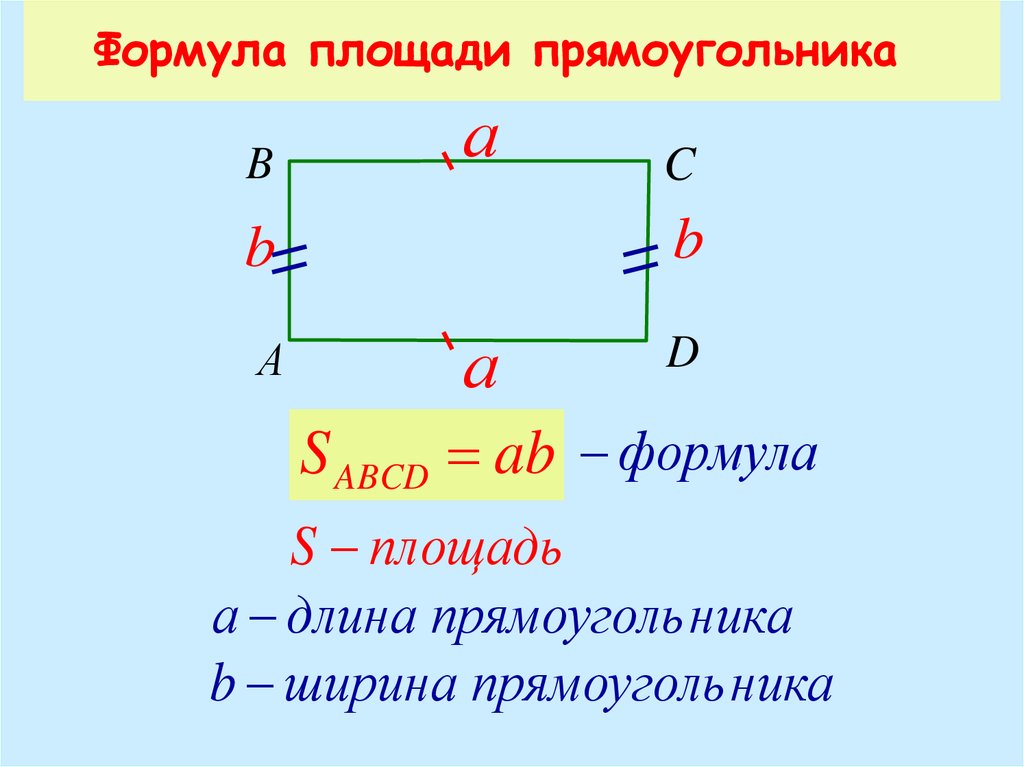 Площадь прямоугольника
Площадь прямоугольника