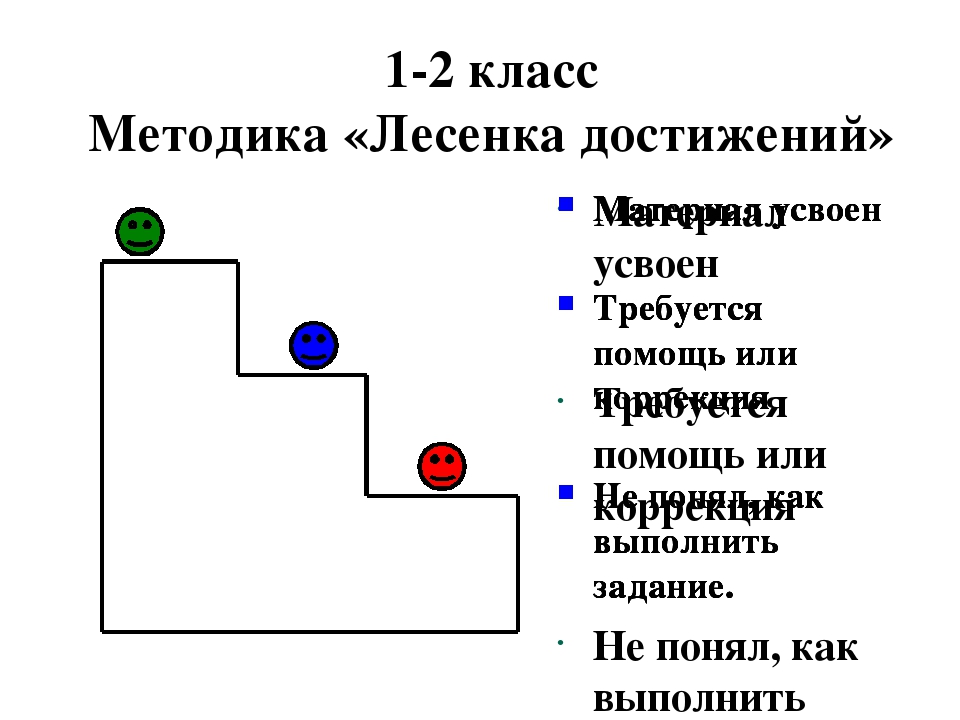
Формирование самооценки у учащихся начальной школы
%PDF-1.5 % 1 0 obj > /Metadata 4 0 R >> endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream
32 841.92]
/Contents 93 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
25 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 94 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
26 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 95 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
27 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 96 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
28 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 97 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
29 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 98 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
30 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 107 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
37 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 108 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
38 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 109 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
39 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 111 0 R
/Group >
/Tabs /S
/StructParents 1
>>
endobj
40 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 112 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
41 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 113 0 R
/Group >
/Tabs /S
/StructParents 2
>>
endobj
42 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 124 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
49 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 125 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
50 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 126 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
51 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 127 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
52 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 128 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
53 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 129 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
54 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.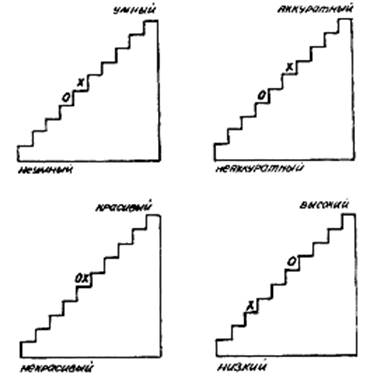
Диагностика самооценки младших школьников
1.5 Методы диагностики самооценки младших школьников
Методика А.И. Липкиной «Три оценки»
Для изучения самооценки можно использовать методику А.И. Липкиной «Три оценки». [9]
Ученикам
предлагается выполнить любое учебное
задание в письменной форме.
Психолог
вместе с учителем дает работе учеников
три оценки: адекватную, завышенную,
заниженную. Перед раздачей тетрадей
ученикам говорят: «Три учительницы из
разных школ проверяли ваши работы. У
каждой сложилось свое мнение о выполненном
задании, и поэтому они поставили разные
оценки. Обведите кружочком ту, с которой
вы согласны». Затем в индивидуальной
беседе с учениками выясняются ответы
на следующие вопросы:
1. Каким учеником ты себя считаешь: средним, слабым или сильным?
2. Твоя работа заслуживает оценки «3», а учительница поставила тебе «5». Обрадуешься ты этому или это тебя огорчит?
3. Какие оценки тебя радуют, какие огорчают?
Уровень самооценки школьников определяется на основе полученных данных по следующим показателям:
— совпадение или несовпадение самооценки с адекватной оценкой учителя;
— характер аргументации самооценки:
а) аргументация, направленная на качество выполненной работы,
б) любая другая аргументация;
—
устойчивость или неустойчивость
самооценки, о которой судят по степени
совпадения выставленной самому себе
отметки и ответов на поставленные
вопросы.
Методика «Справлюсь или нет?»
Уровень притязаний обнаруживается в прогностической, или априорной, самооценке еще не полученного результата. Для ее выяснения у детей начальных классов может быть использована следующая методика. [22]
Разным по успеваемости ученикам даются поочередно три задания: одно — по русскому языку, другое — по математике (оба на основании изученного и понятного материала), третье – не учебное, например, складывание орнамента по заданным образцам. Им предлагается ответить на вопрос: «Сможешь ли ты выполнить задания, на какую оценку и почему?» Затем дети должны ответить на тот же вопрос относительно трех разных по успеваемости одноклассников.
Анализу, позволяющему выявить складывающуюся у ученика оценочную позицию, подлежат следующие данные:
1.
Уровень прогностической самооценки у
разных по успеваемости школьников
(верная, завышенная, заниженная).
2. Особенности прогностической оценки этих школьников.
3. Особенности адаптационной оценочной деятельности, ее направленность — на оценку способностей к учебе или на качества личности.
4. Распространение оценочной деятельности при выполнении учебных заданий на учебные ситуации.
Данный анализ позволяет выяснить складывающуюся у каждого ученика оценочную позицию. Важность выявления у слабоуспевающих школьников формирующейся оценочной позиции доказана в исследованиях отечественных психологов: с возрастом у таких школьников нарастает тенденция к недооценке своих возможностей. Преобладание неуспеха над успехом, подкрепляемое низкими оценками их работы учителем, ведет к увеличению неуверенности в себе, чувству неполноценности и к заниженному, по сравнению с реальными возможностями, уровню притязаний.
Исследование самооценки по методике Дембо-Рубинштейн
Данная
методика основана на непосредственном
оценивании (шкалировании) школьниками
ряда личных качеств, таких как здоровье,
способности, характер и т.
д. Обследуемым
предлагается на вертикальных линиях
отметить определенными знаками уровень
развития у них этих качеств (показатель
самооценки) и уровень притязаний, т. е.
уровень развития этих же качеств, который
бы удовлетворял их. Каждому испытуемому
предлагается бланк методики, содержащий
инструкцию и задание.[9]
Проведение исследования
Инструкция: “Любой человек оценивает свои способности, возможности, характер и др. Уровень развития каждого качества, стороны человеческой личности можно условно изобразить вертикальной линией, нижняя точка которой будет символизировать самое низкое развитие, а верхняя — наивысшее. Вам предлагаются семь таких линий. Они обозначают:
— здоровье;
— ум, способности;
— характер;
— авторитет у сверстников;
— умение многое делать своими руками, умелые руки;
— внешность;
—
уверенность в себе.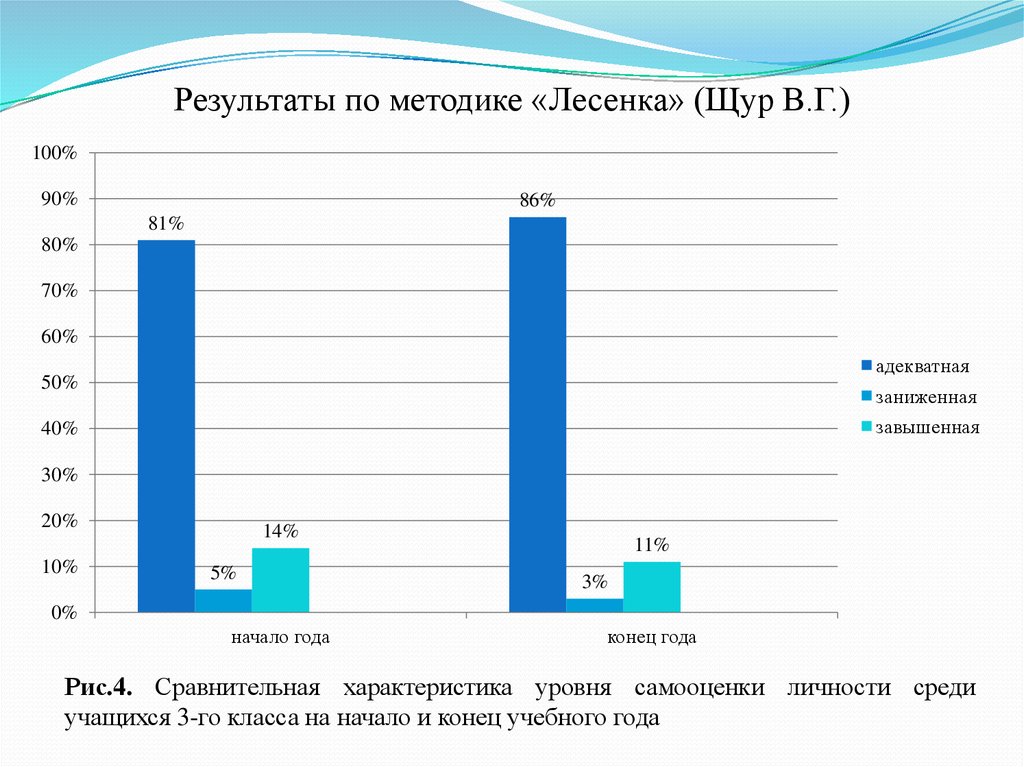
На каждой линии чертой (-) отметьте, как вы оцениваете развитие у себя этого качества, стороны вашей личности в данный момент времени. После этого крестиком (х) отметьте, при каком уровне развития этих качеств, сторон вы были бы удовлетворены собой или почувствовали гордость за себя”.
Испытуемому выдается бланк, на котором изображено семь линий, высота каждой — 100 мм, с указанием верхней, нижней точек и середины шкалы. При этом верхняя и нижняя точки отмечаются заметными чертами, середина едва заметной точкой.
Методика может проводиться как фронтально с целым классом (или группой), так и индивидуально. При фронтальной работе необходимо проверить, как каждый ученик заполнил первую шкалу. Надо убедиться, правильно ли применяются предложенные значки, ответить на вопросы. После этого испытуемый работает самостоятельно. Время, отводимое на заполнение шкалы вместе с чтением инструкции, 10-12 мин.
Обработка и интерпретация результатов
Обработка
проводится по шести шкалам (первая,
тренировочная — «здоровье» — не
учитывается).
Каждый ответ выражается
в баллах. Как уже отмечалось ранее, длина
каждой шкалы 100мм, в соответствии с этим
ответы школьников получают количественную
характеристику (например, 54мм = 54 баллам).
По каждой из шести шкал определить:
уровень притязаний — расстояние в мм от нижней точки шкалы («0») до знака «х»;
высоту самооценки — от «о» до знака «-»;
значение расхождения между уровнем притязаний и самооценкой — расстояние от знака «х» до знака «-», если уровень притязаний ниже самооценки, он выражается отрицательным числом.
Рассчитать среднюю величину каждого показателя уровня притязаний и самооценки по всем шести шкалам.
Уровень притязаний
Норму,
реалистический уровень притязаний,
характеризует результат от 60 до 89 баллов.
Оптимальный — сравнительно высокий
уровень — от 75 до 89 баллов, подтверждающий
оптимальное представление о своих
возможностях, что является важным
фактором личностного развития.
Результат
от 90 до 100 баллов обычно удостоверяет
нереалистическое, некритическое
отношение детей к собственным возможностям.
Результат менее 60 баллов свидетельствует
о заниженном уровне притязаний, он —
индикатор неблагоприятного развития
личности.
Высота самооценки
Количество баллов от 45 до 74 («средняя» и «высокая» самооценка) удостоверяют реалистическую (адекватную) самооценку.
Количество
баллов от 75 до 100 и выше свидетельствует
о завышенной самооценке и указывает на
определенные отклонения в формировании
личности. Завышенная самооценка может
подтверждать личностную незрелость,
неумение правильно оценить результаты
своей деятельности, сравнивать себя с
другими; такая самооценка может указывать
на существенные искажения в формировании
личности — «закрытости для опыта»,
нечувствительности к своим ошибкам,
неудачам, замечаниям и оценкам окружающих.
Количество баллов ниже 45 указывает на
заниженную самооценку (недооценку себя)
и свидетельствует о крайнем неблагополучии
в развитии личности.
Эти ученики
составляют «группу риска», их, как
правило, мало. За низкой самооценкой
могут скрываться два совершенно разных
психологических явления: подлинная
неуверенность в себе и «защитная», когда
декларирование (самому себе) собственного
неумения, отсутствия способности и тому
подобного позволяет не прилагать никаких
усилий.
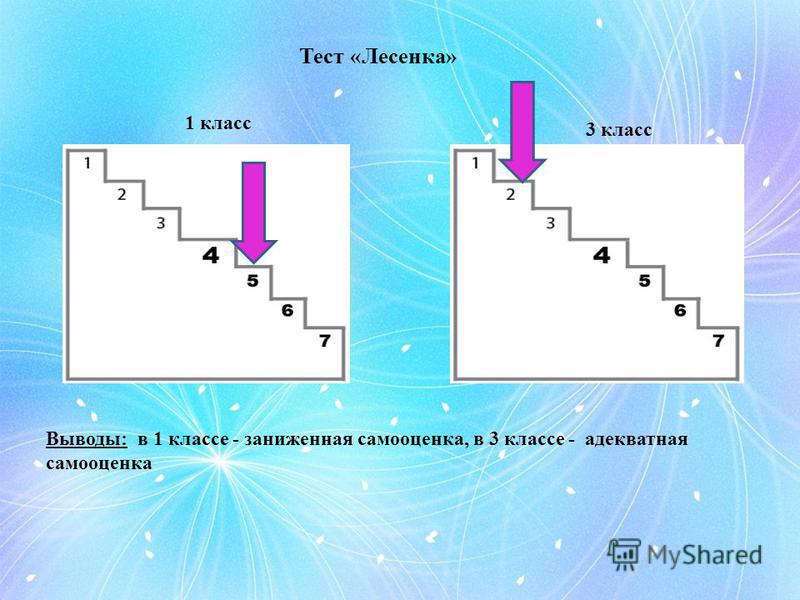
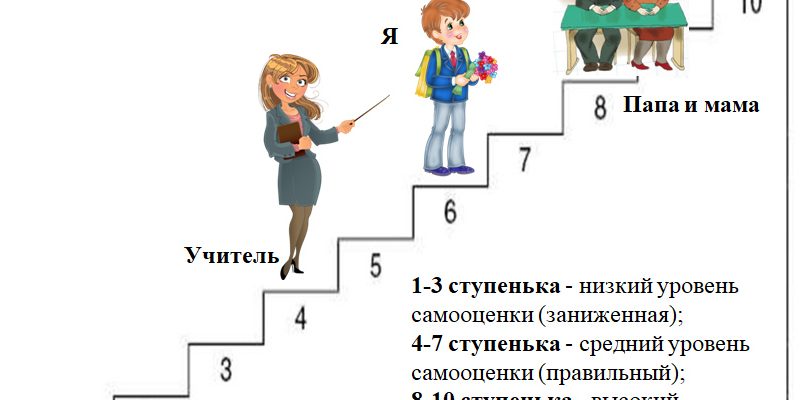
Методика «Лесенка» Щур В.Г., Якобсон С.Г.
Цель: определить особенности самооценки младших школьников и представлений о том, как его оценивают другие люди (когнитивную составляющая самооценки).
Опыт выполняется на основе проективной методики, в которой ребенку предлагается выбрать свое место на лесенке и место, куда бы его поставили его родители, а также аргументировать, почему он так думает.
Материал: макеты двух человечков (мальчик и девочка), макет лесенки, лист бумаги для фиксации аргументов ребенка.
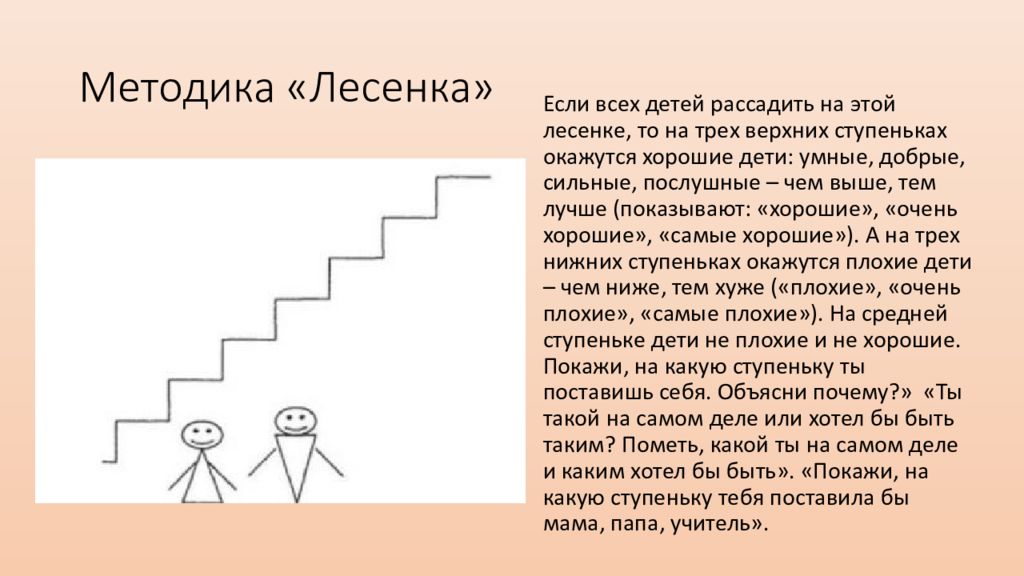
Экспериментатор
предлагает ребенку мысленно рассадить
на лежащей перед ним лесенке детей.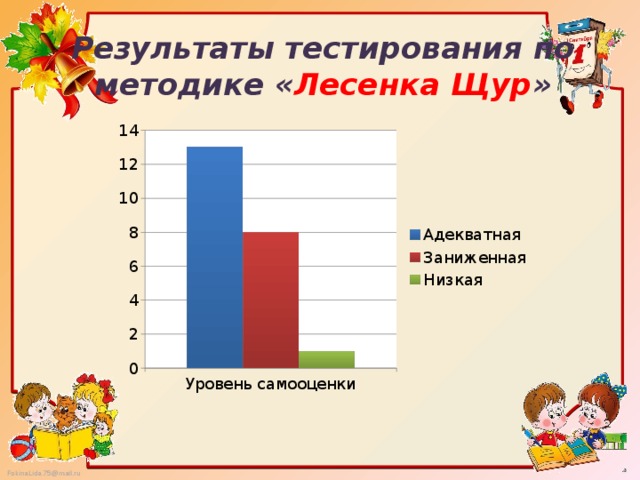
«При
этом на самой верхней ступеньке окажутся
самые хорошие ребята, ниже — просто
хорошие, затее — средние, но еще хорошие
дети. Соответственно распределены
плохие дети. После этого ребенку дается
фигурка человечка и экспериментатор
просит поставить эту фигурку на ту
ступеньку, которой сам ребенок, по его
мнению соответствует. Затем ребенку
предлагается поместить фигурку на
ступеньку, куда по его мнению, его
поставила бы мама.
По мере ответов ребенка психолог фиксирует названные позиции и то как аргументирует эти позиции ребенок.
Обработка и анализ результатов:
если ребенок считает, что мама поставила его выше, чем он сам себя, то это свидетельствует о том, что такие дети ощущают твердую поддержку «за спиной», уже имеют выраженную способность критически оценивать себя, как личность. Этот вариант по мнению автора методики является благоприятным и соответствует адекватной самооценки.
если ребенок считает, что мама его поставила ниже, чем он сам себя, то это характеризует детей, как не благоприятных и этому варианту соответствует заниженной самооценки.
если ребенок считающий, что его мнение и мнение мамы совпадает, это свидетельствует о том, что эти дети менее благополучны или они выдают желаемое за действительное, это говорит о завышенной самооценки.
Помогите своему ребенку понять метод лестницы за меньшее время
Последнее обновление: Thinkster 25 мая 2022 г.
Метод лестницы — полезный способ помочь учащимся понять и решить математические задачи за меньшее время.
Но даже несмотря на то, что это полезный инструмент, который репетиторы и учителя используют в классах сегодня, мы знаем, что многие родители, возможно, не учили математике с помощью того же метода. Если вы родитель, который хочет понять метод лестницы, чтобы вы могли помочь своему ребенку с домашним заданием, оставайтесь с нами.
Мы собираемся превратить эту технику в пошаговое руководство, которое легко понять и начать использовать уже сегодня.
А это означает, что у вас будет больше времени для дополнительных математических заданий и обучения!
Что такое лестничный метод?
Это простая техника, в которой используются простые числа и визуализация в виде ступенчатых линий (похожих на лестницу), чтобы помочь учащимся понять математические задачи.
Это требует от студентов демонстрации своей работы, но помогает им ясно увидеть, как прийти к заданному решению.
Итак, первый шаг — определение и идентификация простых чисел. Возможно, вы помните со времен учебы в классе, что простых чисел — это числа, которые больше 1 и не имеют положительных делителей, кроме 1 и самого себя.
Это означает, что единственный способ получить простое число с помощью умножения — это использовать само число.
Например, вот первые восемь простых чисел: 2, 3, 5, 7, 11, 13, 17 и 19.
Давайте посмотрим на число 7. Вы не может умножать любые числа, кроме 7 и 1, чтобы получить семь, поэтому это простое число.
Что насчет номера 6?
Вы можете умножить 2 х 3, чтобы получить 6, а 6 х 1 также равно 6. Значит, это не простое число.
Лестничный метод можно использовать для решения нескольких различных математических задач. Мы начнем с самого простого и постепенно перейдем к более сложным вещам, чтобы вы могли помочь своему ребенку в любых областях, которые могут доставлять ему проблемы.
Как использовать лестничный метод для факторизации числа 9 на единицу0018
Допустим, вы хотите найти простую факторизацию одного числа. В этом примере мы будем использовать число 24.
Запишите число 24 в скобках. Затем подумайте о наименьшем простом числе, на которое его можно разделить без остатка.
| 24 |
Лучший способ сделать это — вспомнить список простых чисел и начать сначала с наименьшего числа (кроме 1).
Входит ли 2 в 24? Ответ положительный.
Итак, вы напишите 2 слева от скобок, как мы сделали здесь.
2 | 24 |
Далее вам нужно выяснить, сколько раз 2 равномерно переходит в 24, ныряя 24/2.
Вы начнете следующую ступень вашей лестницы ниже первой строки, написав ответ следующим образом:
2 | 24 |
| 12 |
Спросите: «Является ли 12 простым числом?»
Поскольку мы знаем, что можно умножить несколько комбинаций, чтобы получить 12 (например, 3 x 4), мы знаем, что 12 не является простым числом.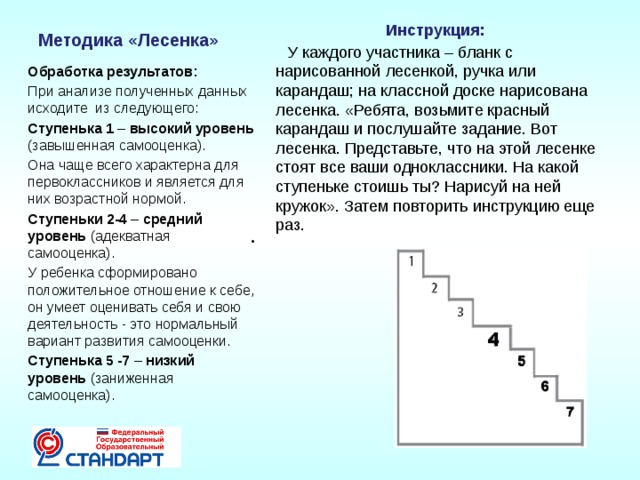
Цель состоит в том, чтобы разбить каждую ступеньку и скобку, чтобы получить простое число.
Итак, начните процесс снова с наименьшего простого числа и продвигайтесь вверх. 2 равномерно входит в 12? Сколько раз?
Запишите простое число (2) слева от скобки и начните следующую ступень лестницы для следующего делителя.
2 | 24 |
2 | 12 |
| 6 |
Теперь перейдите к самой нижней ступени, которую вы только что добавили. Спросите, является ли 6 простым числом. Мы снова знаем, что наше число делится на 2.
Итак, мы снова поместим простое число (2) за пределы скобки и начнем четвертую ступень.
2 | 24 |
2 | 12 |
2 | 6 |
| 3 |
Теперь у нас наконец есть простое число на нижней ступени. Поскольку нет других чисел, которые можно умножить, чтобы получить 3, кроме 1 и 3, мы находимся в конце лестницы.
Разложение числа 24 на простые множители затем выражается как все числа на внешней стороне лестницы или в форме «L»:
2 | 24 |
2 | 12 |
2 | 6 |
| 3 |
Это означает, что простая факторизация числа 24 равна: 2 x 2 x 2 x 3. Что можно записать как 2 3 x 3.
Как использовать лестничный метод для упрощения дробей дробь вроде 24 / 36 и вам нужно упростить, вы будете использовать метод лестницы, как в примере выше. Чтобы учесть оба числа, вы просто добавите еще один столбец.
Определите числитель (число в верхней части дроби) и знаменатель (число в нижней части), поместив их в отдельные столбцы:
N D
| 24 | 36 |
Используя метод лестницы, подумайте о наименьшем простом числе, которое входит в число 24 и 36.
Когда ваш ребенок ответит «2», спросите его, сколько раз 2 входит в число , , 24 и 36.
запишите ответы на отдельных ступенях под номерами.
Вот как должны выглядеть первые две ступени лестницы:
2 | 24 | 36 |
2 | 12 | 18 |
Повторите процесс для следующих двух чисел, которые также делятся на 2:
2 | 24 | 36 |
2 | 12 | 18 |
| 6 | 9 |
Теперь у нас есть числа 6 и 9.
Когда мы начинаем с наименьшего простого числа, 2, мы замечаем, что оно равномерно переходит в 6, но не в 9. Это означает, что мы не можем его использовать. Итак, вы должны перейти к следующему простому числу.
Равномерно ли 3 входит в оба числа?
Если 6 разделить на 3, получится 2; красивое четное число. А можно разделить 9 на 3 и получить 3 простое число. Итак, мы добавим еще одну ступеньку к лестнице.
N D
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
2 3
К этому моменту вы достигли простого числа и больше не сможете добавлять ступени.
Итак, мы вернемся к исходной проблеме: как упростить дробь 24/36.
Правильный ответ находится на нижней ступени лестницы: 2/3
Легко, правда?
Поскольку мы уже проделали всю эту математику, давайте воспользуемся тем же примером, чтобы найти наибольший общий делитель и наименьшее общее кратное.
Как использовать лестничный метод для нахождения наибольшего общего делителянаибольший общий делитель (НОД) — это наибольшее число, которое делится без остатка на все сравниваемые числа.
С помощью лестничного метода легко найти НОД, потому что все, что вам нужно сделать, это посмотреть на множители каждого числа в левой части лестницы и умножить их.
Сможете ли вы найти наибольший общий делитель в приведенном ниже примере?
N D
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
2 3
Если вы ответили 12, вы правы, потому что 2 x 2 x 3 = 12.
Используйте метод лестницы, чтобы найти наименьшее общее кратное
Наименьшее общее кратное (НОК) – это наименьшее кратное, общее для двух (или более) чисел.
Чтобы начать это упражнение, мы сделаем быстрое обновление для кратных. Вы можете найти число, кратное числу , просто умножив его на другое число. Лучший способ сделать это — начать с числа 1.
Вот пример:
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
Затем мы можем перечислить кратные 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44 и т. д.
Различные числа также могут иметь общих кратных . Их можно найти, выписав кратные каждому числу и найдя общие ответы:
Кратные 4: 4, 8, 12, 16, 20 , 24, 28, 32, 36, 4 0 , 44…
Кратные 5: 5, 10, 15, 20 , 25, 30, 35, 40 , 45…
Например, числа, кратные 4 и 5, равны 20 и 40. 20.
Но как найти все кратные двух больших чисел, например 24 и 36, и быстро найти НОК?
Это один из действительно полезных способов использования метода лестницы.
Чтобы показать вам, как это сделать, мы будем использовать построенную выше лестницу с 24 и 36.
Затем вы просто перемножите все числа, образующие букву «L» в левой части лестницы.
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
| 2 | 3 |
Таким образом, НОК находится с помощью следующего уравнения: 2 x 2 x 3 x 2 x 3 = 72.
Это намного более простой способ найти решение, чем определение всех отдельных кратных этих чисел!
Как использовать метод лестницы для сложения и вычитания дробей
Предположим, ваш ребенок должен сложить дроби 1/6 и 3/8.
Прежде чем вы сможете складывать или вычитать дроби, вы должны помнить, что знаменатели должны быть одинаковыми. Мы можем сделать это, создав лестницу из двух столбцов для знаменателей, как таковую:
D D
| 6 | 8 |
Повторим процесс лестничного метода, чтобы найти наименьшее простое число, которое без остатка делится на оба.
В данном случае это 2.
D D
2 | 6 | 8 |
Сколько раз 2 входит и в 6, и в 8?
D D
2 | 6 | 8 |
| 3 | 4 |
Глядя на следующую ступеньку, входит ли 2 и в 3, и в 4?
Нет.
А 3? Опять же, нет.
Так как мы не можем найти больше простых множителей, у нас остаются 3 и 4. Поскольку эти числа не совпадают, мы можем найти НОК, чтобы убедиться, что обе дроби имеют одинаковый знаменатель.
Давайте найдем НОК, снова перемножив все числа в «Г-образной форме»:
D D
2 | 6 | 8 |
3 4
Умножьте 2 x 3 x 4, и вы получите 24.
Это число является наименьшим общим кратным между нашими двумя знаменателями. Это означает, что все, что нам нужно сделать, это заставить обе дроби иметь 24 в качестве их общего нижнего числа.
К счастью, у нас уже есть числа, которые помогут нам в этом.
Мы возьмем исходные дроби и умножим их на числа, находящиеся на нижней ступени нашей лестницы, в данном случае на 3 и 4. В результате обе дроби должны иметь НОК в качестве знаменателя.
Вот как мы это сделали:
1 x (4) + 3 x (3) = 4 + 9
6 x (4) 8 x (3) 24 24
Теперь, когда знаменатели совпадают, мы можем сложить числители. Сумма становится равной 13 / 24.
Как использовать лестничный метод для разложения выражений на множители
Давайте посмотрим на распределительное свойство в математике, которое говорит, что ab + ac = a(b+c ).
В нашем примере мы будем использовать уравнение 18 + 24 = 42. Чтобы продемонстрировать свойство распределения, давайте поместим эти два числа в ступеньку лестницы:
| 18 | 24 |
Следуйте изученному процессу для определения простых чисел и построения ступенек лестницы:
2 | 18 | 24 |
3 | 9 | 12 |
| 3 | 4 |
Теперь можно заполнить уравнение a(b+c), используя числа в нашей лестнице.
2 | 18 | 24 |
3 | 9 | 12 |
| 3 | 4 |
Мы умножим внешние левые числа, чтобы получить «а».
Затем мы будем использовать нижнюю ступень лестницы для чисел в скобках (b+c).
Уравнение должно выглядеть так: a(b+c) = 6(3 + 4)
Но можем ли мы проверить это просто для уверенности? Абсолютно!
Вы можете использовать свойство распределения, чтобы распределить (или умножить) 6 по отдельности на 3 и 4 в скобках:
a(b+c) = 6(3 + 4)
6 x 3 = 18
6 x 4 = 24
18 + 24 = 42.
Или вы можете пойти другим путем и добавить в круглых скобках (3+4), что равняется 7, а затем умножьте это на 6, чтобы получить 42.
В любом случае, получилось!
А как насчет более сложных выражений с такими переменными, как 42x – 56?
Сделайте глубокий вдох и просто используйте тот же метод, который мы практиковали. Начните с верхней ступени лестницы:
| 42x | 56 |
Затем найдите наименьшее простое число, на которое делится каждое число.
В данном случае 2:
2 | 42x | 56 |
| 21x | 28 |
И продолжайте. Наибольшее простое число, на которое эти два числа будут делиться, равно 7.
2 | 42x | 56 |
7 | 21x | 28 |
| 3x | 4 |
Как и в предыдущем примере, мы будем использовать числа в нашей лестнице для заполнения выражения.
Умножьте внешние числа (2 x 7 = 14) и сначала добавьте произведение к вашему выражению.
Затем используйте числа из нижней ступени, чтобы заполнить оставшуюся часть выражения.
2 | 42x | 56 |
7 | 21x | 28 |
| 3x | 4 |
Таким образом, наше исходное выражение 42x – 56 теперь выражается как 14 (3x – 4).
Видишь? В следующий раз, когда ваш ребенок принесет домой математическую задачу, в которой используется метод лестницы, теперь вы можете с уверенностью помочь ему.
Однако, если у вас нет времени, чтобы просмотреть все ответы, работа с онлайн-репетитором по математике может помочь вашему ребенку укрепить свои знания и освоить методы, необходимые для достижения успеха.
Начните работу с Thinkster Math Tutor сегодня, получите доступ к тысячам цифровых математических листов и начните укреплять уверенность своего ребенка прямо сейчас.
Если вы можете изучить совершенно новый метод, подобный этому, всего за одну запись в блоге, представьте, насколько ваш ребенок преуспеет, если в его команде будет специальный онлайн-репетитор Thinkster.
Как дети могут достичь своих целей с помощью лестницы
- Фейсбук37
- Твиттер
Последнее обновление 22 мая 2019 г.
Каждый родитель хочет для своего ребенка самого лучшего.
Поэтому, когда они молоды, вы ставите перед ними цели и помогаете им достичь этих целей. Но в конечном итоге каждый ребенок должен начать ставить свои собственные цели и выяснять, как их достичь.
Но им не обязательно действовать в одиночку. Вместо этого они могут использовать лестницу целей (и небольшое руководство), чтобы начать достигать своих собственных целей! Если у вашего ребенка есть цели, которые он хочет достичь, но не может этого сделать, вот Как дети могут достичь своих целей с помощью лестницы ворот ! Лестницу целей для печати можно найти в конце этого поста!
Прежде чем мы перейдем к тому, как дети могут достичь своих целей с помощью лестницы целей, давайте поговорим о том, что такое лестница целей на самом деле. Лестница целей — это метафорическая лестница и визуальный инструмент. Это способ структурирования шагов к успеху.
Печатная лестница для детей, которую я создал, состоит всего из 5 ступеней. Это делается для того, чтобы упростить задачу и не перегружать детей слишком большим количеством микрошагов.
Каждый шаг должен быть выполнен для достижения вершины (достижения цели). Нижние ступени должны быть завершены, прежде чем переходить к более высоким ступеням, точно так же, как вы не можете пропускать ступени при подъеме по настоящей лестнице.
Читайте: Вам также могут понравиться другие посты о домашнем обучении!
Лестница целей идеально подходит для визуалов или любого ребенка, которому было бы полезно иметь что-то осязаемое, на что можно ссылаться при работе над своими целями . Вы должны помочь своему ребенку в первый раз, когда он делает лестницу целей, просто чтобы убедиться, что шаги идут в логической последовательности.
И первая лестница, которую вы соберете, должна быть для простой цели, чтобы ваш ребенок мог увидеть, как работает лестница, за короткое время. Следующая лестница, которую они делают, может быть более сложной. Но как вы и ваш ребенок придумываете ступени для своей лестницы целей?
Достичь чего угодно: Как ставить цели для детей
Как разработать свою лестницу целей
С помощью лестницы целей легко разработать логические шаги, чтобы ваши дети могли достичь своих целей.
Вам просто нужно мыслить логически в прямом или обратном направлении.
Если вы думаете о будущем, вы проектируете лестницу снизу вверх. Это может быть самый простой способ спроектировать лестницы для простых целей, так как легко придумать их первые шаги. Это также хорошая техника для детей, которые умеют собирать идеи из маленьких частей, чтобы составить окончательное целое.
Жизненные навыки для детей: подготовка ребенка к жизни в реальном миреЖизненные навыки: 100 вещей, которые должен знать каждый ребенок перед выходом из дома
Давайте рассмотрим пример, чтобы вы поняли, о чем я говорю. Допустим, ваш ребенок хочет научиться кататься на велосипеде, но никогда раньше этого не делал, даже с тренировочными колесами.
Для ребенка, который так плохо знаком с ездой на велосипеде, первым шагом, вероятно, должно быть, чтобы он даже не прикасался к велосипеду, а вместо этого видел, как кто-то еще (мама, папа, брат или сестра, может быть, даже человек в видео) катается байк.
Таким образом, шаг № 1 должен состоять в том, чтобы посмотреть, как кто-то едет на велосипеде. Как только ребенок увидит, как делается езда на велосипеде, он готов сесть на велосипед. Но было бы лучше, если бы они сначала научились балансировать, двигаться и ездить на велосипеде.
Таким образом, шаг № 2 должен состоять в том, чтобы мчаться и скользить на велосипеде со снятыми педалями (чтобы они использовали свои ноги для движения). После того, как они двигаются по инерции (ноги отрываются от земли) с хорошим балансом, они могут перейти к шагу № 3 — кататься на велосипеде с тренировочными колесами. Это научит вашего ребенка крутить педали.
Шаг № 4 должен состоять в том, чтобы ездить на велосипеде без тренировочных колес, но с держащимся родителем, на случай, если у него возникнут проблемы с балансировкой и вращением педалей одновременно. Шаг № 5 должен состоять в том, чтобы попрактиковаться в езде на велосипеде полностью самостоятельно.
Видите, как каждый шаг строится на предыдущем? Дети могут достигать своих целей с помощью лестницы целей из-за постепенного наращивания.
Логическая последовательность шагов снижает вероятность неудачи.
В технике обратного мышления шаги были бы такими же, но вы придумали бы их в противоположном направлении. Обратная техника лучше всего подходит для детей, которые хорошо разбирают идеи.
Также хорошо, если у вашего ребенка есть сложная цель, где сложно прописать первые шаги, но легко продумать последние.
Достижение целей обучения с помощью игры: обучение детей младшего возраста с особыми потребностями (международные проблемы раннего вмешательства) Сегодня я катался на велосипеде самостоятельно без тренировочных колес, что я, наверное, делал вчера?»
Ответ: возможно, вы занимались верховой ездой самостоятельно (шаг № 5). Затем вы говорите себе: «Ну, что я сделал, чтобы дойти до того, что смог практиковать самостоятельно?» Ответ: вы тренировались с родителем (шаг № 4).
«И до того, как родитель помог мне с этим велосипедом без тренировочных колес, что я тогда делал?» Вы тренировались с тренировочными колесами (шаг №3).
«Но как я чувствовал себя достаточно комфортно, чтобы ездить на тренировочных колесах?» Вы ехали на велосипеде без педалей (шаг 2). «И как я вообще понял общую идею езды на велосипеде?» Вы наблюдали, как кто-то еще катается на велосипеде (шаг № 1).
В конце концов, вы получите одинаковые результаты при использовании любой техники. Техника мышления назад может потребовать более критического мышления, чем техника мышления вперед, но, как уже упоминалось, может лучше соответствовать некоторым целям.
Чего ты действительно хочешь?: Как поставить цель и идти к ней! Руководство для подростков
Это отличная идея — научить своих детей тому, как достигать своих целей с помощью лестницы целей в раннем возрасте. Если вы используете дополнительную учебную программу Skill Trek для обучения своих детей важным жизненным навыкам, они могут захотеть использовать свою лестницу целей, чтобы помочь им работать с различными целями, которые ставит перед ними учебная программа.
