Корреляция | это… Что такое Корреляция?
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции (или )[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
Содержание
|
Корреляция и взаимосвязь величин
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи.
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи.
Показатели корреляции
Параметрические показатели корреляции
Ковариация
Основные статьи: Ковариация, Неравенство Коши — Буняковского
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент).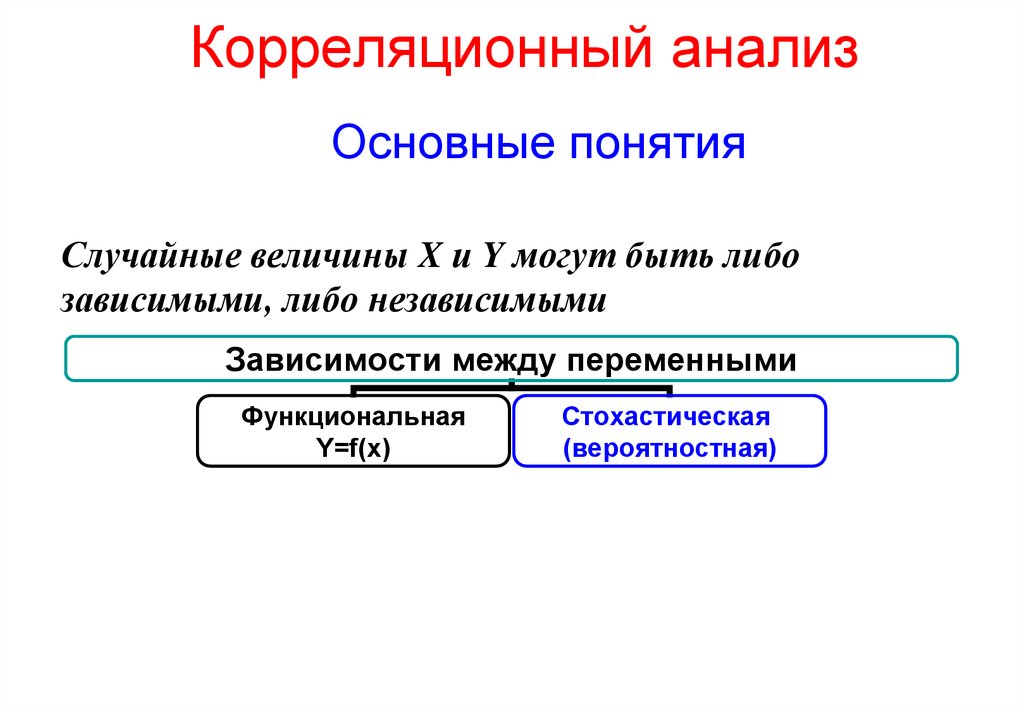 Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
- Ковариация двух независимых случайных величин и равна нулю[8].
Доказательство
Так как и — независимые случайные величины, то и их отклонения и также независимы. Пользуясь тем, что математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей, а математическое ожидание отклонения равно нулю, имеем
- Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий: [9].
Доказательство
Введём в рассмотрение случайную величину (где — среднеквадратическое отклонение) и найдём её дисперсию . Выполнив выкладки получим:
Выполнив выкладки получим:
Любая дисперсия неотрицательна, поэтому
Отсюда
Введя случайную величину , аналогично
Объединив полученные неравенства имеем
Или
Итак,
- Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа
Линейный коэффициент корреляции
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
где , — среднее значение выборок.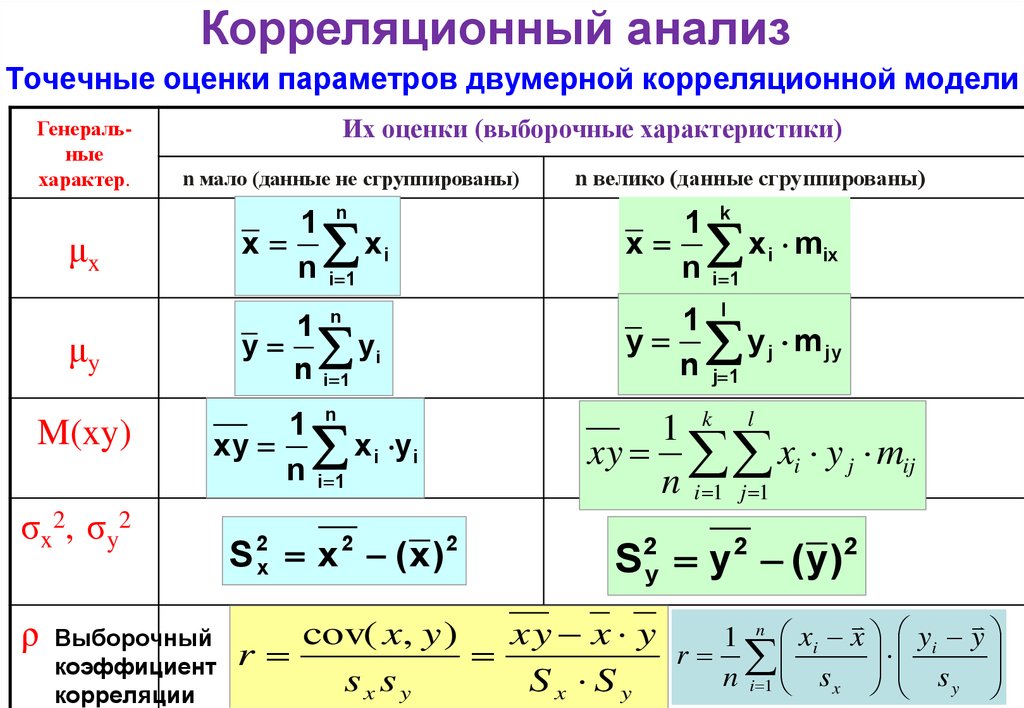
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы[11].
Доказательство
Разделив обе части двойного неравенства на получим
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где — коэффициент регрессии, — среднеквадратическое отклонение соответствующего факторного признака
[12].Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Непараметрические показатели корреляции
Коэффициент ранговой корреляции Кендалла
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где .
— суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
— суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
— число связанных рангов в ряду X и Y соответственно.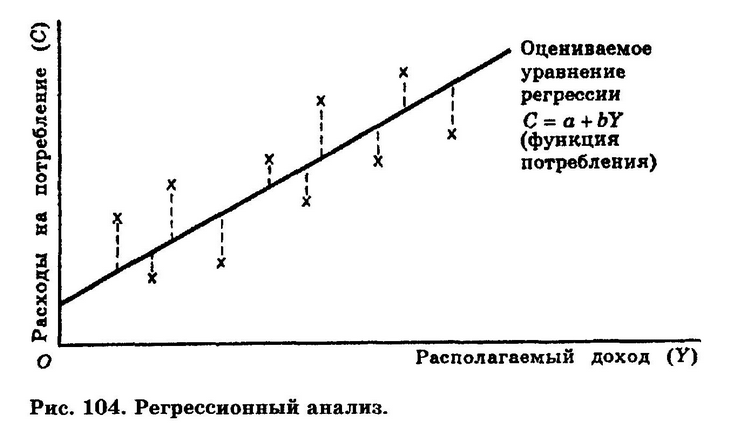
Коэффициент ранговой корреляции Спирмена
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности и вычисляется коэффициент корреляции Спирмена:
Коэффициент корреляции знаков Фехнера
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
Коэффициент множественной ранговой корреляции (конкордации)
— число групп, которые ранжируются.
— число переменных.
— ранг -фактора у -единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Свойства коэффициента корреляции
- Неравенство Коши — Буняковского:
- если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
- .

- Коэффициент корреляции равен тогда и только тогда, когда и линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
- ,
- где . Более того в этом случае знаки и совпадают:
- .
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и . Подсчитаем дисперсию случайной величины :
Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде
Поскольку всегда можно выбрать числа a и b так, чтобы (например, если , то берём произвольное a и ), то при этих a и b дисперсия , и значит почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на , и Y — на .
- Если независимые случайные величины, то . Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Ограничения корреляционного анализа
Множество корреляционных полей. Распределения значений (x,
 Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.
Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.- Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию не менее, чем в 10 раз превышающую количество факторов). В случае, если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний. [13]
- Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае, если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.
 [14].
[14]. - Исходная совокупность значений должна быть качественно однородной.[13]
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Корреляция — взаимосвязь признаков (может быть положительной или отрицательной). Обусловлена сцеплением генов или плейотропией[15]
См. также
- Автокорреляционная функция
- Взаимнокорреляционная функция
- Ковариация
- Коэффициент детерминации
Примечания
- ↑ 1 2 3 Шмойлова, 2002, с. 272
- ↑ 1 2 Елисеева, Юзбашев, 2002, с. 232
- ↑ Елисеева, Юзбашев, 2002, с. 228
- ↑ Елисеева, Юзбашев, 2002, с. 228-229
- ↑ 1 2 Елисеева, Юзбашев, 2002, с. 229
- ↑ Суслов, Ибрагимов, Талышева, Цыплаков, 2005, с. 141
- ↑ Гмурман, 2004, с. 176-177
- ↑ 1 2 3 Гмурман, 2004, с. 177
- ↑ Гмурман, 2004, с.
 178-179
178-179 - ↑ Шмойлова, 2002, с. 300
- ↑ Гмурман, 2004, с. 179
- ↑ Шмойлова, 2002, с. 301
- ↑ 1 2 Елисеева, Юзбашев, 2002, с. 230
- ↑ Шмойлова, 2002, с. 275
- ↑ Самигуллина Н. С. Практикум по селекции и сортоведению плодовых и ягодных культур: Учебное издание. — Мичуринск: Мичуринский государственный аграрный университет, 2006. — 197 с.
Литература
- Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6
- Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9
- Общая теория статистики: Учебник / Под ред. Р.А. Шмойловой. — 3-е издание, переработанное.
 — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8
— Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8 - Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8
Ссылки
- Калькулятор для расчета коэффициента корреляции по Пирсону
- Границы значений коэффициента корреляции
- Иллюстрация: зависимые случайные величины с нулевой корреляцией
Корреляционный анализ
Иллюстрированный самоучитель по SPSS > Корреляционный анализ | ||||||||||||||||||||||||||||||||||
Глава 15. Корреляционный анализ
Корреляция — связь между двумя переменными. Расчёты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок. Если в качестве примера возьмём данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav), то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц. Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным.
Каждая пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» (Scatterplot) для двух зависимых переменных можно построить путём вызова меню
Graphs… (Графики) / Scatter plots. Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц. Статистика говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции. Этот коэффициент, всегда обозначаемый латинской буквой r, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой. Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные:
Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. | ||||||||||||||||||||||||||||||||||
Корреляционные исследования
Корреляционные исследования перейти к содержанию+13236381128
+1519
+61480040096
Book a Demo
TRY A SAMPLE SURVEY
+13236381128
+1519
+61480040096
- Book demo
- Watch demo
- Pricing
- Contact
- Наши клиенты
- Истории клиентов
- Информационные бюллетени
- Ресурсы
Узнайте все о корреляционных исследованиях с определениями корреляционных исследований, примерами корреляционных исследований и методами корреляционных исследований.
Начните свои корреляционные исследования с Voxco
ПОДЕЛИТЕСЬ СТАТЬЕЙ ПО
Содержание
Что такое корреляционные исследования?
Согласно определению корреляционного исследования, корреляционное исследование относится к вид неэкспериментального метода исследования , который изучает взаимосвязь между двумя переменными с помощью статистического анализа.
Корреляционный план исследования не изучает влияние посторонних переменных на изучаемые переменные.
Что касается исследования рынка, то корреляционное исследование обычно используется для изучения количественных данных и определения того, существуют ли какие-либо закономерности, тенденции или идеи между поведением потребителей и рыночными переменными, такими как; реклама, скидки, а также скидки на товары.
Для чего используются корреляционные исследования
План корреляционных исследований полезен для всех видов наборов количественных данных, но обычно он используется в маркетинговых исследованиях. Исследователи рынка считают полезным использовать корреляционный дизайн с опросами по оценке усилий клиентов и их связью с продажами; Опыт клиентов (CX) и его связь с лояльностью клиентов, а также опросы Net Promoter Score и его связь с имиджем бренда или управлением.
Исследователи рынка считают полезным использовать корреляционный дизайн с опросами по оценке усилий клиентов и их связью с продажами; Опыт клиентов (CX) и его связь с лояльностью клиентов, а также опросы Net Promoter Score и его связь с имиджем бренда или управлением.
Эти опросы включают в себя множество актуальных вопросов, которые делают их идеальными для изучения при разработке корреляционных исследований. В исследованиях рынка корреляционные методы помогают выделить переменные и увидеть, как они взаимодействуют друг с другом.
Читайте также: Что такое описательное исследование?
Хотите узнать, сколько будет стоить проведение опроса с использованием Voxco?
Что такое коэффициент корреляции?
Коэффициент корреляции описывает силу и взаимосвязь между переменными.
Это статистическая мера. Существует несколько типов коэффициентов корреляции, наиболее популярным из которых является коэффициент корреляции Пирсона.
Коэффициент корреляции находится в диапазоне от -1 до +1. Коэффициент корреляции +1 указывает на полную положительную корреляцию, тогда как коэффициент корреляции -1 указывает на полную отрицательную корреляцию между двумя переменными. Коэффициент корреляции, равный 0, указывает на отсутствие связи между изучаемыми переменными.
Примеры корреляционного исследования
Вот пример корреляционного исследования:
Рассмотрим гипотетическое исследование гипертонии и удовлетворенности браком, в котором исследователь стремится изучить взаимосвязь между болезнью (гипертонией) и удовлетворенностью браком. Если исследователь обнаружит отрицательную корреляцию между этими двумя переменными, указывающую на то, что по мере увеличения удовлетворенности браком опыт гипертонии уменьшается.
Однако это не означает, что неудовлетворенность в браке вызывает гипертонию, это просто подчеркивает связь между ними. В корреляционном дизайне исследования ни одна из изучаемых переменных не подвергается манипулированию или изменению. Они просто измеряются, и связи между ними наблюдают или изучают.
Они просто измеряются, и связи между ними наблюдают или изучают.
Например, вы хотите понять, существует ли зависимость между вашими доходами и расходами.
Вы можете провести корреляционное исследование, чтобы увидеть, существует ли какая-либо связь между ними.
Если вы обнаружите положительную корреляцию, это означает, что по мере увеличения суммы заработка увеличиваются и расходы.
Давайте рассмотрим еще один пример корреляционного исследования.
Диетолог может выяснить, существует ли связь между вегетарианством и здоровым телом. Диетолог проводит исследование группы людей с разным питанием (веганов, невегетарианцев и вегетарианцев). Затем диетолог статистически анализирует результат, чтобы определить, являются ли люди с вегетарианской диетой более здоровыми, чем другие.
Каковы характеристики корреляционного исследования?
Чтобы лучше понять это, давайте рассмотрим некоторые из важнейших характеристик корреляционного исследования, а именно:
1.
 Это неэкспериментальный метод
Это неэкспериментальный методКорреляционное исследование — это неэкспериментальный метод. Это указывает на то, что исследователям не нужно использовать формальную технику для изменения факторов при согласии или оспаривании такой концепции. Исследователь просто анализирует и исследует взаимосвязь между переменными, никак не изменяя и не модифицируя их.
2. Это ретроспективное исследование
Корреляционное исследование, которое стремится только оглянуться назад на историческую информацию и наблюдать за прошлым. Он используется учеными для оценки и выявления долгосрочных тенденций среди двух факторов. Корреляционный анализ может выявить выгодную связь между переменными, но эта связь может измениться в ближайшие годы.
3. Он динамичен
Результаты корреляционного исследования, включающие 2 фактора, которые никогда не бывают статичными и постоянно развиваются. По разным причинам два параметра с отрицательной корреляцией в прошлом вполне могут иметь положительную корреляционную связь в будущем.
Теперь, когда мы изучили его характеристики, давайте перейдем к пониманию различных существующих типов корреляционных исследований.
Читайте также: Методы выборки
См. аналитическую платформу Voxco в действии
Какие существуют типы результатов корреляционного исследования?
Обычно существует три типа корреляционных исследований:
- Положительная корреляция
- Отрицательная корреляция
- Нулевая корреляция
Положительная корреляция
Положительная корреляция указывает на наличие положительной связи между двумя переменными. В этом виде отношений, когда одна переменная увеличивается, другая переменная также увеличивается. Например, количество автомобилей, которыми владеет человек, положительно коррелирует с его доходом. Больше доход, больше количество автомобилей.
Отрицательная корреляция
Отрицательная корреляция указывает на наличие отрицательной связи между двумя переменными. В этом виде корреляции, когда одна переменная увеличивается, другая переменная уменьшается. Например, существует отрицательная связь между уровнем стресса и удовлетворенностью жизнью. Это указывает на то, что по мере увеличения уровня стресса удовлетворенность жизнью снижается.
В этом виде корреляции, когда одна переменная увеличивается, другая переменная уменьшается. Например, существует отрицательная связь между уровнем стресса и удовлетворенностью жизнью. Это указывает на то, что по мере увеличения уровня стресса удовлетворенность жизнью снижается.
Нулевая корреляция
Нулевая корреляция указывает на отсутствие связи между двумя переменными. Изменение одной переменной не приводит к изменению другой переменной. Примером нулевой корреляции является связь между интеллектом и ростом. Увеличение роста не приводит к каким-либо изменениям интеллекта особи.
Какие существуют методы корреляционного исследования?
Существует два метода сбора данных в корреляционном исследовании:
- Натуристическое наблюдение
- Архивные данные
Натуралистическое наблюдение
В натуралистическом наблюдении за участниками исследования наблюдают в их естественной среде. Натуралистическое наблюдение является своего рода полевым исследованием. Исследователь может наблюдать за участниками в продуктовых магазинах, кинотеатрах, на детских площадках, в школах и т. д.
Натуралистическое наблюдение является своего рода полевым исследованием. Исследователь может наблюдать за участниками в продуктовых магазинах, кинотеатрах, на детских площадках, в школах и т. д.
Исследователи, использующие натуралистическое наблюдение как средство сбора данных, наблюдают за людьми как можно ненавязчивее. Это потому, что они не хотят, чтобы участники осознавали, что за ними наблюдают, поскольку это может повлиять на их поведение, и они могут не быть самими собой.
Например, если исследователь наблюдает за покупателями в продуктовом магазине и за предметами, которые они обычно покупают, это приемлемо с этической точки зрения, поскольку участники знают, что за ними наблюдают в общественных местах. Данные, собранные при натуралистическом наблюдении, могут быть качественными или количественными.
Архивные данные
Архивные данные — это еще один способ сбора данных для разработки корреляционных исследований. Этот тип данных был собран ранее путем проведения аналогичных исследований. Архивные данные обычно собираются в ходе первичных исследований. Архивные данные имеют тенденцию быть более простыми по сравнению с данными, собранными в ходе естественных наблюдений. В архивных данных нет места эффекту наблюдателя.
Архивные данные обычно собираются в ходе первичных исследований. Архивные данные имеют тенденцию быть более простыми по сравнению с данными, собранными в ходе естественных наблюдений. В архивных данных нет места эффекту наблюдателя.
Например, оценить среднюю степень удовлетворенности покупателей электронными продуктами определенного бренда в Америке несложно.
Читайте также: Поисковые исследования
Каковы преимущества корреляционных исследований?
Корреляционное исследование имеет ряд преимуществ:
- Планирование проведения корреляционного исследования мотивирует и вдохновляет исследователей задавать соответствующие вопросы в ходе опроса для оценки отношения клиентов.
- Корреляционный дизайн помогает исследователям определить переменные, которые имеют самые сильные взаимосвязи, и принимать лучшие решения в долгосрочной перспективе.
- Корреляционные методы также могут служить ориентиром для будущих исследований.

- Корреляционный дизайн помогает исследователям определить направление и силу взаимосвязи между различными переменными.
- Корреляционные методы легче интерпретировать, они экономичны и более применимы в повседневном принятии бизнес-решений.
Теперь давайте рассмотрим некоторые из недостатков
Исследуйте все типы вопросов опроса
возможные на Voxco
Каковы недостатки корреляционного исследования?
Несмотря на различные преимущества, у корреляционных исследований есть несколько недостатков, таких как
- Корреляционные методы не позволяют установить причинно-следственную связь. Они только дают нам информацию об ассоциации между двумя переменными.
- Корреляционный план не исключает вероятности других посторонних переменных, влияющих на основные изучаемые переменные. Например, стресс — не единственная переменная, связанная со счастьем.
 Другие переменные, такие как эмоциональный интеллект, субъективное благополучие, а также качество социальных отношений, также влияют на счастье.
Другие переменные, такие как эмоциональный интеллект, субъективное благополучие, а также качество социальных отношений, также влияют на счастье. - Корреляционные методы бесполезны, когда исследователи хотят увидеть изолированное влияние одной переменной на другую.
Заключение
Хотя корреляция не обязательно подразумевает причинно-следственную связь, причинно-следственная связь подразумевает корреляцию. Корреляционное исследование является ступенькой к более мощному экспериментальному методу и более полезно, чем может показаться, потому что некоторые из недавно разработанных комплексных корреляционных моделей допускают очень ограниченные причинно-следственные выводы.
Результаты корреляционного исследования можно использовать для определения распространенности и взаимосвязи между переменными, а также для прогнозирования событий на основе текущих данных и знаний.
Ищете лучшие инструменты для корреляционных исследований?
Подробнее
Карта пути клиента
19 июля 2021 г. Комментариев нет
Комментариев нет
Карта пути клиента Voxco доверяют более 450 мировых брендов в более чем 40 странах Узнайте, какие типы вопросов возможны, с помощью выборочного опроса! Попробуйте
Подробнее »
ResTech: бурно развивающийся метод исследования
7 декабря 2021 г. Комментариев нет
ResTech: бурно развивающийся исследовательский метод ПОДЕЛИТЬСЯ СТАТЬЕЙ В Поделиться на facebookПоделиться в TwitterПоделиться на linkedinСодержание Цифровой прогресс меняет то, как исследователи и
Подробнее »
Логическая статистика: что и как
13 сентября 2021 г. Комментариев нет
Инференциальная статистика: что и как Преобразуйте процесс получения информации Используйте наше подробное онлайн-руководство по проведению опросов, чтобы создать действенный процесс сбора отзывов. Скачать
Подробнее »
Ежедневные активные пользователи
8 марта 2022 г. Комментариев нет
Комментариев нет
Ежедневные активные пользователи ПОДЕЛИТЕСЬ СТАТЬЕЙ В Поделиться на facebook Поделиться в Twitter Поделиться на linkedin Содержание Когда мы в подписной компании,
Подробнее »
Хорошие вопросы для опроса
1 декабря 2021 г. Комментариев нет
Хорошие вопросы опроса ПОДЕЛИТЬСЯ СТАТЬЕЙ В Поделиться на facebookПоделиться в TwitterПоделиться на linkedinСодержание Опросы являются главным инструментом сбора информации.
Подробнее »
Точки взаимодействия с клиентами: что это такое, как их определить, этапы и примеры
15 июля 2021 г. Комментариев нет
Точки соприкосновения с клиентами: что это такое, как их идентифицировать, этапы и примеры Подробнее »
Отличное исследование
Быстрая аналитика
Лучшая в своем классе окупаемость инвестиций
Платформа Voxco помогает собирать многоканальные отзывы, измерять настроения, выявлять идеи и действовать в соответствии с ними.
Присоединяйтесь к
500 + клиентам по всему миру в 40+ странах Great Research
Fast Insights
Лучшая в своем классе окупаемость инвестиций
Платформа Voxco помогает собирать многоканальные отзывы, измерять настроения, находить идеи и действовать в соответствии с ними.
Присоединяйтесь к
500 + клиентам по всему миру в 40+ странахКорреляционные исследования | Когда и как использовать
Опубликован в 7 июля 2021 г. по Прита Бхандари. Отредактировано 10 октября 2022 г.
Корреляционный план исследования исследует отношения между переменными без контроля или манипулирования исследователем какой-либо из них.
Корреляция отражает силу и/или направление связи между двумя (или более) переменными. Направление корреляции может быть как положительным, так и отрицательным.
Направление корреляции может быть как положительным, так и отрицательным.
| Положительная корреляция | Обе переменные изменяются в одном направлении | С ростом роста увеличивается и вес |
|---|---|---|
| Отрицательная корреляция | Переменные изменяются в противоположных направлениях | По мере увеличения потребления кофе снижается усталость |
| Нулевая корреляция | Между переменными нет связи | Потребление кофе не связано с ростом |
Содержание
- Корреляционное и экспериментальное исследование
- Когда использовать корреляционное исследование
- Как собирать корреляционные данные
- Как анализировать корреляционные данные
- Корреляция и причинно-следственная связь
- Часто задаваемые вопросы о корреляционных исследованиях
Корреляционное и экспериментальное исследование
Как корреляционные, так и экспериментальные исследования используют количественные методы для изучения взаимосвязей между переменными. Но есть важные различия в способах сбора данных и типах выводов, которые вы можете сделать.
Но есть важные различия в способах сбора данных и типах выводов, которые вы можете сделать.
| Корреляционные исследования | Экспериментальные исследования | |
|---|---|---|
| Назначение | Используется для проверки силы связи между переменными | Используется для проверки причинно-следственных связей между переменными |
| Переменные | Переменные наблюдаются только без манипуляций или вмешательства исследователей | Производится манипулирование независимой переменной и наблюдается зависимая переменная |
| Управление | Используется ограниченный контроль, поэтому другие переменные могут играть роль в отношениях | Посторонние переменные контролируются, чтобы они не могли повлиять на интересующие вас переменные |
| Срок действия | Высокая внешняя валидность: вы можете с уверенностью обобщать свои выводы на другие группы населения или условия | Высокая внутренняя валидность: вы можете уверенно делать выводы о причинно-следственной связи |
Когда использовать корреляционное исследование
Корреляционные исследования идеально подходят для быстрого сбора данных в естественных условиях. Это поможет вам обобщить ваши выводы на реальные жизненные ситуации внешне обоснованным способом.
Это поможет вам обобщить ваши выводы на реальные жизненные ситуации внешне обоснованным способом.
Есть несколько ситуаций, когда корреляционное исследование является подходящим выбором.
Для исследования непричинных связей
Вы хотите выяснить, есть ли связь между двумя переменными, но не ожидаете найти между ними причинно-следственную связь.
Корреляционные исследования могут дать представление о сложных отношениях в реальном мире, помогая исследователям разрабатывать теории и делать прогнозы.
ПримерВы хотите знать, существует ли какая-либо связь между количеством детей у людей и политической партией, за которую они голосуют. Вы не думаете, что наличие большего количества детей заставляет людей голосовать по-разному — более вероятно, что и то, и другое зависит от других переменных, таких как возраст, религия, идеология и социально-экономический статус. Но сильная корреляция может быть полезна для прогнозирования моделей голосования.Для изучения причинно-следственных связей между переменными
Вы считаете, что между двумя переменными существует причинно-следственная связь, но проводить экспериментальные исследования, в которых манипулируют одной из переменных, нецелесообразно, неэтично или слишком дорого.
Корреляционные исследования могут предоставить первоначальные указания или дополнительную поддержку теорий о причинно-следственных связях.
ПримерВы хотите выяснить, вызывают ли выбросы парниковых газов глобальное потепление. Практически невозможно провести эксперимент, который контролировал бы глобальные выбросы с течением времени, но с помощью наблюдений и анализа вы можете показать сильную корреляцию, подтверждающую теорию.Для тестирования новых измерительных инструментов
Вы разработали новый инструмент для измерения вашей переменной, и вам нужно проверить его надежность или достоверность.
Корреляционное исследование можно использовать для оценки того, последовательно или точно ли инструмент отражает концепцию, которую он призван измерить.
Пример. Вы разрабатываете новую шкалу для измерения одиночества у маленьких детей на основе неофициальных данных во время самоизоляции. Чтобы проверить эту шкалу, вам нужно проверить, действительно ли она измеряет одиночество. Вы собираете данные об одиночестве, используя три разных измерения, включая новую шкалу, и проверяете степень корреляции между различными измерениями. Обнаружение высоких корреляций означает, что ваша шкала действительна.
Вы собираете данные об одиночестве, используя три разных измерения, включая новую шкалу, и проверяете степень корреляции между различными измерениями. Обнаружение высоких корреляций означает, что ваша шкала действительна.Как собирать корреляционные данные
В корреляционных исследованиях можно использовать множество различных методов. В социальных и поведенческих науках наиболее распространенными методами сбора данных для этого типа исследований являются опросы, наблюдения и вторичные данные.
Важно тщательно выбирать и планировать свои методы, чтобы обеспечить надежность и достоверность ваших результатов. Вы должны тщательно отобрать репрезентативную выборку, чтобы ваши данные без предвзятости отражали интересующую вас группу населения.
Опросы
При проведении опросов вы можете использовать анкеты для измерения интересующих вас переменных. Вы можете проводить опросы онлайн, по почте, по телефону или лично.
Опросы — это быстрый и гибкий способ сбора стандартизированных данных от многих участников, но важно убедиться, что ваши вопросы сформулированы беспристрастно и содержат релевантную информацию.
Натуралистическое наблюдение
Натуралистическое наблюдение — это тип полевого исследования, при котором вы собираете данные о поведении или явлении в его естественной среде.
Этот метод часто включает запись, подсчет, описание и классификацию действий и событий. Естественные наблюдения могут включать как качественные, так и количественные элементы, но для оценки корреляции вы собираете данные, которые можно анализировать количественно (например, частоты, продолжительность, масштабы и количества).
Естественные наблюдения позволяют легко обобщать полученные результаты на контексты реального мира и изучать опыт, который невозможно воспроизвести в лабораторных условиях. Но анализ данных может занять много времени и быть непредсказуемым, а предвзятость исследователя может исказить интерпретацию.
Вторичные данные
Вместо сбора исходных данных вы также можете использовать данные, которые уже были собраны для другой цели, например официальные отчеты, опросы или предыдущие исследования.
Использование вторичных данных недорого и быстро, поскольку сбор данных завершен. Однако данные могут быть ненадежными, неполными или не совсем актуальными, и вы не можете контролировать надежность или достоверность процедур сбора данных.
Пример Чтобы выяснить, связано ли рабочее время с психическим здоровьем, вы используете официальную национальную статистику и научные исследования из нескольких разных стран, чтобы объединить данные о среднем рабочем времени и показателях психических заболеваний. Вы статистически анализируете данные, чтобы увидеть, имеют ли страны, которые работают меньше часов, лучшие результаты в области психического здоровья.
Вы статистически анализируете данные, чтобы увидеть, имеют ли страны, которые работают меньше часов, лучшие результаты в области психического здоровья.Как анализировать корреляционные данные
После сбора данных вы можете статистически проанализировать взаимосвязь между переменными с помощью корреляционного или регрессионного анализа или того и другого. Вы также можете визуализировать отношения между переменными с помощью диаграммы рассеяния.
Различные типы коэффициентов корреляции и регрессионного анализа подходят для ваших данных в зависимости от их уровня измерения и распределения.
Корреляционный анализ
Используя корреляционный анализ, вы можете обобщить взаимосвязь между переменными в коэффициент корреляции : одно число, описывающее силу и направление взаимосвязи между переменными. С помощью этого числа вы будете количественно определять степень взаимосвязи между переменными.
Коэффициент корреляции «продукт-момент» Пирсона, также известный как r Пирсона, обычно используется для оценки линейной зависимости между двумя количественными переменными.
Коэффициенты корреляции обычно находятся для двух переменных одновременно, но вы можете использовать множественный коэффициент корреляции для трех или более переменных.
Регрессионный анализ
С помощью регрессионного анализа можно предсказать, насколько изменение одной переменной будет связано с изменением другой переменной. Результатом является уравнение регрессии , которое описывает линию на графике ваших переменных.
Это уравнение можно использовать для прогнозирования значения одной переменной на основе заданного значения (значений) другой переменной (переменных). Лучше всего выполнить регрессионный анализ после проверки корреляции между вашими переменными.
Корреляция и причинно-следственная связь
Важно помнить, что корреляция не подразумевает причинно-следственную связь. Тот факт, что вы нашли корреляцию между двумя вещами, не означает, что вы можете заключить, что одна из них вызывает другую по нескольким причинам.
Проблема направленности
Если две переменные коррелированы, это может быть связано с тем, что одна из них является причиной, а другая следствием. Но корреляционный дизайн исследования не позволяет сделать вывод, что есть что. Из соображений предосторожности исследователи не делают выводов о причинно-следственных связях на основе корреляционных исследований.
Пример. Вы обнаружили положительную корреляцию между уровнем витамина D и депрессией: люди с низким уровнем витамина D более склонны к депрессии. Но вы не можете быть уверены в том, что низкий уровень витамина D вызывает депрессию, или депрессия вызывает снижение потребления витамина D из-за изменения образа жизни или аппетита. Таким образом, вы можете только заключить, что существует связь между этими двумя переменными.Проблема с третьей переменной
Вмешивающаяся переменная — это третья переменная, которая влияет на другие переменные, заставляя их казаться причинно связанными, хотя на самом деле это не так. Вместо этого существуют отдельные причинно-следственные связи между вмешивающимся фактором и каждой переменной.
Вместо этого существуют отдельные причинно-следственные связи между вмешивающимся фактором и каждой переменной.
В корреляционных исследованиях контроль над посторонними переменными ограничен или отсутствует. Даже если вы статистически контролируете некоторые потенциальные искажающие факторы, все равно могут быть другие скрытые переменные, которые маскируют взаимосвязь между переменными вашего исследования.
Пример. Вы обнаружили сильную положительную корреляцию между рабочим временем и стрессом, связанным с работой: люди с меньшим рабочим временем сообщают о более низком уровне стресса, связанного с работой. Однако это не доказывает, что сокращение продолжительности рабочего дня приводит к снижению стресса. Есть много других переменных, которые могут влиять на обе переменные, такие как средний доход, условия труда и ненадежность работы. Вы можете статистически контролировать эти переменные, но вы не можете с уверенностью сказать, что меньшее рабочее время снижает стресс, потому что другие переменные могут усложнить взаимосвязь.
Хотя корреляционное исследование не может продемонстрировать причинно-следственную связь само по себе, оно может помочь вам разработать причинно-следственную гипотезу, проверенную в контролируемых экспериментах.
Часто задаваемые вопросы о корреляционных исследованиях
- Что такое корреляция?
Корреляция отражает силу и/или направление связи между двумя или более переменными.
- Положительная корреляция означает, что обе переменные изменяются в одном направлении.
- Отрицательная корреляция означает, что переменные изменяются в противоположных направлениях.
- нулевая корреляция означает отсутствие связи между переменными.

- В чем разница между корреляционным и экспериментальным исследованием?
Контролируемые эксперименты устанавливают причинно-следственную связь, тогда как корреляционные исследования показывают только связи между переменными.
- В экспериментальном плане вы манипулируете независимой переменной и измеряете ее влияние на зависимую переменную. Другие переменные контролируются, поэтому они не могут повлиять на результаты.
- В корреляционном плане вы измеряете переменные, не манипулируя ни одной из них. Вы можете проверить, изменяются ли ваши переменные вместе, но вы не можете быть уверены, что одна переменная вызвала изменение другой.
В целом корреляционное исследование имеет высокую внешнюю достоверность, в то время как экспериментальное исследование имеет высокую внутреннюю достоверность.

Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Бхандари, П. (2022, 10 октября). Корреляционные исследования | Когда и как использовать. Скриббр. Проверено 31 октября 2022 г., с https://www.scribbr.com/methodology/correlational-research/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса.

 1 Параметрические показатели корреляции
1 Параметрические показатели корреляции
 [14].
[14]. 178-179
178-179 — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8
— Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8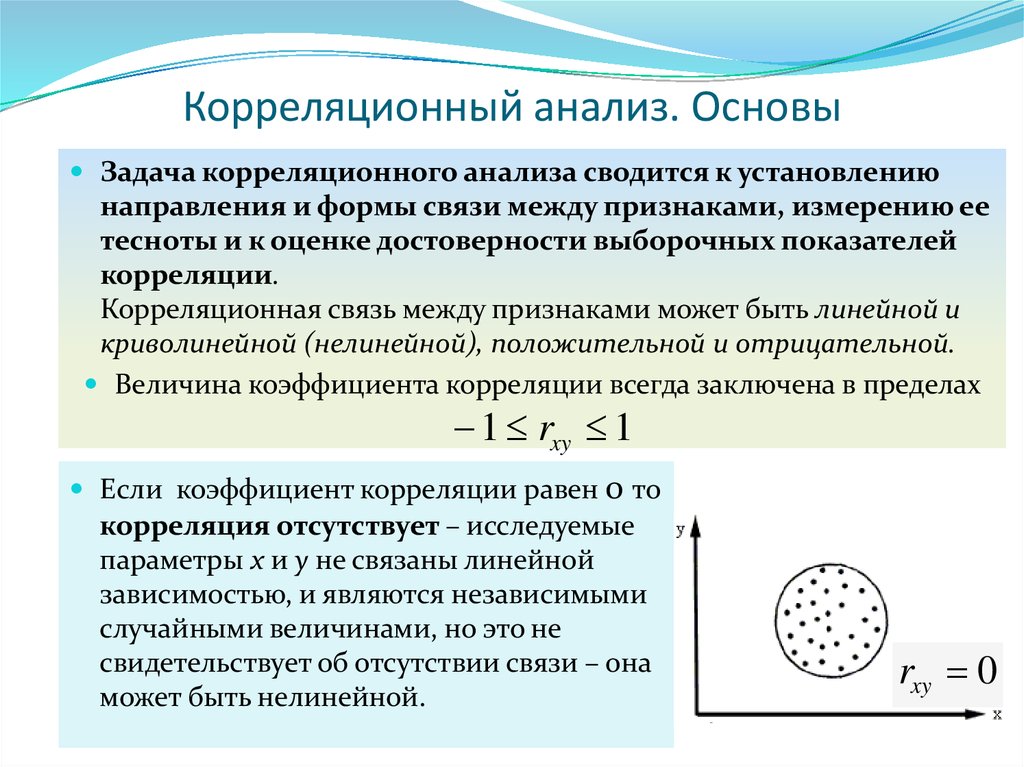 5. Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))
5. Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))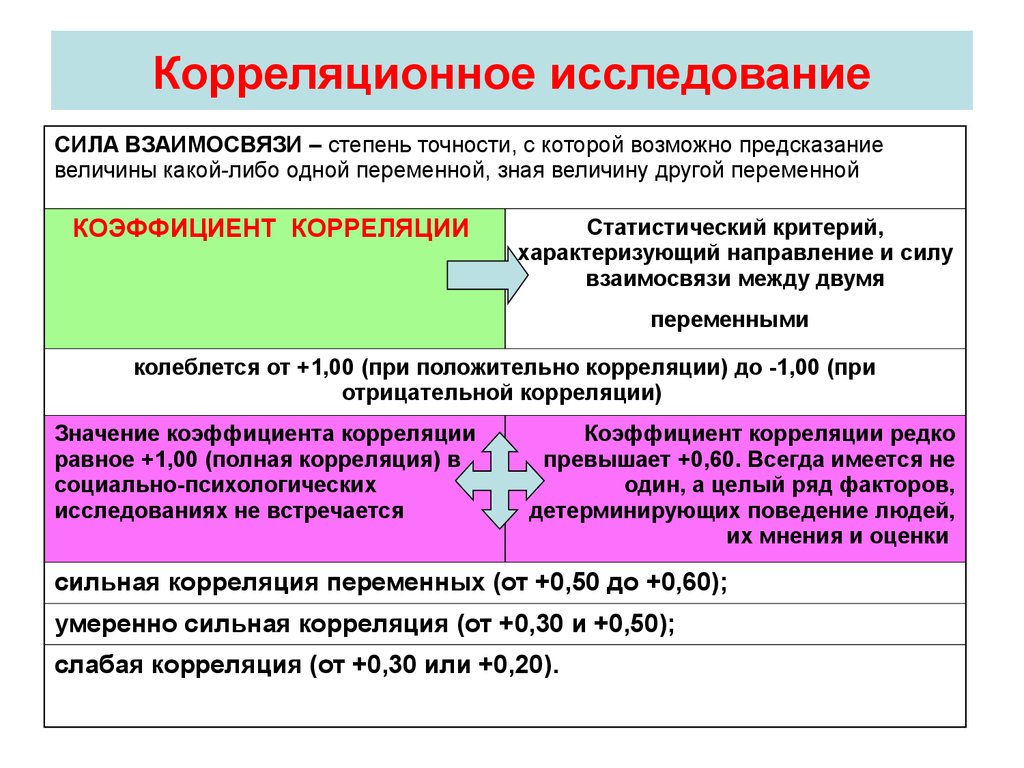 .. (Диаграммы рассеяния) (см. гл. 22.8).
.. (Диаграммы рассеяния) (см. гл. 22.8).
 В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.
В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.
 Другие переменные, такие как эмоциональный интеллект, субъективное благополучие, а также качество социальных отношений, также влияют на счастье.
Другие переменные, такие как эмоциональный интеллект, субъективное благополучие, а также качество социальных отношений, также влияют на счастье.