Методика «Лесенка» для младших школьников
Если рассматривать диагностические методики, применяемые школьным психологом, можно отметить что они различаются между собой не только по направлению исследования, но и по возрастам. Такое разделение связано с уровнем развития, на котором находится тот или иной ребенок. Например, многие задания и вопросы, которые смело можно давать подростку, окажутся сложными и непонятными младшему школьнику. Методики диагностики младших школьников отличаются простотой выполнения заданий и своей наглядностью. Очень часто при работе с младшими школьниками используются проективные методики, как нельзя лучше иллюстрирующие внутренний мир и состояние ребенка.
Одним из важнейших факторов, которые в обязательном порядке отслеживает школьный психолог, является самооценка. Очень важно вовремя выявить и при необходимости скорректировать уровень самооценки ребенка.
На этапе обучения в младшей школе ведущей деятельностью ребенка психологи называют учебную. Формирование того или иного уровня самооценки у маленьких школьников во многом зависит от того, насколько успешны они в обучении и насколько налажен контакт с учителем, являющимся в это время значимым человеком.
Формирование того или иного уровня самооценки у маленьких школьников во многом зависит от того, насколько успешны они в обучении и насколько налажен контакт с учителем, являющимся в это время значимым человеком.
Одной из наиболее популярных методик исследования уровня самооценки младших школьников является методика «Лесенка», позволяющая оперативно проводить исследования, и быстро получать результаты.
Этапы проведения методики «Лесенка»
Диагностическая методика «Лесенка» может проводиться как на группе младших школьников, так и индивидуально с каждым.
Методика «Лесенка» для младших школьников проводится следующим образом:
- Деткам демонстрируется рисунок с изображением лесенки, имеющей семь ступеней;
- Психолог или классный руководитель дает следующую инструкцию: «Давайте представим, что на эту лесенку можно посадить всех-всех деток. На три ступеньки сверху сядут хорошие детки («хорошие», «очень хорошие» и «самые хорошие»).
 Три нижние ступеньки для плохих детей. Среднюю ступеньку оставим для детей, которых нельзя назвать ни плохими, ни хорошими. Возьмите карандашик и отметьте на листочке, на какую бы ступеньку вы посадили бы себя. Объясните почему?»
Три нижние ступеньки для плохих детей. Среднюю ступеньку оставим для детей, которых нельзя назвать ни плохими, ни хорошими. Возьмите карандашик и отметьте на листочке, на какую бы ступеньку вы посадили бы себя. Объясните почему?» - Дополнительно ребенку задается вопрос о том, хочет ли он быть таким, каким отметил себя в ответе. Можно также спросить о том, каким бы ему хотелось быть, и на какую ступеньку посадили бы его близкие, например, мама.
- Высказывается благодарность детям за проделанную работу.
Проводя исследование, нужно обращать особое внимание на то, как ребенок отвечает: сомневается или отвечает сразу, приводит аргументы в пользу своего выбора или просто отвечает по желанию.
Результаты методики «Лесенка»
Методика исследования самооценки «Лесенка» довольно проста в обработке. Анализ результатов производится на основании той ступеньки, которую выбрал для себя ребенок. Именно этот выбор говорит о самооценке.
Первую ступеньку выбирают детки с завышенной самооценкой. Чаще всего такие показатели демонстрируют первоклассники, поскольку для них такой результат находится в пределах нормы. Мотивация для выбора первой ступеньки может быть самой разной и ее непременно нужно принимать во внимание.
Детки, поставившие себя на вторую и третью ступеньку, имеют адекватную самооценку. Такие дети имеют положительное самоотношение и умеют давать оценку себе и своей деятельности.
Выбор четвертой ступеньки свидетельствует о заниженной самооценке и наличии определенной психологической проблемы, требующей проработки. Пояснения ученика могут пролить свет на причины такой оценки себе и своим действиям.
На пятую и шестую ступеньки ставят себя детки с низкой самооценкой. При анализе таких ответов также необходимо учитывать пояснение ребенка. Такая самооценка может быть ситуативной (обусловленной неким конкретным событием) или же быть постоянной. В последнем случае потребуется коррекция, так как данный уровень самооценки может накладывать отпечаток на всю дальнейшую жизнь.
Седьмая ступенька говорит о резко сниженной самооценке и дезадаптации. В этом случае требуется неотложная психологическая помощь, выяснение причины такого состояния, а в крайнем случае – вмешательство социальных служб.
Методика «Лесенка» для младших школьников – это простой в использовании, но достаточно информативный инструмент практикующего психолога в школе.
Бланк методики «Лесенка для детей» (в.В. Ткачева)
Первая инструкция:
Перед тобой лесенка. На ее верхней ступеньке нахо-1шься ты. Расставь на ступеньках лестницы членов твоей семьи и близких тебе людей, отвечая на вопрос: С кем тебе чаще приходится общаться?
Вторая инструкция:
Действуя тем же способом, определи, кто лучше к тебе относится, и кто больше тебя ценит?
Методика «Два дома» {и. Вандвик, п. Экблад)
Эта
методика используется для изучения
общения ребенка с членами своей семьи (Марцинковская, 1997). С ее помощью удается определить
особенности взаимоотношений близких
людей с ребенком и узнать, как он оценивает
эти отношения. В качестве бланка методики
может быть использован стандартный
вариант (см. следующую страницу), или
же предварительно подготовленный
рисунок. Вверху альбомного листа
помещается многоэтажный дом, нарисованный
простым карандашом. Внизу располагаются
два других дома: один большой и красивый,
в виде коттеджа, выполненный в красном
цвете, а другой — поменьше, обычный,
нарисованный простым карандашом.
С ее помощью удается определить
особенности взаимоотношений близких
людей с ребенком и узнать, как он оценивает
эти отношения. В качестве бланка методики
может быть использован стандартный
вариант (см. следующую страницу), или
же предварительно подготовленный
рисунок. Вверху альбомного листа
помещается многоэтажный дом, нарисованный
простым карандашом. Внизу располагаются
два других дома: один большой и красивый,
в виде коттеджа, выполненный в красном
цвете, а другой — поменьше, обычный,
нарисованный простым карандашом.
В начале с ребенком беседуют и выясняют состав семьи. Затем показывают рисунок и просят переселить своих близких из многоэтажного дома в новый дом, расположенный в нижней части листа. Ему объясняют, что в красном большом доме поселится он сам. В свой дом он может взять с собой кого захочет. Те же, кому не хватит места в красном доме, поселятся в домике, расположенном рядом. В конце беседы ребенку задают вопрос: «Кого из членов семьи ты возьмешь в свой новый дом, а кого поселишь рядом?»
При
оценке результатов в первую очередь
обращают внимание на то, всех ли членов
семьи ребенок размещает в «своем» доме. Если он кого-то «забывает» или переселяет
в маленький домик, то это свидетельствует
о неоднозначном или негативном
отношении ребенка к этому члену семьи.
При этом также оценивается быстрота
ответа. Чем больше ребенок думает, тем
менее достоверен ответ. Если в семье
гармоничные отношения и ребенок любим,
то он располагает в «своем» домике всех
близких. Технологии психологического
изучения семей, воспитывающих детей с
отклонениями в развитии
Если он кого-то «забывает» или переселяет
в маленький домик, то это свидетельствует
о неоднозначном или негативном
отношении ребенка к этому члену семьи.
При этом также оценивается быстрота
ответа. Чем больше ребенок думает, тем
менее достоверен ответ. Если в семье
гармоничные отношения и ребенок любим,
то он располагает в «своем» домике всех
близких. Технологии психологического
изучения семей, воспитывающих детей с
отклонениями в развитии
Бланк методики «Два дома» {и. Вандвик, п. Экблад)
Инструкция:
Скажи, кого из членов семьи ты возьмешь в свой новый дом, а кого поселишь рядом?
Детский апперцептивный тест — САТ (Л. Беллак)
Детский
апперцептивный тест САТ предназначен
для изучения особенностей межличностных
отношений ребенка к значимым
близким (родителям, сестрам, братьям и
другим лицам). Этот тест также может
быть использован при изучении личностных
характеристик ребенка, его потребностей
и мотивов.
Стимульный материал представлен в виде картинок с людьми или животными. Их показывают испытуемым с просьбой описать то, что там происходит и составить рассказ. Выбор картинок, предъявляемых ребенку, зависит от проблем, которыми он страдает. Детям с нормальным психическим развитием тест Л. Беллака предъявляется с 3-х до 10-ти лет. Дети с отклонениями в развитии могут диагностироваться с помощью САТ в более старшем возрасте в зависимости от уровня развития мышления и речи.
Инструкция:
Посмотри на эту картинку. Расскажи, что здесь происходит.
В процессе рассказа ребенку задаются дополнительные вопросы. Содержание рассказа анализируется с точки зрения проблем, возникающих в личностной и межличностной сферах ребенка.
Детям
дошкольного возраста рекомендуется
предлагать картинки с животными.
Желательно не задавать ребенку прямых
вопросов о том, что его волнует.
.
Помогите своему ребенку понять метод лестницы за меньшее время
Последнее обновление: Thinkster 25 мая 2022 г.
Метод лестницы — полезный способ помочь учащимся понять и решить математические задачи за меньшее время.
Но даже несмотря на то, что это полезный инструмент, который репетиторы и учителя используют в классах сегодня, мы знаем, что многие родители, возможно, не учили математике с помощью того же метода. Если вы родитель, который хочет понять метод лестницы, чтобы вы могли помочь своему ребенку с домашним заданием, оставайтесь с нами.
Мы собираемся превратить эту технику в пошаговое руководство, которое легко понять и начать использовать уже сегодня.
А это означает, что у вас будет больше времени для дополнительных математических заданий и обучения!
Что такое лестничный метод?
Это простая техника, в которой используются простые числа и визуализация в виде ступенчатых линий (похожих на лестницу), чтобы помочь учащимся понять математические задачи. Это требует от студентов демонстрации своей работы, но помогает им ясно увидеть, как прийти к заданному решению.
Итак, первый шаг — определение и идентификация простых чисел. Возможно, вы помните со времен учебы в классе, что простых чисел — это числа, которые больше 1 и не имеют положительных делителей, кроме 1 и самого себя.
Это означает, что единственный способ получить простое число с помощью умножения — это использовать само число.
Например, вот первые восемь простых чисел: 2, 3, 5, 7, 11, 13, 17 и 19.
Давайте посмотрим на число 7. Вы не может умножать любые числа, кроме 7 и 1, чтобы получить семь, поэтому это простое число.
Что насчет номера 6?
Вы можете умножить 2 х 3, чтобы получить 6, а 6 х 1 также равно 6. Значит, это не простое число.
Лестничный метод можно использовать для решения нескольких различных математических задач. Мы начнем с самого простого и постепенно переходим к более сложным вещам, чтобы вы могли помочь своему ребенку в любых областях, которые могут доставлять ему проблемы.
Как использовать лестничный метод для факторизации числа
Допустим, вы хотите найти простую факторизацию одного числа. В этом примере мы будем использовать число 24.
Запишите число 24 в скобках. Затем подумайте о наименьшем простом числе, на которое его можно разделить без остатка.
| 24 |
Лучший способ сделать это — вспомнить список простых чисел и начать сначала с наименьшего числа (кроме 1).
Входит ли 2 в 24? Ответ положительный.
Итак, вы напишите 2 слева от скобок, как мы сделали здесь.
2 | 24 |
Далее вам нужно выяснить, сколько раз 2 равномерно переходит в 24, ныряя 24/2.
Вы начнете следующую ступень вашей лестницы ниже первой строки, написав ответ следующим образом:
2 | 24 |
| 12 |
Спросите: «Является ли 12 простым числом?»
Поскольку мы знаем, что можно умножить несколько комбинаций, чтобы получить 12 (например, 3 x 4), мы знаем, что 12 не является простым числом. Цель состоит в том, чтобы разбить каждую ступеньку и скобку, чтобы получить простое число.
Итак, начните процесс снова с наименьшего простого числа и продвигайтесь вверх. 2 равномерно входит в 12? Сколько раз?
Запишите простое число (2) слева от скобки и начните следующую ступень лестницы для следующего делителя.
2 | 24 |
2 | 12 |
| 6 |
Теперь перейдите к самой нижней ступени, которую вы только что добавили. Спросите, является ли 6 простым числом. Мы снова знаем, что наше число делится на 2.
Итак, мы снова поместим простое число (2) за пределы скобки и начнем четвертую ступень.
2 | 24 |
2 | 12 |
2 | 6 |
| 3 |
Теперь у нас наконец есть простое число на нижней ступени. Поскольку нет других чисел, которые можно умножить, чтобы получить 3, кроме 1 и 3, мы находимся в конце лестницы.
Разложение числа 24 на простые множители затем выражается как все числа на внешней стороне лестницы или в форме «L»:
2 | 24 |
2 | 12 |
2 | 6 |
| 3 |
Это означает, что простая факторизация числа 24 равна: 2 x 2 x 2 x 3. Что можно записать как 2 3 x 3.
Как использовать лестничный метод для упрощения дробей дробь вроде 24 / 36 и вам нужно упростить, вы будете использовать метод лестницы, как в примере выше. Чтобы учесть оба числа, вы просто добавите еще один столбец.
Определите числитель (число в верхней части дроби) и знаменатель (число в нижней части), поместив их в отдельные столбцы:
N D
| 24 | 36 |
Используя метод лестницы, подумайте о наименьшем простом числе, которое входит в число 24 и 36.
Когда ваш ребенок ответит «2», спросите его, сколько раз 2 входит в число , , 24 и 36. запишите ответы на отдельных ступенях под номерами.
Вот как должны выглядеть первые две ступени лестницы:
2 | 24 | 36 |
2 | 12 | 18 |
Повторите процесс для следующих двух чисел, которые также делятся на 2:
2 | 24 | 36 |
2 | 12 | 18 |
| 6 | 9 |
Теперь у нас есть числа 6 и 9.
Когда мы начинаем с наименьшего простого числа, 2, мы замечаем, что оно равномерно переходит в 6, но не в 9. Это означает, что мы не можем его использовать. Итак, вы должны перейти к следующему простому числу.
Равномерно ли 3 входит в оба числа?
Если 6 разделить на 3, получится 2; красивое четное число. А можно разделить 9 на 3 и получить 3 простое число. Итак, мы добавим еще одну ступеньку к лестнице.
N D
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
2 3
К этому моменту вы достигли простого числа и больше не сможете добавлять ступени. Итак, мы вернемся к исходной проблеме: как упростить дробь 24/36.
Правильный ответ находится на нижней ступени лестницы: 2/3
Легко, правда?
Поскольку мы уже проделали всю эту математику, давайте воспользуемся тем же примером, чтобы найти наибольший общий делитель и наименьшее общее кратное.
Как использовать лестничный метод для нахождения наибольшего общего делителянаибольший общий делитель (НОД) — это наибольшее число, которое делится без остатка на все сравниваемые числа.
С помощью лестничного метода легко найти НОД, потому что все, что вам нужно сделать, это посмотреть на множители каждого числа в левой части лестницы и умножить их.
Сможете ли вы найти наибольший общий делитель в приведенном ниже примере?
N D
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
2 3
Если вы ответили 12, вы правы, потому что 2 x 2 x 3 = 12. Используйте метод лестницы, чтобы найти наименьшее общее кратное
Наименьшее общее кратное (НОК) – это наименьшее кратное, общее для двух (или более) чисел.
Чтобы начать это упражнение, мы сделаем быстрое обновление для кратных. Вы можете найти число, кратное числу , просто умножив его на другое число. Лучший способ сделать это — начать с числа 1.
Вот пример:
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
Затем мы можем перечислить кратные 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44 и т. д.
Различные числа также могут иметь общих кратных . Их можно найти, выписав кратные каждому числу и найдя общие ответы:
Их можно найти, выписав кратные каждому числу и найдя общие ответы:
Кратные 4: 4, 8, 12, 16, 20 , 24, 28, 32, 36, 4 0 , 44…
Клажу 5: 5, 10, 15, 20 , 25, 30, 35, 40 , 45…
Например, кратные 4 и 5 — 20 и 40. и LCM — это 20.
Но как найти все кратные двух больших чисел, например 24 и 36, и быстро найти НОК?
Это один из действительно полезных способов использования метода лестницы. Чтобы показать вам, как это сделать, мы будем использовать построенную выше лестницу с 24 и 36.
Затем вы просто перемножите все числа, образующие букву «L» в левой части лестницы.
2 | 24 | 36 |
2 | 12 | 18 |
3 | 6 | 9 |
| 2 | 3 |
Таким образом, НОК находится с помощью следующего уравнения: 2 x 2 x 3 x 2 x 3 = 72.
Это намного более простой способ найти решение, чем определение всех отдельных кратных этих чисел!
Как использовать метод лестницы для сложения и вычитания дробей
Предположим, ваш ребенок должен сложить дроби 1/6 и 3/8.
Прежде чем вы сможете складывать или вычитать дроби, вы должны помнить, что знаменатели должны быть одинаковыми. Мы можем сделать это, создав лестницу из двух столбцов для знаменателей, как таковую:
D D
| 6 | 8 |
Повторим процесс лестничного метода, чтобы найти наименьшее простое число, которое без остатка делится на оба. В данном случае это 2.
D D
2 | 6 | 8 |
Сколько раз 2 входит и в 6, и в 8?
D D
2 | 6 | 8 |
| 3 | 4 |
Глядя на следующую ступеньку, входит ли 2 и в 3, и в 4?
Нет.
А 3? Опять же, нет.
Поскольку мы не можем найти больше простых множителей, у нас остаются 3 и 4. Поскольку эти числа не совпадают, мы можем найти НОК, чтобы убедиться, что обе дроби имеют одинаковый знаменатель.
Давайте найдем НОК, снова перемножив все числа в «Г-образной форме»:
D D
2 | 6 | 8 |
3 4
Умножьте 2 x 3 x 4, и вы получите 24.
Это число является наименьшим общим кратным между нашими двумя знаменателями. Это означает, что все, что нам нужно сделать, это заставить обе дроби иметь 24 в качестве их общего нижнего числа.
К счастью, у нас уже есть числа, которые помогут нам в этом.
Мы возьмем исходные дроби и умножим их на числа, находящиеся на нижней ступени нашей лестницы, в данном случае на 3 и 4. В результате обе дроби должны иметь НОК в качестве знаменателя.
Вот как мы это сделали:
1 x (4) + 3 x (3) = 4 + 9
6 x (4) 8 x (3) 24 24
Теперь, когда знаменатели совпадают, мы можем сложить числители. Сумма становится равной 13 / 24.
Как использовать лестничный метод для разложения выражений на множители
Давайте посмотрим на распределительное свойство в математике, которое говорит, что ab + ac = a(b+c ).
В нашем примере мы будем использовать уравнение 18 + 24 = 42. Чтобы продемонстрировать свойство распределения, давайте поместим эти два числа в ступеньку лестницы:
| 18 | 24 |
Следуйте изученному процессу для определения простых чисел и построения ступенек лестницы:
2 | 18 | 24 |
3 | 9 | 12 |
| 3 | 4 |
Теперь можно заполнить уравнение a(b+c), используя числа в нашей лестнице.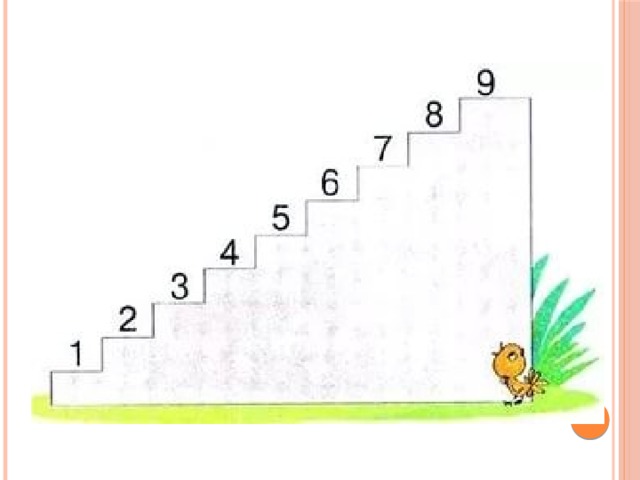
2 | 18 | 24 |
3 | 9 | 12 |
| 3 | 4 |
Мы умножим внешние левые числа, чтобы получить «а».
Затем мы будем использовать нижнюю ступень лестницы для чисел в скобках (b+c).
Уравнение должно выглядеть так: a(b+c) = 6(3 + 4)
Но можем ли мы проверить это просто для уверенности? Абсолютно!
Вы можете использовать свойство распределения, чтобы распределить (или умножить) 6 по отдельности на 3 и 4 в скобках:
a(b+c) = 6(3 + 4)
6 x 3 = 18
6 x 4 = 24
18 + 24 = 42.
Или вы можете пойти другим путем и добавить в круглых скобках (3+4), что равняется 7, а затем умножьте это на 6, чтобы получить 42.
В любом случае, получилось!
А как насчет более сложных выражений с такими переменными, как 42x – 56?
Сделайте глубокий вдох и просто используйте тот же метод, который мы практиковали. Начните с верхней ступени лестницы:
| 42x | 56 |
Затем найдите наименьшее простое число, на которое делится каждое число. В данном случае 2:
В данном случае 2:
2 | 42x | 56 |
| 21x | 28 |
И продолжайте. Наибольшее простое число, на которое эти два числа будут делиться, равно 7.
2 | 42x | 56 |
7 | 21x | 28 |
| 3x | 4 |
Как и в предыдущем примере, мы будем использовать числа в нашей лестнице для заполнения выражения.
Умножьте внешние числа (2 x 7 = 14) и сначала добавьте произведение к вашему выражению.
Затем используйте числа из нижней ступени, чтобы заполнить оставшуюся часть выражения.
2 | 42x | 56 |
7 | 21x | 28 |
| 3x | 4 |
Таким образом, наше исходное выражение 42x – 56 теперь выражается как 14 (3x – 4).
Видишь? В следующий раз, когда ваш ребенок принесет домой математическую задачу, в которой используется метод лестницы, теперь вы можете с уверенностью помочь ему.
Однако, если у вас нет времени, чтобы просмотреть все ответы, работа с онлайн-репетитором по математике может помочь вашему ребенку укрепить свои знания и освоить методы, необходимые для достижения успеха.
Начните работу с Thinkster Math Tutor сегодня, получите доступ к тысячам цифровых математических листов и начните укреплять уверенность своего ребенка прямо сейчас.
Если вы можете изучить совершенно новый метод, подобный этому, всего за одну запись в блоге, представьте, насколько ваш ребенок преуспеет, если в его команде будет специальный онлайн-репетитор Thinkster.
Лестница детского участия – организация взаимодействия
Скачать PDFРаспечатать эту страницу
Впервые опубликовано в Детское участие: от символизма к гражданству , публикация 1992 года Международного центра развития детей Детского фонда Организации Объединенных Наций (ЮНИСЕФ), «Лестница детского участия» Роджера Харта применила концептуальную основу «Лестницы гражданского участия » Шерри Арнштейн к участие детей во взрослых проектах, программах и мероприятиях, включая формы работы, защиту интересов и гражданскую позицию. Как и более ранняя структура Арнштейна, модифицированная лестница участия Харта стала влиятельной и широко применяемой моделью в области детского развития, образования, гражданского участия и демократического принятия решений.
Как и более ранняя структура Арнштейна, модифицированная лестница участия Харта стала влиятельной и широко применяемой моделью в области детского развития, образования, гражданского участия и демократического принятия решений.
«Об участии молодежи нельзя говорить без учета властных отношений и борьбы за равные права. Важно, чтобы у всех молодых людей была возможность научиться участвовать в программах, которые непосредственно влияют на их жизнь. Это особенно касается детей из неблагополучных семей, поскольку благодаря участию с другими такие дети узнают, что борьба против дискриминации и репрессий, а также борьба за свои равные права в знак солидарности с другими – это само по себе основное демократическое право… На мой взгляд, наивысшая возможная степень гражданственности — это когда мы, дети или взрослые, не только чувствуем, что можем сами инициировать некоторые изменения, но и когда мы также признаем, что иногда уместно приглашать других присоединиться к нам из-за их собственных прав и интересов.
Роджер А. Харт, Участие детей: от символизма к гражданствупотому что это касается и их как сограждан».
В 2008 году Харт объяснил причину разработки модели: предмет, которого в то время вообще не хватало… Наиболее полезным качеством модели, вероятно, было то, что она помогла различным профессиональным группам и учреждениям переосмыслить свою работу с молодежью: молодежные работники, директора теле- и радиовещания, лидеры скаутов, игровые работники, уличные работники, работники здравоохранения и даже некоторые школьные учителя. Его простота формы и ясность целей позволяют им найти язык, чтобы системно взглянуть на свои текущие способы работы и, таким образом, придумать что-то более сложное и полезное для их конкретного контекста».
Оригинальная иллюстрация Роджера Харта 1992 года «Лестница детского участия из . Детское участие: от символизма к гражданству ». Модель включает восемь «ступенек», описывающих характеристики, связанные с различными уровнями принятия решений, контроля или власти, которые взрослые могут наделить детей и молодежь.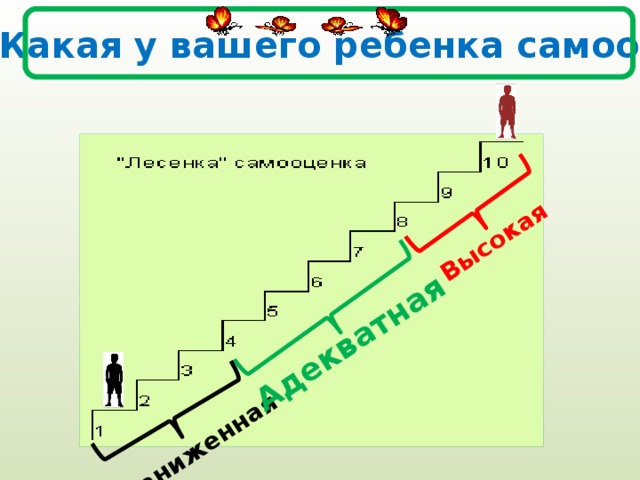 Лестница детского участия
Лестница детского участия Типология детского участия Харта представлена в виде метафорической «лестницы», где каждая восходящая ступенька представляет возрастающие уровни детской активности, контроля или власти. В дополнение к восьми «ступеням» лестница представляет собой континуум власти, восходящий от неучастие (отсутствие участия) до степени участия (повышение уровня участия). Следует отметить, что использование Хартом термина «дети» охватывает всех законных несовершеннолетних от детей дошкольного возраста до подростков.
Восемь ступеней «Лестницы Харта» детского участия:
1.
Манипуляция Участие как манипуляция происходит, когда дети и молодежь не понимают вопросов, мотивирующих процесс участия, или своей роли в этом процессе. По словам Харта: «Иногда взрослые считают, что цель оправдывает средства… Если дети не разбираются в вопросах и, следовательно, не понимают своих действий, то это манипуляция. Такое манипулирование под видом участия вряд ли является подходящим способом вовлечения детей в демократические политические процессы».
Такое манипулирование под видом участия вряд ли является подходящим способом вовлечения детей в демократические политические процессы».
Примеры включают «детей дошкольного возраста, несущих политические плакаты о влиянии социальной политики на детей», когда эти дети не понимают вопросов или своей роли в политическом процессе, и просят детей «нарисовать что-нибудь, например, их идеальная детская площадка», после чего «взрослые собирают рисунки и каким-то скрытым образом синтезируют идеи, чтобы придумать «детский дизайн» детской площадки. Детям не рассказывают о процессе анализа и обычно даже не делают его прозрачным для других взрослых. Дети понятия не имеют, как использовались их идеи».
2.
Украшение Участие в качестве украшения имеет место, когда дети и молодежь выставляются на всеобщее обозрение во время мероприятия, представления или другого мероприятия, организованного с определенной целью, но они не понимают значения или цели своего участие.
Примеры включают «те частые случаи, когда детям выдают футболки, связанные с каким-либо делом, и они могут петь или танцевать на мероприятии в такой одежде, но имеют слабое представление о том, что это такое, и не имеют права голоса в организации мероприятия». повод. Молодёжь здесь из-за угощения или какого-то интересного представления, а не из-за дела. Причина, по которой это описывается как ступень выше «манипуляции», заключается в том, что взрослые не притворяются, что причина вдохновлена детьми. Они просто используют детей для поддержки своего дела относительно косвенным образом».
3.
СимволизмУчастие как символизм происходит в «тех случаях, когда детям явно дается право голоса, но на самом деле у них практически нет выбора в отношении предмета или стиля сообщения о нем, и практически нет возможность сформулировать собственное мнение».
Примеры включают «как детей иногда используют на панелях конференций. Красноречивые, очаровательные дети выбираются взрослыми для участия в комиссии практически без существенной подготовки по этому вопросу и без консультаций со своими сверстниками, которых, как подразумевается, они представляют. Если аудитории или детям не дается никаких объяснений того, как они были выбраны и какие взгляды детей они представляют, этого обычно достаточно, чтобы показать, что проект не является настоящим примером участия».
Если аудитории или детям не дается никаких объяснений того, как они были выбраны и какие взгляды детей они представляют, этого обычно достаточно, чтобы показать, что проект не является настоящим примером участия».
4.
Назначено, но проинформированоУчастие, которое назначено, но проинформировано , имеет место, когда дети и молодежь (1) «понимают намерения проекта», (2) «знают, кто принял решения относительно их участия и почему», (3) «играют значимую (а не «декоративную») роль» и (4) «выступают добровольцами в проекте после того, как им стало ясно, о чем он».
В качестве примера Харт описывает Всемирный саммит в интересах детей, который проходил в штаб-квартире Организации Объединенных Наций. По словам Харта, это было «чрезвычайно крупное мероприятие с большой логистической сложностью», и «было бы трудно искренне привлечь молодых людей к планированию такого мероприятия». Однако «за каждым из 71 мирового лидера был закреплен ребенок. В качестве «пажей» эти дети стали экспертами по зданию Организации Объединенных Наций и этому событию и смогли сыграть важную роль, проводя президентов и премьер-министров в нужные места в нужное время». В данном случае роль детей была одновременно функциональной и символической, а «детские роли пажей были важны и всем понятны».
В качестве «пажей» эти дети стали экспертами по зданию Организации Объединенных Наций и этому событию и смогли сыграть важную роль, проводя президентов и премьер-министров в нужные места в нужное время». В данном случае роль детей была одновременно функциональной и символической, а «детские роли пажей были важны и всем понятны».
5.
Проконсультированы и проинформированыУчастие, составляющее Проведены консультации и проинформированы , имеет место, когда дети выступают в качестве «консультантов для взрослых с большой честностью. Проект разрабатывают и ведут взрослые, но дети понимают процесс и к их мнению относятся серьезно».
Один из примеров, который описывает Харт, — это опрос мнения молодежи под руководством взрослых, в ходе которого молодежь информируют о цели опроса, консультируют по соответствующим вопросам до его разработки и получают возможность высказать свое мнение по окончательному опросу перед его проведением. управляется.
6.
Инициированные взрослыми, совместные решения с детьмиУчастие, которое представляет собой совместные решения, инициированные взрослыми с детьми , имеет место, когда взрослые инициируют совместные проекты, но они делят полномочия по принятию решений или управлению с детьми.
Одним из примеров, описанных Хартом, является молодежная газета. В этом случае газета может быть проектом, инициированным взрослыми, но дети могут управлять всеми аспектами работы — от репортажей, написания и редактирования до рекламы, печати и распространения — только с руководством и технической помощью взрослых.
7.
Инициируется и направляется детьми Участие, которое инициируется и направляется детьми , происходит, когда дети и молодежь разрабатывают и осуществляют сложные проекты, работая совместно в малых или больших группах. Хотя взрослые могут наблюдать за детьми и помогать им, они не вмешиваются в процесс и не играют руководящей или управленческой роли.
Харт отмечает, что трудно «найти примеры общественных проектов, инициированных детьми. Основная причина этого заключается в том, что взрослые обычно плохо реагируют на собственные инициативы молодых людей. Даже в тех случаях, когда взрослые оставляют детей одних, чтобы они сами придумали и раскрасили фреску или украсили собственную комнату отдыха, им сложно не играть руководящую роль».
8.
Инициированные детьми, совместные решения со взрослымиУчастие, которое представляет собой совместные решения, инициированные детьми со взрослыми , имеет место, когда дети — хотя в данном случае в первую очередь подростки — разделяют полномочия по принятию решений, управлению или власть со взрослыми партнерами и союзниками.
Например, учащиеся сотрудничают со взрослыми для сбора средств, разработки и реализации школьной программы или проведения общественной кампании. Основное преимущество этой формы участия молодежи заключается в том, что она может дать молодым людям возможность оказывать значительное влияние на политику, решения или результаты, которые традиционно находились под исключительным контролем и руководством взрослых, например, законодательные или политические процессы.
Харт отмечает, однако, что примеры такой формы детского и молодежного участия редки: «Причина, я думаю, не в отсутствии у подростков желания быть полезными. Это скорее отсутствие заботливых взрослых, настроенных на особые интересы молодежи. Нам нужны люди, способные реагировать на тонкие признаки энергии и сострадания у подростков».
Расширение прав и возможностей детей и молодежи: содействие участию в принятии решений (1997), Фил Треседер преобразовал «Лестницу детского участия» Роджера Харта в конфигурацию со ступицей, чтобы избежать общей критики метафоры лестницы: в реальных условиях участие не разворачивается в упорядоченной последовательности от высшего к низшему, а формирует участия, которые проявляются на более низких ступенях лестницы, по своей сути не хуже, чем на более высоких уровнях — на самом деле, они могут быть уместны в определенных обстоятельствах, например, когда дети и молодежь нуждаются в поддержке и руководстве со стороны взрослых, чтобы в полной мере участвовать в руководстве или принятии решений.
 процесс. Источник изображения: Empowering Young People , Carnegie UK Trust, январь 2008 г. аспекты участия молодежи. В переосмысленной презентации восемь ступеней лестницы Харта размещены на оси X-Y. Вертикальное измерение иллюстрирует возрастающую способность принимать решения и вносить изменения, а горизонтальное измерение иллюстрирует возрастающие уровни взаимодействия и сотрудничества. Источник изображения: Создание лучших городов с детьми и молодежью: пособие для участников .
процесс. Источник изображения: Empowering Young People , Carnegie UK Trust, январь 2008 г. аспекты участия молодежи. В переосмысленной презентации восемь ступеней лестницы Харта размещены на оси X-Y. Вертикальное измерение иллюстрирует возрастающую способность принимать решения и вносить изменения, а горизонтальное измерение иллюстрирует возрастающие уровни взаимодействия и сотрудничества. Источник изображения: Создание лучших городов с детьми и молодежью: пособие для участников . С тех пор, как Харт впервые предложил лестницу, возникло несколько дебатов о подходящем и неподходящем применении этой структуры, отчасти потому, что практики начали использовать модель способами, которые Харт никогда не предполагал. Обращаясь к некоторым из этих дебатов, Харт посвятил главу ограничениям структуры в сборнике 2008 г.
- Лестница предназначена для применения в первую очередь к «программам или проектам, а не к повседневному неформальному участию детей в их сообществах».
 Как пишет Харт, «лестница участия охватывает лишь довольно узкий диапазон способов, которыми большинство детей в мире участвуют в жизни своих сообществ… и в значительной степени ограничивается описанием различных ролей, которые взрослые играют в отношении участия детей».
Как пишет Харт, «лестница участия охватывает лишь довольно узкий диапазон способов, которыми большинство детей в мире участвуют в жизни своих сообществ… и в значительной степени ограничивается описанием различных ролей, которые взрослые играют в отношении участия детей». - Харт также предостерегает от рассмотрения лестницы как модели развития с последовательными стадиями или уровнями участия: «В некотором смысле метафора лестницы неудачна, поскольку она, кажется, подразумевает необходимую последовательность для развития у детей способности к участию. Это не было намерением, но учитывая метафору лестницы, совсем не удивительно, что модель была интерпретирована как ступенчатое восхождение. На самом деле лестница в первую очередь касается степени, в которой взрослые и учреждения позволяют или позволяют детям участвовать… Я думаю о верхних ступенях лестницы как о выражении различных «степеней» активности или участия молодых людей». (Более подробное обсуждение склонности к неверному толкованию лестничных моделей см.
 в 9).0331 Лестница гражданского участия .)
в 9).0331 Лестница гражданского участия .) - Лестница не предназначена для использования в качестве инструмента для оценки программы: «Это простой шаг от размышления о лестнице как модели развития до ее использования в качестве всеобъемлющего инструмента для оценки степени участия программа есть». Но это приложение не входило в первоначальные замыслы Харта: «У него не было намерения служить каким-либо всеобъемлющим оценочным инструментом».
- Лестница не ратует за то, чтобы взрослые уступали всю власть детям или что передача власти детям — это всегда хорошо. По словам Харта, «одним из самых неожиданных критических замечаний по поводу этой модели для меня было желание некоторых превратить верхнюю ступеньку лестницы в «главных детей» или в то, чтобы дети принимали решения без взрослых… Моя цель при создании этой схемы не состояла в том, чтобы наивно утверждать, что мы должны думать о детях как о подавленных личностях, которые должны быть освобождены посредством ряда шагов, посредством которых устраняется всякое участие взрослых.
 Моя забота заключалась скорее в том, чтобы доказать, что потенциал детей как граждан должен быть признан в полной мере, и с этой целью дети должны время от времени иметь возможность участвовать на максимально возможном уровне».
Моя забота заключалась скорее в том, чтобы доказать, что потенциал детей как граждан должен быть признан в полной мере, и с этой целью дети должны время от времени иметь возможность участвовать на максимально возможном уровне». - Как и любая другая модель, лестница отражает некоторую степень культурной предвзятости и может быть менее точной или полезной при применении к определенным культурам. Например, лестница в первую очередь отражает «западную ориентацию», которая имеет тенденцию подчеркивать индивидуализм и ценность прогрессивной независимости и автономии в развитии ребенка, и поэтому она может быть менее полезной или даже проблематичной при общем применении к культурам, которые подчеркивают ценность коллективизм и поддержание семейной или общинной взаимозависимости в развитии ребенка. По словам Харта, «для меня очень удивительно, что я не смог найти больше культурной критики лестницы, особенно из Азии и Африки, поскольку я могу вспомнить некоторые важные из них. Причина вполне может заключаться в том, что многие из тех, кто пишет о проблеме участия детей, сами получили образование на Западе и полагаются на западные теории развития детей, которые, к сожалению, почти полностью доминируют в мировой литературе по развитию детей».


 Три нижние ступеньки для плохих детей. Среднюю ступеньку оставим для детей, которых нельзя назвать ни плохими, ни хорошими. Возьмите карандашик и отметьте на листочке, на какую бы ступеньку вы посадили бы себя. Объясните почему?»
Три нижние ступеньки для плохих детей. Среднюю ступеньку оставим для детей, которых нельзя назвать ни плохими, ни хорошими. Возьмите карандашик и отметьте на листочке, на какую бы ступеньку вы посадили бы себя. Объясните почему?»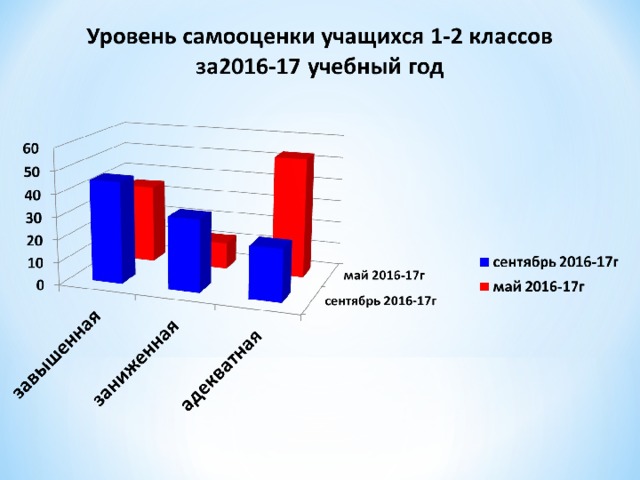 потому что это касается и их как сограждан».
потому что это касается и их как сограждан».