На фигуру произвольной формы наложена палетка. Число целых клеток палетки внутри фигуры равно a, число нецелых клеток-b. Сделай оценку и запиши
Ответы
Знаешь ответ? Добавь его сюда!
Последние вопросы
- Математика
19 часов назад
Добрый времени суток будьте любезны помочь ничего не понимаю.
- Другие предметы
1 день назад
39/корень из 3 - Информатика
2 дня назад
Используя связанные таблицы создать:
— Форму для ввода данных по таблице Студенты.
— Запрос на выборку по которому из базы данных будут отобраны фамилии, имена, специализация и изучаемый язык:
Запрос на выборку по которому из базы данных будут отобраны студенты менеджеры и изучающие английский язык;
— По созданному запросу создать отчет с группировкой по специальности.

- Литература
2 дня назад
61 балл по литературе..все очень плохо? - Математика
2 дня назад
какое аниме посмотреть подскажите
- Физика
3 дня назад
на стройплощадке идет возведение здания на 6 этаже стоит рабочий какие силы действуют на рабочего и на здание если s 100м² вес 70кг
- Химия
4 дня назад
Помогите пожалуйста
- Геометрия
4 дня назад
Помогите пожалуйста
1.
2.
2. Напишите уравнение сферы с центром в точке A(-1;1;-1) проходящей через точку N(3;4;2)
- Математика
4 дня назад
Помогите решить пример,срочно!!!
фото прикрепила
- Физика
5 дней назад
помогите решить пожалуйста!!!
- Обществознание
7 дней назад
47×8:2×2 решите пж этот пример срочно!!! Можно не столбиком - Английский язык
7 дней назад
Помогите пожалуйста очень срочно буду благодарен
- Математика
8 дней назад
https://gamejolt.
 com/invite/Mukhin
com/invite/Mukhin - Математика
9 дней назад
что делать когда скучно
не пишите срать через окно и тому подобное
- Геометрия
9 дней назад
ПОМОГИТЕ С ГЕОМЕТРИЕЙ ПОЖАЛУЙСТА, желательно с рисунком
Площадь. Единицы измерения площади. Палетка
«Площадь. Единицы измерения площади. Палетка.»
Ермакова Ирина Григорьевна
Донецк, 2022
Введение. В школьном курсе математики мы в основном имеем дело с многоугольниками. Между тем, на практике часто возникает необходимость найти площадь фигуры неправильной формы. Например, на уроке физики учитель предложил определить давление ученика на пол, и перед нами стала проблема, как определить площадь опоры (площадь подошвы ботинок) или бывает необходимость определить площадь территории по плану или карте. Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников.
Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников.
Цель исследования состоит в том, чтобы сравнить эффективность различных способов практического измерения площадей, как для реальных физических объектов, так и для фигур, площади которых могут быть найдены по точным формулам.
Объектом исследования являются методы измерения площади фигур произвольной формы:
1) метод взвешивания;
2) использование палетки;
3) применение точных формул.
Предметом исследования является площадь фигур произвольной формы.
Гипотеза исследования заключается в том, что площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.
Для доказательства гипотезы были поставлены следующие задачи:
• знакомство с понятиями измерения и погрешности измерения;
• изучение методов нахождения площади с помощью взвешивания и с помощью палетки;
• измерение с помощью методов взвешивания и палетки площадей контрольных фигур: прямоугольника, квадрата, выявление погрешностей измерения;
• измерение площадей произвольных фигур с помощью изученных методов. 2.Одним из приемов измерения площадей является палетка — сетка квадратов, нанесенной на прозрачный материал. Допустим, что на фигуру F, площадь которой надо измерить, наложена палетка. Тогда по отношению к этой фигуре можно выделить кв. двух видов:
2.Одним из приемов измерения площадей является палетка — сетка квадратов, нанесенной на прозрачный материал. Допустим, что на фигуру F, площадь которой надо измерить, наложена палетка. Тогда по отношению к этой фигуре можно выделить кв. двух видов:
1) кв., которые целиком лежат внутри фигуры F;
2) кв., через которые проходит контур фигуры и которые лежат частью вне, часть. Внутри фигуры F.
Как видим, такая палетка позволяет измерить площадь фигуры F лишь с невысокой точностью. Из определения площади и сути ее измерения вытекают известные правила сравнения площадей и действия над ними.
1) Если фигуры равны, то равны числен. знач. их площадей. фигуры у которых площади равны, называются равновеликие.
2) Если фигура F составлена из фигур F1, F2,… Fn, то числен. знач. площади фигуры F равно сумме числен. знач. площадей фигур F1, F2…Fn.
3) При замене ед. площади числен. знач. площади увеличивается во столько раз, во сколько новая ед. меньше старой.
знач. площади увеличивается во столько раз, во сколько новая ед. меньше старой.
Квадратная палетка представляет собой прозрачный лист, на котором нанесена сеть квадратов со сторонами 2 – 10 мм. Зная длину стороны одного квадрата и масштаб плана, можно вычислить площадь квадрата. Например, масштаб карты (плана) 1:10 000. Следовательно, площадь одного квадрата со стороной 1 см будет равна 10 000 м2 или 1 га.
Рисунок 1. – Определение площади способом палетки
Для определения площади палетку накладывают на замкнутый контур (Рисунок 1.). Площадь подсчитывается как сумма полных и неполных квадратов. Недостаток графического способа заключается в том, что количество неполных квадратов приходится оценивать на глаз. На рисунке 4.4 число полных квадратов 15, а неполных примерно равно 8,5 для каждого неполного квадрата глазомерно определяют, какую часть он составляет от полного. Следовательно, отсюда относительная ошибка определения площади палеткой составляет 1/100.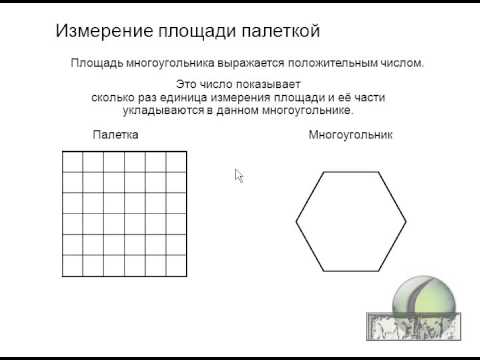
Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур – любая из них обладает площадью. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Величина эта всегда бывает выражена положительным числом. Единицей измерения служит площадь квадрата, чья сторона равняется единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она разбита, на площадь одного квадрата.
Площади плоских фигур правильной геометрической формы, например, прямоугольников, треугольников, кругов, обычно определяют с помощью косвенных измерений. Сначала измеряют линейные размеры фигуры (длину, высоту, ширину, радиус), а потом вычисляют площадь, пользуясь соответствующими математическими формулами.
Площади фигур неправильной формы (произвольных фигур) не имеют определения, определяются лишь способы их вычисления.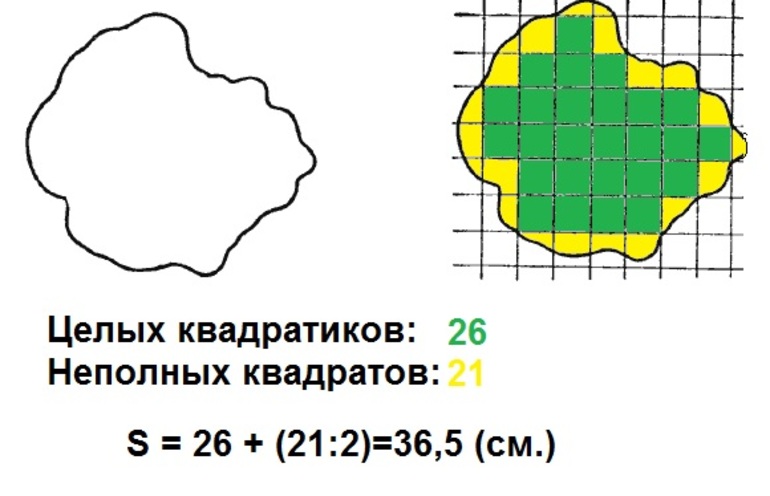
Если фигура имеет неправильную геометрическую форму, то ее площадь можно определить, начертив контур этой фигуры на бумаге в клеточку или с помощью палетки – листом из прозрачного материала, на который нанесена сетка линий, образующих при пересечении квадраты эталонного размера. В этом случае площадь фигуры вычисляют по формуле (2)
где n — количество целых квадратиков; k — количество нецелых квадратиков, С — площадь одного квадратика.
Для контроля расчётов площадь измеряют повторно, развернув палетку на 45° в любую сторону. Среднее значение расчётов до и после поворота и принимают за площадь искомого участка.
Площадь S измеряемой фигуры (рис.1) заключена в пределах , где – площадь фигуры, состоящей из квадратиков, полностью находящихся внутри контура измеряемой фигуры, а – площадь фигуры, состоящей из указанных квадратиков, а также квадратиков, пересекаемых контуром. По формулам (1) получаем: .
Количество квадратиков, пересекаемых контуром, определяет, во сколько раз погрешность больше, чем половина единицы измерения – площади эталонного квадрата. Поэтому способ измерения палеткой не слишком точен. Для измерения площади с меньшей погрешностью нужно измерять некоторую вспомогательную величину, по которой можно легко восстановить значение площади, и для которой существуют измерительные приборы со шкалой, позволяющие измерять вспомогательную величину с наименьшей возможной погрешностью – половиной цены деления шкалы.
Метод измерения вспомогательной величины придуман еще в древности и заключается в измерении массы плоской копии измеряемой фигуры. Если толщина листа, из которого изготовлены взвешиваемая фигура, постоянна, то масса фигуры прямо пропорциональна ее площади. Нужно нанести на плотную бумагу квадрат, площадь которого S0 точно известна, вырезать его и определить на весах его массу m0. На такую же бумагу перенести фигуру с искомой площадью S. Вырезать фигуру и определите её массу m. Затем, пользуясь правилом пропорции – S/S0 = m/m0, вычислить искомую площадь.
Вырезать фигуру и определите её массу m. Затем, пользуясь правилом пропорции – S/S0 = m/m0, вычислить искомую площадь.
Тогда . (3)
В качестве измеряемых фигур были взяты фигуры в форме ладони и подошвы. В качестве эталонных фигур были взяты квадрат со стороной 10 см (эталон 1) и прямоугольник со сторонами 15 см и 6 см (эталон 2), изготовленные из картона. Площадь эталонных фигур можно найти по известным формулам:
.
Для выполнения этой части работы были изготовлены палетки I и II с сеткой 1смсм и 0,5см0,5см.
На палетке I эталон 1: 1кв.ед.=1 см2
n=77
k=38
S1=77 кв.ед.
S2=115 кв.ед.
S= (77+115)/2=96 см2
= (115-77)/2=19
На палетке II эталон 1: 1кв.ед.=0,25 см2
n=364
k=68
S1=364 кв. ед.
ед.
S2=432 кв.ед.
S= ((364+432)/2)0,25=94,5 см2
= ((432-364)/2)0,25=8,5
На палетке I эталон 2: 1кв.ед.=1 см2
n=72
k=40
S1=72 кв. ед.
S2=112 кв. ед.
S= (72+112)/2=92 см2
= (112-72)/2=20
На палетке II эталон 2: 1кв.ед.=0,25 см2
n=330
k=68
S1=330 кв. ед.
S2=398 кв. ед.
S= ((330+398)/2)0,25=91 см2
= ((398-330)/2)0,25=8,5
На палетке I фигура1(ладонь): 1кв.ед.=1 см2
n=75
k=90
S1=75 кв. ед.
S2=165 кв. ед.
S= (75+165)/2=120 см2
= (165-75)/2=45
На палетке II фигура1(ладонь): 1кв.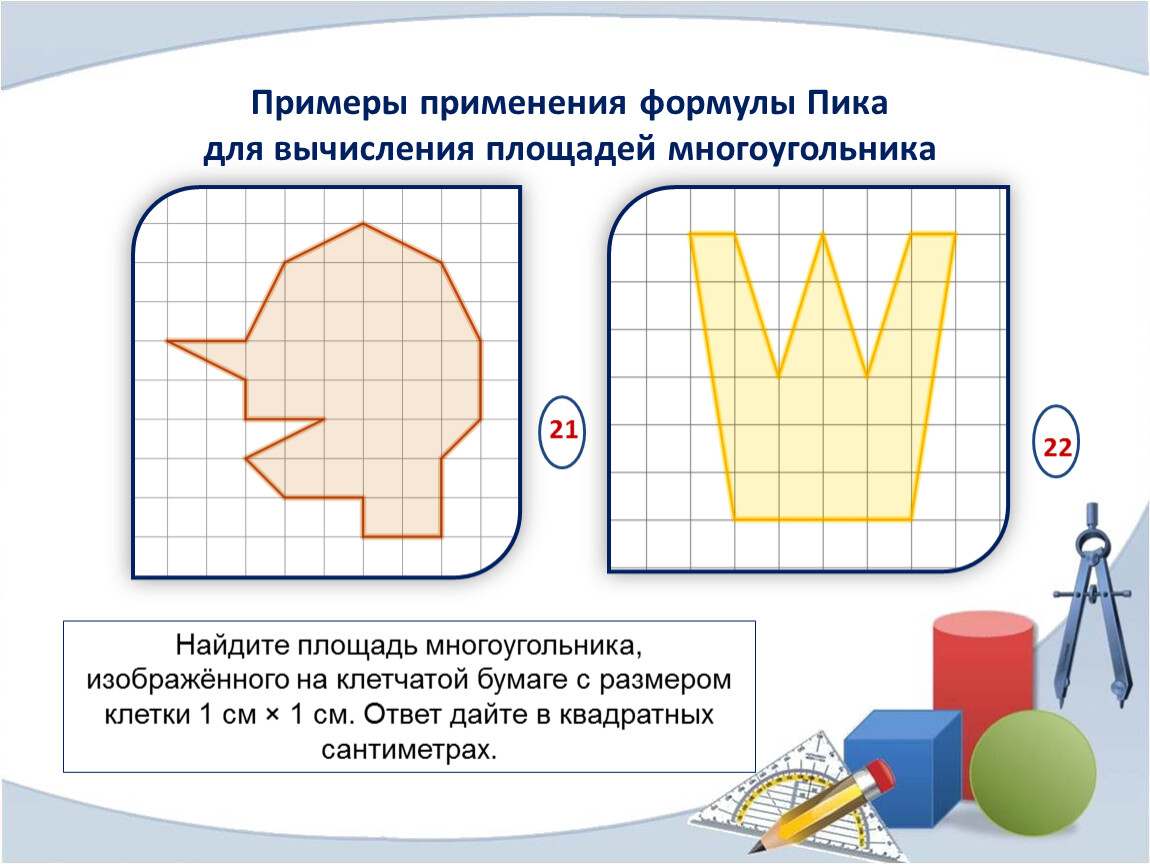 ед.=0,25 см2
ед.=0,25 см2
n=453
k=126
S1=330 кв. ед.
S2=398 кв. ед.
S= ((453+579)/2)0,25=129 см2
=( (579-453)/2)0,25=15,75
На палетке I фигура2(подошва): 1кв.ед.=1 см2
n=142
k=50
S1=142 кв. ед.
S2=192 кв. ед.
S= (142+192)/2=167 см2
= (192-142)/2=25
На палетке II фигура 2(подошва): 1кв.ед.=0,25 см2
n=640
k=86
S1=640 кв. ед.
S2=726 кв. ед.
S= ((640+726)/2)0,25=170,75 см2
= ((726-640)/2)0,25=10,75
Алгоритм вычисления площади с помощью палетки:
1. Наложите палетку на фигуру.
2. Сосчитайте число m, целых клеток внутри фигуры.
3. Сосчитайте число n неполных клеток фигуры и разделите это число на 2.
4. Вычислите значение площади по формуле: S= m + n: 2 (если число – n нечетно, то увеличить или уменьшить его на 1).
Выводы
Как показали проведенные исследования, и метод взвешивания, и измерение площади с помощью палетки являются пригодными для приближенного нахождения площадей фигур сложной формы.
Гипотеза исследования подтверждена.
Точность измерений можно повысить, используя более точные весы или палетки, с разбиением на более мелкие квадратики или площадь измеряют повторно, развернув палетку на 45° в любую сторону. Среднее значение расчётов до и после поворота и принимают за площадь искомого участка.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ:
1. Р.И. Малафеев. Творческие задания по физике VI-VII.
2. Гирке Р., Шпрокхоф Г. Эксперимент по курсу элементарной физики. Часть I. – М.: Учпедгиз, 1959. 368 с.
Часть I. – М.: Учпедгиз, 1959. 368 с.
3. Атанасян Л.С., В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия. 7-9 классы учебник — 3-е изд. — М.: Просвещение, 2014. — 383 с.
4. Болтянский В. О понятиях площади и объема // Научно-популярный физико-математический журнал «Квант» 1977. — №5
5. Новиков И. Метод площадей // Научно-популярный физико-математический журнал «Квант» — 1971. — №12.
6. Садовский Л., Садовский А. Как измеряют площадь? // Научно-популярный физико-математический журнал «Квант». — 1973. — №10.
Микродомен STIM1-ORAI1 — PMC
1. Putney JW., Jr Модель регулируемого рецептором проникновения кальция. Клеточный кальций. 1986; 7: 1–12. [PubMed] [Google Scholar]
2. Путни Дж. В., мл. Еще раз о емкостном введении кальция. Клеточный кальций. 1990; 11: 611–624. [PubMed] [Google Scholar]
3. Penner R, Matthews G, Neher E. Регуляция притока кальция вторичными мессенджерами в тучных клетках крыс. Природа. 1988; 334: 499–504. [PubMed] [Google Scholar]
4. Matthews G, Neher E, Penner R. Активированный вторичным мессенджером приток кальция в перитонеальные тучные клетки крыс. Дж. Физиол. 1989;418:105–130. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Matthews G, Neher E, Penner R. Активированный вторичным мессенджером приток кальция в перитонеальные тучные клетки крыс. Дж. Физиол. 1989;418:105–130. [Бесплатная статья PMC] [PubMed] [Google Scholar]
5. Lewis RS, Cahalan MD. Митоген-индуцированные колебания цитозольного Ca 2+ и трансмембранного Ca 2+ тока в лейкемических Т-клетках человека. Сотовый Регул. 1989; 1: 99–112. [PMC free article] [PubMed] [Google Scholar]
6. Hoth M, Penner R. Истощение запасов внутриклеточного кальция активирует ток кальция в тучных клетках. Природа. 1992; 355:353–356. [PubMed] [Google Scholar]
7. Хот М., Пеннер Р. Активированный высвобождением кальция ток кальция в тучных клетках крыс. Дж. Физиол. 1993;465:359–386. [Бесплатная статья PMC] [PubMed] [Google Scholar]
8. Zweifach A, Lewis RS. Митоген-регулируемый ток Са 2+ Т-лимфоцитов активируется истощением внутриклеточных запасов Са 2+ . Proc Natl Acad Sci USA. 1993;90:6295–6299.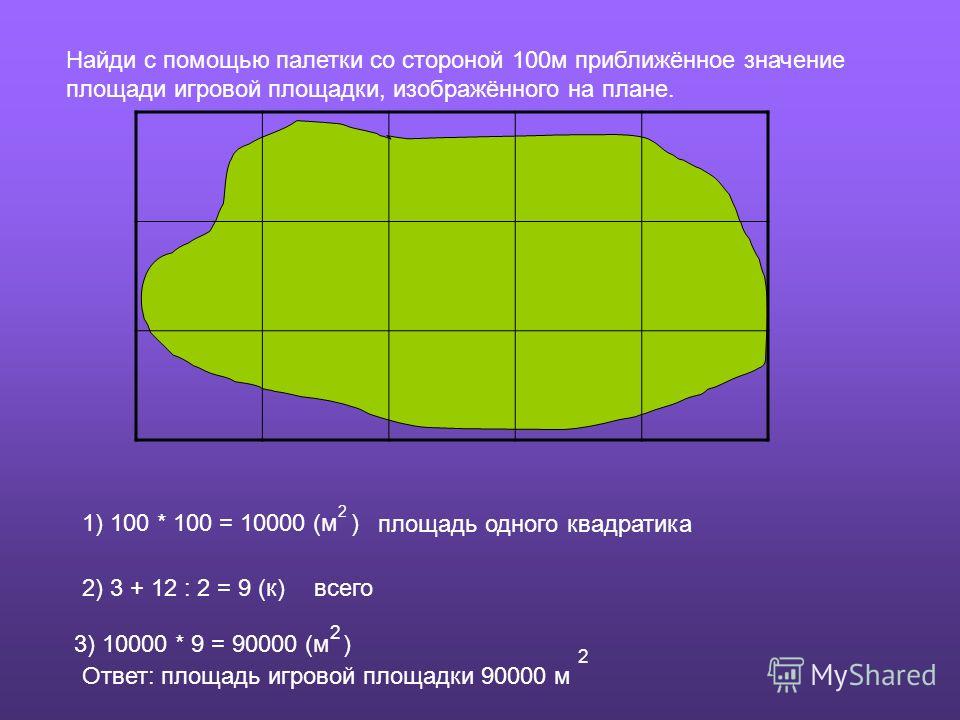 [Бесплатная статья PMC] [PubMed] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [Google Scholar]
9. Roos J, DiGregorio PJ, Yeromin AV, Ohlsen K, Lioudyno M, Zhang S, Safrina O, Kozak JA, Wagner SL, Cahalan MD, Velicelebi G, Stauderman КА. STIM1, важный и консервативный компонент депо-управляемого Ca 2+ функция канала. Джей Селл Биол. 2005; 169: 435–445. [Бесплатная статья PMC] [PubMed] [Google Scholar]
10. Liou J, Kim ML, Heo WD, Jones JT, Myers JW, Ferrell JE, Jr, Meyer T. STIM — датчик Ca 2+ , необходимый для Ca 2+ -вызванное истощением запасов Ca 2+ приток. Карр Биол. 2005; 15:1235–1241. [Бесплатная статья PMC] [PubMed] [Google Scholar]
11. Feske S, Gwack Y, Prakriya M, Srikanth S, Puppel SH, Tanasa B, Hogan PG, Lewis RS, Daly M, Rao A. Мутация в Orai1 вызывает иммунный дефицит, нарушая функцию канала CRAC. Природа. 2006;441:179–185. [PubMed] [Google Scholar]
12. Виг М., Пайнелт С., Бек А., Кумоа Д.Л., Рабах Д., Коблан-Хуберсон М., Крафт С., Тернер Х. , Флейг А., Пеннер Р., Кинет Дж. П. CRACM1 представляет собой белок плазматической мембраны, необходимый для депо-управляемого проникновения Ca 2+ . Наука. 2006; 312:1220–1223. [Бесплатная статья PMC] [PubMed] [Google Scholar]
, Флейг А., Пеннер Р., Кинет Дж. П. CRACM1 представляет собой белок плазматической мембраны, необходимый для депо-управляемого проникновения Ca 2+ . Наука. 2006; 312:1220–1223. [Бесплатная статья PMC] [PubMed] [Google Scholar]
13. Чжан С.Л., Еромин А.В., Чжан XH, Ю.Ю., Сафрина О., Пенна А., Роос Дж., Стаудерман К.А., Кахалан М.Д. Полногеномный скрининг РНКи притока Ca 2+ идентифицирует гены, которые регулируют Ca 2+ активация высвобождения Ca 2+ активность канала. Proc Natl Acad Sci USA. 2006; 103:9357–9362. [Бесплатная статья PMC] [PubMed] [Google Scholar]
14. Cahalan MD. СТИМУЛИРУЮЩИЙ вход Ca 2+ в магазине. Nat Cell Biol. 2009; 11: 669–677. [Бесплатная статья PMC] [PubMed] [Google Scholar]
15. Hogan PG, Lewis RS, Rao A. Молекулярная основа передачи сигналов кальция в лимфоцитах: STIM и ORAI. Анну Рев Иммунол. 2010; 28: 491–533. [Бесплатная статья PMC] [PubMed] [Google Scholar]
16. Соболофф Дж. , Ротберг Б.С., Мадеш М., Гилл Д.Л. Белки STIM: преобразователи динамических сигналов кальция. Nat Rev Mol Cell Biol. 2012; 13: 549–565. [Бесплатная статья PMC] [PubMed] [Google Scholar]
, Ротберг Б.С., Мадеш М., Гилл Д.Л. Белки STIM: преобразователи динамических сигналов кальция. Nat Rev Mol Cell Biol. 2012; 13: 549–565. [Бесплатная статья PMC] [PubMed] [Google Scholar]
17. Гудлур А., Чжоу Ю., Хоган П.Г. Взаимодействия STIM-ORAI, которые контролируют канал CRAC. Лучший член Curr. 2013;71:33–58. [PubMed] [Google Scholar]
18. Шим А.Х., Тирадо-Ли Л., Пракрия Структурно-функциональные механизмы регуляции каналов CRAC. Дж Мол Биол. 2014; 427:77–93. [Бесплатная статья PMC] [PubMed] [Google Scholar]
19. Dickson EJ, Duman JG, Moody MW, Chen L, Hille B. Orai-STIM-опосредованное высвобождение Ca 2+ из секреторных гранул, выявленное с помощью целевого Ca 2+ и pH-зонда. Proc Natl Acad Sci USA. 2012;109:E3539–E3548. [Бесплатная статья PMC] [PubMed] [Google Scholar]
20. Nunes P, Cornut D, Bochet V, Hasler U, Oh-hora M, Waldburger JM, Demaurex N. STIM1 сопоставляет ER с фагосомами, генерируя Ca 2+ горячих точек, которые усиливают фагоцитоз. Карр Биол. 2012; 22:1990–1997. [PubMed] [Google Scholar]
Карр Биол. 2012; 22:1990–1997. [PubMed] [Google Scholar]
21. Stiber J, Hawkins A, Zhang ZS, Wang S, Burch J, Graham V, Ward CC, Seth M, Finch E, Malouf N, Williams RS, Eu JP, Rosenberg Передача сигналов P. STIM1 контролирует депо-управляемое поступление кальция, необходимого для развития и сократительной функции скелетных мышц. Nat Cell Biol. 2008; 10: 688–697. [PMC бесплатная статья] [PubMed] [Google Scholar]
22. Лыфенко А.Д., Дирксен Р.Т. Дифференциальная зависимость входа Ca 2+ , связанного с депо, и связанного с возбуждением в скелетных мышцах от STIM1 и Orai1. Дж. Физиол. 2008; 586:4815–4824. [Бесплатная статья PMC] [PubMed] [Google Scholar]
23. Эдвардс Дж. Н., Мерфи Р. М., Калли Т. Р., фон Вегнер Ф., Фридрих О., Лауниконас Б. С. Сверхбыстрая активация и деактивация депо-управляемого проникновения Ca 2+ в скелетные мышцы. Клеточный кальций. 2010; 47: 458–467. [PubMed] [Google Scholar]
24. Launikonas BS, Murphy RM, Edwards JN. К роли депо-управляемого входа Ca 2+ в скелетные мышцы. Арка Пфлюгера. 2010; 460:813–823. [PubMed] [Google Scholar]
К роли депо-управляемого входа Ca 2+ в скелетные мышцы. Арка Пфлюгера. 2010; 460:813–823. [PubMed] [Google Scholar]
25. Darbellay B, Arnadeau S, Bader CR, Konig S, Bernheim L. STIM1L представляет собой новый актин-связывающий вариант, участвующий в быстром повторении Ca 9.0011 2+ выпуск. Джей Селл Биол. 2011;194:335–346. [Бесплатная статья PMC] [PubMed] [Google Scholar]
26. Wei-LaPierre L, Carrell EM, Boncompagni S, Protasi F, Dirksen RT. Зависимое от Orai1 поступление кальция способствует росту скелетных мышц и ограничивает утомляемость. Нац коммуна 2013. 2013;4:2805. [Бесплатная статья PMC] [PubMed] [Google Scholar]
27. Ву М.М., Бьюкенен Дж., Луйк Р.М., Льюис Р.С. Истощение запасов Ca 2+ вызывает накопление STIM1 в областях ER, тесно связанных с плазматической мембраной. Джей Селл Биол. 2006; 174: 803–813. [Бесплатная статья PMC] [PubMed] [Google Scholar]
28. Orci L, Ravazzola M, Le Coadic M, Shen WW, Demaurex N, Cosson P.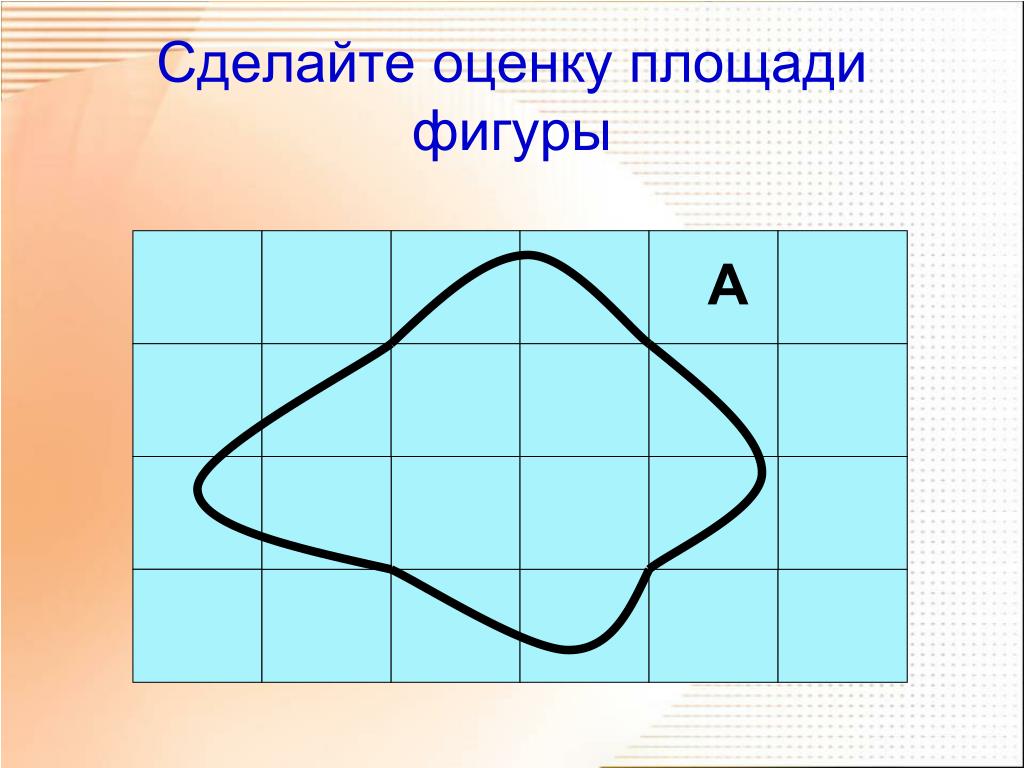 STIM1-индуцированные прекортикальные и кортикальные субдомены эндоплазматического ретикулума. Proc Natl Acad Sci USA. 2009;106:19358–19362. [Бесплатная статья PMC] [PubMed] [Google Scholar]
STIM1-индуцированные прекортикальные и кортикальные субдомены эндоплазматического ретикулума. Proc Natl Acad Sci USA. 2009;106:19358–19362. [Бесплатная статья PMC] [PubMed] [Google Scholar]
29. Luik RM, Wu MM, Buchanan J, Lewis RS. Элементарная единица депо-управляемого проникновения Ca 2+ : локальная активация каналов CRAC с помощью STIM1 в местах соединения ER-плазматической мембраны. Джей Селл Биол. 2006; 174: 815–825. [Бесплатная статья PMC] [PubMed] [Google Scholar]
30. Шарма С., Кинтана А., Финдли Г.М., Меттлен М., Бауст Б., Джейн М., Нильссон Р., Рао А., Хоган П.Г. Скрининг siRNA для активации NFAT идентифицирует септины как координаторы депо-управляемого входа Ca 2+ . Природа. 2013; 499: 238–242. [Бесплатная статья PMC] [PubMed] [Google Scholar]
31. Гудлур А., Кинтана А., Чжоу И., Хирве Н., Махапатра С., Хоган П.Г. STIM1 запускает перестройку ворот во внеклеточном устье канала ORAI1. Нац Коммуна 2014 Октябрь 9. 2014;5:5164. [Бесплатная статья PMC] [PubMed] [Google Scholar]
32. Сампиери А., Зепеда А., Асанов А., Вака Л. Визуализация сборки комплекса управляемых магазином каналов в режиме реального времени: идентификация SERCA2 как нового члена. Клеточный кальций. 2009; 45: 439–446. [PubMed] [Google Scholar]
Сампиери А., Зепеда А., Асанов А., Вака Л. Визуализация сборки комплекса управляемых магазином каналов в режиме реального времени: идентификация SERCA2 как нового члена. Клеточный кальций. 2009; 45: 439–446. [PubMed] [Google Scholar]
33. Ву М.М., Ковингтон Э.Д., Льюис Р.С. Одномолекулярный анализ диффузии и захвата STIM1 и Orai1 в соединениях эндоплазматического ретикулума и плазматической мембраны. Мол Биол Селл. 2014;25:3672–3685. [Бесплатная статья PMC] [PubMed] [Google Scholar]
34. Ji W, Xu P, Li Z, Lu J, Liu L, Zhan Y, Chen Y, Hille B, Xu T, Chen L. Функциональная стехиометрия унитарный кальциевый канал, активируемый высвобождением кальция. Proc Natl Acad Sci USA. 2008; 105:13668–13673. [Бесплатная статья PMC] [PubMed] [Google Scholar]
35. Лур Г., Хейнс Л.П., Приор И.А., Герасименко О.В., Феске С., Петерсен О.Х., Бургойн Р.Д., Тепикин А.В. Свободные от рибосом терминали шероховатого ЭР позволяют формировать точки STIM1 и отделять STIM1 от рецепторов IP 3 . Карр Биол. 2009;19:1648–1653. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Карр Биол. 2009;19:1648–1653. [Бесплатная статья PMC] [PubMed] [Google Scholar]
36. Shen WW, Frieden M, Demaurex N. Ремоделирование эндоплазматического ретикулума во время поступления кальция в депо. Биол Клетка. 2011; 103: 365–380. [PubMed] [Google Scholar]
37. Джордано Ф., Сахеки Ю., Идевалл-Хагрен О., Коломбо С.Ф., Пирруччелло М., Милошевич И., Грачева Е.О., Багрянцев С.Н., Боргезе Н., Де Камилли П. PI(4,5) стр. 2 -зависимое и Ca 2+ -регулируемое взаимодействие ER-PM, опосредованное расширенными синаптотагминами. Клетка. 2013; 153:1494–1509. [Бесплатная статья PMC] [PubMed] [Google Scholar]
38. Várnai P, Tóth B, Tóth DJ, Hunyady L, Balla T. Визуализация и манипулирование сайтами контактов плазматической мембраны и ретикулума указывает на присутствие дополнительных молекулярных компонентов в пределах Комплекс СТИМ1-Орай1. Дж. Биол. Хим. 2007; 282:29678–29690. [PubMed] [Google Scholar]
39. Huang GN, Zeng W, Kim JY, Yuan JP, Han L, Muallem S, Worley PF. Карбоксильный конец STIM1 активирует нативные каналы SOC, Icrac и TRPC1. Nat Cell Biol. 2006; 8: 1003–1010. [PubMed] [Академия Google]
Карбоксильный конец STIM1 активирует нативные каналы SOC, Icrac и TRPC1. Nat Cell Biol. 2006; 8: 1003–1010. [PubMed] [Академия Google]
40. Liou J, Fivaz M, Inoue T, Meyer T. Визуализация живых клеток показывает последовательную олигомеризацию и локальное нацеливание на плазматическую мембрану молекулы стромального взаимодействия 1 после истощения запасов Ca 2+ . Proc Natl Acad Sci USA. 2007; 104:9301–9306. [Статья бесплатно PMC] [PubMed] [Google Scholar]
41. Ercan E, Momburg F, Engel U, Temmerman K, Nickel W, Seedorf M. Консервативный, опосредованный липидами механизм сортировки дрожжей Ist2 и белков STIM млекопитающих для периферическая ЭР. Трафик. 2009 г.;10:1802–1818. [PubMed] [Google Scholar]
42. Чжоу Ю., Шринивасан П., Разави С., Сеймур С., Меранер П., Гудлур А., Статопулос П., Икура М., Рао А., Хоган П.Г. Начальная активация STIM1, регулятора поступления кальция в депо. Nat Struct Mol Biol. 2013;20:973–981. [PMC free article] [PubMed] [Google Scholar]
43. Bhardwaj R, Müller HM, Nickel W, Seedorf M. Олигомеризация и Ca 2+ /кальмодулин контролируют связывание ER Ca 2+ -сенсоры STIM1 и STIM2 к липидам плазматической мембраны. Biosci Rep 2013. 2013;33(5):e00077. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Bhardwaj R, Müller HM, Nickel W, Seedorf M. Олигомеризация и Ca 2+ /кальмодулин контролируют связывание ER Ca 2+ -сенсоры STIM1 и STIM2 к липидам плазматической мембраны. Biosci Rep 2013. 2013;33(5):e00077. [Бесплатная статья PMC] [PubMed] [Google Scholar]
44. Парк С.И., Гувер П.Дж., Маллинз Ф.М., Баххават П., Ковингтон Э.Д., Раунсер С., Вальц Т., Гарсия К.С., Долметч Р.Е., Льюис Р.С. STIM1 кластеризуется и активирует каналы CRAC посредством прямого связывания цитозольного домена с Orai1. Клетка. 2009; 136: 876–890. [PMC бесплатная статья] [PubMed] [Google Scholar]
45. Уолш С.М., Чванов М., Хейнс Л.П., Петерсен О.Х., Тепикин А.В., Бургойн Р.Д. Роль фосфоинозитидов в динамике STIM1 и депонированном поступлении кальция. Биохим Дж. 2009;425:159–168. [Бесплатная статья PMC] [PubMed] [Google Scholar]
46. Муик М., Фришауф И., Дерлер И., Фарнер М., Бергсманн Дж., Эдер П., Шиндл Р., Хеш С., Полцингер Б., Фрич Р., Кар Х., Мадл Дж., Грубер Х., Грошнер К. , Романин С. Динамика соединение предполагаемого спирально-скрученного домена ORAI1 со STIM1 опосредует активацию канала ORAI1. Дж. Биол. Хим. 2008; 283:8014–8022. [PubMed] [Google Scholar]
, Романин С. Динамика соединение предполагаемого спирально-скрученного домена ORAI1 со STIM1 опосредует активацию канала ORAI1. Дж. Биол. Хим. 2008; 283:8014–8022. [PubMed] [Google Scholar]
47. Наварро-Борелли Л., Сомасундарам А., Ямашита М., Рен Д., Миллер Р.Дж., Пракрия М. Взаимодействия STIM1-Orai1 и конформационные изменения Orai1, выявленные с помощью FRET-микроскопии живых клеток. Дж. Физиол. 2008; 586: 5383–5401. [Бесплатная статья PMC] [PubMed] [Google Scholar]
48. Барр В.А., Бернот К.М., Срикант С., Гвак Ю., Балагопалан Л., Риган К.К., Хелман Д.Дж., Соммерс С.Л., Охора М., Рао А., Самельсон Л.Е. Динамическое движение кальциевого сенсора STIM1 и кальциевого канала Orai1 в активированных Т-клетках: точки и дистальные колпачки. Мол Биол Селл. 2008;19:2802–2817. [Бесплатная статья PMC] [PubMed] [Google Scholar]
49. Frischauf I, Muik M, Derler I, Bergsmann J, Fahrner M, Schindl R, Groschner K, Romanin C. Молекулярные детерминанты связи между каналами STIM1 и Orai : дифференциальная активация каналов Orai1-3 мутантом спиральной катушки STIM1.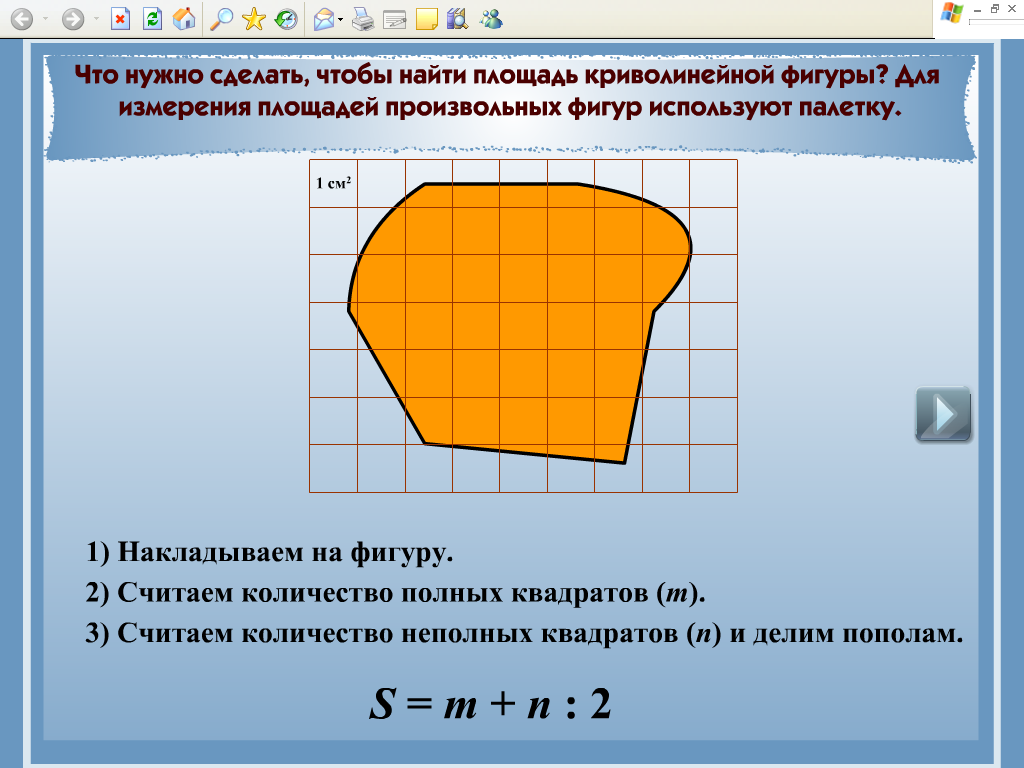 Дж. Биол. Хим. 2009 г.;284:21696–21706. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Биол. Хим. 2009 г.;284:21696–21706. [Бесплатная статья PMC] [PubMed] [Google Scholar]
50. Calloway N, Vig M, Kinet J-P, Holowka D, Baird B. Молекулярная кластеризация STIM1 с Orai1/CRACM1 на плазматической мембране динамически зависит от истощения Ca 2+ накопителей и на электростатические взаимодействия. Мол Биол Селл. 2009; 20: 389–399. [Бесплатная статья PMC] [PubMed] [Google Scholar]
51. Yuan JP, Zeng W, Dorwart MR, Choi YJ, Worley PF, Muallem S. SOAR и многоосновные домены STIM1 блокируют и регулируют каналы Orai. Nat Cell Biol. 2009 г.;11:337–343. [Бесплатная статья PMC] [PubMed] [Google Scholar]
52. Zhou Y, Meraner P, Kwon HT, Machnes D, Oh-hora M, Zimmer J, Huang Y, Stura A, Rao A, Hogan PG. STIM1 управляет депо-управляемым кальциевым каналом ORAI1 in vitro. Nat Struct Mol Biol. 2010;17:112–116. [PMC бесплатная статья] [PubMed] [Google Scholar]
53. Muik M, Fahrner M, Schindl R, Stathopulos P, Frischauf I, Derler I, Plenk P, Lackner B, Groschner K, Ikura M, Romanin C. STIM1 соединяется с ORAI1 через внутримолекулярный переход в расширенную конформацию. EMBO J. 2011; 30: 1678–1689.. [Бесплатная статья PMC] [PubMed] [Google Scholar]
STIM1 соединяется с ORAI1 через внутримолекулярный переход в расширенную конформацию. EMBO J. 2011; 30: 1678–1689.. [Бесплатная статья PMC] [PubMed] [Google Scholar]
54. Prakriya M, Lewis RS. Разделение и характеристика токов через депо-управляемые каналы CRAC и Mg 2+ -ингибированные катионные (MIC) каналы. J Gen Physiol. 2002; 119: 487–507. [Бесплатная статья PMC] [PubMed] [Google Scholar]
55. Prakriya M, Lewis RS. Регулирование активности канала CRAC путем включения молчащих каналов в режим стробирования с высокой вероятностью открытия. J Gen Physiol. 2006; 128: 373–386. [Бесплатная статья PMC] [PubMed] [Google Scholar]
56. Еромин А.В., Роос Дж., Стаудерман К.А., Кахалан М.Д. Депо-управляемый кальциевый канал в клетках дрозофилы S2. J Gen Physiol. 2004; 123:167–182. [Бесплатная статья PMC] [PubMed] [Google Scholar]
57. Abell E, Ahrends R, Bandara S, Park BO, Teruel MN. Параллельная адаптивная обратная связь повышает надежность сигнальной системы Ca 2+ . Proc Natl Acad Sci USA. 2011;108:14485–14490. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Proc Natl Acad Sci USA. 2011;108:14485–14490. [Бесплатная статья PMC] [PubMed] [Google Scholar]
58. Fasolato C, Nilius B. Истощение запасов вызывает кальциевый ток, активируемый высвобождением кальция (I CRAC ) в макрососудистых эндотелиальных клетках; сравнение с линиями клеток Jurkat и эмбриональной почки. Арка Пфлюгера. 1998; 436: 69–74. [PubMed] [Google Scholar]
59. Бугай В., Алексеенко В., Зубов А., Глушанкова Л., Николаев А., Ван З., Казначеева Е., Безпрозванный И., Можаева Г.Н. Функциональные свойства эндогенных рецептор- и депо-управляемых каналов притока кальция в клетках HEK293. Дж. Биол. Хим. 2005; 280:16790–16797. [PubMed] [Google Scholar]
60. Mercer JC, DeHaven WI, Smyth JT, Wedel B, Boyles RR, Bird GS, Putney JW., Jr Большие избирательные потоки кальция, управляемые депо, из-за коэкспрессии Orai1 или Orai2 с внутриклеточным датчиком кальция Stim1. Дж. Биол. Хим. 2006;281:24979–24990. [Бесплатная статья PMC] [PubMed] [Google Scholar]
61. Gonzalez-Cobos JC, Zhang X, Zhang W, Ruhle B, Motiani RK, Schindl R, Muik M, Spinelli AM, Bisaillon JM, Shinde AV, Fahrner M , Singer HA, Matrougui K, Barroso M, Romanin C, Trebak M. Store-независимые каналы Orai1/3, активируемые интракринным лейкотриеном C 4 : роль в неоинтимальной гиперплазии. Цирк Рез. 2013; 112:1013–1025. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Gonzalez-Cobos JC, Zhang X, Zhang W, Ruhle B, Motiani RK, Schindl R, Muik M, Spinelli AM, Bisaillon JM, Shinde AV, Fahrner M , Singer HA, Matrougui K, Barroso M, Romanin C, Trebak M. Store-независимые каналы Orai1/3, активируемые интракринным лейкотриеном C 4 : роль в неоинтимальной гиперплазии. Цирк Рез. 2013; 112:1013–1025. [Бесплатная статья PMC] [PubMed] [Google Scholar]
62. Motiani RK, Hyzinski-Garcia MC, Zhang X, Henkel MM, Abdullaev IF, Kuo Y-H, Matrougui K, Mongin AA, Trebak M. STIM1 и Orai1 опосредуют CRAC активность каналов и необходимы для инвазии глиобластомы человека. Арка Пфлюгера. 2013;465:1249–1260. [Бесплатная статья PMC] [PubMed] [Google Scholar]
63. Peinelt C, Vig M, Koomoa DL, Beck A, Nadler MJS, Koblan-Huberson M, Lis A, Fleig A, Penner R, Kinet J-P. Усиление тока CRAC с помощью STIM1 и CRACM1 (Orai1). Nat Cell Biol. 2006; 8: 771–773. [Бесплатная статья PMC] [PubMed] [Google Scholar]
64. Soboloff J, Spassova MA, Tang XD, Hewavitharana T, Xu W, Gill DL.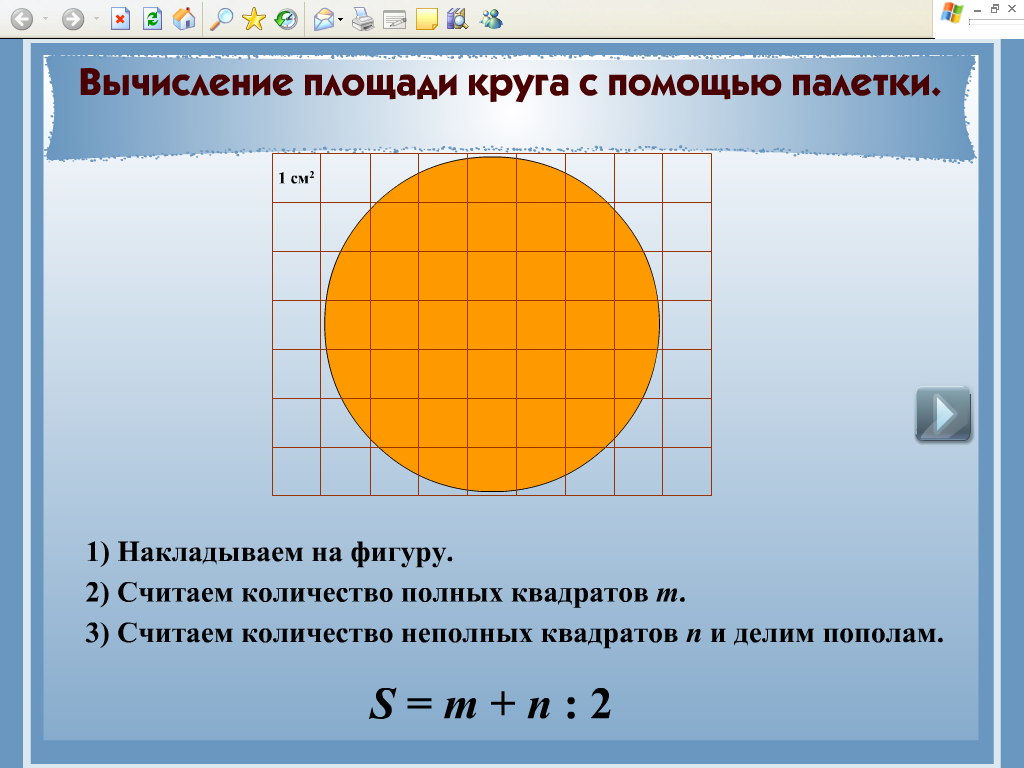 Orai1 и STIM восстанавливают функцию депо-управляемых кальциевых каналов. Дж. Биол. Хим. 2006; 281:20661–20665. [PubMed] [Академия Google]
Orai1 и STIM восстанавливают функцию депо-управляемых кальциевых каналов. Дж. Биол. Хим. 2006; 281:20661–20665. [PubMed] [Академия Google]
65. Bird GS, Hwang SY, Smyth JT, Fukushima M, Boyles RR, Putney JW., Jr STIM1 — датчик кальция, предназначенный для цифровой сигнализации. Карр Биол. 2009;19:1724–1729. [Бесплатная статья PMC] [PubMed] [Google Scholar]
66. McKeown L, Moss NK, Turner P, Li J, Heath N, Burke D, O’Regan D, Gilthorpe MS, Porter KE, Beech DJ. Фактор роста, полученный из тромбоцитов, поддерживает накопленный кальций посредством некластеризующего механизма Orai1, но вызывает кластеризацию, если эндоплазматический ретикулум подвергается стрессу из-за истощения запасов. Цирк Рез. 2012; 111:66–76. [Бесплатная статья PMC] [PubMed] [Google Scholar]
67. Allbritton NL, Meyer T, Stryer L. Диапазон действия мессенджера иона кальция и инозитол 1,4,5-трифосфата. Наука. 1992; 258:1812–1815. [PubMed] [Google Scholar]
68. Donnadieu E, Bismuth G, Trautmann A.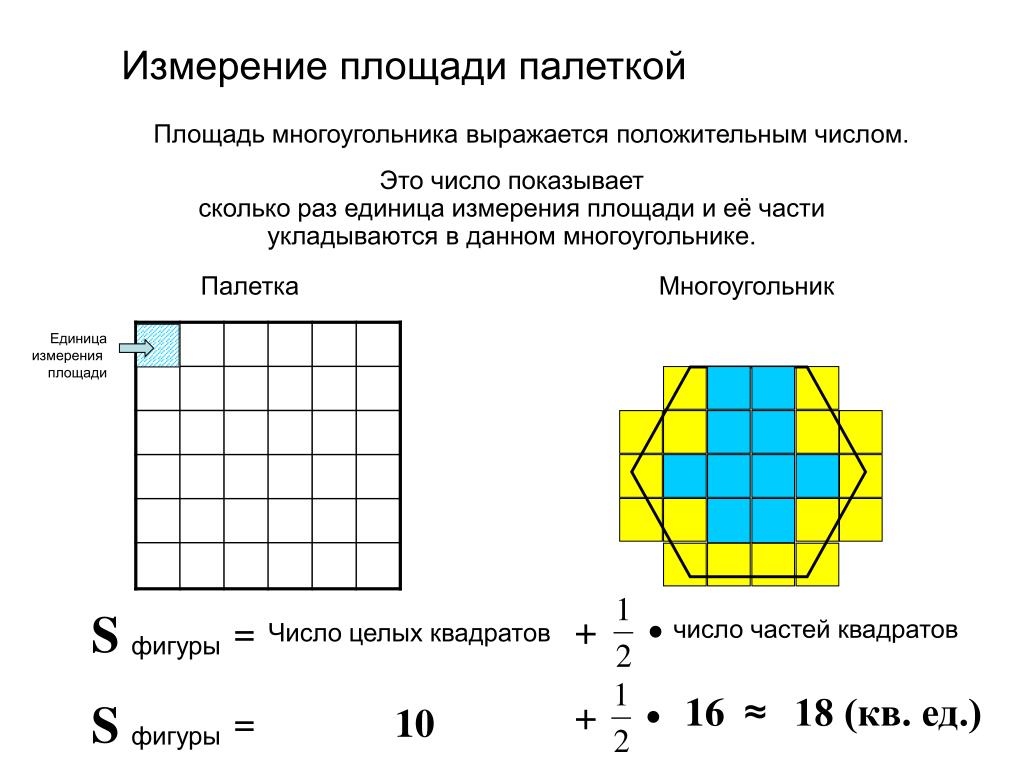 Потоки кальция в Т-лимфоцитах. Дж. Биол. Хим. 1992; 267:25864–25872. [PubMed] [Google Scholar]
Потоки кальция в Т-лимфоцитах. Дж. Биол. Хим. 1992; 267:25864–25872. [PubMed] [Google Scholar]
69. Bauer PJ. Профиль локальной концентрации Ca вблизи кальциевого канала. Клеточная биохимия Биофиз. 2001; 35:49–61. [PubMed] [Google Scholar]
70. Баутиста Д.М., Хот М., Льюис Р.А. Усиление динамики и стабильности передачи сигналов кальция за счет замедленной модуляции кальций-АТФазы плазматической мембраны в Т-клетках человека. Дж. Физиол. 2002; 541: 877–89.4. [Бесплатная статья PMC] [PubMed] [Google Scholar]
71. Bautista DM, Lewis RS. Модуляция активности кальций-АТФазы плазматической мембраны локальными кальциевыми микродоменами вблизи каналов CRAC в Т-клетках человека. Дж. Физиол. 2004; 556: 805–817. [Бесплатная статья PMC] [PubMed] [Google Scholar]
72. Gilabert JA, Parekh AB. Дышащие митохондрии определяют характер активации и инактивации депо-управляемого Ca 2+ тока I CRAC . EMBO J. 2000; 19: 6401–6407. [Бесплатная статья PMC] [PubMed] [Google Scholar]
73. Хот М., Баттон Д.С., Льюис Р.С. Митохондриальный контроль ворот кальциевых каналов: механизм устойчивой передачи сигналов и активации транскрипции в Т-лимфоцитах. Proc Natl Acad Sci USA. 2000;97:10607–10612. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Хот М., Баттон Д.С., Льюис Р.С. Митохондриальный контроль ворот кальциевых каналов: механизм устойчивой передачи сигналов и активации транскрипции в Т-лимфоцитах. Proc Natl Acad Sci USA. 2000;97:10607–10612. [Бесплатная статья PMC] [PubMed] [Google Scholar]
74. Zweifach A, Lewis RS. Медленная кальций-зависимая инактивация кальциевого тока, активируемого истощением. Магазинозависимые и -независимые механизмы. Дж. Биол. Хим. 1995; 279:14445–14451. [PubMed] [Google Scholar]
75. Hoth M, Fanger CM, Lewis RS. Митохондриальная регуляция депо-управляемой передачи сигналов кальция в Т-лимфоцитах. Джей Селл Биол. 1997;137:633–648. [Бесплатная статья PMC] [PubMed] [Google Scholar]
76. Glitsch MD, Bakowski D, Parekh AB. Депо-управляемый вход Ca 2+ зависит от поглощения Ca 2+ митохондриями. EMBO J. 2002; 21: 6744–6754. [PMC free article] [PubMed] [Google Scholar]
77. Giacomello M, Drago I, Bortolozzi M, Scorzeto M, Gianelle A, Pizzo P, Pozzan T. Ca 2+ горячих точек на поверхности митохондрий путем мобилизации Ca 2+ из депо, но не путем активации депо-управляемого Ca 2+ каналов. Мол Ячейка. 2010; 38: 280–290. [PubMed] [Google Scholar]
Ca 2+ горячих точек на поверхности митохондрий путем мобилизации Ca 2+ из депо, но не путем активации депо-управляемого Ca 2+ каналов. Мол Ячейка. 2010; 38: 280–290. [PubMed] [Google Scholar]
78. Spät A, Szanda G, Csordás G, Hajnóczky G. Зависимые от высокого и низкого уровня кальция механизмы митохондриальной передачи сигналов кальция. Клеточный кальций. 2008;44:51–63. [Бесплатная статья PMC] [PubMed] [Google Scholar]
79. Korzeniowski MK, Szanda G, Balla T, Spät A. Депо-управляемый приток Ca2+ и субплазмалеммальные митохондрии. Клеточный кальций. 2009; 46:49–55. [Бесплатная статья PMC] [PubMed] [Google Scholar]
80. Zweifach A, Lewis RS. Быстрая инактивация кальциевого тока, активируемого истощением (I CRAC ) из-за местной обратной связи кальция. J Gen Physiol. 1995; 105: 209–226. [Бесплатная статья PMC] [PubMed] [Google Scholar]
81. Fagan KA, Mons N, Cooper DMF. Зависимость Са 2+ -ингибируемой аденилатциклазы клеток глиомы С6-2В от емкостного входа Са 2+ . Дж. Биол. Хим. 1998; 273:9297–9305. [PubMed] [Google Scholar]
Дж. Биол. Хим. 1998; 273:9297–9305. [PubMed] [Google Scholar]
82. Willoughby D, Cooper DMF. Организация и регуляция Ca 2+ аденилатциклаз в микродоменах цАМФ. Physiol Rev. 2007; 87:965–1010. [PubMed] [Google Scholar]
83. Martin ACL, Willoughby D, Ciruela A, Ayling LJ, Pagano M, Wachten S, Tengholm A, Cooper DMF. Емкостный вход Ca 2+ через Orai1 и стромально взаимодействующую молекулу 1 (STIM1) регулирует аденилатциклазу типа 8. Mol Pharmacol. 2009; 75: 830–842. [Бесплатная статья PMC] [PubMed] [Google Scholar]
84. Ng SW, Nelson C, Parekh AB. Связывание микродоменов Ca 2+ с пространственно и во времени различными клеточными ответами с помощью тирозинкиназы Syk. Дж. Биол. Хим. 2009 г.;284:24767–24772. [Бесплатная статья PMC] [PubMed] [Google Scholar]
85. Кар П., Нельсон С., Парех А.Б. Селективная активация фактора транскрипции NFAT1 кальциевыми микродоменами вблизи каналов Ca 2+ , активируемых высвобождением Ca 2+ (CRAC). Дж. Биол. Хим. 2011; 286:14795–14803. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Биол. Хим. 2011; 286:14795–14803. [Бесплатная статья PMC] [PubMed] [Google Scholar]
86. Chang WC, Di Capite J, Singaravelu K, Nelson C, Halse V, Parekh AB. Локальный приток Ca 2+ через Ca 2+ , активированный высвобождением Ca 2+ (CRAC) каналов стимулирует выработку внутриклеточного мессенджера и межклеточного провоспалительного сигнала. Дж. Биол. Хим. 2008; 283:4622–4631. [PubMed] [Google Scholar]
87. Cheng KT, Liu X, Ong HL, Swaim W, Ambudkar IS. Локальное проникновение Ca 2+ через Orai1 регулирует рекрутирование TRPC1 на плазматической мембране и контролирует цитозольные сигналы Ca 2+ , необходимые для специфических клеточных функций. PLoS Biol 2011. 2011;9(3):e1001025. [Бесплатная статья PMC] [PubMed] [Google Scholar]
88. Willoughby D, Everett KL, Halls ML, Pacheco J, Skroblin P, Vaca L, Klussmann E, Cooper DMF. Прямое связывание между Orai1 и AC8 обеспечивает динамическое взаимодействие между Ca 2+ и передачей сигналов cAMP. Научный сигнал. 2012;5:ra29. (2012) [PubMed] [Google Scholar]
Научный сигнал. 2012;5:ra29. (2012) [PubMed] [Google Scholar]
89. Кар П., Саманта К., Крамер Х., Моррис О., Баковски Д., Парех А.Б. Динамическая сборка мембранного сигнального комплекса обеспечивает избирательную активацию NFAT с помощью Orai1. Карр Биол. 2014; 24:1361–1368. [Бесплатная статья PMC] [PubMed] [Google Scholar]
90. Уиллоуби Д., Вахтен С., Масада Н., Купер Д.М.Ф. Прямая демонстрация дискретных микродоменов Ca 2+ , связанных с различными изоформами аденилатциклазы. Дж. Клеточные науки. 2010; 123:107–117. [Бесплатная статья PMC] [PubMed] [Google Scholar]
91. Willoughby D, Masada N, Crossthwaite AJ, Ciruela A, Cooper DMF. Локализованная экспрессия обменника 1 Na + /H + защищает аденилатциклазы, регулируемые Ca 2+ , от изменений внутриклеточного pH. Дж. Биол. Хим. 2005; 280:30864–30872. [PubMed] [Академия Google]
92. Ведель Б., Бойлз Р.Р., Путни Дж.В., младший, Берд Г.С. Роль депо-управляемых белков входа кальция Stim1 и Orai1 в колебания кальция, стимулированные мускариновыми холинергическими рецепторами, в эмбриональных клетках почек человека. Дж. Физиол. 2007; 579: 679–689. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Физиол. 2007; 579: 679–689. [Бесплатная статья PMC] [PubMed] [Google Scholar]
93. Kar P, Nelson C, Parekh AB. Каналы CRAC управляют цифровой активацией и обеспечивают аналоговый контроль и синергию с Ca 2+ -зависимой регуляцией генов. Карр Биол. 2012; 22: 242–247. [PubMed] [Академия Google]
94. Brandman O, Liou J, Park WS, Meyer T. STIM2 представляет собой регулятор обратной связи, который стабилизирует базальные уровни цитозольного и эндоплазматического ретикулума Ca 2+ . Клетка. 2007; 131:1327–1339. [Бесплатная статья PMC] [PubMed] [Google Scholar]
95. Охора М., Ямасита М., Хоган П.Г., Шарма С., Ламперти Э., Чанг В., Пракрия М., Феске С., Рао А. Двойные функции эндоплазматического датчики кальция ретикулума STIM1 и STIM2 в активации и толерантности Т-клеток. Нат Иммунол. 2008; 9: 432–443. [Бесплатная статья PMC] [PubMed] [Google Scholar]
96. Thiel M, Lis A, Penner R. STIM2 управляет колебаниями Ca 2+ через вход Ca 2+ , управляемый хранилищем, вызванный умеренным истощением запасов. Дж. Физиол. 2013; 591:1433–1445. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Физиол. 2013; 591:1433–1445. [Бесплатная статья PMC] [PubMed] [Google Scholar]
97. Малли Р., Фриден М., Хункова М., Тренкер М., Грайер В.Ф. Заполнение эндоплазматического ретикулума Ca 2+ в значительной степени сохраняется, хотя вход Ca 2+ в эндотелиальные клетки снижен. Клеточный кальций. 2007; 41: 63–76. [Бесплатная статья PMC] [PubMed] [Google Scholar]
98. Alonso MT, Manjarres IM, Garcia-Sancho J. Привилегированная связь между входом Ca 2+ через депо Ca 2+ , управляемым плазматической мембраной, и насосом Ca 2+ эндоплазматического ретикулума. Мол Селл Эндокринол. 2012; 353:37–44. [PubMed] [Google Scholar]
99. Гарсия-Санчо Дж. Связь входа кальция в плазматической мембране с поглощением кальция эндоплазматическим ретикулумом и митохондриями. Дж. Физиол. 2014; 592: 261–268. [Бесплатная статья PMC] [PubMed] [Google Scholar]
100. Jousset H, Frieden M, Demaurex N. Нокдаун STIM1 показывает, что депо-управляемые каналы Ca 2+ , расположенные близко к сарко/эндоплазматической Ca 2+ АТФазам (SERCA), молча пополняют эндоплазматический ретикулум. Дж. Биол. Хим. 2007; 282:11456–11464. [PubMed] [Google Scholar]
Дж. Биол. Хим. 2007; 282:11456–11464. [PubMed] [Google Scholar]
101. Lytton J, Westlin M, Burk SE, Shull GE, MacLennan DH. Функциональные сравнения между изоформами семейства саркоплазматического или эндоплазматического ретикулума кальциевых насосов. Дж. Биол. Хим. 1992; 267:14483–14489. [PubMed] [Google Scholar]
102. Минс С., Смит А.Дж., Шеперд Дж., Шадид Дж., Фаулер Дж., Войцикевич Р.Дж.Х., Мазель Т., Смит Г.Д., Уилсон Б.С. Реакционно-диффузионное моделирование динамики кальция с реалистичной геометрией ЭР. Биофиз Дж. 2006; 91: 537–557. [Бесплатная статья PMC] [PubMed] [Google Scholar]
103. Vaca L. SOCIC: комплекс притока кальция с запасом. Клеточный кальций. 2010;47:199–209. [PubMed] [Google Scholar]
104. Соболов Дж., Спасова М.А., Хевавитарана Т., Хе Л.П., Сюй В., Джонстон Л.С., Дзиадек М.А., Гилл Д.Л. STIM2 является ингибитором STIM1-опосредованного депо-управляемого Ca 9.0011 2+ запись. Карр Биол. 2006; 16:1465–1470. [PubMed] [Google Scholar]
105. Dupont G, Combettes L, Bird GS, Putney JW. Кальциевые колебания. Колд Спринг Харб Перспект Биол. 2011;3:a004226. 2011. [Статья бесплатно PMC] [PubMed] [Google Scholar]
Dupont G, Combettes L, Bird GS, Putney JW. Кальциевые колебания. Колд Спринг Харб Перспект Биол. 2011;3:a004226. 2011. [Статья бесплатно PMC] [PubMed] [Google Scholar]
106. Bird GS, Putney JW., Jr Емкостный вход кальция поддерживает кальциевые колебания в эмбриональных клетках почек человека. Дж. Физиол. 2005; 562: 697–706. [Бесплатная статья PMC] [PubMed] [Google Scholar]
107. Di Capite J, Ng SW, Parekh AB. Расшифровка цитоплазматического Ca 2+ колебаний через пространственную сигнатуру управляет экспрессией генов. Карр Биол. 2009; 19: 853–858. [PubMed] [Google Scholar]
108. Korzeniowski MK, Popovic MA, Szentpetery Z, Varnai P, Stojilkovic SS, Balla T. Зависимость STIM1/Orai1-опосредованного входа кальция в фосфоинозитиды плазматической мембраны. Дж. Биол. Хим. 2009; 284:21027–21035. [Бесплатная статья PMC] [PubMed] [Google Scholar]
109. Calloway N, Owens T, Corwith K, Rodgers W, Holowka D, Baird B. Стимулированная ассоциация STIM1 и Orai1 регулируется балансом PtdIns(4, 5)п 2 между отдельными пулами мембран. Дж. Клеточные науки. 2011;124:2602–2610. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Клеточные науки. 2011;124:2602–2610. [Бесплатная статья PMC] [PubMed] [Google Scholar]
110. Малет Дж., Чой С., Муаллем С., Ахуджа М. Транслокация между PI(4,5)P 2 -бедный и PI(4,5)P 2 -богатые микродомены во время истощения хранилища определяют конформацию STIM1 и ворота Orai1. Nat Commun 2014 17 декабря 2014; 5: 5843. [Бесплатная статья PMC] [PubMed] [Google Scholar]
111. Chang CL, Hsieh TS, Yang TT, Rothberg KG, Azizoglu DB, Volk E, Liao JC, Liou J. Обратная регуляция индуцированного рецептором Ca 2+ передача сигналов, опосредованная E-Syt1 и Nir2 в соединениях эндоплазматического ретикулума и плазматической мембраны. Cell Rep. 2013; 5:813–825. [PubMed] [Google Scholar]
112. Schauder CM, Wu X, Saheki Y, Narayanaswamy P, Torta F, Wenk MR, De Camilli P, Reinisch KM. Структура расширенного синаптотагмина, связанного с липидами, указывает на его роль в переносе липидов. Природа. 2014; 510:552–555. [Бесплатная статья PMC] [PubMed] [Google Scholar]
113. Fernandez-Busnadiego R, Saheki Y, De Camilli P. Трехмерная архитектура расширенных синаптотагмин-опосредованных участков контакта эндоплазматического ретикулума с плазматической мембраной. Proc Natl Acad Sci USA. 2015;112:E2004–E2013. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Fernandez-Busnadiego R, Saheki Y, De Camilli P. Трехмерная архитектура расширенных синаптотагмин-опосредованных участков контакта эндоплазматического ретикулума с плазматической мембраной. Proc Natl Acad Sci USA. 2015;112:E2004–E2013. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Визуализация данных в Python с помощью plt.scatter() — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание:
Использование plt.scatter() для визуализации данных в Python Важной частью работы с данными является возможность визуализировать их. В Python есть несколько сторонних модулей, которые вы можете использовать для визуализации данных. Одним из самых популярных модулей является Matplotlib и его подмодуль pyplot , часто упоминаемый с использованием псевдонима plt . Matplotlib предоставляет очень универсальный инструмент под названием
Matplotlib предоставляет очень универсальный инструмент под названием plt.scatter() , который позволяет создавать как базовые, так и более сложные точечные диаграммы.
Ниже вы ознакомитесь с несколькими примерами, которые покажут вам, как эффективно использовать эту функцию.
В этом уроке вы узнаете, как:
- Создать точечную диаграмму
plt.scatter() - Используйте обязательные и дополнительные входные параметры
- Настройка точечных диаграмм для базовых и более сложных графиков
- Представление более двух измерений на точечной диаграмме
Чтобы получить максимальную отдачу от этого руководства, вы должны быть знакомы с основами программирования Python и основами NumPy и его объекта ndarray . Вам не нужно быть знакомым с Matplotlib, чтобы следовать этому руководству, но если вы хотите узнать больше о модуле, ознакомьтесь с Python Plotting With Matplotlib (Руководство).
Бесплатный бонус: Нажмите здесь, чтобы получить доступ к бесплатному руководству по ресурсам NumPy, в котором вы найдете лучшие учебные пособия, видео и книги для улучшения ваших навыков работы с NumPy.
Создание точечных диаграмм
Точечная диаграмма — это визуальное представление того, как две переменные связаны друг с другом. Вы можете использовать точечные диаграммы, чтобы исследовать взаимосвязь между двумя переменными, например, ища любую корреляцию между ними.
В этом разделе руководства вы познакомитесь с созданием базовых диаграмм рассеяния с помощью Matplotlib. В последующих разделах вы узнаете, как дополнительно настраивать графики для представления более сложных данных с использованием более двух измерений.
Удалить рекламуНачало работы с
plt.scatter() Прежде чем вы сможете начать работать с plt.scatter() , вам необходимо установить Matplotlib. Вы можете сделать это с помощью стандартного диспетчера пакетов Python,
Вы можете сделать это с помощью стандартного диспетчера пакетов Python, pip , выполнив в консоли следующую команду:
$ python -m pip установить matplotlib
Теперь, когда вы установили Matplotlib, рассмотрите следующий вариант использования. Кафе продает шесть различных видов апельсиновых напитков в бутылках. Владелец хочет понять взаимосвязь между ценой напитков и количеством каждого из них, которое он продает, поэтому он отслеживает, сколько каждого напитка он продает каждый день. Вы можете визуализировать эту связь следующим образом:
импортировать matplotlib.pyplot как plt цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40] продаж_за_день = [34, 62, 49, 22, 13, 19] plt.scatter (цена, продажи_за_день) plt.show()
В этом скрипте Python вы импортируете подмодуль pyplot из Matplotlib, используя псевдоним plt . Этот псевдоним обычно используется по соглашению для сокращения имен модулей и подмодулей. Затем вы создаете списки с ценой и средними продажами в день для каждого из шести проданных апельсиновых напитков.
Наконец, вы создаете точечную диаграмму, используя plt.scatter() с двумя переменными, которые вы хотите сравнить, в качестве входных аргументов. Поскольку вы используете сценарий Python, вам также необходимо явно отобразить фигуру с помощью plt.show() .
Когда вы используете интерактивную среду, такую как консоль или Jupyter Notebook, вам не нужно вызывать plt.show() . В этом уроке все примеры будут в виде скриптов и будут включать вызов plt.show() .
Вот результат этого кода:
Этот график показывает, что, как правило, чем дороже напиток, тем меньше товаров продается. Однако напиток, который стоит 4,02 доллара, является исключением, что может свидетельствовать о том, что это особенно популярный продукт. При таком использовании точечных диаграмм тщательная проверка может помочь вам изучить взаимосвязь между переменными. Затем вы можете провести дальнейший анализ, используя линейную регрессию или другие методы.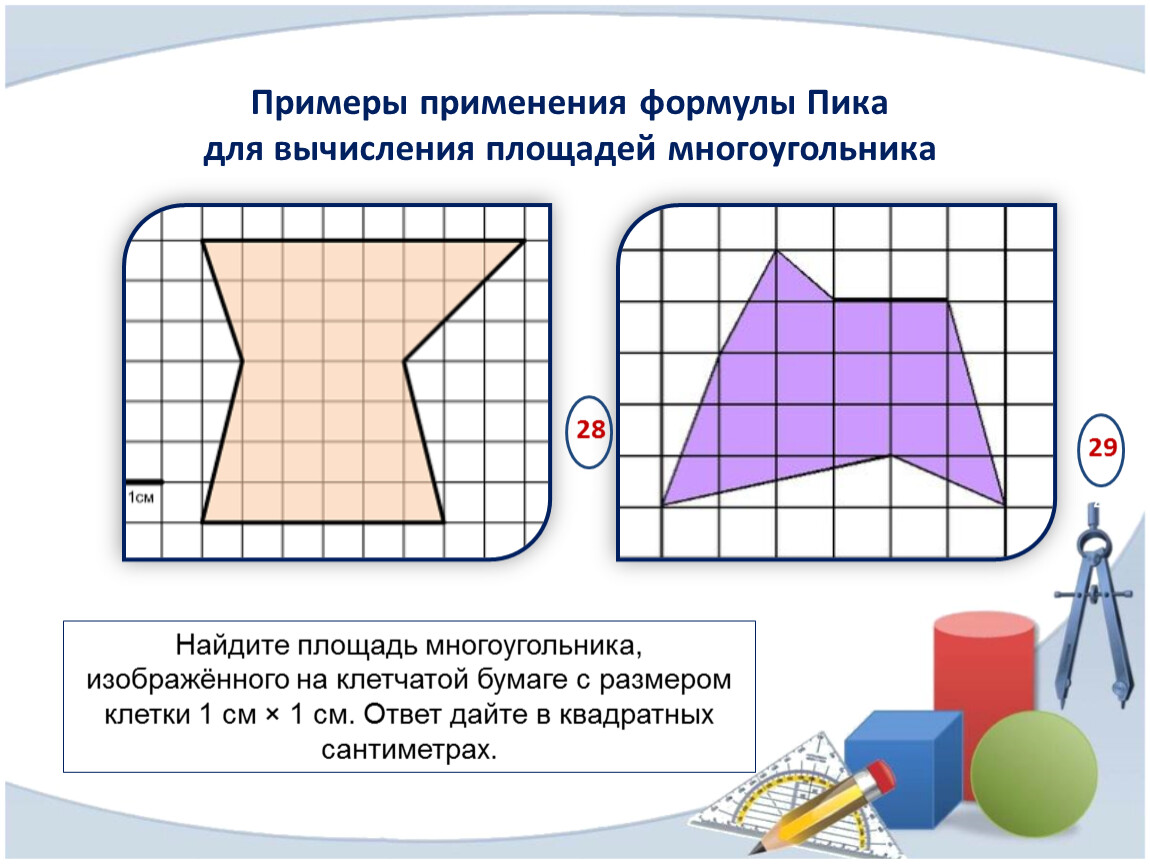
Сравнение
plt.scatter() и plt.plot() Вы также можете создать диаграмму рассеяния, показанную выше, с помощью другой функции в matplotlib.pyplot . Matplotlib plt.plot() — это функция построения графиков общего назначения, которая позволит вам создавать различные линейные или маркерные графики.
Вы можете получить тот же точечный график, что и в предыдущем разделе, с помощью следующего вызова plt.plot() , используя те же данные:
plt.plot(цена, продажи_за_день, "o") plt.show()
В этом случае вы должны были включить маркер "o" в качестве третьего аргумента, иначе plt.plot() построит линейный график. График, который вы создали с помощью этого кода, идентичен графику, который вы создали ранее с помощью
plt.scatter() . В некоторых случаях для базовой диаграммы рассеяния, которую вы строите в этом примере, может быть предпочтительнее использовать plt.. Вы можете сравнить эффективность двух функций, используя  plot()
plot() timeit модуль:
время импорта
импортировать matplotlib.pyplot как plt
цена = [2,50, 1,23, 4,02, 3,25, 5,00, 4,40]
продаж_за_день = [34, 62, 49, 22, 13, 19]
Распечатать(
"plt.scatter()",
время.время(
"plt.scatter(цена, продажи_за_день)",
число=1000,
глобальные = глобальные(),
),
)
Распечатать(
"plt.plot()",
время.время(
"plt.plot(цена, продажи_за_день, 'o')",
число=1000,
глобальные = глобальные(),
),
)
Производительность будет разной на разных компьютерах, но когда вы запустите этот код, вы обнаружите, что
plt.plot() значительно эффективнее, чем plt.scatter() . При запуске приведенного выше примера в моей системе plt.plot() работал более чем в семь раз быстрее. Если вы можете создавать точечные диаграммы с помощью plt.plot() , и это намного быстрее, зачем вам вообще использовать plt. ? Вы найдете ответ в оставшейся части этого руководства. Большинство настроек и расширенных возможностей, о которых вы узнаете в этом руководстве, возможны только при использовании  scatter()
scatter() plt.scatter() . Вот эмпирическое правило, которое вы можете использовать:
- Если вам нужен базовый точечный график, используйте
plt.plot(), особенно если вы хотите отдать приоритет производительности. - Если вы хотите настроить точечный график, используя более продвинутые функции построения графиков, используйте
plt.scatter().
В следующем разделе вы начнете изучать более сложные варианты использования plt.scatter() .
Настройка маркеров на точечных диаграммах
Вы можете визуализировать более двух переменных на двумерной диаграмме рассеяния, настроив маркеры. Существует четыре основных функции маркеров, используемых в точечной диаграмме, которые можно настроить с помощью plt. : scatter()
scatter()
- Размер
- Цвет
- Форма
- Прозрачность
В этом разделе руководства вы узнаете, как изменить все эти свойства.
Изменение размера
Вернемся к владельцу кафе, которого вы встретили ранее в этом уроке. Различные апельсиновые напитки, которые он продает, поступают от разных поставщиков и имеют разную норму прибыли. Вы можете отобразить эту дополнительную информацию на точечной диаграмме, отрегулировав размер маркера. Маржа прибыли указана в процентах в этом примере:
импортировать matplotlib.pyplot как plt импортировать numpy как np цена = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40]) sales_per_day = np.asarray([34, 62, 49, 22, 13, 19]) profit_margin = np.asarray([20, 35, 40, 20, 27,5, 15]) plt.scatter(x=цена, y=продажи_за_день, s=прибыль_маржа * 10) plt.show()
Вы можете заметить несколько изменений по сравнению с первым примером. Вместо списков теперь вы используете массивы NumPy. Для данных можно использовать любую структуру данных, подобную массиву, и массивы NumPy обычно используются в приложениях такого типа, поскольку они позволяют поэлементных операций которые выполняются эффективно. Модуль NumPy зависит от Matplotlib, поэтому вам не нужно устанавливать его вручную.
Для данных можно использовать любую структуру данных, подобную массиву, и массивы NumPy обычно используются в приложениях такого типа, поскольку они позволяют поэлементных операций которые выполняются эффективно. Модуль NumPy зависит от Matplotlib, поэтому вам не нужно устанавливать его вручную.
Вы также использовали именованных параметра в качестве входных аргументов в вызове функции. Параметры x и y являются обязательными, но все остальные параметры являются необязательными.
Параметр s обозначает размер маркера. В этом примере вы используете размер прибыли в качестве переменной для определения размера маркера и умножаете его на 9.0395 10 для более четкого отображения разницы в размерах.
Вы можете увидеть точечную диаграмму, созданную этим кодом ниже:
Размер маркера указывает размер прибыли для каждого продукта. Два апельсиновых напитка, которые продаются больше всего, также приносят наибольшую прибыль.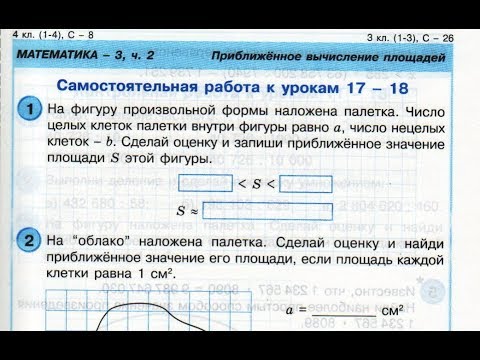 Хорошая новость для владельца кафе!
Хорошая новость для владельца кафе!
Изменение цвета
Многие посетители кафе любят внимательно читать этикетки, особенно чтобы узнать содержание сахара в напитках, которые они покупают. Владелец кафе хочет подчеркнуть свой выбор здоровых продуктов в своей следующей маркетинговой кампании, поэтому он классифицирует напитки на основе содержания в них сахара и использует систему светофора, чтобы указать низкое, среднее или высокое содержание сахара в напитках.
Вы можете раскрасить маркеры на точечной диаграмме, чтобы показать содержание сахара в каждом напитке:
# ...
низкий = (0, 1, 0)
средний = (1, 1, 0)
высокий = (1, 0, 0)
сахар_содержание = [низкий, высокий, средний, средний, высокий, низкий]
plt.scatter(
х=цена,
у=продажи_за_день,
с=прибыль_маржа * 10,
c=sugar_content,
)
plt.show()
Вы определяете переменные low , medium и high как кортежи, каждый из которых содержит три значения, представляющие компоненты красного, зеленого и синего цветов, в указанном порядке. Это значения цвета RGB. Кортежи для
Это значения цвета RGB. Кортежи для низкий , средний и высокий представляют зеленый, желтый и красный соответственно.
Затем вы определили переменную «сахар_содержание» для классификации каждого напитка. Вы используете необязательный параметр c в вызове функции, чтобы определить цвет каждого маркера. Вот точечная диаграмма, созданная этим кодом:
Владелец кафе уже решил убрать из меню самый дорогой напиток, так как он плохо продается и имеет высокое содержание сахара. Должен ли он также прекратить закупать самые дешевые напитки, чтобы повысить репутацию бизнеса в отношении здоровья, даже несмотря на то, что они хорошо продаются и приносят хорошую прибыль?
Удалить рекламуИзменение формы
Владелец кафе нашел это упражнение очень полезным и хочет исследовать другой продукт. В дополнение к апельсиновым напиткам вы теперь также нанесете аналогичные данные для ассортимента зерновых батончиков, доступных в кафе:
.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
низкий = (0, 1, 0)
средний = (1, 1, 0)
высокий = (1, 0, 0)
price_orange = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40])
sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19])
profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15])
Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий]
price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95])
sales_per_day_cereal = np.asarray([67, 34, 36, 12])
profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18])
сахара_content_cereal = [низкий, высокий, средний, низкий]
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
)
plt.show()
В этом коде вы реорганизуете имена переменных, чтобы учесть, что теперь у вас есть данные для двух разных продуктов. Затем вы строите оба графика рассеяния на одном рисунке. Это дает следующий вывод:
Затем вы строите оба графика рассеяния на одном рисунке. Это дает следующий вывод:
К сожалению, вы больше не можете понять, какие точки данных относятся к апельсиновым напиткам, а какие к зерновым батончикам. Вы можете изменить форму маркера для одной из точечных диаграмм:
импортировать matplotlib.pyplot как plt
импортировать numpy как np
низкий = (0, 1, 0)
средний = (1, 1, 0)
высокий = (1, 0, 0)
price_orange = np.asarray([2,50, 1,23, 4,02, 3,25, 5,00, 4,40])
sales_per_day_orange = np.asarray([34, 62, 49, 22, 13, 19])
profit_margin_orange = np.asarray([20, 35, 40, 20, 27,5, 15])
Sugar_content_orange = [низкий, высокий, средний, средний, высокий, низкий]
price_cereal = np.asarray([1,50, 2,50, 1,15, 1,95])
sales_per_day_cereal = np.asarray([67, 34, 36, 12])
profit_margin_cereal = np.asarray([20, 42,5, 33,3, 18])
сахара_content_cereal = [низкий, высокий, средний, низкий]
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
)
plt. scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
)
plt.show()
scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
)
plt.show()
Вы сохраняете форму маркера по умолчанию для данных апельсинового напитка. Маркером по умолчанию является "o" , что представляет собой точку. Для данных батончика хлопьев вы устанавливаете форму маркера на "d" , что представляет собой ромбовидный маркер. Вы можете найти список всех маркеров, которые вы можете использовать на странице документации по маркерам. Вот два графика рассеяния, наложенные на одну и ту же цифру:
Теперь вы можете отличить точки данных для апельсиновых напитков от точек данных для злаковых батончиков. Но есть одна проблема с последним созданным вами графиком, которую вы исследуете в следующем разделе.
Изменение прозрачности
Исчезла одна из точек данных апельсиновых напитков. Оранжевых напитков должно быть шесть, но на рисунке видно только пять круглых маркеров. Одна из точек данных зернового батончика скрывает точку данных апельсинового напитка.
Одна из точек данных зернового батончика скрывает точку данных апельсинового напитка.
Вы можете исправить эту проблему визуализации, сделав точки данных частично прозрачными, используя альфа-значение:
# ...
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
альфа=0,5,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
3.2,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.show()
Вы установили значение альфа обоих наборов маркеров на 0,5 , что означает, что они полупрозрачны. Теперь вы можете увидеть все точки данных на этом графике, включая совпадающие:
Теперь вы можете увидеть все точки данных на этом графике, включая совпадающие:
Вы также добавили заголовок и другие метки к графику, чтобы дополнить рисунок дополнительной информацией о том, что отображается.
Настройка цветовой карты и стиля
На созданных вами диаграммах рассеяния вы использовали три цвета для обозначения низкого, среднего или высокого содержания сахара в напитках и зерновых батончиках. Теперь вы измените это, чтобы цвет напрямую отображал фактическое содержание сахара в продуктах.
Сначала необходимо реорганизовать переменные Sugar_content_orange и Sugar_content_cereal , чтобы они представляли значение содержания сахара, а не только значения цвета RGB:
Sugar_content_orange = [15, 35, 22, 27, 38, 14] сахар_содержание_зерна = [21, 49, 29, 24]
Теперь это списки, содержащие процент рекомендуемого ежедневного количества сахара в каждом продукте. Остальной код остается прежним, но теперь вы можете выбрать цветовую карту для использования. Это сопоставляет значения цветам:
Это сопоставляет значения цветам:
# ...
plt.scatter(
х=цена_оранжевый,
y=продажи_за_день_оранжевый,
s=profit_margin_orange * 10,
c=sugar_content_orange,
смап = "самолет",
альфа=0,5,
)
plt.scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
смап = "самолет",
маркер = "д",
альфа=0,5,
)
plt.title("Продажи и цены на апельсиновые напитки и зерновые батончики")
plt.legend(["Апельсиновые напитки", "Злаковые батончики"])
plt.xlabel("Цена (денежная единица)")
plt.ylabel("Средние продажи за неделю")
пл.текст(
2,7,
55,
"Размер маркера = размер прибыли\n" "Цвет маркера = содержание сахара",
)
plt.colorbar()
plt.show()
Цвет маркеров теперь основан на непрерывной шкале, и вы также отобразили цветовую полосу , которая действует как легенда для цвета маркеров. Вот результирующая диаграмма рассеяния:
Все графики, которые вы построили до сих пор, были отображены в собственном стиле Matplotlib. Вы можете изменить этот стиль, используя один из нескольких вариантов. Вы можете отобразить доступные стили с помощью следующей команды:
Вы можете изменить этот стиль, используя один из нескольких вариантов. Вы можете отобразить доступные стили с помощью следующей команды:
>>> тип.табл.доступен
[
"Соляризация_Свет2",
"_classic_test_patch",
"бмх",
"классический",
"темный_фон",
"быстрый",
"пять тридцать восемь",
"ггплот",
"оттенки серого",
"морской",
"морской яркий",
"морской дальтоник",
"морской темный",
"морская-темная-палитра",
"мореборн-темная сетка",
"морская глубина",
"морской приглушенный",
"морской блокнот",
"морская бумага",
"морская пастель",
"морской постер",
"морской разговор",
"морские клещи",
"бело-морской",
"сиборн-белая сетка",
"таблица-дальтоник10",
]
Теперь вы можете изменить стиль графика при использовании Matplotlib, используя следующий вызов функции перед вызовом plt.scatter() :
импортировать matplotlib.pyplot как plt импортировать numpy как np plt.style.use («морской рожденный») # ...
Это меняет стиль на стиль Seaborn, еще одного стороннего пакета визуализации. Вы можете увидеть другой стиль, построив окончательный график рассеяния, показанный выше, с использованием стиля Seaborn:
.Вы можете узнать больше о настройке графиков в Matplotlib, а также есть дополнительные руководства на страницах документации Matplotlib.
Использование plt.scatter() для создания точечных диаграмм позволяет отображать более двух переменных. Вот переменные, представленные в этом примере:
| Переменная | Представлен |
|---|---|
| Цена | Ось X |
| Среднее количество проданных | Ось Y |
| Маржа прибыли | Размер маркера |
| Тип продукта | Форма маркера |
| Содержание сахара | Цвет маркера |
Возможность представления более двух переменных делает plt. очень мощным и универсальным инструментом. scatter()
scatter()
Изучение
plt.scatter () Далее plt.scatter() предлагает еще большую гибкость в настройке точечных диаграмм. В этом разделе вы узнаете, как маскировать данные с помощью массивов NumPy и точечных диаграмм на примере. В этом примере вы сгенерируете случайные точки данных, а затем разделите их на две отдельные области на одном графике рассеяния.
Жительница пригородной зоны, увлеченная сбором данных, сопоставила время прибытия автобусов на своей местной автобусной остановке за шестимесячный период. Время прибытия по расписанию составляет 15 минут 45 минут первого часа, но она заметила, что истинное время прибытия следует нормальному распределению вокруг этого времени:
Этот график показывает относительную вероятность прибытия автобуса каждую минуту в течение часа. Это распределение вероятностей может быть представлено с помощью NumPy и np. : linspace()
linspace()
импортировать matplotlib.pyplot как plt
импортировать numpy как np
среднее = 15, 45
сд = 5, 7
x = np.linspace(0, 59, 60) # Представляет каждую минуту в течение часа
first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2)
second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2)
y = первое_распределение + второе_распределение
у = у / макс (у)
plt.plot(x, y)
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
Вы создали два нормальных распределения с центром в 15 и 45 минут после часа и просуммировали их. Вы устанавливаете наиболее вероятное время прибытия в значение 1 путем деления на максимальное значение.
Теперь вы можете смоделировать время прибытия автобуса, используя это распределение. Для этого можно создавать случайные времена и случайные относительные вероятности с помощью встроенного модуля random . В приведенном ниже коде вы также будете использовать списки:
В приведенном ниже коде вы также будете использовать списки:
случайный импорт
импортировать matplotlib.pyplot как plt
импортировать numpy как np
n_автобусов = 40
bus_times = np.asarray([random.randint(0, 59) для _ в диапазоне (n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
Вы смоделировали 40 прибывающих автобусов, которые можно визуализировать с помощью следующей диаграммы рассеивания:
Ваш график будет выглядеть по-другому, поскольку данные, которые вы генерируете, случайны. Однако не все из этих моментов, вероятно, будут близки к реальности, которую пассажирка наблюдала на основе собранных и проанализированных ею данных. Вы можете построить распределение, которое она получила из данных смоделированных прибытий автобусов:
случайный импорт импортировать matplotlib.pyplot как plt импортировать numpy как np среднее = 15, 45 сд = 5, 7 х = np.linspace (0, 59, 60) first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2) second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2) y = первое_распределение + второе_распределение у = у / макс (у) n_автобусов = 40 bus_times = np.asarray([random.randint(0, 59) for _ in range(n_buses)]) bus_likelihood = np.asarray([random.random() for _ in range(n_buses)]) plt.scatter(x=автобус_время, y=автобус_вероятность) plt.plot(x, y) plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность") plt.ylabel("Относительная вероятность прибытия автобуса") plt.xlabel("Минуты после часа") plt.show()
Это дает следующий вывод:
Чтобы моделирование было реалистичным, необходимо убедиться, что случайные прибытия автобусов соответствуют данным и распределению, полученному из этих данных. Вы можете отфильтровать случайно сгенерированные точки, оставив только те, которые попадают в распределение вероятностей. Вы можете добиться этого, создав маску для точечной диаграммы:
Вы можете добиться этого, создав маску для точечной диаграммы:
# ...
in_region = автобус_вероятность < y[автобус_время]
out_region = автобус_вероятность >= y[автобус_время]
plt.scatter(
x=автобусное_время[в_регионе],
y=автобус_вероятность[в_регионе],
цвет = "зеленый",
)
plt.scatter(
x=bus_time[out_region],
y=автобус_вероятность[out_region],
цвет = "красный",
маркер = "х",
)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
Переменные in_region и out_region представляют собой массивы NumPy, содержащие логические значения в зависимости от того, находятся ли случайно сгенерированные вероятности выше или ниже распределения y . Затем вы строите два отдельных графика рассеяния, один с точками, попадающими в распределение, а другой — с точками, не входящими в распределение. Точки данных, находящиеся выше распределения, не являются репрезентативными для реальных данных:
Точки данных, находящиеся выше распределения, не являются репрезентативными для реальных данных:
Вы сегментировали точки данных из исходной диаграммы рассеяния на основе того, попадают ли они в распределение, и использовали другой цвет и маркер для идентификации двух наборов данных.
Удаление рекламыПросмотр основных входных параметров
Вы узнали об основных входных параметрах для создания точечных диаграмм в разделах выше. Вот краткое изложение ключевых моментов, которые следует помнить об основных входных параметрах:
| Параметр | Описание |
|---|---|
x и у | Эти параметры представляют две основные переменные и могут быть любыми типами данных, подобными массивам, например списками или массивами NumPy. Это обязательные параметры. |
с | Этот параметр определяет размер маркера. Это может быть число с плавающей запятой, если все маркеры имеют одинаковый размер, или структура данных, подобная массиву, если маркеры имеют разные размеры. Это может быть число с плавающей запятой, если все маркеры имеют одинаковый размер, или структура данных, подобная массиву, если маркеры имеют разные размеры. |
с | Этот параметр представляет цвет маркеров. Обычно это либо массив цветов, например значения RGB, либо последовательность значений, которые будут отображены на карту цветов с помощью параметра cmap 9039.6 . |
маркер | Этот параметр используется для настройки формы маркера. |
смап | Если для параметра c используется последовательность значений, то этот параметр можно использовать для выбора сопоставления между значениями и цветами, обычно с использованием одной из стандартных карт цветов или пользовательской карты цветов. |
альфа | Этот параметр представляет собой число с плавающей запятой, которое может принимать любое значение от 9 до0395 0 и 1 и представляет прозрачность маркеров, где 1 представляет собой непрозрачный маркер. |
Это не единственные входные параметры, доступные с plt.scatter() . Вы можете получить доступ к полному списку входных параметров из документации.
Заключение
Теперь, когда вы знаете, как создавать и настраивать точечные диаграммы с помощью plt.scatter() , вы готовы начать практиковаться со своими собственными наборами данных и примерами. Эта универсальная функция дает вам возможность исследовать ваши данные и представлять результаты в ясной форме.
В этом уроке вы узнали, как:
- Создайте график рассеяния с помощью
plt.scatter() - Используйте обязательные и дополнительные входные параметры
- Настройка точечных диаграмм для базовых и более сложных графиков
- Представление более чем двух измерений с
plt.scatter()
Вы можете получить максимальную отдачу от визуализации, используя plt.



 com/invite/Mukhin
com/invite/Mukhin scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
)
plt.show()
scatter(
х = цена_зерновых,
y=продажи_за_день_зерновых,
s=прибыль_прибыль_зерновые * 10,
c=сахар_содержание_хлопья,
маркер = "д",
)
plt.show()
 style.use («морской рожденный»)
# ...
style.use («морской рожденный»)
# ...
 pyplot как plt
импортировать numpy как np
среднее = 15, 45
сд = 5, 7
х = np.linspace (0, 59, 60)
first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2)
second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2)
y = первое_распределение + второе_распределение
у = у / макс (у)
n_автобусов = 40
bus_times = np.asarray([random.randint(0, 59) for _ in range(n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()
pyplot как plt
импортировать numpy как np
среднее = 15, 45
сд = 5, 7
х = np.linspace (0, 59, 60)
first_distribution = np.exp(-0,5 * ((x - среднее [0]) / sd[0]) ** 2)
second_distribution = 0,9 * np.exp (-0,5 * ((x - среднее [1]) / sd [1]) ** 2)
y = первое_распределение + второе_распределение
у = у / макс (у)
n_автобусов = 40
bus_times = np.asarray([random.randint(0, 59) for _ in range(n_buses)])
bus_likelihood = np.asarray([random.random() for _ in range(n_buses)])
plt.scatter(x=автобус_время, y=автобус_вероятность)
plt.plot(x, y)
plt.title("Случайно выбранное время прибытия автобуса и относительная вероятность")
plt.ylabel("Относительная вероятность прибытия автобуса")
plt.xlabel("Минуты после часа")
plt.show()