Урок математики «Измерение площадей криволинейных фигур. Палетка». 4-й класс
Оборудование. Учебник Э.И.Александровой (изд-во ВИТА-ПРЕСС), на каждого ученика листочки четырёх цветов, листочки с четырьмя вариантами заданий, непрозрачные конверты с палетками из целлофана, два больших демонстрационных листа с рисунками 2 и 3, 6 листов для работы (по количеству групп) с фигурой на рисунке 2, 12 листов с фигурой на рисунке 3.
Тема. Измерение площадей криволинейных фигур. Палетка.
Цели.
Образовательная: познакомить с способом измерения площадей криволинейных фигур; с устройством для измерения площадей — палеткой; закреплять умение находить площади прямолинейных фигур.
Развивающая: развивать внимание, наблюдательность, умение рассуждать, обобщать и делать выводы.
Воспитательная: воспитывать умение общаться,
аккуратность, внимательность.
1. Учебная ситуация успеха
Учитель. Чем мы занимались на вчерашнем уроке?
Ученики. Находили площади и периметры фигур.
Учитель. Как найти площадь геометрической фигуры?
Ученики. Площадь прямоугольника и треугольника находят по формуле. Если это не прямоугольник и не треугольник, то сначала многоугольник надо разбить или достроить до фигур, площади которых мы уже знаем как находить.
Учитель. Я предлагаю вам выполнить эти задания. Здесь 4 варианта заданий. Посмотрите на них и выберите себе любое. Все 4 варианта лежат у вас на партах.
На доске четыре варианта заданий. Каждое записано своим цветом. У детей на партах кроме карточек с фигурами четырёх цветов, квадраты соответствующих цветов.
На доске
Дети, решив задание, поднимают карточку с
соответствующим заданию цветом. По цвету они
находят группу, сверяют решение, выбирают одного
представителя от группы, который записывает
решение на доске.
Учитель. Ребята, научились мы находить площади геометрических фигур?
Ученики. Да.
2. Постановка учебной задачи
Учитель. А теперь найдите площадь этой фигуры.
Показывает и вывешивает на доску
Ученики молчат.
Учитель. Почему вы не можете выполнить задание?
Ученики. Это не прямоугольник и не треугольник. Это не многоугольник.
Учитель. Чем эта фигура отличаются от нам известных фигур, многоугольников?
Ученики. Непонятно, где длина, ширина. Нет углов. Фигуры некрасивые, какие-то кривые.
Учитель. Да, все многоугольники состоят из прямых линий. Поэтому их называют прямолинейными фигурами. А из каких линий состоят эти фигуры?
Как бы вы их назвали?
Ученики. Кривые.
Учитель. В математике такие фигуры называют криволинейными.
Учитель. Чем же мы будем заниматься сегодня на уроке?
Ученики.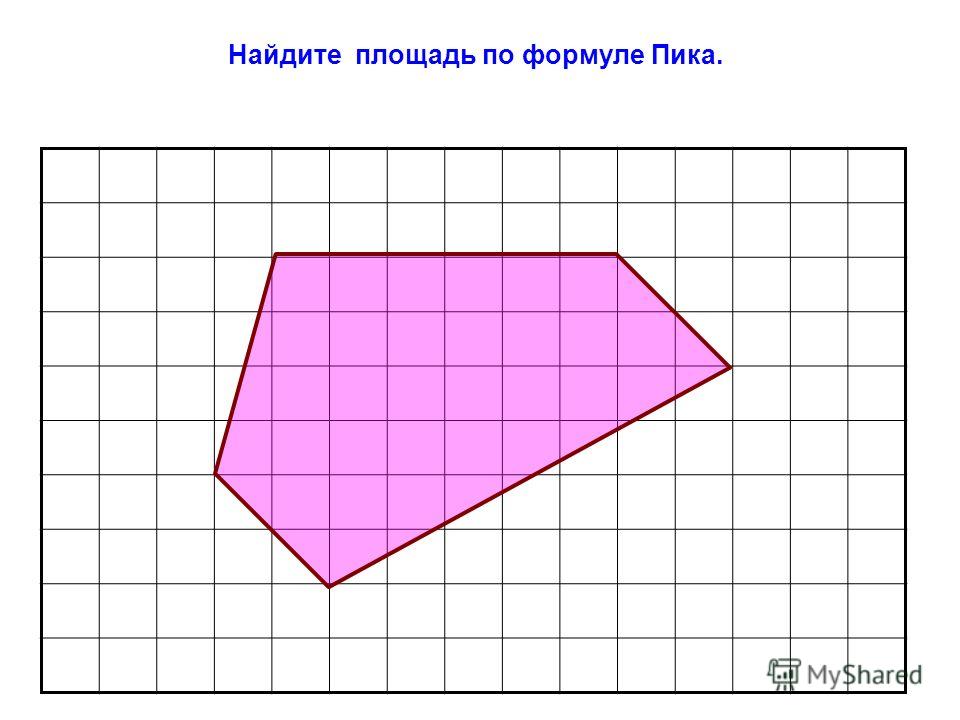 Учиться находить площади
криволинейных фигур.
Учиться находить площади
криволинейных фигур.
Учитель фиксирует проблему на доске:
S = ?
3. Поиск решения поставленной задачи
Учитель. Как же мы будем решать эту задачу? Как вы находили площадь прямоугольника, когда ещё не знали формулу его площади?
Ученики. Мы измеряли площадь прямоугольника с помощью мерки.
Учитель. А для криволинейной фигуры такой способ можно попробовать?
Ученики. Да.
Учитель. Как можно узнать площадь криволинейной фигуры с помощью мерки в одну клетку?
Ученики. Разбить на мерки, продолжив линии клеток-мерок.
Учитель. Что будете делать, когда разобьёте фигуру на мерки, чтобы узнать площадь фигуры?
Ученики. Посчитаем количество мерок в фигуре.
Учитель. Работаем в группах.
Представители от групп записывают свои ответы на доске. Ответы оказываются разными.
Учитель. Почему ответы оказались разными? Наши ребята не умеют считать?
Группа, у которой количество мерок меньше,
объясняют: “Мы не считали нецелые мерки”.
Учитель. Правильно будет вообще не считать неполные мерки?
Ученики. Нет.
Учитель. А считать половинку как полную мерку-квадрат можно?
Ученики. Нет.
Учитель. Что же делать с неполными мерками, ребята? Как их считать?
Ученики. Складывать по две мерки.
Учитель. Да, в математике договорились считать всё количество неполных мерок и делить на 2.
Учитель. Посчитайте ещё раз количество полных мерок. Неполных мерок.
Ученики работают в группах.
Учитель. Скольким квадратным меркам равна площадь фигуры?
Представители от групп называют ответы. Все сверяют со своими ответами.
4. Моделирование
Учитель. Что мы сейчас нашли?
Ученики. Мы узнали площадь криволинейной фигуры.
Учитель. Давайте вспомним, как мы это делали.
Дети говорят, учитель записывает на доске.
1. Разбить на мерки.
1. Посчитать полные мерки.
2. Посчитать неполные мерки и разделить на 2.
3. Сложить.
Учитель. Так можно найти площадь только этой криволинейной фигуры?
Ученики. Можно найти площадь и другой фигуры.
Учитель. Как записать, чтобы было понятно, что таким способом можно воспользоваться для вычисления площади любой криволинейной фигуры?
Как обозначить полные мерки? Неполные мерки?
Дети предлагают разные варианты. Учитель сообщает, что в математике договорились полные мерки обозначать буквой n, а неполные мерки буквой m.
Учитель. Кто закончит запись So = ?
На доске появляется запись: So = n + m : 2
Физминутка
5. Рефлексия
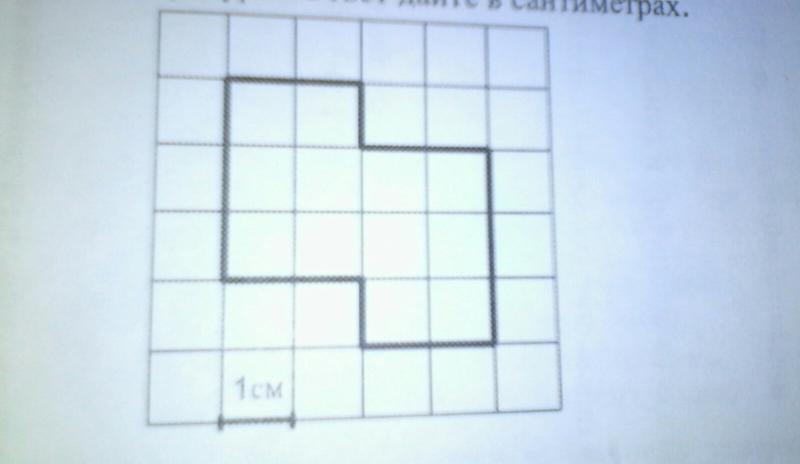
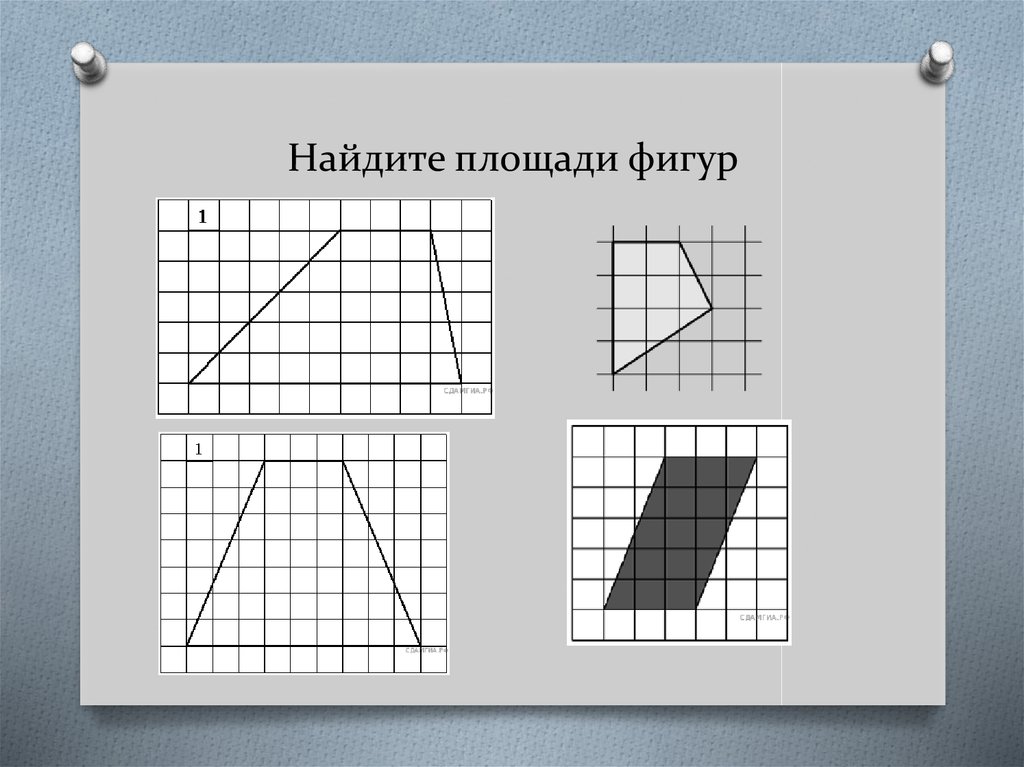
Учитель. Откройте учебники на стр. 61. Найдите №
88. Работая в парах, узнайте площади криволинейных
фигур: 1 ряд – площадь первой фигуры, 2 ряд –
площадь второй фигуры, 3 ряд – площадь третьей
фигуры.
Проверка
Представители от пар, выполнивших задание первыми, записывают на доске ответы. Остальные сравнивают свои ответы с их записями.
Учитель. По какой формуле вы находили площадь криволинейной фигуры?
Ученики. S = n + m : 2
Учитель. При таком способе нахождения площади (путём разбиения фигуры на мерки-квадраты) измерения получаются неточными.
Какие единицы измерения площадей вы знаете?
Ученики. Кв.см, кв.мм, кв.м, кв.км.
Учитель. Откройте учебник на с. 62 , № 89.
Одну и ту же фигуру измеряли сначала в кв.см, потом в кв. мм
Как вы думаете, в каком случае измерения выполнены более точно: в кв. см или в кв.мм?
Ученики. Более точно измерили квадратными мм .
6. Конкретизация способа нахождения площади криволинейной фигуры
Учитель. Мы научились измерять площади криволинейных фигур, разбивая их на клетки – мерки.
А сейчас посмотрите вот на эту фигуру:
Надо узнать площадь этой фигуры с помощью мерки
в 1 кв.
Чем отличается данное задание от предыдущего?
Ученики. Нет клеточек, по которым можно провести линии мерок.
Учитель. Да, здесь нет сетки из квадратов. Как же узнать, сколько полных и неполных кв. см поместилось в данной фигуре?
Все задумались и молчат. Один ученик предлагает свою версию – накинуть сверху какую-нибудь сетку из квадратиков.
Учитель. Да, можно изготовить специальное устройство (показываю). Это палетка.
Достаньте из конверта палетку. Кто догадался, как её сделали?
Ученики. Расчертили на квадраты со стороной в 1 см.
Учитель. А как ей пользоваться?
Ученики. Наложить на фигуру и посчитать количество клеток.
Посчитайте в парах площадь этой криволинейной фигуры.
Учитель. Выполните задание в учебнике № 90.Каждый самостоятельно.
Проверка.
Три первых ученика, выполнивших задание, выходят к доске и записывают свои ответы
Класс сверяет ответы.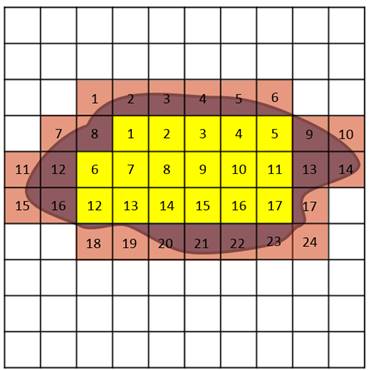
7. Д\з.
Учитель. Дома вам надо найти площади фигур из № 91. Что вам для этого понадобится?
Ученики. Палетка.
Учитель. Кто сможет сделать её сам?
Как это сделать?
Думаю, что все справятся с этой работой.
Если вы увидите фигуру, площадь которой можно найти другим способом, то вычислите площадь такой фигуры двумя способами: с помощью палетки и без неё.
8. Итоговая рефлексия
Учитель. Какую задачу решали на уроке?
Ученики. Учились находить площадь криволинейной фигуры.
Учитель. Кто сможет дома рассказать родителям ,как найти площадь криволинейной фигуры?
Как это сделать?
Учитель. А как вы думаете, чем мы будем заниматься на следующих уроках?
Ученики. Будем решать задачи на нахождение площадей фигур.
Будем находить новые формулы для нахождения площадей фигур.
Учитель. Да, на следующих уроках мы будем
использовать полученные знания в решении задач.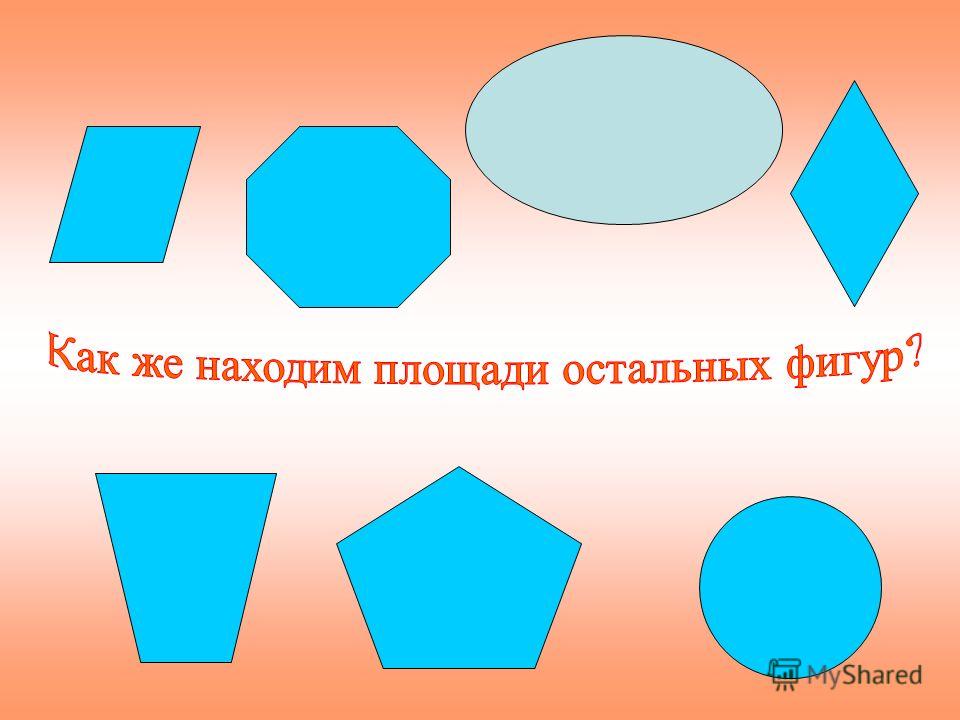
Конспект урока математики «Нахождение площади с помощью палетки»
Муниципальное бюджетное общеобразовательное учреждение Тёпловская средняя общеобразовательная школа
Методическая разработка
открытого урока математики
по теме:
«Измерение площади фигуры с помощью палетки»
4 класс
Разработан
учителем начальных классов
Зиновой А. М.
П. Тёплое
2022 г.
Тема урока: «Измерение площади фигур с помощью палетки»
Уровень образования: начальное общее образование
Класс: 4 класс
Предмет: математика
Тип урока: урок получения новых знаний
Форма урока: урок-путешествие
Используемые учебники и учебные пособия: учебник «Математика» М.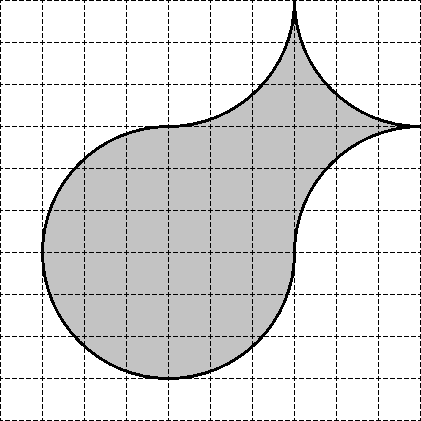 И.Моро: 4 класс – Москва: Просвещение, 2020, 1 часть.
И.Моро: 4 класс – Москва: Просвещение, 2020, 1 часть.
Используемая методическая литература:
Поурочные разработки по математике /Т.Н.Ситникова: 4 класс – Москва: Вако, 2018.
М.И.Моро. Методические рекомендации для учителя – Москва: Просвещение, 2018.
Оборудование:
учебник «Математика» М.И.Моро,
тетрадь для учащихся,
компьютер,
мультимедийный проектор,
презентация по теме урока;
карточки для индивидуальной и групповой работы;
палетки.
Цель: Познакомить учащихся со способом нахождения площади фигур различной формы с помощью палетки, закрепить знание единиц площади и единиц длины.
Познавательные УУД
1. Познакомить учащихся со способом нахождения площади фигур различной формы с помощью палетки.
2. Развивать умение использовать способы решения проблем творческого и поискового характера.
3. Совершенствовать вычислительные навыки при решении задач.
Совершенствовать вычислительные навыки при решении задач.
Коммуникативные УУД
1. Учить формулировать собственное мнение и позицию.
2. Развивать умение сотрудничать и работать в группе; паре.
Регулятивные
Учить принимать и сохранять цели и задачи учебной деятельности, искать и находить средства их достижения.
Определяют наиболее эффективные способы достижения результата.
Оценивают причины успеха/неуспеха в учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха.
Ход урока:
Деятельность учителя | Деятельность учащихся | УУД | |||||||||||||||
1.Орг. момент Чтобы спорилось нужное дело Чтобы в жизни не знать неудач, В мир математики отправимся смело В мир примеров и разных задач. Сегодня мы с вами отправимся в очередное путешествие в страну Геометрии. Чтобы вы пожелали себе и своим друзьям перед уроком? 2.Определить тему и цель урока Чтобы узнать, о какой величине пойдёт речь на сегодняшнем уроке, выполните задание на листе №1 Устный счет 1 м =…см 3 дм =…мм 7 см 8 мм =… мм 1 м = …дм 1 км = … м 6 м = …см 1 м2 =…дм2 Проверяем. Какая единица измерения у нас лишняя? Почему? Над какой величиной будем работать? Определите тему нашего урока. Какую цель поставим перед собой? Какими знаниями вы уже владеете в рамках этой темы? 3.Повторение пройденного. Прием «Кластер» Вспомните всё, что вы знаете о площади. Заполните кластер на листе №2. Расскажите о площади по кластеру. Что осталось незаполненным? Значит, на уроке мы узнаем что-то новое. Чего же мы ещё не знаем? Посмотрите на доску. Площадь каких фигур мы можем найти с помощью формулы? На доске прямоугольник со сторонами 7дм и 2дм. Найдите его площадь. Квадрат со стороной 3см. Найдите его площадь. А как найти площадь у овала? 4.Работа над новым материалом. Выявление причины затруднения. Построение проекта выхода из затруднения. Какая проблема? Можно ли найти площадь криволинейных фигур по формуле? С помощью линейки? Как быть? Оказывается, есть такое приспособление, которое называется палетка. Информацию о ней вы найдёте в учебнике на стр.43. Что вы узнали? Палетка — прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры. С её помощью можно узнать площадь овала. Как это сделать? Коллективное составление кластера «Алгоритм измерение площади фигур с помощью палетки». 1) наложить палетку 2 ) 3 ) : 2 4 ) + ( :2 )Решение задачи с овалом. Как вы думаете. Ответ будет точный? Где мы можем применять палетку? Каким способом мы определили площадь овала? Что можем записать в наш кластер лист №2? Ф и з к у л ь т м и н у т к а 5.Закрепление нового материала. Прием «Логическая цепочка» наших действий. Выполняем задание 191. 1 фигура=14 см2, 2 фигура=12 см2 Продолжаем работу над единицами измерения площади. Работа по учебнику стр.44 №196. Мы постоянно говорим о единицах площади. Можем ли мы эти знания применить в жизни? Где? Как? А можем ли мы измерить площадь нашего класса? С помощью чего? Как записать результат нашего измерения? Дано: Решение: 2 шага=1м а=7 м S=a.b в=5м S=7.5=35 м2 S=? Ответ: S=35м2 Решение геометрической задачи. 6. Итог урока. Возьмите лист №4. Подведём итог нашего урока. Прием «Верные и неверные утверждения» Лист №4.
Достигли мы цели, которую поставили в начале урока? Что нового вы узнали? Оцените себя. Домашнее задание: тетрадь стр.34 №60, 61 | Работают в группах. Ответ: Работа по группам. Ответ: палетка Работа в парах Коллективно, один у доски. Коллективно, один у доски. Работа индивидуально | Интерес к познанию, к новому учебному материалу, к овладению новыми способами познания Осуществляют связь компонентов Навыки сотрудничества со сверстниками в разных ситуациях. Навыки к исследовательской и поисковой деятельности; Ищут варианты Появляется проблема Решение проблемы Находят площадь овала. Делают вывод: Воспринимать и понимать причины успеха/неуспеха в учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха; Сравнивают цели учебной деятельности, какими средствами их достигли. |
Приложения.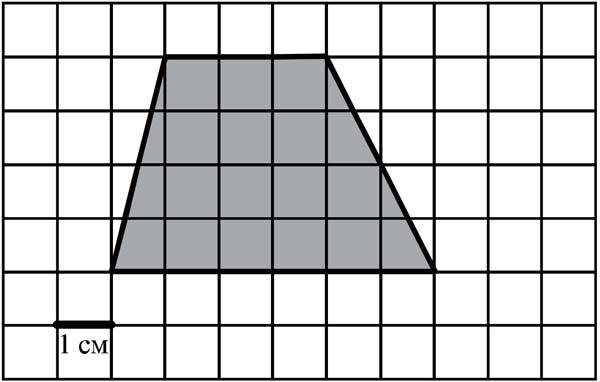
Лист №1
1 м =…см
3 дм =…мм
7 см 8 мм =… мм
1 м = …дм
1 км = … м
6 м = …см
1 м2 =…дм2
Лист №2
Лист №3
Вычисли площадь овала с помощью палетки.
Лист №4
1. | Площадь – это то, что находится внутри фигуры. | |
2. | Площадь измеряется в мм, см, дм, м, км | |
3. | Площадь – это величина | |
4. | Формула площади прямоугольника S = а .в | |
5. | Найти площадь геометрических фигур можно только с помощью линейки |
Извините, страница, которую вы ищете, не может быть найдена.
 (
((1/1)NotFoundHttpException |
|---|
| в RouteCollection.php (строка 179) |
| по адресу RouteCollection ->match( object ( Request ))in Router.php (строка 546) |
| at Router ->findRoute( object |
Итак, наш код #369BE5 в HEX становится (54, 155, 229) в RGB
Как вы называете друзей, которые любят математику?
Alge-bros.
Продолжай улыбаться. Мы продолжаем наше путешествие в мир HSL.
HSL — это обычное представление точек в цилиндрических координатах в цветовой модели RGB. HSL означает оттенок, насыщенность и яркость. Оттенок относится к семейству цветов конкретного цвета, на который мы смотрим. Он указывает фактический доминирующий цвет на цветовом круге RGB. Яркость относится к тому, сколько белого или черного смешано в цвете. Насыщенность показывает количество серого в том же цвете.
Преобразование между RGB и HSL
Яркость
Яркость (также называемая яркостью, яркостью или светимостью) означает интенсивность выходной энергии источника видимого света . Он в основном говорит о том, насколько светлый цвет и измеряется по следующей шкале: L = [0, 1]
Пришло время ввести максимальное и минимальное значения среди наших чисел RGB. Max(RGB) означает наивысшее значение, а Min(RGB) для наименьшего значения для красного, зеленого и синего цветов.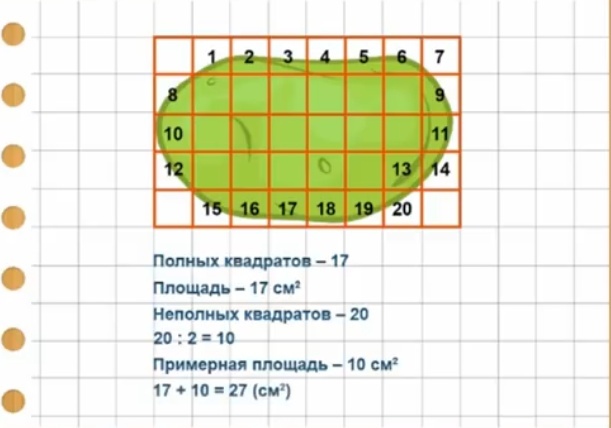 Чтобы наши дальнейшие вычисления работали, нам нужно преобразовать значения RGB в диапазон 0–1. Это можно сделать, разделив их на 255. Возьмем, например, наши существующие значения RGB: (54, 155, 229)
Чтобы наши дальнейшие вычисления работали, нам нужно преобразовать значения RGB в диапазон 0–1. Это можно сделать, разделив их на 255. Возьмем, например, наши существующие значения RGB: (54, 155, 229)
R = 54/255 = 0,212 G = 155/0056 0,608 B = 229 / 255 = 0,898
Яркость цвета RGB (54, 155, 229) можно рассчитать по значениям Max(RGB) и Min(RGB) следующим образом:
L = (1 / 2) x (Max(RGB) + Min(RGB))
Из наших значений R, G и B числа, R кажется самым маленьким, а B самым большим. Теперь мы знаем значения Max(RGB) = B = 0,898 и Min(RGB) = R = 0,212 .
L = (1 / 2) x (0,898 + 0,212) = 0,555 ~ 56%
Оттенок
Большинство источников видимого света содержат энергию в диапазоне длин волн. Оттенок — это длина волны в спектре видимого света, при которой выходная энергия источника максимальна.0024 . Это обозначается его положением (в градусах) на цветовом круге RGB: H= [0°, 360°]
Оттенок — это длина волны в спектре видимого света, при которой выходная энергия источника максимальна.0024 . Это обозначается его положением (в градусах) на цветовом круге RGB: H= [0°, 360°]
Формула для оттенка зависит от того, как значения RGB соотносятся друг с другом. Другими словами, это зависит от того, какой из них представляет значения Max(RGB) и Min(RGB).
(А) Если R ≥ G ≥ B | H = 60° x [(G-B)/(R-B)] (B) Если G > R ≥ B | H = 60° x [2 - (R-B)/(G-B)] (C) Если G ≥ B > R | H = 60° x [2 + (B-R)/(G-R)] (D) Если B > G > R | H = 60° x [4 - (G-R)/(B-R)] (E) Если B > R ≥ G | H = 60° x [4 + (R-G)/(B-G)] (F) Если R ≥ B > G | H = 60° x [6 - (B-G)/(R-G)]
Оттенок цвета RGB (54, 155, 229) можно рассчитать, используя правильную формулу из приведенного выше пула. Не забудьте разделить на 255, прежде чем идти дальше.
R = 54 / 255 = 0,212 G = 155 / 255 = 0,608 B = 229/ 255 = 0,898
B > G > R кажется верным, наше соответствие (D).
H = 60° x [4 - (0,608-0,212)/(0,898-0,212)] = 205,4°
Насыщенность
Насыщенность представляет собой выражение для вывода относительной полосы пропускания видимого диапазона источник света . По мере увеличения насыщенности цвета выглядят более чистыми. По мере уменьшения насыщенности цвета кажутся более размытыми. Измеряется по следующей шкале: S = [0, 1]
Формула для насыщенности использует значения Min(RGB), Max(RGB) и Luminosity.
(А) Если L < 1 | S = (Макс.(RGB) — Мин.(RGB)) / (1 — |2L - 1|) (B) Если L = 1 | S = 0
Мы рассчитали Luminosity ранее, L = 0,555. Наша формула будет (A) , поскольку L = 0,555 < 1. Мы также знаем, что Max(RGB) = 0,898 и Min(RGB) = 0,212 . Наконец-то у нас есть все необходимое для насыщения. Хорошая вещь.
Наша формула будет (A) , поскольку L = 0,555 < 1. Мы также знаем, что Max(RGB) = 0,898 и Min(RGB) = 0,212 . Наконец-то у нас есть все необходимое для насыщения. Хорошая вещь.
S = (0,898 — 0,212) / (1 — |2 x 0,555 - 1|) = 0 ,770 ~ 77%Прямо сейчас это вы.
Теперь мы можем определять свои собственные правила для принятия цветов, опираясь исключительно на HEX-код. Например, мы можем установить желаемый диапазон яркости или исключить определенные цвета из цветового круга с помощью оттенка. С помощью Насыщенности мы также можем влиять на то, насколько размытыми или красочными будут выглядеть наши экраны.
Д = 56% В = 205,4° S = 77%
Мы в Shazam решили принимать только цвета со значением яркости меньше определенного уровня (за исключением слишком светлых) и изменили это правило для определенного спектра на цветовом круге.
Related Posts
на маршрутизатор -> Dispatchtoroute ( объект ( запрос )) в Router.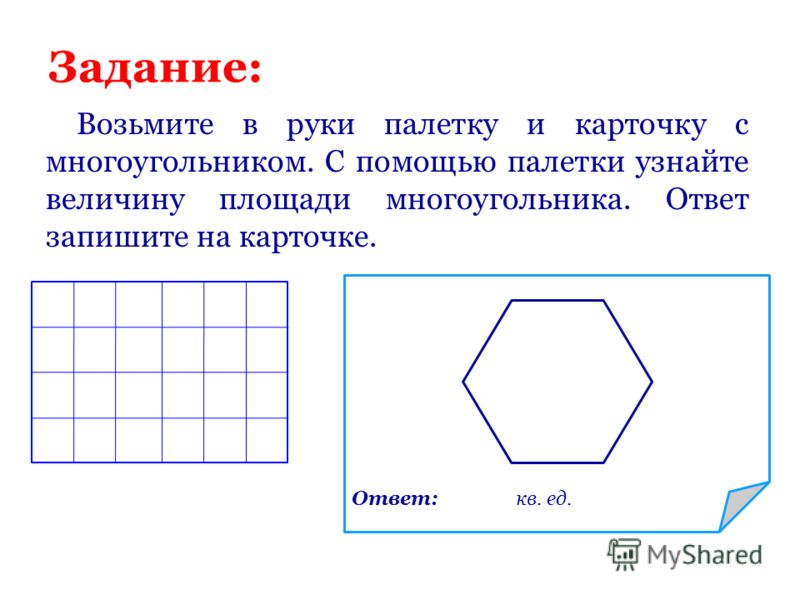 php (строка 511) php (строка 511) | ||||||||||
| на 417 -> | ||||||||||
| по адресу . ( Запрос )) в Kernel.php (строка 176) | ||||||||||
| в Ядро ->Illuminate\Foundation\Http\{close}( object ( Request ))in Pipeline1.php 90 Pipeline1.php 90 30) | ||||||||||
| AT Pipeline -> Oilluminate \ Routing \ {закрытие} ( объект ( запрос )) в Transformsrequest.php (линия 30) | ||||||||||
AT Transformsrece. ( объект ( Запрос ), объект ( Закрытие )) в Pipeline. php (строка 148) php (строка 148) | ||||||||||
в Трубопровод ->Illuminate\Pipeline\{закрытие}(4 объект ) Pipeline.php (line 53))5511115111115111511115111551115115115). Трубопровод -> Освещение \ Трубопровод \ {закрытие} ( объект ( Запрос )) в Трубопровод. объект ( Request ))in Pipeline.php (line 102) Трубопровод -> Освещение \ Трубопровод \ {закрытие} ( объект ( Запрос )) в Трубопровод. объект ( Request ))in Pipeline.php (line 102)
Давайте займемся цветом и математикой.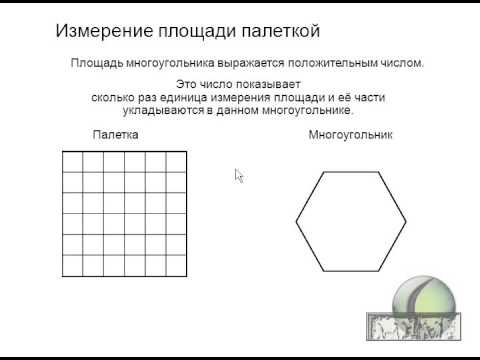 Понимание формул цвета… | by Donat Bali Papp Понимание формул цвета… | by Donat Bali PappПонимание формул преобразования цветаВ Shazam мы представили совершенно новый, визуально более привлекательный способ размещения рекламы в приложении. Этот новый формат рекламы занимает весь экран с плавной анимацией. Опыт не только выглядит лучше, но и кажется менее отвлекающим и намного более увлекательным. Я GIF, который не может обрабатывать более 256 цветов. Извините за мои градиенты.Дизайнеры склонны считать рекламу необходимым злом. Объявления – это внешний контент, которому нужно место на нашем идеальном до пикселя уникальном дизайне. Пользовательский интерфейс имеет цвета, реклама имеет цвета. Непросто применить десяток из них к нашим интерфейсам и заставить их работать вместе. Требуется процесс изучения теории цвета и игры с правилами, чтобы быть уверенным и контролировать то, что хорошо выглядит и работает на экране. В этом случае реклама должна выделяться, не прерывая основной процесс. Цвета — это то, как наш мозг через наши глаза интерпретирует электромагнитное излучение с длиной волны в пределах видимого спектра. Ням. Видимый свет лежит между 400 и 700 нанометрами. Излучение с длиной волны более 750 нм называется инфракрасным, а излучение с длиной волны менее 350 нм — ультрафиолетовым. Цветовой круг — это просто спектр, перекрученный так, что фиолетовый и красный концы соединяются. Это колесо особенно полезно для демонстрации того, как цвета соотносятся друг с другом и как вы можете создавать новые, смешивая два или более цветов. RGB относится к системе представления цветов, которые будут использоваться на дисплее компьютера. RGB представляет собой комбинацию красного, зеленого и синего цветов. Эти цвета можно комбинировать в различных пропорциях, чтобы получить любой цвет в видимом спектре. Каждый уровень измеряется диапазоном десятичных чисел от 0 до 255 (256 уровней для каждого цвета). Например, если в цвете нет синего, он будет смесью красного и зеленого. Это означает, что мы можем сгенерировать 256 x 256 x 256 = 16 777 216 различных цветов с помощью этой модели. Важно отметить, что разные устройства по-разному определяют или воспроизводят заданное значение RGB. Цветовой формат RGB представлен значениями красного, зеленого и синего, здесь нет ничего удивительного: RGB = (54, 155, 229) | Примечание: 54 = красный, 155 = зеленый и 229 = синий HEX — это широко известный и используемый формат для определения цветов в Интернете. Название происходит от фразы «шестнадцатеричный», которая используется людьми для сокращения двоичного кода до более понятной формы. Сам код представляет собой триплет HEX, который представляет 3 отдельных значения, определяющих уровни цветов компонентов. Эти 3 значения называются байтами и составляют шестизначное шестнадцатеричное число, используемое в HTML, CSS, SVG и других вычислительных приложениях. Первая пара значений относится к красному, вторая к зеленому и третья к синему. Один байт представляет собой число в диапазоне от 0 до 255 в десятичном представлении. В шестнадцатеричном представлении шкала идет от самой низкой (00) до самой высокой (FF) интенсивности каждого цвета. HEX-коды начинаются со знака хэштега и следуют в указанном формате: HEX = #A3D645 | Примечание: A3 = красный, D6 = зеленый и 45 = синий
Мы преобразуем код RGB в код HEX. R / 16 = X1 + Y1 G / 16 = X2 + Y2 B / 16 = X3 + 909016 Y30017 В приведенной выше формуле X называется частным, а Y — остатком. Эти два числа используются для представления пары значений HEX для каждого конкретного цвета: красного, зеленого и синего. HEX-код можно рассчитать по этим значениям как #X1Y1X2Y2X3Y3 , где X1Y1 — значения для красного, X2Y2 — для зеленого и X3Y3 — для синего. Давайте посмотрим на это со следующими значениями RGB: (54, 155, 229) R = 54 / 16 = 3 + 6 G = 155 / 16 = 9 + 11 | Примечание: 11 = B в шестнадцатеричном формате B = 229 / 16 = 14 + 5 | Примечание: 14 = E в шестнадцатеричном формате Вуаля, наш код (54, 155, 229) в RGB становится #369BE5 в HEX Мы также можем сделать преобразование в обратном порядке. R = X1 x 16 + Y1 G = X2 x 16 + Y2 B = X3 x 16 + Y39029 (частное уже известно) остатки (Y1, Y2, Y3). Шестнадцатеричный код состоит из этих значений как #X1Y1X2Y2X3Y3 . Давайте попробуем преобразовать обратно наш HEX-код: #369BE5 R = 3 x 16 + 6 = 54 G = 9 x 16 = 17 17 17 + |

 Рассмотрите геометрические фигуры. Назовите их.
Рассмотрите геометрические фигуры. Назовите их. Лист №3. 10+14:2=17 см2
Лист №3. 10+14:2=17 см2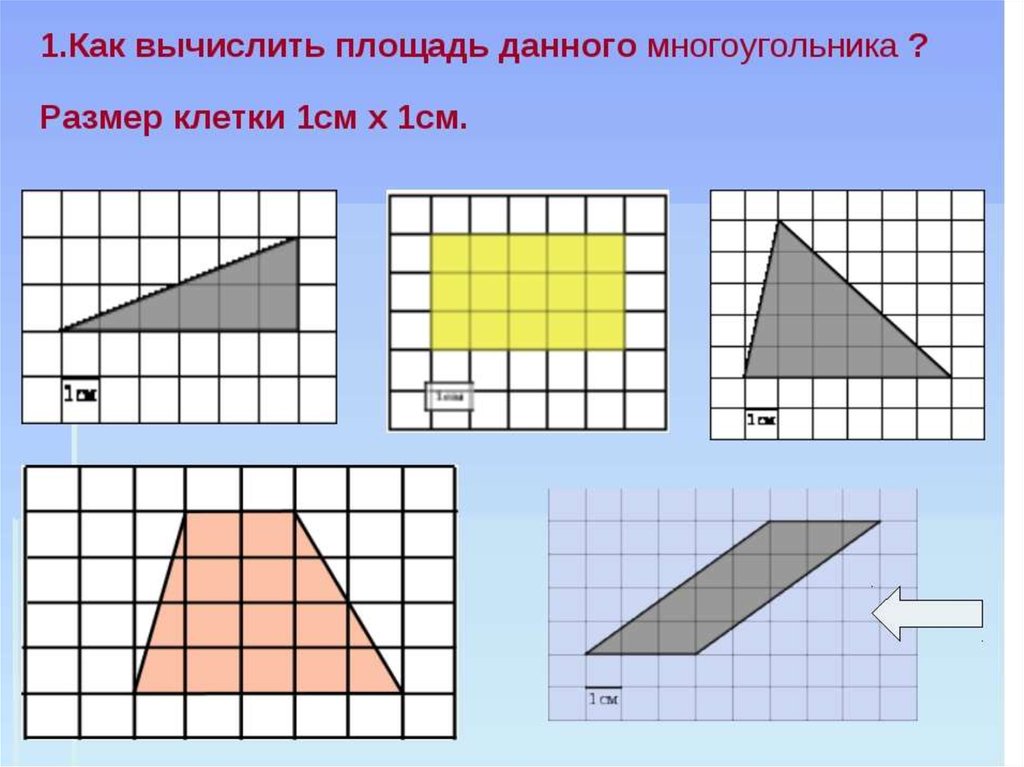 Прочитайте утверждения, если вы с ними согласны, то справа в столбике поставьте +, если нет, то -.
Прочитайте утверждения, если вы с ними согласны, то справа в столбике поставьте +, если нет, то -.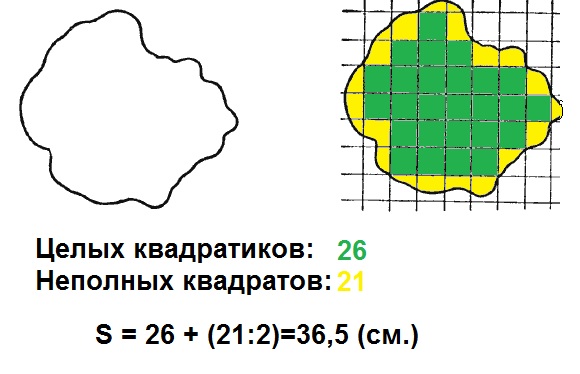

 11php0908)in 27)
11php0908)in 27) Чего мы хотим достичь здесь, так это инструмента для сторонних клиентов, который исключает определенные цвета из приемлемого сочетания. Инструмент, который работает с одним HEX-кодом в качестве входных данных и сообщает, соответствует ли конкретный цвет нашим определенным критериям. Мы хотели бы отфильтровать слишком светлые цвета, которые наносят ущерб удобству использования, и размытые цвета, которые делают работу с сайтом менее приятной. Для этого нам нужно будет выжать эти значения из одного HEX-кода.
Чего мы хотим достичь здесь, так это инструмента для сторонних клиентов, который исключает определенные цвета из приемлемого сочетания. Инструмент, который работает с одним HEX-кодом в качестве входных данных и сообщает, соответствует ли конкретный цвет нашим определенным критериям. Мы хотели бы отфильтровать слишком светлые цвета, которые наносят ущерб удобству использования, и размытые цвета, которые делают работу с сайтом менее приятной. Для этого нам нужно будет выжать эти значения из одного HEX-кода.
 Каждое из шестнадцатеричных чисел использует цифры и буквы для представления значений от 0 до 16. Числа используются в диапазоне 0–9.и буквы A, B, C, D, E, F для диапазона 10–16.
Каждое из шестнадцатеричных чисел использует цифры и буквы для представления значений от 0 до 16. Числа используются в диапазоне 0–9.и буквы A, B, C, D, E, F для диапазона 10–16. На самом деле это означает, что нам нужно преобразовать десятичные числа из заданных значений RGB в шестнадцатеричные. Для этого разделим наши значения на 16.
На самом деле это означает, что нам нужно преобразовать десятичные числа из заданных значений RGB в шестнадцатеричные. Для этого разделим наши значения на 16. Если мы хотим преобразовать HEX-коды в RGB-коды, все, что нам нужно сделать, это умножить частные на 16 и добавить остаток.
Если мы хотим преобразовать HEX-коды в RGB-коды, все, что нам нужно сделать, это умножить частные на 16 и добавить остаток.