Палетка математическая: что она из себя представляет в 4 классе?

что она из себя представляет в 4 классе?

Содержимое

• 1 Палетка как выглядит по математике 4 класс
  • 1.1 Палетка по математике 4 класс
  • 1.2 Что такое палетка и зачем нужна
  • 1.3 Какие элементы входят в палетку для 4 класса
  • 1.4 Какие математические операции можно выполнить с помощью палетки
  • 1.5 Примеры заданий с использованием палетки
  • 1.6 Как правильно использовать палетку для обучения математике
  • 1.7 Какие ошибки могут возникнуть при использовании палетки
  • 1.8 Достоинства и недостатки использования палетки в обучении
  • 1.9 Как выбрать правильную палетку для 4 класса
  • 1.10 Особенности использования палетки в школьном курсе математики
  • 1.11 Как лучше всего совмещать уроки математики с использованием палетки
  • 1.12 Палетка в домашнем обучении математике
  • 1.13 Видео по теме:
  • 1.14 Вопрос-ответ:
    • • 1.14.0.1 Что такое палетка в математике?
      • 1.14.0.2 Как использовать палетку в 4 классе?
      • 1. 14.0.3 Какие математические понятия можно изучить с помощью палетки?
      • 1.14.0.4 Какие типы палеток существуют?
      • 1.14.0.5 Какие преимущества использования палетки в обучении математике?
      • 1.14.0.6 Можно ли использовать палетку для изучения геометрии?
      • 1.14.0.7 Какую роль играет палетка в развитии математической грамотности у детей?

Узнай, как математически выглядит расстановка цветов в палетке для рисования в 4 классе. Разберись в пропорциях и соотношениях, которые лежат в основе создания красивых и интересных комбинаций цветов на бумаге.

Палетка — это набор разноцветных красок, которые используются художниками для создания картин. Но как этот набор цветов представляется в математике? Какие знания нужны у последовательных учеников для того, чтобы научиться работать с палеткой и выбирать нужные цвета?

Первым шагом на пути к пониманию палетки является знание основных цветов. Красный, желтый и синий являются основными цветами. С помощью них можно получить все другие цвета, переплавляя их между собой.

Для создания более сложных цветов ученикам нужно знать о том, что темнота или светлота цвета зависят от количества белого или черного, которые добавляются к нему. Охра — это темный желтый цвет, который получается, если добавить немного черного к желтому цвету. А розовый — это светлый оттенок красного цвета с добавлением немного белого.

В математике ученики изучают не только сами цвета и их комбинации, но и их свойства, такие как цветовая симметрия и сочетание цветов. В общем, работа с палеткой — это уникальное сочетание искусства и науки, которое позволяет создавать яркие и красивые картины.

Палетка по математике 4 класс

Палитра (или палетка) — это набор красок или инструментов, используемых в изобразительном искусстве. Однако, в математике палетка может иметь другое значение.

В 4 классе школьники обучаются базовым арифметическим операциям, таким как сложение, вычитание, умножение и деление. Палетка может помочь им в работе с этими операциями, позволяя легко визуализировать элементы, которые должны быть сложены, вычтены, умножены или разделены.

• Пример палетки для сложения:
  • 1
  • 5
  • 3
  • 2
  • 7
• Пример палетки для умножения:
  • 2
  • 4
  • 3

Таким образом, палетка может быть полезным инструментом для понимания основных арифметических операций 4-классниками.

Что такое палетка и зачем нужна

Палетка — это специальный инструмент для хранения и транспортировки материалов, таких как краски, масла или кисти для рисования. В основном, палетки используются в искусстве, визуальных и графических дизайнах, строительстве, а также в промышленности для хранения и транспортировки товаров.

Основная задача палетки — облегчить процесс работы и сохранить материалы в хорошем состоянии. Работая с палеткой, художник может управлять краской и маслом, мешая их на поверхности палетки, а не на холсте, что позволяет лучше контролировать процесс рисования. Кроме того, палетка может быть многоразовой и легко моется после работы, что экономит время и деньги на покупку новых инструментов.

Зависимости от материала, из которого сделана палетка, она может иметь разную форму, размер и цвет. Некоторые палетки имеют отдельные отверстия для кистей и красок, что повышает удобство их использования. Выбор палетки зависит от индивидуальных потребностей и стиля работы каждого художника, однако её наличие необходимо для успешной работы в сфере искусства и дизайна.

Какие элементы входят в палетку для 4 класса

При выборе палетки для 4 класса нужно учитывать, что она должна содержать необходимые материалы, которые помогут ребенку научиться математике.

• Счетные приспособления: палочки, кубики, бусины, фишки. Они помогают детям понимать абстрактные математические понятия, например, количество, числа, операции.
• Карточки с заданиями: они помогают развивать логическую мысль, способствуют пониманию математических выражений. Карточки могут содержать задания на сложение, вычитание, умножение и деление.
• Геометрические фигуры: круги, треугольники, квадраты, прямоугольники. Они позволяют ребенку лучше понимать пространственные отношения, основные геометрические понятия и их свойства.
• Линейки и угольники: они используются для измерения длины, угла и для построения графиков.
• Тетради: в них записываются домашние задания, задания на уроках и различные математические выражения.

Важно, чтобы палетка была удобной для использования и чтобы в ней содержались все необходимые материалы для обучения математике в 4 классе.

Какие математические операции можно выполнить с помощью палетки

Палетка — это универсальный инструмент для выполнения различных математических операций в четвертом классе. С помощью палетки ученики могут:

• Сложить и вычесть числа. Для этого достаточно использовать квадратики на палетке. Например, чтобы сложить 2 и 3, нужно использовать квадратики, соответствующие этим числам, и сложить их.
• Умножить и разделить числа. Для выполнения этих операций на палетке есть специальные линейки. Например, чтобы умножить 4 на 3, нужно положить линейку, соответствующую 4, на линейку, соответствующую 3, и посчитать количество квадратиков, находящихся под обеими линейками.
• Решать задачи на пропорции. Для этого нужно использовать палетку с двумя линейками, которые различаются по длине. Например, чтобы найти значение неизвестного числа в пропорции 2:3 = 4:x, нужно положить линейку, соответствующую 2, на линейку, соответствующую 3, и подобрать линейку для неизвестного числа, которая будет находиться под линейкой, соответствующей 4.

Таким образом, палетка — это удобный инструмент, который помогает детям быстро и легко решать математические задачи в 4 классе.

Примеры заданий с использованием палетки

Задание 1: Дана палетка с 5 красными деталями и 3 зелеными деталями. Сколько всего деталей на палетке?

Решение: Всего деталей на палетке: 5 + 3 = 8.

Задание 2: Из палетки с 12 деталями нужно выбрать 3 красные. Сколько возможных комбинаций выбора деталей?

Решение: Количество комбинаций выбора 3 красных деталей из 12 будет равно: 12C3 = 220.

Задание 3: Даны две палетки, одна с 7 красными деталями и 5 зелеными, а другая с 3 красными и 4 зелеными деталями. Какая из палеток имеет большую долю красных деталей?

Решение: В первой палетке доля красных деталей: 7 / (7+5) = 0.5833. Во второй палетке доля красных деталей: 3 / (3+4) = 0.4286. Следовательно, первая палетка имеет большую долю красных деталей.

• Задание 4: Используя палетку, создайте геометрическую фигуру в виде треугольника. Рассчитайте площадь этого треугольника.
• Решение: Для создания треугольника на палетке необходимо выбрать 3 детали и расположить их так, чтобы они образовывали треугольник. Расчет площади производится по формуле: S = (a*b*sin(C))/2, где a и b — стороны треугольника, С — угол между этими сторонами. Для этого треугольника можно выбрать стороны a = 4, b = 5 и угол C = 60 градусов. Тогда площадь треугольника будет равна: S = (4*5*sin(60))/2 = 10.

Как правильно использовать палетку для обучения математике

Палетка — это специальный инструмент, который помогает детям изучать математику более эффективно. Однако, чтобы использование палетки было полезным и результативным, необходимо следовать некоторым правилам.

1. Начинайте изучение математики с основных понятий. Используйте палетку для изучения простых математических операций, таких как сложение, вычитание, умножение и деление. Убедитесь, что ваш ребенок хорошо понимает эти понятия, прежде чем переходить к более сложным задачам.
2. Используйте палетку для запоминания таблиц умножения. Например, поместите числа от 1 до 10 на одну сторону палетки, а числа, на которые нужно умножить, на другую. Пусть ребенок переносит фишки на соответствующие числа и легко запомнит таблицу умножения.
3. Используйте палетку в игровой форме. Создайте игры на основе математических задач с использованием палетки. Например, запросите у ребенка, чтобы он использовал одну сторону палетки для представления чисел, а другую сторону для их сложения или вычитания. Это поможет ребенку развивать математические навыки, одновременно играясь.

В целом, палетка является прекрасным инструментом для обучения математике. Следуйте приведенным выше советам и ваш ребенок будет получать удовольствие от изучения математики, при этом усваивать новые знания эффективнее.

Какие ошибки могут возникнуть при использовании палетки

Необходимость выбора подходящей палетки

Одной из основных ошибок, которая может возникнуть при использовании палетки, является выбор не подходящей палетки для конкретной грузоперевозки. Нельзя забывать о весе и размере груза, а также о том, на каком расстоянии нужно перевезти груз для правильного выбора палеты.

Неправильное расположение груза на палете

Еще одна ошибка, которая может быть совершена при использовании палетки – это неправильное расположение груза на палете. Правильное расположение груза на палете поможет избежать объемной массы, которая может проявить себя при транспортировке груза на значительные расстояния.

Неподходящие условия хранения и транспортировки

Кроме того, неподходящие условия хранения и транспортировки могут спровоцировать различные проблемы при использовании палетки. Например, нехватка вентиляции при транспортировке определенных грузов может привести к повреждению самой палеты, ее деформации или менее качественному хранению и транспортировке груза внутри палеты.

Ненадежное крепление груза на палете

И, наконец, еще одна возможная ошибка при использовании палетки – ненадежное крепление груза на палете. Несоблюдение правил и норм при креплении груза может привести к тому, что груз не будет удерживаться на палете, что может привести к проблемам во время транспортировки.

Достоинства и недостатки использования палетки в обучении

Достоинства:

• Упрощает процесс обучения математическим операциям, так как на палетке изображены все цифры и математические знаки.
• Позволяет визуально представлять и сравнивать числа, что помогает выражать идеи и решения более точно и детально.
• Развивает моторику и улучшает понимание математических операций.
• Позволяет создавать игры и задания, которые способствуют более эффективному и интересному обучению.
• Минимизирует ошибки при выполнении математических операций, так как облегчает работу с большими числами и различными знаками.

Недостатки:

• Ограниченный функционал, что делает невозможным выполнение более сложных и изощренных математических задач.
• По сравнению с использованием компьютера или электронных средств, использование палетки требует большего времени на выполнение задания.
• После определенного уровня обучения, палетка может ограничивать развитие навыков и понимание математических операций.
• Палетка может создавать зависимость от визуальной и конкретной репрезентации чисел и операций, что затрудняет переход к абстрактному пониманию.

В целом, палетка является полезным и эффективным инструментом для обучения математическим операциям, однако она не может заменить полностью все другие методы и средства обучения. Палетка должна использоваться в сочетании с другими методами, чтобы добиться наилучшего результата в обучении математике.

Как выбрать правильную палетку для 4 класса

Выбор правильной палетки для 4 класса – это важный шаг, который облегчит занятия рисованием и поможет детям выразить свои творческие способности. Важно учесть несколько критериев, чтобы выбрать палетку, которая будет наилучшим выбором для 4 класса.

Размер палетки:

Для детей 4 класса наиболее удобны палетки среднего размера, которые могут содержать несколько цветов. Они не должны быть слишком большими, чтобы ребенок мог легко держать их в руках и перемещаться по бумаге без проблем.

Материал палетки:

Палетки могут быть сделаны из различных материалов, таких как пластик, дерево или металл.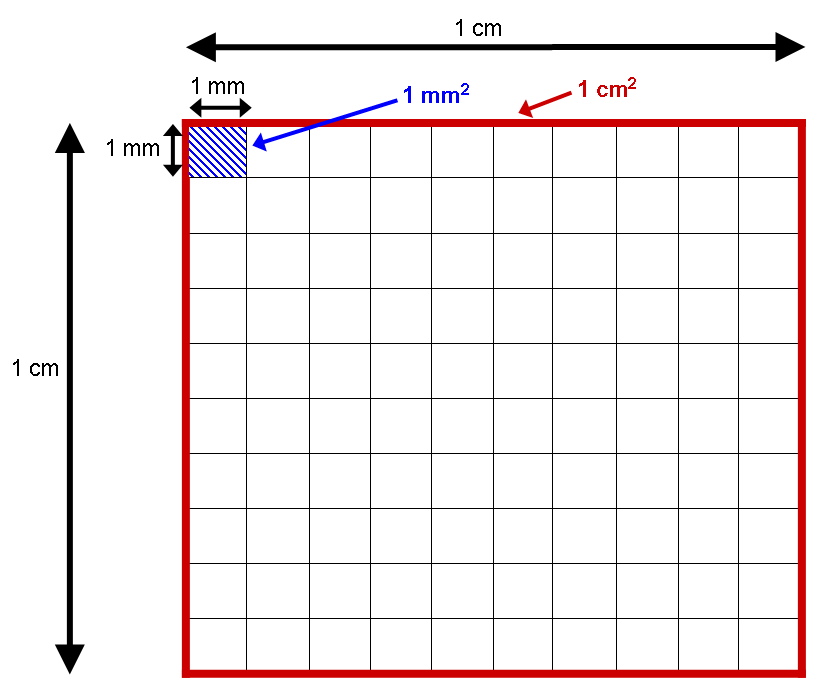 Для 4 класса лучше выбирать пластиковые или деревянные палетки, так как они обеспечивают легкость, долговечность и безопасность.

Количество и форма отверстий на палетке:

Количество отверстий на палетке может варьироваться, но для 4 класса лучше выбирать палетки с от 6 до 10 отверстий. Подходящий выбор – палетки с круглыми отверстиями, которые обеспечивают равномерную подачу краски.

Дополнительные функции:

Палетки могут иметь дополнительные функции, такие как удобный отсек для кисточек или крышку, которая помогает сохранить краску свежей. Эти функции могут быть полезны для учеников и учителей, которые занимаются рисованием.

Выбор правильной палетки для 4 класса – это несложно, если учесть эти критерии. Важно помнить, что палетка должна быть удобной, долговечной и безопасной для использования.

Особенности использования палетки в школьном курсе математики

Палетка – это набор карточек, на которых изображены числа и математические действия. Она используется в школьном курсе математики для обучения основам арифметики.

В школьном курсе математики палетка используется для изучения различных тем, таких как сложение, вычитание, умножение, деление, дроби и т.д. Ученики могут использовать карточки для выполнения заданий, решения примеров или создания своих задач.

Также для использования палетки в школьном курсе математики не обязательно иметь много опыта в математике и знать все возможные операции. Палетка позволяет учиться на практике и делать ошибки, которые можно исправлять, используя другие карточки.

В итоге можно сказать, что палетка является очень полезным инструментом для изучения математики в школе. Она помогает ученикам лучше понимать математические операции, визуально представлять числа и создавать различные задания для закрепления знаний.

Как лучше всего совмещать уроки математики с использованием палетки

Математика — один из самых важных предметов в школе, но не всем ученикам легко даётся решение математических задач. Использование палетки может значительно упростить процесс обучения и помочь ученикам лучше понимать математические концепции.

Одним из способов использования палетки является решение задач на сложение и вычитание. Ученики могут использовать цифры на палетке для создания чисел и совершения нужных действий. Этот метод позволяет более наглядно представлять арифметические операции.

Для лучшего усвоения материала, ученикам также может быть полезна игра с использованием палетки. Например, можно провести игру, где ученики должны использовать цифры на палетке, чтобы создать наибольшее число за ограниченное время. Это поможет ученикам быстрее запомнить числа и понимать, как их сравнивать.

В целом, использование палетки в уроках математики может помочь ученикам лучше понимать математические концепции и совершать арифметические операции быстрее. Кроме того, палетка может быть использована для проведения игр, которые помогут ученикам более эффективно учиться.

Палетка в домашнем обучении математике

Палетка – это небольшая доска с отверстиями, в которые вставляются цветные палочки различной длины. Она является весьма полезным инструментом для изучения математики в домашних условиях.

С помощью палетки ребенок может лучше понять основы математики, такие как счет, разложение чисел на суммы и разности, умножение и деление. Кроме того, палетка помогает развивать логическое мышление и умение решать задачи.

Для начала использования палетки достаточно выложить цветные палочки в заданном порядке. Потом можно переставлять их, чтобы получить различные комбинации. Это помогает научиться безошибочно складывать и вычитать числа.

Использование палетки также помогает ученику научиться работать с отношениями длин и количеством. Он может создавать с помощью палочек геометрические фигуры, изучать симметрию и даже изучать углы.

В итоге, использование палетки в домашнем обучении математике – это один из самых простых и эффективных способов познакомиться с основами математики и развить свой ум, что позволяет ученикам с легкостью освоить дальнейший курс.

Видео по теме:

Вопрос-ответ:

Что такое палетка в математике?

Палеткой в математике называют набор прямоугольных блоков одинаковой ширины и разной высоты, использующихся для моделирования арифметических задач. Каждый блок представляет определенную числовую величину и может быть перемещен и переставлен в соответствии с требованиями задачи.

Как использовать палетку в 4 классе?

Палетку можно использовать для изучения основ арифметики, таких как сложение, вычитание, умножение и деление. С ее помощью можно визуализировать операции и сделать процесс обучения более наглядным и интерактивным.

Какие математические понятия можно изучить с помощью палетки?

С помощью палетки можно изучать такие понятия, как разность, множитель, дробь, десятичная дробь, отношение и многое другое.

Какие типы палеток существуют?

Существует несколько типов палеток, таких как палетки с фиксированной шириной блоков, палетки с переменной шириной блоков и палетки с разноцветными блоками для изучения дробей.

Какие преимущества использования палетки в обучении математике?

Использование палетки в обучении математике позволяет стимулировать воображение, укреплять понимание арифметических операций, развивать логическое мышление и повышать интерес к учебному процессу.

Можно ли использовать палетку для изучения геометрии?

Да, палетку можно использовать для изучения геометрии, например, для изучения площади и периметра прямоугольников и квадратов.

Какую роль играет палетка в развитии математической грамотности у детей?

Палетка играет важную роль в развитии математической грамотности у детей, так как позволяет объяснять абстрактные понятия математики визуально и конкретно. Это особенно важно для детей, у которых есть трудности в усвоении математики.

Разработка программного модуля для оцифровывания геофизических палеток и построения произвольных теоретических кривых зондирования геологической среды

Авторы: Коробейников Павел Александрович, Соколова Анна Сергеевна, Молокова Наталья Викторовна

Рубрика: Технические науки

Опубликовано в Молодой учёный №19 (123) октябрь-1 2016 г.

Дата публикации: 04.10.2016 2016-10-04

Статья просмотрена: 106 раз

Скачать электронную версию

Скачать Часть 1 (pdf)

Библиографическое описание:

Коробейников, П. А. Разработка программного модуля для оцифровывания геофизических палеток и построения произвольных теоретических кривых зондирования геологической среды / П. А. Коробейников, А. С. Соколова, Н. В. Молокова. — Текст : непосредственный // Молодой ученый. — 2016. — № 19 (123). — С. 80-84. — URL: https://moluch.ru/archive/123/34089/ (дата обращения: 16.07.2023).



Данная работа посвящена разработке программного модуля для решения интерпретационных задач с помощью методов идентификации и многовариантного анализа геофизических данных, полученных методом электромагнитного зондирования.

Ключевые слова:

разведочная геофизика, электромагнитное зондирование; программирование; интерпретация данных

Введение

Геологические разрезы имеют сложную слоистую структуру, которая обуславливает практическую ценность данного месторождения. Специалисты различных областей заинтересованы в максимально точной, универсальной и коммерчески выгодной технологии разведки.

Одним из эффективных и универсальных методов разведки на средних глубинах залегания является метод электромагнитного зондирования основанный на теории поля, сопряженной со сложными вычислениями, особенно на этапе интерпретации данных полученных с разведывательного оборудования.

На этом этапе используются графики (в разведке называемые палетками), интерпретация которых требует высокого профессионализма, более того палетки простроены лишь для основных видов разрезов.

Для повышения эффективности проведения анализа данных и сокращения временных затрат необходимо оцифровать имеющиеся палетки, а также расширить возможности построения теоретических кривых для произвольных характеристик разреза, что позволит повысить точность интерпретации результатов разведывательных работ.

Актуальность данной работы обусловлена отсутствием программного обеспечения для интерпретации данных полученных методом электромагнитного зондирования, что мешает активному продвижению и использованию данного метода разведки.

Объект исследования — процесс построения и математическая модель теоретических кривых электромагнитного зондирования.

Предмет исследования — прикладные аспекты многовариантного анализа данных и технологии программирования к решению задач моделирования и анализа.

В связи с вышеизложенным, целью работы является разработка программного обеспечения для автоматизации интерпретации палеток, построении и анализа теоретических кривых зондирования.

Алгоритм решения задачи

Для решения данной задачи необходимо было:

‒ проанализировать литературу посвященную методу электромагнитного зондирования

‒ восстановить алгоритм построения теоретических кривых зондирования

‒ уточнить требования к математической модели

‒ конкретизировать ограничения на входные и выходные параметры

‒ программно реализовать модуль

‒ тестировать корректность работы и соответствие ожидаемым требованиям

Математическая модель

Для создания программного комплекса необходима математическая модель исследования, на основании которой выбирается среда и средства разработки.

Математическая модель основывается на алгоритме решения прямой задачи электроразведки, в котором поэтапно рассчитываются параметры исследуемой слоистой среды, основываясь на входных параметрах.

Входными параметрами модели являются: –разнос, -частота, -диэлектрическая проницаемость, — удельное сопротивление слоев –мощность слоев.

Выходными параметрами являются: — магнитные числа среды, _{— эффективное сопротивление, кривая зависимости от .}

Входные и выходные параметры связаны формулами:

(1)

(2)

где — параметры скин-слоев вычисляемые по формулам:

(3)

— вспомогательные параметры описываемые формулами:

(4)

(5)

(6)

в однородной среде:

(7)

(8)

где — функции Бесселя, а — волновые числа, определяемые по формулам:

(9)

где — круговая частота – абсолютная диэлектрическая проницаемость среды, — абсолютная магнитная проницаемость среды, — электропроводность среды, .

Как видно из формулы, волновое число учитывает электромагнитные свойства среды ( и рабочую частоту съёмки.

Поскольку горные породы на каждом участке исследования обладают определёнными значениями , то и волновое число даже при неизменной частоте на каждом участке и даже каждой точке измерения имеет своё значение и изменяется при изменении рабочей частоты .

Hz и Hr связны с выражениями:

(10)

, при Hz/Hr меньше 0,1(11)

(12)

Средства разработки

Для разработки были выбраны следующие средства:

Язык программирования C# и библиотека ZedGraph

Среда разработки Microsoft Visual Studio

Программный комплекс

Разрабатываемый модуль позволяет строить кривые зависимости от , по известным параметрам среды и и отношения . Данные для построения хранятся в формате.xls, поэтому для работы с ними используются использовать стандартные возможности языка C#.

Кроме того, существует возможность вывести несколько теоретических кривых, как по одной — для этого нужно нажать кнопку выбранной кривой, так и блоком, блоки кривых разделены по исходным параметрам и пронумерованы. При выводе на экран нескольких кривых, они будут различных цветов, цвет кривой отображается справа от кнопки кривой и повторяется в легенде графика — рисунок 1.

Рис. 1. Блок построения основных кривых

Рис. 2. Построенные кривые

Результаты работы программы

Результатом работы программы являются блоки теоретических кривых, построенных на билогарифмическом бланке. Разработанные модули позволят автоматизировать построение теоретических кривых, что дает возможность для дальнейшей интерпретации геофизических данных, полученных с аппаратных комплексов.

Литература:

1. Беляков В. И. Дистанционно-частотные зондирования. Санкт-Петербург, 1995. — 25 с.
2. Жданов М. С. Электроразведка. Недра, 2006. — 316 с.
3. Иголкин В. И. Теоретические основы интерпретации результатов электромагнитного зондирования. Красноярск, 2010. — 50 с.
4. Каратаев Г. Д., Панфилов А. Е. Разработка программного обеспечения для интерпретации результатов электромагнитных методов геологической среды [Электронный ресурс]// Сборник материалов Международной конференции студентов, аспирантов и молодых ученых «Проспект Свободный-2015», посвященной 70-летию Великой Победы — Красноярск, Сибирский федеральный университет, 15–25 апреля 2015 г URL: http://nocmu.sfu-kras.ru/direction/src/техническое/Геология %20и %20разведка %20месторождений.pdf (дата обращения: 14.05.2016)
5. Коробейников П. А., Молокова Н. В. Разработка программного комплекса для интерпретации данных методов электромагнитного зондирования. /Проспект Свободный-2016: материалы науч. Конф., посвященной Году образования и Содружества Независимых Государств (15–25 апреля 2016г.) [Электронный ресурс]/отв. ред. — А. Н. Тамаровская — Электрон.дан. — Красноярск: Сиб.федер.ун-т, 2016. — С.20–23.

Основные термины (генерируются автоматически): электромагнитное зондирование, математическая модель, кривой, волновое число, интерпретация данных, параметр, программное обеспечение, программный комплекс, результат работы программы, средство разработки.

Ключевые слова

программирование, разведочная геофизика, , интерпретация данных, электромагнитное зондирование

разведочная геофизика, электромагнитное зондирование, программирование, интерпретация данных

Похожие статьи

Автоматизированная фильтрация

данных аппаратуры. ..

2. Коробейников П. А., Молокова Н. В. Разработка программного комплекса для интерпретации данных методов электромагнитного зондирования

. / Проспект Свободный-2016: материалы науч. конф…

Разработка программного модуля для исследования связи…

1. Коробейников П. А., Молокова Н. В. Разработка программного комплекса для интерпретации данных методов электромагнитного зондирования. / Проспект Свободный-2016: материалы науч.

Математические модели управления рабочими режимами…

Целью данной работы является разработка программно-аппаратного комплекса (ПАК), имеющего набор программных средств для реализации единого информационного пространства. ..

Исследование и

разработка методов и средств оценки степени…

Он обеспечивает полный цикл обработки данных дистанционного зондирования Земли

Также на экране должны быть представлены результаты работы программы в понятной пользователю форме.

Программное обеспечение удовлетворяет следующим требованием

Проверка корректности

программного обеспечения

Увеличивается количество программных комплексов, призванных решать различные бизнес-задачи, а также увеличивается их сложность.

Похожие статьи. Разработка программного обеспечения для генерации вариантов самостоятельных работ студентов информационного. ..

Анализ современных методов и

программных средств…

Липаев В. В., Филинов Е. Н. Мобильность программ и данных в открытых информационных системах.

Разработка программных средств синтеза и анализа весовых функций в среде MATLAB.

Разработка программы трёхмерного отображения результатов…

Изменяя параметры модели, можно получить наглядную графическую интерпретацию моделируемой ситуации.

Постановка задачи и назначение программы. Основной целью работы была разработка компонента стенда моделирования, обеспечивающего трёхмерное…

Похожие статьи

Автоматизированная фильтрация

данных аппаратуры. ..

2. Коробейников П. А., Молокова Н. В. Разработка программного комплекса для интерпретации данных методов электромагнитного зондирования. / Проспект Свободный-2016: материалы науч. конф…

Разработка программного модуля для исследования связи…

1. Коробейников П. А., Молокова Н. В. Разработка программного комплекса для интерпретации данных методов электромагнитного зондирования. / Проспект Свободный-2016: материалы науч.

Математические модели управления рабочими режимами…

Целью данной работы является разработка программно-аппаратного комплекса (ПАК), имеющего набор программных средств для реализации единого информационного пространства. ..

Исследование и

разработка методов и средств оценки степени…

Он обеспечивает полный цикл обработки данных дистанционного зондирования Земли

Также на экране должны быть представлены результаты работы программы в понятной пользователю форме.

Программное обеспечение удовлетворяет следующим требованием

Проверка корректности

программного обеспечения

Увеличивается количество программных комплексов, призванных решать различные бизнес-задачи, а также увеличивается их сложность.

Похожие статьи. Разработка программного обеспечения для генерации вариантов самостоятельных работ студентов информационного. ..

Анализ современных методов и

программных средств…

Липаев В. В., Филинов Е. Н. Мобильность программ и данных в открытых информационных системах.

Разработка программных средств синтеза и анализа весовых функций в среде MATLAB.

Разработка программы трёхмерного отображения результатов…

Изменяя параметры модели, можно получить наглядную графическую интерпретацию моделируемой ситуации.

Постановка задачи и назначение программы. Основной целью работы была разработка компонента стенда моделирования, обеспечивающего трёхмерное…

Расширение математической палитры для формирования модели развития: пегий

• Дугу, Майкл
;
• Мацца, Кристиан
;
• Шваллер, Бит
;
• Пече, Ласло

Аннотация

Пьебалдизм обычно проявляется в виде белых участков меха, волос или кожи из-за отсутствия клеток, вырабатывающих пигмент, в этих областях. Распределение белых и цветных зон не следует классическим паттернам Тьюринга. Здесь мы представляем структуру моделирования для формирования паттернов, которая позволяет легко модифицировать взаимосвязь между тремя факторами с различными механизмами обратной связи. Эти факторы состоят из двух факторов диффузии и клеточно-автономного неподвижного фактора транскрипции. Глобально модель позволила выделить четыре разные ситуации. Две ситуации приводят к созданию классических паттернов Тьюринга; регулярно расположенные пятна и лабиринтные узоры. Более того, начальный наклон в активации фактора транскрипции дает прямые линии. Третья ситуация не приводит к шаблонам, но приводит к различным однородным цветовым тонам. Наконец, четвертый проливает новый свет на возможные механизмы, ведущие к образованию пегих рисунков, примерами которых служат случайные узоры на шерсти некоторых пород коров и далматинских собак. Мы показываем, что эти пегие паттерны носят преходящий характер, развиваются из случайных начальных условий и зависят от бистабильности системы. Основная новизна заключается в том, что мы обнаружили, что наличие клеточно-автономного фактора не только расширяет диапазон параметров диффузии реакции, в котором может возникнуть паттерн, но и расширяет паттернообразующие способности уравнений реакции-диффузии.

Публикация:

Электронные распечатки arXiv

Дата публикации:

октябрь 2017 г.

DOI:

10.48550/arXiv.1710.03563

архив:

архив: 1710.03563

Биб-код:

2017arXiv171003563D «/>

Ключевые слова:

• Количественная биология – ткани и органы

Mathematical Palette with Bca Ilrna Tutorial & Infotrac: Ronald Staszkow: Hardcover: 9780534403652: Powell’s Books

Synopses & Reviews

MATHEMATICAL PALETTE делает математику увлекательной, актуальной, понятной и информативной для учащихся. Визуально привлекательный текст содержит полноцветные изображения изобразительного искусства, чтобы оживить математические концепции для студентов, изучающих гуманитарные науки. В тексте делается упор на решение проблем посредством открытий и приложений, побуждая учащихся стать активными участниками и прививая глубокое понимание и признательность за красоту математики. Наряду с упором на навыки письма и критического мышления, текст представляет историю математиков с многочисленными повседневными приложениями, чтобы проиллюстрировать эволюцию и практичность математики и провести параллели с творчеством специалистов по гуманитарным наукам. Третье издание THE MATHEMATICAL PALETTE также включает в себя надежный набор онлайн-управления курсами, тестирования и учебных ресурсов для преподавателей и студентов. Это включает в себя BCA / iLrn Testing and Tutorial, онлайн-обучение vMentor в реальном времени и веб-сайт Book Companion с ресурсами онлайн-графического калькулятора.

Краткий обзор

Добейтесь успехов в математике с помощью МАТЕМАТИЧЕСКОЙ ПАЛИТРЫ! Написанные с мыслью о вас, авторы делают математику приятной, актуальной, понятной и информативной. Визуально привлекательный текст содержит полноцветные изображения изобразительного искусства, чтобы оживить математические концепции. Ежедневные приложения включены, чтобы проиллюстрировать эволюцию и практичность математики и параллельны творчеству специальностей гуманитарных наук. Подготовьтесь к экзаменам с помощью многочисленных ресурсов, расположенных в Интернете и по всему тексту, таких как онлайн-репетиторство, учебные пособия, веб-сайт, сопровождающий книги, резюме в конце глав, обзоры, тесты и разделы с точными ответами.

Об авторе

Рональд Сташков родился и вырос в Гонолулу, Гавайи, окончил среднюю школу Сент-Луиса, получил степень бакалавра математики в колледже Святой Марии в Мораге, Калифорния, и получил степень магистра математического образования в Калифорнийском университете в Санта-Барбаре. Он имеет сертификат в области развивающего образования от штата Аппалачи, Северная Каролина, и пожизненные полномочия штата Калифорния в области среднего обучения преподаванию в муниципальных колледжах и надзору за общественными колледжами. После 11 лет работы учителем математики и тренером по легкой атлетике/бегу по пересеченной местности в средней школе Де Ла Саль в Конкорде, Калифорния, он стал штатным инструктором в колледже Олоне, Фремонт, Калифорния, и специализируется на развивающей математике. Он спроектировал Учебный центр математики колледжа Олоне и создал курс математики для студентов гуманитарных наук в колледже Олоне. Роберт Брэдшоу — профессор математики в Колледже Олоне.

Содержание

1. СТАРЫЕ И НОВЫЕ НОМЕРА. Обзор. Краткая история чисел и цифр . Глава 1 Проекты. Древние системы счисления. Индо-арабская система и дроби. Системы счисления с другими основаниями. Числа техники. Типы чисел. Краткое содержание. Обзор. Тест. 2. ЛОГИЧЕСКОЕ МЫШЛЕНИЕ. Обзор. Краткая история логики. Глава вторая Проекты. Логика, утверждения и определения. Индуктивное и дедуктивное мышление. Символическая логика и таблицы истинности. Логика и блок-схемы. Логика и головоломки. Резюме второй главы. Обзор второй главы. Тест второй главы. 3. СЕТЫ И СЧЕТ. Обзор. Краткая история наборов. Глава третья Проекты. Множества: конечное и бесконечное. Установите операции и диаграммы Венна. Приложения наборов. Введение в счет. Краткое содержание. Обзор. Тест. 4. ВЕРОЯТНОСТЬ. Обзор. Краткая история вероятности . Глава четвертая. Проекты. Интуитивные концепции вероятности. Расчет вероятностей. Вероятность и шансы. Вероятность сложных событий. Условная возможность. Ожидаемое значение. Краткое содержание. Обзор. Тест. 5. СТАТИСТИКА И ПОТРЕБИТЕЛЬ. Обзор. Краткая история статистики. Глава пятая Проекты. Организация информации. Меры центральной тенденции. Меры рассеивания. Нормальное распределение. Опросы и погрешность. Регрессия и прогнозирование. Краткое содержание. Обзор. Тест. 6. АЛГЕБРОВОЕ МОДЕЛИРОВАНИЕ. Обзор. Краткая история алгебры . Глава шестая Проекты. Линейные модели. Квадратичные модели. Экспоненциальные модели. Логарифмические модели. Краткое содержание. Обзор. Тест. 7. ГЕОМЕТРИЯ И ИСКУССТВО. Обзор. Краткая история геометрии . Глава седьмая Проекты. Евклидова и неевклидова геометрия. Перспектива. Золотые сечения и прямоугольники. Многоугольники и звезды. Мозаики. Фракталы. Краткое содержание. Обзор. Тест. 8. ТРИГОНОМЕТРИЯ: ДВЕРЬ В НЕИЗМЕРИМОЕ. Обзор. Краткая история тригонометрии. Глава восьмая Проекты. Прямоугольные треугольники, синус, косинус, тангенс. Решение прямоугольных треугольников. Применение прямоугольного треугольника. Законы синусов и косинусов.