Площадь фигуры палетка: » Измерение площади фигур с помощью палетки» (4 класс)

Конспект урока по математике «Измерение площади фигур с помощью палетки» | План-конспект урока по математике (4 класс):

Математика, 4-й класс. 

Тема: «Измерение площади фигуры с помощью палетки».

Цель: найти способ нахождения площади фигур с помощью палетки. 
Задачи урока:

1. систематизировать и обобщать знания о площади фигуры, её свойствах, расширять круг изучения единиц площади.
2.Учить анализировать геометрические фигуры. 
3.Развивать логическое мышление учащихся, умение точно и обоснованно аргументировать, выделять те стороны наблюдаемых явлений, которые необходимы для существа исследования и осмысления задачи. 
4.Создать условия для самостоятельного поиска знаний. 
5.Воспитать интерес к предмету, любознательность, дружеское отношение к одноклассникам в совместной работе. 
Оборудование: авторская презентация «Измерение площади фигуры с помощью палетки», мультимедийная установка.
Дидактические материалы к учебному занятию: учебник «Математика», 4 класс, М. И. Моро; палетки, фигуры из цветного картона.

Ход урока

I. Оргмомент. Создание мотивационной основы учебной деятельности («ситуации успеха». Начинается урок с притчи.

 -Однажды султан решил подвергнуть испытанию своих визирей. «О, мои подданные!” — обратился он к ним, — у меня есть для вас трудная задача. Я хотел бы знать, кто решит её. Повёл он их в сад, в углу была ржавая дверь с огромным замком. «Тот, кто откроет дверь, станет первым визирем”. Одни придворные только качали головами, другие стали замок разглядывать, третьи начали неуверенно толкать дверь, но они были убеждены, что не смогут открыть её. Один за другим отходили. Но один визирь внимательно осмотрел и навалился плечом на дверь. Он толкнул её и — о, чудо! — она стала поддаваться, появилась сначала узкая щель, а потом дверь стала двигаться все быстрее и раскрылась. Тогда падишах сказал: «Ты станешь первым визирем, потому что полагаешься не только на то, что видишь и слышишь, но и веришь в свои силы”.

-Почти на каждом уроке математики мы открываем новые знания. И наш урок сегодня – не исключение. Мы откроем новый секрет математики. И, если вы будете верить в свои силы, то обязательно справитесь со всеми трудностями.

-Давайте представим ситуацию. Однажды ученики 4 Б класса побывали на кондитерской фабрике. Им показывали как делают вафли. В конце экскурсии кондитер отломил каждому ученику от большой пластины по маленькому кусочку хрустящей вафли. Кусочки были неодинаковые. Петя и Вася стали спорить: «Чей кусок оказался больше». Как же им помочь решить их спор?(вычислить площадь поверхности вафли и сравнить) 

-Что такое площадь? Выберите верное утверждение (Слайд 2)

 (число единичных квадратов полностью заполняющих эту фигуру.)

-На какие группы можно разбить данные величины? (Слайд 3)(единицы длины и единицы площади) 

— Запишите в тетрадь единицы измерения площади, расположив их в порядке увеличения.

-Проверьте! (Слайд 4)

-Площадь каких фигур вы можете найти? (5) Вот прямоугольник с заданными сторонами. Найдите его площадь (Слайд 6) – Как находили площадь? (7)

— Можем ли найти таким же способом площадь фигур, напоминающих форму кусочков вафель  №2,3,4? (нет)

— Сформулируйте цель нашего урока (необходимо узнать ещё один способ нахождения площади фигуры)

-Прочитаем тему нашего урока. (Слайд №8) -Что заметили? Новое слово — палетка.

 IV. Новая тема

— Интересное слово, на которое вы обратили внимание. Что же это за приспособление? (от франц. Паллет — «пластинка, планка»)  Найдите ответ в учебнике на с. 43. Вот как она выглядит. (Демонстрация палетки)

-Рассмотрите вашу палетку, чему равна её сторона. (1см) (Слайд 9) 

— На какие квадратные единицы разделена ваша палетка? (кв.см)

Работа в группах. — Давайте подумаем, как можно с помощью палетки измерять площадь. (Дети работают в группах, 2 группы находят площадь фигур, 3-я составляет алгоритм нахождения площади фигуры с помощью палетки)   5-7 мин.

Ответы детей.

— Обозначим последовательность действий. (Слайд 10-12)

1.Наложи палетку на фигуру.

2.Подсчитай кол-во полных см2 .

3.Подсчитай кол-во неполных см2  и раздели на 2.

4.Полученные результаты сложи.

— Как вы думаете, значение площади получилось точное или примерное? (Округляли результат неполных клеток, по-разному накладывали палетку)

V. Первичное закрепление нового понятия

Работа по учебнику. — Предлагаю вам закрепить ваше умение находить площадь фигур, выполнив задание по вариантам и записав решение выражением. (с.43 №191)

№196 – самостоятельно, 1 ученик за доской по карточкам. Проверка по эталону.

№ 198 – устно. Найти разные способы вычисления длины отрезка АВ. (1. Пересчётом количества см между концами отрезков; 2) 13-8=5см – универсальный способ для подобных ситуаций, т.к. точка А лежит на делении 8 см)

Решение задачи №193 – дополнить таблицу и решить самостоятельно

VI. Работа в парах №199

VII. Подведение итогов, рефлексия. (Слайд 16)

Я сегодня научился (ась)…

Мне понравилось…

Мне ещё трудно…

VIII . Домашнее задание (Слайд 15)

4.4. Вычисление площадей с помощью палетки

Для определения площадей небольших участков с криволинейными контурами на плане применяют палетки, в основном прямолинейные. К прямолинейным палеткам относятся известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет собой сеть взаимно перпендикулярных линий, проведенных через 1–2 мм на прозрачном целлулоиде, плексигласе, фотопленке, стекле или кальке.

Площадь фигуры определяется простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитываются на глаз (рис. 13). Квадратной палеткой не рекомендуется определять площади больше 2 см² на плане. Недостаток ее применения (помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз) в том, что подсчет количества целых клеток нередко сопровождается грубыми погрешностями.

Рис. 13

Рис. 14

Рис. 15

Такие недостатки не наблюдаются при определении площадей параллельной палеткой, представляющей собой листок прозрачного целлулоида, плексигласа или кальки, на котором нанесены параллельные линии преимущественно через 2 мм одна от другой. Площадь контура определяют этой палеткой следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посредине между параллельными линиями палетки. Тогда, весь контур оказывается разделенным параллельными линиями на фигуры, близкие к трапециям, с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций (рис.14).

Пунктиром показаны основания этих трапеций.

Сумма площадей трапеций, т.е. площадь контура, равна

.

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т.е. сумму отрезков параллельных прямых внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля, которую определяют по масштабной линейке и полученную длину умножают на h, м (рис.15). Чтобы не выполнять подобных вычислений, для каждого масштаба строят специальную шкалу, по которой отсчитывают площадь контура, зная сумму средних линий.

Расчет шкалы: М 1:10000, h = 2 мм, при длине шкалы 1 см площадь равна (0.2 см  100 м)  (1 см  100 м) = 2000 м² = 0.2 га. Параллельной палеткой не следует определять площади больше 10 см

2 на плане.

При разбивке участка на простейшие фигуры точность вычисления для различных вариантов не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее, чем площади других фигур. Следовательно, площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на другие фигуры (трапеции, прямоугольники). При разбивке участка на треугольники из всех вариантов будет лучшим тот, в котором треугольники будут равносторонними или высота h примерно равна основанию a.

Погрешность уменьшается, если вычислять площадь треугольника не как , а по формуле Герона

,

где . Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане.

При разбивке площади на треугольники погрешность площади участка

,

где M – знаменатель численного масштаба плана. Если вычисляют два раза, то.

Число треугольников, на которое разбивается участок, не влияет на погрешность площади. Поэтому при разбивке участка на треугольники не надо стремиться к тому, чтобы их было меньше. Точность однократного определения площади квадратной и параллельной палетками, а также ротометром характеризуется эмпирической формулой

.

Как выбрать цвета для визуализации данных

(Эта статья была изначально опубликована в Nightingale, журнале Общества визуализации данных.)

Выбор цвета является основным фактором при создании эффективных диаграмм. Хороший набор цветов выделит историю, которую вы хотите рассказать, а плохой скроет или отвлечет от цели визуализации.

В этой статье мы опишем типы цветовых палитр, используемых при визуализации данных, предоставим несколько общих советов и рекомендаций по работе с цветом, а также выделим несколько инструментов для создания и тестирования цветовых палитр для создания собственных диаграмм.

Типы цветовой палитры

Для визуализации данных существует три основных типа цветовой палитры:

• Качественные палитры
• Последовательные паллеты
• Расходящиеся палитры

Тип цветовой палитры, используемой в визуализации, зависит от характера данных, сопоставленных с цветом.

Качественная палитра

Качественная палитра используется, когда переменная является категориальной по своей природе. Категориальные переменные — это переменные, которым присвоены разные метки без присущей им упорядоченности. Примеры включают страну или штат, расу и пол. Каждому возможному значению переменной присваивается один цвет из качественной палитры.

В качественной палитре цвета, присвоенные каждой группе, должны быть разными. Как правило, вы должны попытаться ограничить максимальный размер палитры десятью или менее цветами. С большим количеством цветов вы начинаете сталкиваться с проблемами различения групп. Если у вас есть больше возможных значений, чем цветов, вам следует попытаться объединить значения вместе, например, установить самые маленькие категории в одну «другую» категорию. Многократное перебор цветов — плохая идея, так как это может привести к путанице.

Самые маленькие кусочки слева не только повторяют цвета в палитре, но и довольно трудно отличить друг от друга.

Основной способ различения цветов — через их оттенки. Дополнительные вариации между цветами можно получить, отрегулировав яркость и насыщенность, но лучше не делать различия слишком большими. Слишком большая разница может указывать на то, что одни цвета важнее других, хотя это может быть полезным свойством, если его использовать преднамеренно. Избегайте двух цветов с одинаковым оттенком, но разной яркостью и насыщенностью, если только значения, связанные с этими цветами, не связаны. Например, у вас может быть линейная диаграмма, на которой дневные показания отображаются светлой линией, а недельное скользящее среднее — более темным.

Последовательная палитра

Если переменная, назначенная для окрашивания, является числовой или имеет изначально упорядоченные значения, то ее можно изобразить с помощью последовательной палитры. Цвета назначаются значениям данных в континууме, обычно на основе яркости, оттенка или того и другого.

Наиболее важным параметром цвета для последовательной палитры является его яркость. Как правило, более низкие значения связаны с более светлыми цветами, а более высокие значения — с более темными. Однако это связано с тем, что графики, как правило, находятся на белом или аналогичном светлом фоне. На темном фоне обычно наблюдается обратный случай, когда более высокие значения обозначаются более яркими и светлыми цветами.

Второстепенным параметром последовательной цветовой палитры является ее оттенок. Можно просто использовать один оттенок для вашей цветовой карты, в основном изменяя яркость для обозначения значения. Тем не менее, стоит рассмотреть возможность перехода между двумя цветами в качестве дополнительной помощи при кодировании. Как правило, более теплый цвет (по направлению к красному или желтому) идет на более светлом конце, а более холодный цвет (по направлению к зеленому, синему или пурпурному) — по более темному.

Расходящаяся палитра

Если наша числовая переменная имеет значимое центральное значение, например ноль, то мы можем применить расходящуюся палитру. Расходящаяся палитра — это, по сути, комбинация двух последовательных палитр с общей конечной точкой, находящейся в центре значения. Значения, превышающие центр, назначаются цветам на одной стороне центра, а меньшие значения назначаются цветам на противоположной стороне.

Как правило, для каждой последовательной палитры компонентов используется свой оттенок, чтобы было легче различать положительные и отрицательные значения относительно центра. Как и в случае с последовательными палитрами, центральному значению обычно назначается светлый цвет, поэтому более темные цвета указывают на большее расстояние от центра.

Дискретная или непрерывная палитра

Последовательные и расходящиеся палитры могут быть связаны со значениями данных двумя различными способами: либо как дискретный набор цветов, каждый из которых связан с числовым диапазоном, либо как непрерывная функция между числовым значением и цветом .

Инструменты для создания палитр обычно относятся к первому типу, в то время как инструменты для создания визуализаций часто могут создавать непрерывные ассоциации. Хотя автоматически может показаться, что лучше иметь непрерывную функцию между значением и цветом, у дискретизированной палитры все же есть свои преимущества.

Наша способность различать различия в цвете слабее, чем способность различать положение или длину, поэтому мы уже находимся в невыгодном положении, когда связываем цвет с точными значениями. Дискретизация значений может снизить когнитивную нагрузку, выявляя общие закономерности в данных. Кроме того, мы можем установить диапазоны значений для дискретной палитры таким образом, чтобы лучше представить данные. Если данные содержат выбросы, то непрерывная палитра может привести к тому, что большая часть данных окажется в более узком диапазоне значений. Использование дискретной цветовой палитры означает, что мы можем создавать диапазоны разного размера для лучшего представления различий в данных.

Одним из основных недостатков дискретной цветовой палитры является то, что мы теряем возможность сравнивать элементы, попадающие в одну и ту же корзину. Там, где между близкими значениями с непрерывной палитрой была некоторая цветовая разница (например, между Техасом и Калифорнией в приведенном выше примере), в дискретном случае ее нет.

Дополнительные советы по использованию цвета

Избегайте ненужного использования цвета

Несмотря на то, что цвет является важной частью визуализации данных, разумно проявлять сдержанность и использовать цвет только там, где это уместно. Не для каждой создаваемой вами диаграммы потребуется несколько цветов. Если у вас есть только две переменные для построения графика, они, скорее всего, будут закодированы вертикальным и горизонтальным положением или длиной. Цвет обычно появляется только тогда, когда третья переменная должна быть закодирована в диаграмме или если она является компонентом специализированной диаграммы, такой как круговая диаграмма. Однако бывают случаи, когда цвет может быть добавлен, чтобы подчеркнуть конкретный вывод или в качестве дополнительной кодировки выделения.

Цвета радужной полосы слева не имеют смысла, и их следует избегать. Справа большинство полос окрашены в нейтральный серый цвет, чтобы подчеркнуть сравнение двух цветных полос.

Согласование цветов на диаграммах

Если у вас есть панель мониторинга или отчет, содержащий несколько диаграмм, рекомендуется согласовать цвета между диаграммами, когда они относятся к одной и той же группе или объекту. Если цвета меняют свое значение между диаграммами, читателю может быть труднее понять диаграмму.

Использование значимости цвета

Иногда вы можете использовать восприятие цветов для повышения эффективности визуализации. Если группы, которые вы рисуете, имеют неотъемлемые цветовые соглашения, например спортивные команды и политические партии, назначение соответствующих цветов может облегчить читателям визуализацию. Возможно, вы даже захотите попробовать создать собственные палитры вокруг цветов вашего бренда в качестве основы.

Общее эмпирическое правило заключается в том, чтобы избегать слишком высоких уровней насыщенности и яркости цвета, чтобы снизить нагрузку на глаза.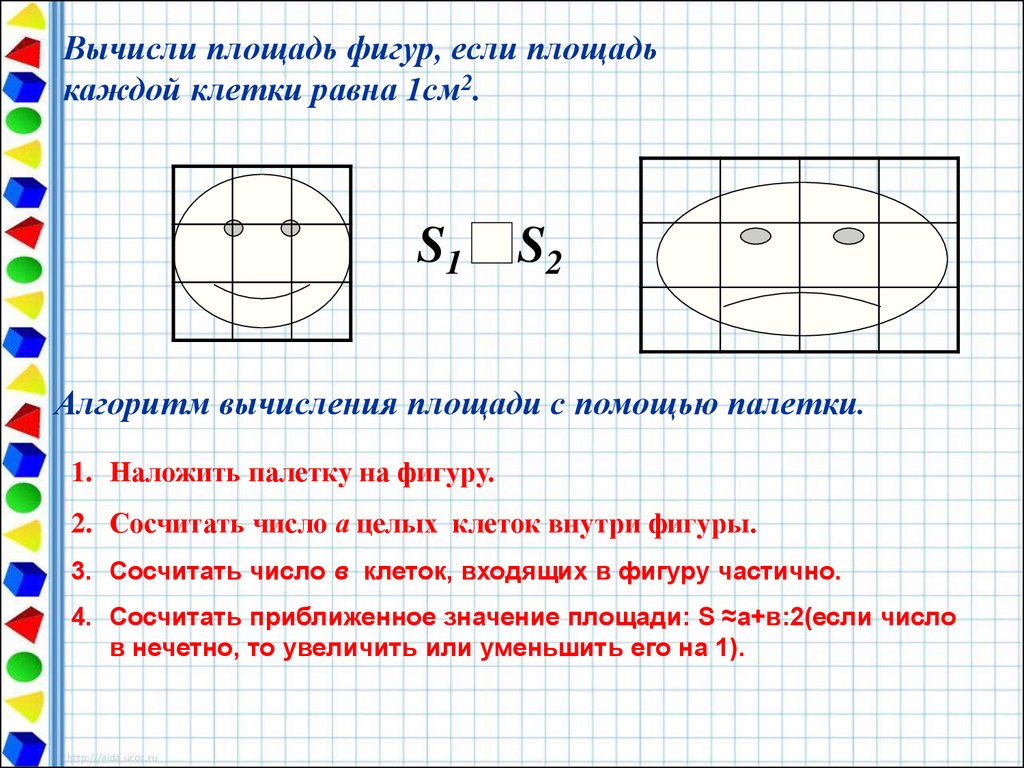 Это также позволяет выделить важные элементы, придав им более смелый вид по сравнению с другими элементами. Точно так же нельзя недооценивать важность серого цвета, чтобы отодвигать неважные данные на задний план, помимо других целей.

В заключение стоит отметить, что разные культуры могут связывать разные значения с каждым оттенком. Например, в некоторых западных культурах красный может ассоциироваться со страстью или опасностью, а в некоторых восточных культурах — с процветанием и удачей. Это может быть не особенно важно, если результаты не представляются широкой аудитории, но это еще один инструмент, о котором следует помнить, чтобы облегчить понимание ваших визуализаций.

Лечение дальтонизма

Около четырех процентов населения страдают дальтонизмом, большинство из них мужчины. Наиболее распространенные формы дальтонизма вызывают смешение определенных оттенков красного и зеленого, хотя существуют также формы дальтонизма, при которых оттенки синего и желтого выглядят одинаково. По этим причинам полезно попробовать изменить измерение, отличное от одного только оттенка, чтобы указать значение, связанное с цветом, например яркость и насыщенность. Вы также можете использовать симуляторы дальтонизма, такие как Coblis, чтобы получить представление о том, будет ли ваша окончательная визуализация понятна другим и есть ли потенциальные двусмысленности.

Инструменты для использования цветов

В Интернете есть много инструментов, которые помогут вам выбрать и протестировать цвета для ваших визуализаций данных. Здесь мы выделим некоторые из самых простых инструментов, которые помогут вам быстро освоиться с выбором цвета.

ColorBrewer

ColorBrewer является классическим справочником по цветовым палитрам и предоставляет ряд различных палитр каждого типа. Некоторые палитры могут быть сомнительными с точки зрения безопасности для дальтоников, поэтому обязательно проверьте значок глаза над панелью цветовых кодов, чтобы проверить, есть ли у набора цветов вероятность возникновения проблем с восприятием (обозначается цифрой 9). 0111 ? и X соответственно).

Средство выбора цвета данных

Средство выбора цвета данных — это быстрый и простой в использовании инструмент для создания последовательных и расходящихся палитр. Вкладку «Палитра» по умолчанию лучше всего использовать для создания последовательных палитр с несколькими оттенками, а не качественных палитр, поскольку интерполяция между конечными точками обязательно оставит некоторый сегмент оттенков в цветовом круге.

Помощник по цветовой палитре Chroma.js

Помощник по цветовой палитре chroma.js немного сложнее, чем Data Color Picker, с его параметрами для коррекции яркости, использования интерполяции Безье и немного более сложного ввода значений цвета. Тем не менее, это также дает некоторую дополнительную свободу в установке нескольких точек остановки для алгоритма, чтобы попытаться подобрать палитру. В качестве дополнительного бонуса приложение также включает симулятор дальтонизма на той же странице, выделяя наиболее распространенные типы дефектов, при которых могут возникнуть проблемы.

Color Thief

Не так много быстрых и простых инструментов для создания качественных палитр, как для последовательных и расходящихся палитр. Я хочу, чтобы hue и Colorgorical быстро генерировали случайные палитры, но с ними немного сложнее работать, когда вы хотите настроить свои значения.

Один из забавных способов создания качественной палитры — черпать вдохновение из изображений и скриншотов с привлекательными естественными палитрами. Есть несколько инструментов, которые помогут сделать это, но Color Thief — один из самых простых в работе, он автоматически извлекает палитру здорового размера из загруженных изображений. Это не обязательно означает, что вы можете использовать извлеченные цвета напрямую и по порядку в качестве палитры визуализации. Хотя они могут быть вдохновляющей отправной точкой для цветов, которые хорошо смотрятся вместе, вам, вероятно, потребуется внести некоторые изменения и изменения, чтобы убедиться, что выбранные вами цвета эффективны в контексте визуализации.

Viz Palette

В предыдущем разделе Coblis был связан как ресурс для проверки того, как ваша окончательная визуализация может выглядеть для тех, у кого проблемы с цветовосприятием. Viz Palette — это инструмент с более широкой цветовой палитрой, который вы можете использовать для проверки своих палитр, прежде чем создавать визуализацию. В дополнение к возможности просматривать наборы цветов в контексте примеров графиков и при смоделированных недостатках восприятия цвета, вы также можете немедленно модифицировать и изменять цвета своей палитры.

Резюме

В этой статье представлен краткий обзор способов использования цвета для эффективной визуализации данных. Различные типы цветовой палитры — качественные, последовательные или расходящиеся — должны использоваться в зависимости от типа данных, сопоставленных с цветом. Убедитесь, что при использовании цвета он имеет смысл и используется последовательно. Постарайтесь обратить внимание на дальтоников, чтобы улучшить доступность вашего сюжета. Всегда старайтесь тщательно обдумывать свой выбор цвета, представляя результаты другим, так как хороший набор цветов значительно облегчит донесение желаемого сообщения до вашей аудитории.

10 Графика и цвет в R

Посмотрите видео этой главы: Часть 1 Часть 2 Часть 3 Часть 4

Цветовые схемы по умолчанию для большинства графиков в R ужасны. Я виноват, как и все остальные, в использовании этих ужасных цветовых схем, но я активно пытаюсь работать над улучшением своих привычек. R имеет гораздо лучшие способы обработки спецификации цветов на графиках и графиках, и вы должны использовать их, когда это возможно. Но для этого важно немного узнать о том, как работают цвета в R.

10.1 Цвета 1, 2 и 3

Довольно часто на графиках, сделанных в R, вы увидите что-то вроде следующего рождественского сюжета.

 > набор семян(19)
> х <- rнорм(30)
> у <- rнорма(30)
> график (x, y, col = rep (1: 3, каждый = 10), pch = 19)
> легенда ("нижняя правая", легенда = паста ("Группа", 1:3), col = 1:3, pch = 19, bty = "n") 

Рисунок 5.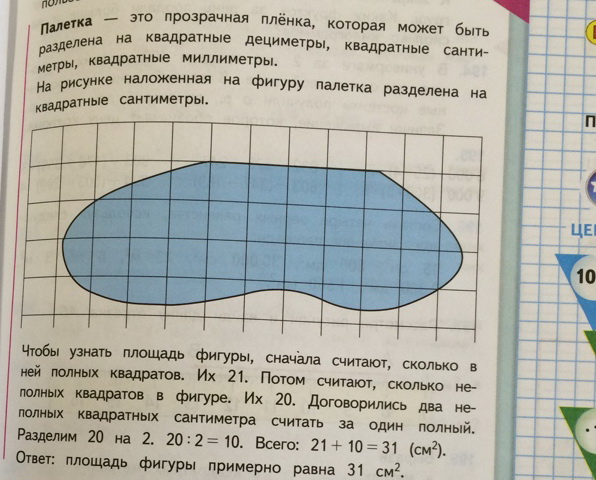 1: Цвета по умолчанию в R

Причина проста. В R черный цвет обозначается как col = 1 в большинстве графических функций, красный обозначается как col = 2 , а зеленый обозначается col = 3 . Так что, если вы рисуете несколько групп вещей, естественно отображать их, используя цвета 1, 2 и 3.

Вот еще один набор общих цветовых схем, используемых в R, на этот раз с помощью функции image() .

 > номинал (mfrow = с (1, 2))
> изображение(вулкан, col = heat.colors(10), main = "heat.colors()")
> изображение(вулкан, col = topo.colors(10), main = "topo.colors()") 

Рисунок 5.2: Графики изображений в R

10.2 Соединение цветов с данными

Обычно мы добавляем цвет на график не для того, чтобы улучшить его художественную ценность, а для того, чтобы добавить еще одно измерение к визуализации (т. Таким образом, имеет смысл, что диапазон и палитра цветов, которые вы используете, будут зависеть от типа данных, которые вы рисуете . Хотя может быть обычным делом просто выбирать цвета наугад, выбор цветов для вашего графика требует тщательного рассмотрения. Потому что тщательный выбор цвета графика может повлиять на то, как люди интерпретируют ваши данные и делают на их основе выводы.

10.3 Цветовые утилиты в R

R имеет ряд утилит для работы с цветами и цветовыми палитрами на ваших графиках. Для начала, пакет grDevices имеет две функции:

• colorRamp : взять палитру цветов и вернуть функцию, которая принимает значения от 0 до 1, указывая крайние значения цветовой палитры (например, см. серый( ) функция)

• colorRampPalette : Возьмите палитру цветов и верните функцию, которая принимает целочисленные аргументы и возвращает вектор цветов, интерполирующий палитру (например,

  heat.colors() или topo.colors() )

Обе эти функции принимают палитры цветов и помогают выполнять интерполяцию между цветами в палитре. Они отличаются только типом объекта, который они возвращают.

Наконец, функция colors() перечисляет названия цветов, которые вы можете использовать в любой функции построения графика. Как правило, вы должны указать цвет в (базовой) функции построения графика с помощью аргумента col .

10,4

colorRamp()

Для colorRamp() и colorRampPalette() представьте, что вы художник и у вас в руках палитра. На вашей палитре есть набор цветов, скажем, красный и синий. Теперь между красным и синим вы можете представить себе целый спектр цветов, которые могут быть созданы путем смешивания разного количества рида и синего. И

colorRamp() , и colorRampPalette() обрабатывают этот процесс «смешивания» за вас.

Начнем с простой палитры «красного» и «синего» цветов и передадим их colorRamp() .

 > приятель <- colorRamp(c("красный", "синий"))
> приятель (0)
     [1] [2] [3]
[1,] 255 0 0 

Обратите внимание, что pal на самом деле является функцией, возвращенной colorRamp() . Когда мы вызываем pal(0) , мы получаем матрицу 1 на 3. Числа в матрице будут находиться в диапазоне от 0 до 255 и обозначать количество красного, зеленого и синего (RGB) в столбцах 1, 2 и 3 соответственно. Простая математика подсказывает нам, что таким образом можно выразить более 16 миллионов цветов. Звонок pal(0) дает нам максимальное значение (255) для красного и 0 для других цветов. Так что это просто красный цвет.

Мы можем передать любое значение от 0 до 1 в функцию pal() .

 > ## синий
> приятель(1)
     [1] [2] [3]
[1,] 0 0 255
>
> ## фиолетовый
> приятель (0,5)
      [1] [2] [3]
[1,] 127,5 0 127,5 

Вы также можете передать последовательность чисел в функцию pal() .

 > приятель (последовательность (0, 1, длина = 10))
           [1] [2] [3]
 [1,] 255,00000 0 0,00000
 [2,] 226,66667 0 28,33333
 [3,] 198,33333 0 56,66667
 [4,] 170,00000 0 85,00000
 [5,] 141,66667 0 113,33333
 [6,] 113,33333 0 141,66667
 [7,] 85. 00000 0 170.00000
 [8,] 56,66667 0 198,33333
 [9,] 28,33333 0 226,66667
[10,] 0.00000 0 255.00000 

Идея здесь в том, что colorRamp() дает вам функцию, которая позволяет интерполировать между двумя цветами, красным и синим. Вам не нужно указывать только два цвета в исходной цветовой палитре; вы можете начать с нескольких цветов и colorRamp() будет выполнять интерполяцию между ними всеми.

10.5

colorRampPalette()

Функция colorRampPalette() похожа на colorRamp(() , однако возвращаемая ею функция дает фиксированное количество цветов, интерполирующих палитру.

 > pal <- colorRampPalette(c("red", "yellow")) 

Снова у нас есть функция pal() , которая была возвращена colorRampPalette() , на этот раз интерполирующая палитру, содержащую красный и желтый цвета. теперь Функция pal() принимает целочисленный аргумент, определяющий количество возвращаемых интерполированных цветов.

 > ## Просто верните красный и желтый
> приятель (2)
[1] "#FF0000" "#FFFF00" 

Обратите внимание, что цвета представлены в виде шестнадцатеричных строк. После символа # первые два символа обозначают красную сумму, вторые два — зеленую, а последние два — синюю. Поскольку каждая позиция может иметь 16 возможных значений (0-9 и A-F), две позиции вместе дают 256 возможностей для каждого цвета. В приведенном выше примере, поскольку мы запросили только два цвета, он дал нам красный и желтый, две крайности палитры.

Мы можем попросить больше цветов.

 > ## Возврат 10 цветов между красным и желтым
> приятель(10)
 [1] "#FF0000" "#FF1C00" "#FF3800" "#FF5500" "#FF7100" "#FF8D00" "#FFAA00"
 [8] «#FFC600» «#FFE200» «#FFFF00» 

Вы увидите, что первый цвет по-прежнему красный («FF» в красном положении), а последний цвет по-прежнему желтый («FF» в обоих случаях). красная и зеленая позиции). Но теперь между ними еще 8 цветов. Эти значения в шестнадцатеричном формате также могут быть указаны для базовых функций построения графика с помощью col аргумент.

Обратите внимание, что функция rgb() может использоваться для получения любого цвета с помощью пропорций красного, зеленого и синего и возврата шестнадцатеричного представления.

 > RGB(0, 0, 234, maxColorValue = 255)
[1] "#0000EA" 

10.6 Пакет RColorBrewer

Часть искусства создания хороших цветовых схем в графических данных состоит в том, чтобы начать с соответствующей цветовой палитры, которую затем можно интерполировать с помощью такой функции, как colorRamp() или colorRampPalette() . Одним из пакетов CRAN, который содержит интересные и полезные цветовые палитры, является пакет RColorBrewer .

Пакет RColorBrewer предлагает три типа палитр

• Последовательно: для числовых данных, которые заказываются

• Расходящиеся: для числовых данных, которые могут быть положительными или отрицательными, часто представляющими отклонения от какой-либо нормы или исходного уровня

• Качественный: для качественных неупорядоченных данных

Все эти палитры можно использовать в сочетании с colorRamp() и colorRampPalette() .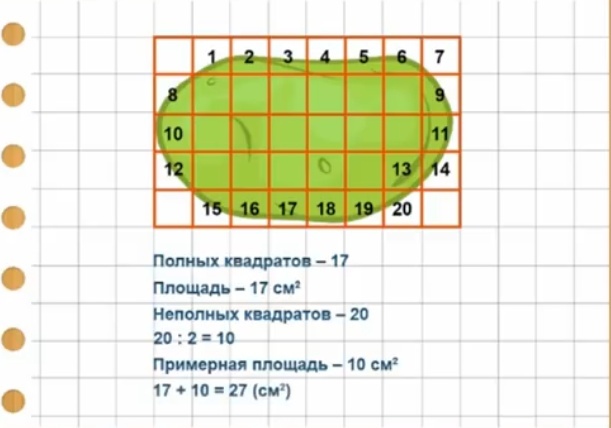

Здесь показаны все цветовые палитры, доступные в пакете RColorBrewer .

 > библиотека (RColorBrewer)
> display.brewer.all() 

Рисунок 6.1: Палитры RColorBrewer

10.7 Использование палитр RColorBrewer

Единственная реальная функция в пакете RColorBrewer — это brewer.pal() функция с двумя аргументами

Ниже мы решили использовать 3 цвета из палитры «BuGn», которая представляет собой последовательную палитру.

 > библиотека (RColorBrewer)
> cols <- brewer.pal(3, "BuGn")
> столбцы
[1] "#E5F5F9" "#99D8C9" "#2CA25F" 

Эти три цвета составляют мою начальную палитру. Затем я могу передать их в colorRampPalette() для создания интерполирующей функции.

 > pal <- colorRampPalette(cols) 

Теперь я могу построить 9Данные вулкана 0161 с использованием этой цветовой шкалы. Обратите внимание, что набор данных вулкана содержит высоты вулкана, которые представляют собой непрерывные упорядоченные числовые данные, для которых подходит последовательная палитра.

 > изображение(вулкан, col = pal(20)) 

Рисунок 10.1: Данные вулкана с палитрой цветовой шкалы

10.8 Функция

smoothScatter()

Функция, использующая преимущества цветовых палитр в RColorBrewer , — это smoothScatter() , которая очень полезна для создания диаграмм рассеивания очень больших наборов данных. Функция smoothScatter() , по сути, дает вам двумерную гистограмму данных с использованием последовательной палитры (здесь «Синий»).

 > набор семян(1)
> х <- rнорм(10000)
> у <- rнорм(10000)
> SmoothScatter(x, y) 

Рисунок 6.4: Функция smoothScatter

10.9 Добавление прозрачности

Цветовая прозрачность может быть добавлена ​​через параметр альфа до rgb() для получения спецификаций цвета с различными уровнями прозрачности. При использовании прозрачности вы заметите, что справа от шестнадцатеричного представления добавляются два дополнительных символа (будет 8 позиций вместо 6).

Например, если мне нужен красный цвет с высоким уровнем прозрачности, я могу указать

 > rgb(1, 0, 0, 0.1)
[1] "#FF00001A" 

Прозрачность может быть полезна при наличии графиков с высокой плотностью точек или линий. Например, на приведенной ниже диаграмме рассеяния много точек перечеркнуты, и трудно увидеть, что происходит в середине области графика.

 > набор.начальных значений(2)
> х <- rнорм(2000)
> у <- rнорм(2000)
> участок (х, у, рч = 19) 

Рисунок 6.6: Диаграмма рассеяния без прозрачности

Если мы добавим немного прозрачности черным кругам, мы сможем лучше понять разную плотность точек на графике.

 > график (х, у, pch = 19, col = rgb (0, 0, 0, 0,15)) 

Рисунок 6.7: Диаграмма рассеяния с прозрачностью

Лучше, да?

10.10 Сводка

• Тщательное использование цветов в графиках, изображениях, картах и ​​других графических данных может облегчить читателю понимание того, что вы пытаетесь сказать (зачем усложнять?).