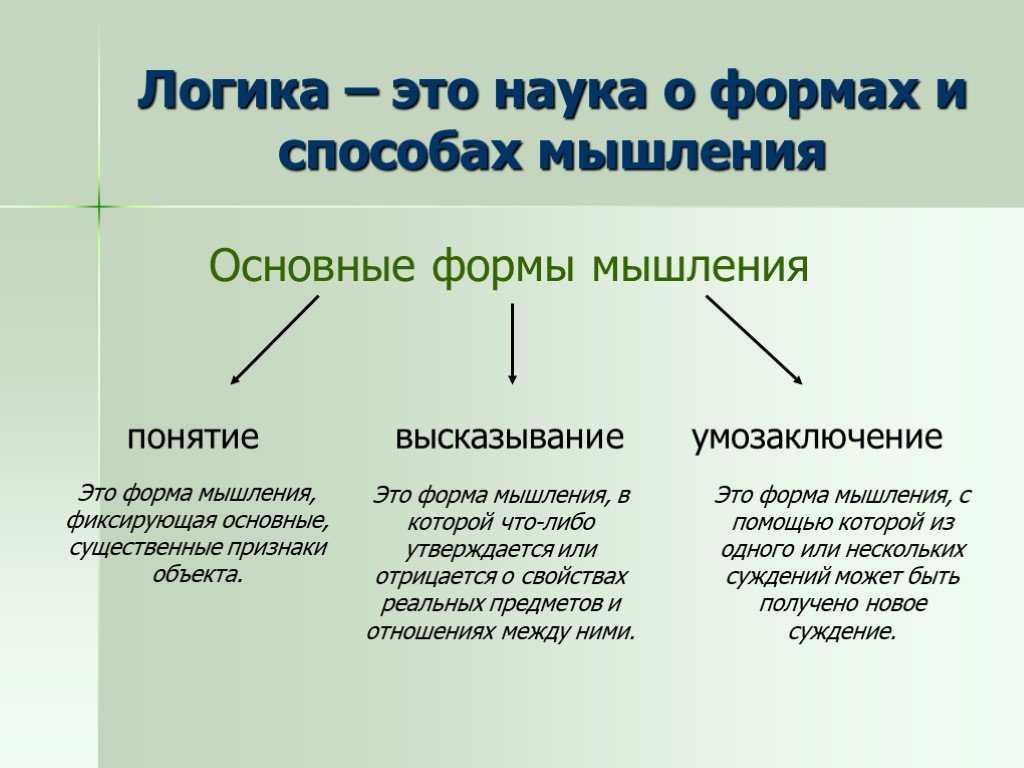
Почему логику называют формальной: Логика формальная это

Содержание

Логическая форма

Два следующих условных суждения имеют одну и ту же форму:

1) «Если железо нагреть, то оно расширяется»;

2) «Если учащийся изучает логику, то он повышает четкость своего мышления». Форма этих суждений такая: «Если S есть Р., то S есть P1».

Формальная логика, как уже говорилось, отделяет правильные способы рассуждения от неправильных и систематизирует первые.

Своеобразие формальной логики связано, прежде всего, с ее основным принципом, в соответствии с которым правильность рассуждения зависит только от его логической формы.

Самым общим образом форму рассуждения можно определить как способ связи входящих в это рассуждение содержательных частей.

Основной принцип формальной логики предполагает – и это следует специально подчеркнуть, что каждое наше рассуждение, каждая мысль, выраженная в языке, имеет не только определенное содержание, но и определенную форму. Предполагается также, что содержание и форма отличаются друг от друга и могут быть разделены.

Содержание мысли не оказывает никакого влияния на правильность рассуждений, и поэтому от него следует отвлечься. Для оценки правильности мысли существенной является лишь ее форма. Ее необходимо выделить в чистом виде, чтобы затем на основе такой «бессодержательной» формы решить вопрос о правильности рассматриваемого рассуждения.

Как известно, все предметы, явления и процессы имеют как содержание, так и форму. Наши мысли не являются исключением из этого общего правила. То, что они обладают определенным, меняющимся от одной мысли к другой содержанием, известно каждому. Но мысли имеют также форму, что обычно ускользает от внимания.

1.2 Язык формальной логики

Формальная логика, есть способ связи составных частей содержания мысли в отличие от самого этого содержания.

Результат отвлечения от «материи» мысли, т.е. от того, какие именно индивиды, свойства, отношения, классы, ситуации и т.п. являются предметами данной мысли. В качестве механизма подобного отвлечения рассматривают процедуру замены переменными (параметрами) отдельных дескриптивных составляющих языкового контекста, выражающего данную мысль.

Приведенное интуитивное понятие логической формы получает в современной логике серьезные уточнения. Считается, что анализ формы концептуальных образований (понятий, суждений, рассуждений и т.п.) не может осуществляться вне языка и существенным образом зависит от выбора языковых средств. Предполагается, что мысленные конструкции адекватно оформлены в виде осмысленных выражений естественного языка. Для фиксации их логической формы используют особые искусственные языки логики. Которые, во-первых, должны иметь точный синтаксис, т.е. точно заданные алфавит и правила образования сложных выражений. Во-вторых, основываться на определенной системе семантических категорий с четким подразделением исходных символов на логические и нелогические, указанием типов возможных значений для различных сортов нелогических символов, фиксацией значений логических символов и формулировкой точных семантических правил установления значений сложных выражений.

С чем же связано наличие собственного языка логики как науки? Дело в том, что естественному языку присущи некоторые недостатки, которые не позволяют логике ограничиваться использованием только его.

Основными недостатками естественного языка являются:

изменение значения слов с развитием общественной практики и по истечении определенного времени;
многозначность некоторых слов;

расплывчатость, неопределенность отдельных слов, не позволяющая с их помощью определить предмет науки;
несовершенство правил построения выражений, которое в логическом смысле несет на себе печать многозначности понимания вербальной мысли;
деление естественного языка на большое количество языков разных стран и народов, в результате чего одна и та же мысль может быть оформлена различными языками.

Формальная логика пытается искоренить данные недостатки в своей области. Это достигается на основе введения специального символического языка. Внутри формальной логики операции с мыслями заменяются действиями со знаками. Общепринятым в современной логике является так называемый язык логики предикатов. Рассмотрим кратко принципы построения и структуру этого языка.

Для выявления логической формы мыслей при анализе естественного языка имеет смысловая или семантическая характеристика языковых выражений. В этом плане в формальной логике используются две группы терминов дескриптивные и логические.

Дескриптивные термины (лат. descriptic — описание) — это имена предметов, предикаторы и функциональные знаки. Они выражаются словами естественного языка и на данный момент речемыслительной деятельности адекватно отражают предмет мышления.

Имена предметов — это слова или словосочетания, которые обозначают отдельные предметы или классы однородных предметов.

Предикаторы — это языковые выражения, которые обозначают свойства или отношения, наличие которых в суждениях утверждается или отрицается.

Функциональные знаки — это принятые обозначения предметных функций, операций (Sin a , «+» и др.).

Логические термины заменяют в естественном языке определенные союзы (логические постоянные, или логические константы).

Выразительные средства языков силлогистики и логики предикатов позволяют учесть внутреннюю структуру³. Однако эти языки базируются на разных системах семантических категорий. В обычной силлогистике имеется лишь один тип нелогических терминов – общие термины, знаки классов. В то время как в логике предикатов содержатся параметры для знаков индивидов, свойств, отношений и предметных функций, поэтому между ними имеется существенное различие в характере и глубине воспроизведения логической формы. Так, форма высказывания «Все планеты вращаются вокруг Солнца» в силлогистическом языке может быть выражена формулой SaP («Всякий S есть P»), где параметрами S и P замещены общие термины «планета» и «тело, вращающееся вокруг Солнца», а само высказывание рассматривается как атрибутивное. В языке логики предикатов имеется возможность передать реляционный характер данного высказывания, выразив его логическую форму посредством формулы ∀x (Q

1 (x) ⊃ R²(x, a)), где параметр Q¹соответствует знаку свойства «быть планетой», R²– знаку отношения «вращается вокруг», а – имени «Солнце».

Уточнение понятия логической формы в рамках теории семантических категорий содержится, в частности, в работе Е.Д.Смирновой «Формализованные языки и проблемы логической семантики» (М., 1982). Различаются понятия логической формы первого уровня, являющейся результатом замещения примитивных знаков в составе выражения индексами. Соответствующих категорий и способной быть представленной в виде графа. И логической формы второго уровня, представленной в виде обобщенного дерева, которое содержит информацию о тождестве и различии дескриптивных составляющих и о значении логических констант.

Таким образом, изучение логики мыслительного процесса, знание логических форм, выраженных в обычном словесном языке, и логических законов, ими управляющих, сохраняет свое значение и актуальность для формирования у человека его логической культуры.

Имея понятие логической формы и логического закона, можно дать определение формальной логике.

Формальная логика – это наука о формах мышления, о формально-логических законах и других связей между мыслями по их логическим формам.

Мышление, которое осуществляется в соответствии с формально-логическими законами, называется правильным. Формальная логика, является наукой о правильном мышлении, исследует и систематизирует также типичные ошибки, совершаемые в процессе мышления, то есть типичные алогизмы.

При применении средств, вырабатываемых формальной логикой, можно отвлекаться от развития знания.

II Основные этапы становления логической формы

2.1 Классификация логических форм

Особым видом деления является классификация, представляющая собой распределение предметов по группам (классам), каждый класс имеет свое постоянное, определенное место.

Целью классификации является систематизация знаний, поэтому от деления она отличается относительно устойчивым характером и сохраняется более или менее длительное время.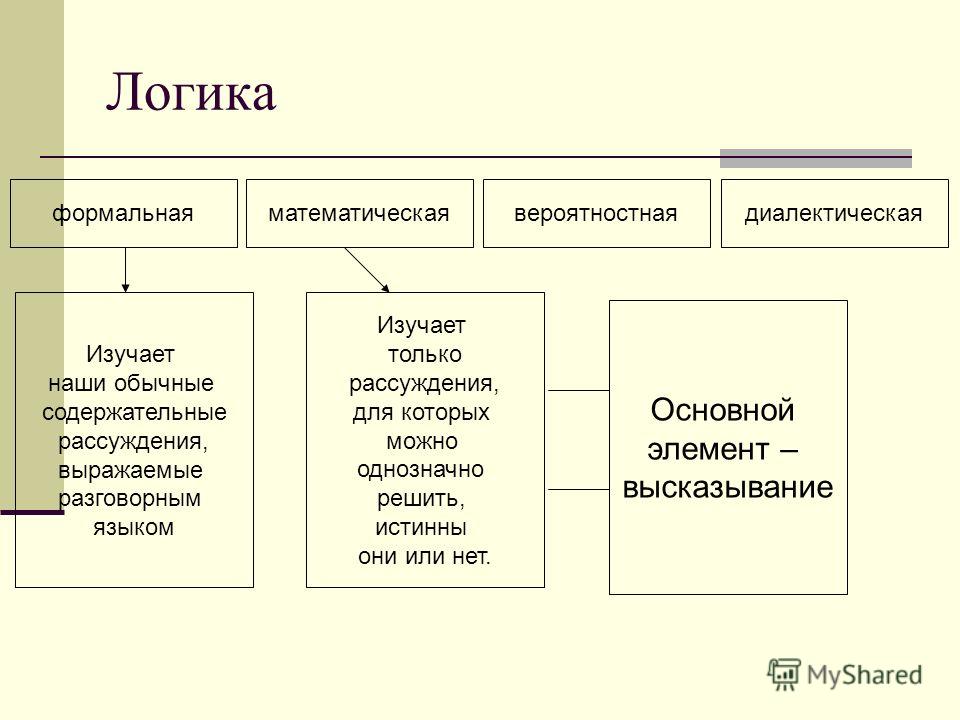 Кроме того, классификация образует развернутую систему, где каждый член деления вновь делится на новые члены, разветвляясь на множество классов, закрепляемых обычно в таблицах, схемах, кодексах и т.п.⁴

Вместе с тем всякая классификация относительна. Многие явления природы и общественной жизни не могут быть отнесены безоговорочно к какой-либо определенной группе явлений.⁵

Кроме того, с развитием знаний классификация, как правило, изменяется, дополняется, иногда заменяется новой, более точной. Поэтому ни к одной классификации нельзя подходить как к завершенной. Необходимо учитывать, что и сама действительность, и знания о ней находятся в непрерывном процессе изменения и развития.

Классификация всегда устанавливает определенный порядок. Она разбивает рассматриваемую область объектов на группы, чтобы упорядочить эту область и сделать ее хорошо обозримой.

Что же такое классификация? Вопрос этот важен, так как классификация — одна из обычных и часто применяемых операций, средство придания нашему мышлению строгости и четкости. Но прежде чем ответить на вопрос, введем несколько вспомогательных понятий.

Классификация является частным случаем деления — логической операции над понятиями. Деление — это распределение на группы, тех предметов, которые мыслятся в исходном понятии. Получаемые в результате деления группы называются членами деления. Признак, по которому производится деление, именуется основанием деления. В каждом делении имеются, таким образом, делимое понятие, основание деления и члены деления.

Классификация представляет собой многоступенчатое, разветвленное деление. Скажем, ощущения можно разделить на зрительные, слуховые, осязательные, обонятельные и вкусовые. Затем внутри отдельных групп выделить подгруппы (например, пространственные и цветовые зрительные ощущения), сами подгруппы подвергнуть более дробному делению и т.д.
К операции деления приходится прибегать едва ли не в каждом рассуждении. Определяя понятие, мы раскрываем его содержание, указываем признаки предметов, мыслимые в этом понятии. Производя деление понятия, мы даем обзор того круга предметов, который отображен в нем. Если у нас есть, скажем, определение понятия «линза», мы знаем наиболее важные признаки линз. Но при этом у нас нет точного представления о видах линз. Только разделив линзы на выпуклые, двояковыпуклые, вогнутые, двояковогнутые и т.д., мы получим знание не только о том, что такое линза, но и о том, какими бывают линзы;
Важно уметь, таким образом, не только определять содержание понятия, но и прослеживать те группы, из которых слагается класс предметов, обозначаемых понятием.

Простой пример из энтомологии — науки о насекомых — еще раз подтвердит эту мысль. На столе энтомолога коробочки с наколотыми на тонкие булавки маленькими мухами-серебрянками. Под микроскопом — иначе не разглядеть — ножницами с иголочнотонкими лезвиями ученый общипывает у этих мух «хвостики» и наклеивает на крошечные стекла. Зачем? В ряде случаев только по «хвостикам» — по особенностям строения отдельных органов — можно точно определить, к какому именно виду относится насекомое. А роспись насекомых по видам и определение территории их обитания важны не только для удовлетворения научной любознательности. Ведь иные из них — потенциальные переносчики ряда болезней, другие — вредители культурных растений, третьи — напротив, враги этих вредителей. Например, трихограммы — крошечные, в полмиллиметра длиной родственники всем известных пчел, шмелей и ос. Трихограммы широко применяются в биологической борьбе с вредителями урожая. Однако недавние исследования показали, что до последнего времени на биофабриках разводили не один вид этого насекомого, а «смесь» из трех видов. Но у каждого свои привязанности: один предпочитает поле, другой — сад, третий — огород. И в каждом случае лучше разводить именно тот вид, который подходит для местных условий.
Это только один из примеров практической отдачи работы систематиков, занимающихся классификацией животных.

Из арифметики хорошо известна операция деления чисел. Деление понятий, или логическое деление, — другая мыслительная операция, имеющая с первой общие не только название, но и структуру: у обеих операций есть «делимое», «делитель» и «результат деления». Логическое деление применяется к понятиям, результат такого деления — несколько новых, видовых понятий. В содержание входят все те признаки, которые мыслились в исходном, родовом понятии, и, кроме того, признаки, отличающие один вид от другого.

2.2 Основные этапы развития логической формы

Логическая форма в своем развитии прошла два основных этапа.

Основанием деления на эти этапы служит различие применяемых в логике средств и методов исследования. Начало первого этапа связано с работами древнегреческого философа и ученого Аристотеля (384—322 гг. до н. э.), в котором впервые дано систематическое изложение логики. Логику Аристотеля и всю доматематическую логику обычно называют «традиционной» формальной логикой. Традиционная формальная логика включала и включает такие разделы, как понятие, суждение, умозаключение (в том числе и индуктивное), законы логики, доказательство и опровержение, гипотеза. Аристотель видел в логике орудие (или метод) исследования. Основным содержанием аристотелевой логики является теория дедукции. В логике Аристотеля содержатся элементы математической (символической) логики, у него имеются «начатки исчисления высказываний».

Второй этап — это появление математической (или символической) логики.

Немецкий философ Г. В. Лейбниц (1646—1716) по праву считается основоположником математической (символической) логики.

Начиная с Лейбница, в логике используется в качестве метода исследования метод формализации, который традиционной логикой относился только к методам математического исследования, а Лейбниц показал, что он имеет общенаучный характер. Лейбниц пытался построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычисления. В XIX в. математическая логика получила интенсивное развитие в работах Д.Буля, Э. Шредера, П. С. Порецкого, Г. Фреге и других логиков.

Математическая (или символическая) логика изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода. При этом в математической логике для выявления структуры вывода строятся различные логические исчисления, прежде всего исчисление высказываний и исчисление предикатов в их различных модификациях. Можно сказать, что математическая логика разрабатывает применение математических методов к анализу форм и законов доказательного рассуждения.

Вопрос 1. Формальная логика как наука.

Формальная логика

Логику можно определить как:

1) науку о правилах мышления, ведущего к истине;

2) объективные закономерности и взаимосвязи в процессе чего-либо (логика событий).

Нас интересует, конечно, первое значение этого слова: логика как наука. Сейчас ее делят на два вида: логика как таковая, или формальная логика, и диалектическая логика. Деление это возникло сравнительно недавно. Долгое время под логикой понимали только то, что сейчас называют формальной логикой, и называли просто логикой.

Возникла она еще в Древней Греции и много столетий считалась основой знания и образованности. В начале XIX в. Гегель подверг эту логику критике и указал на ее ограниченность и недостаточность с точки зрения отражения процесса движения мысли. Он показал, что такая логика отражает не движение содержания мысли, а лишь форму мысли, лишь статическую сторону мышления. Чтобы восполнить этот недостаток, Гегель создал новую логику — диалектическую, а существовавшую до нее назвал формальной. Название это прижилось, потому что оно действительно отражало характер данной науки.

Формальная — значит, связанная с формой, изучающая ее как нечто отдельное, обособленное от содержания, насколько это возможно. В этом отношении формальная логика подобна геометрии, которая является наукой о формах физических тел и совершенно отвлекается, изучая эти формы, от того, что могло бы быть их содержанием. От содержательной стороны процессов и явлений отвлекаются и другие математические науки. Так что существует целый разряд формальных наук, и логика принадлежит к их числу.

Законов таких четыре:

1.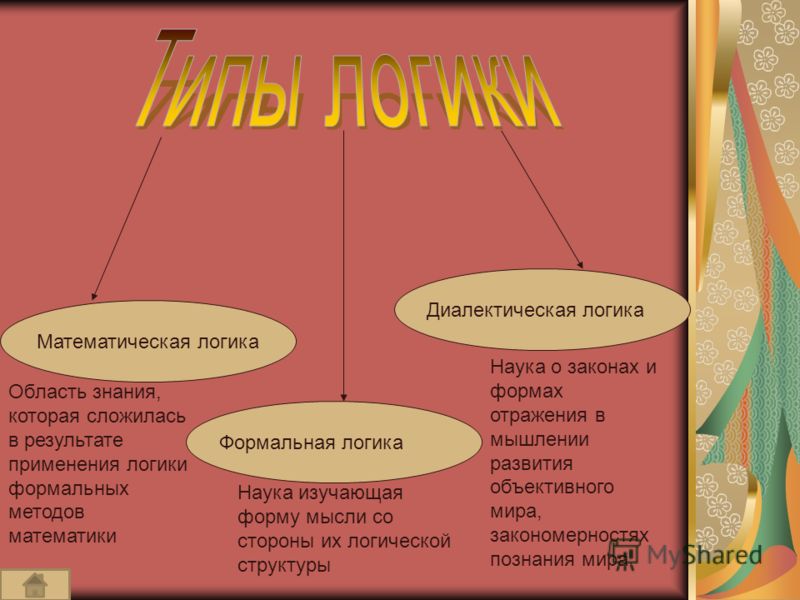 Закон тождества: каждая мысль должна быть тождественна (равнозначна) сама себе, сколько бы раз она ни повторялась в рассуждении. Рассуждая о чем-нибудь, мы должны постоянно иметь в виду одно и то же.

Казалось бы, очень просто. Но этот закон нарушают наиболее часто. Самой распространенной ошибкой при этом является подмена понятий, вследствии чего возникают неправильные умозаключения (учетверение терминов) и доказательства (подмена тезиса). Об этом будет речь впереди, в частности в разделе, посвященном логическим ошибкам.

Символическое выражение закона: А = А.

2. Закон противоречия (его называют также и законом непротиворечия): два противоречащих друг другу суждения об одном и том же предмете, взятом в одном и том же отношении и в одно и то же время, не могут быть одновременно истинными.

Символическое выражение этого закона: А & А.

3. Закон исключенного третьего: из двух противоречащих друг другу суждений одно непременно истинно. А может быть либо Ь, либо Ь. Третьего не дано. Важный вопрос о том, можно ли средствами формальной логики передавать противоречия, мы рассмотрим далее в курсе.

Закон исключенного третьего применяется только:

• К двум единичным противоречащим суждениям.

• К двум суждениям, одно из которых общеутвердительное, а другое частно отрицательное:

• К двум суждениям, одно из которых общеотрицательное, а другое частноутвердительное:

Символическое выражение закона исключенного третьего: AvA.

4. Закон достаточного основания: всякая мысль, чтобы быть истинной, должна быть доказанной, т. е. должны существовать достаточные аргумен- ты в пользу ее истинности. Иными словами, относительно всякого утверждения мы имеем право требовать достаточных доказательств, в противном случае мы можем не принимать его в расчет. Данный закон уже выходит за рамки формально-логического закона, так как требует соотнесения мысли с действительностью. На этом основании некоторые авторы вообще не считают его логическим: «закон достаточного основания не есть логический закон, — писал один автор. — Он является скорее пережитком вольфианской метафизики XVIII века».

В качестве достаточного основания могут фигурировать: очевидные факты, факты, проверенные на опыте, законы и положения науки, подтвержденные практикой, аксиомы.

Символическое выражение закона достаточного основания: В -> А.

Формальная логика | Определение, примеры, символы и факты

Альфред Норт Уайтхед

Смотреть все СМИ

Ключевые люди:: Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано

Похожие темы:: теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод

См. весь связанный контент →

формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.

Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.

Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивное. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.

Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.

Дедуктивные выводы, с которыми имеет дело формальная логика, — это, как следует из названия, выводы, достоверность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .

Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.

С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.

Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.

Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или мысленными конструкциями?