Психика и сознание круги эйлера: Тема 3. Философия сознания.

Содержание

Как совершенствовать логику и перестать заблуждаться

Почему мы верим во всякую чушь? Откуда у людей столько предрассудков? Что такое мистическое мышление? Ответы на эти и другие вопросы дает Никита Непряхин, книга которого описывает самые популярные мифы и заблуждения в истории человечества — от астрологии и гомеопатии до экстрасенсов и призраков — и дает умные, подробные, понятные инструменты для их разоблачения и развития критического мышления. Здесь и понимание своих и чужих когнитивных искажений, и основы формальной и неформальной логики, и теория аргументации, и технологии фактчекинга, и много чего еще. Публикуем отрывок из книги «Анатомия заблуждений», посвященный развитию такой важной части мышления, как логика.

Никита Непряхин

Издательство Альпина Паблишер, 2020

Чтобы погрузиться в науку логику, для начала определим основополагающие понятия. Вот с самого «понятия» и «определения» и начнем. Без грамотного понимания и определения явления или события невозможно разобраться с логикой рассуждений и уяснить их смысл.

Что подразумевает человек, когда произносит какие-либо слова? Что он имеет в виду? Можно ли понять смысл предложения, если в нем есть неизвестное нам слово? Что конкретно имеет в виду человек, когда произносит, например, слово «право»? Имеет ли он в виду общепринятое широкое значение или узкое юридическое? Без понятий и определений мы не смогли бы понимать друг друга. Мы все прекрасно понимаем значение таких слов, как «окно», «компьютер», «собака», «карандаш», «стол». Но задумайтесь, можете ли вы точно дать определения таким терминам, как «справедливость», «инфляция», «возможность», «время»? Это уже гораздо сложнее. Или даже взять элементарные и знакомые всем с детства слова «красный», «теплый», «мягкий». Как их объяснить словами, без демонстрации?

Итак, об этих базовых элементах мышления, фундаменте логики мы и поговорим. Начнем с термина «понятие», а потом перейдем к термину «определение». Мы все мыслим с помощью понятий.

Понятием называется форма мышления, которая обозначает какой-либо объект или его свойство

Вокруг нас бесчисленное множество разных объектов, и каждый из них отражается в нашем сознании как какое-либо понятие.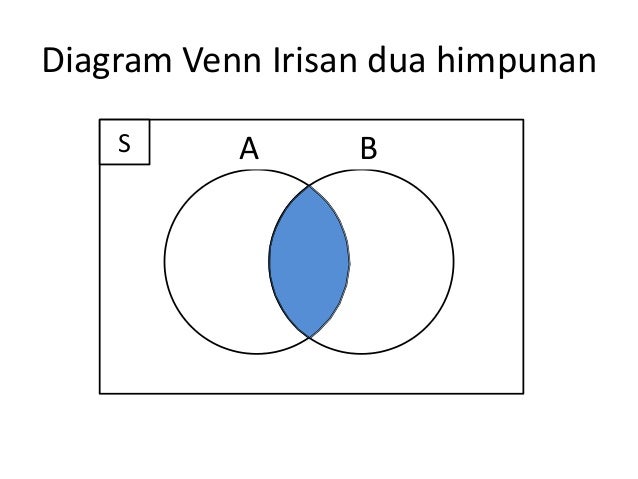 Просто оглянитесь вокруг. Вы видите горы, реки, облака, светящее солнце? А может быть, стол, лампу, календарь и ручку с блокнотом? Каждому объекту или явлению в этом мире мы задаем свои имена. Вот такие имена в логике и называют «понятие». Мы анализируем разные предметы, сравниваем их с другими, выявляем их различные свойства и характеристики, объединяем разные предметы в группы на основании сходных принципов, для того чтобы сформировать их мысленные образы: это все «фрукты», а это «цитрусовые», из них вот это «мандарины», это «грейпфруты», а это «апельсины».

Только подумайте: в объективной реальности никаких понятий нет. Это все плод человеческого разума и воображения, так люди договорились между собой. Все, что мы называем, существует лишь в нашей голове. Нет в объективном мире никаких «прав» и «свобод», нет «демократии» и «денег», нет «юристов» и «учителей», «бакалавров» и «специалистов», не существует «хордовых» и «одноклеточных». Есть понятия, к которым мы обращаемся, чтобы не только общаться и понимать друг друга, но и чтобы наш мозг составил правильную картину окружающего мира.

Не стоит путать «слово» и «понятие»: это все-таки разные вещи. Понятия выражаются словами. Иногда одним словом могут выражаться разные понятия.

Чтобы проиллюстрировать это наглядно, предлагаю обратиться к так называемым кругам (или диаграммам) Эйлера.❓Также используется название «диаграмма Эйлера‒Венна». Если вы думаете, что ничего не знаете о кругах Эйлера, то глубоко ошибаетесь, потому что каждый хоть раз в жизни видел их в виде интернет-мемов.

Научиться контролировать эмоции вам поможет курс «Критическое мышление».

Леонард Эйлер (1707–1783) — известный швейцарский, немецкий и российский математик, член Петербургской академии наук. Он придумал использовать простую визуализацию для обозначения объема понятий и множеств элементов. Круги Эйлера просты и наглядны, они очень упрощают рассуждения и именно поэтому так часто используются в логике, математике, статистике и менеджменте. Они отлично показывают, в каких логических взаимоотношениях могут быть те или иные понятия.

Давайте посмотрим, какие возможны варианты таких взаимоотношений понятий.

Тождество — в данном случае понятия подразумевают один и тот же предмет. Например, А = квадрат, В = равносторонний прямоугольник; А = Москва, В = столица России; А = лучший тренер по технологиям убеждения, В = Никита Непряхин. Ладно, шучу.

Пересечение — в таких случаях объем одного понятия частично входит в объем другого понятия. Например, А = студент, В = спортсмен. Действительно, часть студентов могут быть спортсменами, а часть — нет. И наоборот, кто-то из спортсменов может учиться в вузе, а кто-то нет. Или: А = мужчина, В = врач. Кто-то из мужчин действительно работает врачом, но какая-то часть врачей — явно женщины. Может быть, и большая.

Подчинение — в этих случаях одно понятие включает в себя другое. Например, А = верующий, В = православный. Все православные — верующие. Но среди верующих есть еще и католики, и протестанты, и буддисты, и мусульмане. Или: А = цитрусовые, В = апельсин; А = растение, В = береза.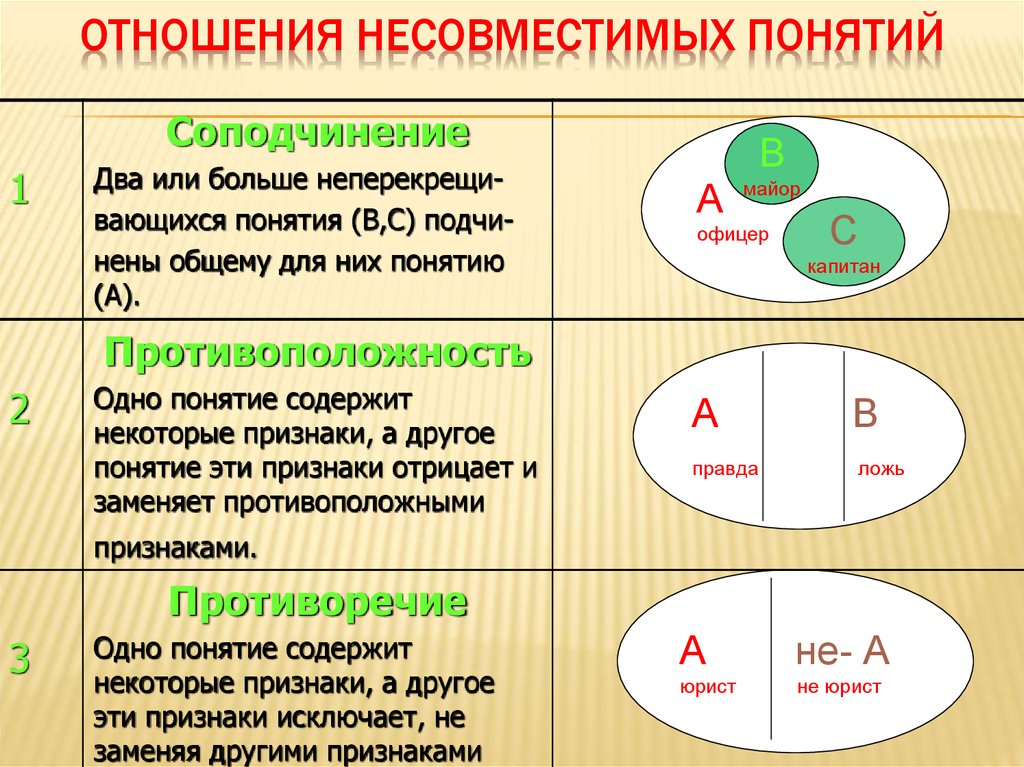

Противоречие понятий представляет собой отрицание одним понятием другого. Например, А = низкий, В = высокий; А = работающий, В = безработный; А = черный, В = белый и т.д.

Давайте рассмотрим несколько примеров использования кругов Эйлера, но уже более сложные варианты.

Что мы видим из схемы, в которой продемонстрировано последовательное подчинение? Каждый мужчина — человек. Но не каждый человек — мужчина. Любой отец — мужского пола. Но не каждый мужчина успел обзавестись потомством. Не каждый отец является дедушкой. При этом любой дедушка всегда является также отцом.

Как читать эту схему? Не все явления природы являются стихийными бедствиями. Например, им не является северное сияние или молния. Равным образом не все стихийные бедствия — это явления природы, некоторые могут возникать в результате деятельности человека. Землетрясение — это всегда явление природы, но не каждое землетрясение признается стихийным бедствием. Наводнение и пожар могут быть как явлением природы, так и следствием человеческой халатности или злого умысла, как, например, в случае прорыва плотины или поджога здания.

И не все наводнения и пожары при этом признаются стихийными бедствиями.

Научиться контролировать эмоции вам поможет курс «Критическое мышление».

Немного практики

Представьте отношения между следующими понятиями с помощью кругов Эйлера.

15.1 Ученый, психолог, кандидат психологических наук.
15.2 Автобус, такси, трамвай, городской транспорт, общественный транспорт.
15.3 Русский писатель, дореволюционный писатель, советский писатель, Достоевский, Пушкин, Шолохов, Булгаков.
15.4 Искусственный спутник, Луна, планета, небесное тело, Земля, планета Солнечной системы, Марс, спутник.
15.5 Человек, имеющий одного ребенка; человек, имеющий двоих детей; человек, имеющий детей; мать.
15.6 Синий свитер; свитер любого цвета, кроме синего.
15.7 Автор романа «Преступление и наказание», автор романа «Братья Карамазовы».
15.8 Диван-кровать, мебель, диван, кровать, табурет.
15.9 Человек, владеющий иностранным языком; человек, владеющий английским языком; человек с высшим образованием; профессиональный переводчик.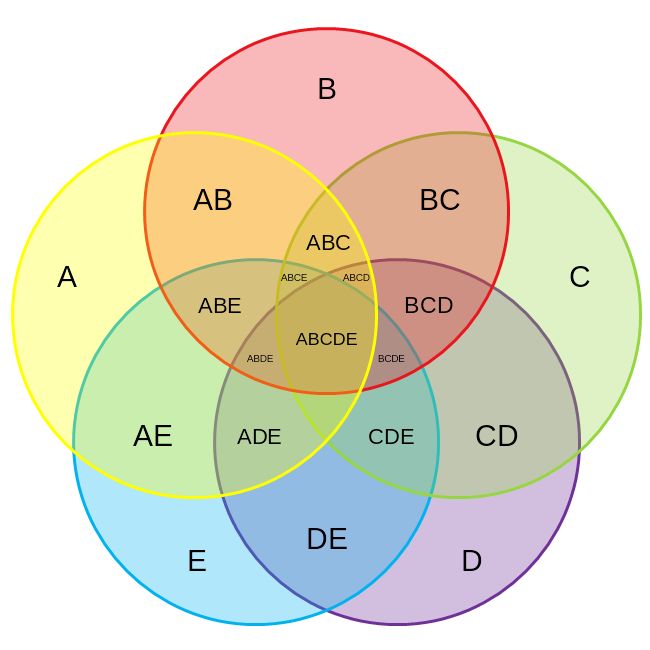
15.10 Врач, пациент, мужчина, женщина.

В рубрике «Открытое чтение» мы публикуем отрывки из книг в том виде, в котором их предоставляют издатели. Незначительные сокращения обозначены многоточием в квадратных скобках.
Мнение автора может не совпадать с мнением редакции.

Что такое круги Эйлера и как найти решение проблемы

Наверняка ты задаешься вопросом: «Геометрия в психологии? Круги Эйлера? Как такое возможно?».

Возможно! Но обо всем по порядку.

Круги Эйлера (на самом деле, может быть любая другая фигура, просто круг – более понятная) были изобретены Леонардом Эйлером, для решения задач. Суть кругов была в том, чтобы показывать отношения между множествами и подмножествами в математике, для наглядного и логического представления. Эйлер считал, что с помощью наглядного изображения можно облегчить размышления человека в решении задач.

Науки всегда связаны, ни одна наука не обходится без математики, а тем более психологи– наука с расчетами и методиками, техниками, самое главное–связанная с организмом и мозгом человека. Исходя из этого, можно сказать, что круги Эйлера можно и нужно использовать для наглядной картинки того, что хочет человек и что с ним происходит в моменте «здесь и сейчас»,, формировать логическое мышление.

В этой статье:

Как применить круги Эйлера в психологииПринцип кругов ЭйлераТехника «капля в луже»Возражаешь? Проработай!Что даёт построение кругов

Как применить круги Эйлера в психологии

Фото автора Karolina Grabowska: Pexels

Ты же смотрела «Зачарованных»? Если нет, то наверняка помнишь, что своеобразным логотипом сериала был трилистник заключённый в круг. И это тоже можно отнести к кругам Эйлера, потому что сёстры три- каждый лепесток символизирует отдельную личность, но внутри этой формы образовывается единая фигура и она говорит о том, что в любом случае сёстры связаны между собой.

Круг, в который заключён трилистник означает то, что объединяет сестёр ещё сильнее–это общее дело.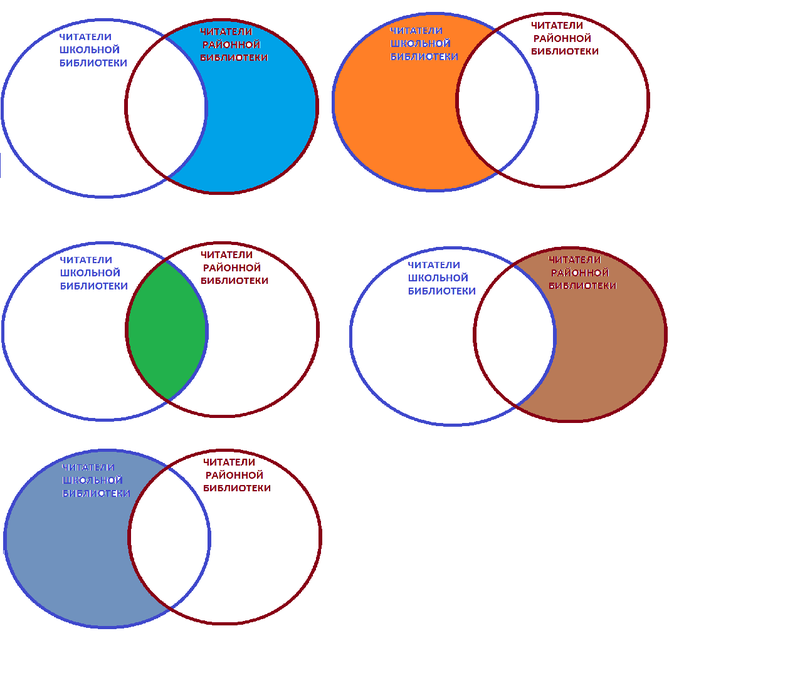 Это был наглядный пример, что бы ты представила, каким образом может простая геометрическая фигура заключить в себе целую логическую цепочку, которая будет очень понятна.

Новости СМИ2

В психологии круги Эйлера применяют для того, чтобы человек смог разобраться в самых разных уголках своей жизни. Эта схема помогает в решении дел, так как сразу становится понятно, что для тебя является важным, какого результата ты ждёшь, а также помогает в отношениях между людьми, тут опять играет роль приоритетность и конкретика конечного исхода.

Схемы Эйлера уникальны, но в тоже время очень универсальны, поскольку помогают детям размышлять и логично мыслить, помогают взрослым распутать клубки и рационализировать свои действия.

Принцип кругов Эйлера

Помни про эмблему из «Зачарованных», она тебе понадобится для визуализации.

Круги Эйлера в реальной жизни

На самом деле, все гениальное просто и самая лучшая и простая техника с техникой Эйлера называется «три круга». Для использования этой несложной техники тебе понадобится три карандаша разного цвета и листок бумаги. Ловкость ума и никакого мошенничества, честно слово! Сейчас ты научишься мыслить ещё более рационально, чем до этого момента!

Определись с задачами, которые ты хочешь решить.

Помни, что один круг–один инструмент. Например: «что я люблю делать?», «что у меня получается лучше всего?», «как из этого извлечь выгоду или заработок?».

Рисуй круги.

Тут нам и понадобится эмблема из нашумевшего сериала. Нарисуй три круга (у каждого круга свой цвет), так, чтобы круги пересекались образовывая внутри трилистник.

Дай кругам названия.

Название круга – это инструмент, присвой каждому кругу свой. Раскрой полностью смысл каждого инструмента. Что-то нравится? Напиши почему нравится. Напиши о том, сколько ты хочешь зарабатывать, укажи причину – поставь себе цель. Напиши, почему у тебя получается делать что-то лучше, чем остальные, похвали себя.

Очень важно рисовать круги до тех пор, пока не образуется этот трилистник. Да, круги могут не пересекаться, тогда нужно думать, как сделать так, чтобы пересеклись, может быть, придётся заменять инструменты. Круги могут быть разного размера, фигура внутри не обязательно должна иметь равные части, самое главное, чтобы эти части были.

Теперь, когда ты нарисовала круги, распределила задачи, в самом центре появилась фигура похожая на треугольник–эта фигура является главным отношением между твоими «подмножествами», она даёт конечный результат. Получившиеся листки – это путь к конечному результату.

Техника «капля в луже»

Эта техника подходит для тебя, если ты не можешь определить свои качества.

Фото автора Jana Kukebal: Pexels

Для этого нужно представить себя каплей, которая, попадая в воду даёт множество кругов.

Обозначь себя главным кругом. Далее подобно капле в луже рисуй круги вокруг себя, делая их все больше и больше. Нарисуй минимум пять кругов и обозначь их своими качествами, прислушиваясь к себе. Самый первый круг определяет тебя, последующие же помогают идти по жизни.

Рисуя такие круги, ты находишь в себе те качества, о которых даже не подозревала, они помогут раскрыть твоё потенциал. Если вдруг тебе не нравится какое-то качество в себе, ты можешь проработать этот момент и избавиться от того, что тебе не нравится. Главная задача техники–это понять, какие качества в тебе вообще есть.

Возражаешь? Проработай!

Есть возражения по поводу составления кругов? Проработай их!

Меня все устраивает, мне просто некомфортно, это пройдёт.

Само по себе ничего не пройдёт. Не пускай жизнь на самотёк. Лучше посмотреть на картину мира в кружках сейчас, принять себя такой, какая ты есть и работать с этим, чем на закате жизни жалеть о том, что прожила жизнь неправильно, потому что осознание придёт в любом случае, но комфорт можешь сотворить только ты!

Фото Martin Sanchez on Unsplash

На работе я прекрасный сотрудник, мне жалко уходить с насиженного места.

Если ты задумалась о том, что тебе «жалко», то вот прямо сейчас рисуй круги, проговаривай плюсы и минусы работы. Во-первых, если ты ценный сотрудник, то тебе могут платить больше! Ищи инструменты для повышения с помощью схемы Эйлера, примеряй все техники.

Меня не любят, потому что я плохая, круги не помогут.

Плохой человек никогда не признается в том, что он плохой. Техника «капля в луже» очень тебе подойдёт сразиться с неуверенностью и найти хорошие качества. Они у тебя точно есть!

Зачем терять время на круги? Это глупо.

Эйлер был неглупым человеком. Он доказал всему миру, как просто решать задачи наглядно изображая их в геометрических фигурах. Логическое мышление есть у каждого, а схема Эйлера поможет тебе его разработать. Поэтому обязательно пробуй!

Что даёт построение кругов

Когда ты начнёшь использовать схему в деле, применяя техники и возьмёшь это за правило, твоё мышление натренируется, и ты станешь понимать этот мир лучше, найдёшь своё предназначение.

Фото Mel Poole on Unsplash

Разовьётся логическое мышление, ты станешь продуктивнее и рациональнее мыслить.

Да, пересечение «трёх кругов» порой даёт отрицательный результат, ты можешь даже по началу расстроиться от того, что тебя это не устроит. Но тебе нужно понимать, что не все тебе по силам, нет на свете совершенных людей, которые могут по щелчку пальца сделать так, как надо им. У тебя попросту может быть другая цель, которую ты не ощущаешь, потому что она находится глубоко в подсознании. Круги Эйлера как раз и предназначены для того, чтобы найти себя с помощью логики и размышлений, которые распространяются на все аспекты жизни.

Техники универсальны, они подойдут абсолютно для всех аспектов жизни: от бытовых мелочей до глобальных целей в жизни. Просто меняй инструменты, применяя техники и жизнь будет становится проще. Главное – это тренировки. Удачи в поиске себя!

причин | Направления мысли: основные концепции когнитивной психологии

Фильтр поиска панели навигации Oxford AcademicLines of Thought: Central Concepts in Cognitive PsychologyCognitive PsychologyBooksJournals Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicLines of Thought: Central Concepts in Cognitive PsychologyCognitive PsychologyBooksJournals Термин поиска на микросайте

Расширенный поиск

Иконка Цитировать Цитировать
Разрешения
Делиться
- Твиттер
- Подробнее

CITE

RIPS, Lance J. ,

‘Причины’

Мышления: центральные концепции в когнитивной психологии

(

2011;

онлайн Edn,

Oxford Academan

, 10002 онлайн Edn,

Oxford

, 10002. январь 2011 г.

), https://doi.org/10.1093/acprof:oso/9780195183054.003.0007,

, по состоянию на 5 ноября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Advanced Search

Abstract

В этой главе делается попытка обосновать возможность того, что за нашу способность распознавать следствия как логически необходимые отношения отвечает отдельный когнитивный процесс. Это показывает, что современные унитарные теории рассуждений — те, в которых все формы рассуждений обусловлены одним психологическим процессом — не имеют ресурсов, чтобы объяснить, что особенного в нашем распознавании следствий. При этом в нем рассматриваются некоторые из основных теорий дедукции, которые использовались в течение последних нескольких лет. Он также опирается на некоторые недавние поведенческие и нейропсихологические данные о диссоциации между дедуктивными и индуктивными рассуждениями. Однако если тип рассуждений, отвечающих за следствия, уникален, то это налагает особое бремя на теории дедукции. Какая способность могла бы воспринять эти необходимые отношения? В главе рассматриваются некоторые альтернативные способы разделения способностей к рассуждению, в том числе основанные на содержании, и утверждается, что эти объяснения не могут дать правдоподобной теории дедукции.

Ключевые слова: дедуктивное рассуждение, индуктивное рассуждение, естественные виды, унитарные теории, познавательный процесс, дедукция

Предмет

Когнитивная психология

В настоящее время у вас нет доступа к этой главе.

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

Щелкните Войти через свое учреждение.
Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

Щелкните Войти через сайт сообщества.
При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Диаграммы Венна и диаграммы Эйлера с объяснением на примерах

Обновлено: 28 июля 2021 г.

Диаграммы Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многим людям трудно понять разницу. Хотя оба типа диаграмм основаны на теории множеств, существуют некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья рассеет ваши сомнения по поводу диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы было понятнее.

Венн против Эйлера: определение

Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между наборами множеств. Но диаграмма Эйлера показывает только те отношения, которые существуют в реальном мире.

Диаграммы Венна и

Диаграммы Эйлера Примеры

Начнем с очень простого примера. Давайте рассмотрим надмножество Animals с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение двух множеств, хотя в реальном мире такой возможности не существует. Диаграмма Эйлера, с другой стороны, не показывает пересечения.

Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии

Теперь давайте рассмотрим более сложный пример с колодой карт. Опять же важно помнить о разнице между двумя типами диаграмм, всеми возможными комбинациями и реальными комбинациями . Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества.

Как одни и те же данные представляются по-разному с использованием диаграмм Венна и диаграмм Эйлера

Как видно из приведенного выше примера, на диаграммах Венна показаны четыре пересечения, для которых нет данных, поскольку они должны отображать все возможные комбинации.

Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Посмотрите эту замечательную вики-статью о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера. Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.

Независимо от того, рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставляет вам все необходимые инструменты. Вы можете быстро приступить к работе, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели. С таким количеством супер крутых функций вы не ошибетесь с Creately.