Технологическая карта урока математики 5 класс «Площадь фигур» | План-конспект урока по математике (5 класс) на тему:
№ | Этап урока | Задачи этапа | Деятельность учителя | Деятельность ученика | Время (в мин.) | Формируемые УУД | ||||||||
Познаватель- ные | Регулятив ные | Коммуникатив- ные | Личностные | |||||||||||
1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||
1 | Организацион-ный этап | Создать благоприятный психологический настрой на работу | Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания; | Готовятся к уроку. Отвечают на вопросы учителя | 2 | Осознанное и произвольное построение речевого высказывания | Прогнозирование своей деятельности | Умение слушать и вступать в диалог | Умение выделять нравственный аспект поведения. | |||||
2 | Актуализация знаний | Актуализация опорных знаний и способов действий | Вступительное слово учителя. Устный счет. Повторение пройденного на прошлом уроке. Слушание домашнего творческого задания |
Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы. | 10 | Логический анализ объектов с целью выделения признаков. Поиск и выделение необходимой информации. | Выделение и осознание того, что уже пройдено. Постановка учебной задачи на основе известного. | Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог | Самоопределение | |||||
3 | Постановка целей, задач урока, мотивационная деятельность учащихся | Обеспечение мотивации учения детьми, принятие ими целей урока | Беседа с проблемным вопросом по будущей теме (отгадывание шарады). Задает учащимся наводящие вопросы. | Определяют цель урока. | 2 | Самостоятельное выделение-формулирование познавательной цели. | Целеполагание | Постановка вопросов | Самоопределение | |||||
4 | Работа по выявлению усвоения знаний | Обеспечение восприятия, осмысления, запоминания детьми изученной темы: площади прямоугольника. | Создает проблемную ситуацию, в ходе решения которой учащиеся делают необходимый вывод. Задача на краеведческом материале. | Делают вывод о формуле нахождения площади прямоугольника, единиц измерения, свойствах площади. Решают задачу на нахождение площади бассейна | 10 | Поиск и выделение необходимой информации. Структурирование знаний. Анализ объектов. Построение логической цепи рассуждений. | Планирование, прогнозирование | Умение слушать и вступать в диалог | Самоопределение | |||||
5 | Проверка усвоения знаний | Установление правильности и осознанности изучения темы. | Объясняет условия выполнения тестовых заданий | Самостоятельно отвечают на вопросы, решая задачи | 5 | Рефлексия способов и условий действия. Анализ объектов и синтез | Планирование своей деятельности для решения поставленной задачи и контроль полученного результата | Умение слушать и понимать, правильно выполнять задания. | Ориента- ция в межлично-стных отношениях | |||||
6 | Самооценка результатов | Самооценка результатов выполнения теста | Объявляет критерии выставления оценки. | Сравнивают результаты своей работы с правильными ответами. | 5 | рефлексия способов и условий действия | контроль полученного результата, коррекция полученного результата, саморегуляция | Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; | Самоопределение | |||||
7 | Создание проблемной ситуации для перехода к проектной деятельности | Создать условия для формулировки темы предполагаемого проекта | Использует игровые моменты, используя опыт детей по просмотру мультфильмов, создает предпосылки для проявления сочувствия и желания помочь. | Принимают решение «построить» дом для бездомных животных | 3 | Выделение и формулирование цели проектной деятельности | Планирование своей деятельности для решения поставленной задачи | Умение слушать, высказывать свою точку зрения, умение вести диалог | Умение выделять нравственный аспект поведения | |||||
8 | Физкультминутка | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. | Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу. | 2 | ||||||||||
9 | Проектная деятельность | Выполнение проекта «Построение» дома для бездомных животных | Формулирует при помощи детей алгоритм проектной деятельности. Выступает в роли тьютора для слабых учащихся при выполнении работы. | Учащиеся выполняют в парах творческое задание по алгоритму Делают записи в проектом листе. После выполнения задания выполняют взаимную проверку. | 15 | Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов | Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция | Умение слушать и вступать в диалог, Интегрироваться в парную деятельность.; Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в коллективном обсуждении проблем. | Профессионалное самоопределение, смыслообразование | |||||
10 | Подведение итогов урока | Самооценка результатов своей деятельности и всего класса | Подводит итоги работы в классе. | Отвечают на поставленные вопросы. Определяют оценку своего труда по количеству заработанных баллов по ходу урока | 5 | Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов | Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция | Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в коллективном обсуждении проблем. | Жизненное самоопределение, ценносто-смысловая ориентация обучающихся | |||||
11 | Информация о домашнем задании, инструктаж по его выполнению. | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания. | Задает домашнее задание | Учащиеся записывают домашнее задание в зависимости от уровня освоения темы урока | 5 | саморегуляция для повышения мотивации учебной деятельности | управление поведением партнёра- контроль, коррекция, оценка | Практико рориентированное | ||||||
12 | Рефлексия. | Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе. | -Кто работал на уроке лучше всех? -Кому еще надо стараться? -С каким настроением вы уйдете с урока? | Оценивают свою работу и работу одноклассников. | 2 | Оценка своей деятельности и других людей | Смыслообразование | |||||||
Вычисление площадей фигур, изображенных на клетчатой бумаге
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник.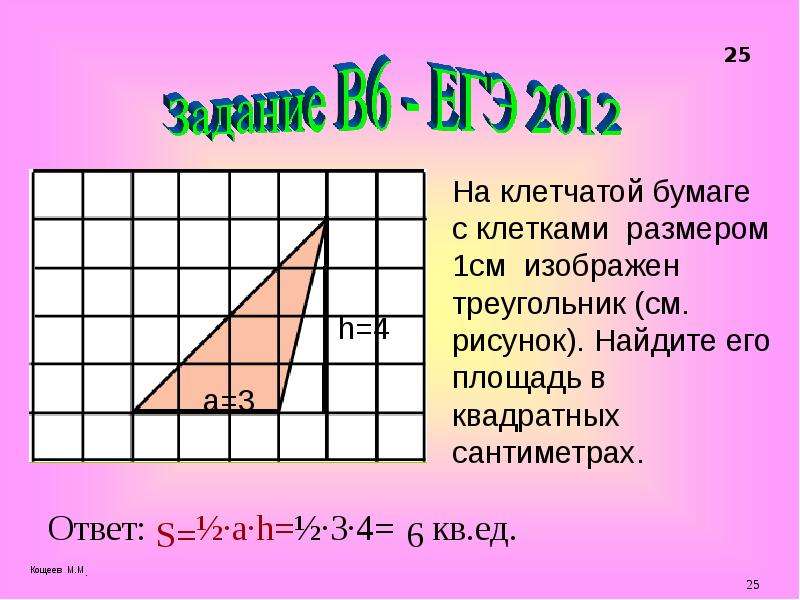 Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник, параллелограмм, трапецию:
1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;
2) подставить найденные величины в формулу площади.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.
Рис. 1. Треугольник
Решение. Подсчитываем клеточки и находим: . По формуле получаем: .
2 Фигура представляет собой многоугольник
Если фигура представляет собой многоугольник то возможно использовать следующие методы.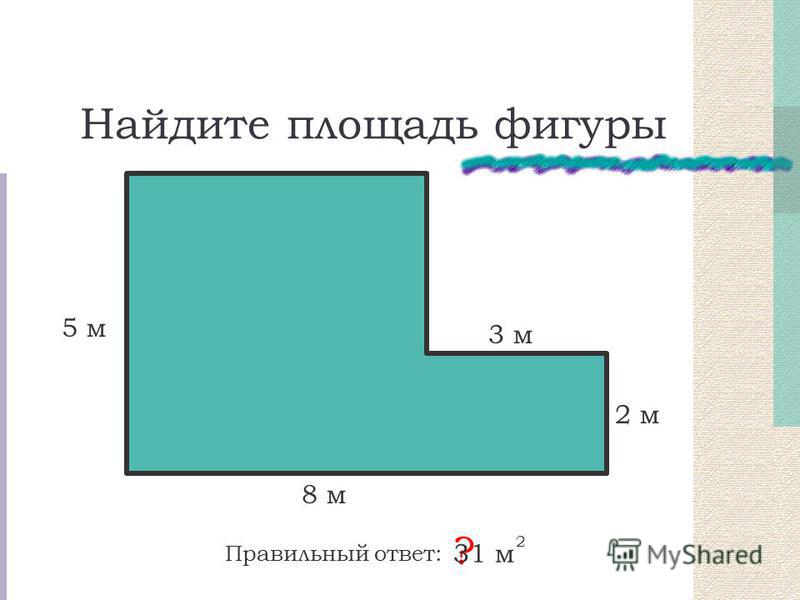
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
2) вычислить площади полученных фигур;
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.
Рис. 2. Многоугольник
Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.
Рис. 3. Многоугольник. Метод разбиения
Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:
Метод дополнительного построения
1) достроить фигуру до прямоугольника
2) найти площади полученных дополнительных фигур и площадь самого прямоугольника
3) из площади прямоугольника вычесть площади всех «лишних» фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.
Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.
Рис. 4. Многоугольник. Метод дополнения
Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.
Формула Пика
Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.
Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Например, для многоугольника, изображенного на рисунке 5.
Рис. 5. Узлы в формуле Пика
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.
Рис. 6. Многоугольник. Формула Пика
Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:
Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.
1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.
Рис. 7. Условие задачи 1
2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Рис. 8. Условие задачи 2
8. Условие задачи 2
3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
Рис. 9. Условие задачи 3
4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.
Рис. 10. Условие задачи 4
5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии.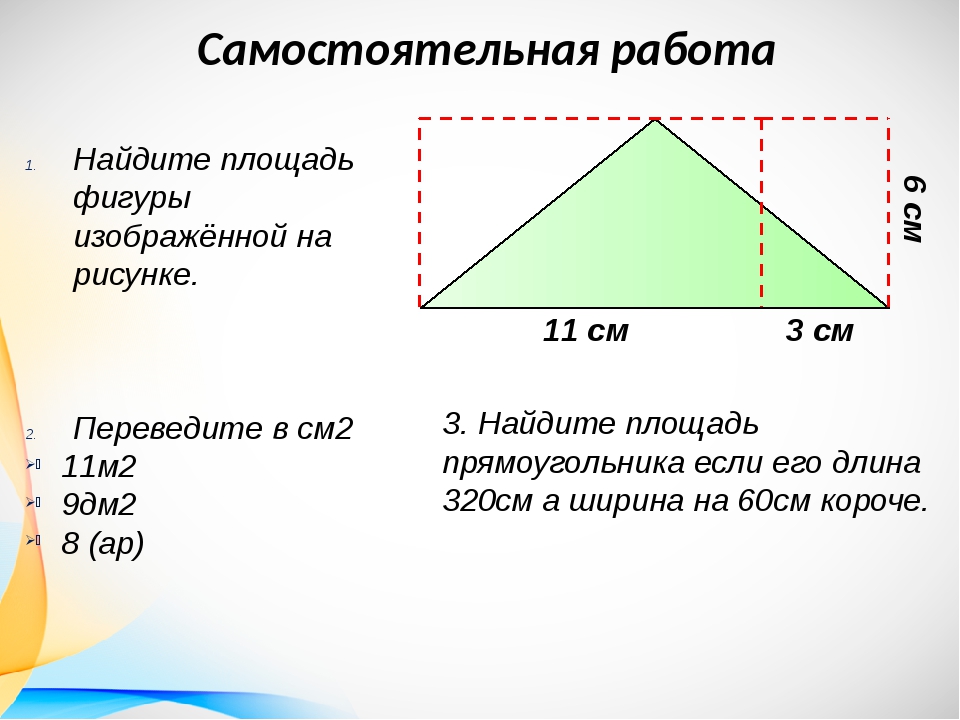
Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.
Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Литература:
- Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
- Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
- Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.
Основные термины (генерируются автоматически): формула Пика, клетчатая бумага, площадь фигуры, фигура, вычисление площадей, многоугольник, площадь, размер клетки, условие задачи, универсальная формула.
Разработка креативного урока в 5 классе по теме «Площади фигур» / Открытый урок
Учителя математики и педагога не могут не интересовать вопросы формирования у школьников креативного мышления, нацеленности на создание творческого продукта, способности проявлять личностную позицию в конкретной научной, культурной сфере жизнедеятельности посредством объединения двух полюсов образования: культуры и жизни. Интересен и процесс формирования у учащихся системы когнитивно-процессуальных и личностных свойств, способных выработать смысловую позицию в отношении ценности научного знания, которая необходима для самореализации человека в современном мире. Исходя из того, что основная цель воспитания – научить человека творить себя как личность, необходимо выделить
воспитывающий потенциал математического образования.Педагогическая система преподавания математики в последнее время претерпела множество изменений и, как мне кажется, в лучшую сторону. Уроки, внеклассные мероприятия, кружки стали менять деятельность школьников. Трансляция готовых знаний и отработка определенных навыков сменилась деятельностным поисково-познавательным подходом. Поэтому и цели, и задачи на урок изменились. Претерпела изменения и сама структура урока и его наполнение. Так нами была использована структура креативного урока схемы целостной системы многоуровневого непрерывного креативного образования – НФТМ-ТРИЗ [1].
Уроки, внеклассные мероприятия, кружки стали менять деятельность школьников. Трансляция готовых знаний и отработка определенных навыков сменилась деятельностным поисково-познавательным подходом. Поэтому и цели, и задачи на урок изменились. Претерпела изменения и сама структура урока и его наполнение. Так нами была использована структура креативного урока схемы целостной системы многоуровневого непрерывного креативного образования – НФТМ-ТРИЗ [1].
1. Блок мотивации. Познакомившись еще в дошкольном возрасте с различными геометрическими фигурами, вы уже тогда пытались выполнять над ними различные действия: из квадрата получать треугольники, собирать из треугольника, квадрата и прямоугольника домик, обклеивать коробочку с подарком для мамы цветной бумагой треугольной формы. Вы не знали свойств одинаковых фигур, не знали таких понятий как периметр и площадь, но достаточно сносно, на радость маме и воспитателю, выполняли все творческие задания, предлагаемые на занятиях. «Как мы это умудрялись делать?» – спросите вы. «Ведь нам это никто не рассказывал?». У вас уже в этом возрасте был достаточно большой жизненный опыт. Давайте и сегодня попробуем на него опереться.
«Как мы это умудрялись делать?» – спросите вы. «Ведь нам это никто не рассказывал?». У вас уже в этом возрасте был достаточно большой жизненный опыт. Давайте и сегодня попробуем на него опереться.
В каких профессиях требуются знания площади фигуры? Это, конечно же, строители, агрономы, конструкторы и вы, если вы решили помочь своим родителям сделать ремонт в своей комнате – поклеить на стены новые обои [3]. Это довольно трудоемко, ведь нужно учесть много факторов, при этом купив обоев столько – сколько нужно: не переплатив за лишних 5 рулонов или не докупив полрулона. Дома вы должны будете выполнить мини-проект «Моя комната». Для этого вам нужно будет сделать все необходимые расчеты для своей комнаты и виртуально поклеить в ней обои. Сегодня нам с вами предстоит решить следующие задачи
— отрабатывать применение теоретических знаний на практике;
— формировать навык самостоятельного переноса и интеграции знаний как результат использования формул и схем;
— принимать решения в проблемной ситуации на основе переговоров.
— осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных ситуаций.
2. Блок творческого разогрева. Выяснив у ребят, куда клеят обои, и с чем у них ассоциируется слово «стена», предлагаю заполнить таблицу, опираясь на их уже имеющиеся знания. В левый столбец нужно записать предметы, на которые похож загаданный объект, а в правый – чем он от них отличается [4].
|
Стена |
|
|
На что похож? |
Чем отличается? |
|
Прямоугольник |
Геометрическая фигура |
|
Окно |
Меньше |
|
Батарея |
Холодная |
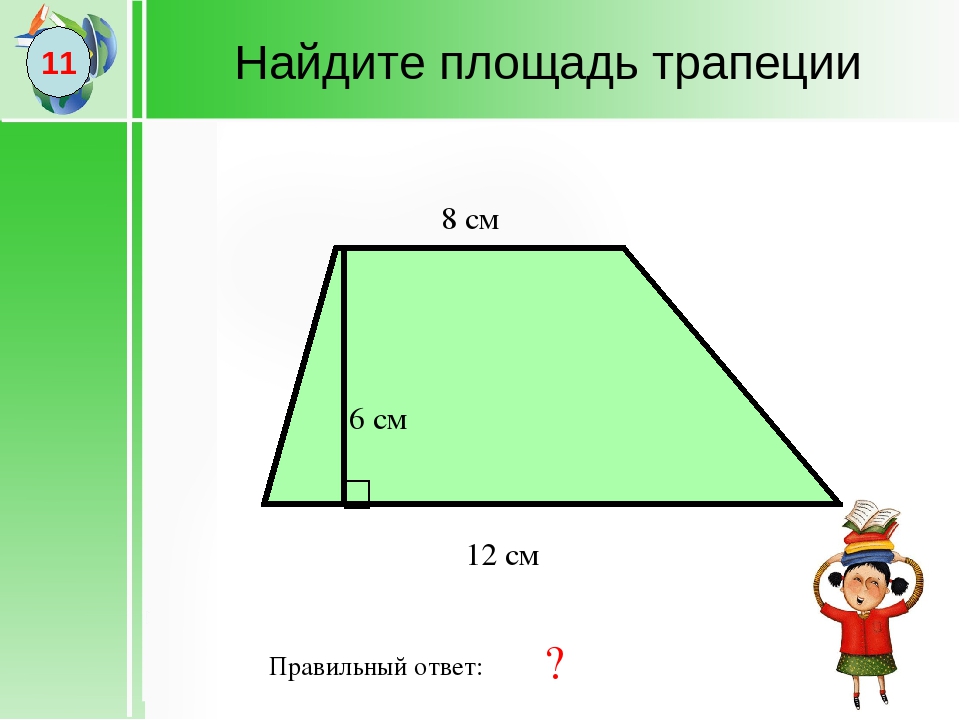
Далее ребятам предлагается рассмотреть план изображенной комнаты и предложенные измерения для расчетов.
Для более эффективной работы, для развития их творческого воображения, для однозначности представления таблицы с расчетами, ученики работают в группах, заполняя таблицу, в которой учитывают количество частей (участвующих в ремонте), составляющих объект (классная комната) [4].
|
Классная комната |
||
|
Части |
Сколько их? |
На что похожи? |
|
Стена |
4 |
На экран в кинотеатре |
|
Длина |
2 |
На плинтус |
|
Высота |
1 |
На трубу от батареи |
|
Окна |
3 |
На зеркала |
|
Двери |
1 |
На рот кита |
|
Батареи |
3 |
На гармошку |
3. Блок (психологическая разгрузка). Продолжая работать также в группах, ребята на этом этапе, представив себя строителями, измеряют: 1 группа – длины стен и высоту классной комнаты; 2 группа – длину и высоту окна; 3 группа – длину и высоту двери; 4 группа – длину и высоту радиаторов. Записывают результаты своих измерений.
Блок (психологическая разгрузка). Продолжая работать также в группах, ребята на этом этапе, представив себя строителями, измеряют: 1 группа – длины стен и высоту классной комнаты; 2 группа – длину и высоту окна; 3 группа – длину и высоту двери; 4 группа – длину и высоту радиаторов. Записывают результаты своих измерений.
4. Блок (головоломка). Ученики всех групп объединяются для построения схемы классной комнаты. Оказывается, что для наклеивания обоев нужно рассчитать площадь фигур различных форм, площадь фигур, у которых внутри или с краю часть вырезана, а бывает, что одну и ту же фигуру вырезают несколько раз. Итак, у нас возникла проблема: как это сделать?
На этом этапе учитель предлагает заготовленную головоломку «Квадраты». Перед вами четыре элемента. Чему равна площадь этих четырех фигур? Как ее найти? Попробуйте в группах выполнить задание.
Площадь каких фигур мы с вами уже умеем находить? Постарайтесь из данных фигур получить квадрат или прямоугольник. Молодцы! У нас получился квадрат, площадь которого мы уже умеем находить.
Молодцы! У нас получился квадрат, площадь которого мы уже умеем находить.
Что нужно знать для нахождения площади квадрата? Проведите в группах необходимые измерения и расчеты.
Итак, перед нами была проблема, решив которую мы познакомились с новым свойством площадей: площадь всей фигуры равна сумме площадей ее частей.
5. Блок (интеллектуальная разминка). Но для того, чтобы решить нашу проблему до конца, нам нужно познакомиться еще с одним важным свойством площадей.
Для этого решим следующую задачу: на рисунке 4 изображены два огорода. На каждый ар нужно 4 кг удобрений. Сколько удобрений потребуется на каждый участок? На какой участок удобрений потребуется больше? [2]
Работу нужно выполнять в парах, предварительно также в парах заполнив таблицу «Я знаю – Я применю» для решения этой задачи. Напротив знания, которое нужно применить для решения данной задачи, нужно поставить плюс или галочку.
|
Я знаю |
Я применю |
|
1. понятие длины отрезка |
+ + — + — — — + — — + |
|
2. понятие площади |
|
|
3. понятие формулы |
|
|
4. формула площади прямоугольника |
|
|
5. формула площади квадрата |
|
|
6. формула периметра прямоугольника |
|
|
7. формула периметра квадрата |
|
|
8. |
|
|
9 единицы измерения площадей |
|
|
10. перевод единиц измерения площадей |
|
|
11. свойства площадей равных фигур |
После решения этой задачи, ребята делают вывод, что площади равных фигур равны. На этапе интеллектуальной разминки могут быть использованы и учебные задачи открытого типа [4, 5].
6. Блок (содержательная часть). На этом этапе возвращаемся к схеме нашей классной комнаты, снова работаем в группах. Вычисляем по формуле нахождения площади прямоугольника площади окон, двери, радиаторов, стен. После этого вычисляем площадь той поверхности, которую нам нужно заклеить обоями. Высчитываем, какое количество рулонов нам нужно купить, если длина рулона 18 м, а ширина 1 м.
Ребята в группах заканчивают работу над проектом «Классная комната» и делают презентацию своего проекта.
После выполнения мини-проекта «Моя классная комната» в группах и всем классом вместе, ребята будут способны вполне самостоятельно провести виртуальный ремонт своей комнаты дома.
7. Блок (компьютерная интеллектуальная поддержка). Как вычислить площадь прямоугольника вы знаете. Как вычислить площади фигур, из которых вырезаны квадраты или прямоугольники – вы тоже знаете. А как все-таки найти площади неправильных фигур? Предложите способы вычисления и приведите свои примеры.
Пример 1. С помощью компьютерной программы на фигуру наложить сетку из одинаковых квадратиков, обработать фигуру. Но есть вероятность того, что точность измерения может быть нарушена.
Пример 2. Фигуру поместить в прямоугольную систему координат. Компьютерная программа зафиксирует координаты вершин фигуры и рассчитает длины сторон.
Этот мини-проект направлен на включение ребенка в процесс творчества средствами создания атмосферы радости поиска. Мини-проекты, связанные с явлениями, встречаемыми детьми в быту: ремонт квартиры (классной комнаты), при изучении темы «Площади и объемы» – вызывают у детей не только радость поиска, но и создают широкое положительное эмоциональное поле для дальнейшего постижения научных знаний по данному вопросу.
Мини-проекты, связанные с явлениями, встречаемыми детьми в быту: ремонт квартиры (классной комнаты), при изучении темы «Площади и объемы» – вызывают у детей не только радость поиска, но и создают широкое положительное эмоциональное поле для дальнейшего постижения научных знаний по данному вопросу.
8. Блок (резюме). На последнем этапе учитель подводит краткие итоги урока, выявляет мнение об уроке, задают домашнее задание.
Вопросы для обратной взаимосвязи могут быть такими:
- Вам понравился сегодняшний урок (кому понравился – поднимите зеленые карточки, кому не понравился – красные).
- Расскажите самый запоминающийся момент урока.
- Сможете ли вы самостоятельно провести виртуальный ремонт своей комнаты?
Великий китайский мудрец Конфуций (около 551-479 лет до н.э.) две с половиной тысячи лет назад сказал: “Когда благородный муж учит и воспитывает, он ведет, но не тянет за собой, побуждает, но не заставляет, указывает путь, но позволяет ученику идти самому. Поскольку он ведет, а не тянет, он пребывает в согласии с учеником. Поскольку он побуждает, а не заставляет, учеба дается ученикам легко. Поскольку он лишь только открывает путь, он предоставляет ученику возможность размышлять”. Такая позиция очень близка современному учителю и современным детям.
Поскольку он ведет, а не тянет, он пребывает в согласии с учеником. Поскольку он побуждает, а не заставляет, учеба дается ученикам легко. Поскольку он лишь только открывает путь, он предоставляет ученику возможность размышлять”. Такая позиция очень близка современному учителю и современным детям.
Ссылки на источники
- Зиновкина М. М. Многоуровневое непрерывное креативное образование в школе // Концепт. – 2012. – № 9 (сентябрь). – ART 12116. – 1,0 п. л. – URL: http://www.covenok.ru/koncept/2012/12116.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X.
- Математика: Учеб. для 5 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 17-е изд., перераб. – М.: Мнемозина, 2005. – 280 с.: ил.
- Развитие компетентности учителя современной гимназии. Практико-ориентированное пособие. Авторы составители: Л.М. Бурнашева, Т.Н. Харламова, П.Л. Зайцев, В.Д. Евсюкова, Л.К. Нефедова, Н.А. Зубачевская, Р.
 Р. Сабирова, Л.Г. Соколина, Н.И. Дорошенко, Л.П. Звягинцева, Ю.А. Нацкевич, С.Л. Попова, М.В. Чернуцкая, Т.В. Свенч. – Омск: Управление образования администрации города Омска 2004г, 135с.
Р. Сабирова, Л.Г. Соколина, Н.И. Дорошенко, Л.П. Звягинцева, Ю.А. Нацкевич, С.Л. Попова, М.В. Чернуцкая, Т.В. Свенч. – Омск: Управление образования администрации города Омска 2004г, 135с. - Горев П.М., Утемов В.В. Путешествие в страну творчества: учебно-методическое пособие. – Киров: Изд-во ВятГГУ, 2012. – 144 с., ил.
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – 4 квартал 2011, ART 11-4-02. – Киров, 2011 г. – URL: http://www.covenok.ru/koncept/2011/11402.htm. – Гос. рег. Эл № ФС 77-46214. – ISSN 2225-1618.
Titovа Maria,
mathematics teacher of MKOU «Nizhneirtyshsky SOSh» of the Sargatsky municipal region of the Omsk region, Omsk
titova_masha@mail.ru
Development of a creative lesson in the 5th class on the subject «Areas of Figures»
Abstract. Development of a creative lesson of the subject «Areas of Figures» is presented in article. The author according to structure of a creative lesson in innovative pedagogical system НФТМш developed all blocks of a lesson. The solution of creative tasks according to the chosen subject is considered.
Development of a creative lesson of the subject «Areas of Figures» is presented in article. The author according to structure of a creative lesson in innovative pedagogical system НФТМш developed all blocks of a lesson. The solution of creative tasks according to the chosen subject is considered.
Keywords: creative tasks, area of figures, creative imagination, positive emotional field.
11.6. Дайте «имя» изображенной фигуре. Выполните необходимые измерения и вычислите периметр и площадь изображенной фигуры.
Все прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
ЛОГИЧЕСКИЕ ЗАДАЧИ НА РАСКРАШИВАНИЕ.
1 ЛОГИЧЕСКИЕ ЗАДАЧИ НА РАСКРАШИВАНИЕ. Задача 1. Квадрат состоит из 9 различных фигур. Четыре из них раскрашены разным цветом: красным, желтым, зеленым, синим (рис. 1, а). Надо раскрасить остальные фигуры
ПодробнееОбразовательный портал «РЕШУ ВПР» (
Задания 12. Геометрические построения 1. 2. На рис. 1 изображены два треугольника. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рис. 2, нарисуйте два треугольника
ПодробнееПЛОЩАДЬ ПРЯМОУГОЛЬНИКА Вариант 1
^САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4.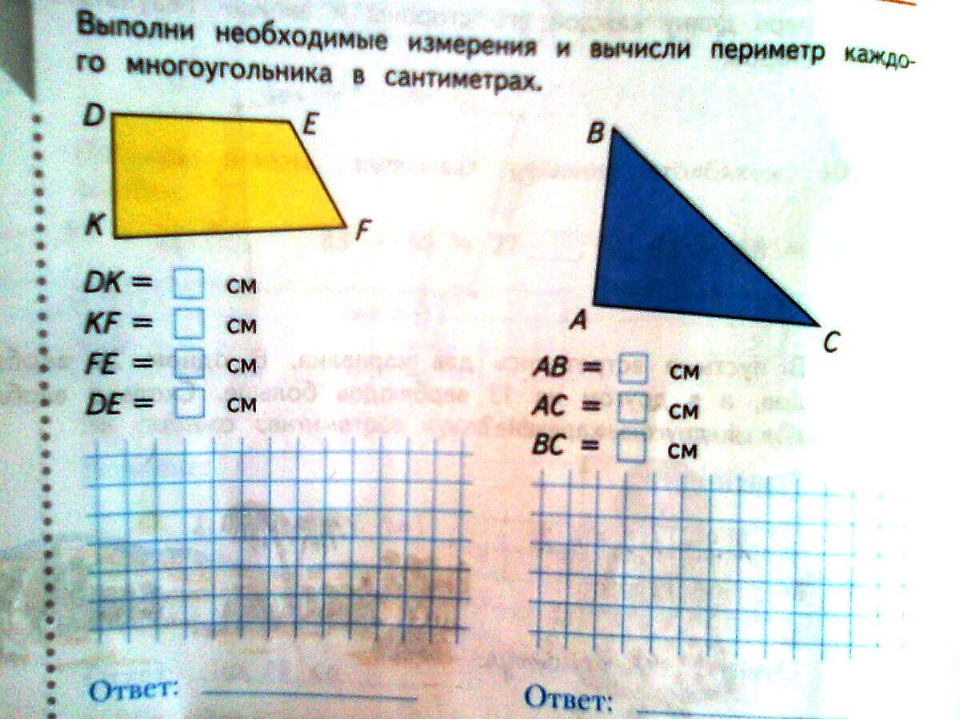 Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
ЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
Подробнее6 Верно ли, что площадь
1 2 Первый ученый, 3 Планиметрия это который систематизировал и изложил основы Параллелограмм это геометрии. 4 5 6 Верно ли, что площадь Две фигуры называются равновеликими, если Площадь трапеции равна
ПодробнееВ.
 А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ
А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬВ.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ 2011 ВВЕДЕНИЕ Выработка умений находить площади фигур на плоскости относится к основным целям обучения геометрии в школе. Задачи на нахождение площадей входят в содержание
ПодробнееПроизвольный четырехугольник
Произвольный четырехугольник 1 На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см рисунок) Найдите ее площадь в квадратных сантиметрах Пояснение Площадь четырехугольника равна разности
ПодробнееМатематика. Задание 1. Задание 2
Математика Задание 1 Цель: выявить умение анализировать условие предложенной задачи, включающей отрицание; умение найти оба способа решения. Инструкция: «Здесь вы будете выполнять первое задание. (Учитель
Подробнее(а) 1 (б) 2 (в) 3 (г) 7 (д) 9
Задача 1 Дано пятизначное число 1379.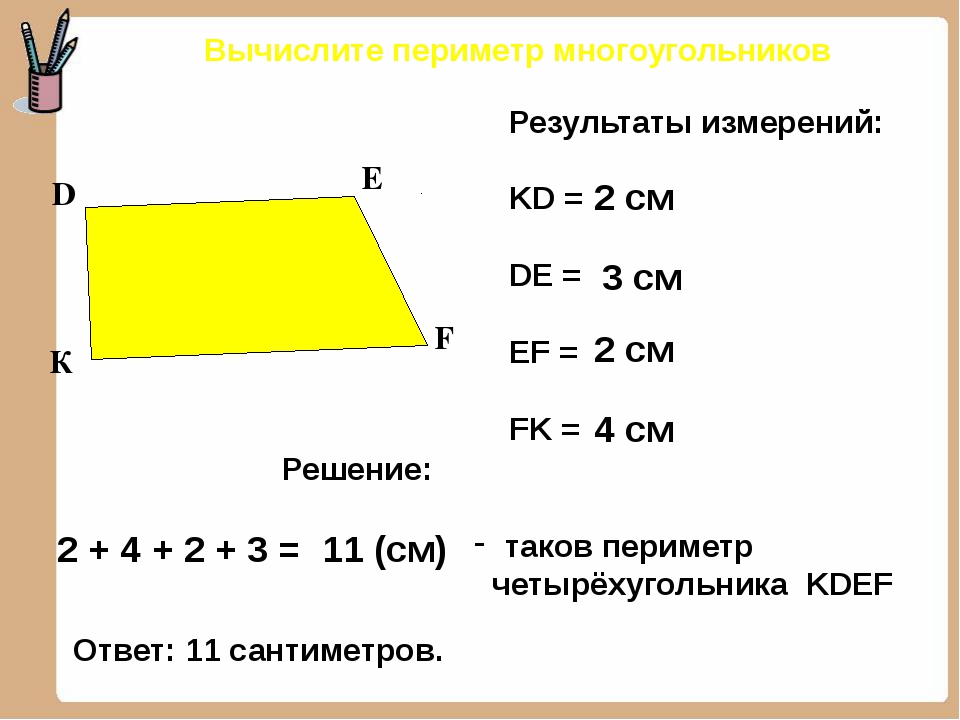 Какую цифру этого числа нужно стереть, чтобы полученное четырехзначное число было наименьшим среди всех четырехзначных чисел полученных таким образом? (а) 1 (б) (в)
Какую цифру этого числа нужно стереть, чтобы полученное четырехзначное число было наименьшим среди всех четырехзначных чисел полученных таким образом? (а) 1 (б) (в)
Многоугольники: вычисление площадей
Многоугольники: вычисление площадей 1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных Площадь прямоугольного треугольника
Подробнее( ) : 5 = < 4, ( ) : 7 = > 4.
XXXV Турнир имени М. В. Ломоносова 30 сентября 0 года Конкурс по математике. Ответы и решения (предварительная версия от 5.0.0) В скобках указано, каким классам рекомендуется задача (решать задачи более
Подробнее0:0 0:1 0:2 0:3 0:4 0:5
Турнир «KamaChallenge-016» Математическая игра «Домино» 0:0 Из квадрата 016 016 вырезана одна угловая клетка 11. На какое наименьшее число равновеликих треугольников можно разрезать получившуюся фигуру?
На какое наименьшее число равновеликих треугольников можно разрезать получившуюся фигуру?
Планиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
ПодробнееЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееID_2420 1/11 neznaika.pro
1 Планиметрия: вычисление длин и площадей Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Запишите ответ без пробелов, запятых и других дополнительных символов.
Развитие сенсорики 1-3 года
Развитие сенсорики 1-3 года Какого цвета предметы? Предложите ребенку рассмотреть картинку. Попросите показать на картинке предмет красного, синего, зеленого, желтого, белого, черного цвета. Что одинакового
ПодробнееПрямоугольник: длины и площади
Прямоугольник: длины и площади 1. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Площадь прямоугольника равна произведению
ПодробнееКоординатная плоскость
Координатная плоскость 1. Найдите площадь ромба, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6). Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных
ПодробнееВ.
 А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ
А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯВ.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ Москва 2011 ВВЕДЕНИЕ Одной из важных целей обучения геометрии в школе является развитие конструктивных умений учащихся, включающих в себя умения изображать различные
Подробнее«Математика» Первоклассник научится: называть: предмет, расположенный левее (правее), выше (ниже) данного предмета, над (под, за) данным предметом,
«Математика» Первоклассник научится: предмет, расположенный левее (правее), выше (ниже) данного предмета, над (под, за) данным предметом, между двумя предметами; натуральные числа от 1 до 20 в прямом и
Подробнее( ) : 5 = < 4, ( ) : 7 = > 4.
XXXV Турнир имени М. В. Ломоносова 30 сентября 01 года Конкурс по математике. Ответы и решения В скобках указано, каким классам рекомендуется задача (решать задачи более старших классов также разрешается,
ПодробнееЗАДАНИЯ ДЛЯ 8 КЛАССА
ЗАДАНИЯ ДЛЯ 8 КЛАССА Задание 1. Из прямоугольного листа бумаги А4 нужно вырезать ромб наибольшей площади. Какое наименьшее количество разрезов для этого потребуется? Опишите процесс складывания и разрезания.
Из прямоугольного листа бумаги А4 нужно вырезать ромб наибольшей площади. Какое наименьшее количество разрезов для этого потребуется? Опишите процесс складывания и разрезания.
Фигуры на клетчатой решетке
Фигуры на клетчатой решетке I. Расстояние между точками 1) На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите
ПодробнееЦЕНТР ПЕДАГОГИЧЕСКОГО МАСТЕРСТВА.
ЦЕНТР ПЕДГОГИЧЕКОГО МТЕРТ. методические материалы проекта «Математическая вертикаль» ГЕОМЕТРИЯ: 7 класс параграф 11 Признаки равенства треугольников. автор: М.. олчкевич 2018 г. ннотация: Данный материал
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Подготовка к ЕГЭ по математике
2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Планиметрия. Комбинации фигур. Александр и Наталья Крутицких
ПодробнееМАТЕМАТИКА 8 и 9 классы
Всероссийская олимпиада школьников «Миссия выполнима. Твое призвание-финансист!» ЗАКЛЮЧИТЕЬНЫЙ (ОЧНЫЙ) ЭТАП МАТЕМАТИКА 8 и 9 классы Задание (0 баллов) Длины сторон AB, ВС, CD и DA выпуклого четырехугольника
Подробнее41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
2. Задание 18 ( 27614) Найдите
ЕГЭ по математике. Вариант 9
ЕГЭ по математике. Вариант 9 Вопрос Найдите значение выражения ( ) :. 4 24 6 Вопрос 2 2 Найдите значение выражения 42 4. 7 4 3 4 Вопрос 3 3 В детский сад завезли 84 упаковки молока, четверть которых рассчитана
Подробнее«Понятие площади многоугольника»
Знание это самое превосходное из владений. Все стремятся к нему, само оно не приходит. Абу-р-Райхан ал-буруни «Понятие площади многоугольника» Геометрия 8 класс 1 ХАРАКТЕРИСТИКА МНОГОЧЛЕНОВ Замкнутая ломаная,
ПодробнееЗАДАНИЯ ДЛЯ 7 КЛАССА
ЗАДАНИЯ ДЛЯ 7 КЛАССА Задание 1 (Задача предложена А.В. Ястребовым). Сформулируйте математическое утверждение, которое ставит под сомнение представленные на рисунке 1 результаты эксперимента. Нужно ли считать
Нужно ли считать
КДР математика 9 класс в среднем по краю
АНАЛИЗ РЕЗУЛЬТАТОВ краевой диагностической работы по МАТЕМАТИКЕ 9 класс (20 февраля 2018 г.) Диагностическую работу выполняли 49541 учащихся 9 х классов, что составляет 89,2 % от всех выпускников образовательных
ПодробнееID_9273 1/10 neznaika.pro
1 Фигуры на квадратной решётке Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. На клетчатой
Подробнее0 А, 1 Ш, 2 П, 3 В, 4 У, 6 Б, 7 Д, 8 Ж.
Квасникова Наталья Юрьевна, МОУ «Средняя общеобразовательная школа 65»г.Кемерово учитель начальных классов Упражнения на развитие логического мышления младших школьников 1. Найти величину слагаемых (по
Найти величину слагаемых (по
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h3=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Урок «Площадь прямоугольника»
Цели урока:
обучающие
- закреплять умение применять табличное умножение при решении числовых выражений;
- закреплять термины «длина», «ширина»;
- сформировать умение находить площадь прямоугольника и квадрата;
- углубить и расширить представление детей о плоскостных фигурах.
развивающие
- способствовать развитию мыслительных операций: анализа, сравнения, обобщения; внимания;
- развитие познавательной активности;
- развивать вычислительные навыки, умения решать задачи;
- развивать конструктивные навыки и воображение;
- развивать умения взаимоконтроля и самоконтроля через оценивание собственной деятельности и деятельности других детей на разных этапах урока.

воспитывающие
- создание благоприятного психологического климата для возможности раскрытия потенциала каждого ребенка;
- воспитывать аккуратность, чувство взаимоподдержки и выручки;
- воспитание культуры учебного труда.
- Оборудование: мультимедийный проектор.
Ход урока
1. Организационный момент(Слайд)
— Здравствуйте, ребята, меня зовут Анастасия Николаевна, сегодня я у вас проведу урок математики.
Ребята, на каждом уроке вы стремитесь сделать для себя открытие, получить новые знания. Вот и сегодня мы постараемся углубить математические знания, узнать новое.
2. Психологический настрой— Посмотрите на доску, что это? (геометрические фигуры)
— Что в них необычного? (на них изображены лица)
— На какие группы, по какому признаку их можно разделить? (лица веселые и грустные)
— А сейчас закройте глазки. Открывайте. Что изменилось? Слайд
Открывайте. Что изменилось? Слайд
— Какое настроение они дарят? (осталисьфигуры веселые, радостные)
— Я тоже желаю вам хорошего настроения, чтобы оно сохранилось в течение всего урока!
— А как называются фигуры. которые остались? (прямоугольники).
— Что такое прямоугольник (четырехугольник, которого все углы прямые, 4 сторон, 4 вершины.
— Сегодня именно они будут чаще всего нам встречаться
3. Актуализайия опорных знанийУстный счет
— Ребята, любите ли вы разгадывать кроссворд. Предлагаю (читаю, отгадывают)
— Первое слово. Сумма длин сторон любой геометрической фигуры. (Периметр)
— Прибор, с помощью которого мы чертим прямые линии. (Линейка)
— Третье слово. Прямая линия, ограниченная с двух сторон. (Отрезок)
— Как называется линия, которая состоит из звеньев. (Ломаная)
— Прямоугольник, у которого все стороны равны. (Квадрат)
(Квадрат)
— Геометрическая фигура , где две противоположные стороны равны, и все углы прямые (прямоугольник)
— Кто догадался, какое слово получается в вертикальном столбике. (Площадь)
— Значит, о чем мы сегодня будем говорить на уроке? (О площади)
Что сразу представляете? – Пожалуйста, поделитесь своими мыслями.(площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.)
— А что означает термин «площадь» в математике? (Ответы детей Площадь — внутренняя часть фигуры (прямоугольника, квадрата)
(площадь — это величина, которая указывает, сколько места занимает фигура на плоскости.
— А как вы думаете площадь какой фигуры мы сегодня с вами рассмотрим? (площадь прямоугольника)
Слайд
— Ребята, а знает, что Первым предложил измерить площадь прямоугольника древнегреческий ученый Архимед, который жил почти 2200 лет назад.
— Хотели ли вы узнать как измеряли площади фигур в древнее время, предлагаю перенестись на тысячи лет назад и побывать в одной из школ.
— Для этого я предлагаю открыть конверт под номером 1. Возьмите фигуры, что за фигуры? Каких цветов?
— Как узнать какой прямоугольник занимает больше место на плоскости? (на глаз)
— Еще как.7 (способом наложения)
— Покажите?Что видим? .Какой прямоугольник занимает больше места на плоскости?Значит площадь какого прямоугольника больше? (красного)
— Теперь Измерьте площади своих прямоугольников.
Провокация: Мерок у детей нет.
Дети не работают.
— Почему не работаете? (Нет мерки.)
Даю нитку. (Не пойдет.)
— Почему? (Площадь нужно мерить меркой площади, например, квадратиком.)
Даю квадратик (мерка у всех одинаковая).
Дети измеряют площади своих прямоугольников путем прикладывания квадратика.
После измерения дети заодно находят, что их прямоугольники имеют одинаковую площадь, хотя длина и ширина у них различна.
Вывод: — Что можете сказать?
(Мы умеем измерять площадь.)
(Мы умеем измерять площадь.)
Задача 2: Измерить площадь пола в классе.
— Почему не можете найти площадь класса? (Нужна мерка.)
— У вас есть квадратик. (Мерка маленькая, ею мерить долго и неудобно.)
Даю на выбор: веревка или кусок обоев. Выбираем кусок обоев.
2 ученика начинают измерять пол в классе.
Остальным детям учитель предлагает изобразить, то, что делают 2 ученика на полу, на доске и в своих тетрадях.
— Всегда ли можно сравнить площади на глаз,или наложением? (нет,бывают фигуры, у которых нельзя определить чья площадь больше или меньше)
— Хотите узнать, как еще мы можем высчитать площадь?
— Посмотрим на экран, скажите площадь какого прямоугольника больше?
При помощи чего высчитать.
— Как же нам вычислить площадь фигур, если квадраты разные по размеру? Будут ли точные подсчеты? (нет)
— Для измерения площадей существуют специальные мерки квадратной формы и Одного размера. Общепринятой меркой является квадрат, но могут быть и другие фигуры.
Общепринятой меркой является квадрат, но могут быть и другие фигуры.
Площадь одного квадрата со стороной 1 см — это 1 квадратный см. В математике одной из общепринятых единицей измерения явл-ся кв.см. слайд
— Сравнивать величины мы можем только тогда, когда они выражены одинаковыми мерками.
— Скажите, площадь каких фигур мы можем измерять такими мерками? (в см кв)
А удобно ли ими измерять площадь больших фигур? Площадь крышки стола, площадь доски, площадь стены?
— Как вы думаете какими единицами измерения еще можем пользоваться (дм, м)
Вывод: Квадратный сантиметр, квадратный дециметр, квадратный метр – единицы площади, ИХ обозначают так: см2, дм2, м2.
— Скажите, а всегда ли удобно использовать мерки ля измерения площади? (нет)
— Может есть более универсальный способ?
— Давайте проверим, предлагаю открыть тетрадь, давайте запишем число. и начертим прямоугольник со сторонами 6 и 3 см.
и начертим прямоугольник со сторонами 6 и 3 см.
— Разобьем на квадратные см. (синий)
— Скажите сколько полос с квадратами в данном прямоугольнике? (3)
— Сколько квадратов в каждой полосе? (6)
— Как нам быстро сосчитать? (умножить 6 на 3)
— А что обозначает нам число 6? (длину)
— А число 3? (ширину)
— Какой вывод сделаем? Чтобы найти площадь, надо длину умножить на ширину.
— Площадь в математике обозначается S, дина a.ширина b. А длину, ширину как найти?
— Кто сможет выйти составить формулу.
— Молодцы!
— Давайте попробуем применять формулы. Предлагаю решить задачу.
Длина нашего класса 9 метров, а ширина 6 метров. Найти площадь класса?
4. Самостоятельная работа с последующей проверкойслайд
— Умение находить площадь прямоугольника в жизни нам необходимо. Людям, каких профессий нужно хорошо знать математику, производить расчёты, находить площадь фигур? (архитектору, конструктору, инженеру, строителю)
— Ребята, в нашем городе реализуется народная программа по благоустройству места отдыха, дорог, спортивных площадок.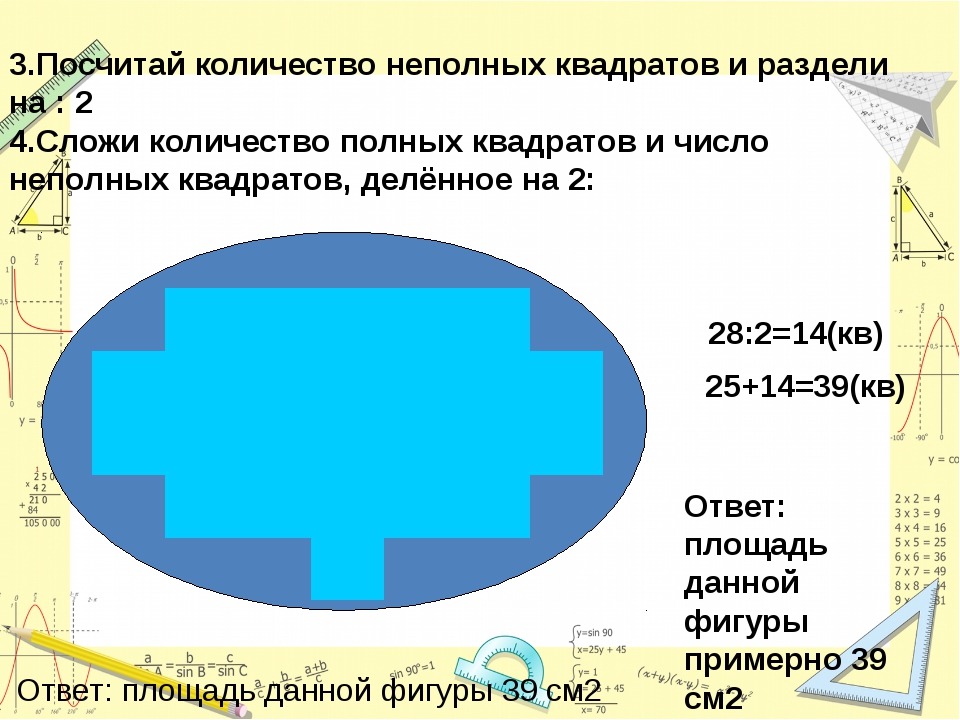 Вот и мне дали задание разработать проект детского парка для нашего города. Поможете мне. У нас будет уменьшенная копия, поэтому все вычисления будут в кв.см 1.
Вот и мне дали задание разработать проект детского парка для нашего города. Поможете мне. У нас будет уменьшенная копия, поэтому все вычисления будут в кв.см 1.
- О какой геометрической фигуре шел разговор на уроке?
- Что нужно знать, чтобы найти площади прямоугольника?
- Пригодятся ли вам в жизни полученные знания? Где?
- Что на уроке было самым сложным, простым?
У вас есть инструкция, которую нужно строго соблюдать.
- Комфортно и все понятно.
- На уроке немного затруднялся. Но было все понятно.
- На уроке было трудно. Ничего не понял.
1. Рассмотреть предложенные картинки
2. Выбрать те, которые вы хотели бы увидеть в парке
3. Наклеить на картон А4
4. Произвести измерения их и высчитать площадь
5. Результаты занести в таблицу
6. Дать название вашему парку
7. Представить своей проект
Общая площадь парка 100 кв. | |
Название объекта | Площадь объекта |
Клумба с цветами |
|
Аттракционы |
|
Спортивная площадка |
|
Фонтан |
|
Детская площадка |
|
Наш парк называется______________________
Мы произвели все необходимые вычисления и решили, что в парке обязательно нужно установить__________________, площадью ______________
___________, площадью______________, площадью
________, площадью
Для этого предлагаю поработать в группах.
Работать будем в группах. Работа в группе – это работа нескольких человек вместе, дружно.
— Давайте, вспомним правила работы в группе
1. Распределить обязанности.
2. Работать дружно.
3. Уважать товарищей.
4. Говорить коротко и понятно.
5.Слушать каждого члена группы
— Детали лежат у вас на столе.
— Чтобы построить дом, надо выполнять правильные расчёты. Листком расчёта будет.
— Продолжим работу.
— Возьмите прямоугольник. Что он вам напоминает из ранее сделанного? (фундамет)
— Как из него сможем сделать дверь?Дверь составляет половину этой фигуры. Как её получить? (согнуть, разрезать)
Чему равняется площадь двери? Расположите дверь правильно.
— Какой наш будет следующий шаг? (окна)
Посмотрите на оставшийся прямоугольник. Сколько окон получится? (2)
— Чему равна площадь будет одного окна?
— Строительство дома завершается крышей.
— Какой формы она бывает?
Но на столах только прямоугольник, равный по площади стенам дома.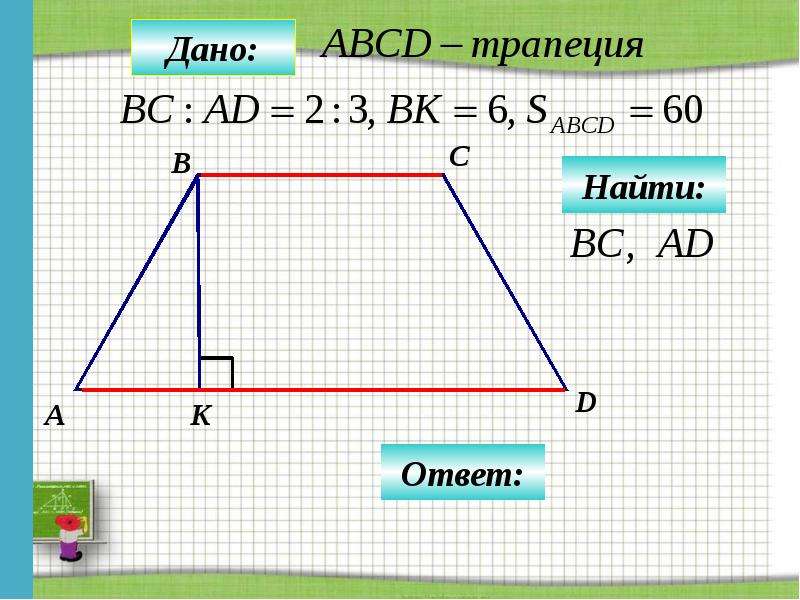 Как быть? (сложить пополам и разрезать)
Как быть? (сложить пополам и разрезать)
— Асможем мы вычислить площадь треугольника? (нет не изучали)
— А что сможем вычислить (периметр)
— По какой формуле (а+б)*2
Вот и готов наш дом.
6. РефлексияЧто нового вы сегодня узнали?
Ребята, послушайте одну притчу.
Шёл мудрец и встретил 3 работников.
«Что ты сегодня делал?» — спросил он каждого.
Первый ответил: — «Я целый день таскал ненавистные камни».
Второй ответил: — «Я немного устал, но добросовестно выполнял свою работу».
Третий ответил: — «Сегодняшняя работа принесла мне радость и большое удовлетворение».
— Спасибо за урок
Инструкция
Выполнить необходимые измерения.
1. Вычислить площадь одной стены, результаты занести в таблицу.
2. Высчитать общую площадь стен дома (4 стороны дома), результаты занести в таблицу.
3. Вычисли площадь одного окна, результат занести в таблицу.
4. Высчитать общую площадь окон (2 окна), результат занести в таблицу.
3. Вычисли площадь трубы (1 труба), результат занести в таблицу.
4. Приклеить все необходимые детали дома на лист А3.
5. Приклеить сводную таблицу.
6. Рассказать, для кого дом построен.
| Кол-во | Площадь одного | Общая площадь |
стен |
|
|
|
окон |
|
|
|
трубы |
|
|
|
единиц площади | 3-й класс по математике
Узнайте о единицах площади
Давайте рассмотрим
Площадь — это площадь поверхности, которую покрывает объект или пространство.
Измеряется на квадратных единицах .
Какова площадь этой формы?
Всего сосчитайте количество квадратов, которые он покрывает. Это область. 000
Так какова площадь синего прямоугольника?
Это 12 квадратных единиц .
Есть еще один способ определить местность.
Получите ширину и высоту. Затем умножьте числа.
Ширина 3, длина 2.
Умножим это:
3 x 2 = 6
Площадь зеленого прямоугольника 6 квадратных единиц .
Насколько велика квадратная единица?
Теперь представьте, что у вас есть игровая комната площадью 6 квадратных единиц.
Нужно накрыть резиновым ковриком.
Сколько резиновых ковриков нужно купить?
Знание количества квадратных единиц вам не поможет, потому что вы не знаете, насколько велика каждая квадратная единица. 000
👉 Вам необходимо знать единиц площади .
Что такое единица площади?
Единица площади показывает, сколько места фактически занимает фигура.
Помните, что вы узнали о единицах длины? С этим тесно связаны единицы площади.
Есть разные типы единиц площади:
Мы используем маленьких единиц площади для маленьких пространств и больших единиц площади для больших пространств .
Квадратный миллиметр используется для действительно маленьких объектов, таких как ноготь.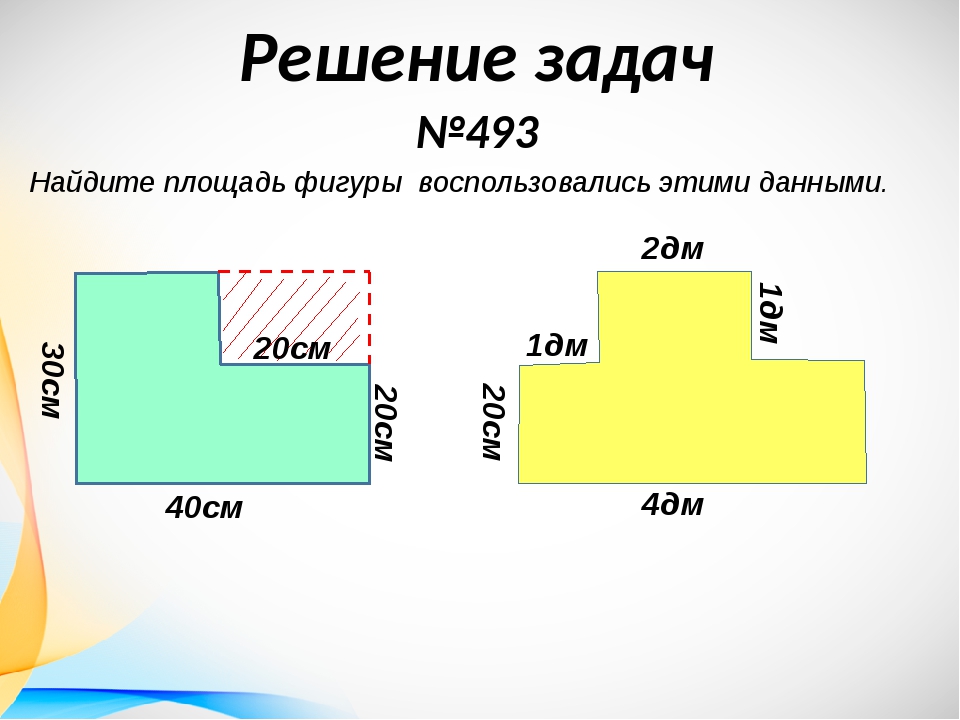
Обычно мы пишем его более коротким образом: мм²
Квадратный дюйм и квадратный сантиметр можно использовать для измерения небольших поверхностей, таких как бумага, изображения или рисунки.
Квадратный дюйм обычно записывается как дюйм² . Квадратный сантиметр часто записывается как см² .
квадратных футов, квадратных ярдов, и квадратных метров используются для больших пространств, таких как площади комнат, домов, садов и полей.
Вот более короткие способы записи этих единиц площади:
квадратных футов = фут²
квадратный ярд = ярд²
квадратных метров = м²
квадратных миль и квадратных километров используются для действительно больших площадей земли. Также используются гектары и акры, но вы узнаете о них в более поздних классах.
Также используются гектары и акры, но вы узнаете о них в более поздних классах.
Квадратные мили сокращаются до миль ². Для квадратных километров используется сокращение км².
Вот значения единиц по сравнению друг с другом.
1 см² = 100 мм²
1 м² = 10 000 см²
1 км² = 1 000 000 м²
1 дюйм² = 6,45 см²
1 фут² = 144 дюйм²
1 ярд² = 9 фут²
1 м² = около 10,9 фут²
1 м² = примерно 2,6 км²
Использование правильной единицы площади
Важно, чтобы использовал правильную единицу измерения при измерении площади.
Допустим, вас попросили найти площадь этого дома.
Правильно ли использовать квадратные миллиметры для его измерения?
❎ Нет! Вы получите число , слишком большое !
Вы можете получить что-то вроде 800 000 мм²! 000
А как насчет квадратных метров (м²)?
✅ Да! Это то, что нужно использовать. 000
✅ Вы также можете использовать квадратные футы (ft²). 000
Итак, будет ли правильно использовать квадратные мили для измерения площади листа бумаги?
❎ No…Вы получите число , слишком маленькое .
В нем будет много десятичных знаков. Вы только посмотрите на это — 0,000868 м². 000
✅ Для измерения бумаги лучше всего использовать меньшие единицы, такие как квадратные сантиметры (см²) или квадратные дюймы (дюйм²).
Как записать единицу площади?
Мы записываем единицу площади, добавляя маленькую 2 после единицы длины.
Например, квадратный сантиметр составит см². Читается как квадратные сантиметры.
Вот другие единицы площади и их символы:
Сравнить единицы площади
👉 Выясните, какая площадь больше.
4 квадратных дюйма или 4 квадратных метра ?
Мы знаем, что квадратный метр больше квадратного дюйма.
Итак …
✅ 4 квадратных метра — это больше, чем 4 квадратных дюйма.
4 м² > 4 дюйма²
👉 Какая из этих двух областей меньше?
50 квадратных футов или 50 квадратных миль ?
Мы знаем, что квадратный фут меньше квадратной мили.
Итак …
✅ 50 квадратных футов — это меньше, чем 50 квадратных миль.
50 фут² < 50 фут²
Смотри и учись
Отличная работа! Теперь попробуйте освоить единицы площади. 000
Нахождение неправильных фигур
Результаты обучения
- Объедините области правильных форм, чтобы найти области неправильных форм.
Итак, мы нашли область для прямоугольников, треугольников, трапеций и кругов. Неправильная фигура — это фигура, не имеющая стандартной геометрической формы. Его площадь не может быть рассчитана ни по одной из стандартных формул площади. Но некоторые неправильные фигуры состоят из двух или более стандартных геометрических фигур. Чтобы найти площадь одной из этих неправильных фигур, мы можем разбить ее на фигуры, формулы которых нам известны, а затем сложить площади фигур.
пример
Найдите площадь заштрихованной области.
Решение
Данный рисунок неправильный, но мы можем разбить его на два прямоугольника. Площадь заштрихованной области будет суммой площадей обоих прямоугольников.
Синий прямоугольник имеет ширину [латекс] 12 [/ латекс] и длину [латекс] 4 [/ латекс]. Красный прямоугольник имеет ширину [латекс] 2 [/ латекс], но его длина не указана. Правая часть рисунка — это длина красного прямоугольника плюс длина синего прямоугольника. Поскольку правая сторона синего прямоугольника имеет длину [латекс] 4 [/ латекс] единиц, длина красного прямоугольника должна быть [латекс] 6 [/ латекс] единиц.
Площадь фигуры [латекс] 60 [/ латекс] квадратных единиц.
Есть ли другой способ разделить эту фигуру на два прямоугольника? Попробуйте и убедитесь, что у вас такая же площадь.
пример
Найдите площадь заштрихованной области.
Показать решение Решение
Мы можем разбить эту неправильную фигуру на треугольник и прямоугольник. Площадь фигуры будет суммой площадей треугольника и прямоугольника.
Прямоугольник имеет длину [латекс] 8 [/ латекс] единиц и ширину [латекс] 4 [/ латекс] единиц.
Нам нужно найти основание и высоту треугольника.
Поскольку обе стороны прямоугольника [латекс] 4 [/ латекс], вертикальная сторона треугольника — [латекс] 3 [/ латекс], то есть [латекс] 7 — 4 [/ латекс].
Длина прямоугольника составляет [латекс] 8 [/ латекс], поэтому основание треугольника будет [латекс] 3 [/ латекс], то есть [латекс] 8 — 4 [/ латекс].
Теперь мы можем добавить области, чтобы найти площадь неправильной фигуры.
Площадь фигуры [латекс] 36,5 [/ латекс] квадратных единиц.
пример
Трасса средней школы имеет форму прямоугольника с полукругом (полукругом) на каждом конце. Прямоугольник имеет длину [латекс] 105 [/ латекс] метров и ширину [латекс] 68 [/ латекс] метров. Найдите область, ограниченную дорожкой. Округлите ответ до ближайшей сотой.
Показать решение Решение
Разобьем фигуру на прямоугольник и два полукруга.Площадь фигуры будет суммой площадей прямоугольника и полукругов.
Прямоугольник имеет длину [латекс] 105 [/ латекс] м и ширину [латекс] 68 [/ латекс] м. Полукруги имеют диаметр [латекс] 68 [/ латекс] м, поэтому каждый имеет радиус [латекс] 34 [/ латекс] м.
Периметр и Площадь | Математика для гуманитарных наук
Периметр
Периметр — это одномерное измерение, которое проводится вокруг внешней части замкнутой геометрической формы.Давайте начнем обсуждение концепции периметра с примера.
Управляемый пример
Рисунок 1.
Рисунок 2.
У Джозефа нет машины, поэтому он должен ездить на автобусе или идти пешком. По понедельникам он должен ехать в школу, на работу и снова домой. Его маршрут изображен на рисунке 1.
В этой ситуации очевиден вопрос: «Сколько миль проезжает Джозеф по понедельникам»? Для вычисления мы каждое расстояние: 3 + 6 + 6 = 15.
Джозеф проезжает 15 миль по понедельникам.
Другой способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и помеченную расстоянием от одного места до другого.
Обратите внимание, что маршрут Джозефа представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. Рисунок 2). Что мы можем спросить об этой форме: «каков периметр треугольника»?
Периметр означает «расстояние вокруг замкнутой фигуры или фигуры», и для вычисления мы складываем каждую длину: 3 + 6 + 6 = 15
Наш вывод тот же, что и выше: Джозеф проезжает 15 миль по понедельникам.
Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили конкретную геометрическую концепцию (периметр , ), чтобы вычислить, как далеко проехал Джозеф.
Записки по периметру
- Периметр — это одномерное измерение, которое представляет собой расстояние вокруг замкнутой геометрической фигуры или фигуры (без промежутков).
- Чтобы найти периметр, сложите длины каждой стороны формы.
- Если есть единицы, включите единицы в окончательный результат.Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. Д.).
Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рисунке 3 показана разница между закрытой фигурой и открытой фигурой.
Рисунок 3.
Пример 1
Найдите периметр для каждой из фигур ниже.
- Сложите длину каждой стороны.
- Иногда приходится делать предположения, если длина не указана.
Решения
- 12 шт.
- 40 футов
Пример 2
Как найти периметр этой более сложной формы?
Решение
Просто продолжайте добавлять длины сторон.6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 шт.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждый периметр в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали, приведенным ниже формулам.
| Форма | Периметр | |
|---|---|---|
| Треугольник со сторонами, a , b , c : | [латекс] P = a + b + c \\ [/ латекс] | |
| Квадрат с длиной стороны a : | [латекс] P = a + a + a + a \\ [/ latex] [латекс] P = 4a \\ [/ latex] | |
| Прямоугольник со сторонами a , b : | [латекс] P = a + b + a + b \\ [/ латекс] [латекс] P = a + a + b + b \\ [/ латекс] [латекс] P = 2a + 2b \\ [ / латекс] | |
Окружность
Как вы понимаете, мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название, называемое окружностью .Чтобы найти длину окружности, воспользуемся этой формулой: C = 2πr
Рисунок 4.
В этой формуле π произносится как «пи» и определяется как длина окружности круга, деленная на его диаметр: [latex] \ displaystyle \ pi = \ frac {C} {d} \\ [/ latex]. Обычно мы заменяем π приближением 3.14. Буква r представляет радиус круга.
Давайте посмотрим, откуда взялась формула для определения окружности. На рис. 4 показан общий круг с радиусом r.
Примечания о
C = 2π rПомните, что в формуле при вычислении длины окружности C = 2π r , мы умножаем , обычно , заменяя 3,14 вместо π:
C = 2 × 3,14 × r
Часто использование () помогает облегчить просмотр различных частей формулы:
С = (2) × (3,14) × ( r )
Происхождение
C = 2π rКак упоминалось ранее, специальное число π определяется как отношение длины окружности к ее диаметру.Мы можем записать это в форме уравнения как: [latex] \ displaystyle \ frac {C} {d} = \ pi \\ [/ latex]
Из нашей предыдущей работы мы знаем, что для определения неизвестного, C , мы можем переместить d на другую сторону уравнения, написав C = π d. Диаметр полностью пересекает середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить C с точки зрения радиуса как C = π (2 r ). После небольшого изменения порядка, в котором написаны наши части, мы можем сказать, что C = 2π r.
Давайте воспользуемся формулой, чтобы найти длину окружности нескольких окружностей.
Пример 3
Найдите длину окружности каждого из следующих кругов. Оставляйте свои ответы сначала в точном виде, а затем в округленном (до сотых разрядов). (Обратите внимание, что когда указан радиус, его значение центрируется над сегментом радиуса. Когда указан диаметр, его значение центрируется над сегментом диаметра.)
Решения
- Точное значение 8π дюймов; округлено от точного ответа 25.13 дюймов; округлено с использованием 3,14 для π 25,12 из
- Точное 12,44π м; округлено от точного ответа 39,08 м; округлено с использованием 3,14 для π 39,06 м
Точная форма против закругленной формы
- π — число в точной форме. Он не округлый.
- 3,14 — это приближение округленной формы для π
Почему важно, какую форму мы используем? Это важно, потому что при округлении мы вносим ошибку в окончательный результат. Для этого класса такая ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, такой уровень точности имеет большое значение.Давайте посмотрим на примере разницы в формах.
Пример 4
Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную, так и округленную форму:
Точное решение
[латекс] C = 2 \ pi {r} = 2 \ pi (1079) = 2158 \ pi \\ [/ latex]
Чтобы округлить от до точного решения, используйте кнопку π на калькуляторе, чтобы получить
.[латекс] 2158 \ pi \ приблизительно 6779,56 \ [/ латекс]
Раствор с закругленными углами
[латекс] C = 2 \ pi {r} = 2 (3.14) (1079) \ приблизительно 6776,12 \ [/ латекс]
Обратите внимание, что наши окончательные результаты отличаются. Эта разница — ошибка, созданная при использовании 3,14 в качестве начального приближения для π. Выполняя домашнее задание и тесты, внимательно читайте инструкции по каждой задаче, чтобы понять, какую форму использовать.
Пример 5
Найдите длину окружности или периметра для каждой описанной ниже ситуации. Включите рисунок формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры рисовать.Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате. Округлите до десятых, если не указано иное.
- Найдите периметр квадрата со стороной 2,17 фута.
- Найдите периметр прямоугольника со сторонами длиной 4,2 и 3,8.
- Найдите периметр треугольника со сторонами длиной 2, 5, 7.
- Найдите длину окружности радиуса 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Представьте округлую форму с точностью до десятых.
- Найдите длину окружности диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 8,68 футов
- 16
- 14
- Точное 12π дюйма, Округленное 37,7 дюйма
- Точное 14,8π дюйма, Округленное 46,5 дюйма
Пример 6
Определение расстояния вокруг нестандартных форм
Основные формулы для периметра прямых фигур и окружности круга помогут нам найти расстояние вокруг более сложных фигур.Найдите расстояние вокруг следующей формы. Округлите окончательный ответ до десятых и используйте 3,14 вместо π.
Решение
34,7 дюйма
Пример 7
Приложения периметра и окружности
Наши знания основных геометрических фигур можно применить для решения «реальных» проблем.
Уолли хочет добавить забор к задней части своего дома, чтобы дети могли безопасно играть (см. Диаграмму ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерения перед тем, как пойти в магазин.Если он помнит, что длина задней стены его дома составляет 15 ярдов, достаточно ли у него информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов ему следует купить?
Решение
81 фут
Площадь
Давайте еще раз посмотрим на задний двор Уолли из примера 7, чтобы представить следующую концепцию: площадь.
Управляемый пример
Уолли успешно огородил свой двор, но теперь хочет добавить немного озеленения и создать лужайку, как показано ниже.
Он направляется в местный магазин по продаже газонов и обнаруживает, что для того, чтобы определить, сколько дерна ему нужно, он должен вычислить квадратные метры площади, на которой он хочет добавить траву. По пути домой он понимает, что если разделит травянистую территорию на участки размером 1 фут на 1 фут, а затем посчитает их, он сможет определить площадь в квадратных футах. Вот информация, которую Уолли собрал, когда вернулся домой.
Уолли правильно определил, что площадь прямоугольного травянистого участка составляет 30 квадратных футов.
Заметки о зоне
- Площадь — это двумерное измерение, которое представляет собой объем пространства внутри двухмерной фигуры.
- Чтобы найти площадь, посчитайте количество единичных квадратов внутри фигуры.
- Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут двухмерными (например, квадратные футы, квадратные ярды, квадратные мили и т. Д.)
Пример 8
Найдите площадь для каждой из фигур ниже.
- Не забудьте посчитать единичные квадраты внутри фигуры.
- Есть ли здесь шаблон, который облегчил бы нашу работу?
Пример 9
Как найти область для более сложных фигур? Разбейте области на формы, которые мы узнаем, и сложите значения областей вместе.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждую область в виде более явной формулы.2 \ [/ латекс] Прямоугольник со сторонами a , b
[латекс] A = a \ cdot {b} \\ [/ latex]
(Вы также увидите это как [latex] A = \ text {length} \ cdot \ text {width} \\ [/ latex])
Формулы площади для фигур ниже сложнее получить, поэтому формулы перечислены для вас в таблице.
| Форма | Форма |
|---|---|
Треугольник высотой h и основанием b [латекс] \ displaystyle {A} = \ frac {1} {2} bh = \ frac {bh} {2} \\ [/ latex] Читается как «половина основания, умноженная на высоту» Обратите внимание, что h — это расстояние по прямой от вершины треугольника до другой стороны.2 \ [/ латекс] Читается как «пи, умноженный на радиус в квадрате» | |
Если ваш треугольник такой, как показано на рисунке слева, то высота нарисована и измерена за пределами треугольника. Формула площади такая же. |
Пример 10
Найдите область для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Используйте 3,14 для π и округляйте ответы до десятых, если необходимо.
- Найдите площадь прямоугольника, длина которого составляет 12,9 метра, а высота — треть этой величины.
- Найдите площадь треугольника с основанием [latex] \ displaystyle {24} \ frac {1} {2} \\ [/ latex] дюймов и высотой 7 дюймов.
- Найдите площадь круга с радиусом [latex] \ displaystyle {2} \ frac {1} {3} \\ [/ latex] дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 55,5 м 2 или 55,5 кв.м (округлено)
- 85,8 дюйма 2 или 85,8 квадратных дюйма (округлено)
- Точное 49/9 π дюйма 2 , Округленное 17,1 дюйма 2
Пример 11
Найдите область в каждой описанной ситуации. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Округляйте ответы до десятых, если не указано иное.
- Найдите площадь квадрата со стороной 4,2 фута.
- Найдите площадь прямоугольника со сторонами длиной 4,2 и 3,8.
- Найдите площадь треугольника высотой 7 дюймов и основанием 12 дюймов.
- Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 17.64 фута 2 или 17,64 квадратных футов
- 16,0
- 42 дюйма 2 или 42 квадратных дюйма
- Точное 36π в 2 или 36π квадратных дюймов, округленное с использованием 3,14 для π 113,0 в 2 или 113,0 квадратных дюймов
Пример 12
Определение области нестандартных форм
Основные формулы площади помогут нам найти площадь более сложных фигур. Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь данной формы.Вычислить, используя 3,14 для π и округлить до ближайшей десятой.
Решение
Округлено с использованием 3,14 для π 25,9 дюйма 2
Пример 13
Приложения площади и периметра
Мы можем объединить наши знания о площади / периметре для решения таких проблем, как эта.
Уолли все еще ремонтирует свой дом, и ему нужно завершить проект полов. Он хочет купить достаточно бамбукового пола, чтобы покрыть пространство в комнатах A, C и коридоре B, а также достаточно бамбуковой кромки для плинтусов во всех помещениях.Сколько квадратных футов пола и сколько футов плинтусов ему следует купить?
Решение
256 футов 2 настил, 108 футов окантовка
Что такое площадь формы?
Площадь фигур
Геометрические фигуры — это фигуры с набором точек, соединенных линиями, в результате чего получается замкнутая фигура.
Например, , треугольник, квадрат, прямоугольник и четырехугольник — это фигуры с 3 и 4 точками, соединенными линиями. Фигуры с ограниченными кривыми не имеют сторон, но имеют окружность.
Зеркала разной формы со сторонами и закруглениями.
ПлощадьПлощадь фигуры — это «пространство, заключенное внутри периметра или границы» данной фигуры. Рассчитываем площадь для разных форм по математическим формулам.
На следующих рисунках заштрихованная область обозначает область для соответствующих форм.
| Имя и форма | Недвижимость | Площадь |
Круг |
| А = πr2 π = 3.14 (постоянная) |
Треугольник |
| A = 1 ⁄ 2 × основание × высота |
Квадрат |
| A = длина стороны 2 |
Ромб |
| А = p × q |
Прямоугольник |
| A = длина × ширина |
Параллелограмм |
| A = основание × высота |
«Текстурированная» область представляет собой область формы
Единица измерения
Единицей измерения площади всегда является квадрат единицы, в которой даны длины.Результирующая единица является произведением единиц данной длины.
Возьмем для примера площадь квадрата со стороной 8 см:
Площадь = (Длина стороны) 2
Площадь = 8 см × 8 см
Площадь = 64 см 2
Заявление
Область применения формулы площади — архитектура, топографическая съемка и проектирование карт. Измененная версия области для данного места полезна при разработке инструментов знаний, таких как глобусы и геофизические карты.Расчет площади для двумерной формы — это первый шаг к интерпретации объема трехмерного объекта, такого как конус, цилиндр, шар и куб.
Интересные факты
|
Сопутствующий математический словарь
Открытые учебники | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Марка 7А
Марка 7Б
Оценка 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8А
Марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 4А
Марка 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Формулы площади
( пи = = 3.141592 …)
Площадь Формулы
Примечание: «ab» означает «a» умножить на «б». «a
2 » означает «квадрат», что то же самое, что «а» умножить на «а».Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений. Примеры
квадрат = a 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2
pi r 2эллипс = pi r 1 r 2
| треугольник = | половина длины основания, умноженная на высоту треугольник |
| равносторонний треугольник = |
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник задан a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
шт.
Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам, умноженным на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.
Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?
НЕ ПРАВИЛЬНО …. 4 раза 6 = 24
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута 2 ).
Измерение площади
Измерение площадиДетские представления об измерении площади имеют тенденцию развиваться предсказуемым образом. Сначала мы рассмотрим ключевые идеи об измерениях, которые были рассмотрены в информационный бюллетень по длине. Эти идеи также помогают детям понять измерение площади. Затем мы опишем стратегии, которые дети используют для измерения площади. Наконец, мы также обсудим несколько распространенных заблуждений, которые есть у детей. по этой теме.
Ключевые идеи об измерении площади.
Если детям просто говорят измерять площадь такими единицами, как квадратный дюйм,
они развивают очень мало понимания больших идей измерения.
Детям нужна возможность сформировать ключевые идеи об измерении площади.
Эти идеи включают:
1) Соответствующие единицы — единицы для измерения площади не совпадают с единицами измерения длины.
2) Идентичные единицы — Сказать, что размер треугольника составляет 14 квадратных дюймов или 9 прямоугольников, означает, что все квадраты одинаковы (квадраты, каждая сторона которых имеет длину 1 дюйм).
3) Полнота покрытия — Единицы устанавливаются так, чтобы полностью покрыть область для области, а затем подсчитываются.
Стратегии, которые дети используют для измерения площади
Хороший способ заставить детей задуматься над этими грандиозными идеями — это попросить их
сравните объем пространства, занимаемого двумя разными цифрами. Сравнение
фигуры неправильной формы или фигуры, которые отличаются по форме, являются проблемами
которые часто вызывают подобные вопросы.Чтобы выяснить, какая рука покрывает больше места,
дети обычно полагаются на простые стратегии. Например, дети часто используют
стратегия наложения — кладет одну руку на другую и ищет
«оставшаяся» область. Этот подход основан на прямом восприятии. Это работает очень
хорошо для похожих фигур (фигурки одинаковой формы, как два прямоугольника), но
это не так хорошо для форм, как руки, потому что две руки не
всегда похожи (например, у одного человека большие пальцы рук могут быть толще и короче).
Вторая стратегия, которую используют дети, чтобы определить, какая фигура больше область состоит в том, чтобы разложить область, покрытую одной фигурой, и попытаться уместить части в другую. Если детали точно подходят друг к другу, две цифры покрывают одинаковые область. Эта стратегия также хорошо работает для знакомых форм, таких как два прямоугольники, показанные ниже, но часто бывает сложно разложить такую форму, как руку на единицы, которые легко воспринимаются.
Благодаря опыту использования таких стратегий, как суперпозиция или разложение, у детей появляются идеи об измерении площадей. Область измерения позволяет детям сказать, какая рука имеет большую площадь, а также узнать, насколько она больше. Дети часто начинают систематические измерения со стратегии прямого моделирования.
Они будут использовать вырезанные квадраты (или прямоугольники или треугольники), чтобы заполнить область и затем подсчитайте количество квадратов (или прямоугольников, или треугольников).Отсюда дети переходят к менее зависимым от восприятия стратегиям, возможно, за счет визуализация фигуры как состоящей из строк и столбцов единичных квадратов (или какую-либо другую подходящую единицу измерения), а затем добавлением строк.
В качестве последнего шага некоторые дети придумывают правила нахождения знакомого места. формы, такие как длина X ширина = площадь для квадратов или прямоугольников. Тогда они могут применяйте эти правила с пониманием.
Обучение детей этим правилам до того, как они получат опыт, приводит к зубрежке. измерение с небольшим пониманием того, почему правило работает.Например, Ученики пятого класса иногда говорят нам, что площадь квадрата 3 на 3 равна 9 квадратные дюймы. Затем они говорят нам, что площадь этого прямоугольного треугольника 14 квадратные дюймы 3X3 = 9 + 4 для диагонали.
Здесь дети просто применяют механические формулы, не понимая, что
площадь квадрата не может быть меньше площади треугольника. Как дети
строят свои представления об измерении площади, они часто занимаются различными
идеи, которые охватывают одни ключевые идеи измерения, но нарушают другие.Тем не менее для них важно опробовать свои идеи, чтобы они увидели
почему некоторые не работают.
Заблуждения
Вот некоторые из наиболее распространенных заблуждений, которые дети используют при измерении площади:
| 1. Все по длине. Дети часто верят, что могут использовать линейки для измерения площади. Следовательно, они часто измеряют периметр (путь вокруг фигуры). | |
| Еще одна ошибка — измерить одну сторону фигуры, переместить линейку «чуть-чуть», еще раз измерить длину, немного сдвинуть линейку, сделайте еще одну меру длины, делая это до тех пор, пока они не решат, что пора «сложите все числа». |
Оба этих подхода представляют собой попытки применить единый размерность длины к площади, которая является двумерной.Эти подходы нарушают первая идея измерения, которую мы отметили ранее (соответствующие единицы).
2. Единицы могут быть разными.
Дети часто считают, что не имеет значения, идентичны ли все блоки.
Они считают, что если они могут заполнить регион (например, руку) единицами
мера (например, фасоль), тогда не имеет значения, есть ли какие-то единицы измерения
(бобы) разного размера — дети просто подсчитывают количество
объекты, содержащиеся в регионе (рука).Такой подход нарушает
вторая идея измерения, которую мы отметили ранее (идентичные единицы).
3. Крышка не обязательно должна быть полной.
Дети часто считают, что хотя единицы измерения должны быть идентичными,
не имеет значения, если они не полностью покрывают регион. Например, девять
бобы того же размера используются для покрытия квадрата, изображенного справа.


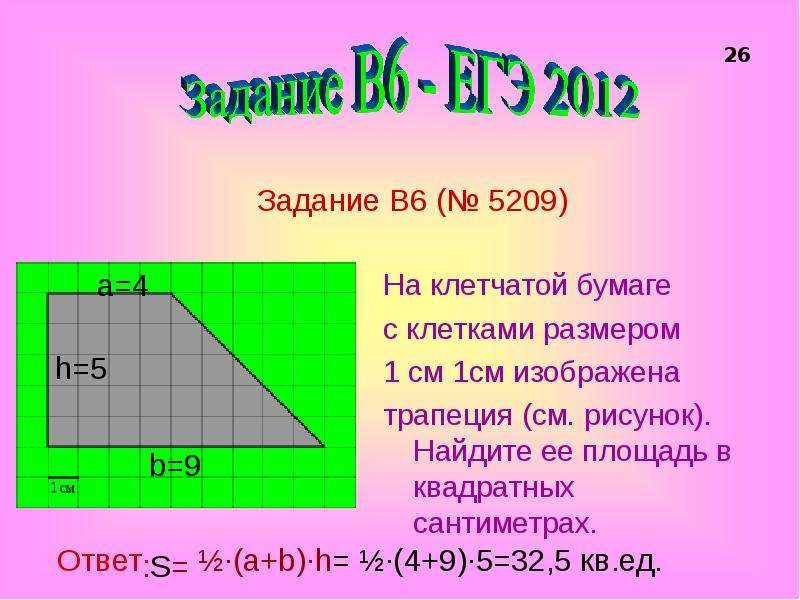
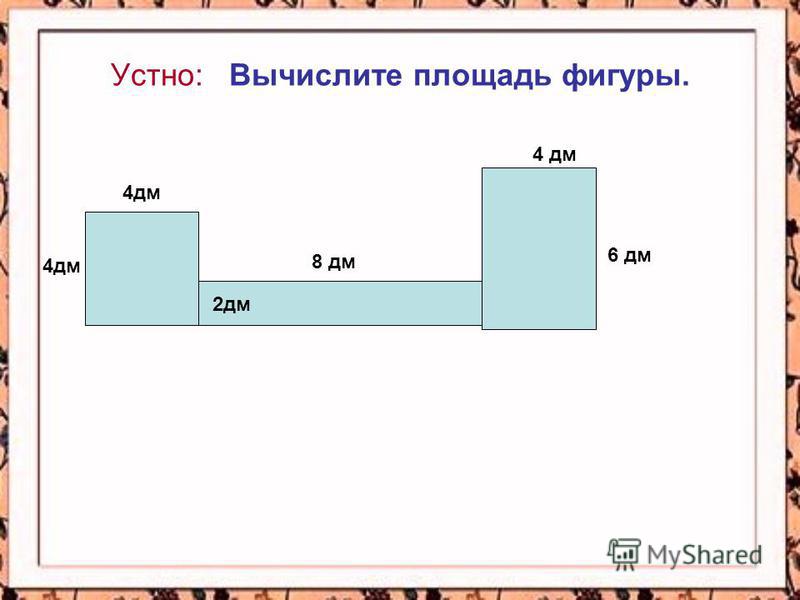

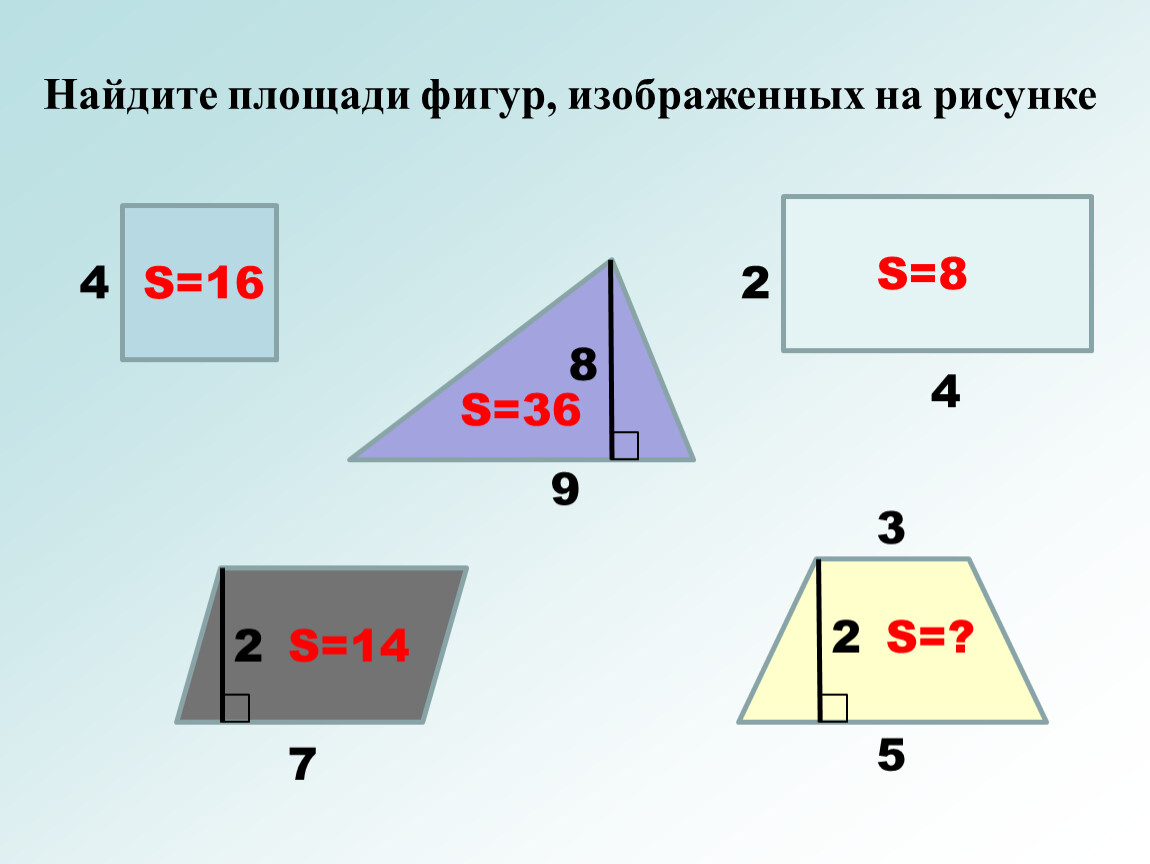 Оценивают себя.
Оценивают себя.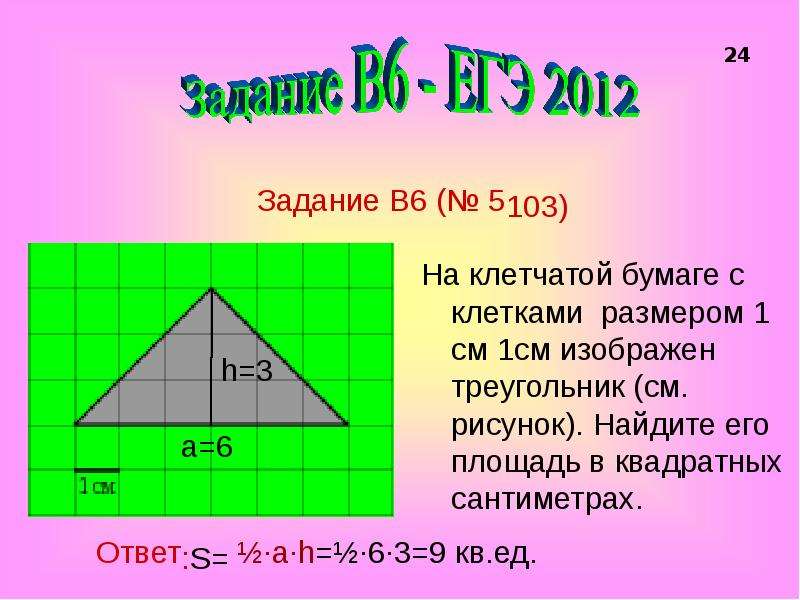
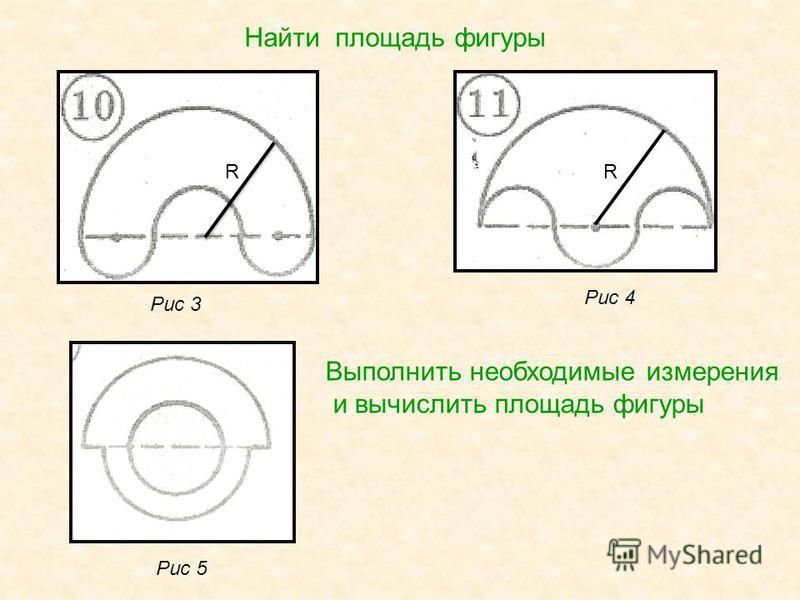
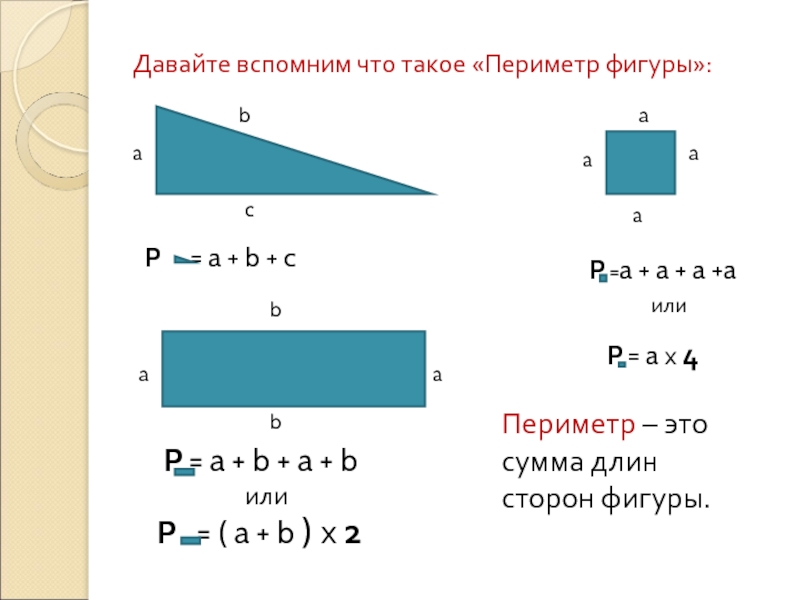

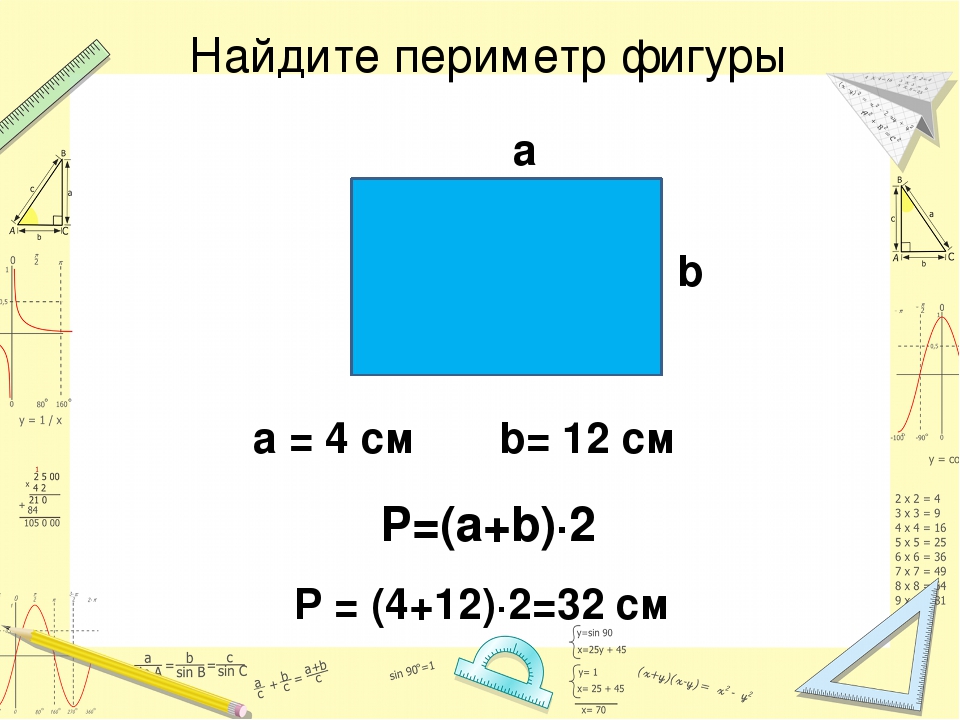 свойства площадей фигур
свойства площадей фигур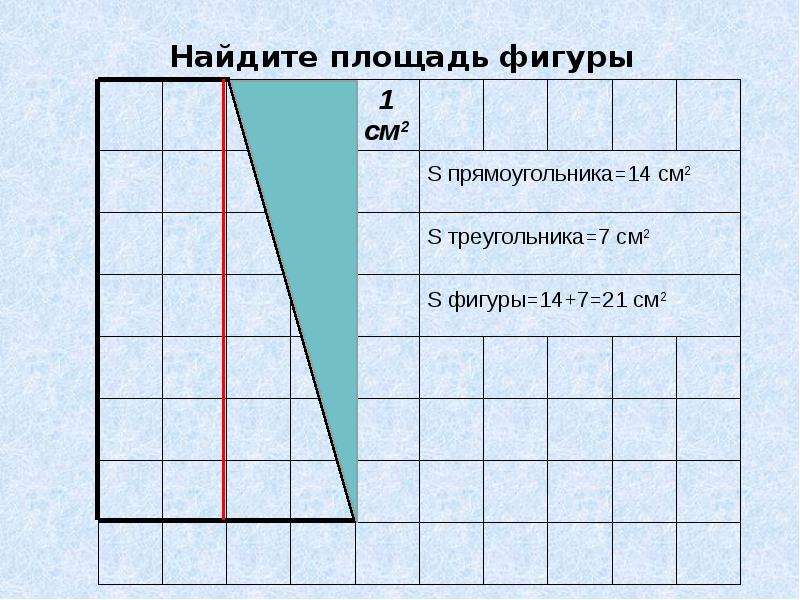 Р. Сабирова, Л.Г. Соколина, Н.И. Дорошенко, Л.П. Звягинцева, Ю.А. Нацкевич, С.Л. Попова, М.В. Чернуцкая, Т.В. Свенч. – Омск: Управление образования администрации города Омска 2004г, 135с.
Р. Сабирова, Л.Г. Соколина, Н.И. Дорошенко, Л.П. Звягинцева, Ю.А. Нацкевич, С.Л. Попова, М.В. Чернуцкая, Т.В. Свенч. – Омск: Управление образования администрации города Омска 2004г, 135с.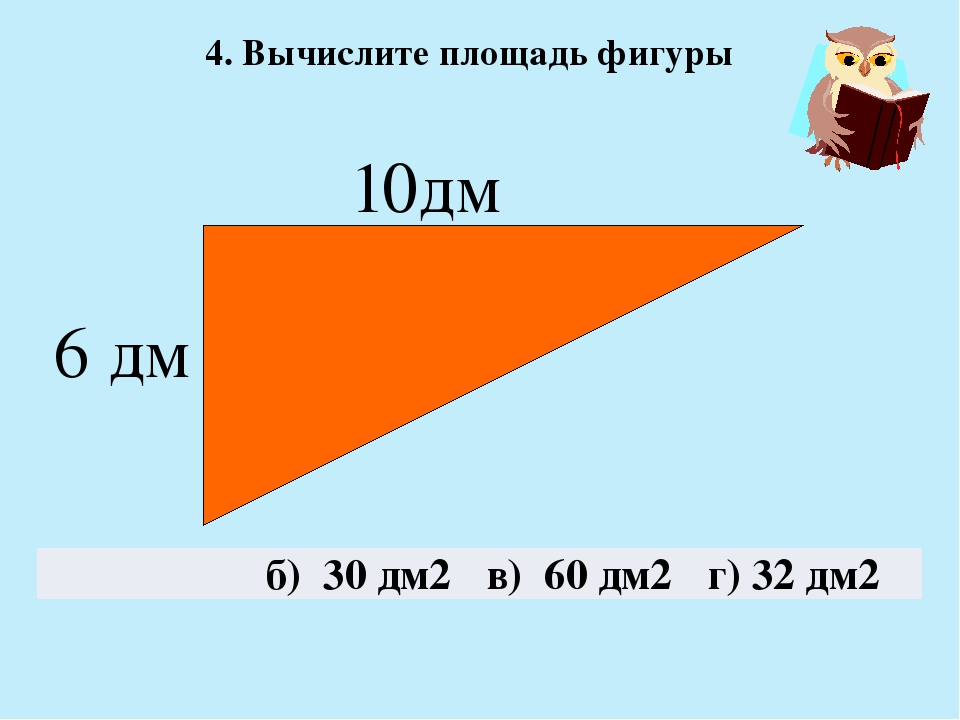
 см.
см.